Chapter 6 - Appendix A: Additions to Brooks (Base) Square (BS): The Architecture of Space-Time (TAOST) and The Conspicuous Absence of Primes (TCAOP) ~copyright 2010-12, Reginald Brooks. All rights reserved.

The well of discoveries to be had in Brooks (Base) Square is enormous ... perhaps infinite. As new discoveries are made we will attempt to bring those highlights here under the banner of "Appendix" ... providing a focused look at a some aspect of the matrix that reveals yet another deep connection between the Inverse Square Law (ISL) and the numbers of the Universe.

Rule 176: Progressive Inner Grid Triangle Sets inform the Prime Diagonal (PD)

Here we are taking a look at how sequentially larger "parent" Triangle Sets ... and their "child" triangle sets contained within ... all work in concert to support the next ISL number on the PD. Yes it is true, once the pattern is discerned it only seems inevitable that the progression works as it does. But don't be fooled into thinking that now what is obvious must be mundane, for it is the very nature of the matrix that complex patterns are simply simple patterns in a choreographed dance. Learn the simple steps so that you may be able to realize the full dance. See Rules 176A-176J.

In the spirit of discovery ... especially in that one discovery often leads to another ... a quick look at the triangles inside the PTOP embedded in Brooks (Base) Square has revealed yet another prime pattern. See Rules 177A-177E.

The simplest and most basic pattern of the simple whole number sequence ... 1,2,3,... forming a truly fundamental base layer ... a sub-matrix ... lying below the original grid. Every number on that original grid is predicated on this simple pattern of 1,2,3,....

Fixed numbers of nodes, i.e. number units, forming a fixed length string, have conserved number differences when they lie over the two shorter sides of a right triangle ...suggesting a natural link to how the conservation laws of Nature might numerically unfold.

~click to enlarge image

Review A

BS Review A: A simple review of some basics of Brooks (Base) Square:

We know from Rule 31 that Column numbers, going from left to right on the Inner Grid, decrease as -1,-3,-5,-7,-9,-11,...;
We know from Rule 32 that Row numbers, going from top to bottom on the Inner Grid, increase by 5,7,,9,11,13,...;
And, that the sums of the mulitpliers of the difference, ∆, in the Row sums, ∑, increase by 3 as shown in the first table below;
And, from Rule 33, we know that the numbers in the 1st, 2nd, 3rd, ..., diagonals from the Prime Diagonal (PD), increase as 2,4,6,8,10,...;
The diagonals that run perpendicular to the PD have their own distinct pattern to the differences, ∆, of their sums, ∑, as shown in the second table below;
And finally, from Rule 11, we know that the PD itself increases by 1,3,5,7,9,...;

Note:

∑	∆	=	Core #s	Addition of Core #s	=	∑	∆
3
13	10	=	2 x 5	2 + 5	=	7	3
34	21	=	3 x 7	3 + 7	=	10	3
70	36	=	4 x 9	4 + 9	=	13	3
125	55	=	5 x 11	5 + 11	=	16	3
203	78	=	6 x 13	6 + 13	=	19	3
308	105	=	7 x 15	7 + 15	=	22	3
444	136	=	8 x 17	8 + 17	=	25	3
615	171	=	9 x 19	9 + 19	=	28	3
825	210	=	10 x 21	10 + 21	=	31	3

∑	∆	=	Core #s	odd/even
3
8	5	=	1 x 5	odd
20	12	=	4 x 3	even
36	16	=	4 x 4	even
63	27	=	3 x 9	odd
96	33	=	3 x 11	odd
144	48	=	8 x 6	even
200	56	=	8 x 7	even
275	75	=	5 x 15	odd
360	85	=	5 x 17	odd
468	108	=	12 x 9	even
588	120	=	12 x 10	even

[ TOP ]

Rule 176: Progressive Inner Grid Triangle Sets inform the Prime Diagonal (PD)

~click to enlarge image

176

BS Rule 176 Overview: Now with these review rules in mind, let's look at number patterns and weights (sums) of progressive Inner Grid Triangle Sets all under the banner of Rule 176. Common to all Inner Grid Triangle Sets in Brooks (Base) Square:

Note the symmetry between sums, ∑, of the parallel diagonals;

Note that the difference, ∆, (end-end, 2nd in-2nd in, 3rd in-3rd in, etc.) between Triangle Sets...e.g. end diagonals increase as 5,7,9,11,13, ...;

Note that the diagonal sums, ∑, for a given Triangle Set reduce to set patterns of a core number ... that core number, #, progresses as 3,4,5,6,7, ..., and, that those core patterns themselves can be patterned as even (2,4,6,8,...a0 or odd (1,3,5,7, ...) progressions in the first table below;

Note, in the second table below, that the difference, ∆, between the progressive total sums of each Triangle Set is the same as the difference, , in the Row sums, ∑, shown earlier (13,34,70,125,...0;

Note that the sums, ∑, of all number units within a given Triangle Set, divided by the # of units, gives us two patterns, both of which relate back to the pattern of the PD:

The whole number quotients follow as 3x1, 3x4, 3x9, 3x16, ...)
Dividing each quotient by 1/3 gives the PD sequence (9,16,25,36,49,64,81,100,...);

Note that the sums, ∑, of the apex #'s of all the unique isosceles triangles formed from a given Triangle Set are:

identical and equal the next PD #, and,
their aggregate sums, ∑, equal the sums, ∑, of the parallel diagonals from that parent Triangle Set (The latter is simply the result of adding up the unit #'s within a Triangle Set in two different ways.). Restated: A series of unique child isosceles triangles within a given parent Triangle Set can account for all the number units of that parent set (the exception being a single perfectly centered units). The sum of each unique child triangle equals the next PD #, and, the aggregate child triangle sums (plus any centered unit) equals the total sum, ∑all.

Note:

∆	Core #	Diagonal ∑ #
0	1 x 3	= 3
1	2 x 4	= 8
1	3 x 5 4 x 5	= 15 = 20
2	4 x 6 6 x 6	= 24 = 36
3 1	5 x 7 8 x 7 9 x 7	= 35 = 56 = 63
4 2	6 x 8 10 x 8 12 x 8	= 48 = 80 = 96
5 3 1	7 x 9 12 x 9 15 x 9 16 x 9	= 63 = 108 = 135 = 144
6 4 2	8 x 10 14 x 10 18 x 10 20 x 10	= 80 = 140 = 180 = 200
7 5 3 1	9 x 11 16 x 11 21 x 11 24 x 11 25 x 11	= 99 = 176 = 231 = 264 = 275
The Core number patterns themselves can be patterned as even (2,4,6,8,...) or odd (1,3,5,7,...) progressions.

*TS	∑_all	=	**∆	∑_all/ # units	=	=	÷ by 1/3
A	3	3 x 1		3/1	3.00	3x1	9
B	16	4 x 4	13	16/3	5.33		16
C	50	5 x 10	34	50/6	8.33		25
D	120	6 x 20	70	120/10	12.00	3x4	36
E	245	7 x 35	125	245/15	16.33		49
F	448	8 x 56	203	448/21	21.33		64
G	756	9 x 84	308	756/28	27.00	3x9	81
H	1200	10x120	444	1200/36	33.33		100
I	1815	11x165	615	1815/45	40.33		121
J	2640	12x220	825	2640/55	48.00	3x16	144
* Triangular Set (progressive "Parent" sets). **Note that the difference, ∆, in Triangle Sets is simply the ∆ in the Row sums shown earlier.

[ TOP ]


~click to enlarge image
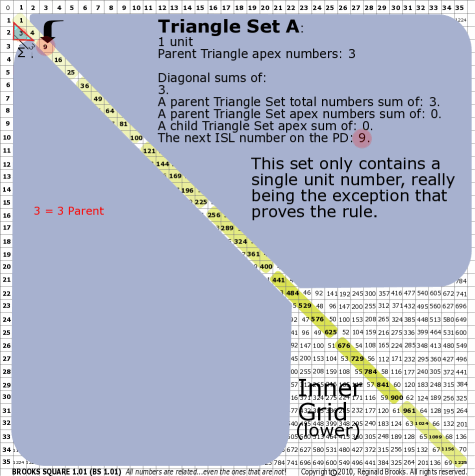
176A	BS Rule 176-Set A: Triangle Set A: 1 unit, with apex numbers: 3.
Note: Diagonal sums of: 3. A parent Triangle Set total numbers sum of: 3. A parent Triangle Set apex numbers sum of: . A child Triangle Set apex sum of: . The next ISL number on the PD: 9. This set only contains a single unit number, really being the exception that proves the rule.

[ TOP ]


~click to enlarge image
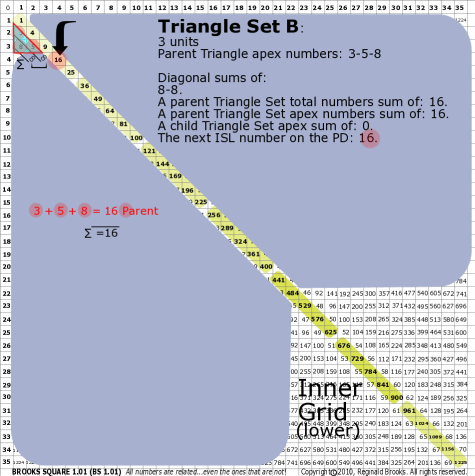
176B	BS Rule 176-Set B: Triangle Set B: 3 units, with apex numbers: 3-5-8.
Note: Diagonal sums of: 8-8. A parent Triangle Set total numbers sum of: 16. A parent Triangle Set apex numbers sum of: 16. A child Triangle Set apex sum of: . The next ISL number on the PD: 16.

[ TOP ]


~click to enlarge image
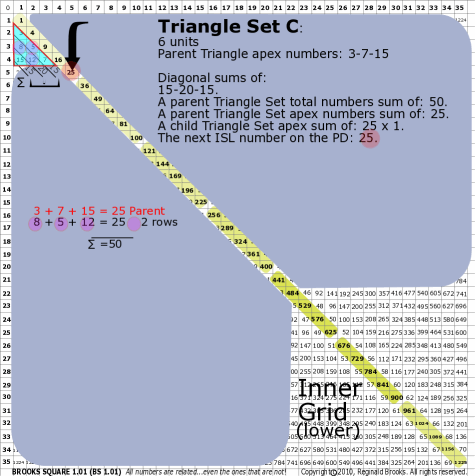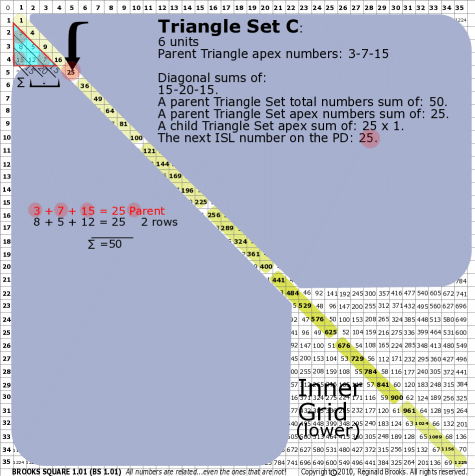
176C	BS Rule 176-Set C: Triangle Set C: 6 units, with apex numbers: 3-7-15.
Note: Diagonal sums of: 15-20-15. A parent Triangle Set total numbers sum of: 50. A parent Triangle Set apex numbers sum of: 25. A child Triangle Set apex sum of: 25. The next ISL number on the PD: 25.


~click to enlarge image
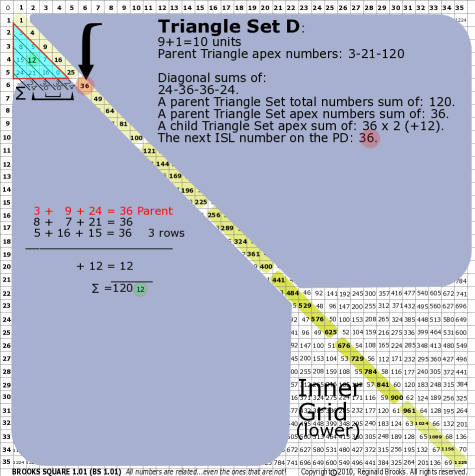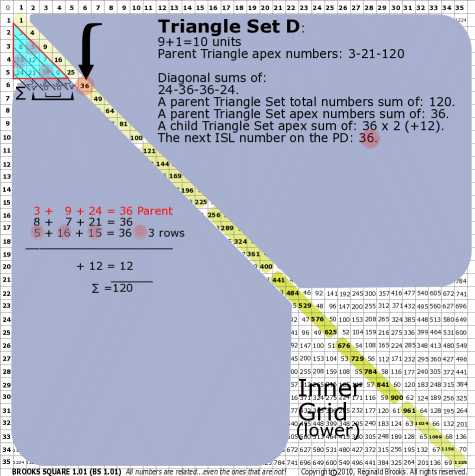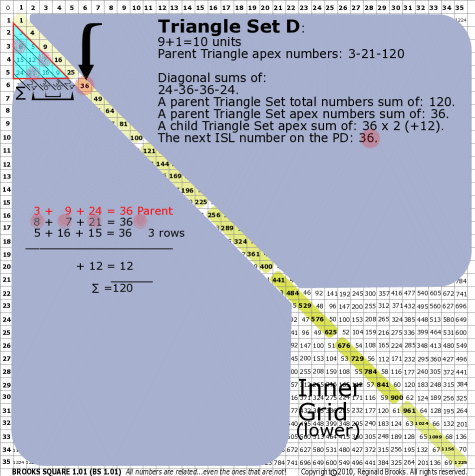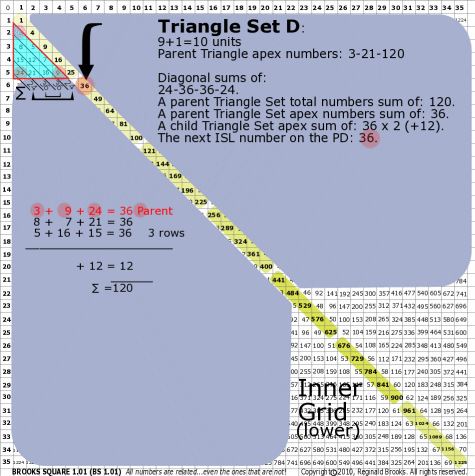
176D	BS Rule 176-Set D: Triangle Set D: 9+1=10 units, with apex numbers: 3-9-24.
Note: Diagonal sums of: 24-36-36-24. A parent Triangle Set total numbers sum of: 120. A parent Triangle Set apex numbers sum of: 36. A child Triangle Set apex sum of: 36-36 (+12). The next ISL number on the PD: 36.

[ TOP ]


~click to enlarge image
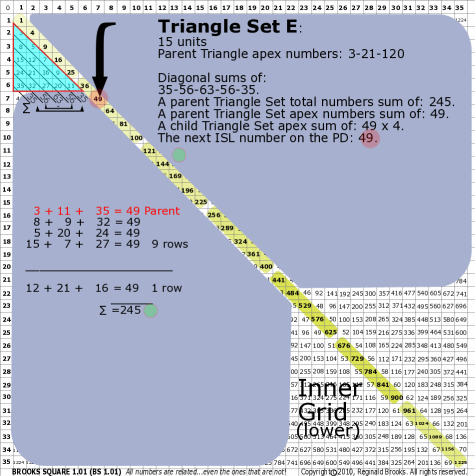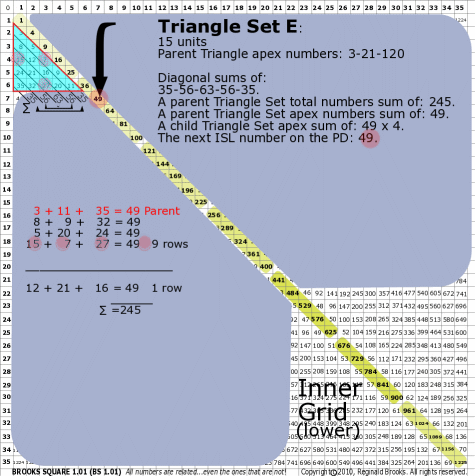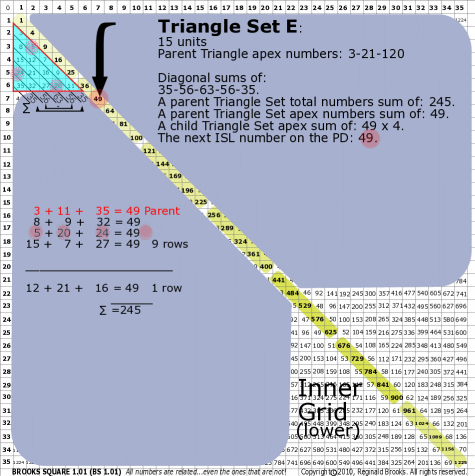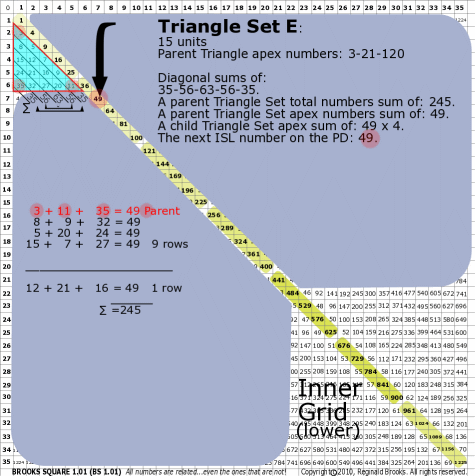
176E	BS Rule 176-Set E: Triangle Set E: 15 units, with apex numbers: 3-11-35.
Note: Diagonal sums of: 35-56-63-56-35. A parent Triangle Set total numbers sum of: 245. A parent Triangle Set apex numbers sum of: 49. A child Triangle Set apex sum of: 49-49-49-49. The next ISL number on the PD: 49.


~click to enlarge image
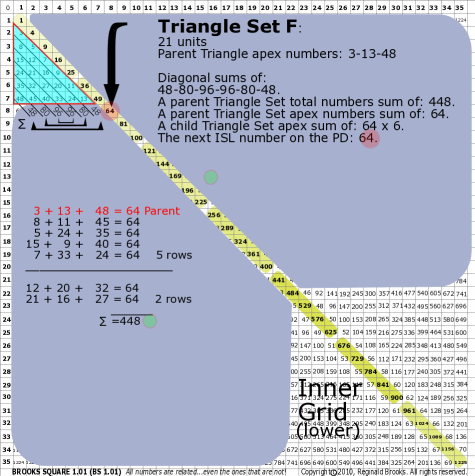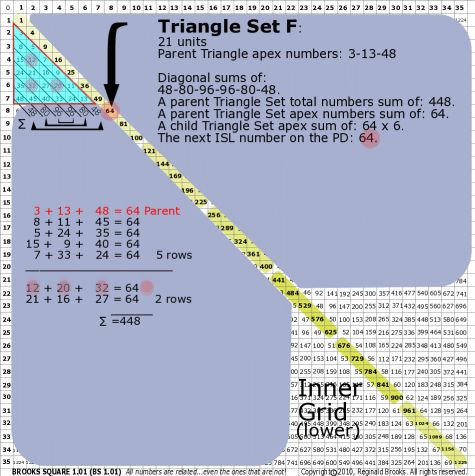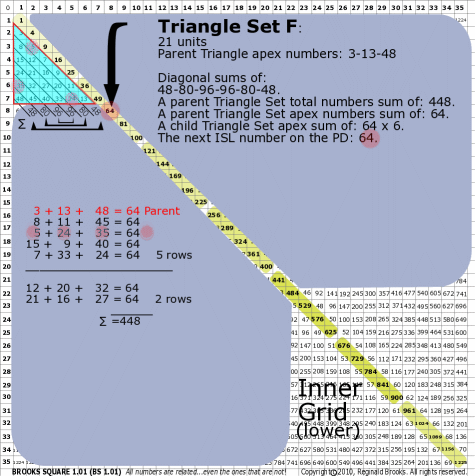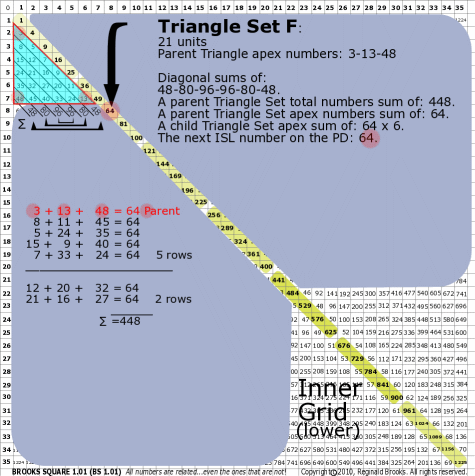
176F	BS Rule 176-Set F: Triangle Set F: 21 units, with apex numbers: 3-13-48.
Note: Diagonal sums of: 48-80-96-96-80-48. A parent Triangle Set total numbers sum of: 448. A parent Triangle Set apex numbers sum of: 64. A child Triangle Set apex sum of: 64-64-64-64-64-64. The next ISL number on the PD: 64.

[ TOP ]


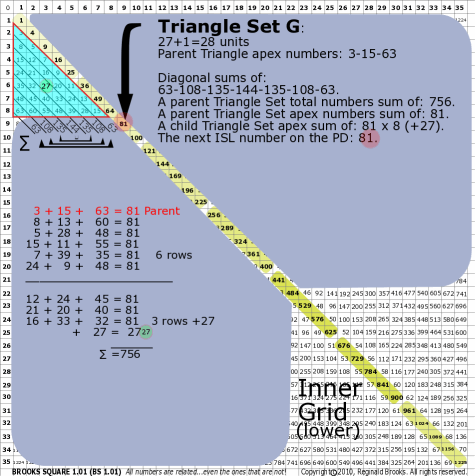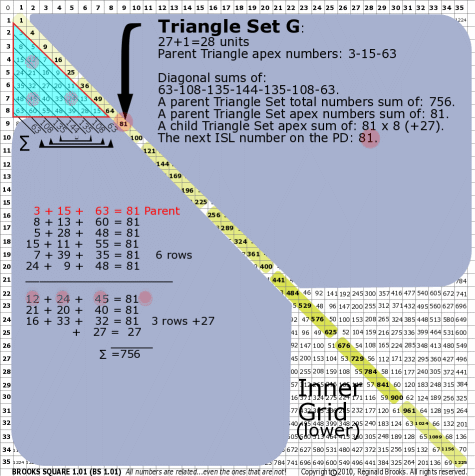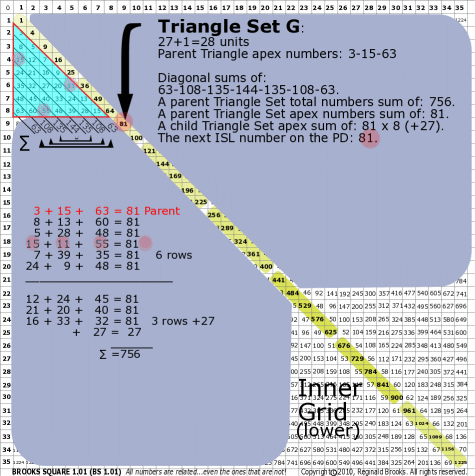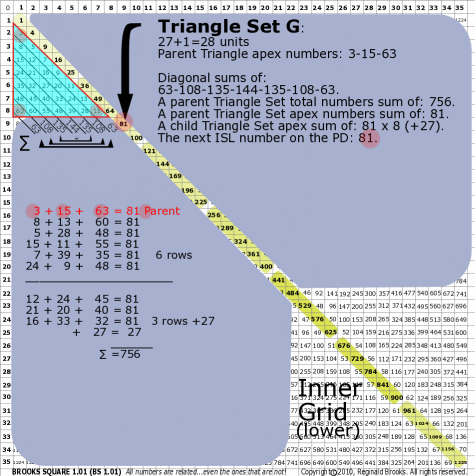
~click to enlarge image
176G	BS Rule 176-Set G: Triangle Set G: 27+1=28 units, with apex numbers: 3-15-63.
Note: Diagonal sums of: 63-108-135-144-135-108-63. A parent Triangle Set total numbers sum of: 756. A parent Triangle Set apex numbers sum of: 81. A child Triangle Set apex sum of: 81-81-81-81-81-81-81-81 (+27). The next ISL number on the PD: 81.

[ TOP ]


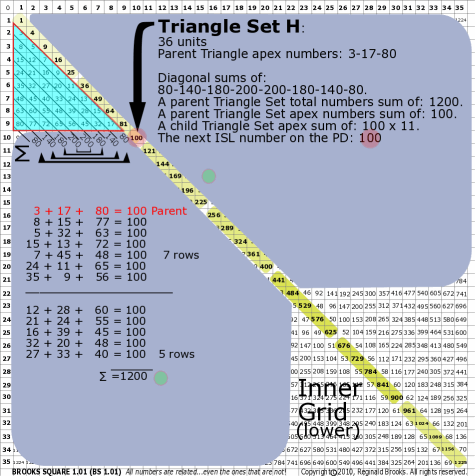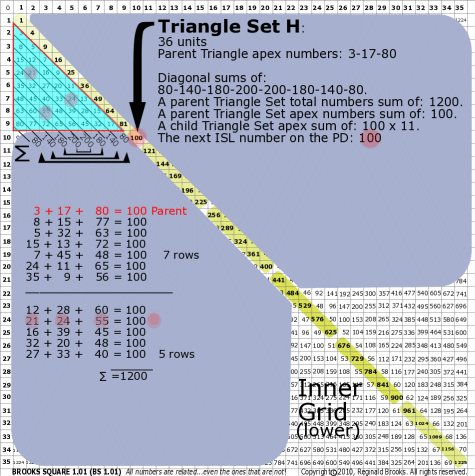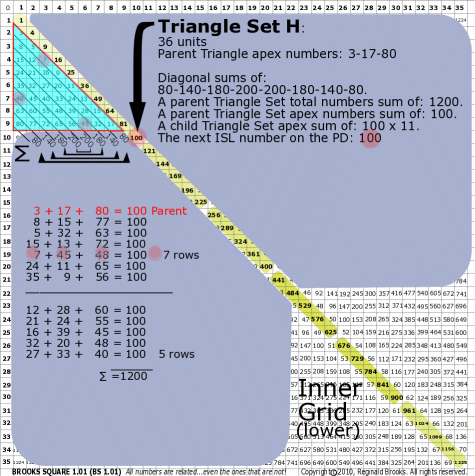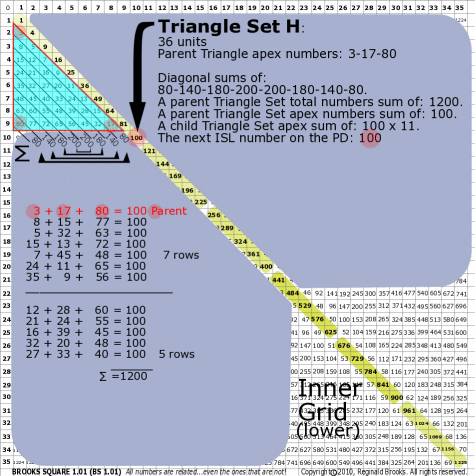
~click to enlarge image
176H	BS Rule 176-Set H: Triangle Set H: 36 units, with apex numbers: 3-17-80.
Note: Diagonal sums of: 80-140-180-200-200-180-140-80. A parent Triangle Set total numbers sum of: 1200. A parent Triangle Set apex numbers sum of: 100. A child Triangle Set apex sum of: 100 x 11. The next ISL number on the PD: 100.

[ TOP ]


~click to enlarge image
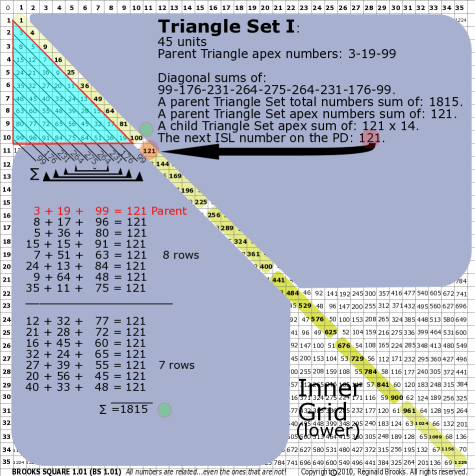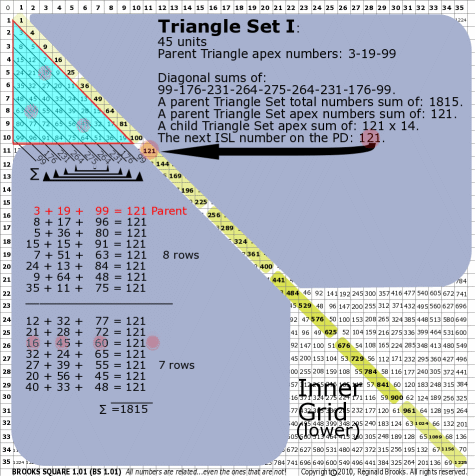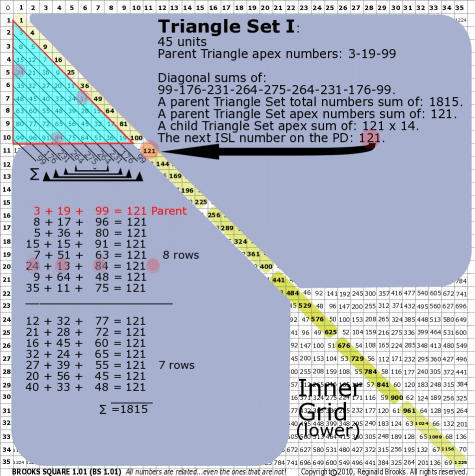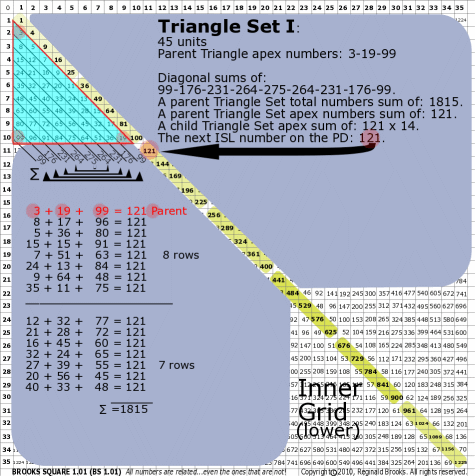
176I	BS Rule 176-Set I: Triangle Set I: 45 units, with apex numbers: 3-19-99.
Note: Diagonal sums of: 99-176-231-264-275-264-231-176-99. A parent Triangle Set total numbers sum of: 1815. A parent Triangle Set apex numbers sum of: 121. A child Triangle Set apex sum of: 121 x 14. The next ISL number on the PD: 121.

[ TOP ]


~click to enlarge image
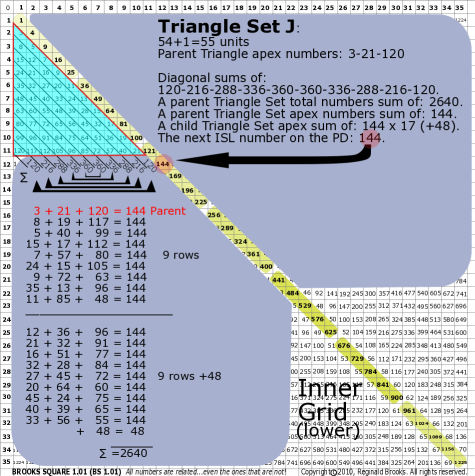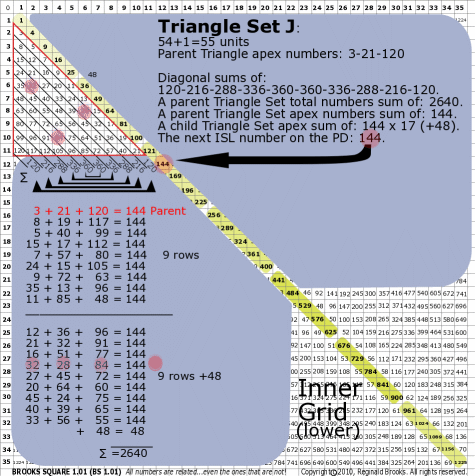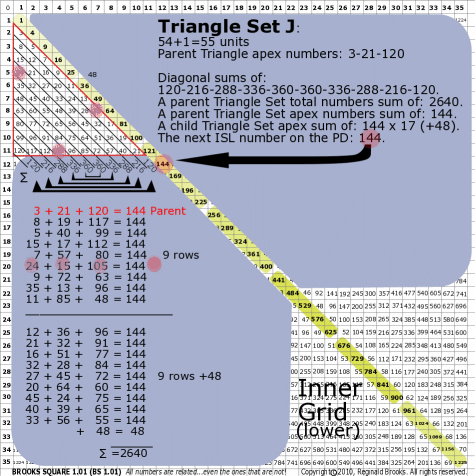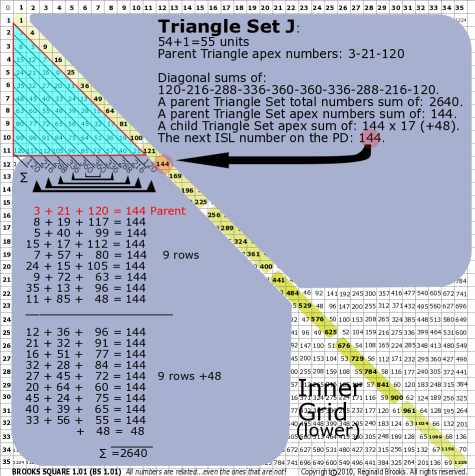
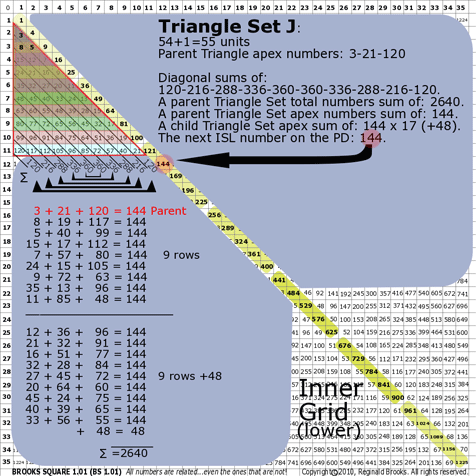
176J	BS Rule 176-Set J: Triangle Set J: 54+1=55 units, with apex numbers:3-21-120 .
Note: Diagonal sums of: 120-216-288-336-360-360-336-288-216-120. A parent Triangle Set total numbers sum of: 2640. A parent Triangle Set apex numbers sum of: 144. A child Triangle Set apex sum of: 144 x 17 (+48). The next ISL number on the PD: 144.

[ TOP ]

From this analysis of the Brooks (Base) Square, we can see that progressively lager Triangle Sets within the Inner Grid increase their total sums ... and the patterns they contain ... in a simple and orderly manner, not the least of which is that the number progression of the Inverse Square Law Pd (1,4,9,16,25,36,...) is recoverable in those total sums.

Rule 177: Prime Triangle Sets within the Periodic Table of Primes (PTOP)


~click to enlarge image
177A	BS Rule 177-Set A: The number sums, ∑, from a Triangle Set formed from two odd numbers from the upper horizontal axis and, the right-angle apex number of the isosceles triangle formed within the Inner Grid, are prime at least once in every row and every column in that grid.
Note: Rows 1-3. Bold numbers are prime. Example shown is for Triangle Sets up to number 37 on the axis and PD. Row 1 sums (e.g. 3+5+15=23): 23-47-79-119-167-223-287-359-439-527-623-727-839-959-1087-1223. Row 2 sums (e.g. 3+7+21=31): 31-59-95-139-191-251-319-395-479-571-671-779-895-1019-1151-1291. Row 3 sums (e.g. 3+9+27=39): 39-71-111-159-215-279-351-431-519-615-719-831-951-1079-1215.

[ TOP ]


~click to enlarge image
177B	BS Rule 177-Set B: The number sums, ∑, from a Triangle Set formed from two odd numbers from the upper horizontal axis and, the right-angle apex number of the isosceles triangle formed within the Inner Grid, are prime at least once in every row and every column in that grid.
Note: Rows 4-6. Bold numbers are prime. Example shown is for Triangle Sets up to number 37 on the axis and PD. Row 4 sums (e.g. 3+11+33=47): 47-83-127-179-239-307-383-467-559-659-767-8831007. Row 5 sums (e.g. 3+13+39=55): 55-95-143-199-263-335-415-503-599-703-815-935-1063-1199. Row 6 sums (e.g. 3+15+45=63): 63-107-159-219-287-363-447-539-639-747-863-987.

[ TOP ]


~click to enlarge image
177C	BS Rule 177-Set C: The number sums, ∑, from a Triangle Set formed from two odd numbers from the upper horizontal axis and, the right-angle apex number of the isosceles triangle formed within the Inner Grid, are prime at least once in every row and every column in that grid.
Note: Rows 7-9. Bold numbers are prime. Example shown is for Triangle Sets up to number 37 on the axis and PD. Row 7 sums (e.g. 3+17+51=71): 71-119-175-239-311-391-479-575-679-791-911. Row 8 sums (e.g. 3+19+57=79): 79-131-191-259-335-419-511-611-719-835. Row 9 sums (e.g. 3+21+75=87): 87-143-207-279-359-447-543-647-759


~click to enlarge image
177D	BS Rule 177-Set D: The number sums, ∑, from a Triangle Set formed from two odd numbers from the upper horizontal axis and, the right-angle apex number of the isosceles triangle formed within the Inner Grid, are prime at least once in every row and every column in that grid.
Note: Rows 10-12. Bold numbers are prime. Example shown is for Triangle Sets up to number 37 on the axis and PD. Row 10 sums (e.g. 3+23+69=95): 95-155-223-299-383-475-575-683. Row 11 sums (e.g. 3+25+75=103): 103-167-239-319-407-503-607. Row 12 sums (e.g. 3+27+81=111): 111-179-255-339-431-531.

[ TOP ]


~click to enlarge image
177E	BS Rule 177-Set E: The number sums, ∑, from a Triangle Set formed from two odd numbers from the upper horizontal axis and, the right-angle apex number of the isosceles triangle formed within the Inner Grid, are prime at least once in every row and every column in that grid.
Note: Rows 13-17. Bold numbers are prime. Example shown is for Triangle Sets up to number 37 on the axis and PD. Row 13 sums (e.g. 3+29+87=119): 119-191-271-359-455. Row 14 sums (e.g. 3+31+93=127): 127-203-287-379. Row 15 sums (e.g. 3+33+99=135): 135-215-303 Row 16 sums (e.g. 3+35+105=143): 143-227. Row 17 sums (e.g. 3+37+111=151): 151. Notice that Row 15, with three entries, actually has no primes. If we simply expand our beginning Triangle Sets, e.g. from 37-41, sure enough the extra data sets generated include a prime in this row as 11+41+451=503.

Rules 178-180: Sub-Matrix: The distillation of the Brooks (Base) Square

[ TOP ]

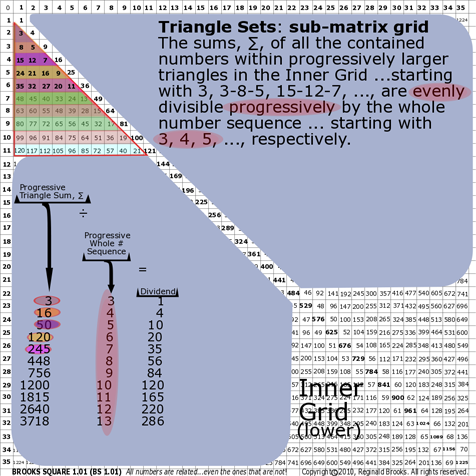
~click to enlarge image

178

BS Rule 178- The Sub-Matrix: The sums, ∑, of all the contained numbers within progressively larger triangles in the Inner Grid ...starting with 3, 3-8-5, 15-12-7, ..., are evenly divisible progressively by the whole number sequence ... starting with 3, 4, 5, ..., respectively.

Note: Same occurs for Rule 176.

Progressive Triangle Sum, ∑	÷	Progressive Whole # Sequence	=	Dividend
3		3		1
16		4		4
50		5		10
120		6		20
245		7		35
448		8		56
756		9		84
1200		10		120
1815		11		165
2640		12		220
3718		13		286

[ TOP ]


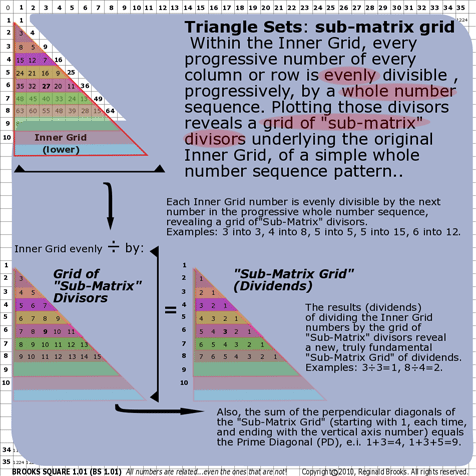
~click to enlarge image
179	BS Rule 179- The Sub-Matrix: Within the Inner Grid, every progressive number of every column or row is evenly divisible , progressively, by a whole number sequence. Plotting those divisors reveals a "sub-matrix" grid, underlying the original Inner Grid, of a simple whole number sequence pattern.

[ TOP ]


~click to enlarge image
180	BS Rule 180- The Sub-Matrix: Within the Inner Grid, every progressive number of every column or row is evenly divisible , progressively, by a whole number sequence. Plotting those dividends reveals a truly fundamental "sub-matrix" grid, underlying the original Inner Grid, of repeating simple whole number sequences, i.e. 1,2,3, ..., horizontally and vertically ...forming the simplest, most basic grid pattern possible, that also includes the axis numbers. All numbers of the original Brooks (Base) Square are predicated on this simple whole number sequence pattern.
Note: This amazing sub-matrix grid pattern explains the entire parent grid matrix and the Inverse Square Law, ISL, relationship that unfolds. See an animated example by CLICKING IMAGE above. Patience. Follow the bold numbers.

Rule 181: Conservation (Laws) in the Brooks (Base) Square

[ TOP ]

~click to enlarge image

181

BS Rule 181- The Conservation Laws: Take any number of sequential nodes, i.e. number units, from a diagonal array (parallel to the Prime Diagonal) to form a fixed length string of nodes. Wrapping that fixed length string variously around the short sides of the right triangle so formed from this diagonal and the one 90 degrees perpendicular ... with the long-side hypotenuse formed from the beginning and end of said string ... the differences between the numbers included in that fixed string length will remain a constant, conserved quantity. The fixed node length string acts like a conserved unit in that no matter how it is manipulated ... in this case wrapped around a corner vertice forming a triangle ... the difference between the end and the beginning of the strings is no different from the difference of the two-legged route around the short-sides of the triangle formed. Advance the string and the results are the same. It is the difference in the number unit values which implies the conservation laws. The loss in number value in going from LEFT to RIGHT equals the gain in number values going from TOP to BOTTOM when going through the same vertice node. Furthermore, for those fixed length node strings formed along the 1st diagonal from the Prime Diagonal, the values of those differences are actually delineated to the side and bottom of the short-side vertice number unit. See examples.

Note: Restated: A new form of the Pythagorean Theory has been found. Within Brooks (Base) Square, it is the difference between the vertices of the right triangle that reveals a Pythagorean-like relationship whereby the sums of those vertice differences on the short side equal that of the long side: C-A=(C-B)+(B-A). As "A", "B" and "C" are the number values of the vertices of a right triangle, we call this the Pythagorean Theorem of Vertices (PTOV). The difference, ∆, in the sums of those number values at A, B, & C remains a constant within any right triangle formed with a given string node length and passing through the same short-side vertice. See an animated example by CLICKING IMAGE above. Patience. Follow the bold numbers.

Fixed length node strings, A to C	Vertices A,B,C	Triangle Vertices Sum, ∑	∆	Vertices C-A	Vertices--- (C-B)+(B-A)	∆
1 3 5 7 9 11	3+11+33	47	24	33-3=30	22+8=30	20
1 3 5 7 9 11	5+11+55	71	24	55-5=50	44+6=50	20
1 3 5 7 9 11	7+11+77	95	24	77-7=70	66+4=70	20
1 3 5 7 9 11 13	3+13+39	55	28	39-3=36	26+10=36	24
1 3 5 7 9 11 13	5+13+65	83	28	65-5=60	52+8=60	24
1 3 5 7 9 11 13	7+13+91	111	28	91-7=84	78+6=84	24
3 15 21 27 33	15+33+55	103	28	55-15=40	22+18=40	16
3 15 21 27 33	21+33+77	131	28	77-21=56	44+12=56	16
3 15 21 27 33	27+33+99	159	28	99-27=72	66+6=72	16
4 24 32 40 48	24+48+72	144	32	72-24=48	24+24=48	16
4 24 32 40 48	32+48+96	176	32	96-32=64	48+16=64	16
4 24 32 40 48	40+48+120	208	32	120-40=80	72+8=80	16

The Pythagorean Theorem of Vertices (PTOV)

C-A=(C-B)+(B-A).
As "A", "B" and "C" are the number values of the vertices of a right triangle.

The Conservation Laws: Conservation of energy, momentum, angular momentum, electric charge, mass (as mass-energy), leptons, baryons, and, spacetime (as proposed by the author), in essence, the total energy of spacetime, as revealed by the matter and energy fields that are its expression, is a constant ... it can neither be created or destroyed.

The quantities, as expressed by numbers, that hold, tie, interconnect, transform, transcend and ultimately account for these principles ... these laws ... of Nature, are contained within the Inverse Square Law matrix ... i.e. "Brooks (Base) Square".

The numerical connection to the Conservation Laws has to be built into the same numerical connection to that law of Nature that fundamentally defines the relationship of light, electromagnetism and gravity (amongst others). And that law, of course, is the ISL.

In the Conservation Rule, we see that a fixed length string of numbers, when wrapped around a fixed vertice of a right triangle, maintains a constant difference between the numbers, despite the number's values changing. This occurs throughout the grid.

Examination of the simple rules of the right triangles so formed reveals not only the source of this constancy ... it's built into the sub-matrix ... but a straightforward connection to that most famous of mathematical (geometrical) laws, the Pythagorean Theorem. c²=a²+b², the hypotenuse of a right triangle equals the square root of the sums of its sides. As "a", "b" and "c" are the lengths of the sides of a right triangle, it is the Pythagorean Theorem of Sides (PTOS).

Now, in rule 181, the Conservation Rule, a new form of the Pythagorean Theory has been found. Within Brooks (Base) Square, it is the difference between the vertices of the right triangle that reveals a Pythagorean-like relationship whereby the sums of those vertice differences on the short side equal that of the long side: C-A=(C-B)+(B-A). As "A", "B" and "C" are the number values of the vertices of a right triangle, we call this the Pythagorean Theorem of Vertices (PTOV). The difference in the progressive right triangles, all with the same vertice at the short sides, remains a constant, conserved quantity. The Pythagorean Theorem of Vertices (PTOV), in the context of the ISL matrix, becomes the source description of the Conservation Laws.

[ TOP ]

TCAOP: Rule 154 | Rules 155-157 | Rules 158-159 | Rule 160 |

Interconnectedness: Rules 161-175 |

Appendix A: Rules 176-181 |

Appendix B: Rules 182-200 |

Page 2d- PIN: Butterfly Prime Determinant Number Array (DNA) ~conspicuous abstinence~.

Page 7- The LUFE Matrix Supplement: Examples and Proofs: Introduction-Layout & Rules

Page 13- GoMAS: The Geometry of Music, Art and Structure ...linking science, art and esthetics. Part I

Page 14- GoMAS: The Geometry of Music, Art and Structure ...linking science, art and esthetics. Part II

Page 15- Brooks (Base) Square (BS): The Architecture of Space-Time (TAOST) and The Conspicuous Absence of Primes (TCAOP) - a brief introduction to the series

Page 16- Brooks (Base) Square (BBS) interactive matrix: BASICS (Part I)~ 5 presentations

Page 17- The Architecture Of SpaceTime (TAOST) as defined by the Brooks (Base) Square matrix and the Inverse Square Law (ISL).

The LUFE Matrix \| The LUFE Matrix Supplement \| The LUFE Matrix: Infinite Dimensions \| The LUFE Matrix: E=mc² \| Dark Matter=Dark Energy \| The History of the Universe in Scalar Graphics \| The History of the Universe_update: The Big Void \| Quantum Gravity ...by the book \| The Conservation of SpaceTime \| LUFE: The Layman's Unified Field Expose`

net.art index \| netart01: RealSurReal...aClone \| netart02: funk'n DNA/Creation GoDNA \| netart03: 9-11_remembered \| netart04: Naughty Physics (a.k.a. The LUFE Matrix) \| netart05: Your sFace or Mine? \| netart06: Butterfly Primes \| netart07: Geometry of Music Color \| net.games \| Art Theory 101 / White Papers Index