[ TOP ]
Brooks (Base) Square (BS) 101
~ The Architecture of Space-Time (TAOST)
&
The Conspicuous Absence of Primes (TCAOP) ~
I. TAOST / B. Geometrics - shapes
I. TAOST - the network
B. Geometrics - shapes <---
II. TCAOP - everything minus the network
|
TAOST: Rules 1-50 | Rules 51-80 | Rules 81-99 | Rules 100-107 | Rules 108-153 | TCAOP: Rule 154 | Rules 155-157 | Rules 158-159 | Rule 160 | Interconnectedness: Rules 161-175 | Appendix A: Rules 176-181 | Appendix B: Rules 182-200 | |
I B. Geometrics - Shapes
There are two parts to this section on shapes. In the first part, we will be looking at shapes formed of diagonal lines within the grid. To illustrate these numerical relationships, we will be using the original Base Square (BS 1.00). The exact symmetry of the lower and upper triangles in the base version of the matrix grid show the patterns to the best advantage.
In the second part, individual geometric shapes will be the focus. For this part, we will revert back to the default Brooks Square (BS 1.01+) version.
Part 1- shaped by diagonals within the grid (BS 1.00).
[ TOP ]
[ TOP ]
[ TOP ]
|
TAOST: Rules 1-50 | Rules 51-80 | Rules 81-99 | Rules 100-107 | Rules 108-153 | TCAOP: Rule 154 | Rules 155-157 | Rules 158-159 | Rule 160 | Interconnectedness: Rules 161-175 | Appendix A: Rules 176-181 | Appendix B: Rules 182-200 | |
[ TOP ]
[ TOP ]
[ TOP ]
|
TAOST: Rules 1-50 | Rules 51-80 | Rules 81-99 | Rules 100-107 | Rules 108-153 | TCAOP: Rule 154 | Rules 155-157 | Rules 158-159 | Rule 160 | Interconnectedness: Rules 161-175 | Appendix A: Rules 176-181 | Appendix B: Rules 182-200 | |
Part 2- individual shapes within the grid (BS 1.01+).

|
|
| ~click to enlarge image | |
| 62 | BS Rule 62: Any equilateral triangle formed in Column C, and labeled A (top), B, © and C, will have the difference, ∆, between the sums, ∑, A+B+© and A+C+© is 8. Simplified: B-C=8 |
Note: This follows from BS Rule 31, where the ∆ in number values from Column B to C=3, Column C to D=5, Column D to E=7,... and therefore, Column B to D=8 as the columns decrease in value by -1, -3, -5, ...left to right, respectively. |
|
[ TOP ]

|
|
| ~click to enlarge image | |
| 63 | BS Rule 63: The same Rule 62 in reverse, A, ©, B and C (bottom) is true. |

|
|
| ~click to enlarge image | |
| 64 | BS Rule 64: Following BS Rule 31 ... and similar to Rules 62 and 63 above ... as one moves the triangle to the right, Columns D, E, F,... the difference, ∆, in values goes as: 12, 16, 20, ... |
Note: C to E=12, D to F=16, E to G=20, ... and so on. |
|
[ TOP ]
Square and Rectangles
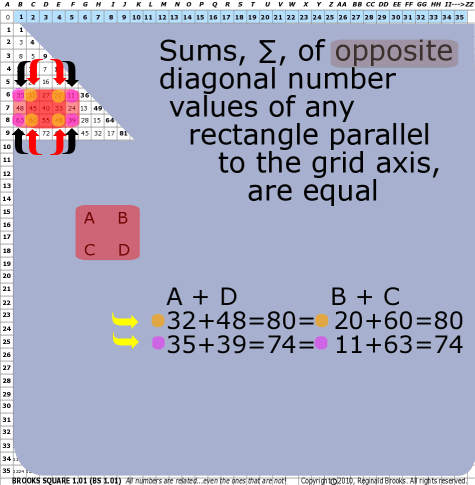
|
|||||||
| ~click to enlarge image | |||||||
| 65 | BS Rule 65: Additions of opposite diagonal number values of any rectangle parallel to the grid axis, are equal. |
||||||
Note:
|
|||||||
[ TOP ]
Diamond-Squares
|
TAOST: Rules 1-50 | Rules 51-80 | Rules 81-99 | Rules 100-107 | Rules 108-153 | TCAOP: Rule 154 | Rules 155-157 | Rules 158-159 | Rule 160 | Interconnectedness: Rules 161-175 | Appendix A: Rules 176-181 | Appendix B: Rules 182-200 | |

|
|||||||||
| ~click to enlarge image | |||||||||
| 66 | BS Rule 66: The difference, ∆, in the sums, ∑, of the opposite diagonal values of any 2x2 grid point unit diamond-squares = 4, or 22 |
||||||||
Note:
|
|||||||||

|
|||||||||||||||||||||
| ~click to enlarge image | |||||||||||||||||||||
| 67 | BS Rule 67: The central number value, ©, of any square or diamond-square equals the sum, ∑, of the perimeter number values divided by the number (quantity, #) of perimeter units, p-units. |
||||||||||||||||||||
Note: ∑p-units ÷ #p-units = ©
|
|||||||||||||||||||||
[ TOP ]

|
|||||||||
| ~click to enlarge image | |||||||||
| 68 | BS Rule 68: The difference, ∆, in the sums, ∑, of the opposite diagonal number values of any 3x3 grid point unit diamond-squares = 16, or 42. |
||||||||
Note:
|
|||||||||

|
|||||||||||||||||||||
| ~click to enlarge image | |||||||||||||||||||||
| 69 | BS Rule 69: The central number value, ©, of any square or diamond-square equals the sum, ∑, of opposite side perimeter number values divided by the number (quantity, #) of perimeter units, p-units. |
||||||||||||||||||||
Note: ∑p-units ÷ #p-units = ©
|
|||||||||||||||||||||
[ TOP ]

|
|||||||||
| ~click to enlarge image | |||||||||
| 70 | BS Rule 70: The difference, ∆, in the sums, ∑, of the opposite diagonal number values of any 4x4 grid point unit diamond-squares = 36, or 62. |
||||||||
Note:
|
|||||||||
[ TOP ]
|
TAOST: Rules 1-50 | Rules 51-80 | Rules 81-99 | Rules 100-107 | Rules 108-153 | TCAOP: Rule 154 | Rules 155-157 | Rules 158-159 | Rule 160 | Interconnectedness: Rules 161-175 | Appendix A: Rules 176-181 | Appendix B: Rules 182-200 | |

|
|||||||||||||||||||||
| ~click to enlarge image | |||||||||||||||||||||
| 71 | BS Rule 71: The central number value, ©, of any square or diamond-square equals the sum, ∑, of opposite side perimeter number values divided by the number (quantity, #) of perimeter units, p-units. |
||||||||||||||||||||
Note: ∑p-units ÷ #p-units = ©
|
|||||||||||||||||||||

|
|||||||||||||||||||||
| ~click to enlarge image | |||||||||||||||||||||
| 72 | BS Rule 72: The central number value, ©, of any square or diamond-square equals the sum, ∑, of symmetrically opposite individual perimeter number values divided by the number (quantity, #) of perimeter units, p-units. |
||||||||||||||||||||
Note: ∑p-units ÷ #p-units = ©
|
|||||||||||||||||||||
[ TOP ]

|
|||||||||
| ~click to enlarge image | |||||||||
| 73 | BS Rule 73: The difference, ∆, in the sums, ∑, of the opposite diagonal number values of any 5x5 grid point unit diamond-squares = 64, or 82, and so on. |
||||||||
Note:
|
|||||||||

|
|||||||||||||||||||||||||||||
| ~click to enlarge image | |||||||||||||||||||||||||||||
| 74 | BS Rule 74: As in Rules 69, 71, and 72, as the number of perimeter units increase, so do the number of combinations of symmetrically opposite p-unit number values that, when divided by the # of p-units, will = ©. |
||||||||||||||||||||||||||||
Note:
|
|||||||||||||||||||||||||||||
[ TOP ]

|
|||||||||||||||||||||||||||||
| ~click to enlarge image | |||||||||||||||||||||||||||||
| 75 | BS Rule 75: Combining the perimeter number values of diamond-squares 2x2, 3x3, 4x4,and 5x5, and dividing by the total number,#, of p-units = ©. |
||||||||||||||||||||||||||||
Note: ∑p-units ÷ #p-units = ©
|
|||||||||||||||||||||||||||||
[ TOP ]
|
TAOST: Rules 1-50 | Rules 51-80 | Rules 81-99 | Rules 100-107 | Rules 108-153 | TCAOP: Rule 154 | Rules 155-157 | Rules 158-159 | Rule 160 | Interconnectedness: Rules 161-175 | Appendix A: Rules 176-181 | Appendix B: Rules 182-200 | |
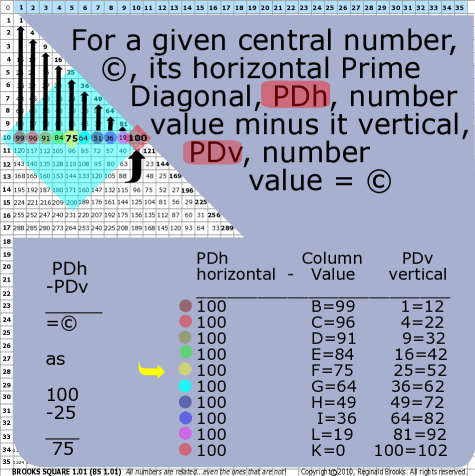
|
|||||||||||||||||||||||||||||||||||||||||||||
| ~click to enlarge image | |||||||||||||||||||||||||||||||||||||||||||||
| 76 | BS Rule 76: For a given central number, ©, its horizontal Prime Diagonal, PDh, number value minus it vertical, PDv, number value = ©. |
||||||||||||||||||||||||||||||||||||||||||||
Note: PDh-PDv=© as 100-25=75 Restated: PDh-Column Value=PDv
|
|||||||||||||||||||||||||||||||||||||||||||||
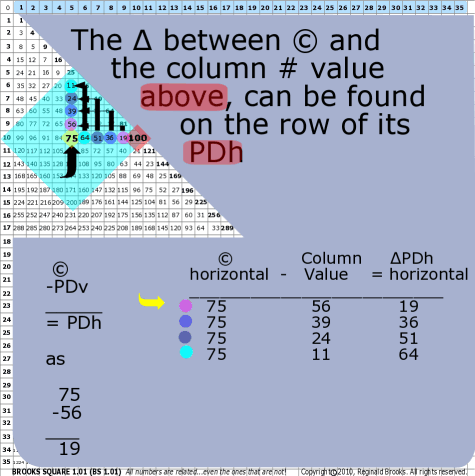
|
|||||||||||||||||||||
| ~click to enlarge image | |||||||||||||||||||||
| 77 | BS Rule 77: For a given central number, ©, the difference,∆, between it and the 1st vertical number value above it is found on the 1st Diagonal intersecting that row. For a given central number, ©, the difference,∆, between it and the 2nd vertical number value above it is found on the 2nd Diagonal intersecting that rowr. For a given central number, ©, the difference,∆, between it and the 3rd vertical number value above it is found on the 3rd Diagonal intersecting that row, and so on. |
||||||||||||||||||||
Note: Restated: The ∆ between © and the column # value above, can be found on the row of its PDh.
|
|||||||||||||||||||||
[ TOP ]
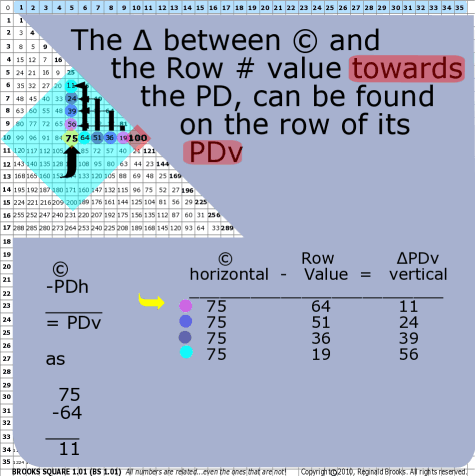
|
|||||||||||||||||||||
| ~click to enlarge image | |||||||||||||||||||||
| 78 | BS Rule 78: Similarly, for a given central number, ©, the difference, ∆, between it and the 1st horizontal row number towards the PD is found vertically in the column above © on the 1st Diagonal intersecting that column. For a given central number, ©, the difference, ∆, between it and the 2nd horizontal row number towards the PD is found vertically in the column above © on the 2nd Diagonal intersecting that column. For a given central number, ©, the difference, ∆, between it and the 3rd horizontal row number towards the PD is found vertically in the column above © on the 3rd Diagonal intersecting that column, and so on. |
||||||||||||||||||||
Note: Restated: The ∆ between © and the row # towards the PD, can be found on the column of its PDv.
|
|||||||||||||||||||||

|
|||||||||||||||||||||
| ~click to enlarge image | |||||||||||||||||||||
| 79 | BS Rule 79: Similarly, for a given central number, ©, the difference, ∆, between it and the 1st horizontal row number away from the PD is found vertically in the column above that 1st horizontal row # on the 1st Diagonal intersecting that column. For a given central number, ©, the difference, ∆, between it and the 2nd horizontal row number away from the PD is found vertically in the column above that 2nd horizontal row # on the 2nd Diagonal intersecting that column. For a given central number, ©, the difference, ∆, between it and the 3rd horizontal row number away from the PD is found vertically in the column above that 3rd horizontal row # on the 3rd Diagonal intersecting that column, and so on. |
||||||||||||||||||||
Note: Restated: The ∆ between © and the row # away from the PD, can be found on the row of its respective vertical PDv.
|
|||||||||||||||||||||
[ TOP ]

|
|||||||||||||||||||||
| ~click to enlarge image | |||||||||||||||||||||
| 80 | BS Rule 80: Similarly, for a given central number, ©, the difference, ∆, between it and the 1st vertical column number below, away from the PD is found horizontally in the row where the the 1st Diagonal intersects. For a given central number, ©, the difference, ∆, between it and the 2nd vertical column number below, away from the PD is found horizontally in the row where the the 2nd Diagonal intersects. For a given central number, ©, the difference, ∆, between it and the 3rd vertical column number below, away from the PD is found horizontally in the row where the the 3rd Diagonal intersects. |
||||||||||||||||||||
Note: Restated: The ∆ between © and the column of #s below, away from the PD, can be found on the column below ©’s respective horizontal PDh.
|
|||||||||||||||||||||
[ TOP ]
|
TAOST: Rules 1-50 | Rules 51-80 | Rules 81-99 | Rules 100-107 | Rules 108-153 | TCAOP: Rule 154 | Rules 155-157 | Rules 158-159 | Rule 160 | Interconnectedness: Rules 161-175 | Appendix A: Rules 176-181 | Appendix B: Rules 182-200 | |
NEXT: On to
I. TAOST>IC. Geometrics-relationships- Brooks (Base) Square
Back to I. TAOST>IA. Geometrics-lines - Brooks (Base) Square
Page 2a- PIN: Pattern in Number...from primes to DNA.
Page 2b- PIN: Butterfly Primes...let the beauty seep in..
Page 2c- PIN: Butterfly Prime Directive...metamorphosis.
Page 2d- PIN: Butterfly Prime Determinant Number Array (DNA) ~conspicuous abstinence~.
Page 3- GoDNA: the Geometry of DNA (axial view) revealed.
Page 4- SCoDNA: the Structure and Chemistry of DNA (axial view).
Page 5a- Dark-Dark-Light: Dark Matter = Dark Energy
Page 5b- The History of the Universe in Scalar Graphics
Page 5c- The History of the Universe_update: The Big Void
Page 6a- Geometry- Layout
Page 6b- Geometry- Space Or Time Area (SOTA)
Page 6c- Geometry- Space-Time Interactional Dimensions(STID)
Page 6d- Distillation of SI units into ST dimensions
Page 6e- Distillation of SI quantities into ST dimensions
Page 7- The LUFE Matrix Supplement: Examples and Proofs: Introduction-Layout & Rules
Page 7c- The LUFE Matrix Supplement: References
Page 8a- The LUFE Matrix: Infinite Dimensions
Page 9- The LUFE Matrix:E=mc2
Page 10- Quantum Gravity ...by the book
Page 11- Conservation of SpaceTime
Page 12- LUFE: The Layman's Unified Field Expose`
Page 13- GoMAS: The Geometry of Music, Art and Structure ...linking science, art and esthetics. Part I
Page 14- GoMAS: The Geometry of Music, Art and Structure ...linking science, art and esthetics. Part II
Page 15- Brooks (Base) Square (BS): The Architecture of Space-Time (TAOST) and The Conspicuous Absence of Primes (TCAOP) - a brief introduction to the series
Page 16- Brooks (Base) Square interactive (BBSi) matrix: Part I "BASICS"- a step by step, multi-media interactive
Page 17- The Architecture Of SpaceTime (TAOST) as defined by the Brooks (Base) Square matrix and the Inverse Square Law (ISL).
| The LUFE Matrix | The LUFE Matrix Supplement | The LUFE Matrix: Infinite Dimensions | The LUFE Matrix: E=mc2 | Dark Matter=Dark Energy | The History of the Universe in Scalar Graphics | The History of the Universe_update: The Big Void | Quantum Gravity ...by the book | The Conservation of SpaceTime | LUFE: The Layman's Unified Field Expose` | |||||
| net.art index | netart01: RealSurReal...aClone | netart02: funk'n DNA/Creation GoDNA | netart03: 9-11_remembered | netart04: Naughty Physics (a.k.a. The LUFE Matrix) | netart05: Your sFace or Mine? | netart06: Butterfly Primes | netart07: Geometry of Music Color | net.games | Art Theory 101 / White Papers Index | |||||