Brooks (Base) Square (BS) 101
~ The Architecture of Space-Time (TAOST)
&
The Conspicuous Absence of Primes (TCAOP) ~
III. Interconnectedness
A Brief Introduction
Table of Contents
I. TAOST - the network
II. TCAOP - everything minus the network
III. Interconnectedness <---
Conclusion
References
Appendix A
Appendix B
III Interconnectedness
How is all this number-pattern-relationship of Brooks (Base) Square integrated in a meaningful way into the larger Multiverse? How might numbers on a chart ... a matrix grid ... tell us something about just this Universe?
About dark matter, dark energy, black holes, worm holes, quasars, supernova, galactic clusters, our own spiral Milky Way Galaxy, the sun, the earth, the soil beneath your feet, the organization of space between the nucleus and the electrons within the atoms of your brain, the rhythm of the beat of your heart?
About the light ... the parts of the enormous electromagnetic spectrum ... composed of individual quantum units called photons ... that seem to be intricately and intimately connected to the very individual quantum units called SpaceTime (ST)? That these particles of light ... these photons ... and their combinations as gravitons and Higgs bosons ... are the source of all energy, and therefore all matter ... and yet ... they are fundamentally defined by the very same ST that they apparently, seemingly ... traverse?
Apparently, seemingly traverse ... whereas in actuality, they are one and the same whose expressions we see, measure and interpret as separate.
The ST unit is composed of photon, graviton and Higgs bosons. Their pulse (propagation) defines the pulse propagation of ST itself. And, as Einstein showed us, the light, the gravity, the energy is itself modulated by the ST field it is emerged ... or traversing ... in.
Thus we have the Conservation Laws. The Conservation of Energy is intimately related to the Conservation of the Velocity of Light. This constant speed of light is a consequence of the Conservation of SpaceTime. All seemingly different and yet all ultimately related back to a dynamic, pulsing, fluctuating ST whose total expression in sum ... that is all the high energy, tiny wavelengths and all the low energy, large wavelengths, together ... will be fixed, constant, conserved. And by definition, the Conservation Laws mean there is an interconnectness of the parts to the whole such that the former never exceeds or retreats from the total of the whole.
Now, back to those silly numbers on the square. We started with the whole integer numbers on the axis and their squares where they meet on the Prime Diagonal (PD). Of course, this simple relationship charts out the Inverse Square Law (ISL). Next, instead of filling in the grid like a simple multiplication table (as was done for the Butterfly Primes), we decided to see if we could find a number on each of the Inner Grid spaces that would show a connection ... an interconnectedness ... to the axis, PD and the numbers (that we would have to discover) of its neighbors. Open Pandora’s Box!
The numbers starting pouring out. Pandora’s Box was white hot ... pure light ... so overwhelmingly giving of one number pattern relationship connected to another and all connected back to the PD of the ISL that we had to stop looking ... least we become blinded by its glory ... and present this for other to see, feel, grow and shine.
Remembering that numbers are simply symbols ... although commonly they are symbols for quantities. If all the matter-energy-ST is conserved and we can put a quantity value on it and all of its parts ... and that numbers as symbols for quantities are applied ... then we can assign ... count ... numbers of parts and their sums.
And, if the parts over time must equal the same whole ... as our Conservation Laws require ... then our numbers must be interconnected. Interconnected such that when the sums of all the parts ... positive and negative ... are taken over time, that sum must be 1 ... or zero, depending on how you like to look at it. As the Universe pulse-propagates into existence at one point in time, that total sum is one. As it pulse-propagates back out of existence, the endpoint, the whole sum of the pulse in + the whole sum of the pulse out ... equal and opposite ... must be zero.
Here is a matrix-grid-table, a truly base square, that interconnects all the numbers as the Universe pulse-propagates into existence. And, while it contains all the whole numbers ... all the quantities ... including the prime numbers within its axis and PD ... it is a pattern of patterns and as such its Strict Inner Grid (SIG) is specifically and uniquely devoid of prime numbers ... those numbers left over when all the patterned numbers are removed. The prime numbers are like the negative space of the patterned, positive space non-primes. Each defining the other.
That ST units ... that together must be conserved ... are themselves of so much space over so much time. As it pulse-propagates into and out of existence ... as a part of the whole ... it must have quantities of extension into (and out of) space.
Extension takes time. So there must be a reciprocal quantity of time to allow for the spatial extension. Short extension, short time multiplied by a high pulse frequency gives high energy and vice versa. Short time appears short ... in the sense of a smaller quantity of temporal units (seconds), but actually ... on the quantum level ... the short time means the clock rate is slowed (it takes longer for each clock second ... time is expanded, dilated), such that a slower internal clock combined with a shorter extension equals ... in terms of its quantum Planck energy (h)... a longer ST extension with longer apparent time. That longer time has it clock rate moving reciprocally faster (it takes less time for each clock second ... time is contracted), such that the apparent time (seconds) seems longer. This is the basis for all Planck energy units, h, being equal and their energy, E, presented being dependent on the frequency, ν, at which they pulse-propagate into and out of existence, E=hν.
The speed of light, c, equals the wavelength, λ, per second or cyclic period of time (frequency) as: c=λν.
The conserved speed of light is built into the Conservation of SpaceTime ... which forms the basis for the Conservation of Energy. Energy density defines the curvature of ST (and vice versa). The ISL defines the ST distribution (curvature) of energy. The interrelationships ... the interconnectedness ... of the numbers and their patterns of the ISL are revealed by the Brooks (Base) Square. It is The Architecture Of SpaceTime (TAOST).
Anything that purports to inform the architecture of spacetime must have these qualities inherent:
- It must begin with nothing, with zero, and build out (+1) ... and back down(-1) ... to zero;
- It must account for all ... in this case ... numbers;
- It must be imminently flexible;
- It must be interconnected on all levels of design ... from the most simple to complex;
- It must be transformable by symmetry.
Brooks (Base) Square easily fulfills each of these requirements. in fact, looking at these requirements from the vantage point of ST units and comparing their fulfillment to that of Brooks (Base) Square and one can see no difference ... they are interchangeable.
Imagine this scenario that was taken from my work “Conservation of SpaceTime” and now briefly elaborated on. ST units are composed of bosons. When relatively stable ST units appear, they represent one of two types of bosons ... both being composed of yet a third type, the photon. Light (EM spectrum) represents moving ST units and these are none other than the photon bosons.
Photons come with spin 1 and have either left or right handed spin. When two moving photons with the same spin constructively interfere, they generate a new, temporary, relatively static boson with spin 2 (L+L or R+R). That is our graviton boson.
When two photons with opposite spin combine, it is the Higgs boson that is generated ... having spin 0 (L=R or R+L).
The graviton, with its very active spin 2 configuration ... and its dependency on its source of radiating photons ... conveys its enhanced curvature of spacetime locally ... as gravity. And just like the EM spectrum, the force of gravity falls off inversely with the square of the distance of separation from its focused source (ISL). The graviton is difficult to measure as a discrete quantum particle because of the tenuous nature of its existence. Its movement is dependent on the movement of its photon-generated interference pattern.
The Higgs boson ... contrary to the modern notion of it being massive ... is, in fact, massless, chargeless and spinless. It will not be detected by modern techniques (like the LHC, Large Hadron Collider) that look for massive particles. The Higgs boson does hold the maximum symmetry of opposing fundamentals of physical expression in the Universe. Its mass, charge and spin are all neutral ... effectively zero ... because it contains equal and opposite vectors of each. It is, thus, the mother of all ST units (bosons) and the ST particles (fermions) that it creates. Because net spin greater than zero is required for motion, it is also motionless. It represents both the zero and the full matrix grid of number values of the Brooks (Base) Square. And, like all ST units, it pulses into and out of existence. It may decouple its perfect symmetry forming two child photon ST units ... with equal and opposite spin ... blasting off in opposite directions. These new bosons so formed ... these photons ... carry the signature energy of ST ... always traveling as ST is wont to do, at the velocity of light, c.
Misc. Interconnectedness - Ϝ, Φ, ⎄, 2½, 1.37
Now that our heads are spinning with the possibilities of interconnectedness, let’s utilize those propellers to sweep over a couple of speculative associations with far reaching implications.
We’ll start with the one that is pretty solid and finish with the one that ... while being provocative to the extreme ... is, nevertheless ... quite a speculative leap ... and don’t we just love to leap!
The Golden Mean, Φ=1.618 ... and its siblings the Golden Rectangle, ⎄, Golden Section, Golden Spiral, etc. ... is so universal in both the natural and artificial, human-designed world that surely its presence must be felt in the ISL and Brooks (Base) Square. The difficulty of fixing an easy to see association ... an interconnectedness ... between the two is one of fractions (proportions) versus whole numbers. Φ is expressed in decimal terms as 1.618, or 1:1.618 or 1:1:.618.
The Fibonacci series, Ϝ, has addressed the fraction problem head on by describing a simple number progression of whole integer numbers whose ratios of successive pairs of numbers in sequence nicely approaches the value of Φ...1-1-2-3-5-8-13-34-55-89-144-233-.... Each Ϝ # is formed by adding the pair of numbers immediately preceding. And the difference, ∆, between the Ϝ #s is Φ once you move along the progression.
Now that we have some whole numbers to look at, we can examine Φ, ⎄, 2½ (square root of 2), all within the Ϝ # series and how it might interact with the ISL and Brooks (Base) Square. See Rules 161-166.
Lastly, we look further into the abstract abyss of pure number relationships ... in this case a brief look at 1-3-7.
When a dimensionless number is part of an equation ... especially when present as a fundamental universal constant ... it has two functions, scale and value. How large (or small) and what is the amount of leverage (ratio value). The ratio value is informing the rest of the equation how much, proportionally and strictly relevant, it will modify the rest of the equation’s value. Of course it matters on which side of the line, numerator or denominator, it is positioned ... at least, sort of, for the mechanics of the equation ... because we know we can always flip it to the opposite side of the line by simply using its inverse ... dividing it into one. With that in mind, we fancy a speculative interconnectedness of the 1.37 number that arises from the Ϝ series and 1/137 the Fine Structure Constant. See Rules 167-168.
Should you elect to simply scan or skip over the marvelous, but esoterically challenging Rules 167-168, remiss NOT the final section below on the PTOP (Periodic Table of Primes) and the solution to Euler's "strong" form of the Goldbach Conjecture and the little discoveries that follow. Rules 169-175..
Misc. Interconnectedness - Prime Numbers, Even Numbers, Goldbach Conjecture and PTOP
Finally, we take a look at one more remarkable interconnection ... this time between all the Even Numbers and the Prime Numbers, Euler’s “strong” form of the Goldbach Conjecture, and the Periodic Table of Primes (PTOP). See Rules 169-175.
Misc. Interconnectedness - Ϝ, Φ, ⎄, 2½, 1.37

|
| ~click to enlarge image
|
| 161 |
BS Rule 161: The even numbers of the 1st Diagonal leg of the Brooks (Base) Square fall into two groups, excluded and included:
- the included even #s ... 4-8-12-16-20-... are both on the upper 1st Diagonal, present in the Strict Inner Grid (SIG) and all are divisible by 4;
- the excluded even #s ... 2-6-10-14-18-... are only on the upper 1st Diagonal, excluded from the SIG and not divisible by 4;
- the excluded #s, when divided by 2 equal the odd numbers ... 1-3-5-7-... of the other 1st Diagonal, of odd number and below the PD. When multiplied by 2, they become a subset of the included evens above;
- both excluded and included #s have 1st # values of 2-6-0-4-8;
- both excluded and included #s have 2nd # values that fall into a pattern of clusters containing a 2:3 ratio of the lower to higher 2nd # values, e.g. 22-26 | 30-34-38, and, 12-16 | 20-24-28 ;
- the sums, ∑, of the excluded even #s grow as: 50-150-250-...;
- the sums, ∑, of the included even #s grow as: 100-200-300-...;
- both excluded and included 2nd # values increase by 10 when going across the chart.
|
Note:
|
Excluded Even #s (non-4-based) Chart
|
|
2nd
#s
|
Excl.
#s
|
∑
|
2nd
#s
|
Excl.
#s
|
∑
|
2nd
#s
|
Excl.
#s
|
∑
|
|
2
|
(0)2
|
50
5x10
|
2
|
10 2
|
550
5x110
|
2
|
20 2
|
1050
5x210
|
|
(0)6
|
10 6
|
20 6
|
|
3
|
1 0
|
3
|
11 0
|
3
|
21 0
|
|
1 4
|
11 4
|
21 4
|
|
1 8
|
11 8
|
21 8
|
|
2
|
2 2
|
150
5x30
|
2
|
12 2
|
650
5x130
|
2
|
22 2
|
1150
5x230
|
|
2 6
|
12 6
|
22 6
|
|
3
|
3 0
|
3
|
13 0
|
3
|
23 0
|
|
3 4
|
13 4
|
23 4
|
|
3 8
|
13 8
|
23 8
|
|
2
|
4 2
|
250
5x50
|
2
|
14 2
|
750
5x150
|
2
|
24 2
|
1250
5x250
|
|
4 6
|
14 6
|
24 6
|
|
3
|
5 0
|
3
|
15 0
|
3
|
25 0
|
|
5 4
|
15 4
|
25 4
|
|
5 8
|
15 8
|
25 8
|
|
2
|
6 2
|
350
5x70
|
2
|
16 2
|
850
5x170
|
2
|
26 2
|
1350
5x270
|
|
6 6
|
16 6
|
26 6
|
|
3
|
7 0
|
3
|
17 0
|
3
|
27 0
|
|
7 4
|
17 4
|
27 4
|
|
7 8
|
17 8
|
27 8
|
|
2
|
8 2
|
450
5x90
|
2
|
18 2
|
950
5x190
|
2
|
28 2
|
1450
5x290
|
|
8 6
|
18 6
|
28 6
|
|
3
|
9 0
|
3
|
19 0
|
3
|
29 0
|
|
9 4
|
19 4
|
29 4
|
|
9 8
|
19 8
|
29 8
|
|
|
∆=500
|
|
|
|
∆ =500
|
|
2nd # ⬆ by 10 across rows - left to right
|
|
Included Even #s (4-based) Chart
|
|
2nd
#s
|
Incl.
#s
|
∑
|
2nd
#s
|
Incl.
#s
|
∑
|
2nd
#s
|
Incl.
#s
|
∑
|
|
3
|
(0)0
|
_____
100
5x20
_____
200
5x40
_____
300
5x60
_____
400
5x80
_____
500
|
3
|
10 0
|
500
5x100
_____
600
5x120
_____
700
5x140
_____
800
5x160
______
900
5x180
_____
1000
|
3
|
20 0
|
1000
5x200
_____
1100
5x220
_____
1200
5x240
_____
1300
5x260
_____
1400
5x280
_____
1500
|
|
(0)4
|
10 4
|
20 4
|
|
(0)8
|
10 8
|
20 8
|
|
2
|
1 2
|
2
|
11 2
|
2
|
21 2
|
|
1 6
|
11 6
|
21 6
|
|
3
|
2 0
|
3
|
12 0
|
3
|
22 0
|
|
2 4
|
12 4
|
22 4
|
|
2 8
|
12 8
|
22 8
|
|
2
|
3 2
|
2
|
13 2
|
2
|
23 2
|
|
3 6
|
13 6
|
23 6
|
|
3
|
4 0
|
3
|
14 0
|
3
|
24 0
|
|
4 4
|
14 4
|
24 4
|
|
4 8
|
14 8
|
24 8
|
|
2
|
5 2
|
2
|
15 2
|
2
|
25 2
|
|
5 6
|
15 6
|
25 6
|
|
3
|
6 0
|
3
|
16 0
|
3
|
26 0
|
|
6 4
|
16 4
|
26 4
|
|
6 8
|
16 8
|
26 8
|
|
2
|
72
|
2
|
172
|
2
|
27 2
|
|
7 6
|
17 6
|
27 6
|
|
3
|
8 0
|
3
|
18 0
|
3
|
28 0
|
|
8 4
|
18 4
|
28 4
|
|
8 8
|
18 8
|
28 8
|
|
2
|
9 2
|
2
|
19 2
|
2
|
29 2
|
|
9 6
|
19 6
|
29 6
|
|
|
∆=500
|
|
|
|
∆ =500
|
|
2nd # ⬆ by 10 across rows - left to right
|
|
[ TOP ]
|
| ~click to enlarge image
|
| 162 |
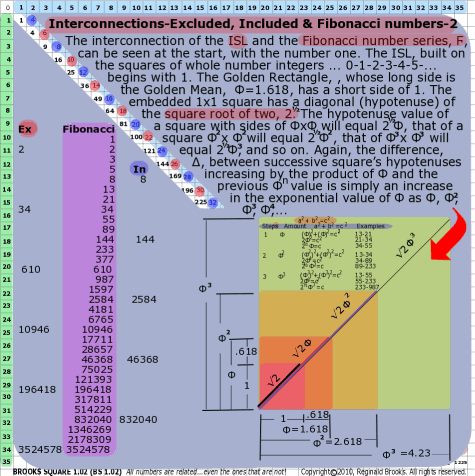
BS Rule 162: The interconnection of the ISL and the Fibonacci number series, Ϝ, can be seen at the start, with the number one. The ISL, built on the squares of whole number integers ... 0-1-2-3-4-5-... begins with 1. The Golden Rectangle, ⎄, whose long side is the Golden Mean, Φ=1.618, has a short side of 1. The embedded 1x1 square has a diagonal (hypotenuse) of the square root of two, 2½. The hypotenuse value of a square with sides of ΦxΦ will equal 2½Φ, that of a square Φ2xΦ2 will equal 2½Φ2, that of Φ3xΦ3 will equal 2½Φ3, and so on. Again, the difference, ∆, between successive square’s hypotenuses increasing by the product of Φ and the previous Φn value is simply an increase in the exponential value of Φ as Φ, Φ2, Φ3, Φ4,...
|
Note: Example: 144xΦ=233; 233xΦ=377; 377xΦ=610;
144xΦ2=377, 144xΦ3=610
|
a2 + b2 =c2
|
|
Steps
|
Amount
|
a2 + b2 =c2
|
Examples
|
|
1
|
Φ
|
(Φ)2+(Φ)2=c2
2Φ2=c2
2½Φ=c
|
13-21
21-34
34-55
|
|
2
|
Φ2
|
(Φ2)2+(Φ2)2=c2
2Φ4=c2
2½Φ2=c
|
13-34
34-89
89-233
|
|
3
|
Φ3
|
(Φ3)2+(Φ3)2=c2
2Φ6=c2
2½Φ3=c
|
13-55
55-233
233-987
|
|
Every 3rd # on the Ϝ series = one 360〫spiral rotation
Every 3rd # on the Ϝ series = an even #
Every 3rd # on the Ϝ series = Φ3 x the original #
|
|
[ TOP ]
|
| ~click to enlarge image
|
| 163 |
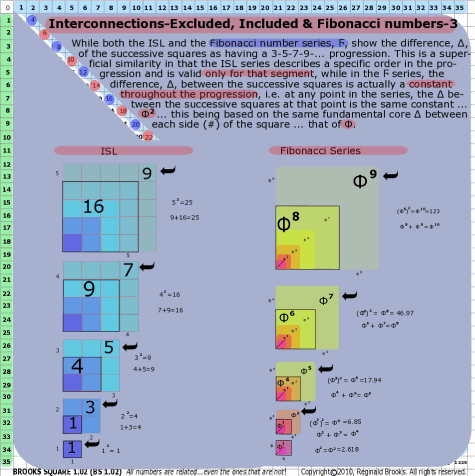
BS Rule 163: While both the ISL and the Fibonacci number series, Ϝ, show the difference, ∆, of the successive squares as having a 3-5-7-9-... progression. This is a superficial similarity in that the ISL series describes a specific order in the progression and is valid only for that segment, while in the Ϝ series, the difference, ∆, between the successive squares is actually a constant throughout the progression, i.e. at any point in the series, the ∆ between the successive squares at that point is the same constant ... Φ2 ... this being based on the same fundamental core ∆ between each side (#) of the square ... that of Φ.
|
Note: The ISL increases sequentially as the odd-number summation series: (1-2-3-4-5-...)2=1-4-9-16-25-... and differences, ∆, of (1)-3-5-7-9-... respectively. The Ϝ series increases, not additively as in the ISL, but by a constant factor of Φ squared, or Φ2, as the sides are increased exponentially as: Φ-Φ2-Φ3-... (and not as Φ-2Φ-3Φ).
|
ISL- successive squares
|
|
Side
|
Side2
|
Original
|
Additional Added
|
∑
|
|
1
|
12=1
|
0
|
1
|
1
|
|
2
|
22=4
|
1
|
3
|
4
|
|
3
|
33=9
|
4
|
5
|
9
|
|
4
|
42=16
|
9
|
7
|
16
|
|
5
|
53=25
|
16
|
9
|
25
|
|
Fibonacci Series- successive squares-1
|
|
Side
|
Side2
|
Original
|
Additional
Added
|
∑
|
|
Φ
|
(Φ)2=Φ2
|
0
|
Φ
|
Φ2
|
|
Φ2
|
(Φ2)2=Φ4
|
Φ2
|
Φ3
|
Φ4
|
|
Φ3
|
(Φ3)2=Φ6
|
Φ4
|
Φ5
|
Φ6
|
|
Φ4
|
(Φ4)2=Φ8
|
Φ6
|
Φ7
|
Φ8
|
|
Φ5
|
(Φ5)2=Φ10
|
Φ8
|
Φ9
|
Φ10
|
|
Fibonacci Series- successive squares-2
|
|
Side
|
Side2
|
Original
|
Additional
Added
|
∑
|
|
Φ
|
(Φ)2=Φ2
|
Φ2 = 2.618
|
|
Φ2
|
(Φ2)2=Φ4
|
(Φ2)2= Φ4 = 6.85
Φ2 + Φ3 = Φ4
|
|
Φ3
|
(Φ3)2=Φ6
|
(Φ3)2 = Φ6 = 17.94
Φ4 + Φ5 = Φ6
|
|
Φ4
|
(Φ4)2=Φ8
|
(Φ4)2 = Φ8 = 46.97
Φ6 + Φ7 = Φ8
|
|
Φ5
|
(Φ5)2=Φ10
|
(Φ5)2 = Φ10 = 123
Φ8 + Φ9 = Φ10
|
|
Areas go as: Φ2 - Φ4 - Φ6 - Φ8 - Φ10...
Note: Adding exponentials sequentially, e.g. Φ2+Φ3=Φ4, only works for the Golden Mean, Φ.
|
|
Φ
|
value
(approx.)
|
|
Φ
|
1.618
|
|
Φ2
|
2.618
|
|
Φ3
|
4.235
|
|
Φ4
|
6.85
|
|
Φ5
|
11.09
|
|
Φ6
|
17.94
|
|
Φ7
|
29.03
|
|
Φ8
|
46.97
|
|
Φ9
|
76
|
|
Φ10
|
123
|
|
Φ11
|
199
|
|
Φ12
|
323
|
|
[ TOP ]
|
| ~click to enlarge image
|
| 164 |
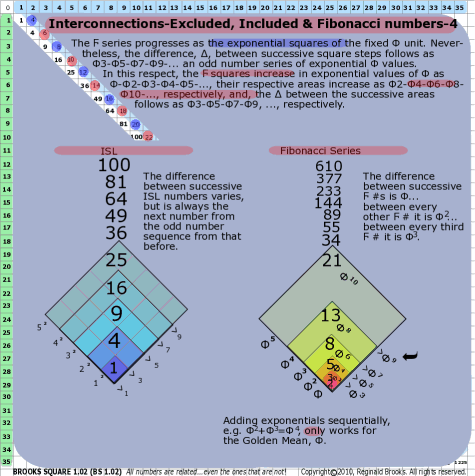
BS Rule 164: The Ϝ series progresses as the exponential squares of the fixed Φ unit. Nevertheless, the difference, ∆, between successive square steps follows as Φ3-Φ5-Φ7-Φ9-... an odd number series of exponential Φ values. In this respect, the Ϝ squares increase in exponential values of Φ as Φ-Φ2-Φ3-Φ4-Φ5-..., their respective areas increase as Φ2-Φ4-Φ6-Φ8-Φ10-..., respectively, and, the ∆ between the successive areas follows as Φ3-Φ5-Φ7-Φ9, ..., respectively.
|
Note: The difference between successive Ϝ #s is Φ... between every other Ϝ # it is Φ2... between every third Ϝ # it is Φ3. In the charts below, we see that the differences between Φ-Φ2-Φ3-... is itself yet another Ϝ-like series. The difference, ∆, between the subsequent Φn values follows exactly as a Ϝ series. Each subsequent value of Φn is the sum,∑, of the two preceding values.
Another way to look at this is the progression of squares, as above, where the sides grow as Φ-Φ2-Φ3-.... In actuality, as:
Φ1=0+1Φ
Φ2=1+1Φ
Φ3=1+2Φ
Φ4=2+3Φ
Φ5=3+5Φ
Φ6=5+8Φ
Φ7=8+13Φ
Φ8=13+21Φ
Every new side is the sum, ∑, of the two preceding sides.
|
5 steps along three sequential Fibonacci series numbers & Φ
|
|
Ϝ#
|
x Φn
|
Ϝ#
|
x Φn
|
Ϝ#
|
x Φn
|
*Equivalent
|
|
13
|
x Φ = 21
|
|
|
|
|
|
|
13
|
x Φ2 = 34
|
21
|
x Φ = 34
|
|
|
|
|
13
|
x Φ3= 55
|
21
|
x Φ2 = 55
|
34
|
x Φ = 55
|
34 x (0 + Φ1)
|
|
13
|
x Φ4= 89
|
21
|
x Φ3 = 89
|
34
|
x Φ2= 89
|
34 x (1 + Φ1)
|
|
13
|
x Φ5 = 144
|
21
|
x Φ4 = 144
|
34
|
x Φ3= 144
|
34 x (Φ1 + Φ2)
|
|
|
|
21
|
x Φ5 = 233
|
34
|
x Φ4 = 233
|
34 x (Φ2 + Φ3)
|
|
|
|
|
|
34
|
x Φ5 = 377
|
34 x (Φ3 + Φ4)
|
|
Note: *Adding exponentials sequentially, e.g. Φ2+Φ3=Φ4, only works for the Golden Mean, Φ.
If Φ= (0+Φ1), as in the first row, then substituting this value into the second row gives: (1 + Φ1)= [1 + (0 + Φ1)]=1+Φ1=2.618=Φ2.
Now, onto the third row.
If Φ2= (1 + Φ1), then (Φ1 + Φ2)= [Φ1 + (1 + Φ1)]=1+2Φ1=4.236=Φ3.
In the fourth row:
If Φ3= (Φ1 + Φ2), then (Φ2 + Φ3)= (1 + Φ1)+ (Φ1 + Φ2)= (1 + Φ1)+ [Φ1 + (1 + Φ1)]=
1 + Φ1+ Φ1 + 1 + Φ1=2+3Φ1=6.854=Φ4.
In the fifth row:
If Φ4= (Φ2 + Φ3),
then (Φ3 + Φ4)= (Φ1 + Φ2) + (Φ2 + Φ3) = [Φ1 + (1 + Φ1)]+[(1 + Φ1)+ (Φ1 + Φ2)]=
[Φ1 + (1 + Φ1)]+[(1 + Φ1)+ (Φ1 + [1 + Φ1])] =3+5Φ1=11.09=Φ5, and so on.
Clearly,
Φ1=0+1Φ
Φ2=1+1Φ
Φ3=1+2Φ
Φ4=2+3Φ
Φ5=3+5Φ
Φ6=5+8Φ
Φ7=8+13Φ
Φ8=13+21Φ
...
The difference, ∆, between the subsequent Φn values follows exactly as above.
Each subsequent value of Φn is the sum,∑, of the two preceding values.
Φ1=0+1Φ
Φ2=1+1Φ
Φ3=1+2Φ
Φ3=1+2Φ
Φ4=2+3Φ
Φ5=3+5Φ
Φ5=3+5Φ
Φ6=5+8Φ
Φ7=8+13Φ
|
|
[ TOP ]
|
| ~click to enlarge image
|
| 165 |
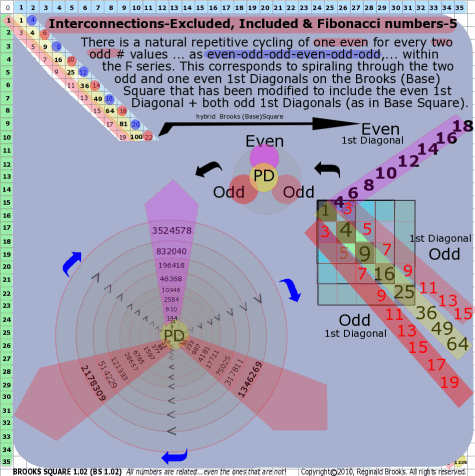
BS Rule 165: There is a natural repetitive cycling of one even for every two odd # values ... as even-odd-odd-even-odd-odd,... within the Ϝ series. This corresponds to spiraling through the two odd and one even 1st Diagonals on the Brooks (Base) Square that has been modified to include the even 1st Diagonal + both odd 1st Diagonals (as in Base Square).
Every even #, excluded and included, alternately, that is included in the Ϝ series is Φ3 (approximately 2½x3) larger or smaller than its next or previous even #, respectively.
|
Note:
|
Ϝ #
|
Excl.Even #
|
Incl. Even #
|
|
0
|
|
|
|
1
|
|
|
|
1
|
|
|
|
2
|
2
|
|
|
3
|
|
|
|
5
|
|
|
|
8
|
|
8
|
|
13
|
|
|
|
21
|
|
|
|
34
|
34
|
|
|
55
|
|
|
|
89
|
|
|
|
144
|
|
144
|
|
233
|
|
|
|
377
|
|
|
|
610
|
610
|
|
|
987
|
|
|
|
1597
|
|
|
|
2584
|
|
2584
|
|
4181
|
|
|
|
6765
|
|
|
|
10946
|
10946
|
|
|
17711
|
|
|
|
28657
|
|
|
|
46368
|
|
46368
|
|
75025
|
|
|
|
121393
|
|
|
|
196418
|
196418
|
|
|
317811
|
|
|
|
514229
|
|
|
|
832040
|
|
832040
|
|
1346269
|
|
|
|
2178309
|
|
|
|
3524578
|
3524578
|
|
|
Every 3rd Ϝ # is even, follows symmetrical pattern.
Each Excluded and Included even # is 2½ x 3 = Φ3 larger than its even # predecessor.
|
|
[ TOP ]
|
| ~click to enlarge image
|
| 166 |
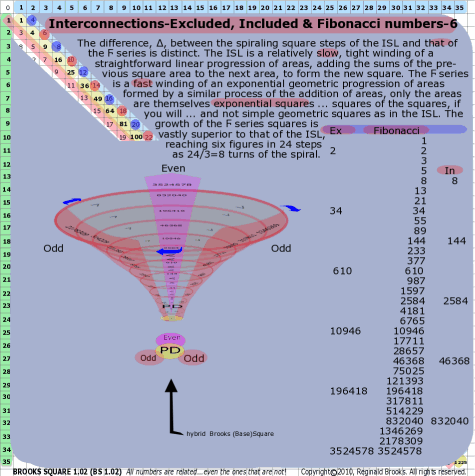
BS Rule 166: The difference, ∆, between the spiraling square steps of the ISL and that of the Ϝ series is distinct. The ISL is a relatively slow, tight winding of a straightforward linear progression of areas, adding the sums of the previous square area to the next area, to form the new square. The Ϝ series is a fast winding of an exponential geometric progression of areas formed by a similar process of the addition of areas, only the areas are themselves exponential squares ... squares of the squares, if you will ... and not simple geometric squares as in the ISL. The growth of the Ϝ series squares is vastly superior to that of the ISL, reaching six figures in 24 steps as 24/3=8 turns of the spiral.
|
Note:
- A square with sides of 1 has a hypotenuse of 2½.
- A square with sides of 3, has a hypotenuse of 4.2426=2½x3.
1.6180339887 x 1.6180339887 x 1.6180339887 = 4.23606798 Φ3=4.2358. Close, but not exact.
- A square with sides of Φ has a hypotenuse of 2½xΦ=2.288=[(Φ)2+(Φ)2]½.
|
[ TOP ]

|
| ~click to enlarge image
|
| 167 |
BS Rule 167: Take any Fibonacci, Ϝ, # and divide it sequentially by the Golden Mean, Φ, and it will resolve down to 1.17105. (1.17105)2=1.37137.
The Fine Structure Constant (FSC), or α, equals approximately 1/137. The FSC is one of the pure number, dimensionless universal constants of physics. It defines the fundamental interaction ... coupling constant (strength)... of the electromagnetic force (EMF). (See “GoDNA: The Geometry of DNA” to see how 1.37(α) and 1.618 (Φ) are fundamental in the DNA Master Table ... defining the geometric structure of the DNA double helix in the axial view.)
The FSC is actually about 1/137. It simply represents a pure dimensionless # that functions as a proportion ... a ratio factor ... in the mathematical description of other dimension-based physical parameters that yield the coupling strength of the EM interaction. It is extremely intriguing that 1.37 shows up here in the Ϝ series, but for now, we will call it a speculative interconnection.
|
Note: Example: 144/Φ4=1.17105 (1.17105)2=1.37137
|
[ TOP ]
|
| ~click to enlarge image
|
| 168 |
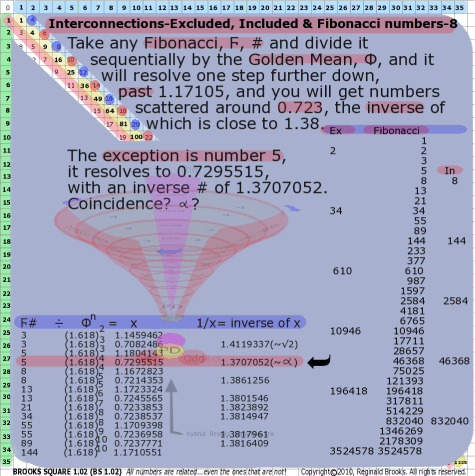
BS Rule 168: Take any Fibonacci, Ϝ, # and divide it sequentially by the Golden Mean, Φ, and it will resolve one step further down, past 1.17105, and you will get numbers scattered around 0.723, the inverse of which is close to 1.38. The exception is number 5, it resolves to 0.7295515, with an inverse # of 1.3707052. Coincidence?
|
|
|
Misc. Interconnectedness - Prime Numbers, Even Numbers, Goldbach Conjecture and PTOP
Please refer to
for in depth review of prime numbers as it applies here.
(Weisstein, Eric W. "Goldbach Conjecture." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/GoldbachConjecture.html)
|
| ~click to enlarge image
|
| 169 |
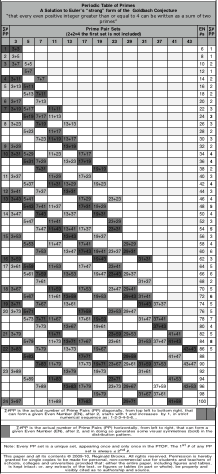
BS Rule 169: The solution to the strong form of the Goldbach Conjecture ... as modified by Euler ... “that every even positive integer greater than or equal to 4 can be written as a sum of two primes” is presented here as the Periodic Table of Primes (PTOP), an unequivocal pattern of primes, in sets of two, which account for every even positive whole number integer. (Please donate any prize money associated with this proof to the help, nutrition, education, shelter and prevention of abuse of the underprivileged children of the world.)
A simple graphical plot of the pairs of prime numbers whose sum, ∑, equals the next sequential even whole number integer ... 4-6-8-10-12-14-16-... reveals a series of patterns amongst those prime pairs:
- horizontally, across the grid left to right, one or more prime pair sets will form the even number and the first prime number will increase while the second prime number decreases;
- vertically, down each column of prime pairs, the second prime number of that pair set, after 2, increases exactly in the order of the primes from 3 to infinity;
- diagonally, from top left to bottom right, the first prime number of that pair set, after 2, increases exactly in the order of the primes from 3 to infinity;
- diagonally, from top left to bottom right, the actual number of prime pairs that can form a given even number, after 2, starts with 1 and increases by 1, in strict numerical sequence as: 1-2-3-4-5-6... the progressive sum of these prime pairs being designated as ∑#PP;
- combining the information about the prime pairs (PP) pattern distribution above, one can use the PTOP to help determine the “next” prime, from the smallest to the largest, by simply extending the PP pattern into the next corresponding even number ... or the one thereafter ... or the one thereafter, and so on ... until the pattern is fulfilled. Double-checking that the horizontal, vertical and diagonal pattern requirements are all met, you will now have assurance that that “next” prime number is indeed, prime. In doing so, you will also reconfirm the validity of the solution of Euler’s reformulated version ... a.k.a. the “strong” version ... of the Goldbach Conjecture. The conjecture has been confirmed up to 4x1014 numbers.
|
Note: The sum, ∑, of the actual numbers of prime pair (PP) sets in the first column ... ∑#PP ... increases by one, giving the sequence: 1-2-3-.... These PP sets run diagonally from top-left to bottom-right. We are simply adding one new PP set. Note that for any given set, the first prime # of that set increases in strict prime sequence order (no primes are missing!), while the second # remains fixed, e.g. 3+7, 5+7, 7+7. The sums, ∑, of the PP sets grow as one goes down the diagonal. The empty blank spaces going down diagonally, while not being prime, do follow the strict odd number sequence ... as if they were there ... acting as place holders, e.g. 3+11, 5+11, 7+11 and 11+11 has a blank diagonal space where 9+11 would go if 9 were prime, but it’s not, nevertheless, it acts as a blank placeholder for the odd number sequence, and the next valid prime number 11 is over and down diagonally 2 spaces from its predecessor, 7. Restated: If all the odd numbers were prime then the diagonals would all line up, corner to corner, to give a straight line; but for those odd numbers which are not prime, the diagonal corners are staggered with blanks stacked for each non-prime odd number. See the PTOP.
Going down vertically from the top, this time it is the second prime # of that set increases in strict prime sequence order (no primes are missing!), while the first # remains fixed, e.g. 5+5, 5+7, 5+11,.... The sums, ∑, of the PP sets grow as one goes down the column. The empty blank spaces going down vertically, while not being prime, do follow the strict odd number sequence ... as if they were there ... acting as place holders, e.g. above the 5+9 set is blank as 9 is not prime, but it does follow the odd number sequence as 5-7-9-11.
Going horizontally across, the prime #s of the PP sets both change. The first prime # increases, while the second decreases. And while they both do respect the natural sequence of primes, they do NOT do so in strict order, i.e. there are jumps along the sequence, bypassing some of those primes that are in strict order sequence, e.g. 3+19, 5+17, 11+11 (forming ∑=22), the first prime #s of the PP sets are 3-5-11 ... missing the 7 between the 5 and 11, and the second prime #s going in the reverse direction are 11-17-19 ... missing the 13 between the 11 and 17, and if you look at the chart there is a blank space at exactly this position of the missing PPs (naturally since 7+13=20 and does not belong on this row). What this points out is that the horizontal PP set pattern actually does follow the strict prime number sequence but for those PP sets that do NOT add up to the even number that that row represents, a blank naturally occurs there, causing the jumps in the strict prime number sequence. This is valuable information in confirming the horizontal, vertical and diagonal patterns of the PP sets are properly in place and accounted for.
|
Periodic Table of Primes
A Solution to Euler’s “strong” form of the Goldbach Conjecture
“that every even positive integer greater than or equal to 4 can be written as a sum of two primes”
|
|
∑#
PP
|
Prime Pair Sets
(2+2=4 the first set is not included)
|
EN #s
|
∑#
PP
|
|
|
3
|
5
|
7
|
11
|
13
|
17
|
19
|
23
|
29
|
31
|
37
|
41
|
43
|
|
|
|
1
|
3+3
|
|
|
|
|
|
|
|
|
|
|
|
|
6
|
1
|
|
2
|
3+5
|
|
|
|
|
|
|
|
|
|
|
|
|
8
|
1
|
|
3
|
3+7
|
5+5
|
|
|
|
|
|
|
|
|
|
|
|
10
|
2
|
|
|
|
5+7
|
|
|
|
|
|
|
|
|
|
|
|
12
|
1
|
|
4
|
3+11
|
|
7+7
|
|
|
|
|
|
|
|
|
|
|
14
|
2
|
|
5
|
3+13
|
5+11
|
|
|
|
|
|
|
|
|
|
|
|
16
|
2
|
|
|
|
5+13
|
7+11
|
|
|
|
|
|
|
|
|
|
|
18
|
2
|
|
6
|
3+17
|
|
7+13
|
|
|
|
|
|
|
|
|
|
|
20
|
2
|
|
7
|
3+19
|
5+17
|
|
11+11
|
|
|
|
|
|
|
|
|
|
22
|
3
|
|
|
|
5+19
|
7+17
|
11+13
|
|
|
|
|
|
|
|
|
|
24
|
3
|
|
8
|
3+23
|
|
7+19
|
|
13+13
|
|
|
|
|
|
|
|
|
26
|
3
|
|
|
|
5+23
|
|
11+17
|
|
|
|
|
|
|
|
|
|
28
|
2
|
|
|
|
|
7+23
|
11+19
|
13+17
|
|
|
|
|
|
|
|
|
30
|
3
|
|
9
|
3+29
|
|
|
|
13+19
|
|
|
|
|
|
|
|
|
32
|
2
|
|
10
|
3+31
|
5+29
|
|
11+23
|
|
17+17
|
|
|
|
|
|
|
|
34
|
4
|
|
|
|
5+31
|
7+29
|
|
13+23
|
17+19
|
|
|
|
|
|
|
|
36
|
4
|
|
|
|
|
7+31
|
|
|
|
19+19
|
|
|
|
|
|
|
38
|
2
|
|
11
|
3+37
|
|
|
11+29
|
|
17+23
|
|
|
|
|
|
|
|
40
|
3
|
|
|
|
5+37
|
|
11+31
|
13+29
|
|
19+23
|
|
|
|
|
|
|
42
|
4
|
|
12
|
3+41
|
|
7+37
|
|
13+31
|
|
|
|
|
|
|
|
|
44
|
3
|
|
13
|
3+43
|
5+41
|
|
|
|
17+29
|
|
23+23
|
|
|
|
|
|
46
|
4
|
|
|
|
5+43
|
7+41
|
11+37
|
|
17+31
|
19+29
|
|
|
|
|
|
|
48
|
5
|
|
14
|
3+47
|
|
7+43
|
|
13+37
|
|
19+31
|
|
|
|
|
|
|
50
|
4
|
|
|
|
5+47
|
|
11+41
|
|
|
|
23+29
|
|
|
|
|
|
52
|
3
|
|
|
|
|
7+47
|
11+43
|
13+41
|
17+37
|
|
23+31
|
|
|
|
|
|
54
|
5
|
|
15
|
3+53
|
|
|
|
13+43
|
|
19+37
|
|
|
|
|
|
|
56
|
3
|
|
|
|
5+53
|
|
11+47
|
|
17+41
|
|
|
29+29
|
|
|
|
|
58
|
4
|
|
|
|
|
7+53
|
|
13+47
|
17+43
|
19+41
|
23+37
|
29+31
|
|
|
|
|
60
|
6
|
|
16
|
3+59
|
|
|
|
|
|
19+43
|
|
|
31+31
|
|
|
|
62
|
3
|
|
17
|
3+61
|
5+59
|
|
11+53
|
|
17+47
|
|
23+41
|
|
|
|
|
|
64
|
5
|
|
|
|
5+61
|
7+59
|
|
13+53
|
|
19+47
|
23+43
|
29+37
|
|
|
|
|
66
|
6
|
|
|
|
|
7+61
|
|
|
|
|
|
|
31+37
|
|
|
|
68
|
2
|
|
18
|
3+67
|
|
|
11+59
|
|
17+53
|
|
23+47
|
29+41
|
|
|
|
|
70
|
5
|
|
|
|
5+67
|
|
11+61
|
13+59
|
|
19+53
|
|
29+43
|
31+41
|
|
|
|
72
|
6
|
|
19
|
3+71
|
|
7+67
|
|
13+61
|
|
|
|
|
31+43
|
37+37
|
|
|
74
|
5
|
|
20
|
3+73
|
5+71
|
|
|
|
17+59
|
|
23+53
|
29+47
|
|
|
|
|
76
|
5
|
|
|
|
5+73
|
7+71
|
11+67
|
|
17+61
|
19+59
|
|
|
31+47
|
37+41
|
|
|
78
|
7
|
|
|
|
|
7+73
|
|
13+67
|
|
19+61
|
|
|
|
37+43
|
|
|
80
|
4
|
|
21
|
3+79
|
|
|
11+71
|
|
|
|
23+59
|
29+53
|
|
|
41+41
|
|
82
|
5
|
|
|
|
5+79
|
|
11+73
|
13+71
|
17+67
|
|
23+61
|
|
31+53
|
37+47
|
41+43
|
|
84
|
8
|
|
22
|
3+83
|
|
7+79
|
|
13+73
|
|
19+67
|
|
|
|
|
|
43+43
|
86
|
5
|
|
|
|
5+83
|
|
|
|
17+71
|
|
|
29+59
|
|
|
41+47
|
|
88
|
|
|
|
|
|
7+83
|
11+79
|
|
17+73
|
19+71
|
23+67
|
29+61
|
31+59
|
37+53
|
|
43+47
|
90
|
|
|
23
|
3+89
|
|
|
|
13+79
|
|
19+73
|
|
|
31+61
|
|
|
|
92
|
|
|
|
|
5+89
|
|
11+83
|
|
|
|
23+71
|
|
|
|
41+53
|
|
94
|
|
|
|
|
|
7+89
|
|
13+83
|
17+79
|
|
23+73
|
29+67
|
|
37+59
|
|
43+53
|
96
|
|
|
|
|
|
|
|
|
|
19+79
|
|
|
31+67
|
37+61
|
|
|
98
|
|
|
24
|
3+97
|
|
|
11+89
|
|
17+83
|
|
|
29+71
|
|
|
41+59
|
|
100
|
|
|
|
|
∑#PP is the actual number of Prime Pairs (PP) diagonally, from top left to bottom right, that can form a given Even Number (EN), after 2, starts with 1 and increases by 1, in strict numerical sequence as: 1-2-3-4-5-6...
|
|
|
|
|
|
|
∑#PP is the actual number of Prime Pairs (PP) horizontally, from left to right, that can form a given Even Number (EN), after 2, and in doing so generates some visual symmetries (bold) in the distribution pattern.
|
|
|
|
Note: Every PP set is a unique set, appearing once and only once in the PTOP. The 1st # of any PP set is always ≤ 2nd #.
|
|
This paper and all its contents © 2009-10, Reginald Brooks. All rights reserved. Permission is hereby granted for single copies to be made for personal, non-commercial use for students and teachers of schools, colleges and universities provided that: either the entire paper, including figures and tables, is kept intact; or, any extracts of the text, or figures or tables (in part or whole), be properly and visibly cited as to authorship and source.
|
Remembering that:
- all primes above 2 are odd;
- that the double of every prime gives an even number not divisible by 4 [the numbers from the excluded evens of the 1st Diagonal on Brooks (Base) Square];
- all even numbers are the product of two primes (Euler’s Goldbach Conjecture);
- those even #s that are the result of doubling a prime are always separated by a difference of a multiple of 4 from previous even #s so formed;
- the even numbers in between being those that are divisible by 4 [the numbers from the included evens of the 1st Diagonal on Brooks (Base) Square] and even numbers not divisible by 4 [the numbers from the excluded evens of the 1st Diagonal on Brooks (Base) Square];
let’s proceed to an example of a series of primes providing both a visual and mathematical solution to the solution of the conjecture.
- take prime numbers: 1601-1607-1609-1613-1621-1627-1637-1657-1663-1667-1669-1697-1699-1709;
- their gaps run: 6-2-4-6-2-6-10-20-6-4-2-24-4-2-10, respectively;
- we know that their doubles=even #s that are NOT divisible by 4 (excluded evens): 3202-3214-3218-3226-3238-3242-3254-3274-3314-3326-3334-3338-3386-3394-3398-3418;
- in between these double prime even #s are 92 other even #s (included and excluded);
- on the PTOP, the # of diagonals of PP sets increase by 1, starting with 3+3;
- prime # 1601 is ∑#PP = 251, i.e. there are 251 PP sets forming the 1601 diagonal;
- as each diagonal member occupies one prime column across, there are also 251 unique,
possible PP sets going across the PTOP whose 2nd PP set # is 1601;
- the last PP set, consisting of 1601 + 1601 equals 3202;
- the other 250 PP sets occupy 1PP set/even # less than 3202;
- the ∑#PP starts at column 3 PP set: 3 + 1601 = 1604;
- therefore, the ∑#PP 251 runs from 3=1601=1604 to 1601+1601=3202;
- between 1604 and 3202 there are 1598 total numbers, divided by 2 = 799 even #s;
- add 1 to include the 1st even, 799 + 1 = 800 even #s;
- ∑#PP occupies 251 of 800, or 251/800, possible PP sets that sum up to those even #s;
- now, do the same distribution analysis for each subsequent prime: 1607-1609-1613-...;
- 1607+1607=3214 and 3214-(3+1607)=1604 and 1604/2=802 and 802+1=803 for 252/803;
- 1609+1609=3218 and 3218-(3+1609)=1606 and 1606/2=803 and 803=1=804 for 253/804;
- 1613+1613=3226 and 3226-(3+1613)=1610 and 1610/2=805 and 805+1=806 for 254/806;
- simplifying the calculation;
- (1619x2)-(3+1619)=1616 and (1616/2)+1=809 or (1619-1)/2=809 to give 255/809;
- (1621-1)/2=810 for 256/810;
- (1627-1)/2=813 for 257/813;
- (1637-1)/2=818 for 258/818;
- (1657-1)/2=828 for 259/828;
- (1663-1)/2=831 for 260/831
- (1667-1)/2=833 for 261/833;
- (1669-1)/2=834 for 262/834;
- (1693-1)/2=846 for 263/846;
- (1697-1)/2=848 for 264/848;
- (1699-1)/2=849 for 265/849;
- (1709-1)/2=854 for 266/854;
- knowing that every PP set is unique and appears only one time on the PTOP, and;
- knowing that every PP set has the 1st # ≤ to the 2nd # of the set, then;
- it would appear that the combined # of unique PP sets, as members of the ∑#PP, overlaps every possible even # to such an extent that it is statistically improbable ... impossible ... for any even #, greater than or equal to 4, NOT to be composed of at least one PP set;
- the ratio of 251/800 tells us that of the 800 possible even #s between 1604-3202, 251 PP sets, each of who's sums equal one of the the 800 even #s, 31+% are immediately covered by the 1601 diagonal of PP sets ... and, of course, the 1st (1604) and last (3202) are known to be covered;
- when we move down to the next number, 1607, and apply the same distribution analysis, the 252/803 ratio shows a similar 31+% coverage for even #s 1607-3214;
- we see that most of the 803 even #s overlap and include the same even #s from the first analysis (1601);
- and so on, down the line;
- in fact, the amount of overlap of the PP sets covering the even #s is so vast that it is statistically improbably ... impossible ... for all the even #s NOT to be covered;
- not to forget, there are a number of PP diagonal sets both before prime 1601 and after 1709 that also overlap the even # sequences we have been looking at here but have not be included in the distribution analysis ... further strengthening the case presented;
- in order to find a hole/holes in the PP set coverage of the even #s, the gap between subsequent prime numbers would have to be so large, AND, such gaps would have to occur in succession over multiple neighboring primes to break through the extensive overlapping of PP sets that ensures that Euler’s “strong” form of the Goldbach Conjecture is satisfied;
- as of early 2010, no such violation in over 4x1014 tested numbers have been found, the largest confirmed gap between primes is 1476 ... and is rare ... and Bertrand’s Postulate, proved in 1850 by Chebyshev, that between every number (>3) and its double-2, there exists a prime, highly suggests ... along with Periodic Table of Primes (PTOP) ... that the solution to the conjecture is no longer an open question.
|
gap
|
Prime #
|
Prime #+3
|
∑#PP
possible
even
#s
|
Prime X2
|
|
0
|
1601
|
1604
|
251/800
|
3202
|
|
6
|
1607
|
1610
|
252/803
|
3214
|
|
2
|
1609
|
1612
|
253/804
|
3218
|
|
4
|
1613
|
1616
|
254/806/
|
3226
|
|
6
|
1619
|
1621
|
255/809
|
3238
|
|
2
|
1621
|
1624
|
256/810
|
3242
|
|
6
|
1627
|
1630
|
257/813
|
3254
|
|
10
|
1637
|
1640
|
258/818
|
3274
|
|
20
|
1657
|
1660
|
259/828
|
3314
|
|
6
|
1663
|
1660
|
260/831
|
3226
|
|
4
|
1667
|
1666
|
261/833
|
3334
|
|
2
|
1669
|
1670
|
262/834
|
3338
|
|
24
|
1693
|
1672
|
263/846
|
3386
|
|
4
|
1697
|
1696
|
264/848
|
3394
|
|
2
|
1699
|
1700
|
265/849
|
3398
|
|
10
|
1709
|
1702
|
266/854
|
3418
|
|
[ TOP ]

|
| ~click to enlarge image
|
| 170 |
BS Rule 170: The Periodic Table of Primes (PTOP) is present ... albeit hidden ... within
the Brooks (Base) Square. Each prime pair (PP) set forms an even
number. All even numbers are formed from one or more PP sets. The
overlap of the two right-angled diagonals (one diagonal is yellow, the
other is blue-green) forms a right-angled isosceles triangle with a series of
apexes culminating finally onto the the even numbers of the upper 1st
Diagonal. The apexes formed along the way are the products of that
triangle ... i.e. they reside on the upper axis as the base vertices of that
triangle. Multiplied together, their product at the apex of the triangle is
revealed. However, adding them together, instead, reveals their even sum
at the final apex along the upper even 1st Diagonal. Thus they are hidden.
The double of any horizontal axis number is also directly below on the 1st
Diagonal.
Example:
11 & 13
11+13=24
11x13=143, going
down the column
119=7x17 and
7+17=24, next PP set
down the same column is
95=5x19 and
5+19=24.
24 has 3 PP sets and each is
shown as the diagonals cross:
11+13, 7+17, and 5+19.
|
|
|
[ TOP ]
A natural finding resulting from the discovery that the PTOP was already embedded within Brooks (Base) Square were the Right-Angle Isosceles Triangle Multiplication Rules (Rules 171-175). Remember that the only difference between the Base Square (BS 1.00) and the Brooks (Base) Square (BS1.01+) is the even-numbered upper 1st Diagonal of the latter.
|
| ~click to enlarge image
|
| 171 |
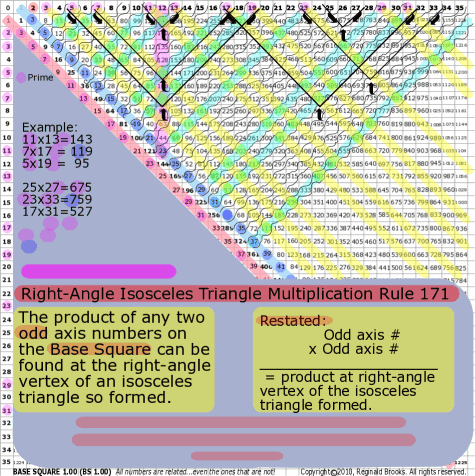
BS Rule 171: The product of any two odd axis numbers on
the Base Square can be found at the right-angle vertex of an isosceles triangle so
formed.
Restated:
Odd axis # x Odd axis # = product at right-angle vertex of the isosceles triangle formed.
|
|
|
[ TOP ]
|
| ~click to enlarge image
|
| 172 |
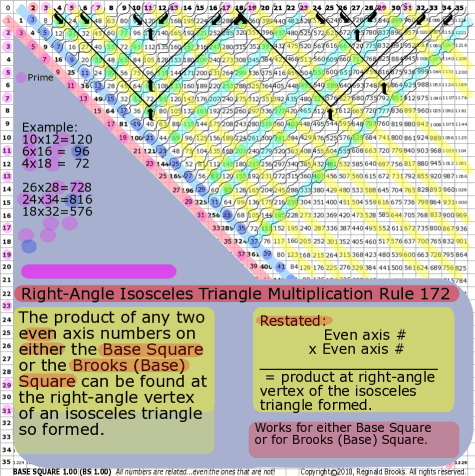
BS Rule 172: The product of any two even axis numbers on either
the Base Square or the Brooks (Base) Square can be found at the right-angle vertex of an isosceles triangle so
formed.
Restated:
Even axis # x Even axis # = product at right-angle vertex of the isosceles triangle formed.
|
|
|
[ TOP ]
|
| ~click to enlarge image
|
| 173 |
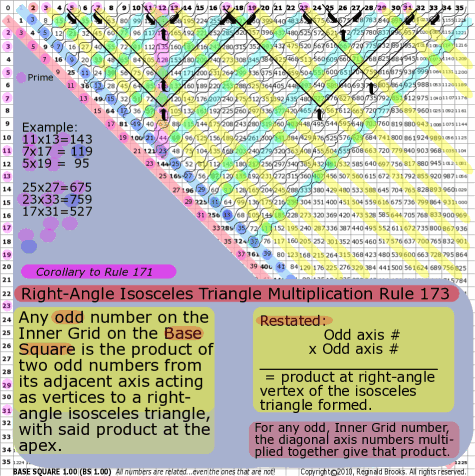
BS Rule 173: Corollary to Rule 171: Any odd number on the Inner Grid on
the Base Square is the product of two odd numbers from its adjacent axis acting as vertices to a right-angle isosceles triangle, with said product at the apex.
Restated:
For any odd, Inner Grid number, the diagonal axis numbers multiplied together give that product.
|
|
|
[ TOP ]
|
| ~click to enlarge image
|
| 174 |
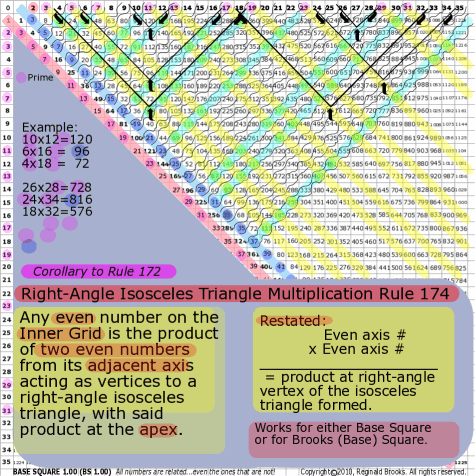
BS Rule 174:Corollary to Rule 172: Any even number on the Inner Grid on either
the Base Square or the Brooks (Base) Square is the product of two even numbers from its adjacent axis acting as vertices to a right-angle isosceles triangle, with said product at the apex.
Restated:
For any even, Inner Grid number, the diagonal axis numbers multiplied together give that product.
|
|
|
[ TOP ]

|
| ~click to enlarge image
|
| 175 |
BS Rule 175: Every number in the Inner Grid on
the Base Square is the difference, ∆, between two PD numbers and can be found as the right-angle vertex of an isosceles triangle whose base vertices are those two PD numbers.
Restated-1:
For any Inner Grid # the PD row # - PD column # = Inner Grid #.
Restated-2:
From any two PD #s, form a right-angle isosceles triangle on the Inner Grid and the difference, ∆, is at the apex.
|
|
|
With this we have now come full circle ...
though, without a doubt, we will find many, many more complete circuits of interconnectedness. Here
we see how the primes, normally hidden from the Strict Inner Grid ... and by definition singularly
devoid of pattern ... become embedded in the very fabric of the square by their combinations with
other numbers (TCAOP) or by being part of the simple Prime Pair (PP) sets that we have now found to
not only form the core of the Periodic Table of Primes (PTOP), but to actually have a one to one
presence from the PTOP to the SIG within Brooks (Base) Square. This remarkable
interconnectedness came about this time, not from looking for a connection ... no, quite the
opposite ... in this case it came from looking quite independently at the Goldbach Conjecture and
wondering how the primes as pair sets and the even numbers might be somehow patterned together.
Finding that the double of every prime summed up to an even number ... but not just any even number,
but only an even number that was NOT divisible by 4 and thus a member of the "excluded" evens
(6-10-14-18-22-26-...) ... that first the PTOP was formed and then it was found to fit embedded and
"hidden" within the square itself. Every PP set of the PTOP has it corresponding PP set embedded in
an orderly array within the grid. Truly remarkable. Nature is spelled number.
Rules 171-175 have truly brought us back...full circle... to the original quest: How might the axes and Prime Diagonal (PD) of the ISL be related to the Inner Grid numbers? As we can see ... intimately ...in a full spectrum of interconnectedness from the simple to the sublime. To leave you with an example of the former, indeed, every number on the Inner Grid is both a product of the axis numbers and the difference of the PD numbers!
[ TOP ]
NEXT: On to
Conclusion
Back to II. TCAOP>IIC.
TCAOP=BS-network>2. Prime Locator - diagonal addition
Page 2a-
PIN: Pattern in Number...from primes to DNA.
Page 2b-
PIN: Butterfly Primes...let the beauty seep in..
Page 2c-
PIN: Butterfly Prime Directive...metamorphosis.
Page 2d-
PIN: Butterfly Prime Determinant Number Array (DNA) ~conspicuous abstinence~.
Page 3-
GoDNA: the Geometry of DNA (axial view) revealed.
Page 4-
SCoDNA: the Structure and Chemistry of DNA (axial view).
Page 5a-
Dark-Dark-Light: Dark Matter = Dark
Energy
Page 5b-
The History of the Universe in Scalar
Graphics
Page 5c-
The History of the Universe_update: The Big
Void
Page
6a- Geometry-
Layout
Page
6b- Geometry- Space Or Time Area
(SOTA)
Page 6c- Geometry-
Space-Time Interactional
Dimensions(STID)
Page
6d- Distillation of SI units into ST
dimensions
Page
6e- Distillation of SI quantities into ST
dimensions
Page
7- The LUFE Matrix Supplement: Examples and Proofs: Introduction-Layout &
Rules
Page 7c-
The LUFE Matrix Supplement:
References
Page
8a- The LUFE Matrix: Infinite
Dimensions
Page 9-
The LUFE
Matrix:E=mc2
Page 10-
Quantum Gravity ...by the
book
Page
11- Conservation of
SpaceTime
Page
12- LUFE: The Layman's Unified Field Expose`
Page
13- GoMAS: The Geometry of Music, Art and Structure ...linking science, art and esthetics. Part I
Page
14- GoMAS: The Geometry of Music, Art and Structure ...linking science, art and esthetics. Part II
Page
15- Brooks (Base) Square (BS): The Architecture of Space-Time (TAOST) and The Conspicuous Absence of Primes (TCAOP) - a brief introduction to the series
Page
16- Brooks (Base) Square interactive (BBSi) matrix: Part I "BASICS"- a step by step, multi-media interactive
Page
17- The Architecture Of SpaceTime (TAOST) as defined by the Brooks (Base) Square matrix and the Inverse Square Law (ISL).
Copyright©2009-12 Reginald Brooks, BROOKS DESIGN. All Rights
Reserved.
(function() {
var toJsLink = function(link) {
// Check the escape conditions
if (link.href === undefined) { return; }
if (link.onclick) { return; }
if (link.className.indexOf('bkry-link-ignore') !== -1) { return; }
var handler = function(evt) {
// Look out for escape conditions
if (link.href.indexOf('#')) {
var targetUrl = link.href.split('#')[0];
var currentUrl = window.location.href.split('#')[0];
if (targetUrl === currentUrl) {
return;
}
}
// Salt in the query string argument to make sure it always gets passed around
var url = link.href;
var hash = url.split('#')[1];
url = url.split('#')[0];
var qs = url.split('?')[1];
url = url.split('?')[0];
evt.preventDefault();
window.location = url + '?' + (qs || '') + (qs ? '&' : '') + 'bkry-rewrite-links=true' + (hash ? '#' + hash : '')
return false;
};
// Bind the event handler down
if(link.addEventListener) {
link.addEventListener('click', handler, false)
} else if(link.attachEvent) { // old ie support
link.attachEvent('onclick', handler)
}
};
if (window.location.search.indexOf('bkry-rewrite-links=true') !== -1) {
// Look for new nodes
window.addEventListener('DOMNodeInserted', function(e) {
if (e.target.tagName = 'A') { toJsLink(e.target); }
}, false);
// Look for existing nodes
var links = document.getElementsByTagName('a');
for (var i = 0; i < links.length; i++) {
toJsLink(links[i]);
}
}
})();














