Brooks (Base) Square (BS) 101
~ The Architecture of Space-Time (TAOST)
&
The Conspicuous Absence of Primes (TCAOP) ~
I. TAOST / C. Geometrics – relationships / 1. Pythagorean
Table of Contents
I. TAOST - the network
A. Geometrics – lines
B. Geometrics - shapes
C. Geometrics - relationships
1. Pythagorean <---
2. Parallelogram
3. Penta
II. TCAOP - everything minus the network
I C. Geometrics - Relationships_1. Pythagorean
As we head deeper into the matrix, examining numerical relationships that include both lines and shapes that often move beyond the simple considerations we have touched on so far ... looking for those larger patterns. Hang on, for some of these new patterns are simply mind blowing in the majesty and beauty of their presence. What started as a simple table of relationships between the axial numbers and their square number counterparts depicting the Inverse Square Law (ISL) soon became much, much more.
How is it so? What is the mystery here in this magical mystery tour?
How does the Pythagorean Theorem (a2+b2=c2) appear?
Part 1-Pythagorean ((a2+b2=c2)
It does so in the form of triples ... Pythagorean triples ... of whole integer numbers. From Wikipedia (http://en.wikipedia.org/wiki/Pythagorean_theorem) we see a list of “Primitive Pythagorean triples up to 100.”
3,4,5 16,63,65
5,12,13 20,21,29
7,24,25 28,45,53
8,15,17 33,56,65
9,40,41 36,77,85
11,60,61 39,80,89
12,35,37 48,55,73
13,84,85 65,72,97
(listed by http://creativecommons.org/licenses/by-sa/3.0/)
Yet it is multiples of the simplest ratio ... 3, 4, 5 ... that appear redundantly on the grid as an ever expanding pattern. Perhaps it is the very simplicity of the matrix that lends itself to the simplest of patterns.
It was the pattern itself that led down the path of parallelograms, in general, ultimately to that watershed of numerical relationships ... the penta- ... and the symmetry of numbers.
|
| ~click to enlarge image
|
| 81 |
BS Rule 81: The base Pythagorean triple (3, 4, 5 as 32+42=52) presents itself repeatedly on Brooks (Base) Square as multiples of 12, 16, 20 as collective “generations.” These generations are oriented along both diagonals (like parallelograms) and distinguish themselves from each other by the number of diagonal steps between the constituent elements.
|
|
|
|
| ~click to enlarge image
|
| 82 |
BS Rule 82: The 1st generation of Pythagorean parallelograms extend parallel to the Prime Diagonal (PD) and consist of only even multiples of 12, 16, 20 separated by one step. The 2nd generation by two steps, 3rd generation by four steps, the 4th generation by eight steps, and so on.
|
Note: The even multiples of 12, 16, 20 continue outward, away from the PD as 2x, 4x, 6x, 8x, 10x....
|
Generation
|
Steps
|
|
1
|
1
|
|
2
|
2
|
|
3
|
4
|
|
4
|
8
|
|
[ TOP ]
|
| ~click to enlarge image
|
| 83 |
BS Rule 83: The 1st generation of Pythagorean parallelograms that extend perpendicular to the Prime Diagonal (PD) and consist of all, even and odd, multiples of 12, 16, 20 separated by one step. The 2nd generation by two steps, 3rd generation by four steps, the 4th generation by eight steps, and so on.
|
Note: The sequential multiples of 12, 16, 20 continue downward from the PD as 4x, 5x, 6x, 7x, 8x, 9x, 10x, ....
|
Generation
|
Steps
|
|
1
|
1
|
|
2
|
2
|
|
3
|
4
|
|
4
|
8
|
|
|
| ~click to enlarge image
|
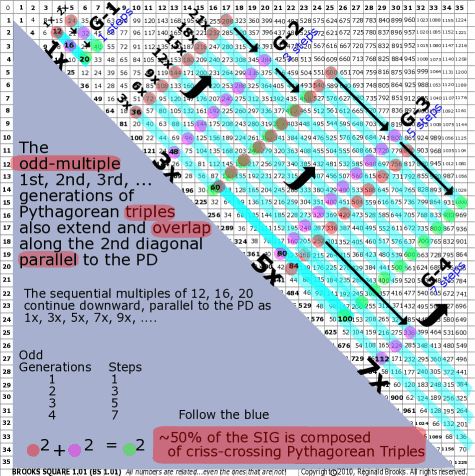
| 84 |
BS Rule 84: The odd-multiple 1st, 2nd, 3rd, ... generations of Pythagorean triples also extend and overlap along the 2nd diagonal parallel to the PD.
|
Note:
|
Generation
|
Steps
|
|
1
|
1
|
|
3
|
3
|
|
5
|
5
|
|
7
|
7
|
|
9
|
9
|
|
[ TOP ]
|
| ~click to enlarge image
|
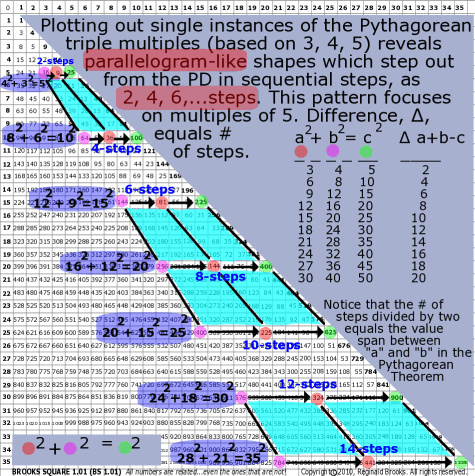
| 85 |
BS Rule 85: Plotting out single instances of the Pythagorean triple multiples (based on 3, 4, 5) reveals parallelogram-like shapes which step out from the PD in sequential steps, as 2, 4, 6,...steps.
|
Note: This pattern focuses on multiples of 5. Difference, ∆, steps.
|
a2
|
+
|
b2
|
=
|
c2
|
∆
a+b-c
|
|
3
|
|
4
|
|
5
|
2
|
|
6
|
|
8
|
|
10
|
4
|
|
9
|
|
12
|
|
15
|
6
|
|
12
|
|
16
|
|
20
|
8
|
|
15
|
|
20
|
|
25
|
10
|
|
18
|
|
24
|
|
30
|
12
|
|
21
|
|
28
|
|
35
|
14
|
|
24
|
|
32
|
|
40
|
16
|
|
27
|
|
36
|
|
45
|
18
|
|
30
|
|
40
|
|
50
|
20
|
|
[ TOP ]
|
| ~click to enlarge image
|
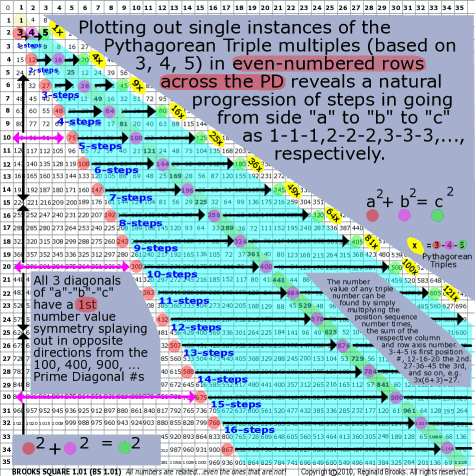
| 86 |
BS Rule 86: Plotting out single instances of the Pythagorean Triple multiples (based on 3, 4, 5) in even-numbered rows across the PD reveals a natural progression of steps in going from side "a" to "b" to "c" as 1-1-1,2-2-2,3-3-3,..., respectively.
|
Note: This pattern focuses on multiples of 2,3,4 and 5 in that each new Pythagorean Triple ... horizontally placed on a row, based on 3-4-5, that has side "a" in the lower SIG triangle, side "b" on the PD, and the hypotenuse, "c" in the upper SIG triangle... is located on the even numbered rows of the side axis. The first triple number ("a") is 3 and all subsequent "a's" are multiples of 3. The first "b" triple number is 4 and all subsequent "b's" on the PD are multiples of 4. The "c's" are all multiples of 5.
All 3 diagonals
of "a"-"b"-"c"
have a 1st
number value
symmetry splaying
out in opposite
directions from the
100, 400, 900, ...
Prime Diagonal #s.
The number
value of any triple
number can be
found by simply
multiplying the
position sequence
number times,
the sum of the
respective column
and row axis number.
3-4-5 is first position
#, 12-16-20 the 2nd,
27-36-45 the 3rd,
and so on, e.g.
3x(6+3)=27 and 3x(6+6)=36 and 3x(6+9)= 45 for the 3rd position Pythagorean Triple.
The triples follow a natural sequence of 1xP, 4xP, 9xP, 16xP, 25xP, 36xP,... where P= the original 3-4-5 Pythagorean Triple.
|
a2
|
+
|
b2
|
=
|
c2
|
Steps
|
|
3
|
|
4
|
|
5
|
1
|
|
12
|
|
16
|
|
20
|
2
|
|
27
|
|
36
|
|
45
|
3
|
|
48
|
|
64
|
|
80
|
4
|
|
75
|
|
100
|
|
125
|
5
|
|
108
|
|
144
|
|
180
|
6
|
|
147
|
|
196
|
|
245
|
7
|
|
192
|
|
256
|
|
320
|
8
|
|
243
|
|
324
|
|
405
|
9
|
|
300
|
|
400
|
|
500
|
10
|
|
[ TOP ]
While I told myself I was not going to look for ... and describe ... any other simple number patterns before stopping and writing up what has been found thus far, I must digress ... briefly. This pattern below is so blatantly obvious, yet I didn’t see it before. It, along with a few other others ought to be in your, dear reader, toolbox before we really get into the best part of this tour.
|
| ~click to enlarge image
|
| 87 |
BS Rule 87: Add the horizontal axis number to the vertical axis number to give the sum, ∑, at their intersecting grid point at the 1st Diagonal.
Note: The number next to it on the row at the 2nd diagonal is the sum of its horizontal and vertical axis number values x2.
The number next to it on the row at the 3rd diagonal is the sum of its horizontal and vertical axis number values x3.
The number next to it on the row at the 4th diagonal is the sum of its horizontal and vertical axis number values x4, and so on.
|
Note:
|
Sequence, adding every
|
∆∑
|
|
2nd #
|
x2
|
|
3rd #
|
x3
|
|
4th #
|
x4
|
|
5th #
|
x5
|
|
|
| ~click to enlarge image
|
| 88 |
BS Rule 88: The difference, ∆, in the sums, ∑, of the axial numbers in sequence ...1,2,3,...follows as the sequence spacing, 2=2,3=3, 4=4,...
|
Note:
|
Sequence, adding every
|
∆∑
|
|
2nd #
|
2
|
|
3rd #
|
3
|
|
4th #
|
4
|
|
5th #
|
5
|
|
[ TOP ]
|
| ~click to enlarge image
|
| 89 |
BS Rule 89: The difference, ∆, in the sums, ∑, of the PD numbers in sequence ...1,4,9,...follows as the double of the sequence spacing, 2=4,3=6, 4=8,...
|
Note:
|
Sequence, adding every
|
∆∑
|
|
|
2nd #
|
4
|
8,12,16,...
|
|
3rd #
|
6
|
15,21,27,...
|
|
4th #
|
8
|
24,32,40,...
|
|
5th #
|
10
|
35,45,55,...
|
|
|
| ~click to enlarge image
|
| 90 |
BS Rule 90: Within the Inner Grid, the difference, ∆, in the sums, ∑, of the sums of successive rows reduces ultimately to 4. With the addition of the number values in the PD, the difference, ∆, in the sums, ∑, of the sums of the successive rows reduces ultimately to 4.
|
Note: And includes every other odd # before reduction to 4.
|
∑
|
>
|
∆∑
|
>
|
∆
|
>
|
∆
|
|
3
|
|
10
21
36
55
78
105
|
|
11
15
19
23
27
|
|
4
4
4
4
|
|
13
|
|
34
|
|
70
|
|
125
|
|
203
|
|
308
|
|
∑
|
>
|
∆∑
|
>
|
∆
|
>
|
∆
|
|
7
|
|
15
28
45
66
|
|
13
17
21
|
|
4
4
|
|
22
|
|
50
|
|
95
|
|
161
|
|
[ TOP ]
|
| ~click to enlarge image
|
| 91 |
BS Rule 91: Within the Inner Grid, the difference, ∆, in the sums, ∑, of the running sums of successive number values in a given column reduces to 2.
|
Note: And includes every odd # before reduction to 2.
|
∑
|
>
|
∆∑
|
>
|
∆
|
>
|
∆
|
|
3
|
|
8
15
24
35
48
63
|
|
7
9
11
13
15
|
|
2
2
2
2
|
|
11
|
|
26
|
|
50
|
|
85
|
|
133
|
|
196
|
|
276
|
|
|
| ~click to enlarge image
|
| 92 |
BS Rule 92: Within the Inner Grid, the difference, ∆, in the sum, ∑, of the last row minus the sum of the number values in Column B = the difference, ∆, in the sum of Column C number values minus the sum from the row above.
|
Note: ∆(∑last row - ∑Col B) = ∆(∑Col C -∑row above)
|
[ TOP ]
|
| ~click to enlarge image
|
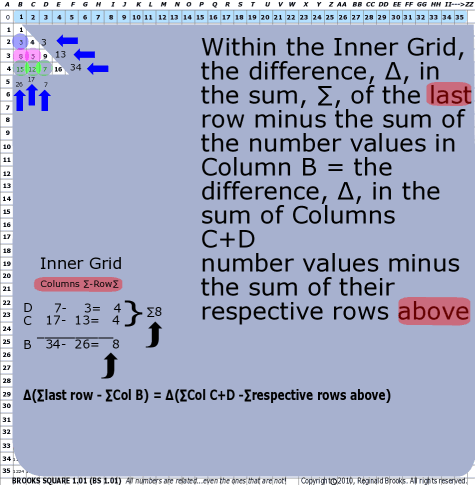
| 93 |
BS Rule 93: Within the Inner Grid, the difference, ∆, in the sum, ∑, of the last row minus the sum of the number values in Column B = the difference, ∆, in the sum of Columns C+D number values minus the sum from their respective rows above.
|
Note: ∆(∑last row - ∑Col B) = ∆(∑Col C+D -∑respective rows above)
|
|
| ~click to enlarge image
|
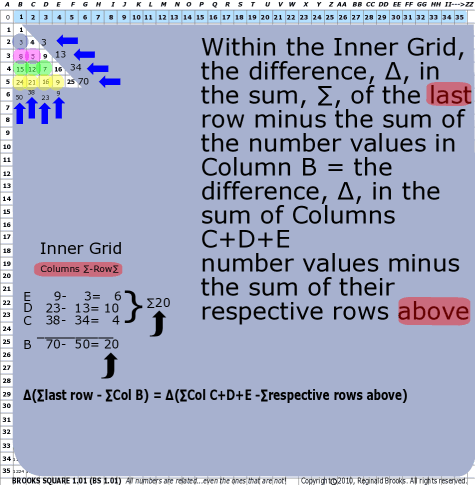
| 94 |
BS Rule 94:Within the Inner Grid, the difference, ∆, in the sum, ∑, of the last row minus the sum of the number values in Column B = the difference, ∆, in the sum of Columns C+D+E number values minus the sum of their respective rows above.
|
Note: ∆(∑last row - ∑Col B) = ∆(∑Col C+D+E -∑respective rows above)
|
[ TOP ]
|
| ~click to enlarge image
|
| 95 |
BS Rule 95: Within the Inner Grid, the difference, ∆, in the sum, ∑, of the last row minus the sum of the number values in Column B = the difference, ∆, in the sum of Columns C+D+E+F number values minus the sum of their respective rows above.
|
Note: ∆(∑last row - ∑Col B) = ∆(∑Col C+D+E+F-∑respective rows above)
|
[ TOP ]
|
| ~click to enlarge image
|
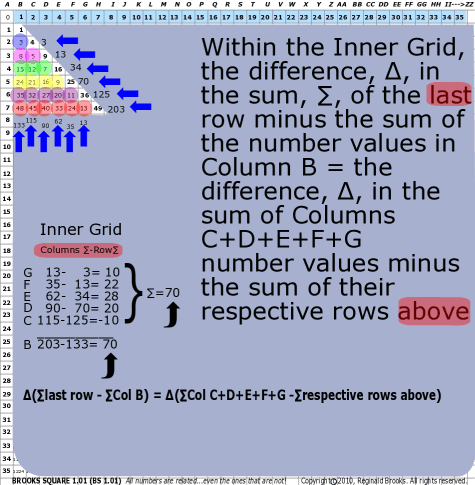
| 96 |
BS Rule 96: Within the Inner Grid, the difference, ∆, in the sum, ∑, of the last row minus the sum of the number values in Column B = the difference, ∆, in the sum of Columns C+D+E+F+G number values minus the sum of their respective rows above.
|
Note: ∆(∑last row - ∑Col B) = ∆(∑Col C+D+E+F+G -∑respective rows above)
|
|
| ~click to enlarge image
|
| 97 |
BS Rule 97: Within the Inner, the difference, ∆, in the sum, ∑, of the last row minus the sum of the number values in Column B = the difference, ∆, in the sum of Column C+D+E+F+G+H number values minus the sum of their respective rows above.
|
Note: ∆(∑last row - ∑Col B) = ∆(∑Col C+D+E+F+G+H -∑respective rows above)
|
[ TOP ]
|
| ~click to enlarge image
|
| 98 |
BS Rule 98: Within the Inner Grid, the difference, ∆, in the sum, ∑, of the last row minus the sum of the number values in Column B = the difference, ∆, in the sum of Columns C+D+E+F+G+H+I number values minus the sum of their respective rows above.
|
Note: ∆(∑last row - ∑Col B) = ∆(∑Col C+D+E+F+G+H+I -∑respective rowsabove)
|
|
| ~click to enlarge image
|
| 99 |
BS Rule 99: On the Strict Inner Grid (SIG), the number,#, of diagonal steps to reach the numerical value that is the sum, ∑, of the two even-numbered grid values further down that even diagonal continues in an orderly and predictable pattern.
|
Note: Likewise, the # of steps down the diagonal to the first addition number grid value (starting with 2, it always being counted as two steps; starting with 4, it always being counted as 3 steps; starting with 6, it always being counted as 4 steps, and so on for each successive even diagonal) = the number of steps from the last addition number to the sum number of the two number values. Example: On the 2 diagonal: 28+32=60 and 60 is 7 steps down the diagonal from 32. It is also 7 steps from 2 ... the axial number topping the 8, 12, 16... diagonal, and remember it has a built-in count of 2, so 2 + 5=7 steps. If you go to the next even diagonal starting at axial number 4, its built-in step count is 3. Axial 6 has a built-in step count of 4, and so on. As the axial number grows by 2, the built-in step count grows by 1.
|
Generation
|
Even
Axis
#
Diagonal
|
Diagonal
#s
added
|
∑
|
#
Steps
from last #
to
∑
|
# of
Steps
from
axis #
to
first #
|
|
1st
|
2
|
8+12
|
20
|
2
|
2
|
|
2
|
12+16
|
28
|
3
|
3
|
|
2
|
16+20
|
36
|
4
|
4
|
|
2
|
16+24
|
40
|
4
|
4
|
|
2
|
20+24
|
44
|
5
|
5
|
|
2
|
20+32
|
52
|
5
|
5
|
|
2
|
16+40
|
56
|
4
|
4
|
|
2
|
24+32
|
56
|
6
|
6
|
|
2nd
|
4
|
24+32
|
56
|
3
|
3
|
|
4
|
32+40
|
72
|
4
|
4
|
|
4
|
80+96
|
176
|
10
|
10
|
|
3rd
|
6
|
48+60
|
108
|
4
|
4
|
|
6
|
48+72
|
120
|
4
|
4
|
|
6
|
48+96
|
144
|
4
|
4
|
|
4th
|
8
|
80+96
|
176
|
5
|
5
|
|
8
|
80+176
|
256
|
5
|
5
|
|
5th
|
10
|
120+140
|
260
|
6
|
6
|
|
6th
|
12
|
168+192
|
360
|
7
|
7
|
|
[ TOP ]
NEXT: On to
I. TAOST>IC. Geometrics-relationships>IC2. Parallelograms - Brooks (Base) Square
Back to I. TAOST>IC. Geometrics-relationships- Brooks (Base) Square
Page 2a-
PIN: Pattern in Number...from primes to DNA.
Page 2b-
PIN: Butterfly Primes...let the beauty seep in..
Page 2c-
PIN: Butterfly Prime Directive...metamorphosis.
Page 2d-
PIN: Butterfly Prime Determinant Number Array (DNA) ~conspicuous abstinence~.
Page 3-
GoDNA: the Geometry of DNA (axial view) revealed.
Page 4-
SCoDNA: the Structure and Chemistry of DNA (axial view).
Page 5a-
Dark-Dark-Light: Dark Matter = Dark
Energy
Page 5b-
The History of the Universe in Scalar
Graphics
Page 5c-
The History of the Universe_update: The Big
Void
Page
6a- Geometry-
Layout
Page
6b- Geometry- Space Or Time Area
(SOTA)
Page 6c- Geometry-
Space-Time Interactional
Dimensions(STID)
Page
6d- Distillation of SI units into ST
dimensions
Page
6e- Distillation of SI quantities into ST
dimensions
Page
7- The LUFE Matrix Supplement: Examples and Proofs: Introduction-Layout &
Rules
Page 7c-
The LUFE Matrix Supplement:
References
Page
8a- The LUFE Matrix: Infinite
Dimensions
Page 9-
The LUFE
Matrix:E=mc2
Page 10-
Quantum Gravity ...by the
book
Page
11- Conservation of
SpaceTime
Page
12- LUFE: The Layman's Unified Field Expose`
Page
13- GoMAS: The Geometry of Music, Art and Structure ...linking science, art and esthetics. Part I
Page
14- GoMAS: The Geometry of Music, Art and Structure ...linking science, art and esthetics. Part II
Page
15- Brooks (Base) Square (BS): The Architecture of Space-Time (TAOST) and The Conspicuous Absence of Primes (TCAOP) - a brief introduction to the series
Page
16- Brooks (Base) Square interactive (BBSi) matrix: Part I "BASICS"- a step by step, multi-media interactive
Page
17- The Architecture Of SpaceTime (TAOST) as defined by the Brooks (Base) Square matrix and the Inverse Square Law (ISL).
Copyright©2009-12 Reginald Brooks, BROOKS DESIGN. All Rights
Reserved.
(function() {
var toJsLink = function(link) {
// Check the escape conditions
if (link.href === undefined) { return; }
if (link.onclick) { return; }
if (link.className.indexOf('bkry-link-ignore') !== -1) { return; }
var handler = function(evt) {
// Look out for escape conditions
if (link.href.indexOf('#')) {
var targetUrl = link.href.split('#')[0];
var currentUrl = window.location.href.split('#')[0];
if (targetUrl === currentUrl) {
return;
}
}
// Salt in the query string argument to make sure it always gets passed around
var url = link.href;
var hash = url.split('#')[1];
url = url.split('#')[0];
var qs = url.split('?')[1];
url = url.split('?')[0];
evt.preventDefault();
window.location = url + '?' + (qs || '') + (qs ? '&' : '') + 'bkry-rewrite-links=true' + (hash ? '#' + hash : '')
return false;
};
// Bind the event handler down
if(link.addEventListener) {
link.addEventListener('click', handler, false)
} else if(link.attachEvent) { // old ie support
link.attachEvent('onclick', handler)
}
};
if (window.location.search.indexOf('bkry-rewrite-links=true') !== -1) {
// Look for new nodes
window.addEventListener('DOMNodeInserted', function(e) {
if (e.target.tagName = 'A') { toJsLink(e.target); }
}, false);
// Look for existing nodes
var links = document.getElementsByTagName('a');
for (var i = 0; i < links.length; i++) {
toJsLink(links[i]);
}
}
})();