(Part II) this page

Oceans of Numbers Part I

(Intro: Butterfly Fractal)

Part II of an overview of the relationship between the Mersenne Prime Squares and the Mersenne Primes -- Perfect Numbers -- Butterfly Fractal 1 -- and the Exponential Power of 2.

An artist, mathematician, and choreographer are sitting up at the bar squabbling with the bartender about numbers — you know, those simple whole numbers 1,2,3,… Just how does one show that these simple symbols of quantities have so much mystery combined with such sublime beauty that it defies one’s imagination? How can there be so many, many interconnections? How does the world we see come from this?

The artist wants to see the visuals: the geometry. “Show me the geometry and I will know everything,” he/she says!

The mathematician, besides seeing all the arithmetic adding up correctly, really wants to see the equations. “A good equation is worth all the images in the world when it comes to succinctly stating what those connections between quantities — and the symbols that represent them — really are all about!”

The choreographer, without hesitation, says: “Show me the dance! Without dance, it is all meaningless! Show me the dance!”

Arched eyebrows and a little smirk on his face, the bartender exclaims: “Hold on ladies and gents! I think we might have some answers!” As three ones entered the bar.

~~~

Three identical “1”s sit on two bar stools. You see, “1” is simple quantity “one,” and if you double it you get quantity “two” — which, of course, is really just two “1”s. At least, that’s what one said!

“So do you guys and gals need a diagram?” quipped the bartender.

“Wouldn’t hurt,” said the visualizing artist-geometer. “Let’s see:”

“It’s simply a matter of multiplying 1x2,” exclaimed the mathematician.

1•2 = 2

“and, of course, you must add in original “1” to get a total of three.” he added.

“You know, when you line them up like a chorus line it really does emphasize that there are three individual ones!” marveled the choreographer.

1—1—1

“Simple!”

“Well then, let’s move on. What happens to the whole picture when quantity “2” is doubled?” the bartender asks.

“If we let every instance of quantity “1” be represented by a 1x1 square, we simply double the number of quantity “2” squares!” barks the visualizer.

“Two times two plus three equals seven!” says the mathematician.

2•2+3=7

“Musically, one becomes two, two becomes four, and if you line them up in a staggered chorus line you have a dance!” sang out the choreographer.

I

I I

I I I I

“Not only that, but a symmetry line down the middle divides all the EVENS into two identical sides, each now repeats the I to I I pattern starting on the second Row. It’s the beginning of the fractal pattern!”

“When the staggered line collapses back to one single chorus line, we see 7 individuals!”

“Wait a second, please,” cried out the mathematician. We have the beginnings of kind of matrix here:

2

7—1— — 3

4

“We started with “1” on the Horizontal Row, doubled that to “2” on the upper Vertical Column. The sum of 1+2=3 and “3” is on the right side of the Horizontal Row. This is followed by the doubling of “2” to give “4” that is placed on the lower Vertical Column of EVENS. The running sum of 3+4=7 and “7” is placed on the outer left side of the Horizontal Row of ODDS!

The bartender popped in with one raised eyebrow, “ Is that right? News to me! Seems a bit complicated.”

“No, not at all!” exclaimed the mathematician. While the geometer will surely show it is best visualized in a grid, it is more expedient to condense the Areas of the square grid cells down to just their symbolic numbers. The connections are more apparent!”

“Well, maybe to you and your mindset! rebuffed the artist, “but for me, seeing the Areas actually form and add up, just makes sense. Any child can see that!”

“Again!” inserted the choreographer, “If it doesn’t dance, it doesn’t really exist! I recently saw a dancer wearing a shirt that said: “So if I think, then I can dance!” Love it!”

“What do you say we see how this all plays out by doing another doubling, this time double the “4” says the bartender.

“Visuals make it direct and simple!” claims the artist. “We now add 8 additional squares.”

To which the mathematician can hardly contain her/his-self, “8+7=15, the new running sum!”

8

2

7— 1— — 3—15

4

“Quite naturally, the chorus line is starting to get rather long. Soon we will not be able to fit everyone on stage, but you get the idea. Staggering each doubling helps. It also really does point out the evolving fractal nature of the doubling of quantities starting with quantity “1.” Again, draw a central bilateral symmetry line down the middle and each side now has I, I I, I I I I. Not only that, but the pattern repeats again starting with each I, I I in the third to fourth Rows! We have the beginnings of “The Butterfly Fractal 1.”

I

I I

I I I I

I I I I I I I I

“So what do you think barkeep?” chimed in all three.

“I think we need another round, of course. Right now it’s Even Steven. Let’s get doubling! We’ve done three doublings, how about another three?”

To which the geometer adds:

Followed by the mathematician:

32

8

2

127—31—7— 1— — — 3—15—63

4

16

64

And wonderfully completed by our dance choreographer

I

I I

I I I I

I I I I I I I I

I I I I I I I I I I I I I I I I

I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I

I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I

“As the bilateral symmetry line divides the “Butterfly Fractal” into two equal sides, one finds that for each “1” located on the EVEN Rows, there is a corresponding “Butterfly Fractal” that mirrors the whole and the running sum of fractals grows as 1, 3, 7, 15, 31, and 63 thus far!” shouts out the choreographer. “Our dance would show each half of the “Butterfly Fractal” as its own staggered chorus line that kicks and bows first together, then alternately, followed by each inner fractal on a given side taking a brief separate turn before sparkling back into the whole. Amazing!”

“Guess what?” declared the visual artist-geometer, “One can show all that and a whole lot more on a simple grid of square Areas — especially on the BIM grid of the Inverse Square Law. (We will come to that shortly. Last year, July, 2021, we showed in the “The MPS Project (Mersenne Prime Squares Project)” installation in Building 5, that all these exponential power of 2 numbers and their running sums translate directly into Areas all within the Mersenne Prime Square (MPS). Since then a whole treasure trove of connections have been found and are exquisitely visualized on the *BIM.)

~

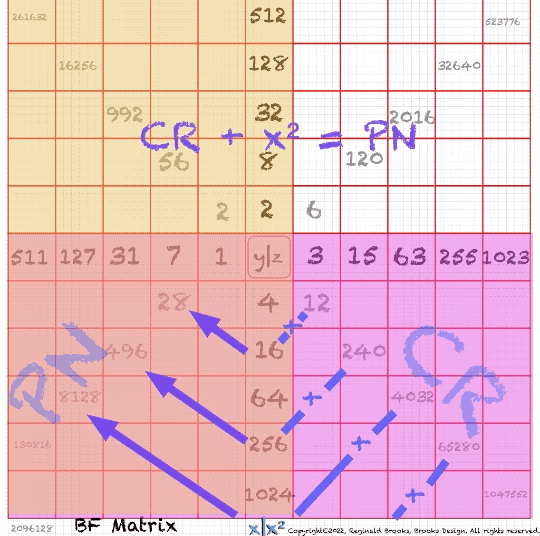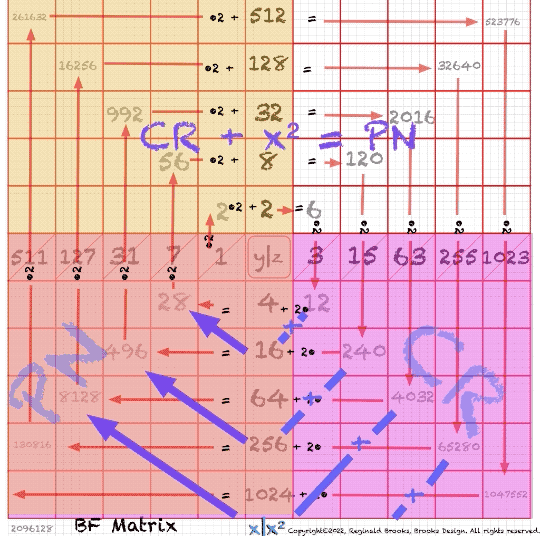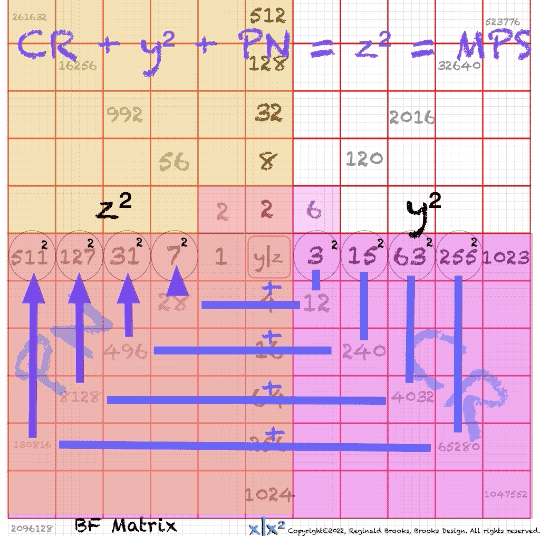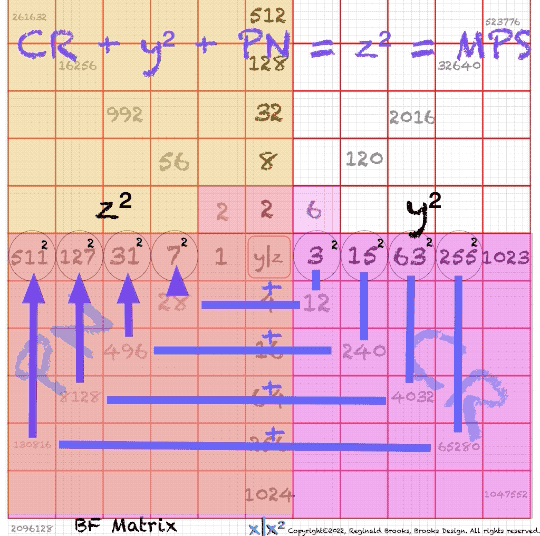
“Ahem! Well, you had better hold on to your hat, because once again good old algebra — or at least what we might call algebraic geometry — is going to blow your socks off! Everything you’ve seen in the straight-forward geometry and everything you have experienced in the choreographed dance — and much more — can be eloquently distilled into our simple little — but infinitely expandable — Butterfly Fractal Matrix (BFM)! And herein lies the secret sauce. To be fair, you can see it visually in the geometry, and perhaps with some very clever choreography, in the dance. But only here can you readily crunch the numbers that provides the proof is in the pudding or more succinctly the proof of the pudding is in the eating.

“If one fills out the BFM as we have been doing, there are four quadrants clockwise starting at the top left: A, B, C, and D made from Horizontal Row of the ODD running sums and the Vertical Column of EVEN exponential powers of 2 (doubling of twos as in the doubling of twos, fours, eights, …). Both alternate values as the matrix is formed as an expanding spiral of sequential values of 2ⁿ with their running sums as we have shown earlier.

“Now for the secret sauce: If the axis values in each quadrant A, B and C are multiplied together, the resulting values are key Areas within the Mersenne Prime Square (MPS) that each Mersenne Prime - Perfect Number (PN) make. The same goes for quadrant D, only the Row values are offset by square.

“Turns out the diagonal of values so formed make up the Complement Rectangle (CR) values on the descending diagonal and the Perfect Numbers (PN) on the ascending diagonal.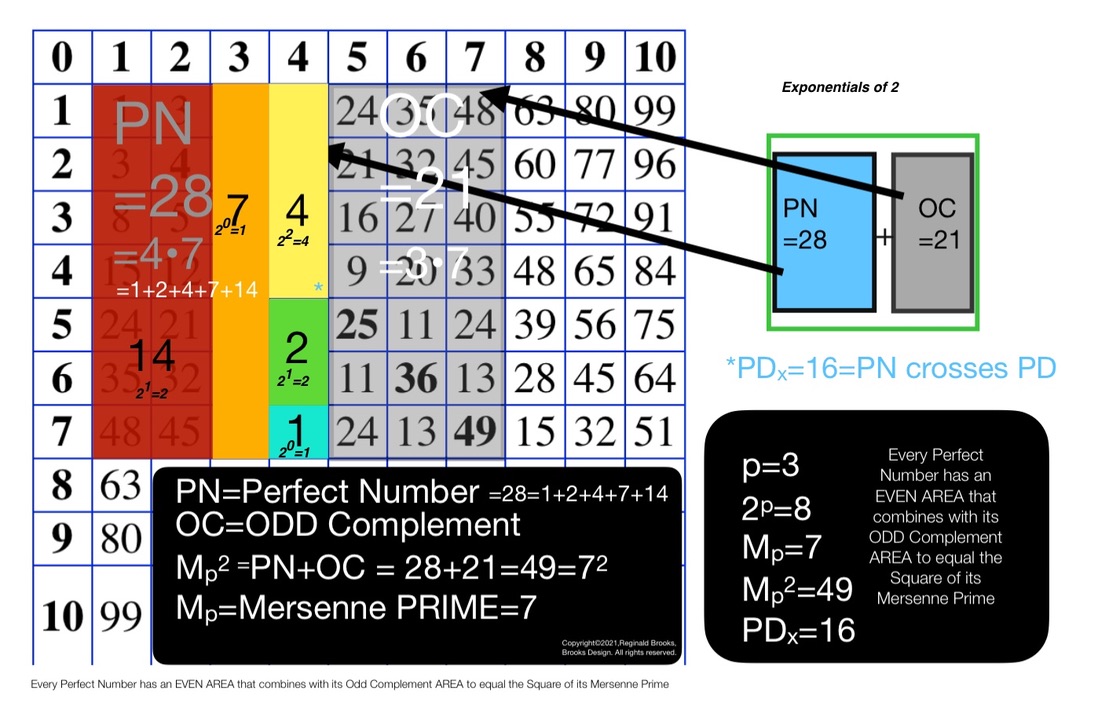

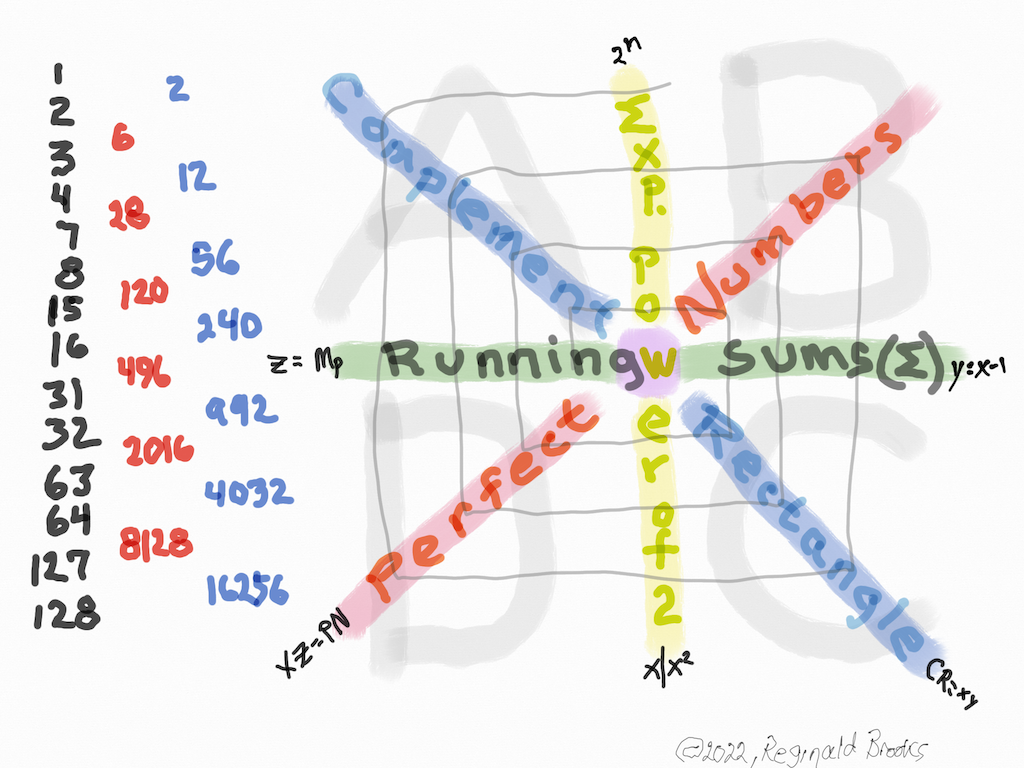
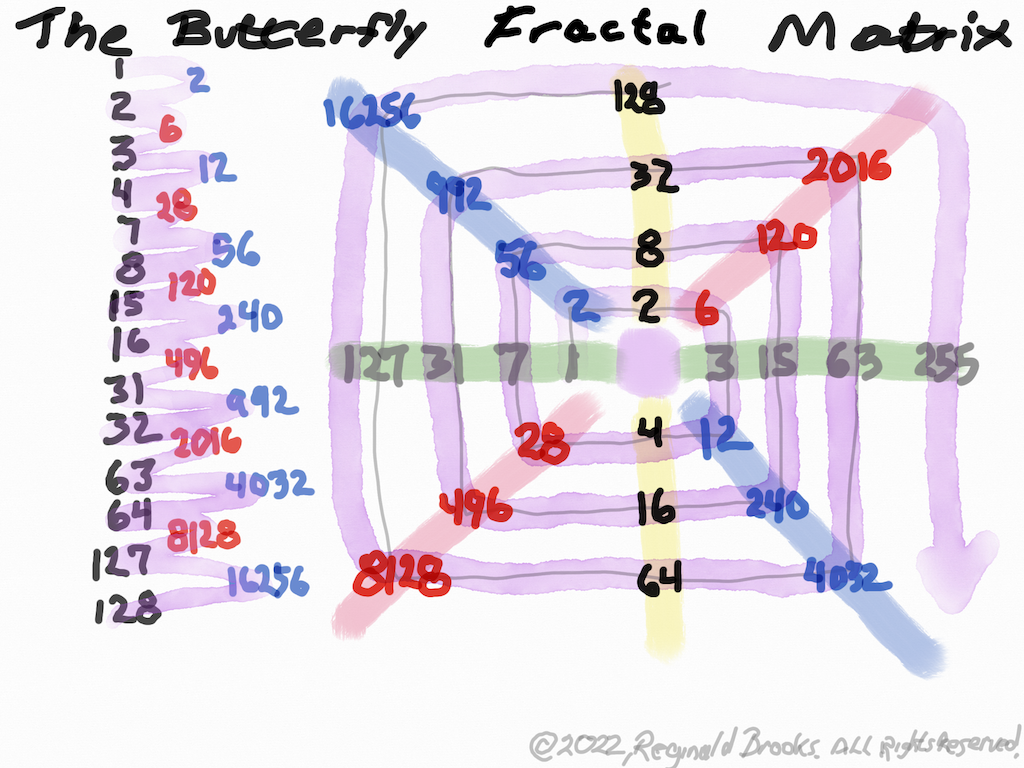
“And, one can start anywhere on these diagonal matrix values of CR and PN and get to the next spot by simply doubling the current spot value, and — if and only if one is passing Horizontally over the Vertical Column of EVENS — adding that EVEN value to the doubling product. One can start with “1” and spiral out. Every possible CR and PN value is revealed. Of, course, being a product of mathematics, one can also just multiply the appropriate Horizontal and Vertical Axis values to get the same result!”

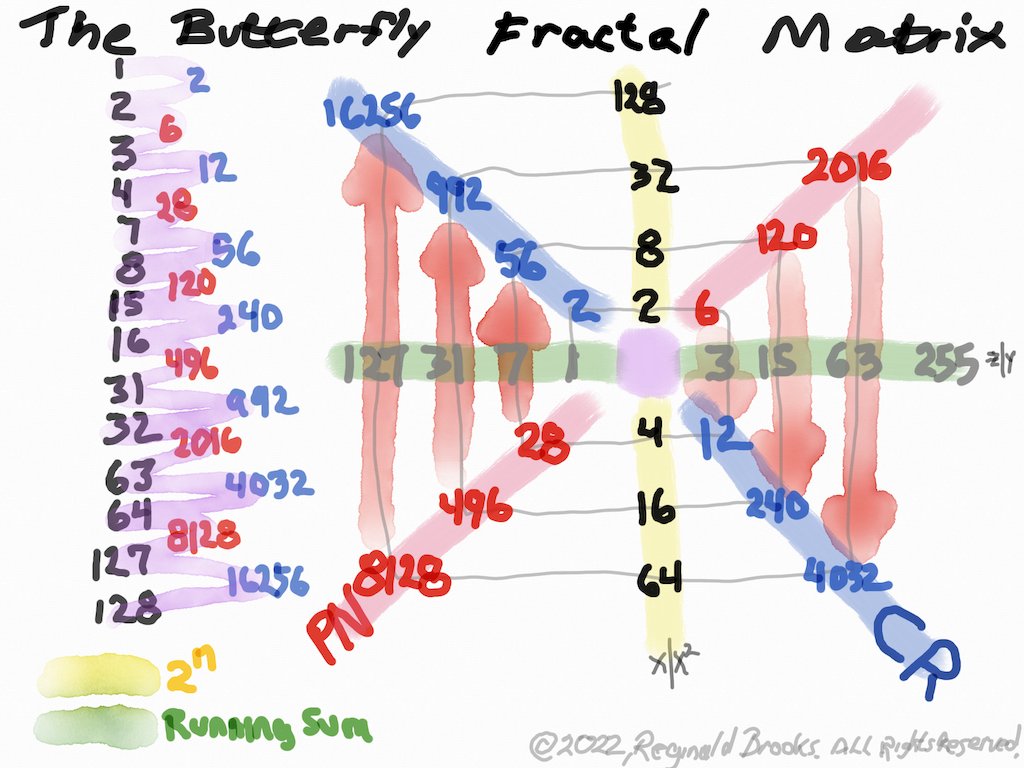
“Hate to break the news, burst your bubble, or steal your thunder, but anyone with a tad bit of imagination and even a little bit of math intuition can see all of that in the staggered chorus line dance. The Butterfly Fractal, or perhaps we should call it The Butterfly Fractal Dance — or simply The Butterfly Dance — has this same information built right in! No need to make some complicated-looking matrix!,” exclaimed the exasperated choreographer.

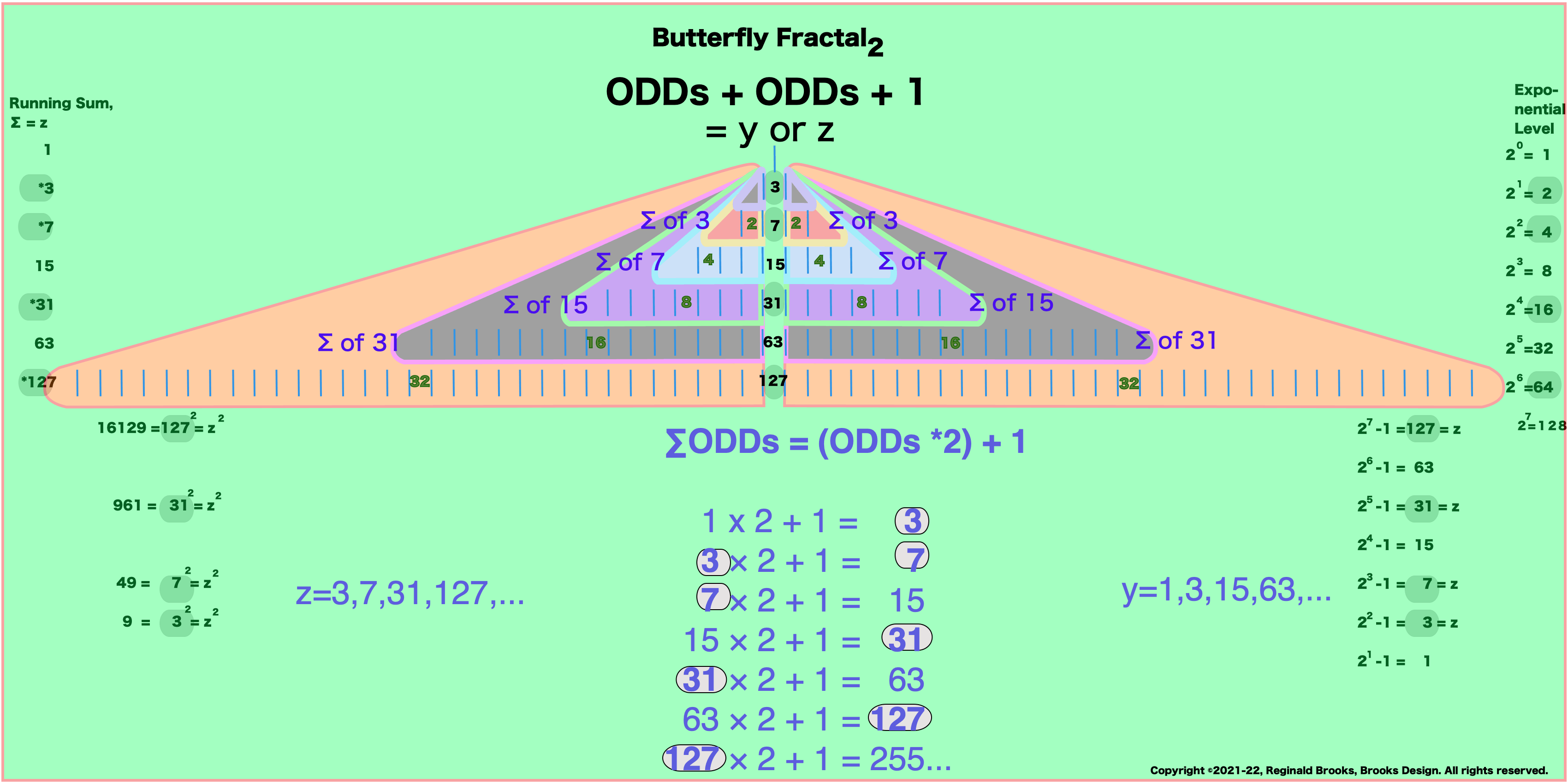
“If I may interject here,” the artist-geometer interrupted, “and I mean no disrespect for the wonders of either the mathematician or choreographer’s expression, the geometry-based view gives one the most informed view: it visualizes everything in terms of a conventional and traditional viewing platform (grid), every part of which can be restated in algebraic terms, and, though one of its major strengths is its breakdown into static plane visuals (frames, if you will), it can always be serially animated into a choreographed dance! Now, how about them apples! Gotcha!”

The barkeep blew out a jet-trail of exhale from his puffed checks and followed with a sigh, “Seems like we have hit an impasse. I feel like — depending on which day of the week I get out of bed — that I could favor any one of these views over the other two! What do you two — oh, excuse me — what do you three drink? I mean think?”

Numbers “1” and “1” and “1” — the latter two a.k.a. as “2” began to talk together all at once. “Ahem, since I am numero uno,” says “1,” “let me shed some light on all of this, or at least emphasize some basics.

“Each of us are quantities, identical quantities when taken as the parts — 1-1-1 — but when grouped we are symbolized by the number of parts in each group: thus number “1” for quantity one, and number “2” for two units of quantity one. Keep that in mind. The symbols are hugely important, convenient and a great simplification to keeping track of all the individual unit parts of quantity one. In the end, though, we are still dealing with quantities, be that quantities of spacetime, energy or flower petals on a Dahlia!

“There are two key dynamics going on with our simple natural numbers, especially when we are doubled:

1. We double the result of the previous doubling: 1-2–4–8–16–32,…(Exponential power of 2: 2⁰=1, 2¹=2, 2²=4, 2³=8, 2⁴=16, 2⁵=32,… that, after “1” are all EVENS)

2. Adding up the sums — the running sums (∑) — of each subsequent doubling gives new connections and interconnections: 1+2=3, 3+4=7, 7+8=15, 15+16=31,… (all ODDS including, but not exclusively, all the PRIMES — especially the Mersenne Primes.)

“To that, we would add that by adding and/or multiplying combinations of 1 and 2 above, we can easily generate all the Mersenne Primes Squares (MPS) and all of their geometric “parts” including:

x=short side of the xz=PN rectangle=2ᵖ⁻¹ , where p=prime #

y=x-1=short side of the yz=OC rectangle

z=Mp=Mersenne Prime=2ᵖ -1, where p=prime #

PN=xz=Perfect Number

OC=yz=ODD Complement

PNS=x²=Perfect Number Square

OCS=y²=ODD Complement Square

CR=xy=Complement Rectangle

Each of our distinguished artists are all correct. They are all envisioning and expressing the same inherent beauty of simply doubling our quantities: The Butterfly Fractal Dance!”

“Enough of the details!,” cried out the bartender. “Life is short! Exactly what is the big picture here. Why do we care?”

"Well, get ready!" warns "1," everything up to this point has been a cakewalk. You know, solid ground stuff. Simple arithmetic -- adding, subtracting, multiplying and dividing -- will get you to everything found so far. A curious child will love to do it!

"But now you want interpretation, hey!

"That will rely on intuition, imagination, risk taking, and courage, not to mention a bit of pure reasoning.

"What seems like an illusion is really fact, and, I hate to say this, but what sometimes seems like fact is really an illusion!

“1” explains, “One is everything — everything else is just detail — everything else is but a repeating, reiterated, self-similar duplicate doubling of the same “1.” Only the difference is, all that follows is really both identical to the starting “1” and a self-similar — but smaller (by sequential division of the running sum). Let me explain this essential paradox:

“If one starts with a large fractal — a fractal that represents, encompasses all — then by definition, as one drills down looking at the smaller “parts” of said fractal-1, one finds exactly the same fractal as fractal-1. Let’s call it fractal-2. Now repeat drilling down and an exact same fractal — fractal-4— is found. It is the nature of the fractal that at each level the “reality” is self-similarly the same! Sounds like Special Relativity (based on constant velocity) and/or General Relativity (based on accelerated velocity). The latter often visualized as the curved spacetime (viz. bowling ball on a rubber mat).

“If all energy — that is, all spacetime — is conserved — that is, neither net created or destroyed — is not “1” then every bit of energy here and energy there is but as fractal-bit-2, -4, -8,… part of that whole “1” fractal. The paradox is that each energy fractal bit-2, -4, -8, … is self-similar to the whole energy fractal-1! So how can you double something, have each of the parts be equal to the original, and yet not have the sum of parts exceed the original - the original that is suppose to hold it all?

“When "I" doubles to "I I," we now have "I I I," i.e. each “I” is 1/3 as 3•1/3=1. One must always end up with a net of “I.” Another example: I + I I + I I I I = 7 and each “I” now equals 1/7 as 7•1/7=I.

“Yes, the paradox here is that original “1” equals “I” and they must always equal the sum total of all the other, doublings of “1” or “I” with no net exceptions. It’s not that “1” — or as “I” — is actually fluid, it’s not, it is fixed as the total amount of all ST energy, but in any particular ST frame of reference — doubling(s)— one must sum up all the values, including the initial “1” value such that it remains a constant. Thus the running sums (∑) gain a truly hierarchal significance –– the inverse equals the value of "1" for that particular ST frame of reference. Summing up the "parts" restores the constant value of "1!"

“Not only is the number doubled and the quantity it represents seemingly doubled, but in actuality, the spacetime that it is composed of and seems to reside in, is correspondingly reduced — so relatively, it occupies the same density as its original, only now there are double the number, so that the fractional values add back up — including the original value — to equal their original! This is entanglement. We pure numbers don’t distinguish between our generic entanglement and what is referred to as quantum entanglement. The latter has a lot of physical world baggage — a.k.a. particles — associated with its implementation. Below any physical level of expression is where the generic level of quantities, numbers, fractals, entanglement,… all perform their dance!”

The absolute takeaway here is that every “1” and/or “one” is a fractally, entangled part of a larger “1” and/or “one!” Once again, we reaffirm that every number counts!”

To which the entire bar falls into a deep slumber.

“Just look at the children. They don’t even realize that while in their somber slow-wave and/or deep REM sleep that they are actually re-aligning their own numbers with their opposing anti-matter selves! Such bliss!”

“Like the ‘Sandman,’ let me insert this little closer into your dream(s): While the Mersenne Primes and Perfect Numbers — all 51 of the known ones — seem to be randomly distributed across the number landscape, in fact, each and every one is connected! On the BIM this shows as a straight-line connection between the PNs and CRs. On the whirling “square” matrix, each informs the next, and of course, on the pure ‘Butterfly Fractal’ one only has to watch the dance to experience this essential fractal expression!

—

—

—

—

Sneek Peak: Table 124: Mersenne Prime-Perfect Number "containers"

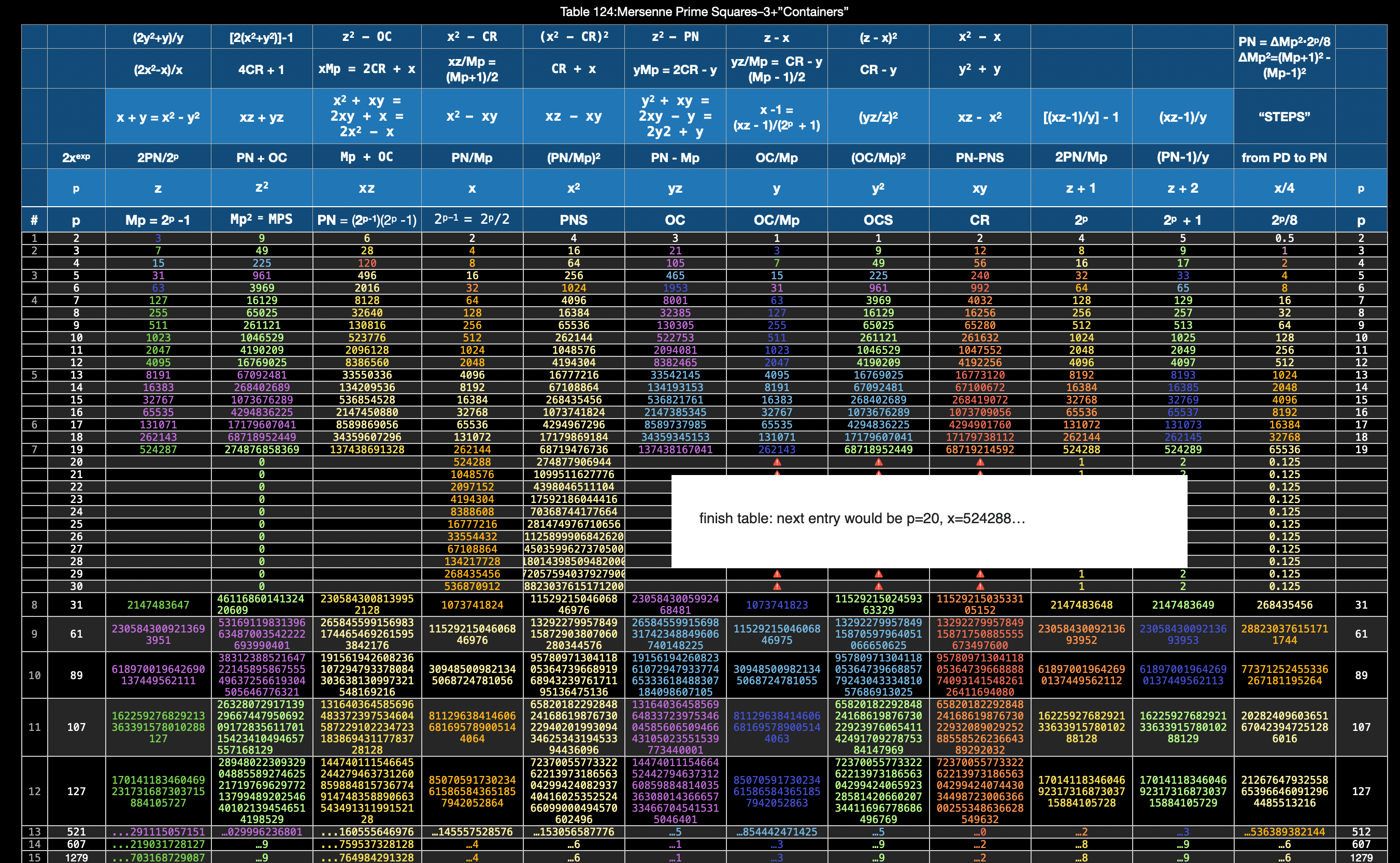
“Wow, that might even put me to sleep! But let’s not end on that note. Just one little exercise that even your children will enjoy: the basic idea is that we are going to make a list of numbers (from the Exponential Power of 2 —>Butterfly Fractal) and populate those numbers around a square-spiral:

First, make a list:

• 1
• leave blank for now
• 2
• leave blank for now
• 3
• leave blank for now
• 4
• leave blank for now
• 7
• leave blank for now
• 8
• leave blank for now
• 15
• leave blank for now
• 16
• leave blank for now
• 31
• leave blank for now
• 32
• leave blank for now
• 63
• leave blank for now
• 64
• leave blank for now
• 127
• leave blank for now
• 128

Now, with two different RED and BLUE colors, fill in the blanks;

• 1
• 2 (line 1•line 3 = 1•2 = 2) in BLUE
• 2
• 6 (line 3•line 5 = 2•3 =6) in RED
• 3
• 12 (line 5•line 7 = 3•4 = 12) in BLUE
• 4
• 28 (line 7•line 9 = 4•7 = 28) in RED
• 7
• 56 (line 9•line 11 = 7•8 = 56) in BLUE
• 8
• 120 (line 11•line 13 = 8•15 = 120) in RED
• 15
• 240 (line 13•line 15 = 15•16 = 12) in BLUE
• 16
• 496 (line 15•line 17 = 16•31 = 496) in RED
• 31
• 992 (line 17•line 19 = 31•32 = 992) in BLUE
• 32
• 2016 (line 19•line 21 = 32•63 = 2016) in RED
• 63
• 4032 (line 21•line 23 = 63•64 = 4032) in BLUE
• 64
• 8128 (line 23•line 25 = 64•127 = 8128) in RED
• 127
• 16256 (line 25•line 27 = 127•128 = 16256) in BLUE
• 128

Notice that the BLUE is ALWAYS 2x the RED. The BLUE and RED alternate starting with the BLUE. Both are ALWAYS EVEN numbers divisible by 4.

Cleaned up it should look something like this:

• 1
• 2 BLUE
• 2
• 6 RED
• 3
• 12 BLUE
• 4
• 28 RED
• 7
• 56 BLUE
• 8
• 120 RED
• 15
• 240 BLUE
• 16
• 496 RED
• 31
• 992 BLUE
• 32
• 2016 RED
• 63
• 4032 BLUE
• 64
• 8128 RED
• 127
• 16256 BLUE
• **128

Secondly:

• Make a simple grid: say 13x13 with large enough squares to put in the numbers.
• At or near the center, mark that grid with “0” or a large PURPLE DOT.

Thirdly:

• Insert the numbers from your list above, starting with “1” placed next to the center “0” and following a square-spiral outward, place “2 BLUE” above the “1”, the BLACK “2” to the right (above the center “0”), 6 RED to the right of that, BLACK “3” below the “6”, 12 BLUE below the BLACK “3”, and “4” to the left of 12 BLUE (under the center “0”).
• The 28 RED will bypass the next grid square on the left, moving under what will be the BLACK “7”, with 56 BLUE above it, and so on.

Fourthly:

• With a YELLOW Marker, underline or highlight the center Vertical Axis going from 128 to 64. This is the x or x² Axis.
• With a GREEN Marker, underline or highlight the center Horizontal Axis going from 127 to 63. This is the z = Mersenne Prime (Mp) or y = x-1 Axis.
• With a BLUE Marker, underline or highlight the 45° Diagonal going from 16256 to 4032. This is the Complement Rectangle (CR) Axis.
• With a RED Marker, underline or highlight the other 45° Diagonal going from 2016 to 8128. This is the Perfect Number (PN) Axis

Fifthly:

• Notice that CR and PN values on the Diagonals are the product of the respective x & y Axis values, e.i. 7•8 = 56 and 8•15 = 120.
• Notice that the BLUE CR values are simply double the respective RED PN values, e.i. 56=2•28
• Notice that the RED PN values equal the previous BLUE CR values + the YELLOW x value it crosses, e.i. 56•2 + 8 = 120.
• Notice that sum of the BLUE CR + YELLOW x diagonally below it equals the RED PN across, e.i. CR + x = PN = 12 + 16 = 28.
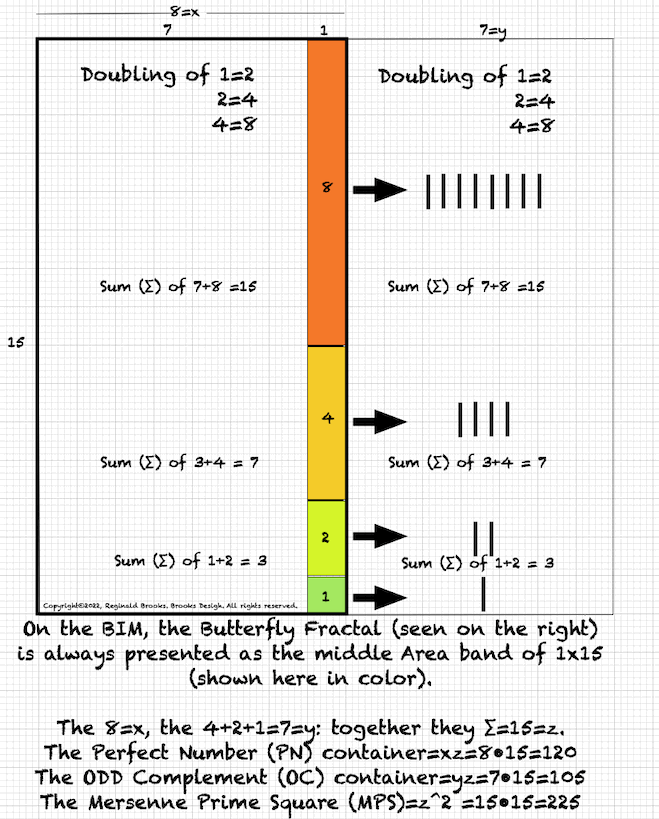
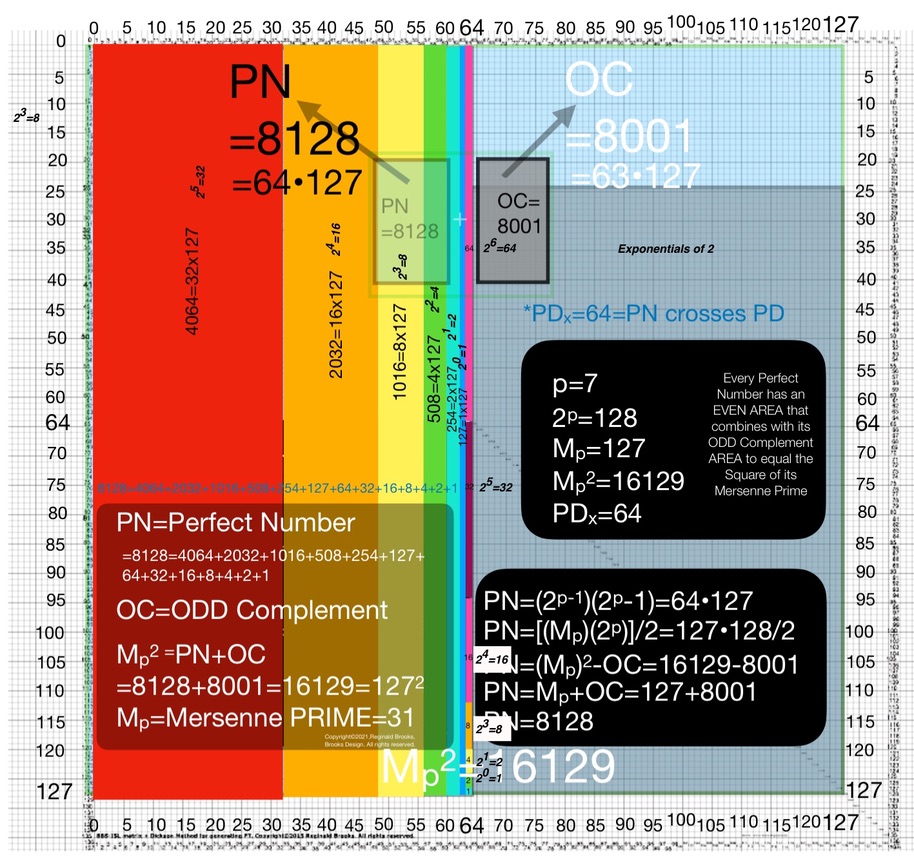
• Notice that CR + y² + PN = z² = Mersenne Prime Square (MPS), e.i. CR + y² + PN = z² = 12 + 3² + 28 = 7² = 49.

Note: In a strict Cartesian coordinate system, “x” is the designated horizontal axis, “y” the vertical. Being a bit dyslectic — or perhaps overly tuned to the symmetries — I have rotated the axis so “y” or “z” is on the horizontal and “x” or “x²” is on the vertical. It pleases my eye and the relational information is the same. This also occurs in some computer graphics applications (https://en.wikipedia.org/wiki/Cartesian_coordinate_system ). 

One can easily make the Butterfly Fractal Matrix (BFM) by starting the initial placement of “1” on left, top, right, or bottom of the center square and achieve a perfectly workable matrix. It all spirals out to give the same data points and connections placed at 0°, 90°, 180° and 270° positions, respectively. And they are all derived from that simple I  I I  I I I I,… Butterfly Fractal based on the Exponential Power of 2!

NEXT: BOOK IV: Not to be outdone-the Artist-Geometer: MPSnext & 10 Common Parameters ALL MPS follow

LINKS:

Mersenne Prime Squares (Part I) the Introductory white paper.

Mersenne Prime Squares (Part II) 3 Simple Intros.

Mersenne Prime Squares (Part III) the Advanced white paper.

The MPS Project The Mersenne Prime Squares Project.