Reference:
"A New Kind of Prime
The twin primes conjecture’s most famous prediction is that there are infinitely many prime pairs with a difference of 2. But the statement is more general than that. It predicts that there are infinitely many pairs of primes with a difference of 4 (such as 3 and 7) or 14 (293 and 307), or with any even gap that you might want."
Quote is from Quanta Mag 9/26/19 article: Big Question About Primes Proved in Small Number Systems
by Kevin Hartnett
~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~
- Twin Primes
- Primes separated by other EVEN numbers
- Euler's 6n+1 and 6n-1
- Fermat-Euler's 4n + 1= Sum of Two Squares Theorem (Pythagorean Primes)
- Dickson's Conjectures: Sophie Germain Primes
- Goldbach Conjecture (Euler's "strong" form)
- Primes - BIM - Pythagorean Triples
~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~
A new and easy visualization!
PRIME GAPS
Game Board
There is a new game board in town. It has actually been around for awhile, but few know of it. It's basically a matrix grid of natural numbers that defines the Inverse Square Law (ISL). It's called the BIM, short for the BBS-ISL Matrix. Every grid cell is uniquely occupied by a given number that is simply the difference between the horizontal and vertical intercept values of the main "Prime Diagonal" (not Prime number diagonal) that mirror-divides the whole matrix.
If you show all the matrix values that are evenly divisible by 24, a criss-crossing pattern of diamond-diagonal lines will appear and this ends up giving us a unique visual on the distribuition of ALL PRIMES!
Basically, all ODDs (3 and greater for this presentation) fall into a repetitive pattern of:
ODD ÷3—Not÷3—Not÷3—÷3—Not÷3—Not÷3—÷3—Not÷3—Not÷3—÷3—Not÷3—Not÷3—÷3...
The matrix ÷24 described above, nicely picks out these sets of —Not÷3—Not÷3 that we call Active Row Sets (ARS). Each ODD member of the ARS is referred to as an Active Row (AR).
The ÷3 ODD Rows that lie between are called Non-Active Rows, or NA.
It is a necessary, but not sufficient condition, that ALL PRIMES are strictly located on ARs. NO exceptions, except for some ARs have NO PRIMES.
Another striking visualization is that ALL Primitive Pythagorean Triples (PPTs) also lie only on the ARs, following the same necessary, but not sufficient, condition. NO exceptions here as well, except for some ARs also have NO PPTs. In addition, only one of the ARs within an ARS can have a PPT.
So any AR within an ARS can have 0/1 PRIMES and/or 0/1 PPTs in any combination, only with the one caveat: that only 1 PPT/ARS is allowed.
Now, not to belabor this BIM game board, let's talk PRIME GAPS!
Prime Gaps
Let's refer to the lower number value for the ARS as "Lower" and the higher as "Upper." All are ODDs. As will become apparent, you can always tell if your ODD AR is "Lower/Upper" simply by adding 2 and ÷3: if the result evenly ÷3 it is "Upper" and if not, "Lower."
The Even Gap between primes strictly follows this pattern: (all are necessary but not sufficient conditions for primality)
For any given set of twin primes, or any single prime, that is the smaller "Lower" of an AR set:
- Even Gap must be 2, 6, 8, 12, 14, 18, 20, 24, 26, 30, 32, 36, 38, 42, 44, 48, 50,…
- Example: P=5: 7, 11, 13, 17, 19, 23, (25), 29, 31, (35), 37, 41, 43, 47, (49), 53, (55)
- P + 2, P + 2+4, P + 2+6, P + 2+10, P + 2+12, P + 2+16, P + 2+18, P + 2+22, P + 2+24,…
- P+21, P+2+22, P+23, P+22+23, P+2+22+23, P+2+24, P+22+24, P+23+24, P+2+2324
- The Even Gap difference pattern follows: 2-4-2-4-2-4-….
For any given set of twin primes, or any single prime, that is the larger "Upper" of an AR set:
- Even Gap must be 4, 6, 10, 12, 16, 18, 22, 24, 28, 30, 34, 36, 40, 42, 46, 48, 52, 54.…
- Example: P=7: 11, 13, 17, 19, 23, (25), 29, 31, (35), 37, 41, 43, 47, (49), 53, (55), 59, 61
- P + 4, P + 2+4, P + 2+8, P + 2+10, P + 2+14, P + 2+16, P + 2+20, P + 2+22, P + 2+26, P + 2+28,
- P+22, P+2+22, P+2+23, P+22+23, P+24, P+2+24, P+2+22+24, P+23+24, P+22+23+24, P+2+22+23+24,
- The Even Gap difference pattern follows: 4-2-4-2-4-2-…. and is identical in the middle, not the start!
One can readily see that all this is simply the natural result of two ARs alternating with a NA row:
AR—AR—NA—AR—AR—NA—AR—AR—NA—AR—AR—NA—…
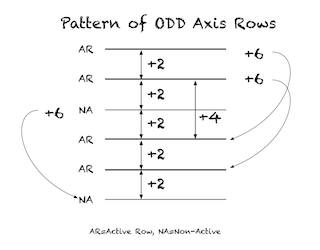
“Lower” AR number
AR—5
AR—7
NA—9
AR—11
AR—13
NA—15
AR—17
AR—19
NA—21
AR—23
AR—25
NA—27…
It is 6 steps, i.e. +6, from any NA to the next NA, from any “Lower” AR to the next “Lower” AR, from any “Upper” AR to the next “Upper” AR. ALL of the various EVEN GAPS may be shown to be a direct consequence of the natural number sequence and easily visualized on the BIM.
To any “Lower” Active Axis Row ODD:
- Add 2, 4, or 6,…
- If sum is ÷3, it is a NA
- If sum is NOT÷3, it is an AR number and a PRIME (or PPT) candidate.
“Upper” AR number
AR—7
NA—9
AR—11
AR—13
NA—15
AR—17
AR—19
NA—21
AR—23
AR—25
NA—27…
To any “Upper” Active Axis Row ODD:
- Add 2, 4, or 6,…
- If sum is ÷3, it is a NA
- If sum is NOT÷3, it is an AR number and a PRIME (or PPT) candidate.
Again, It is 6 steps, i.e. +6, from any NA to the next NA, from any “Lower” AR to the next “Lower” AR, from any “Upper” AR to the next “Upper” AR. ALL of the various EVEN GAPS may be shown to be a direct consequence of the natural number sequence and easily visualized on the BIM.
The ARS pattern on the BIM clearly shows the above patterns and may be extrapolated to infinity:
pg3.png)
PRIME Conjectures
A number of PRIME conjectures have been shown to be easily visualized on the BIM:
Reference: TPISC IV: Details: BIM + PTs + PRIMES
The factors of 24 — 1,24–2,12–3,8–4,6 — when increased or decreased by 1, ultimately pick out ALL ARs. Euler's 6n +/-1 is the most direct, Fermat's 4n + 1 gets the Sums of Two Squares = Pythagorean Primes(while 4n + 3 gets the rest).
Fermat's Little Theorem (as opposed to the more familiar "Fermat's Last Theorem") tests for primality.
But now there is a dead simple way to test for primality:
The difference in the squares between ANY 2 PRIMES (≧5) ALWAYS = n24.
For example, take any random ODD # - 25 —> it must be ÷24 n times to be PRIME. (n=1,2,3,...)
741
7412-52/24 = n= 22877.3 NOT PRIME
189
1892-52/24 = n = 1487.3 NOT PRIME
289
2892-52/24 = n = 3479 PRIME
PRIMES vs NO-PRIMES
I would be remiss if I did not mention that throughout this long journey that began with the Inverse Square Law and the Primtive Pythagorean Triples that the PRIMES kinda of just fell out. They just kept popping up. Not the least, but certainly not without effort, the BIM actually directly visualizes ALL of the NO-PRIMES. In doing so, one is left with information that is simply the inverse of the PRIMES. Subtract the NO-PRIMES information from the list of ODDS (disregarding 2) and what remains are ALL the PRIMES! A simple algebraic expression falls out from that:
NP = 6yx +/- y
letting x=1,2,3,… and y=ODDs 3,5,7,… with the only caveat is that if you don't first eliminate all the ÷3 ODDS, you must include exponentials of 3 (3x) in the NP tally.
Goldbach Conjecture (Euler's "strong" form)
In 2009-10, a solution to Euler's "strong" form of the Goldbach Conjecture "that every even positive integer greater than or equal to 4 can be written as a sum of two primes" was presented as the BBS-ISL Matrix Rule 169 and 170. This work generated a Periodic Table of Primes (PTOP) in which Prime Pair Sets (PPsets) that sequentially formed the EVEN numbers were laid out. It is highly patterned table. A recently annotated version is included with the original below. (See above link for details.)
It turned out this PTOP was actually embedded — albeit hidden — within the BIM itself as shown in Rule 170 and here, too, a recently annotated version is included below. (See above link for details.)
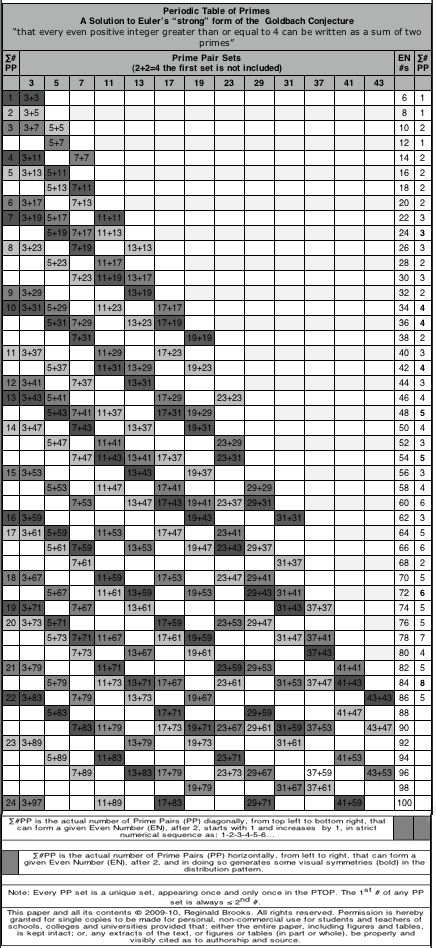
Rule 169: Periodic Table of Primes.
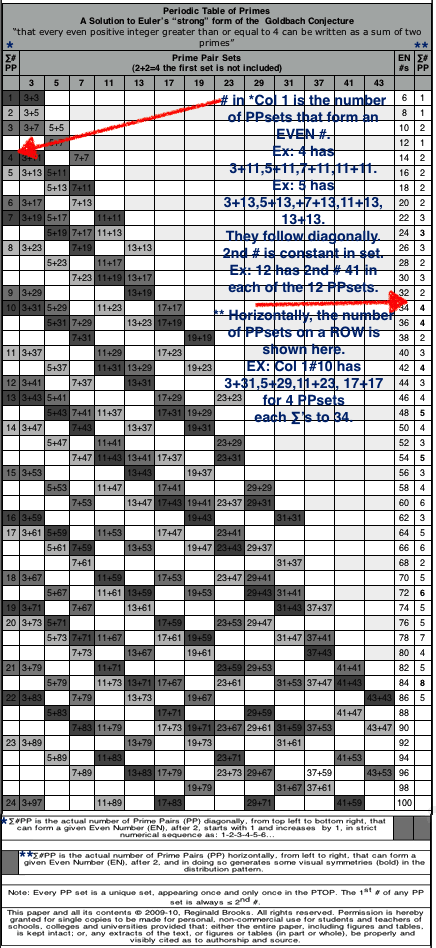
Rule 169: annotated
 Rule 170: Periodic Table of Primes (PTOP): embedded within Brooks (Base) Square.
Rule 170: Periodic Table of Primes (PTOP): embedded within Brooks (Base) Square.
 Rule 170: annotated
Rule 170: annotated


MathspeedST: TPISC Media Center
Artist Link in iTunes Apple Books Store: Reginald Brooks

Reginald Brooks
Brooks Design
Portland, OR
brooksdesign-ps.net
~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~