TPISC_IV:_Details ~A MathspeedST Supplement~
Copyright©2018-19, Reginald Brooks. All rights reserved.
TPISC_IV:_Details_BIM+PTs+PRIMES
Preface
C. How — but NOT why — 24 connects the PTs and PRIMES to the BIM.(Also see Appendix A/Notes2016-2018/Section 4C/Pages 0000-50c, and thereafter: see Appendix A/Notes2016-2018/Sections 1 and 2/ ALL Pages for more. Appendix B will be the go-to appendix for BIM/24, PPTs and PRIMES, as well as the DSEQEC.)
Sub-Matrix
(Also see Appendix Figures and Tables for BIM/24, PPTs and PRIMES, as well as the DSEQEC.)
Rules 178-180 introduced the “sub-matrix grid” briefly as:
180 BS Rule 180- The Sub-Matrix: Within the Inner Grid, every progressive number of every column or row is evenly divisible , progressively, by a whole number sequence. Plotting those dividends reveals a truly fundamental "sub-matrix" grid, underlying the original Inner Grid, of repeating simple whole number sequences, i.e. 1,2,3, ..., horizontally and vertically ...forming the simplest, most basic grid pattern possible, that also includes the axis numbers. All numbers of the original Brooks (Base) Square are predicated on this simple whole number sequence pattern.
“Note: This amazing sub-matrix grid pattern explains the entire parent grid matrix and the Inverse Square Law, ISL, relationship that unfolds. See an animated example by CLICKING IMAGE above. Patience. Follow the bold numbers.
Here we find the simplest and most basic pattern of the simple whole number sequence ... 1,2,3,... forming a truly fundamental base layer ... a sub-matrix ... lying below the original grid. And every number on that original grid is predicated on this simple pattern of 1,2,3,... in both the horizontal and vertical arrays. In fact, we now have complete integration of the axis numbers with the Inner Grid numbers ... together forming the Prime Diagonal (PD) of the Inverse Square Law (ISL). We have come full circle. And it begs the question: Who is the parent and who is the child. It seems the parent has become the child. How many more fractal matrix layers are there?”
Henceforth, we will call this Sub-Matrix 2.
A new sub-matrix, Sub-Matrix 1, results in the Active Row Sets (ARS) grid formed by dividing ALL Inner Grid numbers by 24.
Together Sub-Matrix 1 and Sub-Matrix 2 will provide the visual-geometric and algebraic-geometric location of ALL PPTs and PRIMES.
First Sub-Matrix 1:
The simple — and some of the not so simple — geometries of the BIM and BIMtree have been laid out in a series of interactive canvases. Each canvas opens up on its own webpage. Once open, you just click/touch and drag the geometry around, apart, this way and that way, even rebuilding the initial geometry side by side until you can really see how the parts are so simply related. It's deconstruction!
The entire geometry on canvas series was produced initially without any supporting text to keep it as clean, simple and intuitive as possible. The accompanying text will certainly help fill in the gaps, but it should be noted that the geometry on canvas series sequentially builds from one canvas to another.
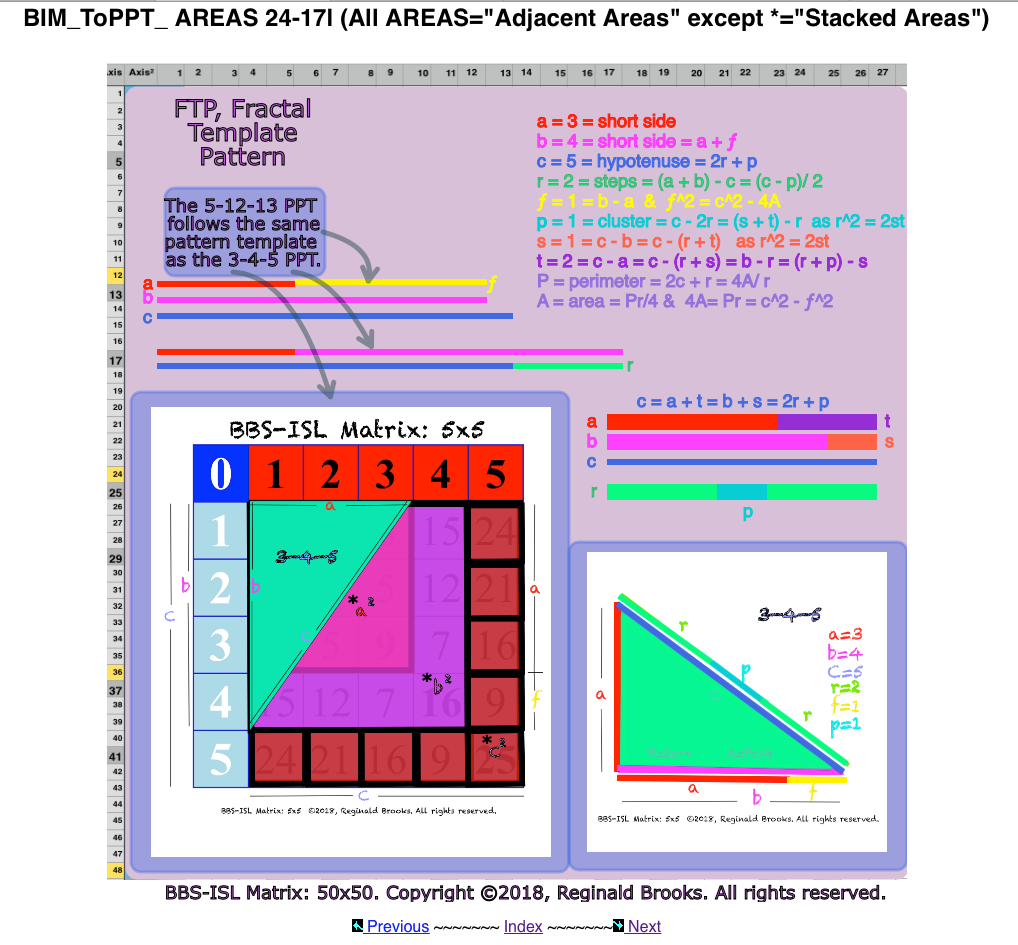
The algebraic binomials and their square proofs are widely known. Here the very same proofs overlap with that of the BIM, BIMtree and the ToPPTs! This, too, can be readily seen.
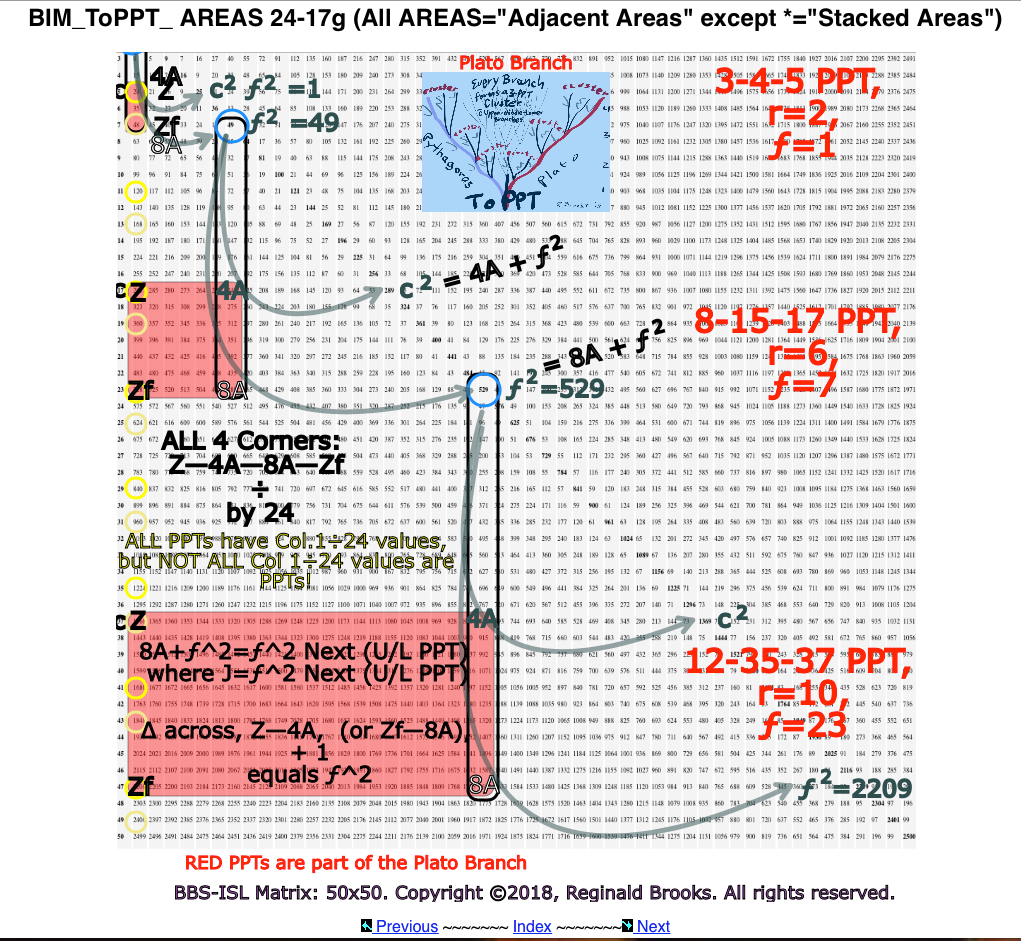
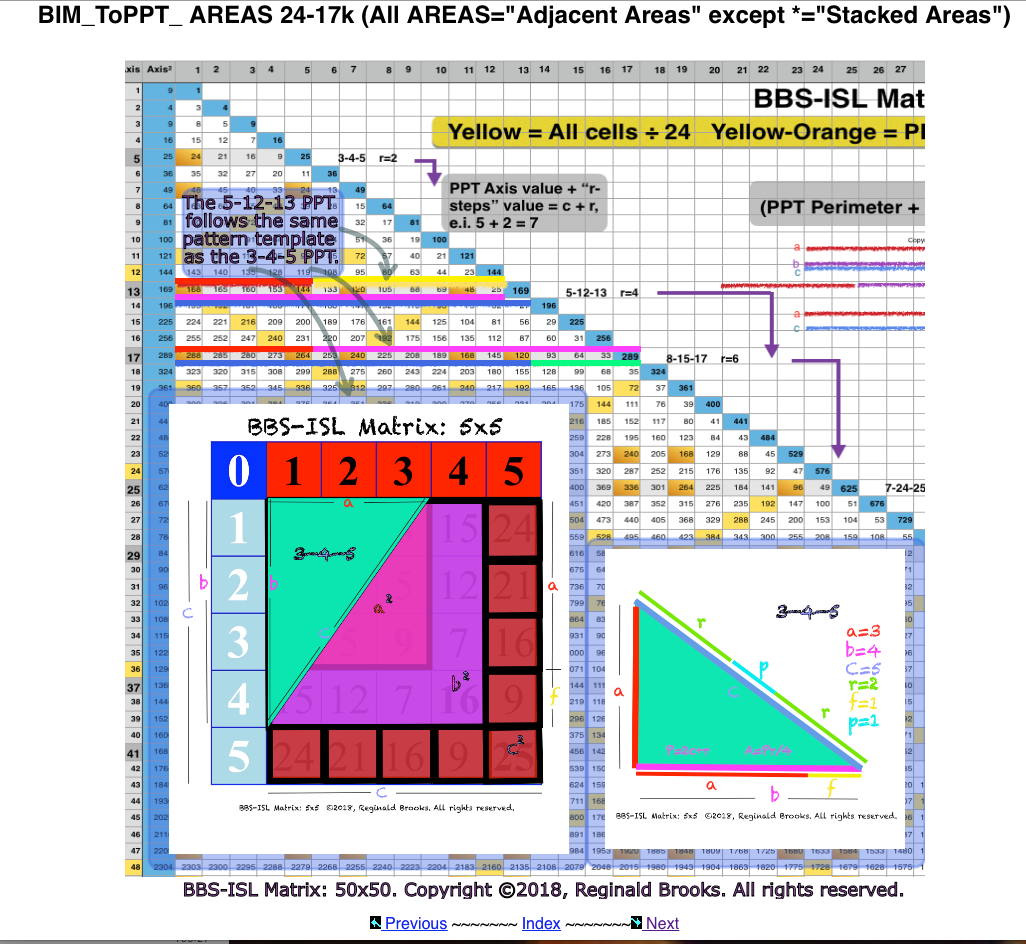
The number 24 — and its factors of 1-24, 2-12, 3-8, and 4-6 have shown, once again, to be integral to both the BIM in general (remember, the EVEN Inner Grid cell numbers are all evenly divisible by 4), and, the ToPPTs. HOW SO? Well, this is new, really new, so just the surface has been touched, but so far:
- Marking (YELLOW) all BIM cells evenly ➗ by 24 generates a striking diamond-grid, criss-crossing pattern with 4 additional YELLOW marked cells in the center of each diamond; (TPISC IV: Details)
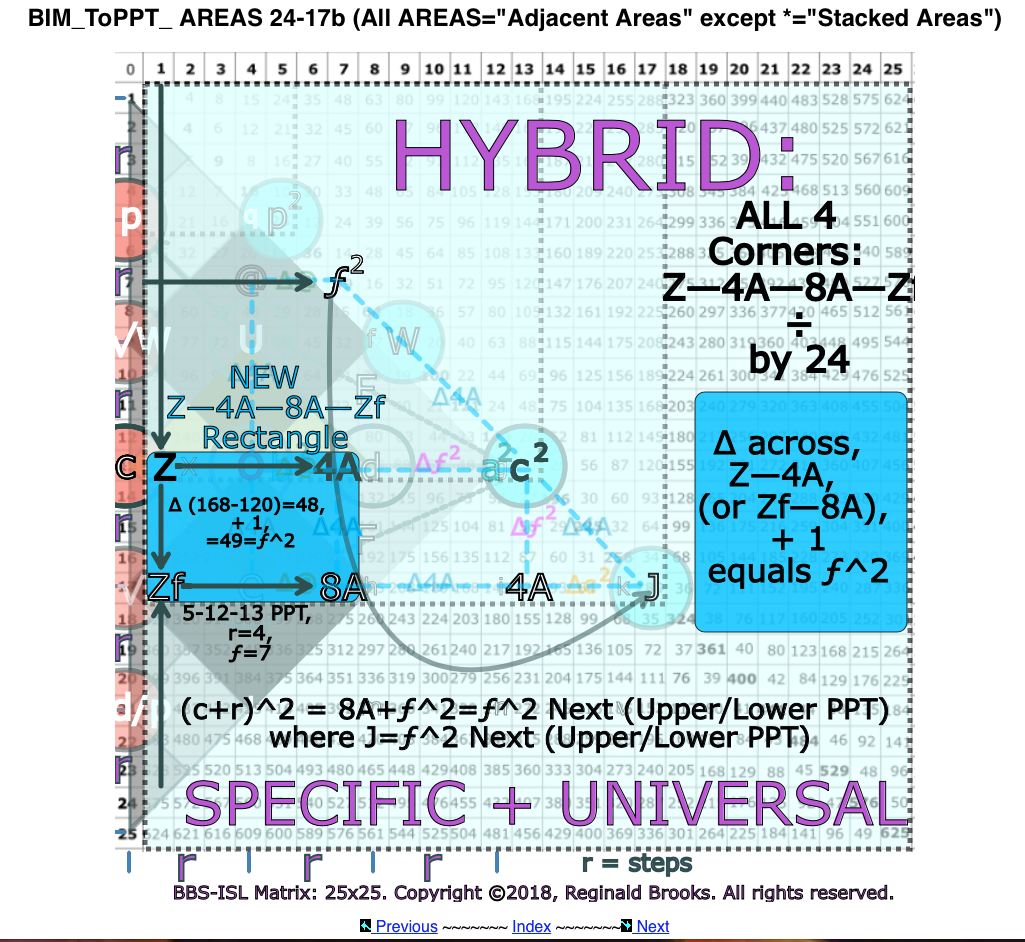
- Every PPT is found to exist on —and ONLY on — those Rows whose 1st Column grid cell are ➗ by 24 (YELLOW, with 1st Column grid cell marked as 'Z'), though not every such YELLOW marked Row contains a PPT. nPPT are only present on such Rows if accompanied by a PPT; (TPISC IV: Details)
- The “step-sister” of any given PT Row is found r-steps down the Axis from that Row (with 1st Column grid cell marked as 'Zf') and it, too, always and only exists on a YELLOW marked Row (“r” is part of the FTP originally derived from the Dickson Method for algebraically calculating all PTs); (TPISC IV: Details)
- The PPT Row (and nPPT Row) always contains the 4A (A=area) value of that PT and the “step-sister” PPT Row always contains the 8A value, both landing exclusively on YELLOW marked grid cells, giving a striking visualization of ALL PPTs and their r-based “step-sisters;” (TPISC III: Clarity & TPISC IV: Details)
- The significance of the “step-sister” is that it becomes the mathematical link to the “NEXT” PPT within the ToPPT — like the Russian-Doll model; (TPISC III: Clarity)
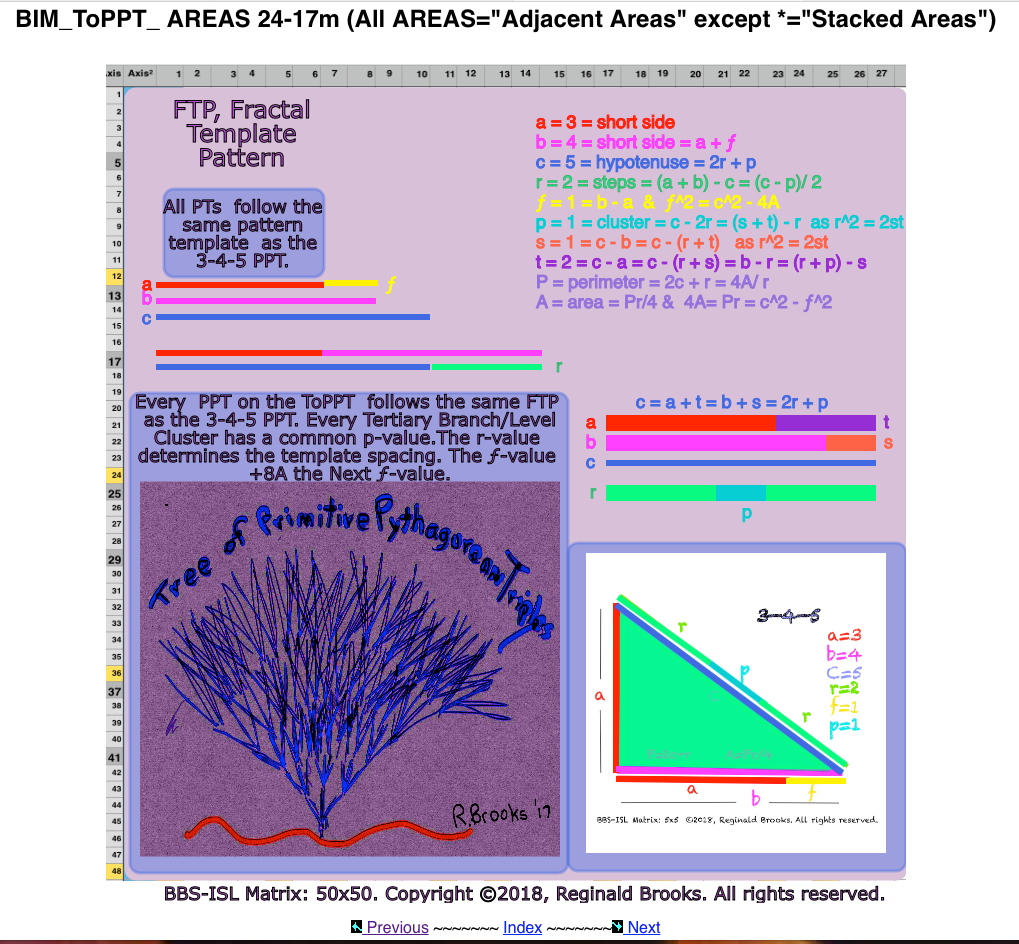
- The significance of the expanding and increasingly inter-connected PTs, as the BIM itself expands, is one in which the perfect-symmetry geometry of regular shapes and solids — equal triangles, squares, circles,… of the BIM allows — at certain articulation nodes (i.e., Rows) — the introduction of the slightly less-perfect-symmetry geometry (i.e., bilateral symmetry) of the full rectangle and oval that the non-isosceles right triangle PTs represent, into the unfolding structural framework, working from the ground up, if you will. The roots of fractals-based self organization are first to grow here! (TPISC III: Clarity & TPISC IV: Details) more…
- ALL self organization of any sort — be it force field or particulate matter — must have an organizing mathematical layer below driving it!
Besides intimately tying the ToPPTs to a natural fractal pattern within the BIM:
- Thereafter, ALL PTs — primitive “parents” (PPT) and non-primitive “children” (nPPT) —are found on select Rows of the BIM by simply following the squared numbers on the the Prime Diagonal down to intersecting Rows; ( TPISC I: Basics & TPISC II: Advanced) more…
- The mathematical basis relating the PPTs was found, as was the consistent Fractal-Template Profile (FTP) that every PT follows; (TPISC II: Advanced & TPISC III: Clarity) more…
- A yet to be explained tie-in with the prime numbers and 24: The difference (∆) between the squares of ALL primes is evenly ➗ by 24!!! (Pattern in Number: from Primes to DNA; GoDNA: The Geometry of DNA; SCoDNA: Structure and Chemistry of DNA; Butterfly Primes: ~let the beauty seep in~; Butterfly Prime Directive: ~metamorphosis ~ ; and, Butterfly Prime Determinate Number Array (DNA): ~conspicuous abstinence ~; and an interactive Butterfly Primes new media net.art project.
- The FTP allowed all the PPTs to be sorted out and organized into a definitive Tree of Primitive Pythagorean Triples (ToPPT) that co-extends infinitely throughout the infinitely expanding BIM —>BIMtree or BIM-ToPPT; (TPISC III: Clarity) more… and more…
One could simply say that: subtract one from the squared values of any natural, whole integer number (WIN) and if it is evenly ➗ by 24, it is a candidate for being a PPT or 'step-sister' if that same squared value - 25 is ALSO ➗ by 24.
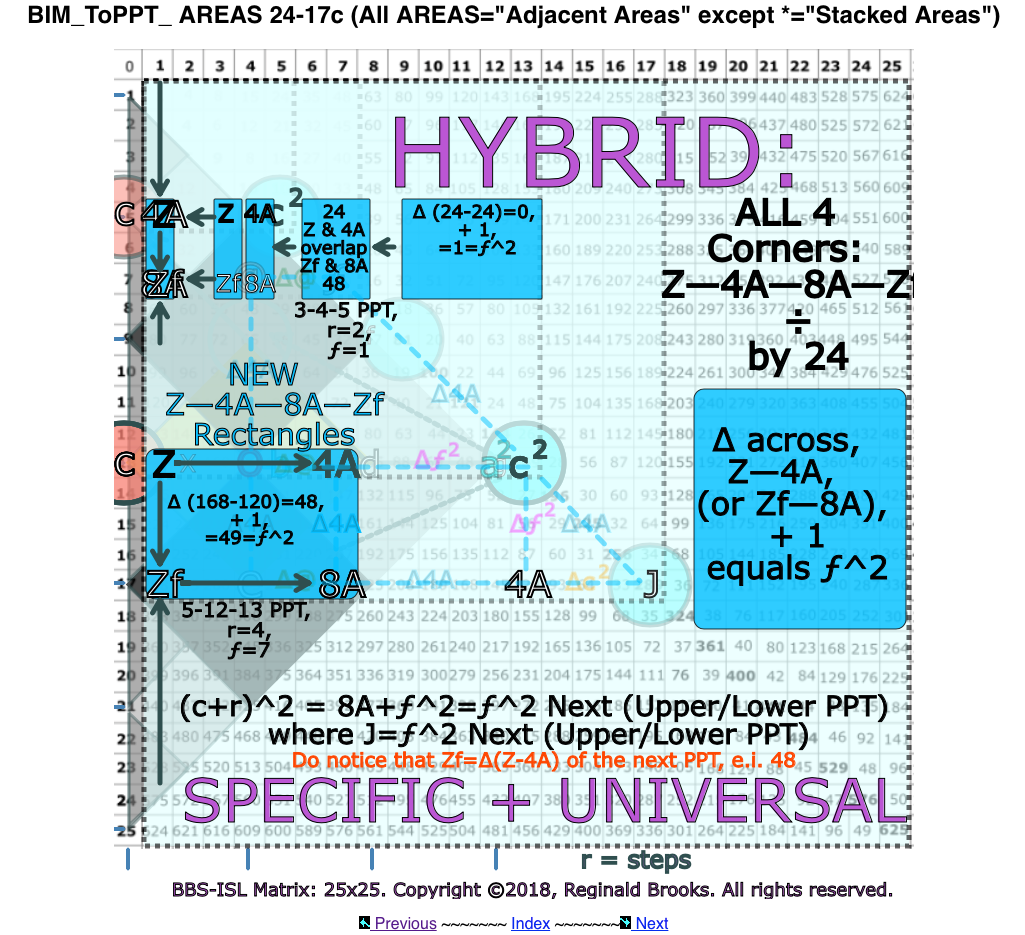
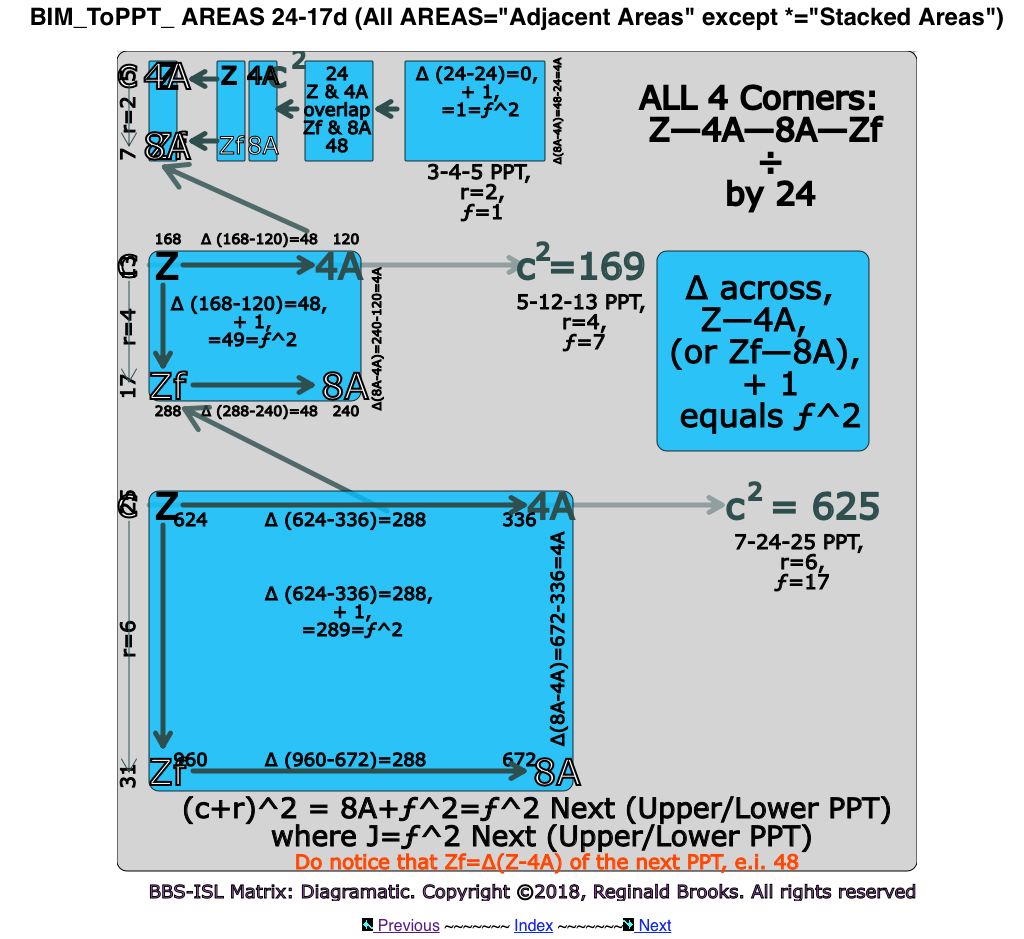
If the Row contains BOTH a Factor Pair Set (two squared values that = a2 and b2) and the 4A value ONLY, it is a PPT Row.
If it contains BOTH the 4A and 8A values, it is a 'step-sister' Row, i.e. (c2-1)/24 and (c2-25)/24, if evenly divisible, are PPT and/or PPT 'step-sister' Rows, e.i. Row 17 is the PPT Row of the 8-15-17 PPT, but is also the 'step-sister' Row of the 5-12-13 PPT.
(NOTE: The PPTs intersect with grid cells/24 at: the subtraction of 1,5,7,11,13,17,19,23,25,… from the squared Axis number (c2) and that gives a cell spacing of 4-2-4-2-4-2-4-2-… respectively, or a blank step ∆ between of 3,1,3,1,3,1,3,1,... )
Take the BIM and divide all numbers evenly divisible by 24.
This gives you a criss-cross pattern based on 12, i.e. 12, 24, 36 ,48,… from Axis.
Halfway between, are the rows based on 6.
On either side of this 6-based and 12-based frequency, the rows just before and just after, are ACTIVE Rows. These are ALWAYS ODD # Rows. They form an Active Row Set (ARS). Later colored in PURPLE.
Their Axis #s are NEVER ➗3.They ALWAYS have their 1st Col value ➗ by 24.
Adding 24 to ANY of the ODD # NOT ➗3 ACTIVE Row Axis values ALWAYS sums to a value NOT ➗3 and thus to another ACTIVE Row Axis value (as adding 2 + 4 = 6, ➗3 added to a value NOT ➗3 = NOT ➗3 sum*).
Another ODD Axis # Row lies before and after each pair of ACTIVE Rows, i.e. between EVERY set of two ACTIVE Rows, is an ODD non-ACTIVE Row and their Col 1value is NOT ➗by 24.
Adding 24 to ANY of these ODD # ➗3 Axis values ALWAYS sums to a value also ➗3 (as 2 + 4 = 6, ➗3 added to a value already ➗3 = ➗3 sum *).
While not an exclusive condition, it is a necessary condition, that ALL PPTs and ALL Primes have Col 1 evenly ➗ by 24.
Together, two ACTIVEs + one non-ACTIVE form a repetitive pattern down the Axis, i.e. ARS + non-Active Row.
*While 24 seems to define this relationship, any EVEN # ➗3 will pick out much if not all of this pattern, e.i., 6, 12, 18,…
It follows that:
ALL PTs (gray with small black dot) fall on an ACTIVE Row.
ALL PRIMES (RED with faint RED circle) fall on an ACTIVE Row.
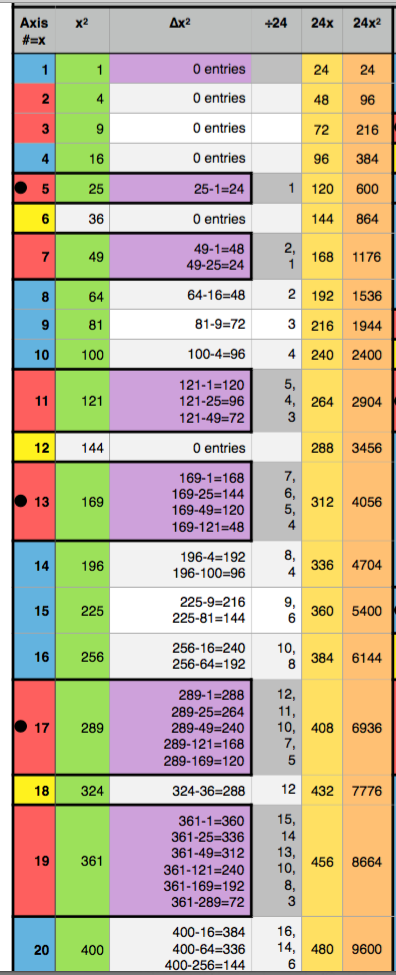
The difference, ∆, in the SQUARED Axis #s on any two ACTIVE Rows is ALWAYS divisible by 24.
The difference, ∆, in the SQUARED Axis #s on an non-ACTIVE ODD Row and an ACTIVE Row is NEVER divisible by 24.
The difference, ∆, in the SQUARED Axis #s on any non-ACTIVE ODD Row and another non-ACTIVE ODD Row is ALWAYS divisible by 24.
Going sequentially down the Axis, every ODD number in the series follows this pattern:
nA—A-A—nA—A-A—nA—A-A—
#3—5-7—9—11-13—15—17-19—21... Every 3rd ODD # (starting with 3) is ➗by 3 = nA .
#5-7—9—11-13—15—17-19 Every 1st & 2nd, 4th & 5th, 7th & 8th,… ODD # is NOT ➗ by 3 = A.
In other words, the two consecutive ODD #s, between the the nA ODD #s, are A ODD #s and are NOT ➗ by 3.
#3,4,5 re-stated: let A = ACTIVE Row Axis #, nA = non-ACTIVE Row Axis #
A22-A12= ➗ 24 and A ≠ ➗by 3
nA2-A2≠ ➗ 24
nA22-nA12= ➗ 24 and nA = ➗by 3
6,7,8 re-stated:
ODD Axis #s ➗by 3 (every 3rd ODD #) are NEVER ACTIVE Row members — thus never PT/PRIME
ODD Axis #s NOT ➗by 3 (every 1,2 — 4,5 — 7,8….ODD #s ) are ALWAYS ACTIVE Row members and candidates for being PT and/or PRIME.
In brief:
An ACTIVE Row ODD Axis # squared + a multiple of 24 (as 24x) = Another ACTIVE Row ODD Axis # squared , and the Square Root = a PT and/or a PRIME # :
A12+ 24x = A22 and √A22 = A2 = a PT and/or PRIME candidate;
ODD12+ 24x = ODD22 and √ODD22 = ODD2 = a PT and/or PRIME candidate, if and only if, its 1st Col. value is ➗ by 24.
The difference in the squared values of any two PTs/PRIME #s (>3) is ALWAYS a multiple of 24!
On the Prime Diagonal, the ODD #s follow the same pattern as on the Axis (see No.7).
BIM➗PPTs and PRIMES: (Latest: as this work was being prepared, a NEW relationship was found.) See below under Why?
Now that have overloaded the field with details, let's simply (again)!:
ALL PTs and ALL PRIMES are exclusively on Rows that:
• are referred to as “ACTIVE."
• bookend the Rows that are multiples (evenly ➗ by) 6: i.e. 6,12,18,24,30,36…
• some of these bookend on 6-based Rows do NOT have a PT and/or Prime, e.i. Rows 35, 49, 55, 77, 91, 95,… (Certainly, those ➗ by factors other than themselves and one, are NOT Prime.)
• as one progresses across the Matrix Row, the YELLOW and YELLOW-ORANGE cells on “ACTIVE” Rows follow a pattern under Column #: 1–5—7—11—13—17—19—23—25…i.e., + - - - + - + - - - + - + - - - + - + - - - and so on (see Gray-Violet & White on the Table below).
• the cell value numbers of the YELLOW and YELLOW-ORANGE cells on “ACTIVE” Rows follow exactly the numbers on Col C of the Table VII: Axis_Sqd_Diff_24x.numbers.
• the Table view gives the number values and relationships in tabular form, the Matrix in a more visual, geometric form.
• remember: ALL candidates for PTs and/or Primes MUST have Col 1/24 = (x2 - 1)/24 as TRUE.
Distilling the BIM/24 into the underlying "sub-matrix" of ➗24 Actives, as shown in Figure below. ___ , reveals exactly why the BIM/24 pattern is what it is.
NOTES: Sections 1-10
Section 1: 2018 (29pgs)

~~ ~~ ~~
In that the discovery that ALL PRIMES land only on ARS — exactly as do the PPTs — yet most emphatically do NOT follow the exact same distribution pattern leads to some open questions:
- what exactly is the relationship between PPTs and PRIMES?
- why do they BOTH land on ARS?
- why do some ARS have both, neither, or one or the other?
- can the PRIMES be used to predict the PPTs?
- can the PPTs be used to predict the PRIMES?
While a great deal in the way of proof of the PRIMES dependency on the ARS for their distribution will be presented in a number of tables (Tables 1-23, mostly redirected to the APPENDIX), we must keep these questions in mind as we pursue the PPTs and their relationship to the BIM (Tables 24-28).
Now, we introduce
Sub-Matrix 2:
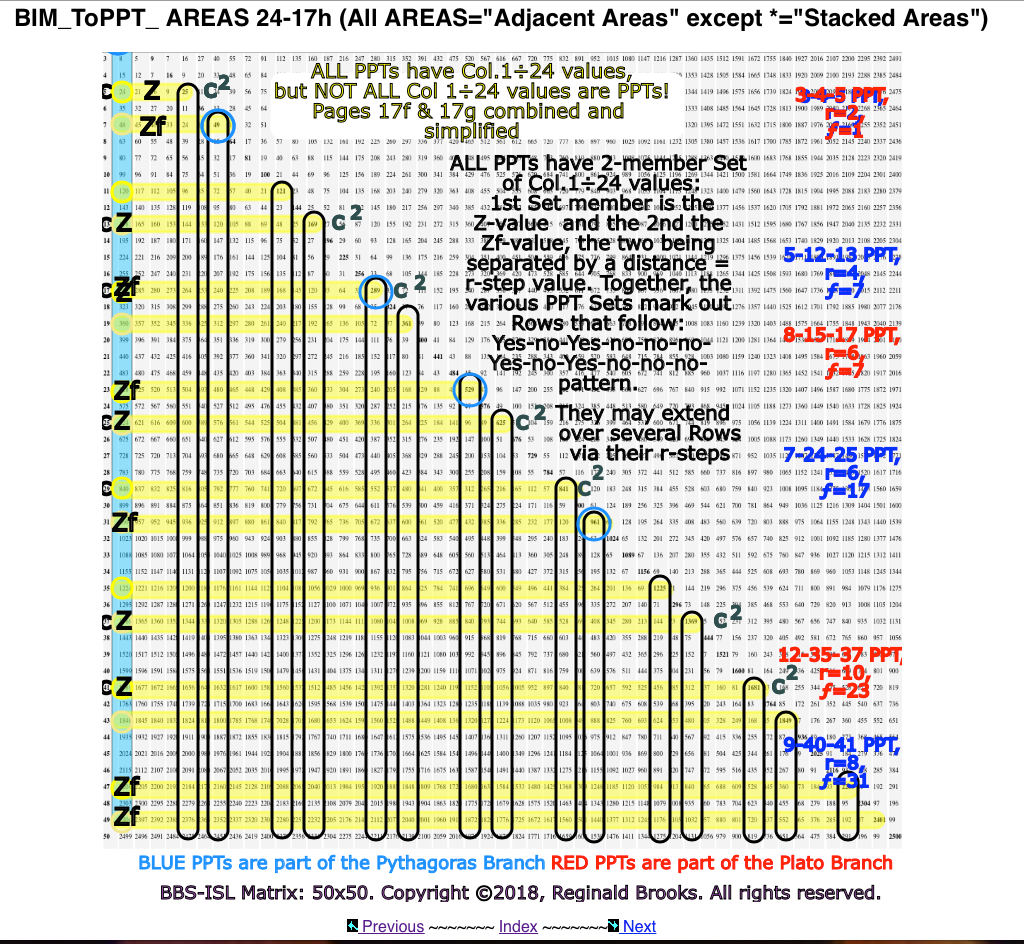
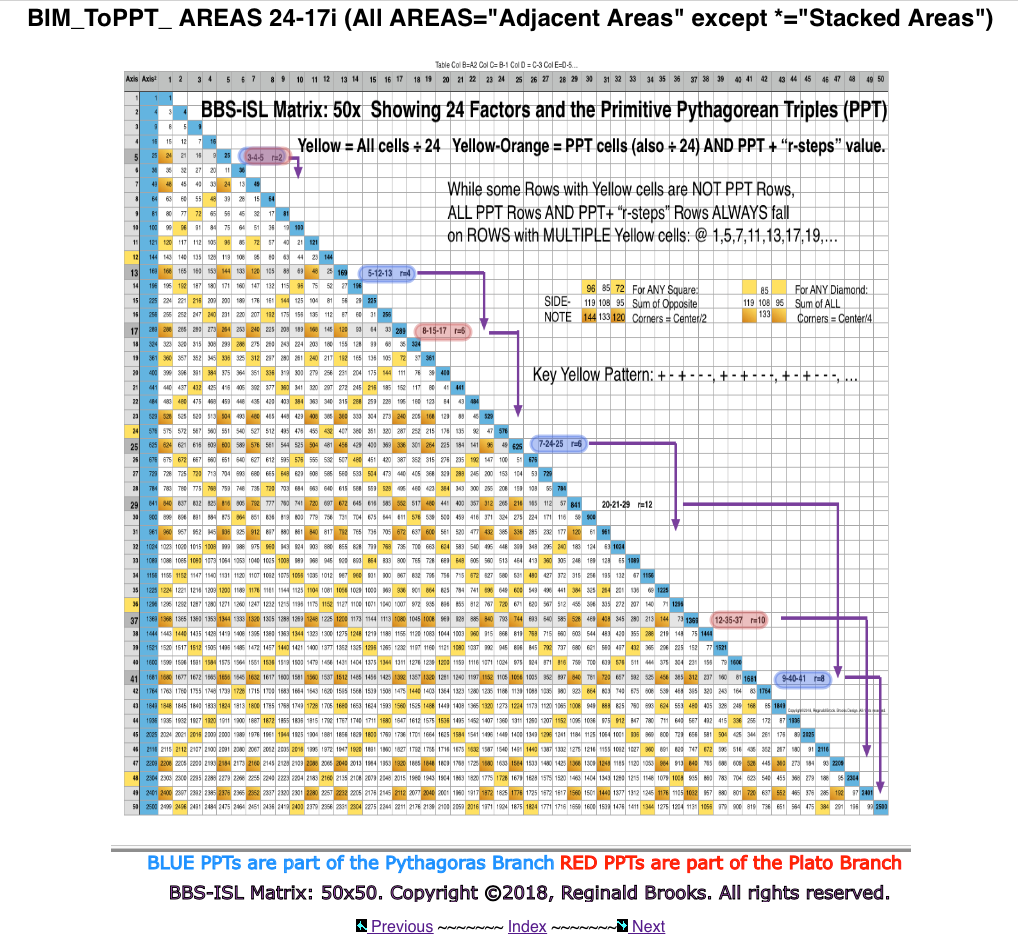
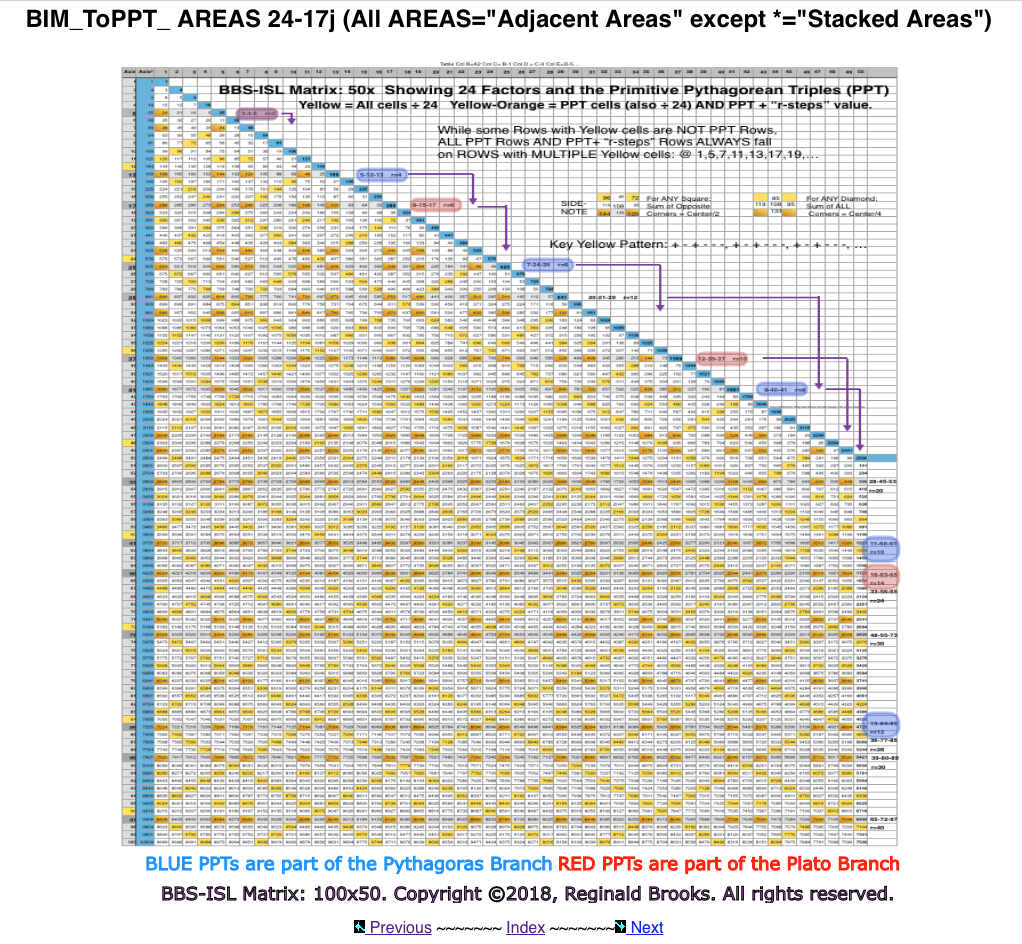
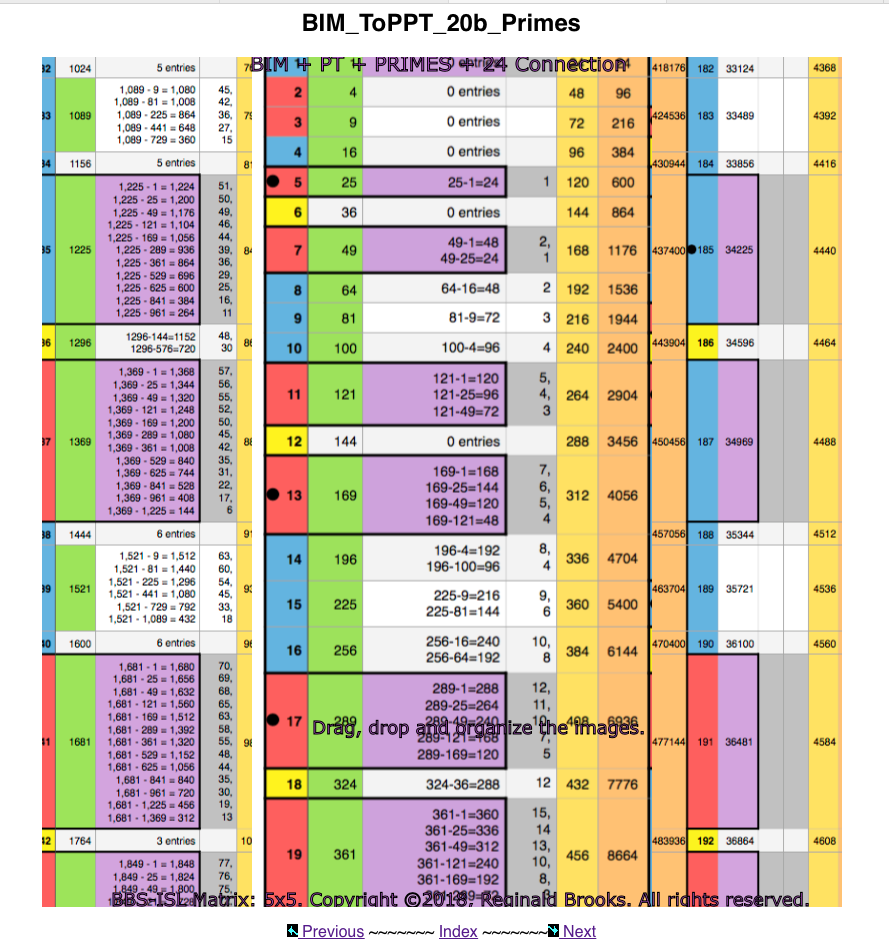
- Table 24 re-introduces the Sub-Matrix 1 and how the PPTs (and PRIMES) are distributed strictly on the ARS.
- Table 25 introduces the full Sub-Matrix 2, with the Columns 1,5,7,11,13,17,19,23,25,29,31,35,37,41,43,47, and 49 values shown in the colored inset boxes across the BIM.
- Table 26 reduces Table 25 down to a 5x1000 BIM to focus primarily on the Col 1 Sub-Matrix 2 values (shown in the colored box insets).
- Table 27 reduces this further to a 5x100 BIM.
- Table 28 reduces this further to a 5x50 BIM.
The details are the same:
These (colored inset boxes) Sub-Matrix 2 values:
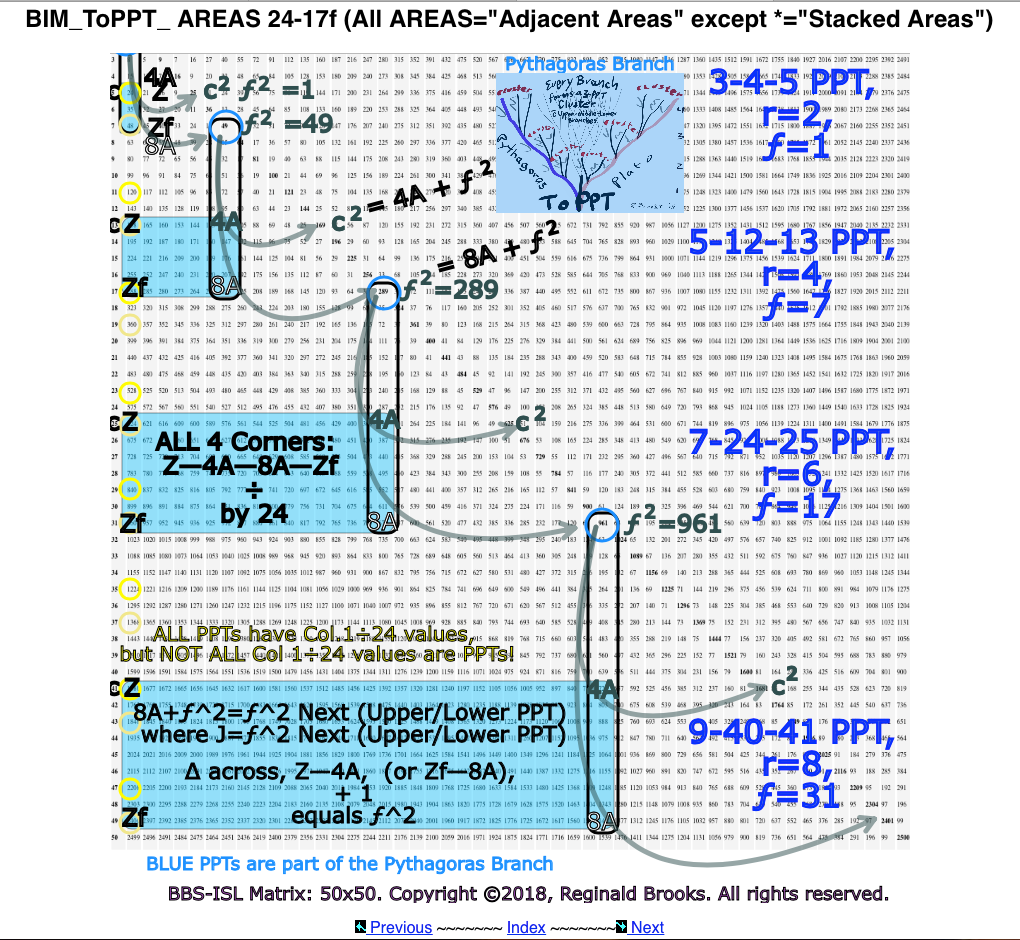
- ALL PPTs have Col 1 ➗4;
- NO PPTs have Col 1 NOT ➗4;
- For any given Active Rows Set, only 1 Row is a ➗4 Row PPT, never both;
- SOME Col 1 ➗4 Rows are NOT PPTs ( starred );
- The NOT PPTs ( starred ) Axis #s are ➗Prime Factors*.
Fool-proof Steps to Find ALL PPTs:
Axis# must be ODD, NOT ➗3 = Active Row Set (ARS) member;
Only 1 of the 2 ARS can be a PPT;
Sub-Matrix Col 1 # MUST be ➗4;
SOME may NOT be PPT if ➗Prime Factor (>5);
Remaining Axis # is a PPT. Exceptions:
Squared #s that are PPTs, remain PPTs when x2 or √x:
- ALL Squared #s that are PPTs, remain PPTs. ANY PPT #(x) times itself, times its square (x2) and/or times it serial products = NEW PPT;
- Example1: 5x5=25, 5x25=125, 5x125=625, 5x625=3125, 5x3125=15625=1252, 5x15625=78125, 5x78125=390625=6252,… products are ALL PPTs;
- Example 2: 97x97=9409, 97x9409=912,673, 97x912,673=88,529,281=94092=ALL PPTs.
Squared #s that are NOT, remain NOT when x2 or √x, as above.
Sub-Matrix 2 Sidebar: Exponentials of the PPTs
Table 29 Exponentials of the first 10 PPTs c-values to be used in Tables 30a-g.
Tables 30a-g The Sub-Matrix 2, when ➗4, and the difference (∆) between this and the next exponential PPT treated this way, is subsequently ➗ by its Sub-Matrix 2 variable, the PREVIOUS exponential within the series is revealed. Restated as an example: When one subtracts 1 from the exponential values of c (the c-value of the PPT) you get the Sub-Matrix 2 value. Divide that by 4 and take the difference (∆) between it and the next. Divide that by 3 to give the PREVIOUS PPT c-value in the series.
The Sub-Matrix 2 variable divisor = 3 = Sub-Matrix 2 value/4 = 12/4. These variables run: 1,3,4,6,7,9,10,...
As to answers to the open questions called above:
what exactly is the relationship between PPTs and PRIMES?
- a loosely threaded connection is quite apparent;
why do they BOTH land on ARS?
- they both must be ODD #s, not ➗3, whose (x2-1)/24 is true;
why do some ARS have both, neither, or one or the other?
- some clouds, some clarity, at least for the PPTs;
can the PRIMES be used to predict the PPTs?
- yes, in the sense that if the PPT candidate is ➗Prime Factor (>5), it will not be a PPT;
can the PPTs be used to predict the PRIMES?
- currently, NO, yet the threaded connections are so great that the pattern will eventually emerge!
BIM÷24: SubMatrix Sidebar: What is the role of 24 in the underlying structure?
SEE: Tables: 33a, 33b, 33c and 33d towards the end of Appendix B for some very NEW INFO on the BIM÷24.
The underlying geometry of the BIM÷24 PRE-SELECTS the Axis Rows into TWO Groups: ARs and NON-ARs. The PPTs and PRIMES are EXCLUSIVELY — as a sufficient, but not necessary condition — found on the ARs and NEVER on the NON-ARs. While both Groups follow (PD2 - PD2)÷24, they do so ONLY within their own respective Groups. They do NOT crossover. This Grouping divide occurs naturally within the BIM as shown in these images below.
The ISL as presented in the BIM is deeply, intimately structured around the number 24 — and its factors: 4,6, 3,8 2,12, and 1,24.
The interplay between these small sets of Numbers generates an incredible amount of richness and complexity with seemingly simplistic BIM itself. This has led to TPISP: The Pythagorean-Inverse Square Connection, and the PRIMES.
 Open in separate browser tab/window to see all.
Open in separate browser tab/window to see all.
BIM➗PPTs and PRIMES
BIM➗PPTs and PRIMES: (Latest: as this work was being prepared, a NEW relationship was found.)
A dovetailing of PPTs and PRIMES on the BIM
The discovery of the Active Row Sets (ARS) — the direct result of the BIM ➗24 — in which it has been found that ALL PPTs and ALL PRIMES are exclusively found on, was in and of itself, a slow an arduous journey.
Once found, it has added a great deal of visual graphic clarity! In simple terms, it simply marks out the obvious. Both the PPTs and the PRIMES can not be on Axis Row #s that are EVEN, nor ➗3. This leaves ONLY Rows that are ODD #s and not ➗3.
The BIM ➗24 marked those Active Row Sets indirectly, by being on either side — i.e., +/- 1 — of the Axis Row # intercepted by the ➗24. Directly, the ARS was shown to be picked out by Sub-matrix 1 and 2 values of the 1st cell Column of those Rows.
So we have the PPTs and the PRIMES occupying the same footprint rows, the ARS Rows. Both as a necessary, but not sufficient requirement, i.e., some ARS Rows do NOT have a PPT or PRIME, or both. ALL PPTs and ALL PRIMES are ALWAYS found on an ARS Row, NEVER on a non-ARS Row. Some ARS Rows may have none, either a PPT or a PRIME, or both.
Nevertheless, on this vast matrix array of ISL whole integer numbers, that the PPTs and PRIMES exclusively occupy the same ➗24-based footprint points to an underlying connection!
The 1st connection was found and written about in the three white papers of 2005-6 on PRIMES:
- Page 2b: Butterfly Primes...let the beauty seep in.
- Page 2c: Butterfly Prime Directive...metamorphosis.
- Page 2d: Butterfly Prime Determinant Number Array (DNA) ~conspicuous abstinence~.
The 2nd connection, as referenced below, has been the latest discovery that Euler’s 6n+1 and 6n-1 pick out, as a necessary — but not sufficient for primality — condition ALL the PRIMES.
When you look at the BIM➗24, you can readily see how this theorem simply picks out the very same ARS Rows! (For ARS 5 and above.)
The BIM➗24 becomes a DIRECT GRAPHIC VISUALIZATION of EULER’s PRIMES = 6n+1 and 6n-1, where n=1,2,3,..
The same holds true for Fermat's (Fermat-Euler) 4n + 1 = Sum of Two Squares Theorem, where 4n + 3 ≠ Sum of Two Squares. The 4n + 1 = Sum of Two Squares = Pythagorean Primes (PTs where c = Prime #).
These are simply those ARs that contain BOTH a PRIME (red circle) AND a PPT (black dot) in the figures.
Note: In any given ARS, only one of the two ARs may be a PPT, while both, neither, or one or the other ARs may be PRIME.
Black dot in a Red circle = Pythagorean Triple = 4n + 1 PRIME candidate = Sum of Two Squares.
The 3rd connection is that for those ARS Rows that do NOT contain PRIMES — e.i., 25, 35, 49, … and have been shown to negate the possibility of the # being prime because it is itself prime factorable — divisible by another set of primes — is ALSO DIRECTLY VISUALIZABLE ON THE BIM➗24 AS THE INTERSECTING PRIME COLUMNS!!!
The 4th connection reveals that the BIM Prime Diagonal (PD) — the simple squares of the Axis #s — defines:
- The ISL itself, as every BIM Inner Grid cell value is simply the difference between its horizontal and vertical PD values;
- The Pythagorean Triples, as every PD cell value points to a PT when one drops down from it to its ARS intercept;
- The PRIMES, as the difference in the squares of any two PRIMES (≧5) — every PD value of a PRIME Axis # — is evenly ➗24.
The 5th connection is that for those ARS Rows— that may or may not contain PPTs and/or PRIMES — their 1,5,7,11,13,17,19,23,25,.. ODD intersecting Columns NOT ➗3, ARE ALL➗24, and, this is ALSO DIRECTLY VISUALIZABLE ON THE BIM➗24 AS THE INTERSECTING COLUMNS (usually depicted graphically in YELLOW-ORANGE boxes/cells on the BIM as part of the diamond with centers pattern) !!!
 This is revealed in the Sub-Matrix 1 figures and tables: the BIM ÷24.
Additionally, Sub-Matrix 2 also selects for ALL ARS as Column 1 ALWAYS ÷4. (See figures.)
In ALL cases, the PRIMES (≧5) are necessary — but not sufficient to insure primality — located on ODD # Rows NOT ÷3. It is as simple as that!
The factors of 24 — 1,24–2,12–3,8–4,6 — when increased or decreased by 1, ultimately pick out ALL ARs. Euler's 6n +/-1 is the most direct, Fermat's 4n + 1 gets the Sums of Two Squares = Pythagorean Primes (while 4n + 3 gets the rest).
Fermat's Little Theorem (as opposed to the more familiar "Fermat's Last Theorem") tests for primality.
But now there is a dead simple way to test for primality:
The difference in the squares between ANY 2 PRIMES (≧5) ALWAYS = n24.
For example, take any random ODD # - 25 —> it must be ÷24 n times to be PRIME. (n=1,2,3,...)
741
7412-52/24 = n= 22877.3 NOT PRIME
189
1892-52/24 = n = 1487.3 NOT PRIME
289
2892-52/24 = n = 3479 PRIME





 If P = X, evenly ➗24, then P = a PRIME Candidate
where, X=evenly➗24, P=Prime, P22=larger Prime Squared, P21=smaller PRIME Squared, n=1,2,3,…
TPISC, The Pythagorean-Inverse Square Connection, has evolved into a connection with the PRIMES (TPISC-P).
How Visualization of the PRIMES on the BIM ÷24 Simplifies Much of the Mysteries of the PRIME Conjectures and What This Means!
Much is made of the PRIME Conjectures: https://primes.utm.edu/notes/conjectures/ & site:primes.utm.edu Prime Gap conjecture
- Goldbach (Strong) Conjecture (every even # is made of two primes)
- Goldbach Tertiary (Weak) Conjecture (every odd # is made of three primes)
- Twin Prime Conjecture (there are an infinite # of primes separated by 2)
- Twin Primes Conjecture (there are an infinite # of primes separated by a fixed # gap)
- Prime Gap (size between consecutive primes)
- Prime Triple Conjecture (there are an infinite # of 3 consecutive primes with ∆ of 6, first and last)
- Prime Quadruple Conjecture (there are an infinite # of 4 consecutive primes with ∆ of 8, first and last)
- Prime k-tuplet Conjecture (there are an infinite # of prime k-tuplets for each* k*)
- Dickson’s Conjecture (there are a lot of primes, Twin, Sophie Germain, k-tuplet,…)
- Pythagorean Primes Conjecture(Pythagorean triples with prime # hypotenuse)
A look at the BIM÷24 grid will quickly give one a visualization of the limits — and expanses — of these conjectures!
(1 above.) This was examined and a proof-solution was offered in 2010 with the Periodic Table of Primes (PTOP), hidden within the BIM.
(2 above.) Work remains.
(3 above.) ALL Primes fall on Active Rows (ARs) within an Active Row Set (ARS) of three Axis #s: two ODDs with an EVEN in-between. The difference (∆) between the ODDs = 2. Thus ANY and ALL Twin Primes — separated by 2 — are seen right here, and only here, directly, on the ARS.
(4-8 above.) Because the ARSs follow a strict Number Pattern Sequence (NPS) in that the EVEN #s are ÷12 — being the endpoint of BIM÷24 — and the bookcased ODD #s are NEVER ÷3, there is a built-in ∆, a natural gap, between the ARS and ODD #s ÷ 3. This means the ARs — that provide a necessary, but not sufficient requirement for ANY PRIME — must necessarily have gaps that are:
taken from the lower ARS #:
- (Twins of) 2, 6, 8, 12, 14, 18, 20,… i.e., up 2, 4, 2, 4, 2, 4, 2,….
taken from the higher ARS #:
- (Twins of) 4, 6, 10, 12, 16, 18, 22,… i.e., up 4, 2, 4, 2, 4, 2, 4,….
(9 above.) Dickson’s Conjecture leads to many of the individual conjectures above. One, the Sophie Germain Prime Conjecture states that if a PRIME #, p, has another PRIME # generated at 2p + 1, it is a Sophie Germain PRIME and that there are an infinite number of these. On the BIM, it is easy to see that any Sophie PRIME is simply taking the lower AR # and ADDING a multiple of 6 — 6x — to get to the next PRIME. Try it: (≧5)5, 11, 23, 29, 41, 53, 83, 89, 113, 131, 173, 179, 191, 233, 239, 251, 281, 293, 359, 419, 431, 443, 491, 509, 593, 641, 653, 659, 683, 719, 743, 761, 809, 911, 953, ... OEIS: A005384. (https://en.wikipedia.org/wiki/Sophie_Germain_prime)
*the lower AR + 2 = higher AR — neither is ÷ by 3, while the lower AR - 2 = ODD# that is ÷ by 3 and NOT an AR.
This works for p≧5:
5+6=11, 11+(2)6=23, 23+6=29, 29+(2)6=41, 53+(5)6=83, 83+6=89, 89+(4)6=113, 113+(3)6=131, 131+(7)6=173, 173+(1)6=179, 179+(2)6=191, 191+(7)6=233, 233+(1)6=239, 239+(2)6=251, 251+(5)6=281, 281+(2)6=293, 293+(11)6=359, 359+(10)6=419, 419+(2)6=431, 431+(2)6=443, 443+(8)6=491, 491+(3)6=509, 509+(14)6=593, 593+(8)6=641, 641+(2)6=653, 653+(1)6=659, 659+(4)6=683, 683+(6)6=719, 719+(4)6=743, 743+(3)6=761, 761+(8)6=809, 809+(17)6=811, 911+(7)6=953, …
It appears that this conjecture really is simply restating Euler’s 6n+1 and 6n-1 — where n=1,2,3,… method for determining ALL PRIMES.
(10 above.) Ironically, the Pythagorean Triples were first to be found on the ARS, and only after reviewing earlier work — the Butterfly Primes — that the connection of the PRIMES to the BIM÷24 was made. Both the Primitive Pythagorean Triples (PPTs) and the PRIMES have the same — again, necessary, but not sufficient requirement — that they occupy EXCLUSIVELY the ARs potentially of any ARS. When the PPTs overlap the PRIMES, we get the Pythagorean Primes. An interesting note is that unlike the PRIMES that can occupy BOTH ARs of a given ARS, the PPTs will NEVER do this, occupying either one or the other, but NEVER BOTH, ARs within a ARS.
Fermat's (Fermat-Euler) 4n + 1 = Sum of Two Squares Theorem, where 4n + 3 ≠ Sum of Two Squares. The 4n + 1 = Sum of Two Squares = Pythagorean Primes (PTs where the hypotenuse, c = Prime #).
Remember, not only does the BIM÷24 reveal the ARs within the ARS, the∆ BETWEEN THE SQUARES OF ANY PAIR OF AR Axis #s (≧5) IS A MULTIPLE OF 24. The latter becomes a necessary, but not sufficient test of both primality, and, PPT validity.
Note that this same ∆ occurs with pairs of two non-AR ODD #s, i.e. 9 and 15. Both are ÷3. 152 - 92 = 144, and 144/24 = 6. A hybrid of an AR and a non-AR ODD pair set will NOT show a ∆ of 24x.
This points to underlying NPS within the BIM (see the pattern below the links):
For the ODD #s2:
∆÷24 vs NOT ∆÷24
∆÷24 in ARS vs ∆÷24 in non-ARS, NEVER a mix of the two
For the EVEN #s2:
∆÷24 vs NOT ∆÷24
∆÷24 includes those in progressive NPS series ∆2, ∆4, ∆6, ∆8, ∆10,… (see Table in Appendix ).
The PPTs and PRIMES are STRICTLY following this NPS within the BIM!
Perhaps the biggest finding here is: The PRIMES — Inverse Square Law Connection! Just like the PPTs! TPISC stands for both The Pythagorean-Inverse Square Connection, AND, The PRIMES-Inverse Square Connection. TP-P-ISC, TP/P-ISC, TP/PISC, TPPISC, or TP-IS-PC,...
The connection between that Universal Law, the ISL, — the underlying law of ALL of spacetime —and the PRIMES — the fundamental "quarks" of the number quantity system, AND, the Pythagorean Triples — the fundamental right-triangle/rectangle form of that same geometry — is without out a doubt the most intriguing, beguiling, and misunderstood relationship we are only just NOW getting a real glimpse at. The future looks very promising!
Reference:
"A New Kind of Prime
The twin primes conjecture’s most famous prediction is that there are infinitely many prime pairs with a difference of 2. But the statement is more general than that. It predicts that there are infinitely many pairs of primes with a difference of 4 (such as 3 and 7) or 14 (293 and 307), or with any even gap that you might want."
Quote is from Quanta Mag 9/26/19 article: Big Question About Primes Proved in Small Number Systems
by Kevin Hartnett
- Twin Primes
- Primes separated by other EVEN numbers
- Euler's 6n+1 and 6n-1
- Fermat-Euler's 4n + 1= Sum of Two Squares Theorem (Pythagorean Primes)
- Dickson's Conjectures: Sophie Germain Primes
- Goldbach Conjecture (Euler's "strong" form)
- Primes - BIM - Pythagorean Triples
~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~
A new and easy visualization!
PRIME GAPS
Game Board
There is a new game board in town. It has actually been around for awhile, but few know of it. It's basically a matrix grid of natural numbers that defines the Inverse Square Law (ISL). It's called the BIM, short for the BBS-ISL Matrix. Every grid cell is uniquely occupied by a given number that is simply the difference between the horizontal and vertical intercept values of the main "Prime Diagonal" (not Prime number diagonal) that mirror-divides the whole matrix.
If you show all the matrix values that are evenly divisible by 24, a criss-crossing pattern of diamond-diagonal lines will appear and this ends up giving us a unique visual on the distribuition of ALL PRIMES!
Basically, all ODDs (3 and greater for this presentation) fall into a repetitive pattern of:
ODD ÷3—Not÷3—Not÷3—÷3—Not÷3—Not÷3—÷3—Not÷3—Not÷3—÷3—Not÷3—Not÷3—÷3...
The matrix ÷24 described above, nicely picks out these sets of —Not÷3—Not÷3 that we call Active Row Sets (ARS). Each ODD member of the ARS is referred to as an Active Row (AR).
The ÷3 ODD Rows that lie between are called Non-Active Rows, or NA.
It is a necessary, but not sufficient condition, that ALL PRIMES are strictly located on ARs. NO exceptions, except for some ARs have NO PRIMES.
Another striking visualization is that ALL Primitive Pythagorean Triples (PPTs) also lie only on the ARs, following the same necessary, but not sufficient, condition. NO exceptions here as well, except for some ARs also have NO PPTs. In addition, only one of the ARs within an ARS can have a PPT.
So any AR within an ARS can have 0/1 PRIMES and/or 0/1 PPTs in any combination, only with the one caveat: that only 1 PPT/ARS is allowed.
Now, not to belabor this BIM game board, let's talk PRIME GAPS!
Prime Gaps
Let's refer to the lower number value for the ARS as "Lower" and the higher as "Upper." All are ODDs. As will become apparent, you can always tell if your ODD AR is "Lower/Upper" simply by adding 2 and ÷3: if the result evenly ÷3 it is "Upper" and if not, "Lower."
The Even Gap between primes strictly follows this pattern: (all are necessary but not sufficient conditions for primality)
For any given set of twin primes, or any single prime, that is the smaller "Lower" of an AR set:
- Even Gap must be 2, 6, 8, 12, 14, 18, 20, 24, 26, 30, 32, 36, 38, 42, 44, 48, 50,…
- Example: P=5: 7, 11, 13, 17, 19, 23, (25), 29, 31, (35), 37, 41, 43, 47, (49), 53, (55)
- P + 2, P + 2+4, P + 2+6, P + 2+10, P + 2+12, P + 2+16, P + 2+18, P + 2+22, P + 2+24,…
- P+21, P+2+22, P+23, P+22+23, P+2+22+23, P+2+24, P+22+24, P+23+24, P+2+2324
- The Even Gap difference pattern follows: 2-4-2-4-2-4-….
For any given set of twin primes, or any single prime, that is the larger "Upper" of an AR set:
- Even Gap must be 4, 6, 10, 12, 16, 18, 22, 24, 28, 30, 34, 36, 40, 42, 46, 48, 52, 54.…
- Example: P=7: 11, 13, 17, 19, 23, (25), 29, 31, (35), 37, 41, 43, 47, (49), 53, (55), 59, 61
- P + 4, P + 2+4, P + 2+8, P + 2+10, P + 2+14, P + 2+16, P + 2+20, P + 2+22, P + 2+26, P + 2+28,
- P+22, P+2+22, P+2+23, P+22+23, P+24, P+2+24, P+2+22+24, P+23+24, P+22+23+24, P+2+22+23+24,
- The Even Gap difference pattern follows: 4-2-4-2-4-2-…. and is identical in the middle, not the start!
One can readily see that all this is simply the natural result of two ARs alternating with a NA row:
AR—AR—NA—AR—AR—NA—AR—AR—NA—AR—AR—NA—…
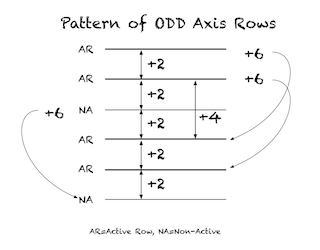
“Lower” AR number
AR—5
AR—7
NA—9
AR—11
AR—13
NA—15
AR—17
AR—19
NA—21
AR—23
AR—25
NA—27…
It is 6 steps, i.e. +6, from any NA to the next NA, from any “Lower” AR to the next “Lower” AR, from any “Upper” AR to the next “Upper” AR. ALL of the various EVEN GAPS may be shown to be a direct consequence of the natural number sequence and easily visualized on the BIM.
To any “Lower” Active Axis Row ODD:
- Add 2, 4, or 6,…
- If sum is ÷3, it is a NA
- If sum is NOT÷3, it is an AR number and a PRIME (or PPT) candidate.
“Upper” AR number
AR—7
NA—9
AR—11
AR—13
NA—15
AR—17
AR—19
NA—21
AR—23
AR—25
NA—27…
To any “Upper” Active Axis Row ODD:
- Add 2, 4, or 6,…
- If sum is ÷3, it is a NA
- If sum is NOT÷3, it is an AR number and a PRIME (or PPT) candidate.
Again, It is 6 steps, i.e. +6, from any NA to the next NA, from any “Lower” AR to the next “Lower” AR, from any “Upper” AR to the next “Upper” AR. ALL of the various EVEN GAPS may be shown to be a direct consequence of the natural number sequence and easily visualized on the BIM.
The ARS pattern on the BIM clearly shows the above patterns and may be extrapolated to infinity:
pg3.png)
PRIME Conjectures
A number of PRIME conjectures have been shown to be easily visualized on the BIM:
Reference: TPISC IV: Details: BIM + PTs + PRIMES
The factors of 24 — 1,24–2,12–3,8–4,6 — when increased or decreased by 1, ultimately pick out ALL ARs. Euler's 6n +/-1 is the most direct, Fermat's 4n + 1 gets the Sums of Two Squares = Pythagorean Primes(while 4n + 3 gets the rest).
Fermat's Little Theorem (as opposed to the more familiar "Fermat's Last Theorem") tests for primality.
But now there is a dead simple way to test for primality:
The difference in the squares between ANY 2 PRIMES (≧5) ALWAYS = n24.
For example, take any random ODD # - 25 —> it must be ÷24 n times to be PRIME. (n=1,2,3,...)
741
7412-52/24 = n= 22877.3 NOT PRIME
189
1892-52/24 = n = 1487.3 NOT PRIME
289
2892-52/24 = n = 3479 PRIME
PRIMES vs NO-PRIMES
I would be remiss if I did not mention that throughout this long journey that began with the Inverse Square Law and the Primtive Pythagorean Triples that the PRIMES kinda of just fell out. They just kept popping up. Not the least, but certainly not without effort, the BIM actually directly visualizes ALL of the NO-PRIMES. In doing so, one is left with information that is simply the inverse of the PRIMES. Subtract the NO-PRIMES information from the list of ODDS (disregarding 2) and what remains are ALL the PRIMES! A simple algebraic expression falls out from that:
NP = 6yx +/- y
letting x=1,2,3,… and y=ODDs 3,5,7,… with the only caveat is that if you don't first eliminate all the ÷3 ODDS, you must include exponentials of 3 (3x) in the NP tally.
Goldbach Conjecture (Euler's "strong" form)
In 2009-10, a solution to Euler's "strong" form of the Goldbach Conjecture "that every even positive integer greater than or equal to 4 can be written as a sum of two primes" was presented as the BBS-ISL Matrix Rule 169 and 170. This work generated a Periodic Table of Primes (PTOP) in which Prime Pair Sets (PPsets) that sequentially formed the EVEN numbers were laid out. It is highly patterned table. A recently annotated version is included with the original below. (See above link for details.)
It turned out this PTOP was actually embedded — albeit hidden — within the BIM itself as shown in Rule 170 and here, too, a recently annotated version is included below. (See above link for details.)
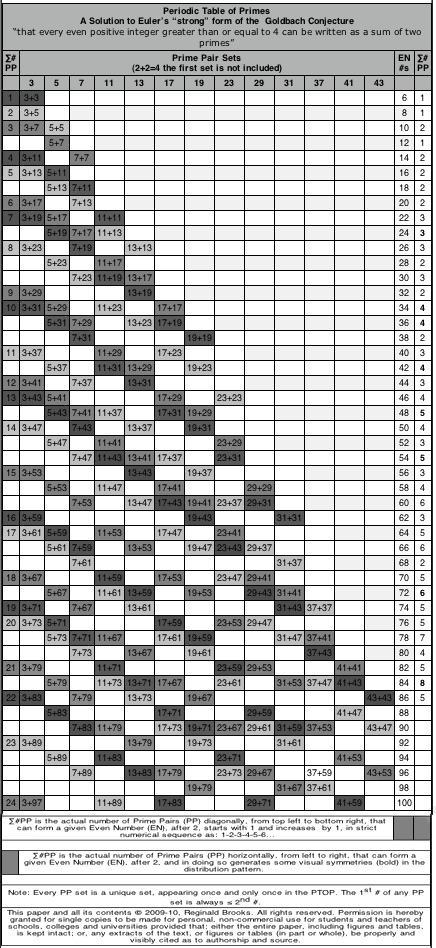
Rule 169: Periodic Table of Primes.
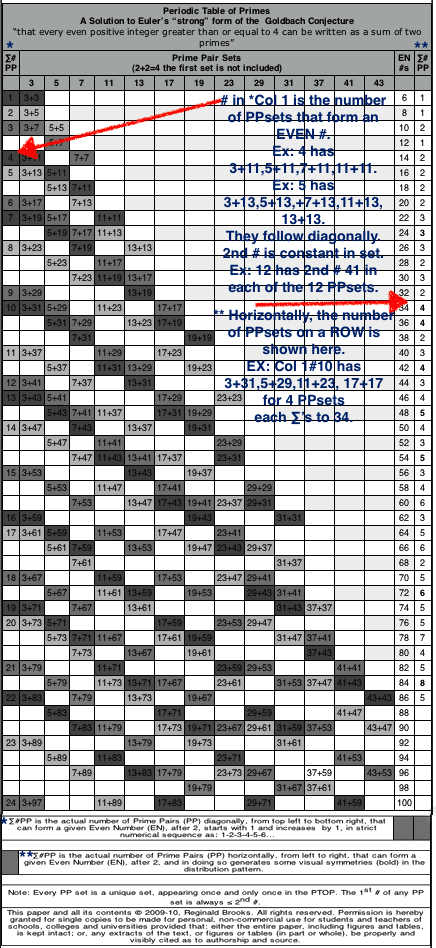
Rule 169: annotated
 Rule 170: Periodic Table of Primes (PTOP): embedded within Brooks (Base) Square.
Rule 170: Periodic Table of Primes (PTOP): embedded within Brooks (Base) Square.
 Rule 170: annotated
Rule 170: annotated
LINKS:
MathspeedST: TPISC Media Center
BACK: ---> Simple Path BIM to PRIMES on a separate White Paper
BACK: ---> PRIMES vs NO-PRIMES on a separate White Paper
BACK: ---> TPISC_IV: Details_BIM+PTs+PRIMES on a separate White Paper
BACK: ---> PRIME GAPS on a separate White Paper (This work.)
A NEW UPDATE: scroll down below these references!
Additional useful links:
See Appendix B: Tables 31-33 for more info.
https://en.wikipedia.org/wiki/Goldbach%27s_conjecture
https://en.wikipedia.org/wiki/Goldbach%27s_weak_conjecture
https://en.wikipedia.org/wiki/Pythagorean_triple
https://en.wikipedia.org/wiki/Twin_prime
https://en.wikipedia.org/wiki/Prime_gap
https://en.wikipedia.org/wiki/Prime_triplet
https://en.wikipedia.org/wiki/Prime_quadruplet
https://en.wikipedia.org/wiki/Prime_quadruplet#Prime_quintuplets
https://en.wikipedia.org/wiki/Prime_k-tuple
https://en.wikipedia.org/wiki/Dickson%27s_conjecture
https://en.wikipedia.org/wiki/Sophie_Germain_prime
https://en.wikipedia.org/w/index.php?search=Pythagorean+Primes&title=Special%3ASearch&go=Go
https://en.wikipedia.org/wiki/Prime_k-tuple
https://en.wikipedia.org/wiki/Fermat%27s_theorem_on_sums_of_two_squares
https://en.wikipedia.org/wiki/Pythagorean_prime
https://en.wikipedia.org/wiki/Fermat%27s_little_theorem
https://en.wikipedia.org/wiki/Euler%27s_theorem
https://en.wikipedia.org/wiki/Euclid–Euler_theorem
http://mathworld.wolfram.com/Eulers6nPlus1Theorem.html
What is the underlying NPS of the BIM ÷24?
Earlier we found:
For the ODD #s2
- ∆÷24 vs NOT ∆÷24
- ∆÷24 in ARS vs ∆÷24 in non-ARS, NEVER a mix of the two
For the EVEN #s2
- ∆÷24 vs NOT ∆÷24
- ∆÷24 includes those in progressive NPS series ∆2, ∆4, ∆6, ∆8, ∆10,… (see Table in Appendix ).
The PPTs and PRIMES are STRICTLY following this NPS within the BIM!
But what about just the BIM ÷24. How does this pattern out?
Let’s dispense with the EVENs first.
If one takes the EVEN #s on either side of the ARS + the EVEN # in the MIDDLE of the ARS, we have a new set. Let’s call it the EVENs Set (ES).
Well, it turns out there are two versions of the ESs and they alternate down the PD. Let’s call them ES1 and ES2 and they go: ES1-ES2-ES1-ES2,…
If we plot the ESs along the PD it will look like this (remember these are the squares of the EVEN Axis #s):
16 — 36 — 64 100 —144 — 196
256 —324— 400 484 — 576 — 676
784 —900—1024 1156—1296—1444
1600—1764—1936 2116—2304—2500
The ES1 are on the Left, the ES2 are on the Right.
The ÷24 NPS of the ES1 andES2 play out as:
Both group sets bookend the ARS with an ODD #÷3 (NON-ARS ODD) between.
The OUTER ends of ES1 are ∆/24 and the OUTER ends of ES2 are ∆/24.
The MIDDLE of ES1 are ∆/24 and the MIDDLE of ES2 are ∆/24.
There is NO MIXING between sets and NO MIXING OUTER with MIDDLE #s.
- The MIDDLE ES1 is ÷ by the 1st MIDDLE of the whole ES1 set.
- The MIDDLE ES2 is ÷ by the 1st MIDDLE of the whole ES2 set.
ES1 ÷ 16 ÷ 8 ÷ 4 ÷ 2 OUTER; MIDDLE ÷ 36, NEVER ÷ 24. (NOTE: these are the PD#s and not the ∆ in PD#s.)
ES2 ————÷ 4 ÷ 2 OUTER; MIDDLE ÷ 36, ALWAYS ÷ 24. (NOTE: these are the PD#s and not the ∆ in PD#s.)
A look at the BIM ÷24 shows that ALL MIDDLE PDs of their ESs are ÷12 and graphically: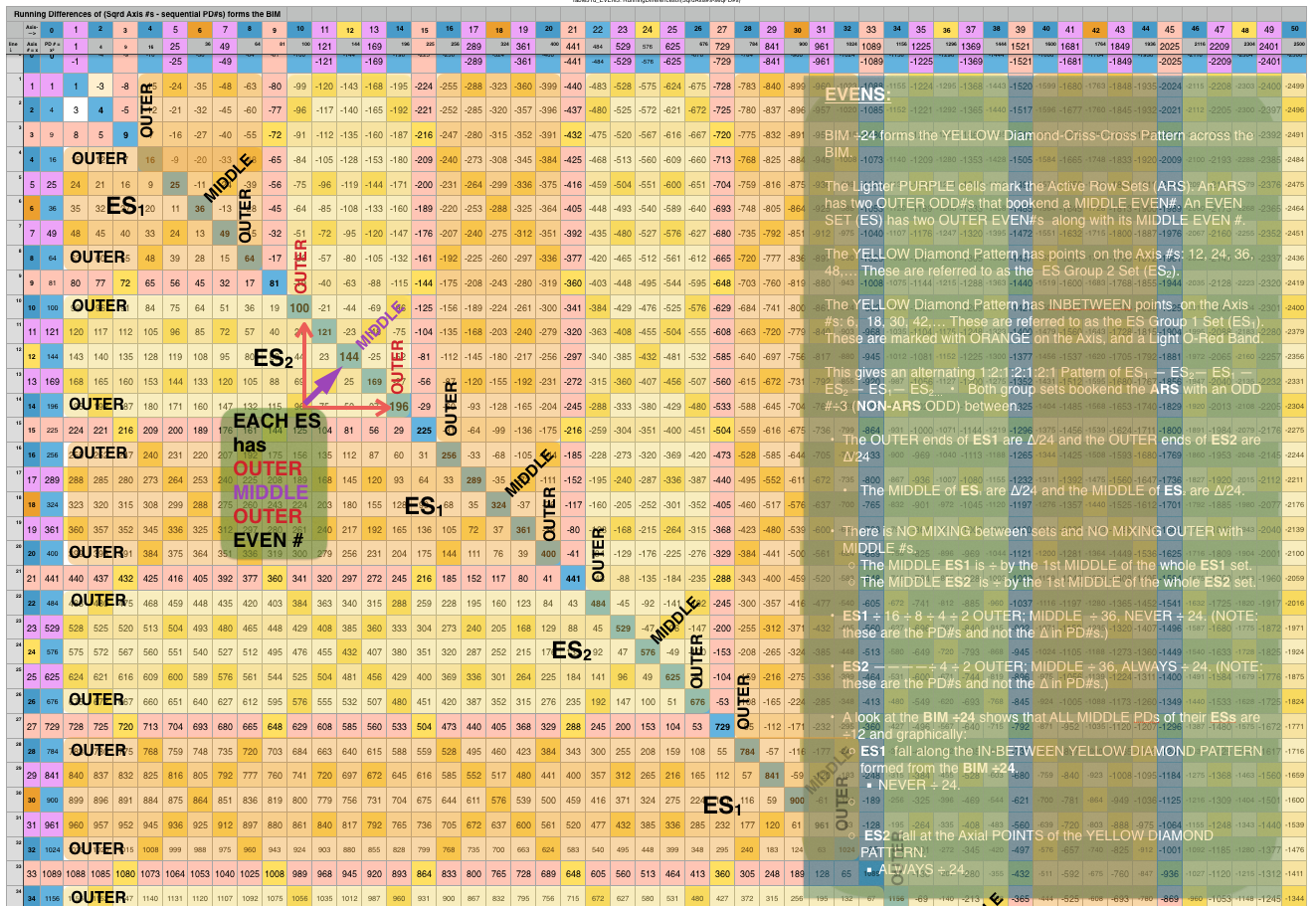 Table 31d. Snapshot of the PDF showing the EVENS role in the BIM ÷24 Distribution.
Table 31d. Snapshot of the PDF showing the EVENS role in the BIM ÷24 Distribution.
ES1 fall along the IN-BETWEEN YELLOW DIAMOND PATTERN formed from the BIM ÷24.
- NEVER ÷ 24.
ES2 fall at the Axial POINTS of the YELLOW DIAMOND PATTERN.
- ALWAYS ÷ 24.
 Table31d PDF sequence. The EVENS. Open the PDFs in a separate tab/window to see all pages.
Table31d PDF sequence. The EVENS. Open the PDFs in a separate tab/window to see all pages.
 Table 33c. The EVENS
Table 33c. The EVENS
So now that we have established that the EVENS, too, reveal a ÷24 expression within the BIM, let's move on the ODDS.
What about the ODDs?
We know that the ODDs ÷3 are the separators of the EVEN's ES1 and ES2 . They are also a separate player in the whole ODDs set in that though their PDs are ÷24, they are NOT part of the ARS. And as NON-ARs they do NOT MIX with the AR ODDs.
We will continue to label the two groups as ARs and NON-ARs.
Earlier we found:
For the ODD #s2
- ∆÷24 vs NOT ∆÷24
- ∆÷24 in ARS vs ∆÷24 in non-ARS, NEVER a mix of the two.
More precisely:
ALL ARs2 are ∆/24, and, NEVER ÷3, and after subtracting (-1) are ALWAYS ÷24, and, ALL now ÷3.
ALL NON-ARs2 are ∆/24, and, ALWAYS ÷3, and after subtracting (-1) NEVER ÷24, but ALL ÷9 ÷3.
There is NO MIXING between groups.
Additionally, the ODD AR group may be further divided into:
ODD Set 1 (OS1): (Like the EVENS, ES1) for IN-BETWEEN YELLOW DIAMOND Rows 6,18,30,42,...
ODD Set 2 (OS2): (Like the EVENS, ES2) for the POINTS of the YELLOW DIAMOND Rows 12,24,36,...
However, here, BOTH groups ARE MIXABLE, i.e. ∆/24 across OS1 and OS2.
What really becomes interesting about the ODDs on the BIM ÷24 is that, all by themselves without regard to the PPTs or PRIMES, they form a deep, underlying NPS ALL BASED ON THEIR ∆s/24!
In a nutshell, if you take each ODD #, square it (that's the PD#) and now sequentially substract the ODD PDs below it, and then ÷24, the results will generate a tightly connected NPS across the ODDS on the BIM.
The ARs2 1-25-49-121-169-289-361-529-625,… (12-52-72-112-132-172-192-232-252,) subtraction=ALL ARs.
The NON-ARs2 9-81-225-441-729,… (32-92-152-212-272,…) subtraction=ALL NON-ARs.
pg2.png) Here is a quick look at the AR and NON-AR Distribution. Open the PDFs below in a separate tab/window.
Here is a quick look at the AR and NON-AR Distribution. Open the PDFs below in a separate tab/window.
pg3.png) Here is a quick look at the AR and NON-AR Distribution. Open the PDFs below in a separate tab/window.
Here is a quick look at the AR and NON-AR Distribution. Open the PDFs below in a separate tab/window.
+50x50.pdf) Table 33a. ODDs AR and NON-AR Distribution PDF. Open the PDFs in a separate tab/window to see all pages.
Table 33a. ODDs AR and NON-AR Distribution PDF. Open the PDFs in a separate tab/window to see all pages.
 Table 33b. ODDs sequenced PDF. Open the PDFs in a separate tab/window to see all pages.
Table 33b. ODDs sequenced PDF. Open the PDFs in a separate tab/window to see all pages.
 Table 33c ODDs_more detail PDF. Open the PDFs in a separate tab/window to see all pages.
Table 33c ODDs_more detail PDF. Open the PDFs in a separate tab/window to see all pages.
 Table 33d-2-1
Table 33d-2-1

Table 33d-2-2
 Table 33d-2
Table 33d-2
UPDATE: Finally, the NEW relationship between the BIM÷24 and the PRIMES has been found! See the bottom of APPENDIX B for the tables that document this work! From the APPENDIX B:
Back to the Table 31 sequences. Table 31a... series, along with the previous Table33 series, uncovers how the PRIMES were found within the BIM both by algebra and geometry. This has been reduced to a focus white paper: "PRIMES vs NO-PRIMES that is a condensed summary of this work. One may benefit from looking over this paper prior to the study of these more elaborate tables. A summary from the paper is presented here:
SUMMARY*
(~from "*Simple Path from the BIM to the PRIMES" that presents the algebraic-geometry method.)
How do we go from the simple grid of the BIM (BBS-ISL Matrix) to identifying the PRIMES?
The BIM is a symmetrical grid — divided equally down its diagonal center with the Prime Diagonal (PD) — that illuminates the Number Pattern Sequence (NPS) of the Inverse Square Law (ISL) via simple, natural Whole Integer Numbers (WIN).
The BIM Axis numbers are 1,2,3,.. with 0 at the origin.
The Inner Grid (IG) contains EVEN and ODD WIN, but except for the 1st diagonal next to the PD — a diagonal that contains ALL the ODD WIN — there are NO PRIMES (NO-PRIMES, NP) on the SIG (Strict Inner Grid).
The PD WIN are simple the square of the Axis WIN.
ALL the IG WIN result from subtracting the horizontal from the vertical intersection of the PD.
Dropping down a given PD Squared WIN (>4) until it intersects with another squared WIN on a Row below will ALWAYS reveal that Row to be a Primitive Pythagorean Triple (PPT) Row, whose hypotenuse, c, lies on the intersecting PD. ALL PPTs may be identified this way.
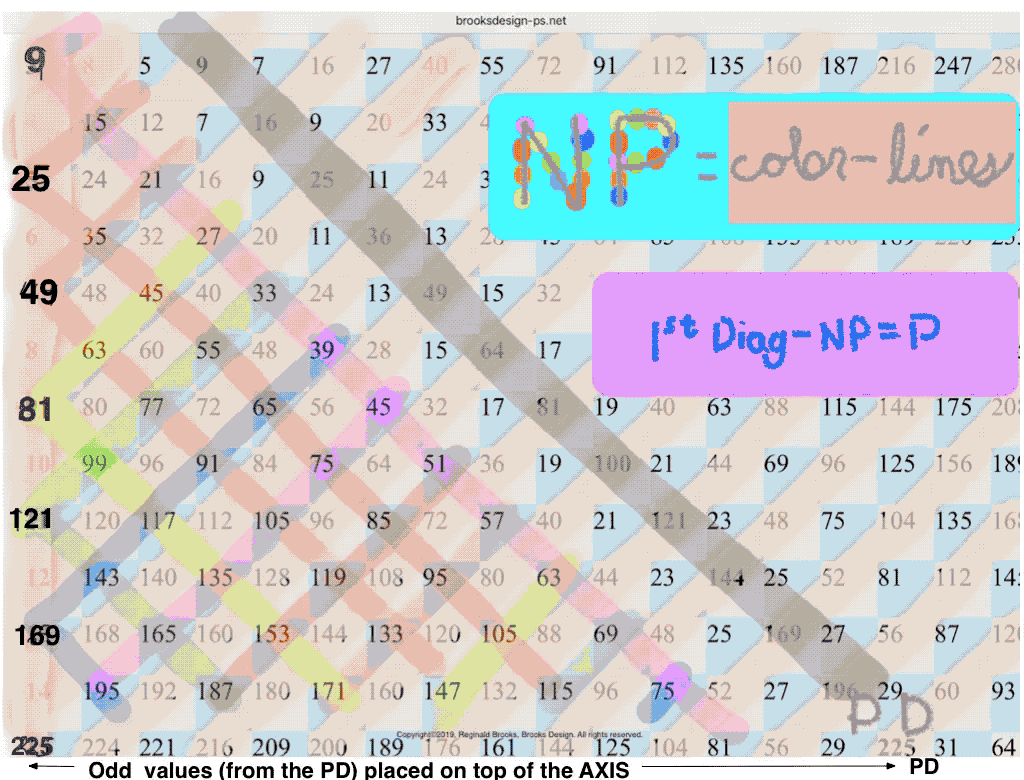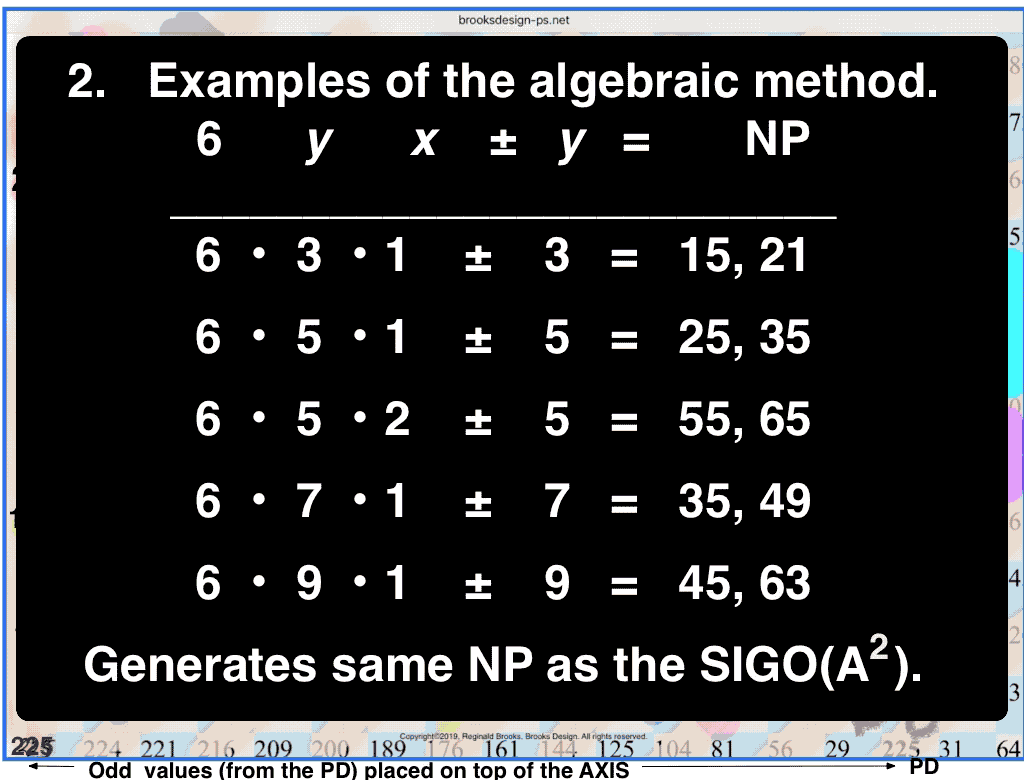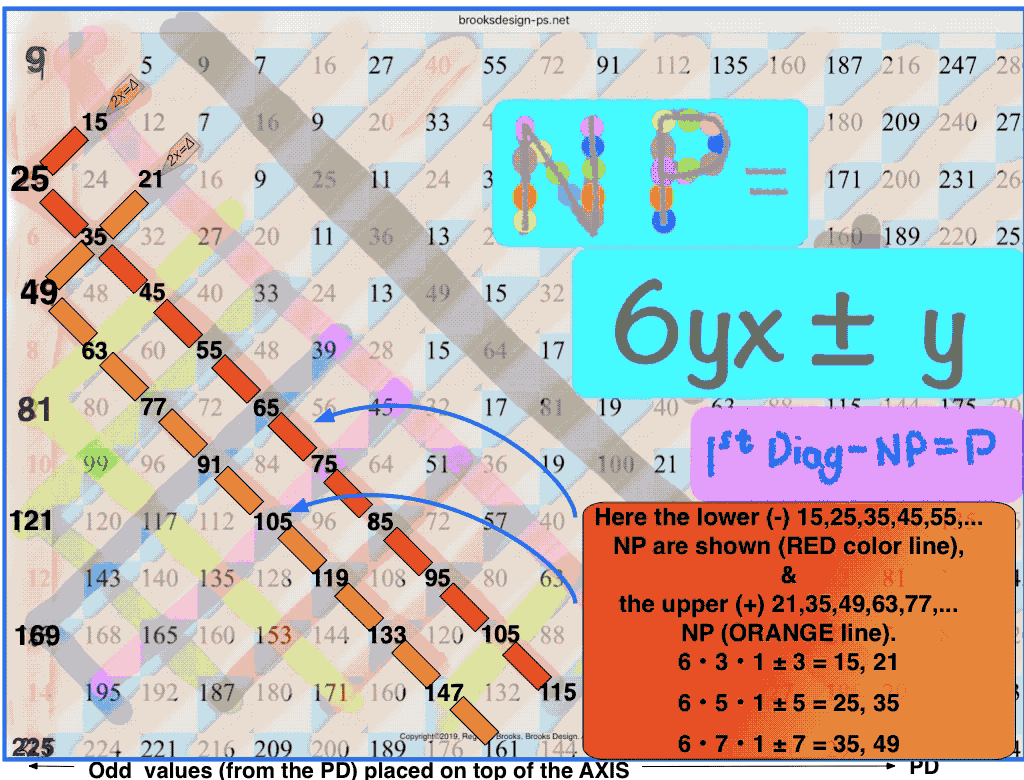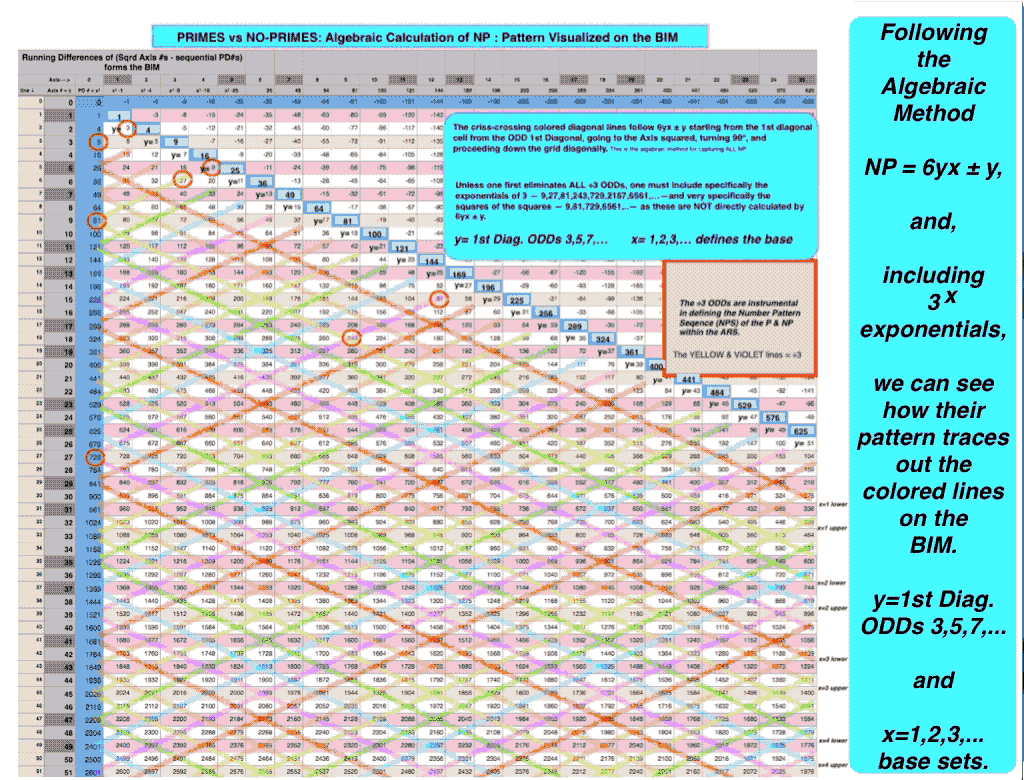
Dividing the BIM cell values by 24 — BIM÷24 — forms a criss-crossing DIAMOND NPS that divides the overall BIM into two distinct and alternating Row (and Column) bands or sets:
- ODD WIN that are ÷3 and referred to as NON-ARs;
- ODD WIN that are NOT ÷3 and referred to as ARs, or Active Rows;
- The ARs ALWAYS come in pairs — with an EVEN WIN between — as the UPPER and LOWER AR of the ARS (Active Row Set);
ALL PPTs and ALL PRIMES ALWAYS are found exclusively on the ARs — no exceptions.
By applying:
(1) *
let y = odd number (ODD) 3, 5, 7,… and x = 1, 2, 3,... one generates a NP table containing ALL the NP;
*True if ÷3 ODDs are first eliminated, otherwise ADD exponentials of 3 to the NP pool;
Eliminating the NP — and the NP contain a NPS — from ALL the ODD WIN, reveals the PRIMES (P).
A necessary, but not sufficient confirmation — but not proof — of primality is found by finding the even division of 24 into the difference of the square of ANY two PRIMES as:
(2) (P2)2 - (P1)2 =
let
Be aware that this also holds true for ALL the AR NP. The P and NP are NOT ÷3, and are both part of the ARS and therefore any combination of the two squared differences will be ÷24:
(3) (NP2)2 - (NP1)2 =
(4) (NP2)2 - (P1)2 =
(5) (P2)2 - (NP1)2 =
The ÷3 NON-AR set is separately ÷24, but can NOT be mixed with members of the AR set (ARS) as:
(6) (NON-AR-NP2)2 - (NON-AR-NP1)2 = n24
(7) (NON-AR-NP2)2 - (NP1)2 ⧣
(8) (NP2)2 - (NON-AR-NP1)2 ⧣
(9) (P2)2 - (NON-AR-NP1)2 ⧣
(10) (NON-AR-NP2)2 - (P1)2 ⧣
The division into AR and NON-AR sets has a NPS that ultimately define the elusive pattern of the P.
Furthermore, may be re-arranged to:
(11)
(12)
asking whether any given ODD (>3) is a P or NP, it is exclusively a NP if, and only if, y reduces to the same value after applying x. As y is effectively an ODD of either a PRIME or composite of PRIMES factor*, one only needs to satisfy a single instance to validate NON-Primality.
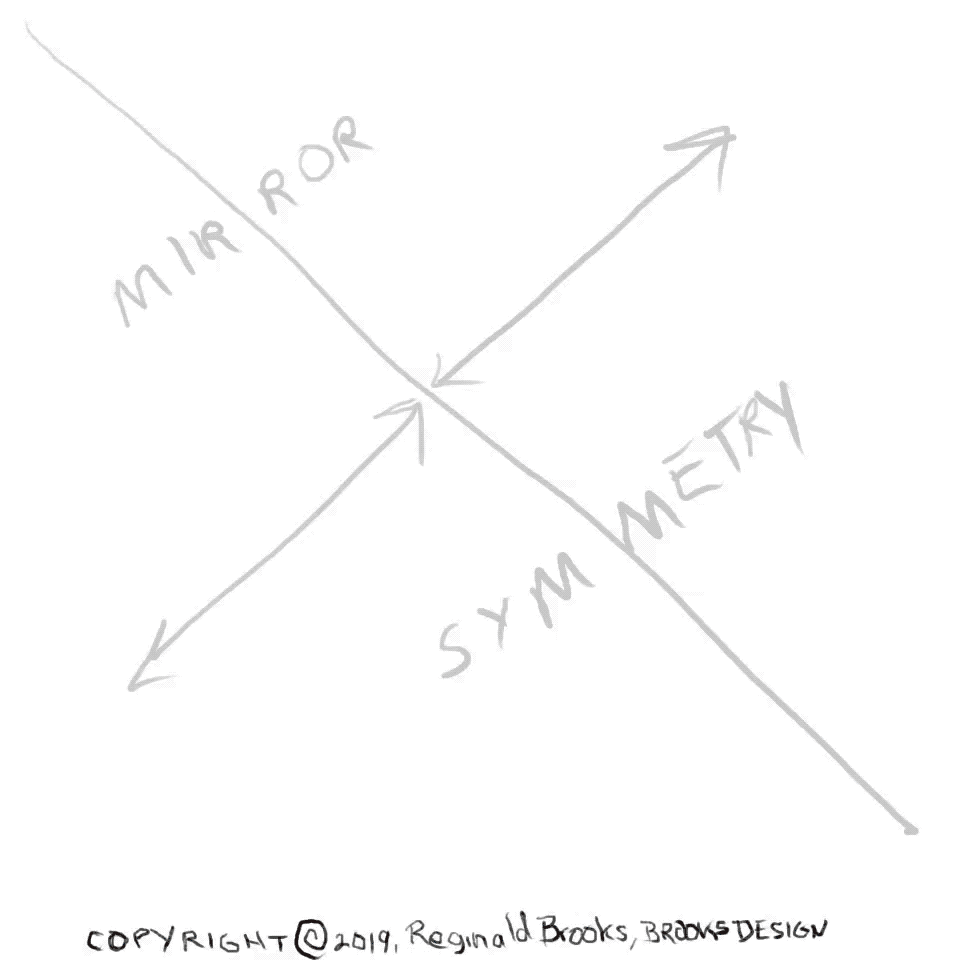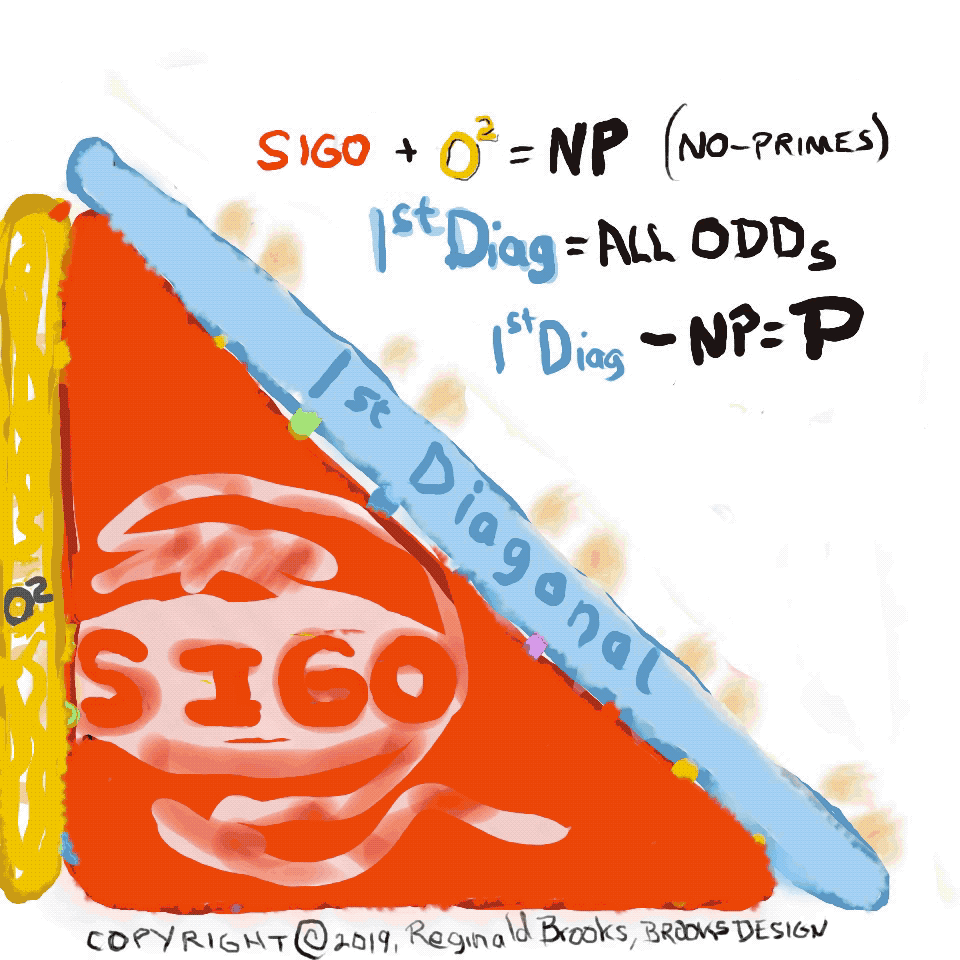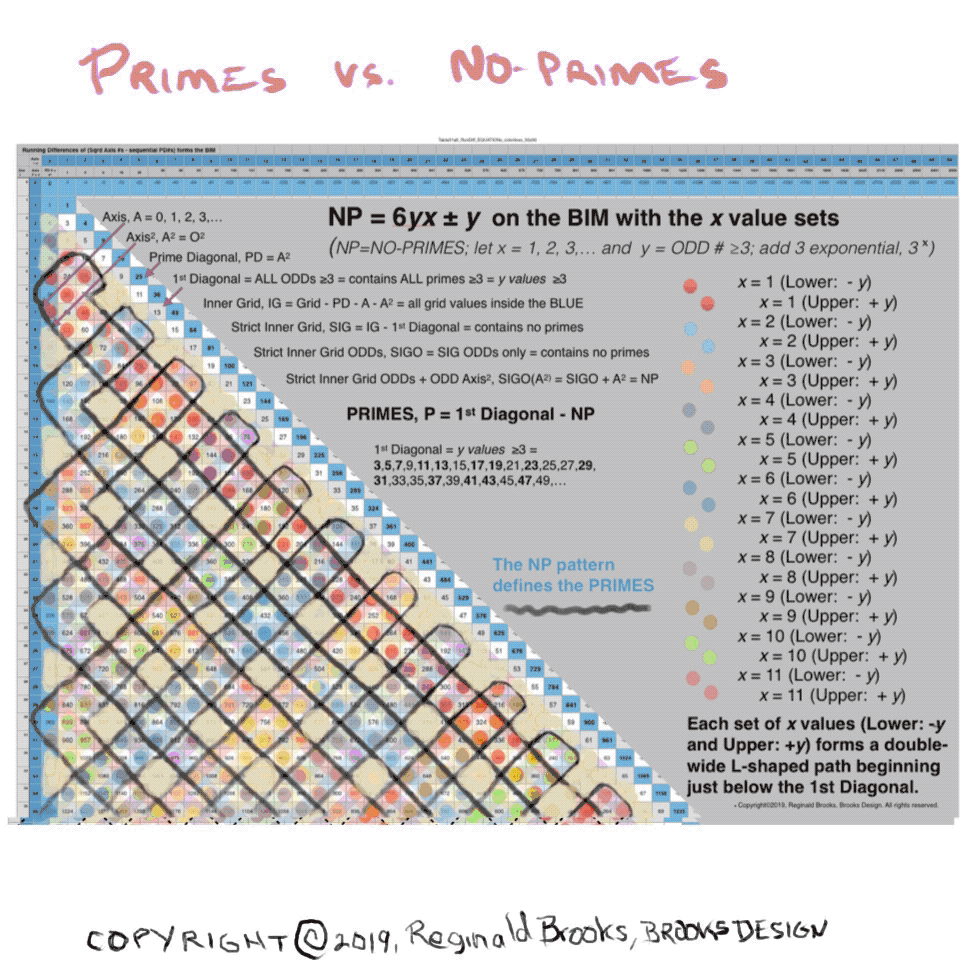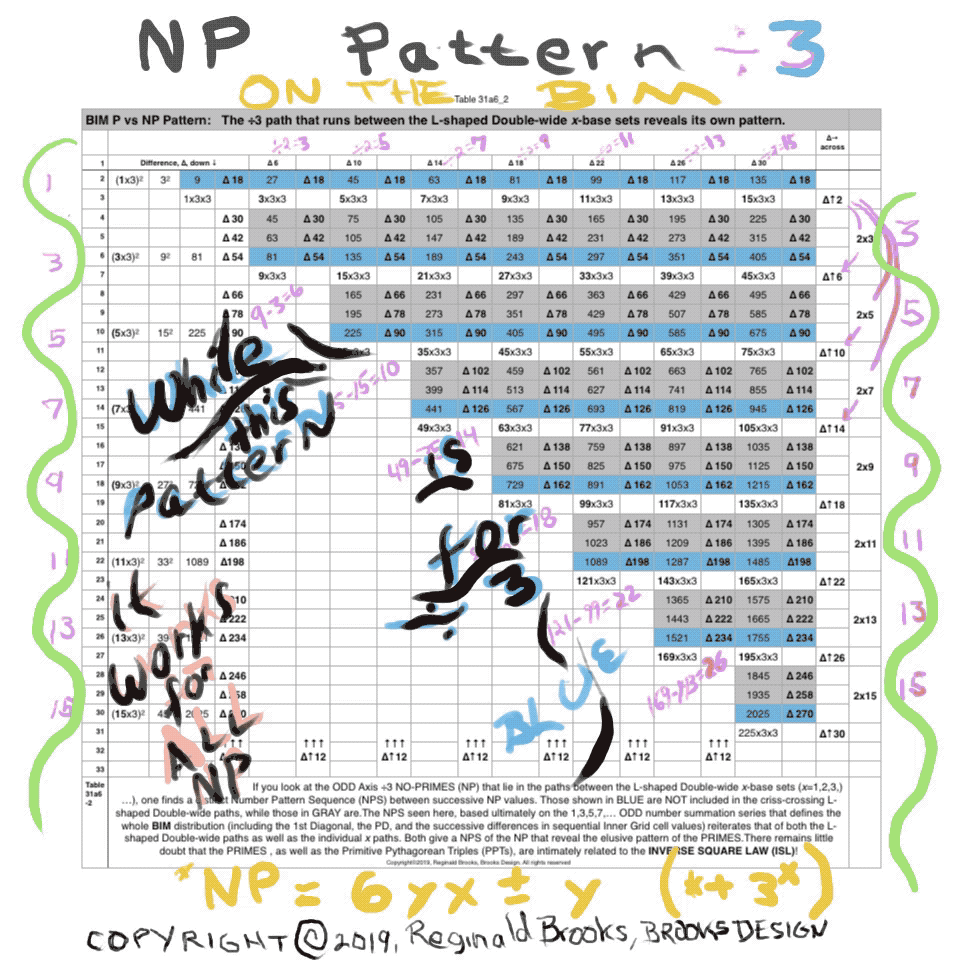
One can also obtain ALL the P by eliminating the BIM SIGO and O2 from the 1st Diagonal WIN, where SIGO = Strict Inner Grid ODDs, O2 = ODDs2, and the 1st Diagonal = the 1st Diagonal Parallel to the PD.
This itself is further simplified by switching out the ODD AXIS values with the O2 — the O2 being the PD values — such that we now have:
(13) SIGO(A2) = Strict Inner Grid ODDS & ODD AXIS2 giving a distinct visualization advantage; (14) NP = SIGO(A2)
(15) 1st Diagonal - SIGO(A2) = P.
This second method — the algebraic geometry method — as presented here.
Introduction
Two methods — one pure algebraic and the other a more visual algebraic geometry presented here — have been found that capture ALL the NO-PRIMES (NP). While they process slightly different, they dovetail nicely into a very visual Number Pattern Sequence (NPS) here on the BIM. They both give identical NP results.
So what is the significance of capturing ALL the NP?
The NP are the highly NPS that define the elusive pattern of the P. P + NP = ALL ODD WINs (≥3).
In any group of WIN, if you know the NP, you also know the P. Here is the highly visualizable geometric method for capturing ALL NP. In fact, it is just as simply stated in 12. of the SUMMARY.
Algebraic Geometry Method
One can obtain ALL the P by eliminating the BIM SIGO and O2 from the 1st Diagonal WIN, where SIGO = Strict Inner Grid ODDs, O2 = ODDs2, and the 1st Diagonal = the 1st Diagonal Parallel to the PD.
This itself is further simplified by switching out the ODD AXIS values with the O2 — the O2 being the PD values — such that we now have:
One can also obtain ALL the P by eliminating the BIM SIGO and O2 from the 1st Diagonal WIN, where SIGO = Strict Inner Grid ODDs, O2 = ODDs2, and the 1st Diagonal = the 1st Diagonal Parallel to the PD.
This itself is further simplified by switching out the ODD AXIS values with the O2 — the O2 being the PD values — such that we now have:
(13) SIGO(A2) = Strict Inner Grid ODDS & ODD AXIS2 (14) NP = SIGO(A2)
(15) 1st Diagonal - SIGO(A2) = P.
The PDFs will follow these animated gifs. Videos and other supporting graphics thereafter.
Animated Gifs:
PRIMES vs NO-PRIMES-2: algebraic method.

PRIMES vs NO-PRIMES-1: algebraic-geometry method.
PRIMES vs NO-PRIMES-3: algebraic and algebraic geometry method.

PRIMES vs NO-PRIMES-4: algebraic method in detail.
PDFs +


PRIMES vs NO-PRIMES: snapshot-1 showing dovetailing visualization of the algebraic method of calculating the NP with that of the geometric method on the BIM. The larger PDF is below.
25x200Annot.pdf)
PRIMES vs NO-PRIMES PDF: snapshot-1 showing dovetailing visualization of the algebraic method of calculating the NP with that of the geometric method on the BIM. The NPS of the NP define the elusive pattern of the P.

PRIMES vs NO-PRIMES: snapshot-2 showing dovetailing visualization of the algebraic method of calculating the NP with that of the geometric method on the BIM. Here the x=1,2,3,... base value sets -- Lower -y an Upper +y--as double-wide, L-shaped paths beginning just below the 1st Diagonal. These double rows alternate with divisible by 3--or divisible by 9 Axis squared--paths. The larger PDF is below.

PRIMES vs NO-PRIMES PDF: snapshot-2 showing dovetailing visualization of the algebraic method of calculating the NP with that of the geometric method on the BIM. The larger PDF is below. Here the x=1,2,3,... base value sets -- Lower -y an Upper +y--as double-wide, L-shaped paths beginning just below the 1st Diagonal. These double rows alternate with divisible by 3--or divisible by 9 Axis squared--paths.

PRIMES vs NO-PRIMES: snapshot-3 showing dovetailing visualization of the algebraic method of calculating the NP with that of the geometric method on the BIM. Here the x=1,2,3,... base value sets -- Lower -y an Upper +y--as double-wide, L-shaped paths beginning just below the 1st Diagonal. These double rows alternate with divisible by 3--or divisible by 9 Axis squared--paths. The larger PDF is below.

PRIMES vs NO-PRIMES PDF: snapshot-3 showing dovetailing visualization of the algebraic method of calculating the NP with that of the geometric method on the BIM. The larger PDF is below. Here the x=1,2,3,... base value sets -- Lower -y an Upper +y--as double-wide, L-shaped paths beginning just below the 1st Diagonal. These double rows alternate with divisible by 3--or divisible by 9 Axis squared--paths.

PRIMES vs NO-PRIMES PDF: snapshot-4 showing dovetailing visualization of the algebraic method of calculating the NP with that of the geometric method on the BIM. The larger PDF is below. Here the x=1,2,3,... base value sets -- Lower -y an Upper +y--as double-wide, L-shaped paths beginning just below the 1st Diagonal. These double rows alternate with divisible by 3--or divisible by 9 Axis squared--paths.
+50x500+.pdf)
Table31a4: PRIMES vs NO-PRIMES PDF: Open in a separate tab/window to see all 11 pages. Here the x=1,2,3,... base value sets -- Lower -y an Upper +y--are shown individually and collectively as sets. The full Upper and Lower tables conclude.

Table31a6_2: PRIMES vs NO-PRIMES PDF: If you look at the ODD Axis ÷3 NO-PRIMES (NP) that lie in the paths between the L-shaped Double-wide x-base sets (x=1,2,3,)…), one finds a distinct Number Pattern Sequence (NPS) between successive NP values. Those shown in BLUE are NOT included in the criss-crossing L-shaped Double-wide paths (seen in the snapshots above), while those in GRAY are. The NPS seen here, based ultimately on the 1,3,5,7,… ODD number summation series that defines the whole BIM distribution (including the 1st Diagonal, the PD, and the successive differences in sequential Inner Grid cell values) reiterates that of both the L-shaped Double-wide paths as well as the individual x paths. Both give a NPS of the NP that reveal the elusive pattern of the PRIMES. There remains little doubt that the PRIMES , as well as the Primitive Pythagorean Triples (PPTs), are intimately related to the INVERSE SQUARE LAW (ISL)!
Videos:
PRIMES vs NO-PRIMES-1-long from Reginald Brooks on Vimeo.
PRIMES vs NO-PRIMES-2-long from Reginald Brooks on Vimeo.
PRIMES vs NO_PRIMES 3 from Reginald Brooks on Vimeo.
PRIMES_vs_NO-PRIMES-4 from Reginald Brooks on Vimeo.
...more supporting graphics and tables:
+10x10+.pdf) Table31a4-5_+RunDiff_EQUATIONsDEMO(÷3Filter)+10x10+. A simple table to demo the NP process.
Table31a4-5_+RunDiff_EQUATIONsDEMO(÷3Filter)+10x10+. A simple table to demo the NP process.
 Table31a4_+RunDiff_EQUATION-PATTERNS-LOWER+UPPER+Annotated. NP Table with layout notes.
Table31a4_+RunDiff_EQUATION-PATTERNS-LOWER+UPPER+Annotated. NP Table with layout notes.
+50x500+.pdf.pdf) Table31a4_+RunDiff_EQUATIONs(SqrdAxis-seqPD)+50x500+.pdf. From the BIM to the NP/P Tables.
Table31a4_+RunDiff_EQUATIONs(SqrdAxis-seqPD)+50x500+.pdf. From the BIM to the NP/P Tables.
 BIM35-Table31a4-5_NO-PRIMES_Factores-withARS-YELLOW-numbAnnotated. The NP pattern on the BIM.
BIM35-Table31a4-5_NO-PRIMES_Factores-withARS-YELLOW-numbAnnotated. The NP pattern on the BIM.
 Table33a,c,d_ODDsqrd÷24_sheets. The NP pattern – an amazing NPS – defines the P.
Table33a,c,d_ODDsqrd÷24_sheets. The NP pattern – an amazing NPS – defines the P.
 BIMrows1-1000+Primes_sheets+Sub-Matrix2. A BIM reference showing ÷24 ARS, PPTs, NP an P.
BIMrows1-1000+Primes_sheets+Sub-Matrix2. A BIM reference showing ÷24 ARS, PPTs, NP an P.
For the full documentation of all the graphics and pdfs — including history, development, expanded tables, and more — see Appendix B below.
REFERENCES
While there are no specific references for this work other than referring back to my own original work, there are many references involved in the study and research on the PRIMES in general. These have been well documented in the TPISC_IV: Details_BIM+PPT+PRIMES focus white paper. This paper also contains the background graphics and tables leading up to this current work. The focus page is part of the much larger TPISC_IV: Details ebook project that is freely available as an HTML webpage. The quick reference outline can be found here.
(See Appendix B below: BIM ➗24 PPTs and PRIMES for ALL the Figures and Tables relating to BIM ➗24. Note: open the PDFs into a separate tab/page to see the full content. The png image files give a quick-look only.)
REFERENCES:
https://primes.utm.edu/notes/faq/six.html
“Are all primes (past 2 and 3) of the forms 6n+1 and 6n-1?
"Perhaps the most rediscovered result about primes numbers is the following:
"I found that every prime number over 3 lies next to a number divisible by six. Using Matlab with the help of a friend, we wrote a program to test this theory and found that at least within the first 1,000,000 primes this holds true.
"Checking a million primes is certainly energetic, but it is not necessary (and just looking at examples can be misleading in mathematics). Here is how to prove your observation: take any integer n greater than 3, and divide it by 6. That is, write
n = 6q + r
where q is a non-negative integer and the remainder r is one of 0, 1, 2, 3, 4, or 5.
- If the remainder is 0, 2 or 4, then the number n is divisible by 2, and can not be prime.
- If the remainder is 3, then the number n is divisible by 3, and can not be prime.
"So if n is prime, then the remainder r is either
- 1 (and n = 6q + 1 is one more than a multiple of six), or
- 5 (and n = 6q + 5 = 6(q+1) - 1 is one less than a multiple of six).
"Remember that being one more or less than a multiple of six does not make a number prime. We have only shown that all primes other than 2 and 3 (which divide 6) have this form.”
From Another prime page by Chris K. Caldwell caldwell@utm.edu
~~~
"Euler's 6n+1 Theorem
"Every Prime of the form  can be written in the form
can be written in the form  ."
."
https://archive.lib.msu.edu/crcmath/math/math/e/e282.htm
~~~
~~~
http://www2.mae.ufl.edu/~uhk/sixnplusone.pdf.
~~~
~~~
https://en.m.wikipedia.org/wiki/Formula_for_primes
~~
http://www2.mae.ufledu/~uhk/PRIME-TEST.pdf **
http://www2.mae.ufl.edu/~uhk/NUMBER- FRACTION.pdf
~~~
http://mathworld.wolfram.com/Eulers6nPlus1Theorem.html
~~
http://eulerarchive.maa.org See Number Theory Section
E744en.pdf **!!!!!!*!!!!! MOST IMPORTANT READ
http://eulerarchive.maa.org/docs/translations/E744en.pdf
NOTE: These article links from the Euler Archive/Number Theory/ INDEX are IMPORTANT READS for PRIMES & Squares. You can link directly from the Index as well.
http://eulerarchive.maa.org/pages/E026.html
http://eulerarchive.maa.org/pages/E054.html
http://eulerarchive.maa.org/pages/E134.html
http://eulerarchive.maa.org/pages/E175.html
http://eulerarchive.maa.org/pages/E191.html
http://eulerarchive.maa.org/pages/E241.html
http://eulerarchive.maa.org/pages/E242.html
http://eulerarchive.maa.org/pages/E243.html
http://eulerarchive.maa.org/pages/E244.html
http://eulerarchive.maa.org/pages/E256.html
http://eulerarchive.maa.org/pages/E262.html
http://eulerarchive.maa.org/pages/E270.html
http://eulerarchive.maa.org/pages/E279.html
http://eulerarchive.maa.org/pages/E283.html
http://eulerarchive.maa.org/pages/E369.html
http://eulerarchive.maa.org/pages/E394.html
http://eulerarchive.maa.org/pages/E405.html
http://eulerarchive.maa.org/pages/E445.html
http://eulerarchive.maa.org/pages/E449.html
http://eulerarchive.maa.org/pages/E467.html
http://eulerarchive.maa.org/pages/E523.html
http://eulerarchive.maa.org/pages/E542.html
http://eulerarchive.maa.org/pages/E552.html
http://eulerarchive.maa.org/pages/E554.html
http://eulerarchive.maa.org/pages/E564.html
http://eulerarchive.maa.org/pages/E596.html
http://eulerarchive.maa.org/pages/E610.html
http://eulerarchive.maa.org/pages/E699.html
http://eulerarchive.maa.org/pages/E708.html
http://eulerarchive.maa.org/pages/E715.html
http://eulerarchive.maa.org/pages/E718.html
http://eulerarchive.maa.org/pages/E719.html
744 On divisors of numbers of the form mxx + nyy
http://eulerarchive.maa.org original 744 Euler article
https://www.britannica.com/science/Fermats-theorem
http://mathworld.wolfram.com/FermatsLittleTheorem.html
http://mathworld.wolfram.com/EulersTotientTheorem.html
http://mathworld.wolfram.com/TotientFunction.html
https://www.geeksforgeeks.org/fermats-little-theorem/
https://www.geeksforgeeks.org/eulers-totient-function/
http://mathworld.wolfram.com/Eulers6nPlus1Theorem.html
https://brilliant.org/wiki/fermats-little-theorem/
https://brilliant.org/wiki/eulers-theorem/
https://primes.utm.edu/notes/proofs/FermatsLittleTheorem.html
https://primes.utm.edu/notes/conjectures/ Conjectures
https://primes.utm.edu/notes/faq/ FAQ Index
https://primes.utm.edu/notes/faq/one.html One
https://primes.utm.edu/notes/faq/six.html Six —>Important Page
http://unsolvedproblems.org/index.htm Unsolved Problems Index
https://en.m.wikipedia.org/wiki/Proofs_of_Fermat%27s_little_theorem
https://en.m.wikipedia.org/wiki/Fermat%27s_little_theorem
https://en.m.wikipedia.org/wiki/Euler%27s_theorem
~~NEW REFERENCE LIST 11-08-2018~Fermat’s Little Theorem ++++Euler
https://web.math.princeton.edu/swim/SWIM%202010/Shi-Xie%20Presentation%20SWIM%202010.pdf
http://mathworld.wolfram.com/Fermats4nPlus1Theorem.html
http://nonagon.org/ExLibris/euler-proves-fermats-theorem-sum-two-squares
https://storyofmathematics.com/17th_fermat.html
https://en.wikipedia.org/wiki/Prime_number
http://mathworld.wolfram.com/PrimeNumberTheorem.html
https://www.britannica.com/science/prime-number-theorem
https://going-postal.com/2018/02/fermats-little-theorem/
https://ibmathsresources.com/2014/03/15/fermats-theorem-on-the-sum-of-two-squares/
https://en.wikipedia.org/wiki/Fermat%27s_theorem_on_sums_of_two_squares *
https://en.wikipedia.org/wiki/Pythagorean_prime *
https://oeis.org/A002144 Pythagorean Primes of the form 4n + 1
https://oeis.org/A002144/list List of Pythagorean Primes of the form 4n + 1
http://nonagon.org/ExLibris/fermat-sum-two-squares-calculator *
https://www.britannica.com/science/Mersenne-prime Mersenne Primes
https://primes.utm.edu/mersenne/
https://en.wikipedia.org/wiki/Mersenne_prime#About_Mersenne_primes
http://mathworld.wolfram.com/MersenneNumber.html
http://mathworld.wolfram.com/MersennePrime.html
https://www.encyclopediaofmath.org/index.php/Mersenne_number
https://www.mersenne.org GIMPS
https://www.mersenne.org/primes/
https://primes.utm.edu/lists/small/millions/ Primes LIST by section
http://compoasso.free.fr/primelistweb/page/prime/liste_online_en.php Primes LIST by section
http://primerecords.dk/primegaps/gaps20.htm Prime Gaps
http://primerecords.dk/primegaps/maximal.htm
https://en.wikipedia.org/wiki/Prime_gap
https://primes.utm.edu/notes/GapsTable.html
https://en.wikipedia.org/wiki/Prime_k-tuple
https://primes.utm.edu/glossary/page.php?sort=ktuple
https://en.wikipedia.org/wiki/Twin_prime
http://mathworld.wolfram.com/TwinPrimes.html
https://primes.utm.edu/notes/faq/
~~
https://oeis.org/wiki/Pythagorean_primes Pythagorean vs non-Pythagorean Primes
http://oeis.org/A002145 non-Pythagorean Primes of the form 4n + 3
http://oeis.org/A002144 Pythagorean Primes of the form 4n + 1
https://en.wikipedia.org/wiki/Double_Mersenne_number Double Mersenne Primes
https://primes.utm.edu/mersenne/index.html#unknown Questions remain
~~~~~~~~~~NEW REFERENCE LIST 12-13-2018~~~videos——must watch~~~~
See: Animated math: videos by 3Blue1Brown (Grant Sanderson, et al.)
https://www.3blue1brown.com/videos/
Feynman's Lost Lecture (ft. 3Blue1Brown)
https://www.youtube.com/watch?v=xdIjYBtnvZU
But WHY is a sphere's surface area four times its shadow?: video by 3Blue1Brown
https://youtu.be/GNcFjFmqEc8
Why is pi here? And why is it squared? A geometric answer to the Basel problem: video by 3Blue1Brown
https://www.youtube.com/watch?v=d-o3eB9sfls&frags=pl%2Cwn
Pi hiding in prime regularities: video by 3Blue1Brown
https://youtu.be/NaL_Cb42WyY
Visualizing the Riemann hypothesis and analytic continuation: video by 3Blue1Brown
https://youtu.be/sD0NjbwqlYw
All possible pythagorean triples, visualized: video by 3Blue1Brown
https://www.youtube.com/watch?v=QJYmyhnaaek
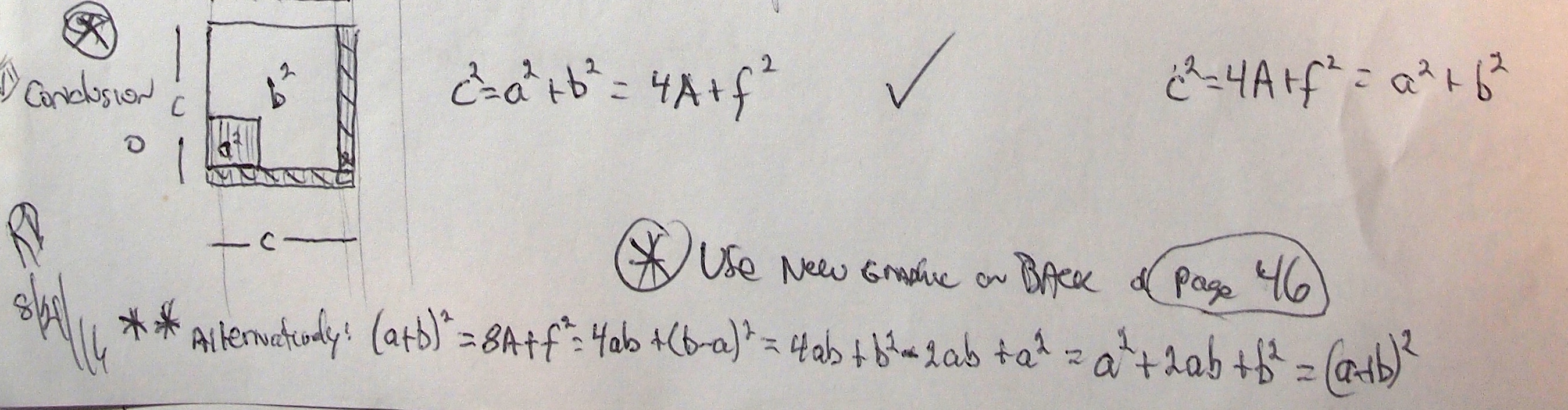
((((Table VI series is really the whole evolution of the BIMrow1-1000+sheets/Primes_sheets+PF, etc here and appendix.)))
 referenced as Table VI a
referenced as Table VI a
 referenced as Table VI b
referenced as Table VI b
 referenced as Table VI b
referenced as Table VI b
 Table VII.
Table VII.
(See Appendix B below: BIM ➗24 PPTs and PRIMES for ALL the Figures and Tables relating to BIM ➗24.)
BACK: ---> Part I of II CaCoST-DSEQEC on a separate White Paper
BACK: ---> Part II of II CaCoST-DSEQEC on a separate White Paper
BACK: ---> Simple Path BIM to PRIMES on a separate White Paper
BACK: ---> PRIMES vs NO-PRIMES on a separate White Paper
BACK: ---> TPISC_IV: Details_BIM+PTs+PRIMES on a separate White Paper
BACK: ---> PRIME GAPS on a separate White Paper
Artwork referencing TPISC.
Summation:
Here’s the thing. Amongst a myriad of other connections, there exist an intimate connection between three number systems:
- The ISL as laid out in the BIM;
- PTs — and most especially PPTs — as laid out on the BIM;
- The PRIME numbers — PRIMES — as laid out on the BIM.
The BIM is the FIXED GRID numerical array of the ISL.
Amongst its vast array of inter-connecting Number Pattern Sequences (NPS) — i.e., number systems — two such systems stick out and do so in such an overtly visual — as well as mathematical — way that their connection to each other is more than implied.
You see, both the PPTs and PRIMES strictly align themselves on the SAME paths within the BIM.
Now, their footprints upon these paths are not identical, yet their paths chosen are. If you divide the number array — i.e., the Inner Grid numbers — of the BIM by 24, a Sub-Matrix 1 grid is formed.
Upon that Sub-Matrix 1, pathways are formed on every ODD Axis number NOT ➗3.** EVERY PPT and PRIME lies on these paths!**
Yes, while in the details we show how:
- The 1st Col. on the BIM — that which is the square of the Axis number (i.e., the Prime Diagonal number) - 1, when then ➗ by 24, equals a Whole Integer Number (WIN);
- This defines the path — the “Active Row” upon the BIM;
- While every Active Row path may or may not contain a PPT and/or PRIME, every PPT and/or PRIME is ALWAYS located on one of these paths;
- The difference (∆) between the squares of any two PRIMES (>5) is also ➗24;
- The serial — and exponential — products of ANY and ALL PPTs remain PPTs, whilst those NOT remain NOT.
Furthermore, by distilling the BIM to Sub-Matrix 2 — i.e., every number across a Row is progressively divided by a growing sequence series starting with the Col. 1 as the Axis number - 1 — every such serial-exponential PPT is clearly predicted by its neighbors within the sequence. One more example of the extremely intimate relationship between The Pythagorean - Inverse Square Connection (TPISC).
One simply can not ignore how the PRIMES, the PTs and ultimately the ISL define the architecture of SpaceTime!
In the original MathspeedST, an artificial division was made, separating the content into:
- TAOST, The Architecture Of SpaceTime,
- TCAOP, The Complete Absence Of Primes.
Now we have come full circle.
ALL PRIMES and ALL PPTs follow — although individually with their own respective footprints — the SAME, HIGHLY PATTERNED NPS path on the BIM.
This is no coincidence. The ➗24 Active Row Pattern that defines this path on the BIM does so in a highly ordered pattern. The energy density that expresses itself as curved ST does so precisely by the numerical architect of the built-in ISL.
We now have some very strong evidence that the numbers that define the PPTs and the numbers that define the PRIMES are ubiquitously linked throughout the entire number pattern array that defines the ISL. This is revealed on the BIM!
Surely their interplay provides some very significant contributions to the overall Architecture of SpaceTime!
feel the beat: + - + - - - + - + - - - + - + - - - + - + - - - ...
VIMEO "BIM_PRIMES_24"1! )
BIM_PT_PRIMES_24 from Reginald Brooks on Vimeo.
TPISC_IV:_Details ~A MathspeedST Supplement~
Copyright©2018-19, Reginald Brooks. All rights reserved.
BACK: ---> Part I of II CaCoST-DSEQEC on a separate White Paper
BACK: ---> Part II of II CaCoST-DSEQEC on a separate White Paper
BACK: ---> TPISC_IV: Details:_PRIMES_vs_NO-PRIMES on a separate White Paper
BACK: ---> Simple Path BIM to PRIMES on a separate White Paper
BACK: ---> PRIMES vs NO-PRIMES on a separate White Paper
BACK: ---> TPISC_IV: Details_BIM+PTs+PRIMES on a separate White Paper
BACK: ---> PRIME GAPS on a separate White Paper
BACK: ---> TPISC IV: Details White Paper
Artwork referencing TPISC.
TPISC_IV:_Details ~PRIMES vs NO-PRIMES~
Copyright©2019, Reginald Brooks. All rights reserved.
~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~
SEE Page 50 (Art Theory101: White Papers) for spreadsheets: BIM: How to Make.
TABLES 1-9 (r-sets, Z➗24,Axis squared, differences, groundwork tables)







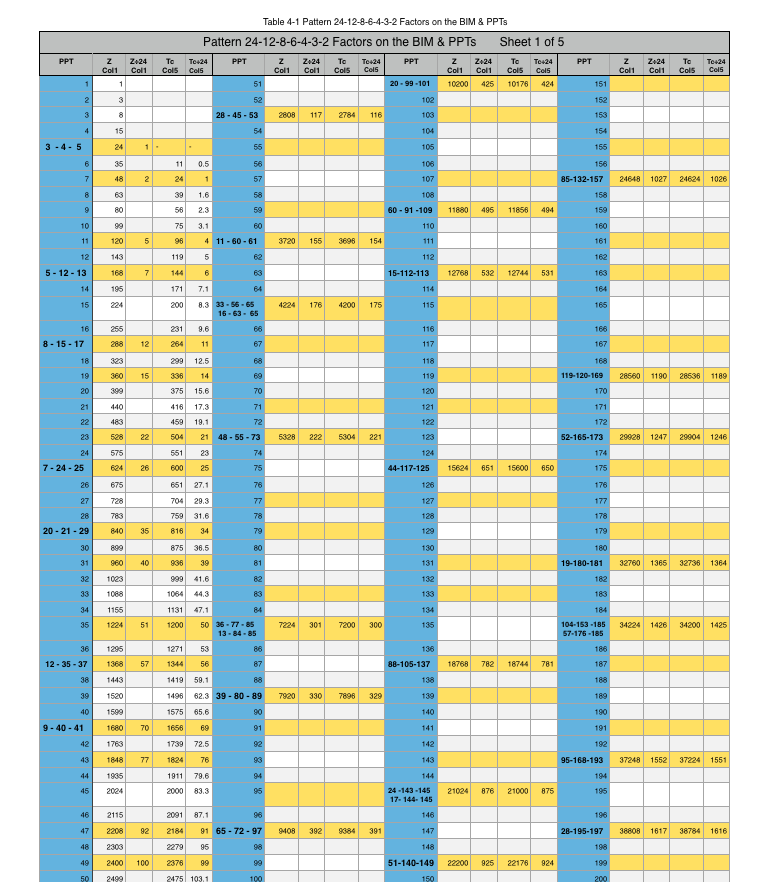
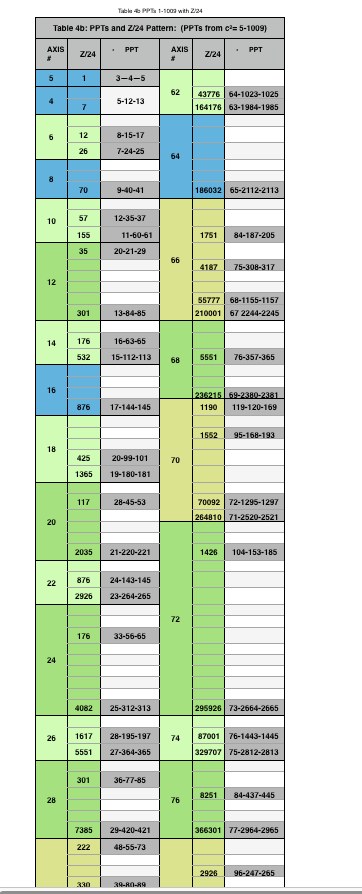
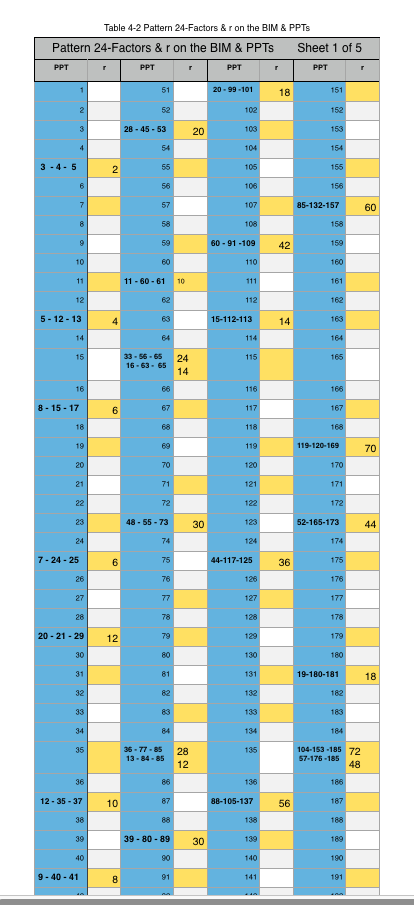

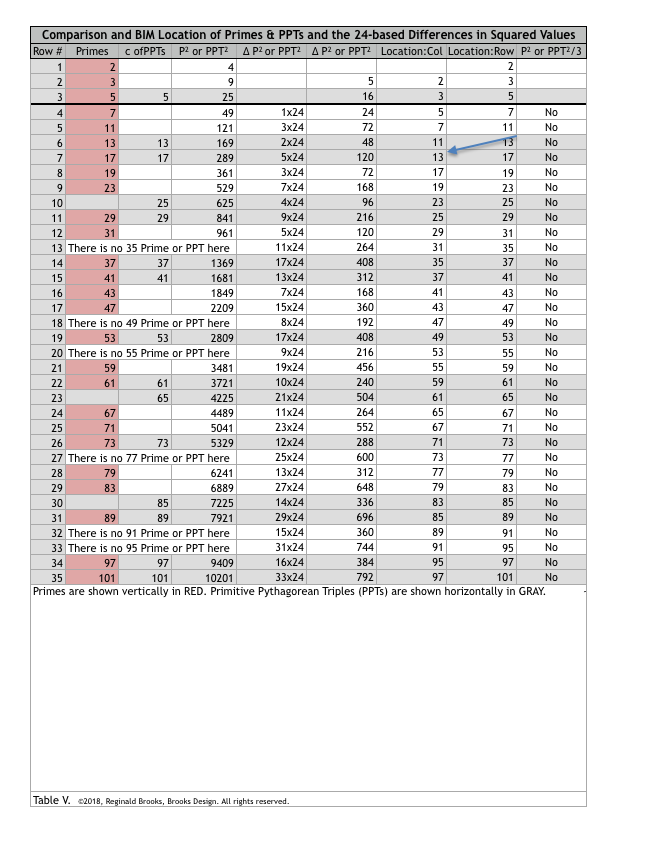

Table VI b fully expanded 1-1010 PTs and Primes with ALL ACTIVE Rows color-coded in Violet














(Once renamed, ALL Tables — as pdf/pngs—will be listed here with links to and fro main article)
TABLES 10-19 (PRIMEs-gaps and random differences)
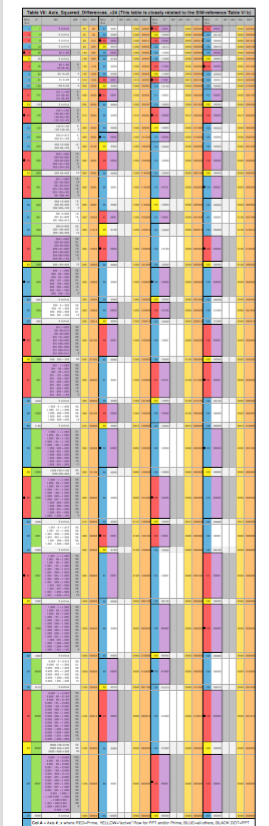

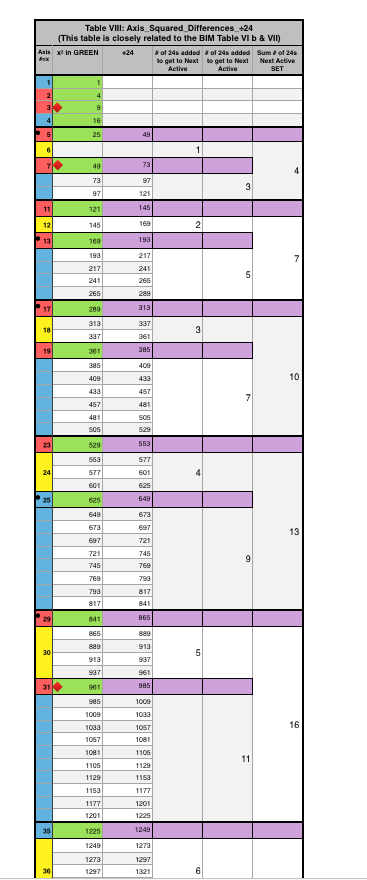


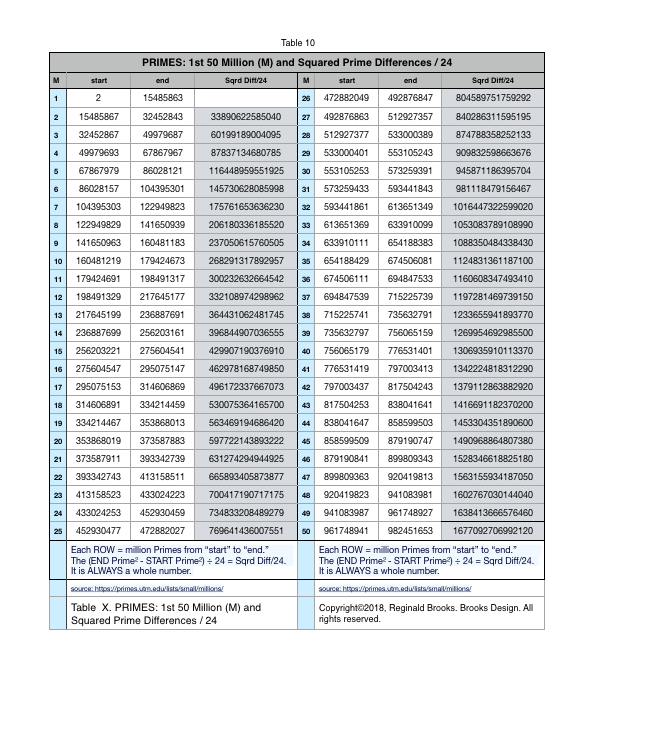

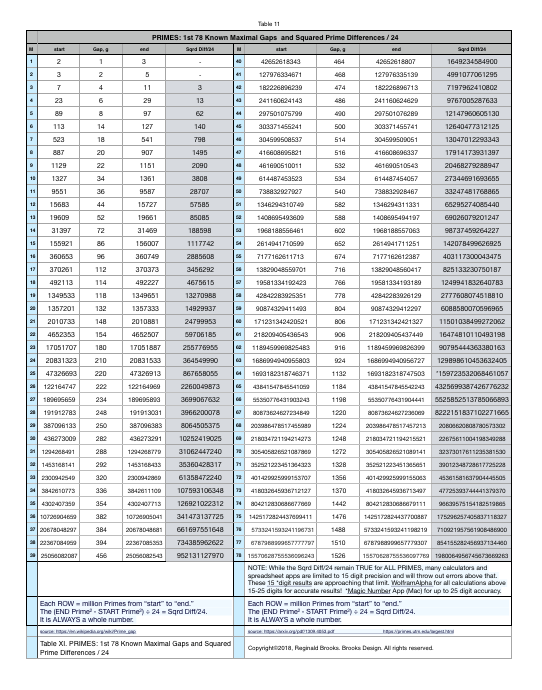








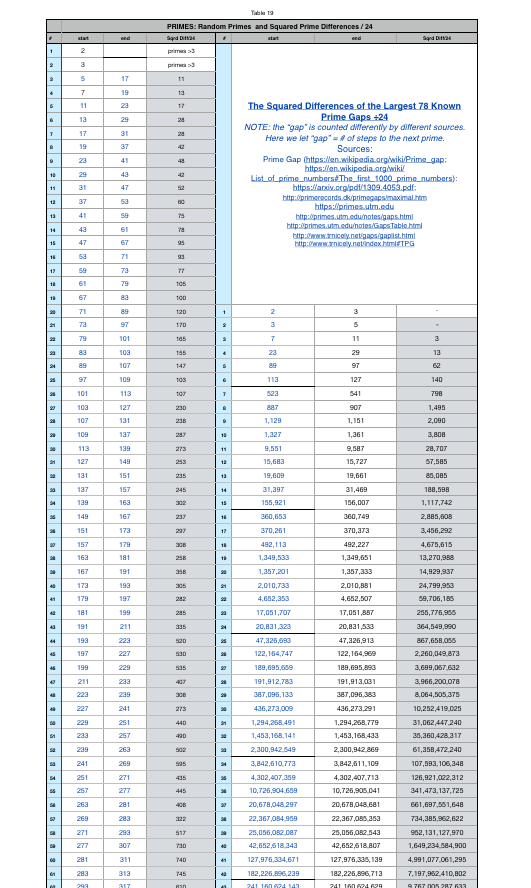

TABLES 20-23 (PRIME-PPT or not with r-values)





TABLES 24-28 (Sub-Matrix 2 )








TABLES 29-30 (Sub-Matrix 2 Sidebar: Exponentials of the PPTs)
Sub-Matrix 2 Sidebar: Exponentials of the PPTs
Table 29 Exponentials of the first 10 PPTs c-values to be used in Tables 30a-g.
Tables 30a-g The Sub-Matrix 2, when ➗4, and the difference (∆) between this and the next exponential PPT treated this way, is subsequently ➗ by its Sub-Matrix 2 variable, the PREVIOUS exponential within the series is revealed. Restated as an example: When one subtracts 1 from the exponential values of c (the c-value of the PPT) you get the Sub-Matrix 2 value. Divide that by 4 and take the difference (∆) between it and the next. Divide that by 3 to give the PREVIOUS PPT c-value in the series.
The Sub-Matrix 2 variable divisor = 3 = Sub-Matrix 2 value/4 = 12/4. These variables run: 1,3,4,6,7,9,10,...








Tables: 31a, a+, a++, ++MP, a+++ and 31b
.pdf)
.pdf)
.pdf)
.pdf)
.pdf)
-sheets.pdf)
Tables: 32a,32b and 32c



BIM÷24: SubMatrix Sidebar: What is the role of 24 in the underlying structure?
SEE: Tables: 33a, 33b, 33c and 33d. towards the end of Appendix B for some very NEW INFO on the BIM÷24.
The underlying geometry of the BIM÷24 PRE-SELECTS the Axis Rows into TWO Groups: ARs and NON-ARs. The PPTs and PRIMES are EXCLUSIVELY — as a sufficient, but not necessary condition — found on the ARs and NEVER on the NON-ARs. While both Groups follow (PD2 - PD2)÷24, they do so ONLY within their own respective Groups. They do NOT crossover. This Grouping divide occurs naturally within the BIM as shown in these images below.
The ISL as presented in the BIM is deeply, intimately structured around the number 24 — and its factors: 4,6, 3,8 2,12, and 1,24.
The interplay between these small sets of Numbers generates an incredible amount of richness and complexity with seemingly simplistic BIM itself. This has led to TPISP: The Pythagorean-Inverse Square Connection, and the PRIMES.
 Open in separate browser tab/window to see all.
Open in separate browser tab/window to see all.



Supporting Graphics forTables: 33a, 33b, 33c and 33d. Open in separate browser tab/window to see all.



















xxxxxxxx
Back to the Table 31 sequences. Table 31a... series, along with the previous Table33 series, uncovers how the PRIMES were found within the BIM both by algebra and geometry. This has been reduced to a focus white paper: "PRIMES vs NO-PRIMES that is a condensed summary of this work. One may benefit from looking over this paper prior to the study of these more elaborate tables. A summary from the paper is presented here:
SUMMARY*
(~from "*Simple Path from the BIM to the PRIMES" that presents the algebraic-geometry method.)
How do we go from the simple grid of the BIM (BBS-ISL Matrix) to identifying the PRIMES?
The BIM is a symmetrical grid — divided equally down its diagonal center with the Prime Diagonal (PD) — that illuminates the Number Pattern Sequence (NPS) of the Inverse Square Law (ISL) via simple, natural Whole Integer Numbers (WIN).
The BIM Axis numbers are 1,2,3,.. with 0 at the origin.
The Inner Grid (IG) contains EVEN and ODD WIN, but except for the 1st diagonal next to the PD — a diagonal that contains ALL the ODD WIN — there are NO PRIMES (NO-PRIMES, NP) on the SIG (Strict Inner Grid).
The PD WIN are simple the square of the Axis WIN.
ALL the IG WIN result from subtracting the horizontal from the vertical intersection of the PD.
Dropping down a given PD Squared WIN (>4) until it intersects with another squared WIN on a Row below will ALWAYS reveal that Row to be a Primitive Pythagorean Triple (PPT) Row, whose hypotenuse, c, lies on the intersecting PD. ALL PPTs may be identified this way.
Dividing the BIM cell values by 24 — BIM÷24 — forms a criss-crossing DIAMOND NPS that divides the overall BIM into two distinct and alternating Row (and Column) bands or sets:
- ODD WIN that are ÷3 and referred to as NON-ARs;
- ODD WIN that are NOT ÷3 and referred to as ARs, or Active Rows;
- The ARs ALWAYS come in pairs — with an EVEN WIN between — as the UPPER and LOWER AR of the ARS (Active Row Set);
ALL PPTs and ALL PRIMES ALWAYS are found exclusively on the ARs — no exceptions.
By applying:
(1) *
let y = odd number (ODD) 3, 5, 7,… and x = 1, 2, 3,... one generates a NP table containing ALL the NP;
*True if ÷3 ODDs are first eliminated, otherwise ADD exponentials of 3 to the NP pool;
Eliminating the NP — and the NP contain a NPS — from ALL the ODD WIN, reveals the PRIMES (P).
A necessary, but not sufficient confirmation — but not proof — of primality is found by finding the even division of 24 into the difference of the square of ANY two PRIMES as:
(2) (P2)2 - (P1)2 =
let
Be aware that this also holds true for ALL the AR NP. The P and NP are NOT ÷3, and are both part of the ARS and therefore any combination of the two squared differences will be ÷24:
(3) (NP2)2 - (NP1)2 =
(4) (NP2)2 - (P1)2 =
(5) (P2)2 - (NP1)2 =
The ÷3 NON-AR set is separately ÷24, but can NOT be mixed with members of the AR set (ARS) as:
(6) (NON-AR-NP2)2 - (NON-AR-NP1)2 = n24
(7) (NON-AR-NP2)2 - (NP1)2 ⧣
(8) (NP2)2 - (NON-AR-NP1)2 ⧣
(9) (P2)2 - (NON-AR-NP1)2 ⧣
(10) (NON-AR-NP2)2 - (P1)2 ⧣
The division into AR and NON-AR sets has a NPS that ultimately define the elusive pattern of the P.
Furthermore, may be re-arranged to:
(11)
(12)
asking whether any given ODD (>3) is a P or NP, it is exclusively a NP if, and only if, y reduces to the same value after applying x. As y is effectively an ODD of either a PRIME or composite of PRIMES factor*, one only needs to satisfy a single instance to validate NON-Primality.
One can also obtain ALL the P by eliminating the BIM SIGO and O2 from the 1st Diagonal WIN, where SIGO = Strict Inner Grid ODDs, O2 = ODDs2, and the 1st Diagonal = the 1st Diagonal Parallel to the PD.
This itself is further simplified by switching out the ODD AXIS values with the O2 — the O2 being the PD values — such that we now have:
(13) SIGO(A2) = Strict Inner Grid ODDS & ODD AXIS2 giving a distinct visualization advantage; (14) NP = SIGO(A2)
(15) 1st Diagonal - SIGO(A2) = P.
This second method — the algebraic geometry method — as presented here.
Introduction
Two methods — one pure algebraic and the other a more visual algebraic geometry presented here — have been found that capture ALL the NO-PRIMES (NP). While they process slightly different, they dovetail nicely into a very visual Number Pattern Sequence (NPS) here on the BIM. They both give identical NP results.
So what is the significance of capturing ALL the NP?
The NP are the highly NPS that define the elusive pattern of the P. P + NP = ALL ODD WINs (≥3).
In any group of WIN, if you know the NP, you also know the P. Here is the highly visualizable geometric method for capturing ALL NP. In fact, it is just as simply stated in 12. of the SUMMARY.
Algebraic Geometry Method
One can obtain ALL the P by eliminating the BIM SIGO and O2 from the 1st Diagonal WIN, where SIGO = Strict Inner Grid ODDs, O2 = ODDs2, and the 1st Diagonal = the 1st Diagonal Parallel to the PD.
This itself is further simplified by switching out the ODD AXIS values with the O2 — the O2 being the PD values — such that we now have:
One can also obtain ALL the P by eliminating the BIM SIGO and O2 from the 1st Diagonal WIN, where SIGO = Strict Inner Grid ODDs, O2 = ODDs2, and the 1st Diagonal = the 1st Diagonal Parallel to the PD.
This itself is further simplified by switching out the ODD AXIS values with the O2 — the O2 being the PD values — such that we now have:
(13) SIGO(A2) = Strict Inner Grid ODDS & ODD AXIS2 (14) NP = SIGO(A2)
(15) 1st Diagonal - SIGO(A2) = P.
The PDFs will follow these animated gifs. Videos and other supporting graphics thereafter.
Animated Gifs:

PRIMES vs NO-PRIMES-2: algebraic method.

PRIMES vs NO-PRIMES-1: algebraic-geometry method.

PRIMES vs NO-PRIMES-3: algebraic and algebraic geometry method.

PRIMES vs NO-PRIMES-4: algebraic method in detail.
PDFs +


PRIMES vs NO-PRIMES: snapshot-1 showing dovetailing visualization of the algebraic method of calculating the NP with that of the geometric method on the BIM. The larger PDF is below.
25x200Annot.pdf)
PRIMES vs NO-PRIMES PDF: snapshot-1 showing dovetailing visualization of the algebraic method of calculating the NP with that of the geometric method on the BIM. The NPS of the NP define the elusive pattern of the P.

PRIMES vs NO-PRIMES: snapshot-2 showing dovetailing visualization of the algebraic method of calculating the NP with that of the geometric method on the BIM. Here the x=1,2,3,... base value sets -- Lower -y an Upper +y--as double-wide, L-shaped paths beginning just below the 1st Diagonal. These double rows alternate with divisible by 3--or divisible by 9 Axis squared--paths. The larger PDF is below.

PRIMES vs NO-PRIMES PDF: snapshot-2 showing dovetailing visualization of the algebraic method of calculating the NP with that of the geometric method on the BIM. The larger PDF is below. Here the x=1,2,3,... base value sets -- Lower -y an Upper +y--as double-wide, L-shaped paths beginning just below the 1st Diagonal. These double rows alternate with divisible by 3--or divisible by 9 Axis squared--paths.

PRIMES vs NO-PRIMES: snapshot-3 showing dovetailing visualization of the algebraic method of calculating the NP with that of the geometric method on the BIM. Here the x=1,2,3,... base value sets -- Lower -y an Upper +y--as double-wide, L-shaped paths beginning just below the 1st Diagonal. These double rows alternate with divisible by 3--or divisible by 9 Axis squared--paths. The larger PDF is below.

PRIMES vs NO-PRIMES PDF: snapshot-3 showing dovetailing visualization of the algebraic method of calculating the NP with that of the geometric method on the BIM. The larger PDF is below. Here the x=1,2,3,... base value sets -- Lower -y an Upper +y--as double-wide, L-shaped paths beginning just below the 1st Diagonal. These double rows alternate with divisible by 3--or divisible by 9 Axis squared--paths.

PRIMES vs NO-PRIMES PDF: snapshot-4 showing dovetailing visualization of the algebraic method of calculating the NP with that of the geometric method on the BIM. The larger PDF is below. Here the x=1,2,3,... base value sets -- Lower -y an Upper +y--as double-wide, L-shaped paths beginning just below the 1st Diagonal. These double rows alternate with divisible by 3--or divisible by 9 Axis squared--paths.
+50x500+.pdf)
Table31a4: PRIMES vs NO-PRIMES PDF: Open in a separate tab/window to see all 11 pages. Here the x=1,2,3,... base value sets -- Lower -y an Upper +y--are shown individually and collectively as sets. The full Upper and Lower tables conclude.

Table31a6_2: PRIMES vs NO-PRIMES PDF: If you look at the ODD Axis ÷3 NO-PRIMES (NP) that lie in the paths between the L-shaped Double-wide x-base sets (x=1,2,3,)…), one finds a distinct Number Pattern Sequence (NPS) between successive NP values. Those shown in BLUE are NOT included in the criss-crossing L-shaped Double-wide paths (seen in the snapshots above), while those in GRAY are. The NPS seen here, based ultimately on the 1,3,5,7,… ODD number summation series that defines the whole BIM distribution (including the 1st Diagonal, the PD, and the successive differences in sequential Inner Grid cell values) reiterates that of both the L-shaped Double-wide paths as well as the individual x paths. Both give a NPS of the NP that reveal the elusive pattern of the PRIMES. There remains little doubt that the PRIMES , as well as the Primitive Pythagorean Triples (PPTs), are intimately related to the INVERSE SQUARE LAW (ISL)!
Videos:
PRIMES vs NO-PRIMES-1-long from Reginald Brooks on Vimeo.
PRIMES vs NO-PRIMES-2-long from Reginald Brooks on Vimeo.
PRIMES vs NO_PRIMES 3 from Reginald Brooks on Vimeo.
PRIMES_vs_NO-PRIMES-4 from Reginald Brooks on Vimeo.
...more supporting graphics and tables:
+10x10+.pdf) Table31a4-5_+RunDiff_EQUATIONsDEMO(÷3Filter)+10x10+. A simple table to demo the NP process.
Table31a4-5_+RunDiff_EQUATIONsDEMO(÷3Filter)+10x10+. A simple table to demo the NP process.
 Table31a4_+RunDiff_EQUATION-PATTERNS-LOWER+UPPER+Annotated. NP Table with layout notes.
Table31a4_+RunDiff_EQUATION-PATTERNS-LOWER+UPPER+Annotated. NP Table with layout notes.
+50x500+.pdf.pdf) Table31a4_+RunDiff_EQUATIONs(SqrdAxis-seqPD)+50x500+.pdf. From the BIM to the NP/P Tables.
Table31a4_+RunDiff_EQUATIONs(SqrdAxis-seqPD)+50x500+.pdf. From the BIM to the NP/P Tables.
 BIM35-Table31a4-5_NO-PRIMES_Factores-withARS-YELLOW-numbAnnotated. The NP pattern on the BIM.
BIM35-Table31a4-5_NO-PRIMES_Factores-withARS-YELLOW-numbAnnotated. The NP pattern on the BIM.
 Table33a,c,d_ODDsqrd÷24_sheets. The NP pattern – an amazing NPS – defines the P.
Table33a,c,d_ODDsqrd÷24_sheets. The NP pattern – an amazing NPS – defines the P.
 BIMrows1-1000+Primes_sheets+Sub-Matrix2. A BIM reference showing ÷24 ARS, PPTs, NP an P.
BIMrows1-1000+Primes_sheets+Sub-Matrix2. A BIM reference showing ÷24 ARS, PPTs, NP an P.
+253x250.pdf) BIM250x250.
BIM250x250.
Various supporting graphics








xxxxxxxxxx
~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~
BACK: ---> Part I of II CaCoST-DSEQEC on a separate White Paper
BACK: ---> Part II of II CaCoST-DSEQEC on a separate White Paper
BACK: ---> Simple Path BIM to PRIMES on a separate White Paper
BACK: ---> PRIMES vs NO-PRIMES on a separate White Paper
BACK: ---> TPISC_IV: Details_BIM+PTs+PRIMES on a separate White Paper
BACK: ---> PRIME GAPS on a separate White Paper
BACK: ---> PeriodicTableOfPrimes(PTOP)_GoldbachConjecture on a separate White Paper
NEWLY ADDED (after TPISC IV published):
Back to Part I of the BIM-Goldbach_Conjecture.
Back to Part II of the BIM-Goldbach_Conjecture.
Back to Part III of the BIM-Goldbach_Conjecture.
Artwork referencing TPISC.
TPISC_IV:_Details ~PRIMES vs NO-PRIMES~
Copyright©2019, Reginald Brooks. All rights reserved.
Artist Link in iTunes Apple Books Store:
Reginald Brooks

~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~
KEYWORDS TAGS:
PTOP, Periodic Table Of PRIMES, PRIMES vs NO-PRIMES, algebraic geometry, BIM, TPISC, The Pythagorean - Inverse Square Connections, Pythagorean Triangles, DNA, Zika virus, pentagon, decagon, double pentagon, composite axial DNA double-helix, Pythagorean Triples, primitive Pythagorean Triples, non-primitive Pythagorean Triples, Pythagorean Theorem, Pythagorus Theorem, The Dickson Method, BBS-ISL Matrix, Expanded Dickson Method, r-sets, s-set, t-sets, Pair-sets, geometric proofs, MathspeedST, leapfrogging LightspeedST FASTER than the speed of light, Brooks (Base) Square- Inverse Square Law (ISL), BBS-ISL Matrix grid, The Architecture Of SpaceTime (TAOST), The Conspicuous Absence Of Primes (TCAOP), A Fresh Piece Of Pi(e), AFPOP, Numbers of Inevitability, LightspeedST, Teachers, Educators and Students (TES), number theory, ubiquitous information, FASTER than the speed of light, primes, prime numbers, fractals, mathematics, Universe, cosmos, patterns in number, DSEQEC, Double-Slit Experiment-Quantum Entanglement Conjecture, CaCost, Creation and Conservation of SpaceTime.
TOP
| 180 | BS Rule 180- The Sub-Matrix: Within the Inner Grid, every progressive number of every column or row is evenly divisible , progressively, by a whole number sequence. Plotting those dividends reveals a truly fundamental "sub-matrix" grid, underlying the original Inner Grid, of repeating simple whole number sequences, i.e. 1,2,3, ..., horizontally and vertically ...forming the simplest, most basic grid pattern possible, that also includes the axis numbers. All numbers of the original Brooks (Base) Square are predicated on this simple whole number sequence pattern. |
The simple — and some of the not so simple — geometries of the BIM and BIMtree have been laid out in a series of interactive canvases. Each canvas opens up on its own webpage. Once open, you just click/touch and drag the geometry around, apart, this way and that way, even rebuilding the initial geometry side by side until you can really see how the parts are so simply related. It's deconstruction!
The entire geometry on canvas series was produced initially without any supporting text to keep it as clean, simple and intuitive as possible. The accompanying text will certainly help fill in the gaps, but it should be noted that the geometry on canvas series sequentially builds from one canvas to another.
The algebraic binomials and their square proofs are widely known. Here the very same proofs overlap with that of the BIM, BIMtree and the ToPPTs! This, too, can be readily seen.
The number 24 — and its factors of 1-24, 2-12, 3-8, and 4-6 have shown, once again, to be integral to both the BIM in general (remember, the EVEN Inner Grid cell numbers are all evenly divisible by 4), and, the ToPPTs. HOW SO? Well, this is new, really new, so just the surface has been touched, but so far:
- Marking (YELLOW) all BIM cells evenly ➗ by 24 generates a striking diamond-grid, criss-crossing pattern with 4 additional YELLOW marked cells in the center of each diamond; (TPISC IV: Details)
- Every PPT is found to exist on —and ONLY on — those Rows whose 1st Column grid cell are ➗ by 24 (YELLOW, with 1st Column grid cell marked as 'Z'), though not every such YELLOW marked Row contains a PPT. nPPT are only present on such Rows if accompanied by a PPT; (TPISC IV: Details)
- The “step-sister” of any given PT Row is found r-steps down the Axis from that Row (with 1st Column grid cell marked as 'Zf') and it, too, always and only exists on a YELLOW marked Row (“r” is part of the FTP originally derived from the Dickson Method for algebraically calculating all PTs); (TPISC IV: Details)
- The PPT Row (and nPPT Row) always contains the 4A (A=area) value of that PT and the “step-sister” PPT Row always contains the 8A value, both landing exclusively on YELLOW marked grid cells, giving a striking visualization of ALL PPTs and their r-based “step-sisters;” (TPISC III: Clarity & TPISC IV: Details)
- The significance of the “step-sister” is that it becomes the mathematical link to the “NEXT” PPT within the ToPPT — like the Russian-Doll model; (TPISC III: Clarity)
- The significance of the expanding and increasingly inter-connected PTs, as the BIM itself expands, is one in which the perfect-symmetry geometry of regular shapes and solids — equal triangles, squares, circles,… of the BIM allows — at certain articulation nodes (i.e., Rows) — the introduction of the slightly less-perfect-symmetry geometry (i.e., bilateral symmetry) of the full rectangle and oval that the non-isosceles right triangle PTs represent, into the unfolding structural framework, working from the ground up, if you will. The roots of fractals-based self organization are first to grow here! (TPISC III: Clarity & TPISC IV: Details) more…
- ALL self organization of any sort — be it force field or particulate matter — must have an organizing mathematical layer below driving it!
Besides intimately tying the ToPPTs to a natural fractal pattern within the BIM:
- Thereafter, ALL PTs — primitive “parents” (PPT) and non-primitive “children” (nPPT) —are found on select Rows of the BIM by simply following the squared numbers on the the Prime Diagonal down to intersecting Rows; ( TPISC I: Basics & TPISC II: Advanced) more…
- The mathematical basis relating the PPTs was found, as was the consistent Fractal-Template Profile (FTP) that every PT follows; (TPISC II: Advanced & TPISC III: Clarity) more…
- A yet to be explained tie-in with the prime numbers and 24: The difference (∆) between the squares of ALL primes is evenly ➗ by 24!!! (Pattern in Number: from Primes to DNA; GoDNA: The Geometry of DNA; SCoDNA: Structure and Chemistry of DNA; Butterfly Primes: ~let the beauty seep in~; Butterfly Prime Directive: ~metamorphosis ~ ; and, Butterfly Prime Determinate Number Array (DNA): ~conspicuous abstinence ~; and an interactive Butterfly Primes new media net.art project.
- The FTP allowed all the PPTs to be sorted out and organized into a definitive Tree of Primitive Pythagorean Triples (ToPPT) that co-extends infinitely throughout the infinitely expanding BIM —>BIMtree or BIM-ToPPT; (TPISC III: Clarity) more… and more…
One could simply say that: subtract one from the squared values of any natural, whole integer number (WIN) and if it is evenly ➗ by 24, it is a candidate for being a PPT or 'step-sister' if that same squared value - 25 is ALSO ➗ by 24.
If the Row contains BOTH a Factor Pair Set (two squared values that = a2 and b2) and the 4A value ONLY, it is a PPT Row.
If it contains BOTH the 4A and 8A values, it is a 'step-sister' Row, i.e. (c2-1)/24 and (c2-25)/24, if evenly divisible, are PPT and/or PPT 'step-sister' Rows, e.i. Row 17 is the PPT Row of the 8-15-17 PPT, but is also the 'step-sister' Row of the 5-12-13 PPT.
(NOTE: The PPTs intersect with grid cells/24 at: the subtraction of 1,5,7,11,13,17,19,23,25,… from the squared Axis number (c2) and that gives a cell spacing of 4-2-4-2-4-2-4-2-… respectively, or a blank step ∆ between of 3,1,3,1,3,1,3,1,... )
Take the BIM and divide all numbers evenly divisible by 24.
This gives you a criss-cross pattern based on 12, i.e. 12, 24, 36 ,48,… from Axis.
Halfway between, are the rows based on 6.
On either side of this 6-based and 12-based frequency, the rows just before and just after, are ACTIVE Rows. These are ALWAYS ODD # Rows. They form an Active Row Set (ARS). Later colored in PURPLE.
Their Axis #s are NEVER ➗3.They ALWAYS have their 1st Col value ➗ by 24.
Adding 24 to ANY of the ODD # NOT ➗3 ACTIVE Row Axis values ALWAYS sums to a value NOT ➗3 and thus to another ACTIVE Row Axis value (as adding 2 + 4 = 6, ➗3 added to a value NOT ➗3 = NOT ➗3 sum*).
Another ODD Axis # Row lies before and after each pair of ACTIVE Rows, i.e. between EVERY set of two ACTIVE Rows, is an ODD non-ACTIVE Row and their Col 1value is NOT ➗by 24.
Adding 24 to ANY of these ODD # ➗3 Axis values ALWAYS sums to a value also ➗3 (as 2 + 4 = 6, ➗3 added to a value already ➗3 = ➗3 sum *).
While not an exclusive condition, it is a necessary condition, that ALL PPTs and ALL Primes have Col 1 evenly ➗ by 24.
Together, two ACTIVEs + one non-ACTIVE form a repetitive pattern down the Axis, i.e. ARS + non-Active Row.
*While 24 seems to define this relationship, any EVEN # ➗3 will pick out much if not all of this pattern, e.i., 6, 12, 18,…
It follows that:
ALL PTs (gray with small black dot) fall on an ACTIVE Row.
ALL PRIMES (RED with faint RED circle) fall on an ACTIVE Row.
The difference, ∆, in the SQUARED Axis #s on any two ACTIVE Rows is ALWAYS divisible by 24.
The difference, ∆, in the SQUARED Axis #s on an non-ACTIVE ODD Row and an ACTIVE Row is NEVER divisible by 24.
The difference, ∆, in the SQUARED Axis #s on any non-ACTIVE ODD Row and another non-ACTIVE ODD Row is ALWAYS divisible by 24.
Going sequentially down the Axis, every ODD number in the series follows this pattern:
nA—A-A—nA—A-A—nA—A-A—
#3—5-7—9—11-13—15—17-19—21... Every 3rd ODD # (starting with 3) is ➗by 3 = nA .
#5-7—9—11-13—15—17-19 Every 1st & 2nd, 4th & 5th, 7th & 8th,… ODD # is NOT ➗ by 3 = A.
In other words, the two consecutive ODD #s, between the the nA ODD #s, are A ODD #s and are NOT ➗ by 3.
#3,4,5 re-stated: let A = ACTIVE Row Axis #, nA = non-ACTIVE Row Axis #
A22-A12= ➗ 24 and A ≠ ➗by 3
nA2-A2≠ ➗ 24
nA22-nA12= ➗ 24 and nA = ➗by 3
6,7,8 re-stated:
ODD Axis #s ➗by 3 (every 3rd ODD #) are NEVER ACTIVE Row members — thus never PT/PRIME
ODD Axis #s NOT ➗by 3 (every 1,2 — 4,5 — 7,8….ODD #s ) are ALWAYS ACTIVE Row members and candidates for being PT and/or PRIME.
In brief:
An ACTIVE Row ODD Axis # squared + a multiple of 24 (as 24x) = Another ACTIVE Row ODD Axis # squared , and the Square Root = a PT and/or a PRIME # :
A12+ 24x = A22 and √A22 = A2 = a PT and/or PRIME candidate;
ODD12+ 24x = ODD22 and √ODD22 = ODD2 = a PT and/or PRIME candidate, if and only if, its 1st Col. value is ➗ by 24.
The difference in the squared values of any two PTs/PRIME #s (>3) is ALWAYS a multiple of 24!
On the Prime Diagonal, the ODD #s follow the same pattern as on the Axis (see No.7).
BIM➗PPTs and PRIMES: (Latest: as this work was being prepared, a NEW relationship was found.) See below under Why?
ALL PTs and ALL PRIMES are exclusively on Rows that:
• are referred to as “ACTIVE."
• bookend the Rows that are multiples (evenly ➗ by) 6: i.e. 6,12,18,24,30,36…
• some of these bookend on 6-based Rows do NOT have a PT and/or Prime, e.i. Rows 35, 49, 55, 77, 91, 95,… (Certainly, those ➗ by factors other than themselves and one, are NOT Prime.)
• as one progresses across the Matrix Row, the YELLOW and YELLOW-ORANGE cells on “ACTIVE” Rows follow a pattern under Column #: 1–5—7—11—13—17—19—23—25…i.e., + - - - + - + - - - + - + - - - + - + - - - and so on (see Gray-Violet & White on the Table below).
• the cell value numbers of the YELLOW and YELLOW-ORANGE cells on “ACTIVE” Rows follow exactly the numbers on Col C of the Table VII: Axis_Sqd_Diff_24x.numbers.
• the Table view gives the number values and relationships in tabular form, the Matrix in a more visual, geometric form.
• remember: ALL candidates for PTs and/or Primes MUST have Col 1/24 = (x2 - 1)/24 as TRUE.
Distilling the BIM/24 into the underlying "sub-matrix" of ➗24 Actives, as shown in Figure below. ___ , reveals exactly why the BIM/24 pattern is what it is.
NOTES: Sections 1-10
Section 1: 2018 (29pgs)

These (colored inset boxes) Sub-Matrix 2 values:
- ALL PPTs have Col 1 ➗4;
- NO PPTs have Col 1 NOT ➗4;
- For any given Active Rows Set, only 1 Row is a ➗4 Row PPT, never both;
- SOME Col 1 ➗4 Rows are NOT PPTs ( starred );
- The NOT PPTs ( starred ) Axis #s are ➗Prime Factors*.
Axis# must be ODD, NOT ➗3 = Active Row Set (ARS) member;
Only 1 of the 2 ARS can be a PPT;
Sub-Matrix Col 1 # MUST be ➗4;
SOME may NOT be PPT if ➗Prime Factor (>5);
Remaining Axis # is a PPT. Exceptions:
Squared #s that are PPTs, remain PPTs when x2 or √x:
- ALL Squared #s that are PPTs, remain PPTs. ANY PPT #(x) times itself, times its square (x2) and/or times it serial products = NEW PPT;
- Example1: 5x5=25, 5x25=125, 5x125=625, 5x625=3125, 5x3125=15625=1252, 5x15625=78125, 5x78125=390625=6252,… products are ALL PPTs;
- Example 2: 97x97=9409, 97x9409=912,673, 97x912,673=88,529,281=94092=ALL PPTs.
Squared #s that are NOT, remain NOT when x2 or √x, as above.
Table 29 Exponentials of the first 10 PPTs c-values to be used in Tables 30a-g.
Tables 30a-g The Sub-Matrix 2, when ➗4, and the difference (∆) between this and the next exponential PPT treated this way, is subsequently ➗ by its Sub-Matrix 2 variable, the PREVIOUS exponential within the series is revealed. Restated as an example: When one subtracts 1 from the exponential values of c (the c-value of the PPT) you get the Sub-Matrix 2 value. Divide that by 4 and take the difference (∆) between it and the next. Divide that by 3 to give the PREVIOUS PPT c-value in the series.
The Sub-Matrix 2 variable divisor = 3 = Sub-Matrix 2 value/4 = 12/4. These variables run: 1,3,4,6,7,9,10,...
what exactly is the relationship between PPTs and PRIMES?
- a loosely threaded connection is quite apparent;
why do they BOTH land on ARS?
- they both must be ODD #s, not ➗3, whose (x2-1)/24 is true;
why do some ARS have both, neither, or one or the other?
- some clouds, some clarity, at least for the PPTs;
can the PRIMES be used to predict the PPTs?
- yes, in the sense that if the PPT candidate is ➗Prime Factor (>5), it will not be a PPT;
can the PPTs be used to predict the PRIMES?
- currently, NO, yet the threaded connections are so great that the pattern will eventually emerge!
The underlying geometry of the BIM÷24 PRE-SELECTS the Axis Rows into TWO Groups: ARs and NON-ARs. The PPTs and PRIMES are EXCLUSIVELY — as a sufficient, but not necessary condition — found on the ARs and NEVER on the NON-ARs. While both Groups follow (PD2 - PD2)÷24, they do so ONLY within their own respective Groups. They do NOT crossover. This Grouping divide occurs naturally within the BIM as shown in these images below.
The ISL as presented in the BIM is deeply, intimately structured around the number 24 — and its factors: 4,6, 3,8 2,12, and 1,24.
The interplay between these small sets of Numbers generates an incredible amount of richness and complexity with seemingly simplistic BIM itself. This has led to TPISP: The Pythagorean-Inverse Square Connection, and the PRIMES.
 Open in separate browser tab/window to see all.
Open in separate browser tab/window to see all.
741
7412-52/24 = n= 22877.3 NOT PRIME
189
1892-52/24 = n = 1487.3 NOT PRIME
289
2892-52/24 = n = 3479 PRIME



How Visualization of the PRIMES on the BIM ÷24 Simplifies Much of the Mysteries of the PRIME Conjectures and What This Means!
Much is made of the PRIME Conjectures: https://primes.utm.edu/notes/conjectures/ & site:primes.utm.edu Prime Gap conjecture
- Goldbach (Strong) Conjecture (every even # is made of two primes)
- Goldbach Tertiary (Weak) Conjecture (every odd # is made of three primes)
- Twin Prime Conjecture (there are an infinite # of primes separated by 2)
- Twin Primes Conjecture (there are an infinite # of primes separated by a fixed # gap)
- Prime Gap (size between consecutive primes)
- Prime Triple Conjecture (there are an infinite # of 3 consecutive primes with ∆ of 6, first and last)
- Prime Quadruple Conjecture (there are an infinite # of 4 consecutive primes with ∆ of 8, first and last)
- Prime k-tuplet Conjecture (there are an infinite # of prime k-tuplets for each* k*)
- Dickson’s Conjecture (there are a lot of primes, Twin, Sophie Germain, k-tuplet,…)
- Pythagorean Primes Conjecture(Pythagorean triples with prime # hypotenuse)
A look at the BIM÷24 grid will quickly give one a visualization of the limits — and expanses — of these conjectures!
(1 above.) This was examined and a proof-solution was offered in 2010 with the Periodic Table of Primes (PTOP), hidden within the BIM.
(2 above.) Work remains.
(3 above.) ALL Primes fall on Active Rows (ARs) within an Active Row Set (ARS) of three Axis #s: two ODDs with an EVEN in-between. The difference (∆) between the ODDs = 2. Thus ANY and ALL Twin Primes — separated by 2 — are seen right here, and only here, directly, on the ARS.
(4-8 above.) Because the ARSs follow a strict Number Pattern Sequence (NPS) in that the EVEN #s are ÷12 — being the endpoint of BIM÷24 — and the bookcased ODD #s are NEVER ÷3, there is a built-in ∆, a natural gap, between the ARS and ODD #s ÷ 3. This means the ARs — that provide a necessary, but not sufficient requirement for ANY PRIME — must necessarily have gaps that are:
taken from the lower ARS #:
- (Twins of) 2, 6, 8, 12, 14, 18, 20,… i.e., up 2, 4, 2, 4, 2, 4, 2,….
taken from the higher ARS #:
- (Twins of) 4, 6, 10, 12, 16, 18, 22,… i.e., up 4, 2, 4, 2, 4, 2, 4,….
(9 above.) Dickson’s Conjecture leads to many of the individual conjectures above. One, the Sophie Germain Prime Conjecture states that if a PRIME #, p, has another PRIME # generated at 2p + 1, it is a Sophie Germain PRIME and that there are an infinite number of these. On the BIM, it is easy to see that any Sophie PRIME is simply taking the lower AR # and ADDING a multiple of 6 — 6x — to get to the next PRIME. Try it: (≧5)5, 11, 23, 29, 41, 53, 83, 89, 113, 131, 173, 179, 191, 233, 239, 251, 281, 293, 359, 419, 431, 443, 491, 509, 593, 641, 653, 659, 683, 719, 743, 761, 809, 911, 953, ... OEIS: A005384. (https://en.wikipedia.org/wiki/Sophie_Germain_prime)
*the lower AR + 2 = higher AR — neither is ÷ by 3, while the lower AR - 2 = ODD# that is ÷ by 3 and NOT an AR.
This works for p≧5:
5+6=11, 11+(2)6=23, 23+6=29, 29+(2)6=41, 53+(5)6=83, 83+6=89, 89+(4)6=113, 113+(3)6=131, 131+(7)6=173, 173+(1)6=179, 179+(2)6=191, 191+(7)6=233, 233+(1)6=239, 239+(2)6=251, 251+(5)6=281, 281+(2)6=293, 293+(11)6=359, 359+(10)6=419, 419+(2)6=431, 431+(2)6=443, 443+(8)6=491, 491+(3)6=509, 509+(14)6=593, 593+(8)6=641, 641+(2)6=653, 653+(1)6=659, 659+(4)6=683, 683+(6)6=719, 719+(4)6=743, 743+(3)6=761, 761+(8)6=809, 809+(17)6=811, 911+(7)6=953, …
It appears that this conjecture really is simply restating Euler’s 6n+1 and 6n-1 — where n=1,2,3,… method for determining ALL PRIMES.
(10 above.) Ironically, the Pythagorean Triples were first to be found on the ARS, and only after reviewing earlier work — the Butterfly Primes — that the connection of the PRIMES to the BIM÷24 was made. Both the Primitive Pythagorean Triples (PPTs) and the PRIMES have the same — again, necessary, but not sufficient requirement — that they occupy EXCLUSIVELY the ARs potentially of any ARS. When the PPTs overlap the PRIMES, we get the Pythagorean Primes. An interesting note is that unlike the PRIMES that can occupy BOTH ARs of a given ARS, the PPTs will NEVER do this, occupying either one or the other, but NEVER BOTH, ARs within a ARS.
Fermat's (Fermat-Euler) 4n + 1 = Sum of Two Squares Theorem, where 4n + 3 ≠ Sum of Two Squares. The 4n + 1 = Sum of Two Squares = Pythagorean Primes (PTs where the hypotenuse, c = Prime #).
Remember, not only does the BIM÷24 reveal the ARs within the ARS, the∆ BETWEEN THE SQUARES OF ANY PAIR OF AR Axis #s (≧5) IS A MULTIPLE OF 24. The latter becomes a necessary, but not sufficient test of both primality, and, PPT validity.
Note that this same ∆ occurs with pairs of two non-AR ODD #s, i.e. 9 and 15. Both are ÷3. 152 - 92 = 144, and 144/24 = 6. A hybrid of an AR and a non-AR ODD pair set will NOT show a ∆ of 24x.
This points to underlying NPS within the BIM (see the pattern below the links):
For the ODD #s2:
∆÷24 vs NOT ∆÷24
∆÷24 in ARS vs ∆÷24 in non-ARS, NEVER a mix of the two
For the EVEN #s2:
∆÷24 vs NOT ∆÷24
∆÷24 includes those in progressive NPS series ∆2, ∆4, ∆6, ∆8, ∆10,… (see Table in Appendix ).
The PPTs and PRIMES are STRICTLY following this NPS within the BIM!
Perhaps the biggest finding here is: The PRIMES — Inverse Square Law Connection! Just like the PPTs! TPISC stands for both The Pythagorean-Inverse Square Connection, AND, The PRIMES-Inverse Square Connection. TP-P-ISC, TP/P-ISC, TP/PISC, TPPISC, or TP-IS-PC,...
The connection between that Universal Law, the ISL, — the underlying law of ALL of spacetime —and the PRIMES — the fundamental "quarks" of the number quantity system, AND, the Pythagorean Triples — the fundamental right-triangle/rectangle form of that same geometry — is without out a doubt the most intriguing, beguiling, and misunderstood relationship we are only just NOW getting a real glimpse at. The future looks very promising!
Reference:
"A New Kind of Prime
The twin primes conjecture’s most famous prediction is that there are infinitely many prime pairs with a difference of 2. But the statement is more general than that. It predicts that there are infinitely many pairs of primes with a difference of 4 (such as 3 and 7) or 14 (293 and 307), or with any even gap that you might want."
Quote is from Quanta Mag 9/26/19 article: Big Question About Primes Proved in Small Number Systems
by Kevin Hartnett
- Twin Primes
- Primes separated by other EVEN numbers
- Euler's 6n+1 and 6n-1
- Fermat-Euler's 4n + 1= Sum of Two Squares Theorem (Pythagorean Primes)
- Dickson's Conjectures: Sophie Germain Primes
- Goldbach Conjecture (Euler's "strong" form)
- Primes - BIM - Pythagorean Triples
~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~
A new and easy visualization!
PRIME GAPS
Game Board
There is a new game board in town. It has actually been around for awhile, but few know of it. It's basically a matrix grid of natural numbers that defines the Inverse Square Law (ISL). It's called the BIM, short for the BBS-ISL Matrix. Every grid cell is uniquely occupied by a given number that is simply the difference between the horizontal and vertical intercept values of the main "Prime Diagonal" (not Prime number diagonal) that mirror-divides the whole matrix.
If you show all the matrix values that are evenly divisible by 24, a criss-crossing pattern of diamond-diagonal lines will appear and this ends up giving us a unique visual on the distribuition of ALL PRIMES!
Basically, all ODDs (3 and greater for this presentation) fall into a repetitive pattern of:
ODD ÷3—Not÷3—Not÷3—÷3—Not÷3—Not÷3—÷3—Not÷3—Not÷3—÷3—Not÷3—Not÷3—÷3...
The matrix ÷24 described above, nicely picks out these sets of —Not÷3—Not÷3 that we call Active Row Sets (ARS). Each ODD member of the ARS is referred to as an Active Row (AR).
The ÷3 ODD Rows that lie between are called Non-Active Rows, or NA.
It is a necessary, but not sufficient condition, that ALL PRIMES are strictly located on ARs. NO exceptions, except for some ARs have NO PRIMES.
Another striking visualization is that ALL Primitive Pythagorean Triples (PPTs) also lie only on the ARs, following the same necessary, but not sufficient, condition. NO exceptions here as well, except for some ARs also have NO PPTs. In addition, only one of the ARs within an ARS can have a PPT.
So any AR within an ARS can have 0/1 PRIMES and/or 0/1 PPTs in any combination, only with the one caveat: that only 1 PPT/ARS is allowed.
Now, not to belabor this BIM game board, let's talk PRIME GAPS!
Prime Gaps
Let's refer to the lower number value for the ARS as "Lower" and the higher as "Upper." All are ODDs. As will become apparent, you can always tell if your ODD AR is "Lower/Upper" simply by adding 2 and ÷3: if the result evenly ÷3 it is "Upper" and if not, "Lower."
The Even Gap between primes strictly follows this pattern: (all are necessary but not sufficient conditions for primality)
For any given set of twin primes, or any single prime, that is the smaller "Lower" of an AR set:
- Even Gap must be 2, 6, 8, 12, 14, 18, 20, 24, 26, 30, 32, 36, 38, 42, 44, 48, 50,…
- Example: P=5: 7, 11, 13, 17, 19, 23, (25), 29, 31, (35), 37, 41, 43, 47, (49), 53, (55)
- P + 2, P + 2+4, P + 2+6, P + 2+10, P + 2+12, P + 2+16, P + 2+18, P + 2+22, P + 2+24,…
- P+21, P+2+22, P+23, P+22+23, P+2+22+23, P+2+24, P+22+24, P+23+24, P+2+2324
- The Even Gap difference pattern follows: 2-4-2-4-2-4-….
For any given set of twin primes, or any single prime, that is the larger "Upper" of an AR set:
- Even Gap must be 4, 6, 10, 12, 16, 18, 22, 24, 28, 30, 34, 36, 40, 42, 46, 48, 52, 54.…
- Example: P=7: 11, 13, 17, 19, 23, (25), 29, 31, (35), 37, 41, 43, 47, (49), 53, (55), 59, 61
- P + 4, P + 2+4, P + 2+8, P + 2+10, P + 2+14, P + 2+16, P + 2+20, P + 2+22, P + 2+26, P + 2+28,
- P+22, P+2+22, P+2+23, P+22+23, P+24, P+2+24, P+2+22+24, P+23+24, P+22+23+24, P+2+22+23+24,
- The Even Gap difference pattern follows: 4-2-4-2-4-2-…. and is identical in the middle, not the start!
One can readily see that all this is simply the natural result of two ARs alternating with a NA row:
AR—AR—NA—AR—AR—NA—AR—AR—NA—AR—AR—NA—…

“Lower” AR number
AR—5
AR—7
NA—9
AR—11
AR—13
NA—15
AR—17
AR—19
NA—21
AR—23
AR—25
NA—27…
It is 6 steps, i.e. +6, from any NA to the next NA, from any “Lower” AR to the next “Lower” AR, from any “Upper” AR to the next “Upper” AR. ALL of the various EVEN GAPS may be shown to be a direct consequence of the natural number sequence and easily visualized on the BIM.
To any “Lower” Active Axis Row ODD:
- Add 2, 4, or 6,…
- If sum is ÷3, it is a NA
- If sum is NOT÷3, it is an AR number and a PRIME (or PPT) candidate.
“Upper” AR number
AR—7
NA—9
AR—11
AR—13
NA—15
AR—17
AR—19
NA—21
AR—23
AR—25
NA—27…
To any “Upper” Active Axis Row ODD:
- Add 2, 4, or 6,…
- If sum is ÷3, it is a NA
- If sum is NOT÷3, it is an AR number and a PRIME (or PPT) candidate.
Again, It is 6 steps, i.e. +6, from any NA to the next NA, from any “Lower” AR to the next “Lower” AR, from any “Upper” AR to the next “Upper” AR. ALL of the various EVEN GAPS may be shown to be a direct consequence of the natural number sequence and easily visualized on the BIM.
The ARS pattern on the BIM clearly shows the above patterns and may be extrapolated to infinity:
pg3.png)
PRIME Conjectures
A number of PRIME conjectures have been shown to be easily visualized on the BIM:
Reference: TPISC IV: Details: BIM + PTs + PRIMES
The factors of 24 — 1,24–2,12–3,8–4,6 — when increased or decreased by 1, ultimately pick out ALL ARs. Euler's 6n +/-1 is the most direct, Fermat's 4n + 1 gets the Sums of Two Squares = Pythagorean Primes(while 4n + 3 gets the rest).
Fermat's Little Theorem (as opposed to the more familiar "Fermat's Last Theorem") tests for primality.
But now there is a dead simple way to test for primality:
The difference in the squares between ANY 2 PRIMES (≧5) ALWAYS = n24.
For example, take any random ODD # - 25 —> it must be ÷24 n times to be PRIME. (n=1,2,3,...)
741
7412-52/24 = n= 22877.3 NOT PRIME
189
1892-52/24 = n = 1487.3 NOT PRIME
289
2892-52/24 = n = 3479 PRIME
PRIMES vs NO-PRIMES
I would be remiss if I did not mention that throughout this long journey that began with the Inverse Square Law and the Primtive Pythagorean Triples that the PRIMES kinda of just fell out. They just kept popping up. Not the least, but certainly not without effort, the BIM actually directly visualizes ALL of the NO-PRIMES. In doing so, one is left with information that is simply the inverse of the PRIMES. Subtract the NO-PRIMES information from the list of ODDS (disregarding 2) and what remains are ALL the PRIMES! A simple algebraic expression falls out from that:
NP = 6yx +/- y
letting x=1,2,3,… and y=ODDs 3,5,7,… with the only caveat is that if you don't first eliminate all the ÷3 ODDS, you must include exponentials of 3 (3x) in the NP tally.
Goldbach Conjecture (Euler's "strong" form)
In 2009-10, a solution to Euler's "strong" form of the Goldbach Conjecture "that every even positive integer greater than or equal to 4 can be written as a sum of two primes" was presented as the BBS-ISL Matrix Rule 169 and 170. This work generated a Periodic Table of Primes (PTOP) in which Prime Pair Sets (PPsets) that sequentially formed the EVEN numbers were laid out. It is highly patterned table. A recently annotated version is included with the original below. (See above link for details.)
It turned out this PTOP was actually embedded — albeit hidden — within the BIM itself as shown in Rule 170 and here, too, a recently annotated version is included below. (See above link for details.)

Rule 169: Periodic Table of Primes.

Rule 169: annotated
 Rule 170: Periodic Table of Primes (PTOP): embedded within Brooks (Base) Square.
Rule 170: Periodic Table of Primes (PTOP): embedded within Brooks (Base) Square.
 Rule 170: annotated
Rule 170: annotated
LINKS:
MathspeedST: TPISC Media Center
BACK: ---> Simple Path BIM to PRIMES on a separate White Paper BACK: ---> PRIMES vs NO-PRIMES on a separate White Paper BACK: ---> TPISC_IV: Details_BIM+PTs+PRIMES on a separate White Paper BACK: ---> PRIME GAPS on a separate White Paper (This work.)
A NEW UPDATE: scroll down below these references!
Additional useful links:
See Appendix B: Tables 31-33 for more info.
https://en.wikipedia.org/wiki/Goldbach%27s_conjecture
https://en.wikipedia.org/wiki/Goldbach%27s_weak_conjecture
https://en.wikipedia.org/wiki/Pythagorean_triple
https://en.wikipedia.org/wiki/Twin_prime
https://en.wikipedia.org/wiki/Prime_gap
https://en.wikipedia.org/wiki/Prime_triplet
https://en.wikipedia.org/wiki/Prime_quadruplet
https://en.wikipedia.org/wiki/Prime_quadruplet#Prime_quintuplets
https://en.wikipedia.org/wiki/Prime_k-tuple
https://en.wikipedia.org/wiki/Dickson%27s_conjecture
https://en.wikipedia.org/wiki/Sophie_Germain_prime
https://en.wikipedia.org/w/index.php?search=Pythagorean+Primes&title=Special%3ASearch&go=Go
https://en.wikipedia.org/wiki/Prime_k-tuple
https://en.wikipedia.org/wiki/Fermat%27s_theorem_on_sums_of_two_squares
https://en.wikipedia.org/wiki/Pythagorean_prime
https://en.wikipedia.org/wiki/Fermat%27s_little_theorem
https://en.wikipedia.org/wiki/Euler%27s_theorem
https://en.wikipedia.org/wiki/Euclid–Euler_theorem
http://mathworld.wolfram.com/Eulers6nPlus1Theorem.html
What is the underlying NPS of the BIM ÷24?
Earlier we found:
For the ODD #s2
- ∆÷24 vs NOT ∆÷24
- ∆÷24 in ARS vs ∆÷24 in non-ARS, NEVER a mix of the two
For the EVEN #s2
- ∆÷24 vs NOT ∆÷24
- ∆÷24 includes those in progressive NPS series ∆2, ∆4, ∆6, ∆8, ∆10,… (see Table in Appendix ).
The PPTs and PRIMES are STRICTLY following this NPS within the BIM!
But what about just the BIM ÷24. How does this pattern out?
Let’s dispense with the EVENs first.
If one takes the EVEN #s on either side of the ARS + the EVEN # in the MIDDLE of the ARS, we have a new set. Let’s call it the EVENs Set (ES).
Well, it turns out there are two versions of the ESs and they alternate down the PD. Let’s call them ES1 and ES2 and they go: ES1-ES2-ES1-ES2,…
If we plot the ESs along the PD it will look like this (remember these are the squares of the EVEN Axis #s):
16 — 36 — 64 100 —144 — 196
256 —324— 400 484 — 576 — 676
784 —900—1024 1156—1296—1444
1600—1764—1936 2116—2304—2500
The ES1 are on the Left, the ES2 are on the Right.
The ÷24 NPS of the ES1 andES2 play out as:
Both group sets bookend the ARS with an ODD #÷3 (NON-ARS ODD) between.
The OUTER ends of ES1 are ∆/24 and the OUTER ends of ES2 are ∆/24.
The MIDDLE of ES1 are ∆/24 and the MIDDLE of ES2 are ∆/24.
There is NO MIXING between sets and NO MIXING OUTER with MIDDLE #s.
- The MIDDLE ES1 is ÷ by the 1st MIDDLE of the whole ES1 set.
- The MIDDLE ES2 is ÷ by the 1st MIDDLE of the whole ES2 set.
ES1 ÷ 16 ÷ 8 ÷ 4 ÷ 2 OUTER; MIDDLE ÷ 36, NEVER ÷ 24. (NOTE: these are the PD#s and not the ∆ in PD#s.)
ES2 ————÷ 4 ÷ 2 OUTER; MIDDLE ÷ 36, ALWAYS ÷ 24. (NOTE: these are the PD#s and not the ∆ in PD#s.)
A look at the BIM ÷24 shows that ALL MIDDLE PDs of their ESs are ÷12 and graphically:
 Table 31d. Snapshot of the PDF showing the EVENS role in the BIM ÷24 Distribution.
Table 31d. Snapshot of the PDF showing the EVENS role in the BIM ÷24 Distribution. ES1 fall along the IN-BETWEEN YELLOW DIAMOND PATTERN formed from the BIM ÷24.
- NEVER ÷ 24.
ES2 fall at the Axial POINTS of the YELLOW DIAMOND PATTERN.
- ALWAYS ÷ 24.
- ALWAYS ÷ 24.


So now that we have established that the EVENS, too, reveal a ÷24 expression within the BIM, let's move on the ODDS.
What about the ODDs?
We know that the ODDs ÷3 are the separators of the EVEN's ES1 and ES2 . They are also a separate player in the whole ODDs set in that though their PDs are ÷24, they are NOT part of the ARS. And as NON-ARs they do NOT MIX with the AR ODDs.
We will continue to label the two groups as ARs and NON-ARs.
Earlier we found:
For the ODD #s2
- ∆÷24 vs NOT ∆÷24
- ∆÷24 in ARS vs ∆÷24 in non-ARS, NEVER a mix of the two.
More precisely:
ALL ARs2 are ∆/24, and, NEVER ÷3, and after subtracting (-1) are ALWAYS ÷24, and, ALL now ÷3.
ALL NON-ARs2 are ∆/24, and, ALWAYS ÷3, and after subtracting (-1) NEVER ÷24, but ALL ÷9 ÷3.
There is NO MIXING between groups.
Additionally, the ODD AR group may be further divided into:
ODD Set 1 (OS1): (Like the EVENS, ES1) for IN-BETWEEN YELLOW DIAMOND Rows 6,18,30,42,...
ODD Set 2 (OS2): (Like the EVENS, ES2) for the POINTS of the YELLOW DIAMOND Rows 12,24,36,...
However, here, BOTH groups ARE MIXABLE, i.e. ∆/24 across OS1 and OS2.
What really becomes interesting about the ODDs on the BIM ÷24 is that, all by themselves without regard to the PPTs or PRIMES, they form a deep, underlying NPS ALL BASED ON THEIR ∆s/24!
In a nutshell, if you take each ODD #, square it (that's the PD#) and now sequentially substract the ODD PDs below it, and then ÷24, the results will generate a tightly connected NPS across the ODDS on the BIM.
The ARs2 1-25-49-121-169-289-361-529-625,… (12-52-72-112-132-172-192-232-252,) subtraction=ALL ARs.
The NON-ARs2 9-81-225-441-729,… (32-92-152-212-272,…) subtraction=ALL NON-ARs.
pg2.png) Here is a quick look at the AR and NON-AR Distribution. Open the PDFs below in a separate tab/window.
Here is a quick look at the AR and NON-AR Distribution. Open the PDFs below in a separate tab/window.
pg3.png) Here is a quick look at the AR and NON-AR Distribution. Open the PDFs below in a separate tab/window.
Here is a quick look at the AR and NON-AR Distribution. Open the PDFs below in a separate tab/window.
+50x50.pdf)


 Table 33d-2-1
Table 33d-2-1

Table 33d-2-2

UPDATE: Finally, the NEW relationship between the BIM÷24 and the PRIMES has been found! See the bottom of APPENDIX B for the tables that document this work! From the APPENDIX B:
Back to the Table 31 sequences. Table 31a... series, along with the previous Table33 series, uncovers how the PRIMES were found within the BIM both by algebra and geometry. This has been reduced to a focus white paper: "PRIMES vs NO-PRIMES that is a condensed summary of this work. One may benefit from looking over this paper prior to the study of these more elaborate tables. A summary from the paper is presented here:
SUMMARY*
(~from "*Simple Path from the BIM to the PRIMES" that presents the algebraic-geometry method.)
How do we go from the simple grid of the BIM (BBS-ISL Matrix) to identifying the PRIMES?
The BIM is a symmetrical grid — divided equally down its diagonal center with the Prime Diagonal (PD) — that illuminates the Number Pattern Sequence (NPS) of the Inverse Square Law (ISL) via simple, natural Whole Integer Numbers (WIN).
The BIM Axis numbers are 1,2,3,.. with 0 at the origin.
The Inner Grid (IG) contains EVEN and ODD WIN, but except for the 1st diagonal next to the PD — a diagonal that contains ALL the ODD WIN — there are NO PRIMES (NO-PRIMES, NP) on the SIG (Strict Inner Grid).
The PD WIN are simple the square of the Axis WIN.
ALL the IG WIN result from subtracting the horizontal from the vertical intersection of the PD.
Dropping down a given PD Squared WIN (>4) until it intersects with another squared WIN on a Row below will ALWAYS reveal that Row to be a Primitive Pythagorean Triple (PPT) Row, whose hypotenuse, c, lies on the intersecting PD. ALL PPTs may be identified this way.
Dividing the BIM cell values by 24 — BIM÷24 — forms a criss-crossing DIAMOND NPS that divides the overall BIM into two distinct and alternating Row (and Column) bands or sets:
- ODD WIN that are ÷3 and referred to as NON-ARs;
- ODD WIN that are NOT ÷3 and referred to as ARs, or Active Rows;
- The ARs ALWAYS come in pairs — with an EVEN WIN between — as the UPPER and LOWER AR of the ARS (Active Row Set);
ALL PPTs and ALL PRIMES ALWAYS are found exclusively on the ARs — no exceptions.
By applying:
(1) *
let y = odd number (ODD) 3, 5, 7,… and x = 1, 2, 3,... one generates a NP table containing ALL the NP;
*True if ÷3 ODDs are first eliminated, otherwise ADD exponentials of 3 to the NP pool;
Eliminating the NP — and the NP contain a NPS — from ALL the ODD WIN, reveals the PRIMES (P).
A necessary, but not sufficient confirmation — but not proof — of primality is found by finding the even division of 24 into the difference of the square of ANY two PRIMES as:
(2) (P2)2 - (P1)2 =
let
Be aware that this also holds true for ALL the AR NP. The P and NP are NOT ÷3, and are both part of the ARS and therefore any combination of the two squared differences will be ÷24:
(3) (NP2)2 - (NP1)2 =
(4) (NP2)2 - (P1)2 =
(5) (P2)2 - (NP1)2 =
The ÷3 NON-AR set is separately ÷24, but can NOT be mixed with members of the AR set (ARS) as:
(6) (NON-AR-NP2)2 - (NON-AR-NP1)2 = n24
(7) (NON-AR-NP2)2 - (NP1)2 ⧣
(8) (NP2)2 - (NON-AR-NP1)2 ⧣
(9) (P2)2 - (NON-AR-NP1)2 ⧣
(10) (NON-AR-NP2)2 - (P1)2 ⧣
The division into AR and NON-AR sets has a NPS that ultimately define the elusive pattern of the P.
Furthermore, may be re-arranged to:
(11)
(12)
asking whether any given ODD (>3) is a P or NP, it is exclusively a NP if, and only if, y reduces to the same value after applying x. As y is effectively an ODD of either a PRIME or composite of PRIMES factor*, one only needs to satisfy a single instance to validate NON-Primality.
One can also obtain ALL the P by eliminating the BIM SIGO and O2 from the 1st Diagonal WIN, where SIGO = Strict Inner Grid ODDs, O2 = ODDs2, and the 1st Diagonal = the 1st Diagonal Parallel to the PD.
This itself is further simplified by switching out the ODD AXIS values with the O2 — the O2 being the PD values — such that we now have:
(13) SIGO(A2) = Strict Inner Grid ODDS & ODD AXIS2 giving a distinct visualization advantage;(14) NP = SIGO(A2)
(15) 1st Diagonal - SIGO(A2) = P.
This second method — the algebraic geometry method — as presented here.
Introduction
Two methods — one pure algebraic and the other a more visual algebraic geometry presented here — have been found that capture ALL the NO-PRIMES (NP). While they process slightly different, they dovetail nicely into a very visual Number Pattern Sequence (NPS) here on the BIM. They both give identical NP results.
So what is the significance of capturing ALL the NP?
The NP are the highly NPS that define the elusive pattern of the P. P + NP = ALL ODD WINs (≥3).
In any group of WIN, if you know the NP, you also know the P. Here is the highly visualizable geometric method for capturing ALL NP. In fact, it is just as simply stated in 12. of the SUMMARY.
Algebraic Geometry Method
One can obtain ALL the P by eliminating the BIM SIGO and O2 from the 1st Diagonal WIN, where SIGO = Strict Inner Grid ODDs, O2 = ODDs2, and the 1st Diagonal = the 1st Diagonal Parallel to the PD.
This itself is further simplified by switching out the ODD AXIS values with the O2 — the O2 being the PD values — such that we now have:
One can also obtain ALL the P by eliminating the BIM SIGO and O2 from the 1st Diagonal WIN, where SIGO = Strict Inner Grid ODDs, O2 = ODDs2, and the 1st Diagonal = the 1st Diagonal Parallel to the PD.
This itself is further simplified by switching out the ODD AXIS values with the O2 — the O2 being the PD values — such that we now have:
(13) SIGO(A2) = Strict Inner Grid ODDS & ODD AXIS2(14) NP = SIGO(A2)
(15) 1st Diagonal - SIGO(A2) = P.
The PDFs will follow these animated gifs. Videos and other supporting graphics thereafter.
Animated Gifs:

PRIMES vs NO-PRIMES-2: algebraic method.

PRIMES vs NO-PRIMES-1: algebraic-geometry method.

PRIMES vs NO-PRIMES-3: algebraic and algebraic geometry method.

PRIMES vs NO-PRIMES-4: algebraic method in detail.
PDFs +


PRIMES vs NO-PRIMES: snapshot-1 showing dovetailing visualization of the algebraic method of calculating the NP with that of the geometric method on the BIM. The larger PDF is below.
PRIMES vs NO-PRIMES PDF: snapshot-1 showing dovetailing visualization of the algebraic method of calculating the NP with that of the geometric method on the BIM. The NPS of the NP define the elusive pattern of the P.

PRIMES vs NO-PRIMES: snapshot-2 showing dovetailing visualization of the algebraic method of calculating the NP with that of the geometric method on the BIM. Here the x=1,2,3,... base value sets -- Lower -y an Upper +y--as double-wide, L-shaped paths beginning just below the 1st Diagonal. These double rows alternate with divisible by 3--or divisible by 9 Axis squared--paths. The larger PDF is below.
PRIMES vs NO-PRIMES PDF: snapshot-2 showing dovetailing visualization of the algebraic method of calculating the NP with that of the geometric method on the BIM. The larger PDF is below. Here the x=1,2,3,... base value sets -- Lower -y an Upper +y--as double-wide, L-shaped paths beginning just below the 1st Diagonal. These double rows alternate with divisible by 3--or divisible by 9 Axis squared--paths.

PRIMES vs NO-PRIMES: snapshot-3 showing dovetailing visualization of the algebraic method of calculating the NP with that of the geometric method on the BIM. Here the x=1,2,3,... base value sets -- Lower -y an Upper +y--as double-wide, L-shaped paths beginning just below the 1st Diagonal. These double rows alternate with divisible by 3--or divisible by 9 Axis squared--paths. The larger PDF is below.
PRIMES vs NO-PRIMES PDF: snapshot-3 showing dovetailing visualization of the algebraic method of calculating the NP with that of the geometric method on the BIM. The larger PDF is below. Here the x=1,2,3,... base value sets -- Lower -y an Upper +y--as double-wide, L-shaped paths beginning just below the 1st Diagonal. These double rows alternate with divisible by 3--or divisible by 9 Axis squared--paths.

PRIMES vs NO-PRIMES PDF: snapshot-4 showing dovetailing visualization of the algebraic method of calculating the NP with that of the geometric method on the BIM. The larger PDF is below. Here the x=1,2,3,... base value sets -- Lower -y an Upper +y--as double-wide, L-shaped paths beginning just below the 1st Diagonal. These double rows alternate with divisible by 3--or divisible by 9 Axis squared--paths.
Table31a4: PRIMES vs NO-PRIMES PDF: Open in a separate tab/window to see all 11 pages. Here the x=1,2,3,... base value sets -- Lower -y an Upper +y--are shown individually and collectively as sets. The full Upper and Lower tables conclude.
Table31a6_2: PRIMES vs NO-PRIMES PDF: If you look at the ODD Axis ÷3 NO-PRIMES (NP) that lie in the paths between the L-shaped Double-wide x-base sets (x=1,2,3,)…), one finds a distinct Number Pattern Sequence (NPS) between successive NP values. Those shown in BLUE are NOT included in the criss-crossing L-shaped Double-wide paths (seen in the snapshots above), while those in GRAY are. The NPS seen here, based ultimately on the 1,3,5,7,… ODD number summation series that defines the whole BIM distribution (including the 1st Diagonal, the PD, and the successive differences in sequential Inner Grid cell values) reiterates that of both the L-shaped Double-wide paths as well as the individual x paths. Both give a NPS of the NP that reveal the elusive pattern of the PRIMES. There remains little doubt that the PRIMES , as well as the Primitive Pythagorean Triples (PPTs), are intimately related to the INVERSE SQUARE LAW (ISL)!
Videos:
PRIMES vs NO-PRIMES-1-long from Reginald Brooks on Vimeo.
PRIMES vs NO-PRIMES-2-long from Reginald Brooks on Vimeo.
PRIMES vs NO_PRIMES 3 from Reginald Brooks on Vimeo.
PRIMES_vs_NO-PRIMES-4 from Reginald Brooks on Vimeo.
...more supporting graphics and tables:
+10x10+.pdf)

+50x500+.pdf.pdf)



For the full documentation of all the graphics and pdfs — including history, development, expanded tables, and more — see Appendix B below.
REFERENCES
While there are no specific references for this work other than referring back to my own original work, there are many references involved in the study and research on the PRIMES in general. These have been well documented in the TPISC_IV: Details_BIM+PPT+PRIMES focus white paper. This paper also contains the background graphics and tables leading up to this current work. The focus page is part of the much larger TPISC_IV: Details ebook project that is freely available as an HTML webpage. The quick reference outline can be found here.
(See Appendix B below: BIM ➗24 PPTs and PRIMES for ALL the Figures and Tables relating to BIM ➗24. Note: open the PDFs into a separate tab/page to see the full content. The png image files give a quick-look only.)
REFERENCES:
https://primes.utm.edu/notes/faq/six.html
“Are all primes (past 2 and 3) of the forms 6n+1 and 6n-1?
"Perhaps the most rediscovered result about primes numbers is the following:
"I found that every prime number over 3 lies next to a number divisible by six. Using Matlab with the help of a friend, we wrote a program to test this theory and found that at least within the first 1,000,000 primes this holds true.
"Checking a million primes is certainly energetic, but it is not necessary (and just looking at examples can be misleading in mathematics). Here is how to prove your observation: take any integer n greater than 3, and divide it by 6. That is, write
n = 6q + r
where q is a non-negative integer and the remainder r is one of 0, 1, 2, 3, 4, or 5.
- If the remainder is 0, 2 or 4, then the number n is divisible by 2, and can not be prime.
- If the remainder is 3, then the number n is divisible by 3, and can not be prime.
"So if n is prime, then the remainder r is either
- 1 (and n = 6q + 1 is one more than a multiple of six), or
- 5 (and n = 6q + 5 = 6(q+1) - 1 is one less than a multiple of six).
"Remember that being one more or less than a multiple of six does not make a number prime. We have only shown that all primes other than 2 and 3 (which divide 6) have this form.”
From Another prime page by Chris K. Caldwell caldwell@utm.edu
~~~
"Euler's 6n+1 Theorem
"Every Prime of the form 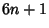 can be written in the form
can be written in the form 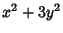 ."
."
https://archive.lib.msu.edu/crcmath/math/math/e/e282.htm
~~~
~~~
http://www2.mae.ufl.edu/~uhk/sixnplusone.pdf.
~~~
~~~
https://en.m.wikipedia.org/wiki/Formula_for_primes
~~
http://www2.mae.ufledu/~uhk/PRIME-TEST.pdf **
http://www2.mae.ufl.edu/~uhk/NUMBER- FRACTION.pdf
~~~
http://mathworld.wolfram.com/Eulers6nPlus1Theorem.html
~~
http://eulerarchive.maa.org See Number Theory Section
E744en.pdf **!!!!!!*!!!!! MOST IMPORTANT READ
http://eulerarchive.maa.org/docs/translations/E744en.pdf
NOTE: These article links from the Euler Archive/Number Theory/ INDEX are IMPORTANT READS for PRIMES & Squares. You can link directly from the Index as well.
http://eulerarchive.maa.org/pages/E026.html
http://eulerarchive.maa.org/pages/E054.html
http://eulerarchive.maa.org/pages/E134.html
http://eulerarchive.maa.org/pages/E175.html
http://eulerarchive.maa.org/pages/E191.html
http://eulerarchive.maa.org/pages/E241.html
http://eulerarchive.maa.org/pages/E242.html
http://eulerarchive.maa.org/pages/E243.html
http://eulerarchive.maa.org/pages/E244.html
http://eulerarchive.maa.org/pages/E256.html
http://eulerarchive.maa.org/pages/E262.html
http://eulerarchive.maa.org/pages/E270.html
http://eulerarchive.maa.org/pages/E279.html
http://eulerarchive.maa.org/pages/E283.html
http://eulerarchive.maa.org/pages/E369.html
http://eulerarchive.maa.org/pages/E394.html
http://eulerarchive.maa.org/pages/E405.html
http://eulerarchive.maa.org/pages/E445.html
http://eulerarchive.maa.org/pages/E449.html
http://eulerarchive.maa.org/pages/E467.html
http://eulerarchive.maa.org/pages/E523.html
http://eulerarchive.maa.org/pages/E542.html
http://eulerarchive.maa.org/pages/E552.html
http://eulerarchive.maa.org/pages/E554.html
http://eulerarchive.maa.org/pages/E564.html
http://eulerarchive.maa.org/pages/E596.html
http://eulerarchive.maa.org/pages/E610.html
http://eulerarchive.maa.org/pages/E699.html
http://eulerarchive.maa.org/pages/E708.html
http://eulerarchive.maa.org/pages/E715.html
http://eulerarchive.maa.org/pages/E718.html
http://eulerarchive.maa.org/pages/E719.html
| 744 | On divisors of numbers of the form mxx + nyy |
|---|---|
http://eulerarchive.maa.org original 744 Euler article
https://www.britannica.com/science/Fermats-theorem
http://mathworld.wolfram.com/FermatsLittleTheorem.html
http://mathworld.wolfram.com/EulersTotientTheorem.html
http://mathworld.wolfram.com/TotientFunction.html
https://www.geeksforgeeks.org/fermats-little-theorem/
https://www.geeksforgeeks.org/eulers-totient-function/
http://mathworld.wolfram.com/Eulers6nPlus1Theorem.html
https://brilliant.org/wiki/fermats-little-theorem/
https://brilliant.org/wiki/eulers-theorem/
https://primes.utm.edu/notes/proofs/FermatsLittleTheorem.html
https://primes.utm.edu/notes/conjectures/ Conjectures
https://primes.utm.edu/notes/faq/ FAQ Index
https://primes.utm.edu/notes/faq/one.html One
https://primes.utm.edu/notes/faq/six.html Six —>Important Page
http://unsolvedproblems.org/index.htm Unsolved Problems Index
https://en.m.wikipedia.org/wiki/Proofs_of_Fermat%27s_little_theorem
https://en.m.wikipedia.org/wiki/Fermat%27s_little_theorem
https://en.m.wikipedia.org/wiki/Euler%27s_theorem
~~NEW REFERENCE LIST 11-08-2018~Fermat’s Little Theorem ++++Euler
https://web.math.princeton.edu/swim/SWIM%202010/Shi-Xie%20Presentation%20SWIM%202010.pdf
http://mathworld.wolfram.com/Fermats4nPlus1Theorem.html
http://nonagon.org/ExLibris/euler-proves-fermats-theorem-sum-two-squares
https://storyofmathematics.com/17th_fermat.html
https://en.wikipedia.org/wiki/Prime_number
http://mathworld.wolfram.com/PrimeNumberTheorem.html
https://www.britannica.com/science/prime-number-theorem
https://going-postal.com/2018/02/fermats-little-theorem/
https://ibmathsresources.com/2014/03/15/fermats-theorem-on-the-sum-of-two-squares/
https://en.wikipedia.org/wiki/Fermat%27s_theorem_on_sums_of_two_squares *
https://en.wikipedia.org/wiki/Pythagorean_prime *
https://oeis.org/A002144 Pythagorean Primes of the form 4n + 1
https://oeis.org/A002144/list List of Pythagorean Primes of the form 4n + 1
http://nonagon.org/ExLibris/fermat-sum-two-squares-calculator *
https://www.britannica.com/science/Mersenne-prime Mersenne Primes
https://primes.utm.edu/mersenne/
https://en.wikipedia.org/wiki/Mersenne_prime#About_Mersenne_primes
http://mathworld.wolfram.com/MersenneNumber.html
http://mathworld.wolfram.com/MersennePrime.html
https://www.encyclopediaofmath.org/index.php/Mersenne_number
https://www.mersenne.org GIMPS
https://www.mersenne.org/primes/
https://primes.utm.edu/lists/small/millions/ Primes LIST by section
http://compoasso.free.fr/primelistweb/page/prime/liste_online_en.php Primes LIST by section
http://primerecords.dk/primegaps/gaps20.htm Prime Gaps
http://primerecords.dk/primegaps/maximal.htm
https://en.wikipedia.org/wiki/Prime_gap
https://primes.utm.edu/notes/GapsTable.html
https://en.wikipedia.org/wiki/Prime_k-tuple
https://primes.utm.edu/glossary/page.php?sort=ktuple
https://en.wikipedia.org/wiki/Twin_prime
http://mathworld.wolfram.com/TwinPrimes.html
https://primes.utm.edu/notes/faq/
~~
https://oeis.org/wiki/Pythagorean_primes Pythagorean vs non-Pythagorean Primes
http://oeis.org/A002145 non-Pythagorean Primes of the form 4n + 3
http://oeis.org/A002144 Pythagorean Primes of the form 4n + 1
https://en.wikipedia.org/wiki/Double_Mersenne_number Double Mersenne Primes
https://primes.utm.edu/mersenne/index.html#unknown Questions remain
~~~~~~~~~~NEW REFERENCE LIST 12-13-2018~~~videos——must watch~~~~
See: Animated math: videos by 3Blue1Brown (Grant Sanderson, et al.) https://www.3blue1brown.com/videos/
Feynman's Lost Lecture (ft. 3Blue1Brown) https://www.youtube.com/watch?v=xdIjYBtnvZU
But WHY is a sphere's surface area four times its shadow?: video by 3Blue1Brown https://youtu.be/GNcFjFmqEc8
Why is pi here? And why is it squared? A geometric answer to the Basel problem: video by 3Blue1Brown https://www.youtube.com/watch?v=d-o3eB9sfls&frags=pl%2Cwn
Pi hiding in prime regularities: video by 3Blue1Brown https://youtu.be/NaL_Cb42WyY
Visualizing the Riemann hypothesis and analytic continuation: video by 3Blue1Brown https://youtu.be/sD0NjbwqlYw
All possible pythagorean triples, visualized: video by 3Blue1Brown https://www.youtube.com/watch?v=QJYmyhnaaek
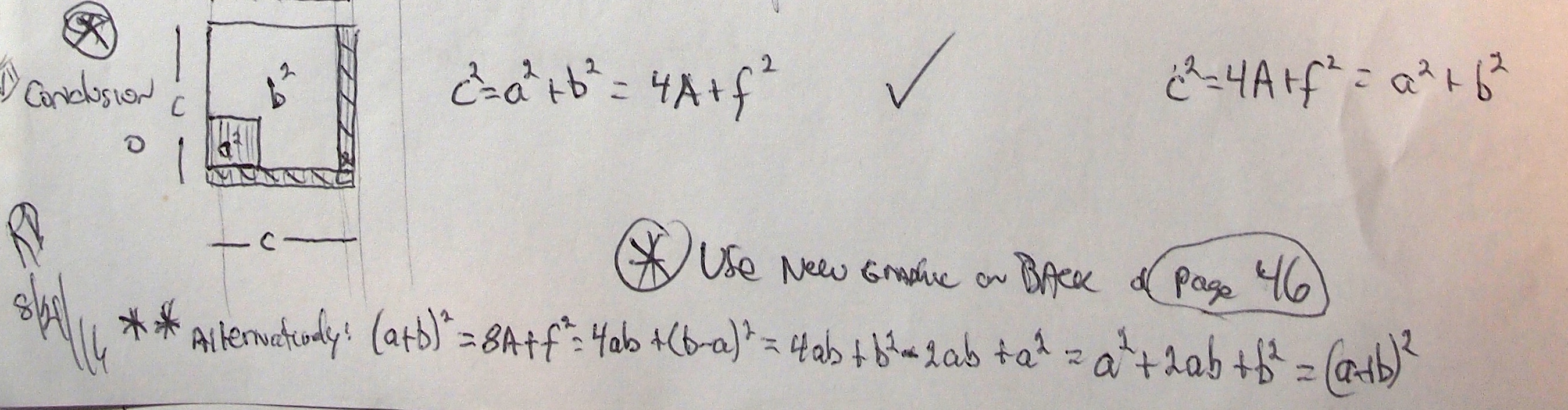
((((Table VI series is really the whole evolution of the BIMrow1-1000+sheets/Primes_sheets+PF, etc here and appendix.)))
referenced as Table VI a
referenced as Table VI b
referenced as Table VI b
Table VII.
(See Appendix B below: BIM ➗24 PPTs and PRIMES for ALL the Figures and Tables relating to BIM ➗24.)
Artwork referencing TPISC.
Summation:
Here’s the thing. Amongst a myriad of other connections, there exist an intimate connection between three number systems:
- The ISL as laid out in the BIM;
- PTs — and most especially PPTs — as laid out on the BIM;
- The PRIME numbers — PRIMES — as laid out on the BIM.
The BIM is the FIXED GRID numerical array of the ISL.
Amongst its vast array of inter-connecting Number Pattern Sequences (NPS) — i.e., number systems — two such systems stick out and do so in such an overtly visual — as well as mathematical — way that their connection to each other is more than implied.
You see, both the PPTs and PRIMES strictly align themselves on the SAME paths within the BIM.
Now, their footprints upon these paths are not identical, yet their paths chosen are. If you divide the number array — i.e., the Inner Grid numbers — of the BIM by 24, a Sub-Matrix 1 grid is formed.
Upon that Sub-Matrix 1, pathways are formed on every ODD Axis number NOT ➗3.** EVERY PPT and PRIME lies on these paths!**
Yes, while in the details we show how:
- The 1st Col. on the BIM — that which is the square of the Axis number (i.e., the Prime Diagonal number) - 1, when then ➗ by 24, equals a Whole Integer Number (WIN);
- This defines the path — the “Active Row” upon the BIM;
- While every Active Row path may or may not contain a PPT and/or PRIME, every PPT and/or PRIME is ALWAYS located on one of these paths;
- The difference (∆) between the squares of any two PRIMES (>5) is also ➗24;
- The serial — and exponential — products of ANY and ALL PPTs remain PPTs, whilst those NOT remain NOT.
Furthermore, by distilling the BIM to Sub-Matrix 2 — i.e., every number across a Row is progressively divided by a growing sequence series starting with the Col. 1 as the Axis number - 1 — every such serial-exponential PPT is clearly predicted by its neighbors within the sequence. One more example of the extremely intimate relationship between The Pythagorean - Inverse Square Connection (TPISC).
One simply can not ignore how the PRIMES, the PTs and ultimately the ISL define the architecture of SpaceTime!
In the original MathspeedST, an artificial division was made, separating the content into:
- TAOST, The Architecture Of SpaceTime,
- TCAOP, The Complete Absence Of Primes.
Now we have come full circle.
ALL PRIMES and ALL PPTs follow — although individually with their own respective footprints — the SAME, HIGHLY PATTERNED NPS path on the BIM.
This is no coincidence. The ➗24 Active Row Pattern that defines this path on the BIM does so in a highly ordered pattern. The energy density that expresses itself as curved ST does so precisely by the numerical architect of the built-in ISL.
We now have some very strong evidence that the numbers that define the PPTs and the numbers that define the PRIMES are ubiquitously linked throughout the entire number pattern array that defines the ISL. This is revealed on the BIM!
Surely their interplay provides some very significant contributions to the overall Architecture of SpaceTime!
feel the beat: + - + - - - + - + - - - + - + - - - + - + - - - ...
VIMEO "BIM_PRIMES_24"1! )
BIM_PT_PRIMES_24 from Reginald Brooks on Vimeo.
TPISC_IV:_Details ~A MathspeedST Supplement~
Copyright©2018-19, Reginald Brooks. All rights reserved.
Artwork referencing TPISC.
TPISC_IV:_Details ~PRIMES vs NO-PRIMES~
Copyright©2019, Reginald Brooks. All rights reserved.
~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~
SEE Page 50 (Art Theory101: White Papers) for spreadsheets: BIM: How to Make.
TABLES 1-9 (r-sets, Z➗24,Axis squared, differences, groundwork tables)







Table VI b fully expanded 1-1010 PTs and Primes with ALL ACTIVE Rows color-coded in Violet
(Once renamed, ALL Tables — as pdf/pngs—will be listed here with links to and fro main article)
TABLES 10-19 (PRIMEs-gaps and random differences)













TABLES 20-23 (PRIME-PPT or not with r-values)

TABLES 24-28 (Sub-Matrix 2 )
TABLES 29-30 (Sub-Matrix 2 Sidebar: Exponentials of the PPTs)
Sub-Matrix 2 Sidebar: Exponentials of the PPTs
Table 29 Exponentials of the first 10 PPTs c-values to be used in Tables 30a-g.
Tables 30a-g The Sub-Matrix 2, when ➗4, and the difference (∆) between this and the next exponential PPT treated this way, is subsequently ➗ by its Sub-Matrix 2 variable, the PREVIOUS exponential within the series is revealed. Restated as an example: When one subtracts 1 from the exponential values of c (the c-value of the PPT) you get the Sub-Matrix 2 value. Divide that by 4 and take the difference (∆) between it and the next. Divide that by 3 to give the PREVIOUS PPT c-value in the series.
The Sub-Matrix 2 variable divisor = 3 = Sub-Matrix 2 value/4 = 12/4. These variables run: 1,3,4,6,7,9,10,...
Tables: 31a, a+, a++, ++MP, a+++ and 31b
Tables: 32a,32b and 32c
BIM÷24: SubMatrix Sidebar: What is the role of 24 in the underlying structure?
SEE: Tables: 33a, 33b, 33c and 33d. towards the end of Appendix B for some very NEW INFO on the BIM÷24.
The underlying geometry of the BIM÷24 PRE-SELECTS the Axis Rows into TWO Groups: ARs and NON-ARs. The PPTs and PRIMES are EXCLUSIVELY — as a sufficient, but not necessary condition — found on the ARs and NEVER on the NON-ARs. While both Groups follow (PD2 - PD2)÷24, they do so ONLY within their own respective Groups. They do NOT crossover. This Grouping divide occurs naturally within the BIM as shown in these images below.
The ISL as presented in the BIM is deeply, intimately structured around the number 24 — and its factors: 4,6, 3,8 2,12, and 1,24.
The interplay between these small sets of Numbers generates an incredible amount of richness and complexity with seemingly simplistic BIM itself. This has led to TPISP: The Pythagorean-Inverse Square Connection, and the PRIMES.

Supporting Graphics forTables: 33a, 33b, 33c and 33d. Open in separate browser tab/window to see all.


















Back to the Table 31 sequences. Table 31a... series, along with the previous Table33 series, uncovers how the PRIMES were found within the BIM both by algebra and geometry. This has been reduced to a focus white paper: "PRIMES vs NO-PRIMES that is a condensed summary of this work. One may benefit from looking over this paper prior to the study of these more elaborate tables. A summary from the paper is presented here:
SUMMARY*
(~from "*Simple Path from the BIM to the PRIMES" that presents the algebraic-geometry method.)
How do we go from the simple grid of the BIM (BBS-ISL Matrix) to identifying the PRIMES?
The BIM is a symmetrical grid — divided equally down its diagonal center with the Prime Diagonal (PD) — that illuminates the Number Pattern Sequence (NPS) of the Inverse Square Law (ISL) via simple, natural Whole Integer Numbers (WIN).
The BIM Axis numbers are 1,2,3,.. with 0 at the origin.
The Inner Grid (IG) contains EVEN and ODD WIN, but except for the 1st diagonal next to the PD — a diagonal that contains ALL the ODD WIN — there are NO PRIMES (NO-PRIMES, NP) on the SIG (Strict Inner Grid).
The PD WIN are simple the square of the Axis WIN.
ALL the IG WIN result from subtracting the horizontal from the vertical intersection of the PD.
Dropping down a given PD Squared WIN (>4) until it intersects with another squared WIN on a Row below will ALWAYS reveal that Row to be a Primitive Pythagorean Triple (PPT) Row, whose hypotenuse, c, lies on the intersecting PD. ALL PPTs may be identified this way.
Dividing the BIM cell values by 24 — BIM÷24 — forms a criss-crossing DIAMOND NPS that divides the overall BIM into two distinct and alternating Row (and Column) bands or sets:
- ODD WIN that are ÷3 and referred to as NON-ARs;
- ODD WIN that are NOT ÷3 and referred to as ARs, or Active Rows;
- The ARs ALWAYS come in pairs — with an EVEN WIN between — as the UPPER and LOWER AR of the ARS (Active Row Set);
ALL PPTs and ALL PRIMES ALWAYS are found exclusively on the ARs — no exceptions.
By applying:
(1) *
let y = odd number (ODD) 3, 5, 7,… and x = 1, 2, 3,... one generates a NP table containing ALL the NP;
*True if ÷3 ODDs are first eliminated, otherwise ADD exponentials of 3 to the NP pool;
Eliminating the NP — and the NP contain a NPS — from ALL the ODD WIN, reveals the PRIMES (P).
A necessary, but not sufficient confirmation — but not proof — of primality is found by finding the even division of 24 into the difference of the square of ANY two PRIMES as:
(2) (P2)2 - (P1)2 =
let
Be aware that this also holds true for ALL the AR NP. The P and NP are NOT ÷3, and are both part of the ARS and therefore any combination of the two squared differences will be ÷24:
(3) (NP2)2 - (NP1)2 =
(4) (NP2)2 - (P1)2 =
(5) (P2)2 - (NP1)2 =
The ÷3 NON-AR set is separately ÷24, but can NOT be mixed with members of the AR set (ARS) as:
(6) (NON-AR-NP2)2 - (NON-AR-NP1)2 = n24
(7) (NON-AR-NP2)2 - (NP1)2 ⧣
(8) (NP2)2 - (NON-AR-NP1)2 ⧣
(9) (P2)2 - (NON-AR-NP1)2 ⧣
(10) (NON-AR-NP2)2 - (P1)2 ⧣
The division into AR and NON-AR sets has a NPS that ultimately define the elusive pattern of the P.
Furthermore, may be re-arranged to:
(11)
(12)
asking whether any given ODD (>3) is a P or NP, it is exclusively a NP if, and only if, y reduces to the same value after applying x. As y is effectively an ODD of either a PRIME or composite of PRIMES factor*, one only needs to satisfy a single instance to validate NON-Primality.
One can also obtain ALL the P by eliminating the BIM SIGO and O2 from the 1st Diagonal WIN, where SIGO = Strict Inner Grid ODDs, O2 = ODDs2, and the 1st Diagonal = the 1st Diagonal Parallel to the PD.
This itself is further simplified by switching out the ODD AXIS values with the O2 — the O2 being the PD values — such that we now have:
(13) SIGO(A2) = Strict Inner Grid ODDS & ODD AXIS2 giving a distinct visualization advantage;(14) NP = SIGO(A2)
(15) 1st Diagonal - SIGO(A2) = P.
This second method — the algebraic geometry method — as presented here.
Introduction
Two methods — one pure algebraic and the other a more visual algebraic geometry presented here — have been found that capture ALL the NO-PRIMES (NP). While they process slightly different, they dovetail nicely into a very visual Number Pattern Sequence (NPS) here on the BIM. They both give identical NP results.
So what is the significance of capturing ALL the NP?
The NP are the highly NPS that define the elusive pattern of the P. P + NP = ALL ODD WINs (≥3).
In any group of WIN, if you know the NP, you also know the P. Here is the highly visualizable geometric method for capturing ALL NP. In fact, it is just as simply stated in 12. of the SUMMARY.
Algebraic Geometry Method
One can obtain ALL the P by eliminating the BIM SIGO and O2 from the 1st Diagonal WIN, where SIGO = Strict Inner Grid ODDs, O2 = ODDs2, and the 1st Diagonal = the 1st Diagonal Parallel to the PD.
This itself is further simplified by switching out the ODD AXIS values with the O2 — the O2 being the PD values — such that we now have:
One can also obtain ALL the P by eliminating the BIM SIGO and O2 from the 1st Diagonal WIN, where SIGO = Strict Inner Grid ODDs, O2 = ODDs2, and the 1st Diagonal = the 1st Diagonal Parallel to the PD.
This itself is further simplified by switching out the ODD AXIS values with the O2 — the O2 being the PD values — such that we now have:
(13) SIGO(A2) = Strict Inner Grid ODDS & ODD AXIS2(14) NP = SIGO(A2)
(15) 1st Diagonal - SIGO(A2) = P.
The PDFs will follow these animated gifs. Videos and other supporting graphics thereafter.
Animated Gifs:

PRIMES vs NO-PRIMES-2: algebraic method.

PRIMES vs NO-PRIMES-1: algebraic-geometry method.

PRIMES vs NO-PRIMES-3: algebraic and algebraic geometry method.

PRIMES vs NO-PRIMES-4: algebraic method in detail.
PDFs +


PRIMES vs NO-PRIMES: snapshot-1 showing dovetailing visualization of the algebraic method of calculating the NP with that of the geometric method on the BIM. The larger PDF is below.
PRIMES vs NO-PRIMES PDF: snapshot-1 showing dovetailing visualization of the algebraic method of calculating the NP with that of the geometric method on the BIM. The NPS of the NP define the elusive pattern of the P.

PRIMES vs NO-PRIMES: snapshot-2 showing dovetailing visualization of the algebraic method of calculating the NP with that of the geometric method on the BIM. Here the x=1,2,3,... base value sets -- Lower -y an Upper +y--as double-wide, L-shaped paths beginning just below the 1st Diagonal. These double rows alternate with divisible by 3--or divisible by 9 Axis squared--paths. The larger PDF is below.
PRIMES vs NO-PRIMES PDF: snapshot-2 showing dovetailing visualization of the algebraic method of calculating the NP with that of the geometric method on the BIM. The larger PDF is below. Here the x=1,2,3,... base value sets -- Lower -y an Upper +y--as double-wide, L-shaped paths beginning just below the 1st Diagonal. These double rows alternate with divisible by 3--or divisible by 9 Axis squared--paths.

PRIMES vs NO-PRIMES: snapshot-3 showing dovetailing visualization of the algebraic method of calculating the NP with that of the geometric method on the BIM. Here the x=1,2,3,... base value sets -- Lower -y an Upper +y--as double-wide, L-shaped paths beginning just below the 1st Diagonal. These double rows alternate with divisible by 3--or divisible by 9 Axis squared--paths. The larger PDF is below.
PRIMES vs NO-PRIMES PDF: snapshot-3 showing dovetailing visualization of the algebraic method of calculating the NP with that of the geometric method on the BIM. The larger PDF is below. Here the x=1,2,3,... base value sets -- Lower -y an Upper +y--as double-wide, L-shaped paths beginning just below the 1st Diagonal. These double rows alternate with divisible by 3--or divisible by 9 Axis squared--paths.

PRIMES vs NO-PRIMES PDF: snapshot-4 showing dovetailing visualization of the algebraic method of calculating the NP with that of the geometric method on the BIM. The larger PDF is below. Here the x=1,2,3,... base value sets -- Lower -y an Upper +y--as double-wide, L-shaped paths beginning just below the 1st Diagonal. These double rows alternate with divisible by 3--or divisible by 9 Axis squared--paths.
Table31a4: PRIMES vs NO-PRIMES PDF: Open in a separate tab/window to see all 11 pages. Here the x=1,2,3,... base value sets -- Lower -y an Upper +y--are shown individually and collectively as sets. The full Upper and Lower tables conclude.
Table31a6_2: PRIMES vs NO-PRIMES PDF: If you look at the ODD Axis ÷3 NO-PRIMES (NP) that lie in the paths between the L-shaped Double-wide x-base sets (x=1,2,3,)…), one finds a distinct Number Pattern Sequence (NPS) between successive NP values. Those shown in BLUE are NOT included in the criss-crossing L-shaped Double-wide paths (seen in the snapshots above), while those in GRAY are. The NPS seen here, based ultimately on the 1,3,5,7,… ODD number summation series that defines the whole BIM distribution (including the 1st Diagonal, the PD, and the successive differences in sequential Inner Grid cell values) reiterates that of both the L-shaped Double-wide paths as well as the individual x paths. Both give a NPS of the NP that reveal the elusive pattern of the PRIMES. There remains little doubt that the PRIMES , as well as the Primitive Pythagorean Triples (PPTs), are intimately related to the INVERSE SQUARE LAW (ISL)!
Videos:
PRIMES vs NO-PRIMES-1-long from Reginald Brooks on Vimeo.
PRIMES vs NO-PRIMES-2-long from Reginald Brooks on Vimeo.
PRIMES vs NO_PRIMES 3 from Reginald Brooks on Vimeo.
PRIMES_vs_NO-PRIMES-4 from Reginald Brooks on Vimeo.
...more supporting graphics and tables:
+10x10+.pdf)

+50x500+.pdf.pdf)



+253x250.pdf)
Various supporting graphics








xxxxxxxxxx
~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~
BACK: ---> Part I of II CaCoST-DSEQEC on a separate White Paper
BACK: ---> Part II of II CaCoST-DSEQEC on a separate White Paper
BACK: ---> Simple Path BIM to PRIMES on a separate White Paper
BACK: ---> PRIMES vs NO-PRIMES on a separate White Paper
BACK: ---> TPISC_IV: Details_BIM+PTs+PRIMES on a separate White Paper
BACK: ---> PRIME GAPS on a separate White Paper
BACK: ---> PeriodicTableOfPrimes(PTOP)_GoldbachConjecture on a separate White Paper
NEWLY ADDED (after TPISC IV published):
Back to Part I of the BIM-Goldbach_Conjecture.
Back to Part II of the BIM-Goldbach_Conjecture.
Back to Part III of the BIM-Goldbach_Conjecture.
Artwork referencing TPISC.
TPISC_IV:_Details ~PRIMES vs NO-PRIMES~
Copyright©2019, Reginald Brooks. All rights reserved.
Artist Link in iTunes Apple Books Store:
Reginald Brooks

~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~
KEYWORDS TAGS:
PTOP, Periodic Table Of PRIMES, PRIMES vs NO-PRIMES, algebraic geometry, BIM, TPISC, The Pythagorean - Inverse Square Connections, Pythagorean Triangles, DNA, Zika virus, pentagon, decagon, double pentagon, composite axial DNA double-helix, Pythagorean Triples, primitive Pythagorean Triples, non-primitive Pythagorean Triples, Pythagorean Theorem, Pythagorus Theorem, The Dickson Method, BBS-ISL Matrix, Expanded Dickson Method, r-sets, s-set, t-sets, Pair-sets, geometric proofs, MathspeedST, leapfrogging LightspeedST FASTER than the speed of light, Brooks (Base) Square- Inverse Square Law (ISL), BBS-ISL Matrix grid, The Architecture Of SpaceTime (TAOST), The Conspicuous Absence Of Primes (TCAOP), A Fresh Piece Of Pi(e), AFPOP, Numbers of Inevitability, LightspeedST, Teachers, Educators and Students (TES), number theory, ubiquitous information, FASTER than the speed of light, primes, prime numbers, fractals, mathematics, Universe, cosmos, patterns in number, DSEQEC, Double-Slit Experiment-Quantum Entanglement Conjecture, CaCost, Creation and Conservation of SpaceTime.
TOP





xxxxxxxxxx~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~
Back to Part I of the BIM-Goldbach_Conjecture.
Back to Part II of the BIM-Goldbach_Conjecture.
Back to Part III of the BIM-Goldbach_Conjecture.
Artwork referencing TPISC.
TPISC_IV:_Details ~PRIMES vs NO-PRIMES~
Copyright©2019, Reginald Brooks. All rights reserved.
Artist Link in iTunes Apple Books Store: Reginald Brooks

~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~