
CLICK for LINKS
BIM-MPS Details, Part IV
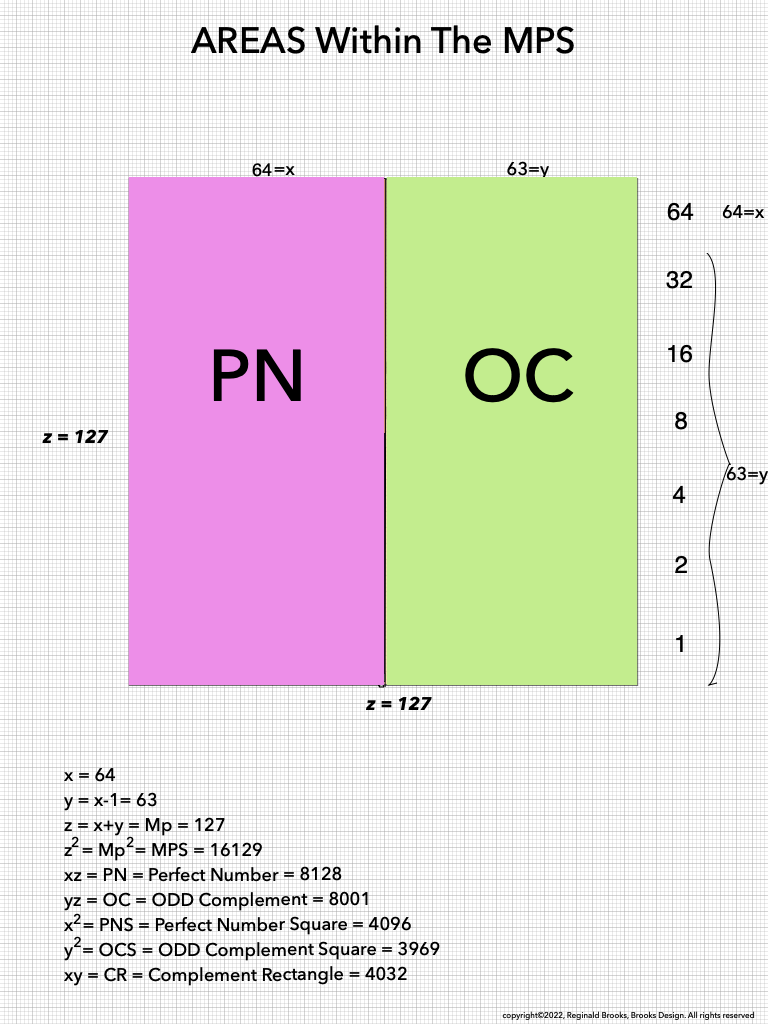
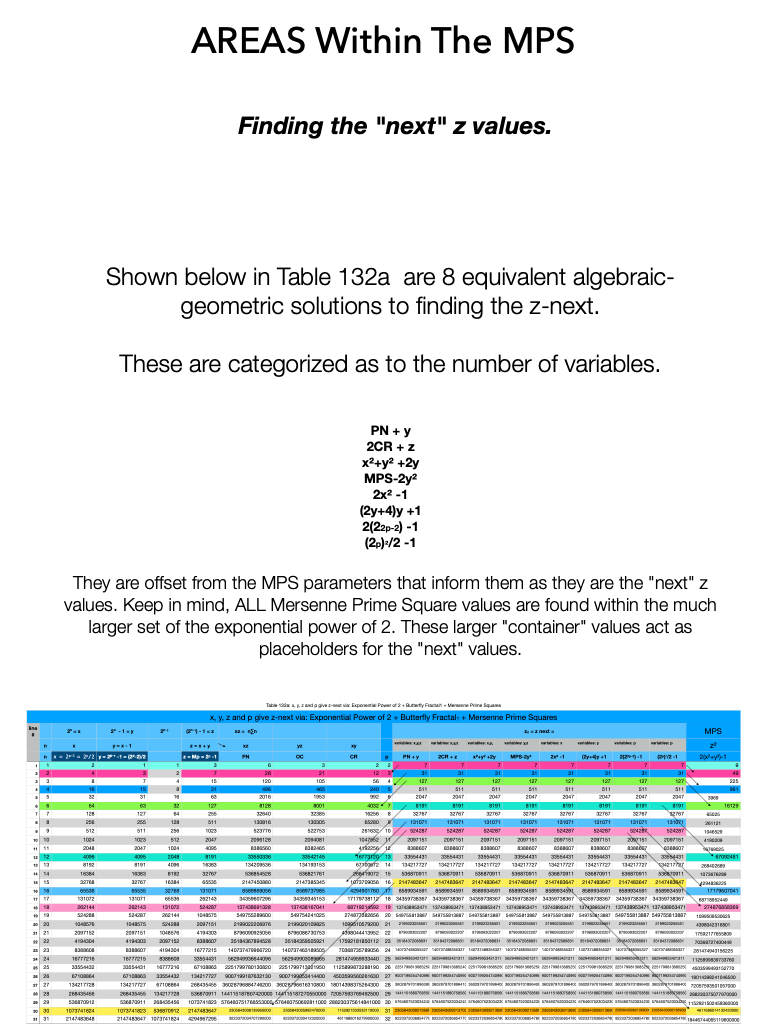
The MPS on the BIM (BIMMPS)
The MPS on the BIM (BIMMPS)
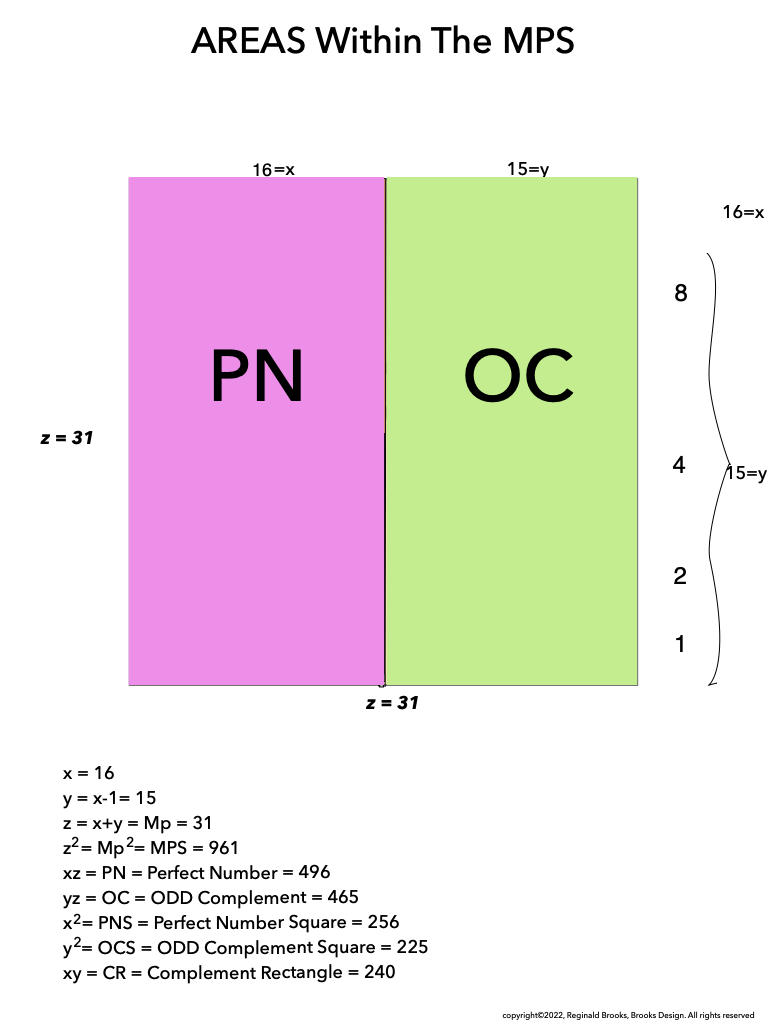
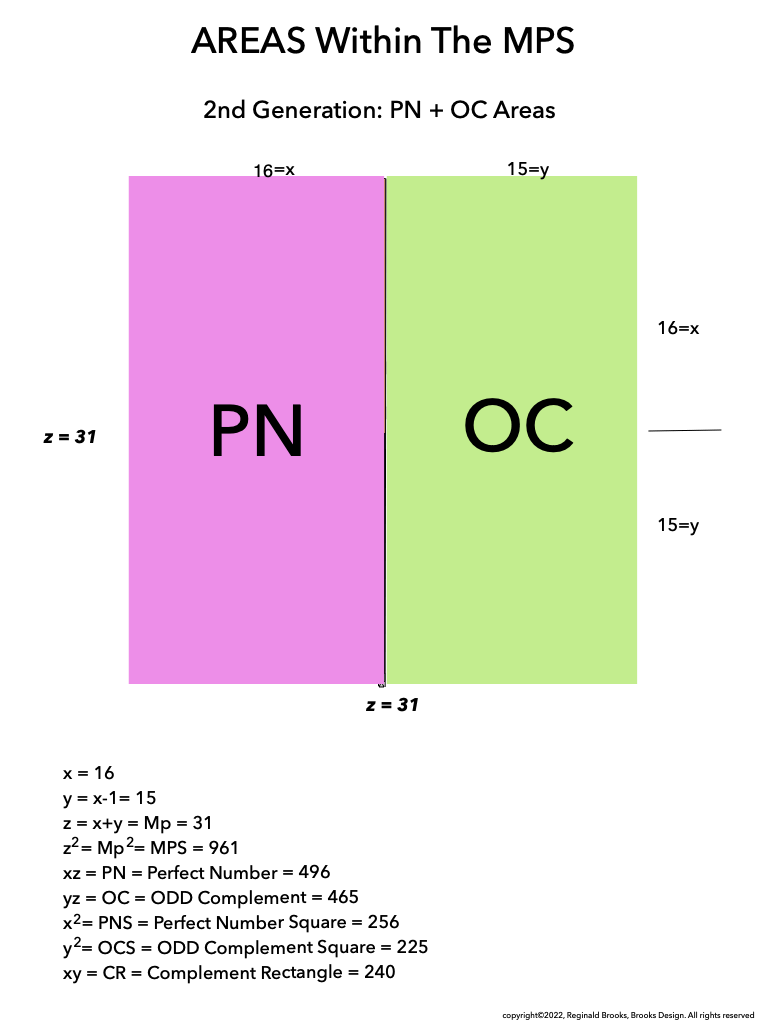
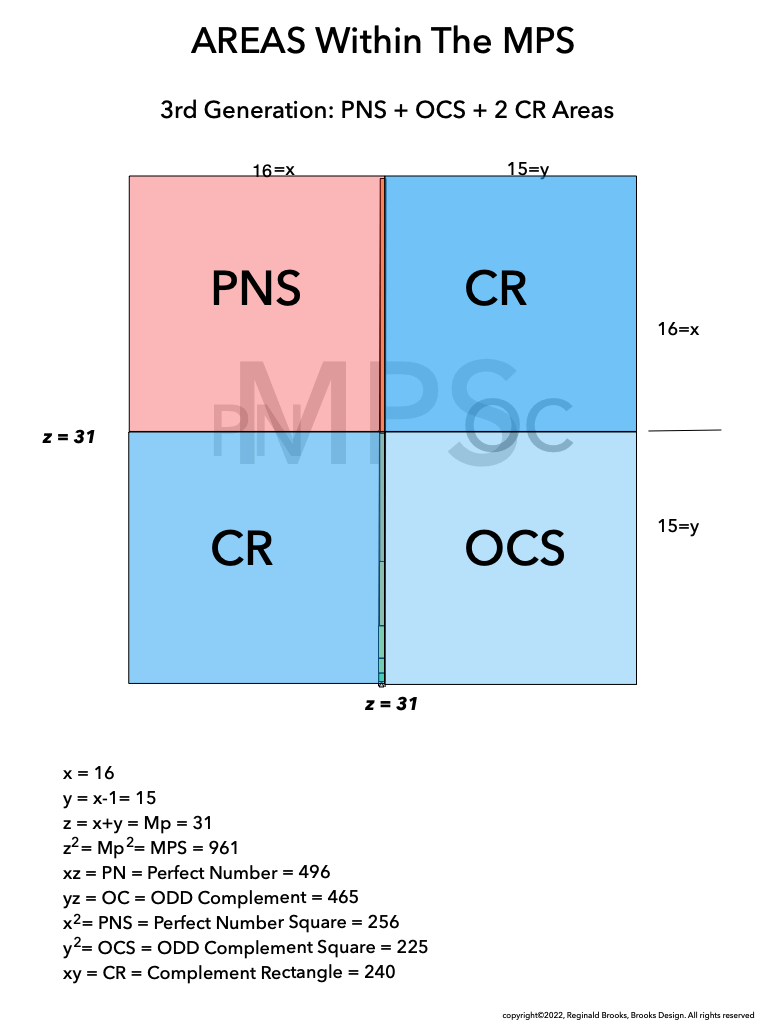
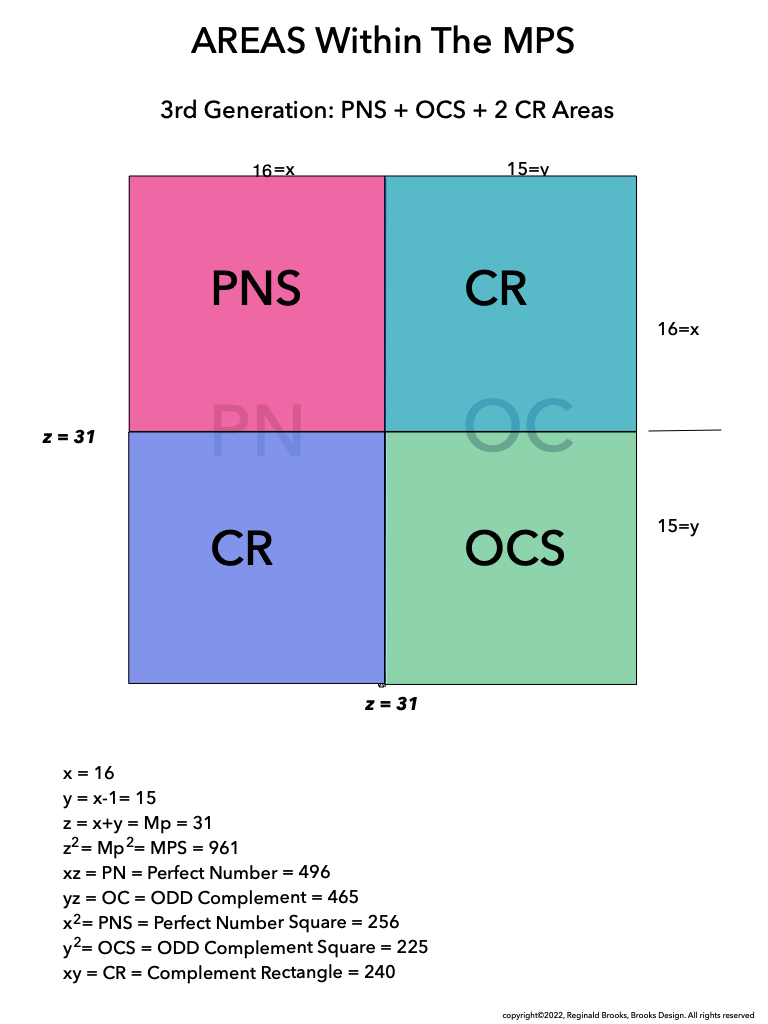
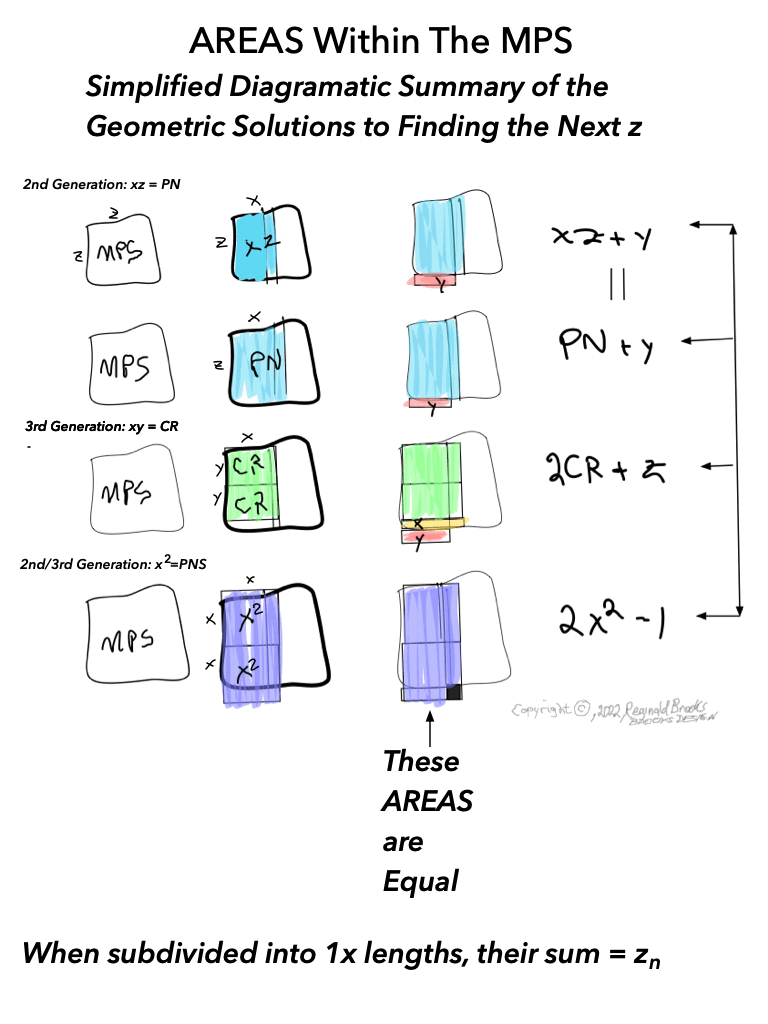
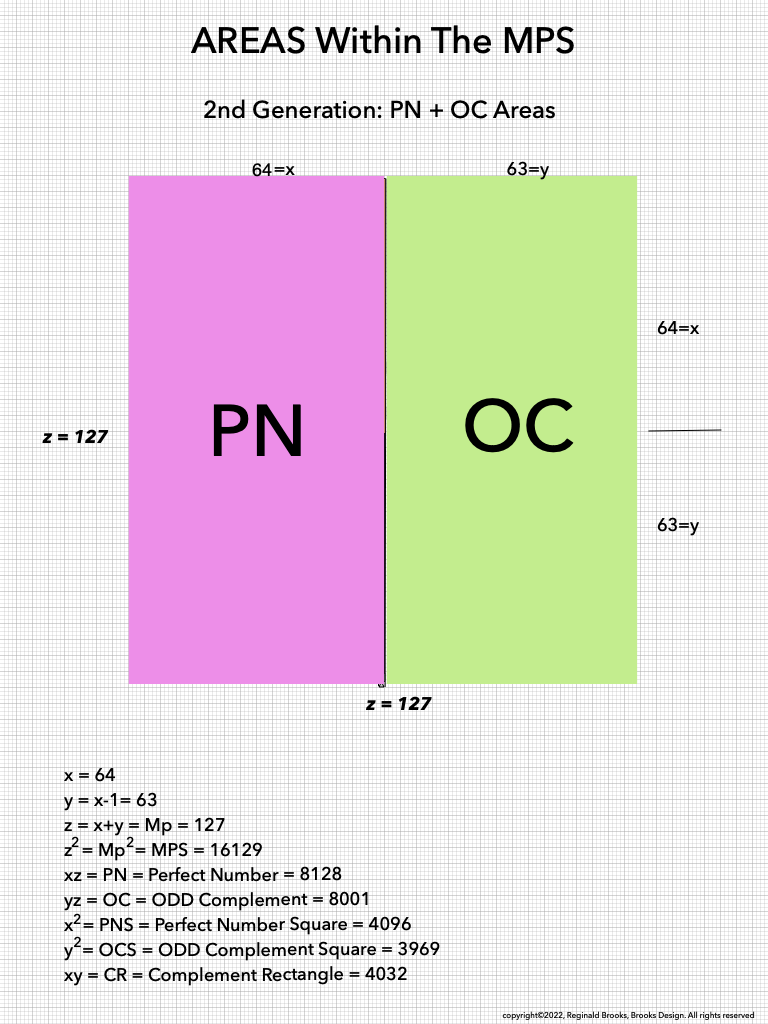
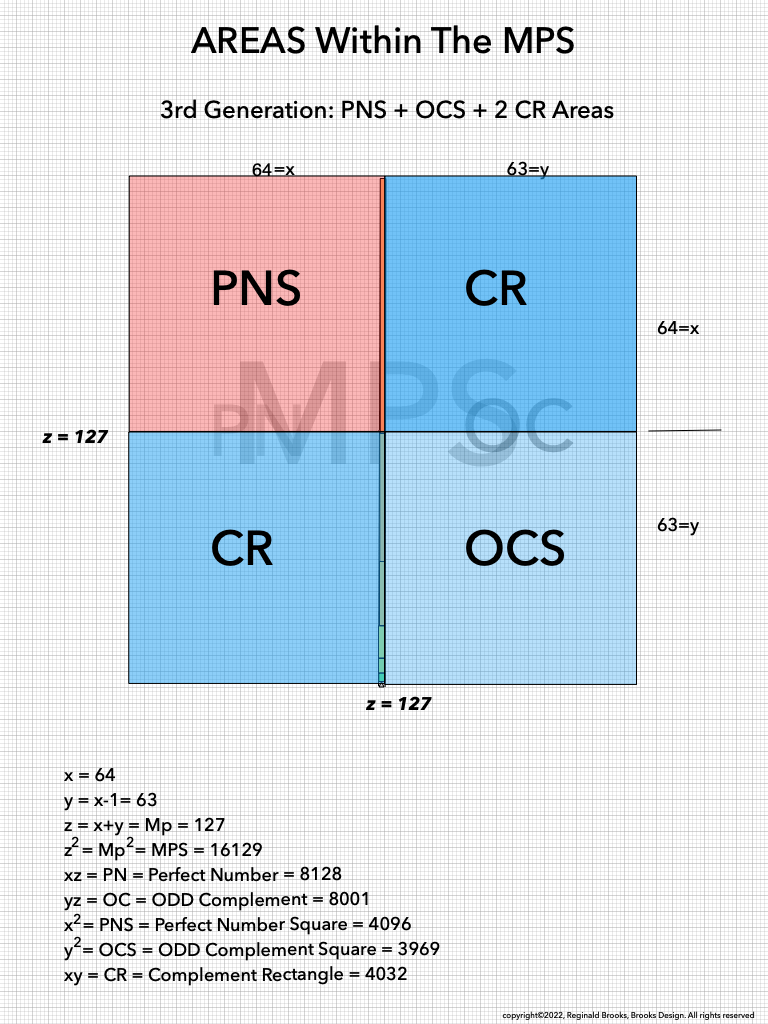
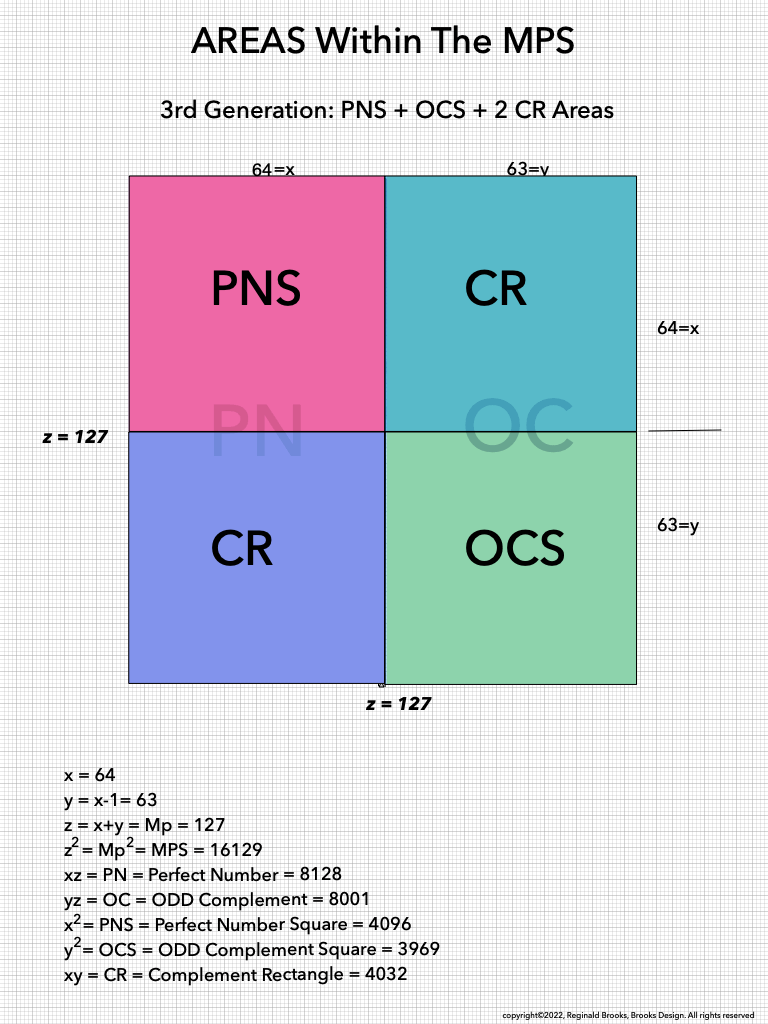
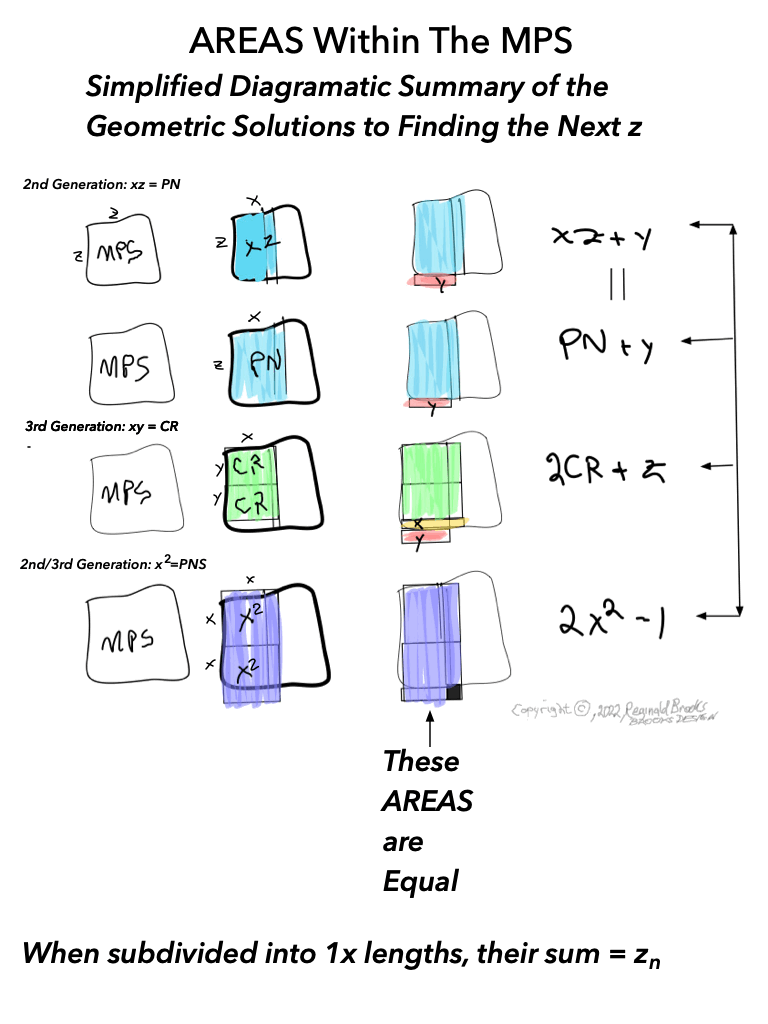
As much as viewing the MPS on a universal grid is absolutely amazing in its combination of simple geometry to visually reveal the basic and fundamental relationships in the form of AREAS -- areas that add and subtract to inform all the AREAS that define all three generations within-- it is truly when we examine the BIMMPS that the numerical, quantity based relationships of these AREAS are unfolded in an in-depth and repeating NPS of their own that the profound connections are realized!
As before, the NPS of the BIMMPS at first looks formidable as a group. Taking a few examples of the smaller MPS and drawing a clear NPS picture will establish a fractal-template that will be repeated with each and every MPS thereafter -- only the numbers will change.
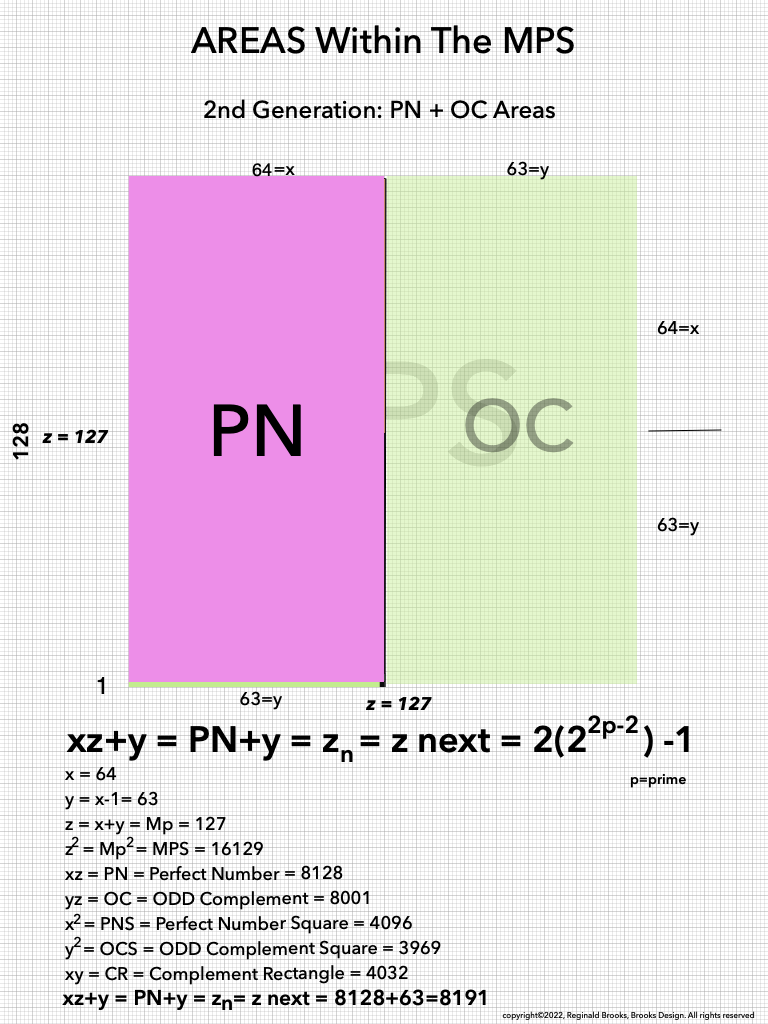
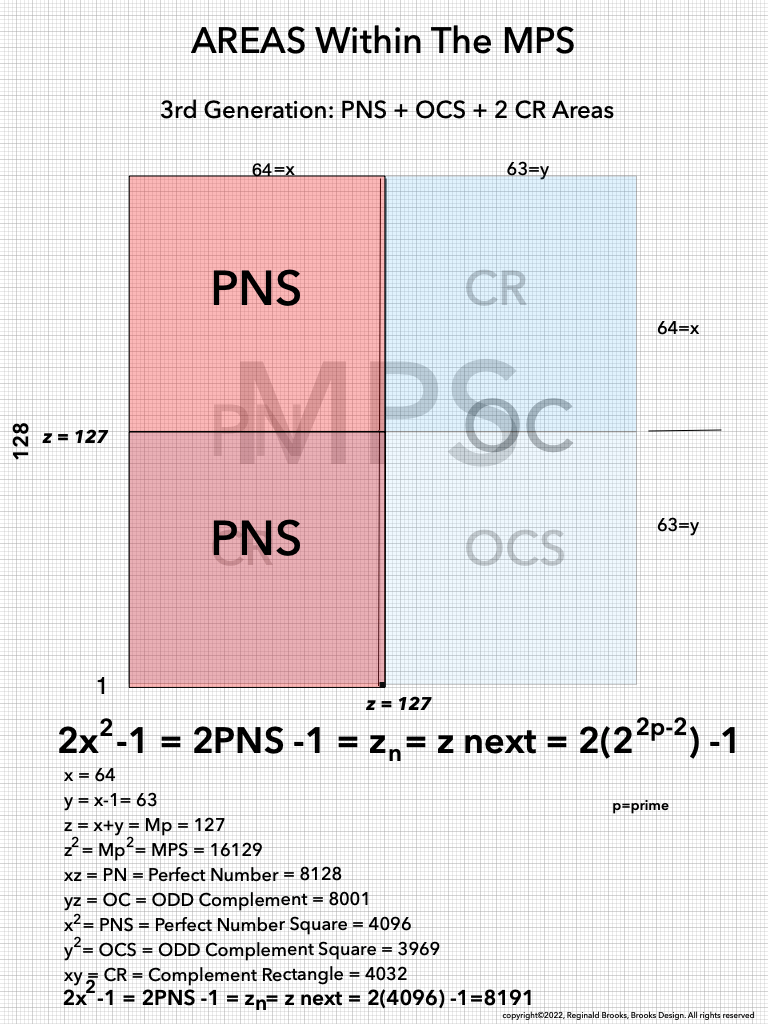
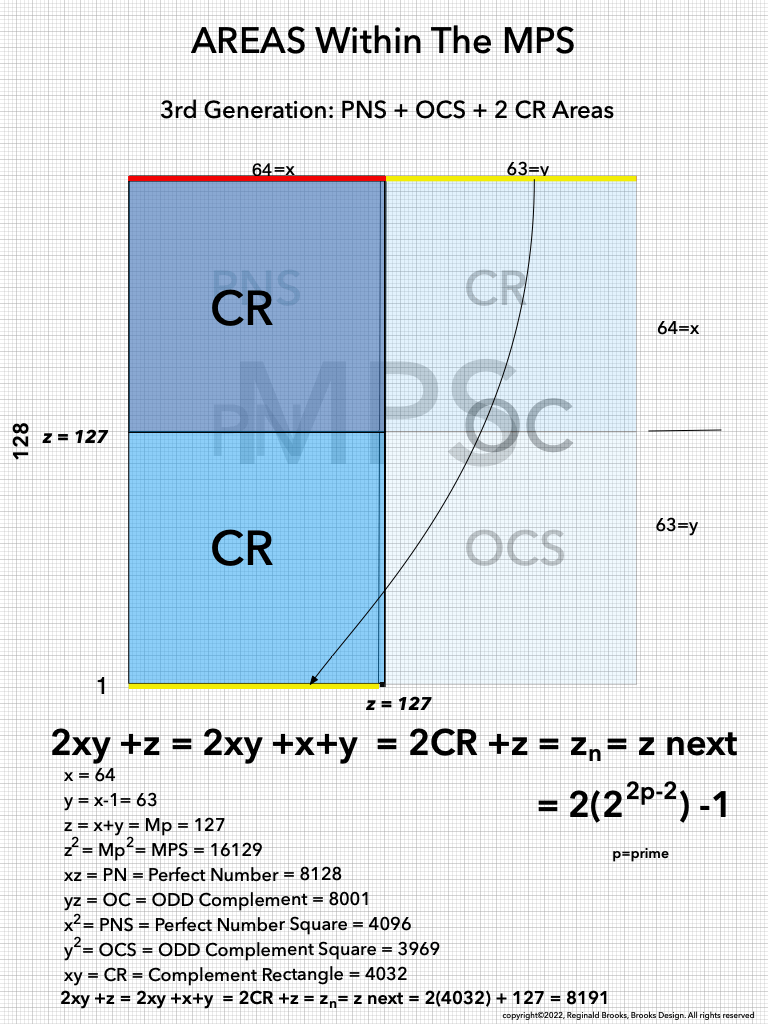
As one can see, the color bands that make up the PN can form all three "generations" withing the MPS space. They do so in a completely fractal manner, based on the exponential power of 2. They do so in a repeating NPS template that is exactly the same for each MPS, with only the relative numbers being different.
BIM-MPS-PN-1--1.mp4

BIM-MPS-PN-1--1.gif
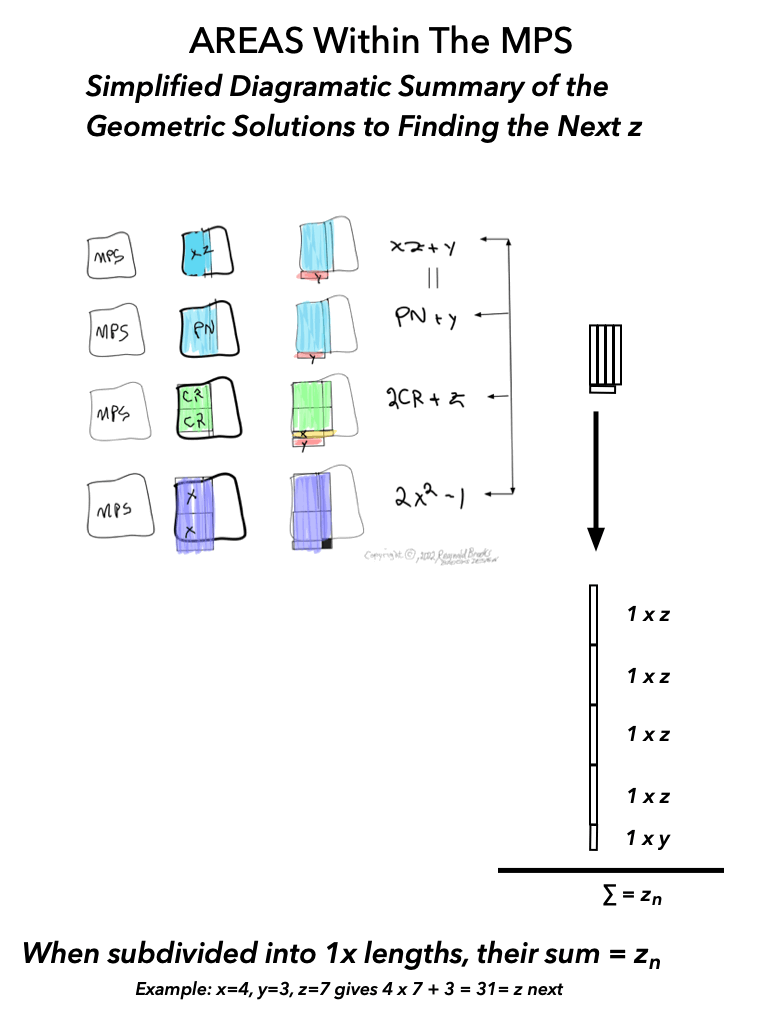
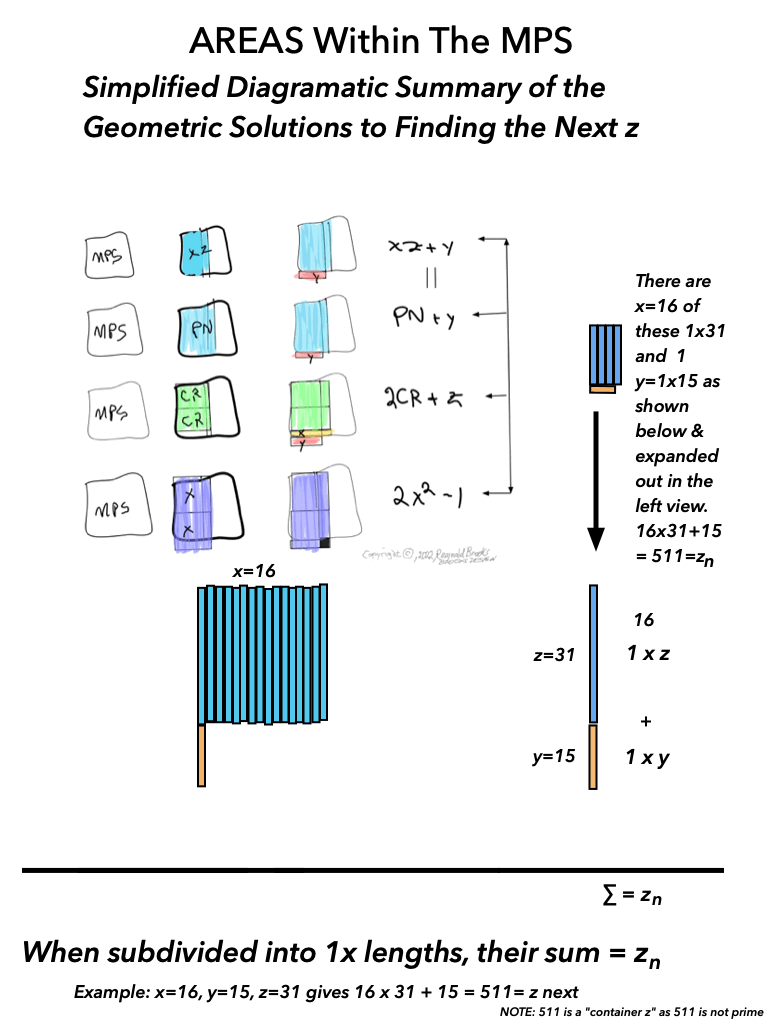
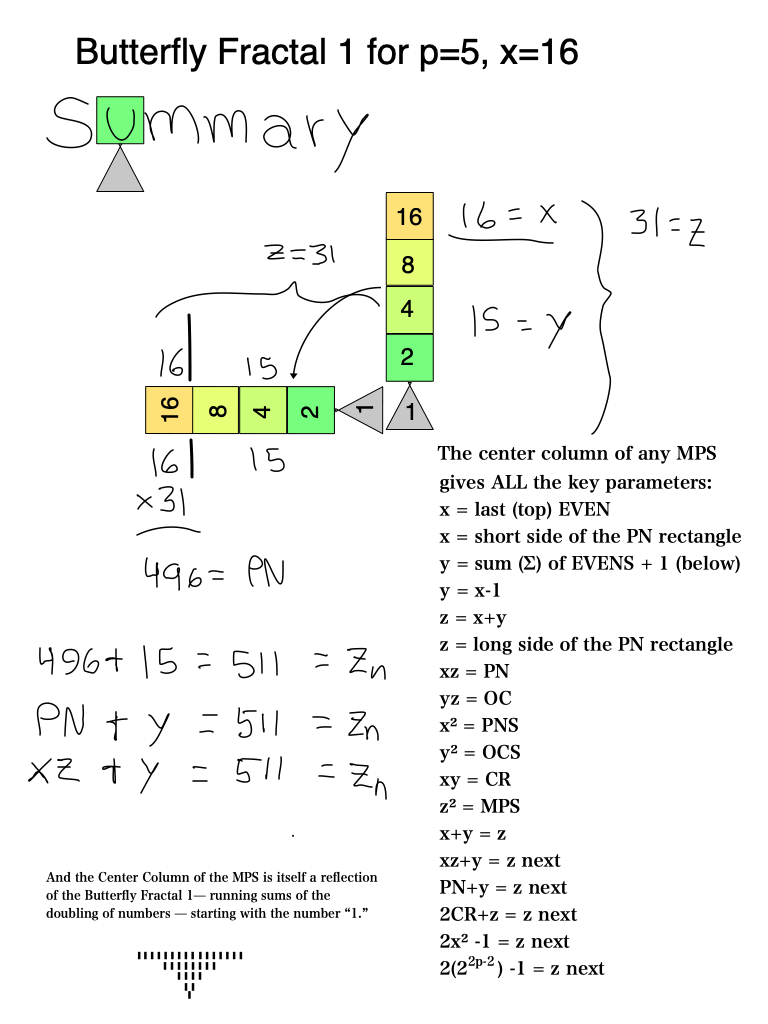
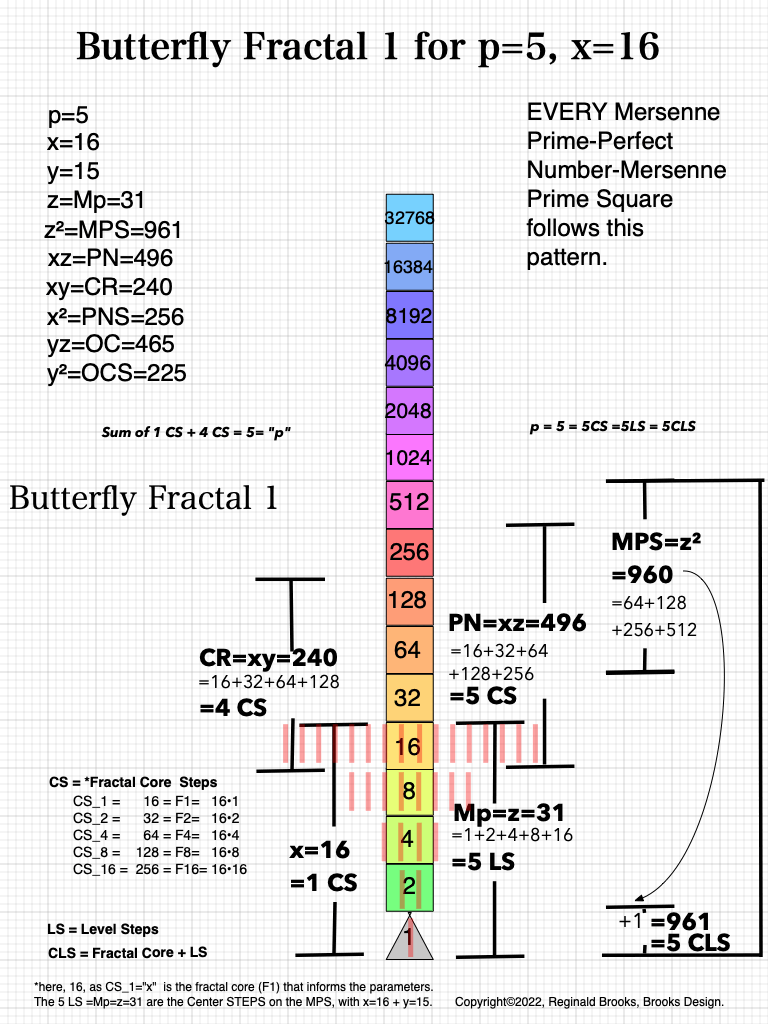
As an overview, let's look at a half a dozen examples before diving in to a more detailed look. To note: only the y values listed are illustrated within the much larger x+y=z central column shown.
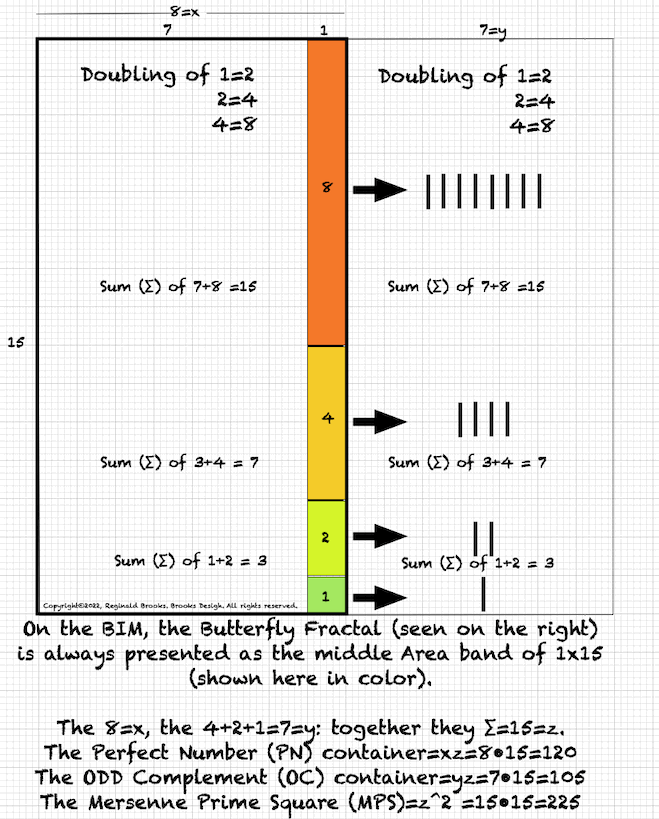
BIM+BF-8.gif

BFsums-x=2_p=2

BFsums-x=4_p=3

BFsums-x=8_p=4
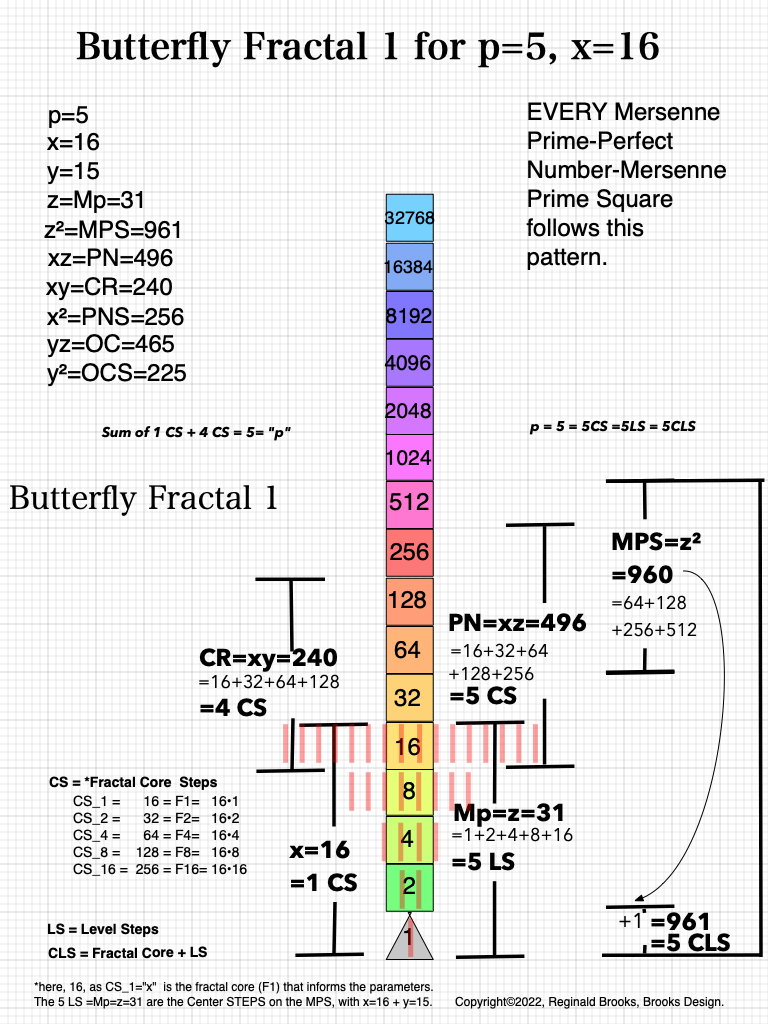
BFsums-x=16_p=5
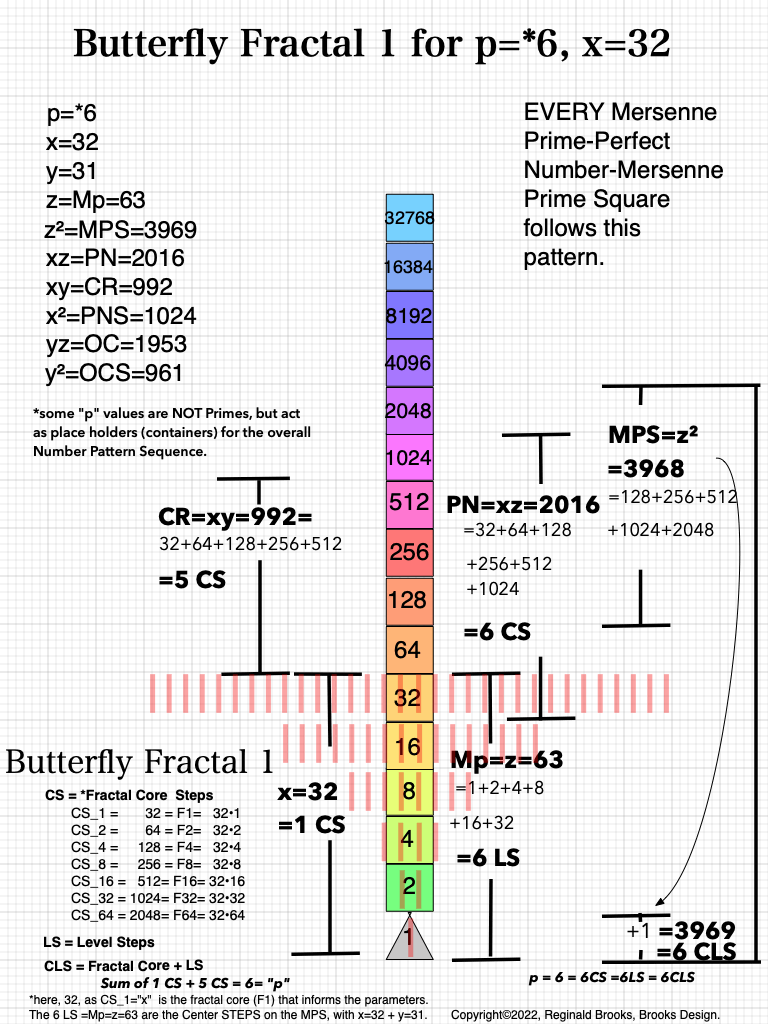
BFsums-x=32_p=6
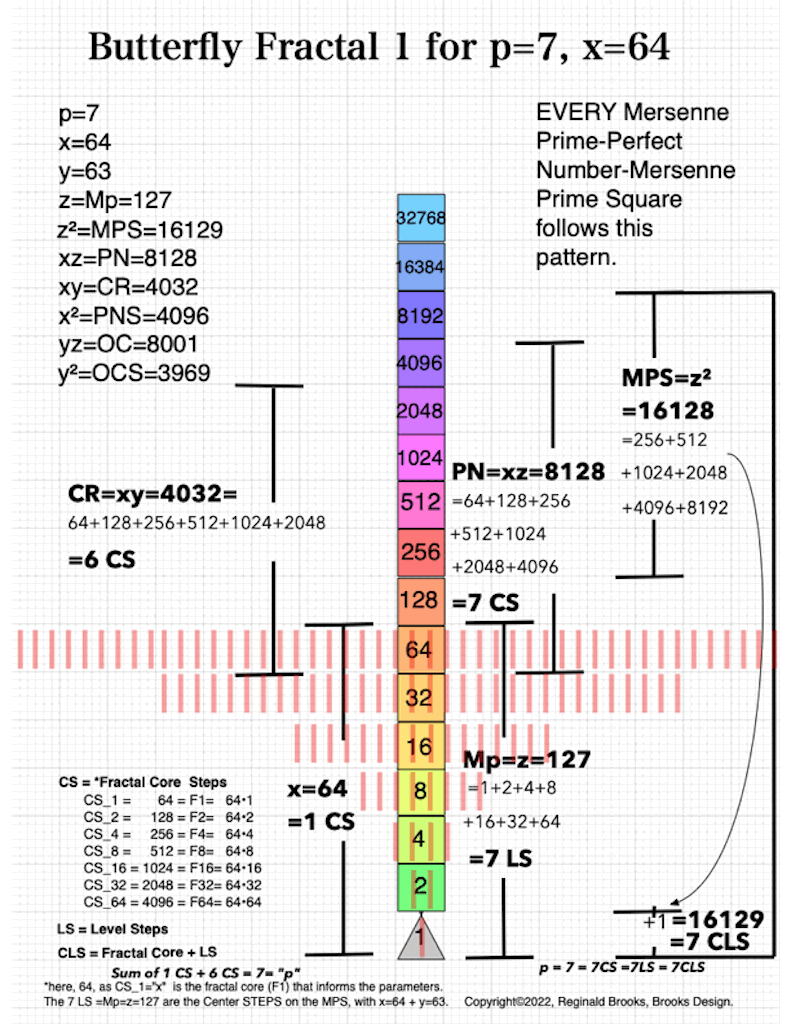
BFsums-x=64_p=7
Looking at BFsums-x=16_p=5MPS-0-22 in detail:
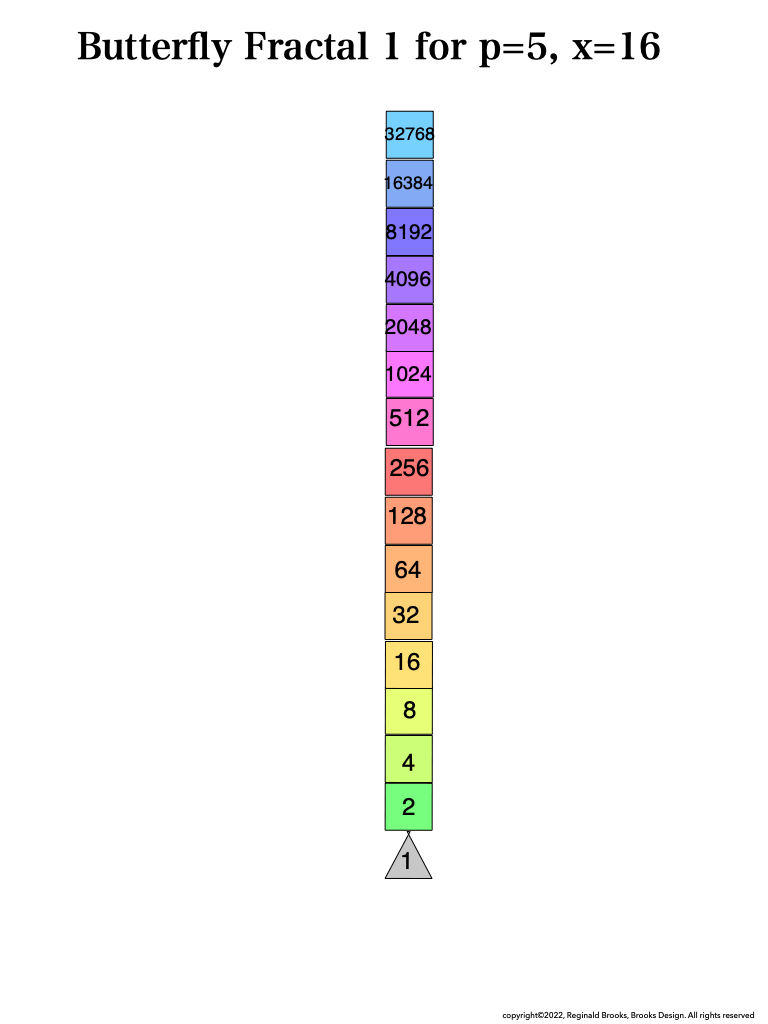
BFsums-x=16_p=5MPS-0
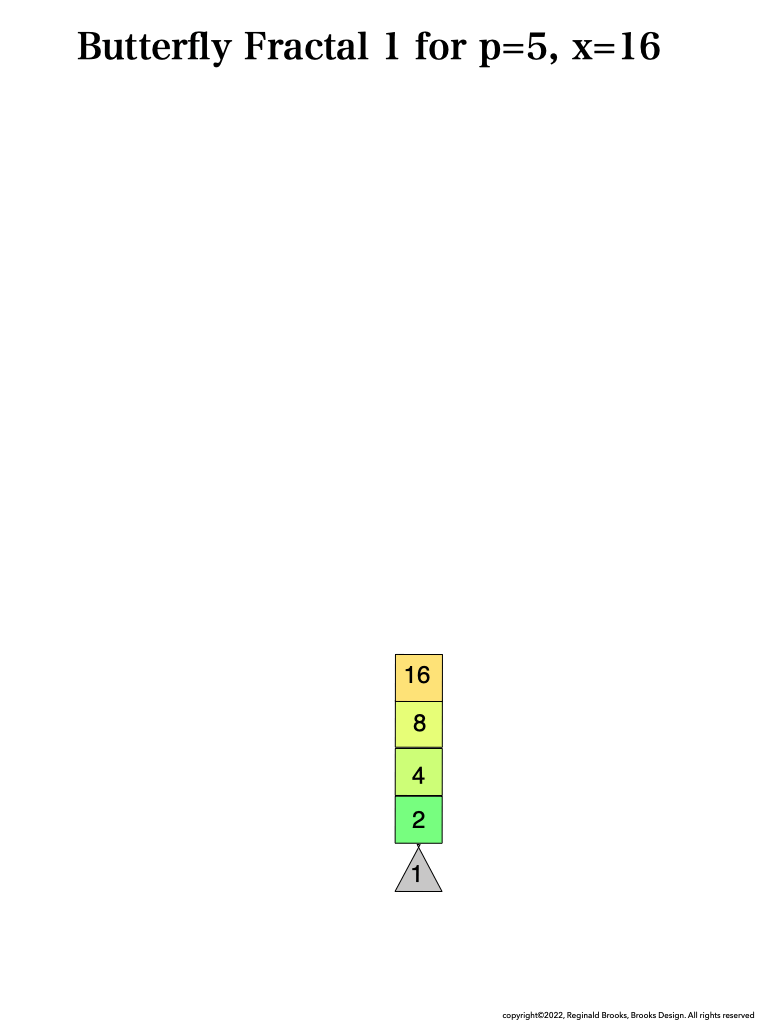
BFsums-x=16_p=5MPS-1
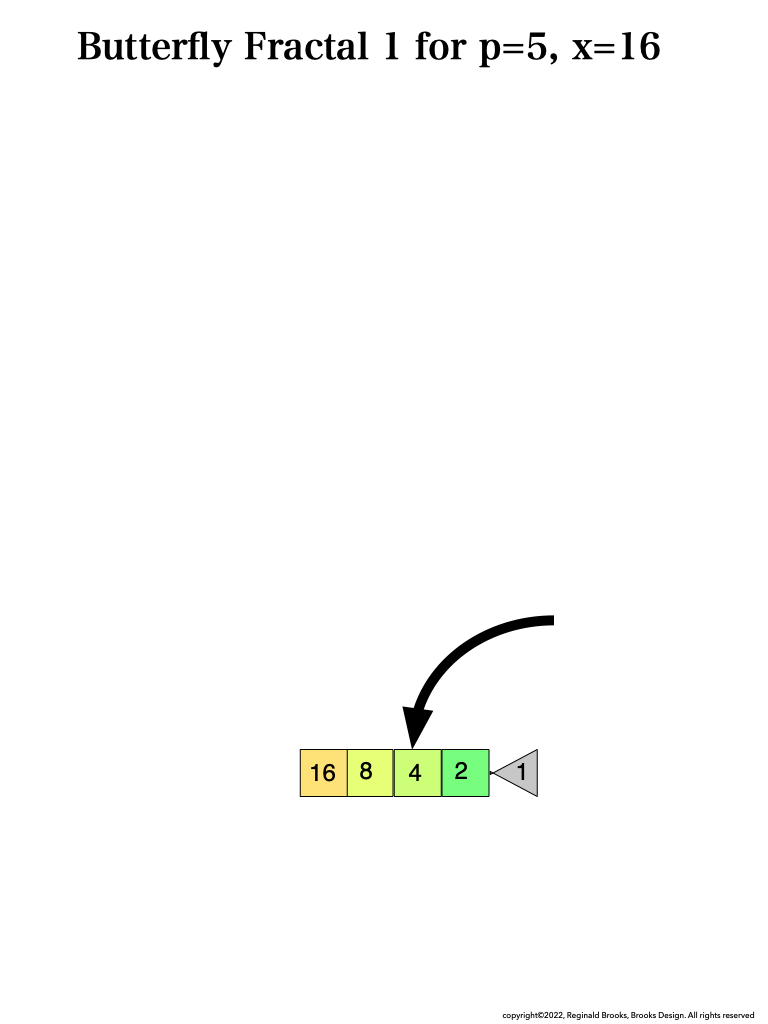
BFsums-x=16_p=5MPS-2

BFsums-x=16_p=5MPS-3
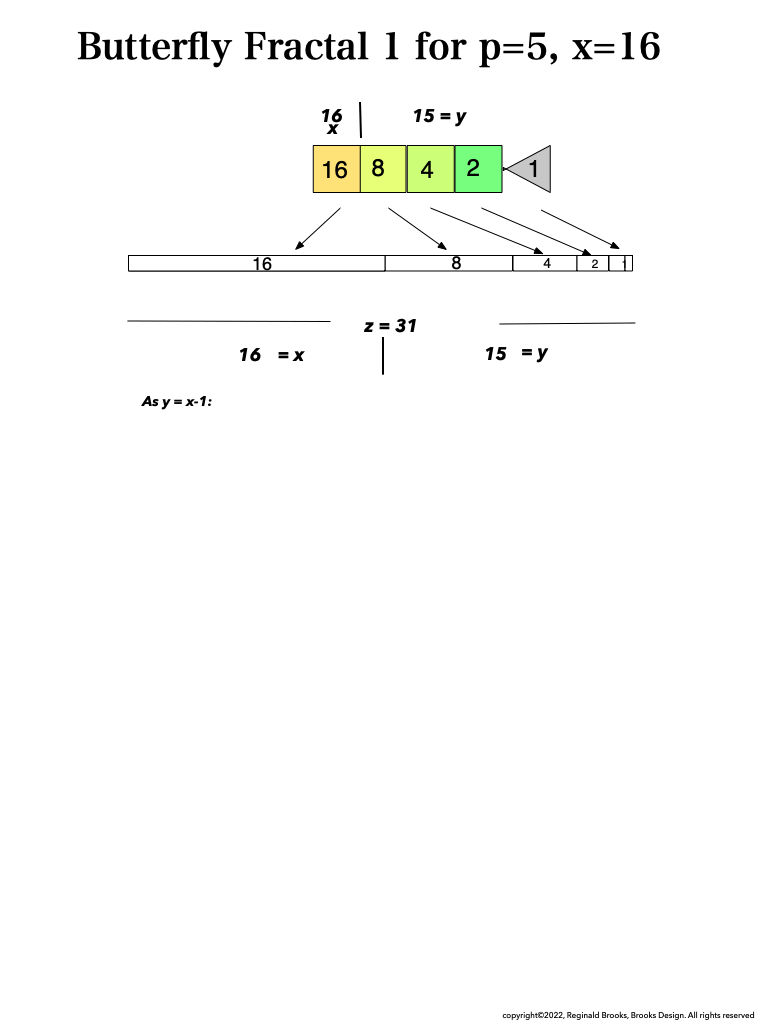
BFsums-x=16_p=5MPS-4
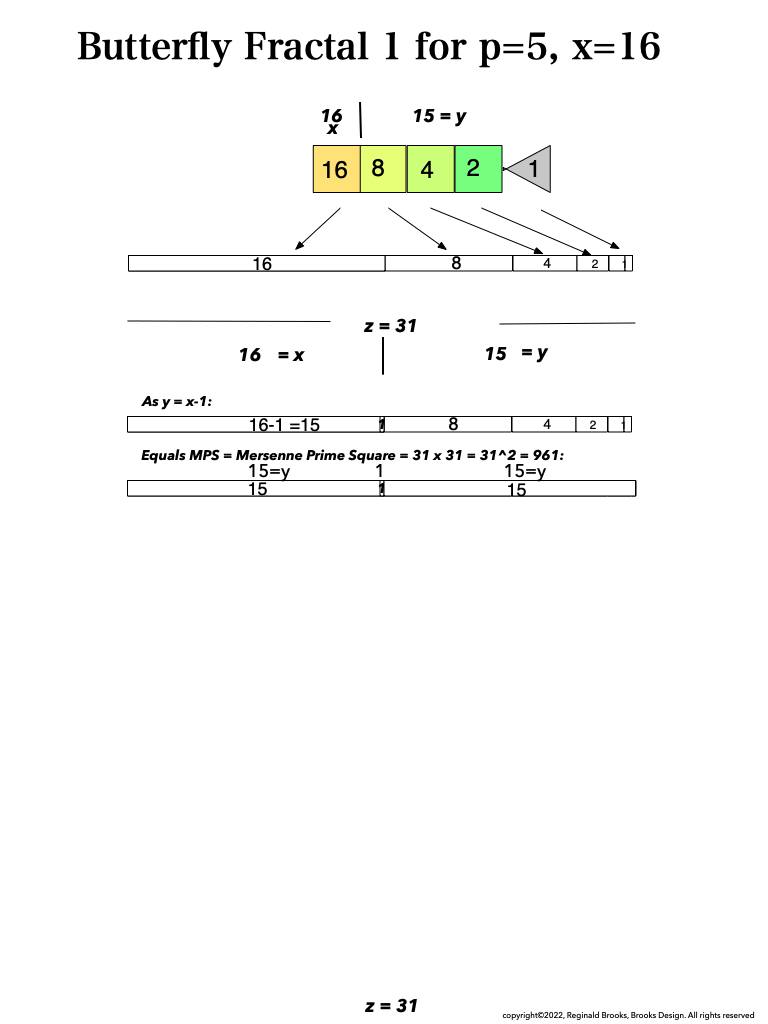
BFsums-x=16_p=5MPS-5
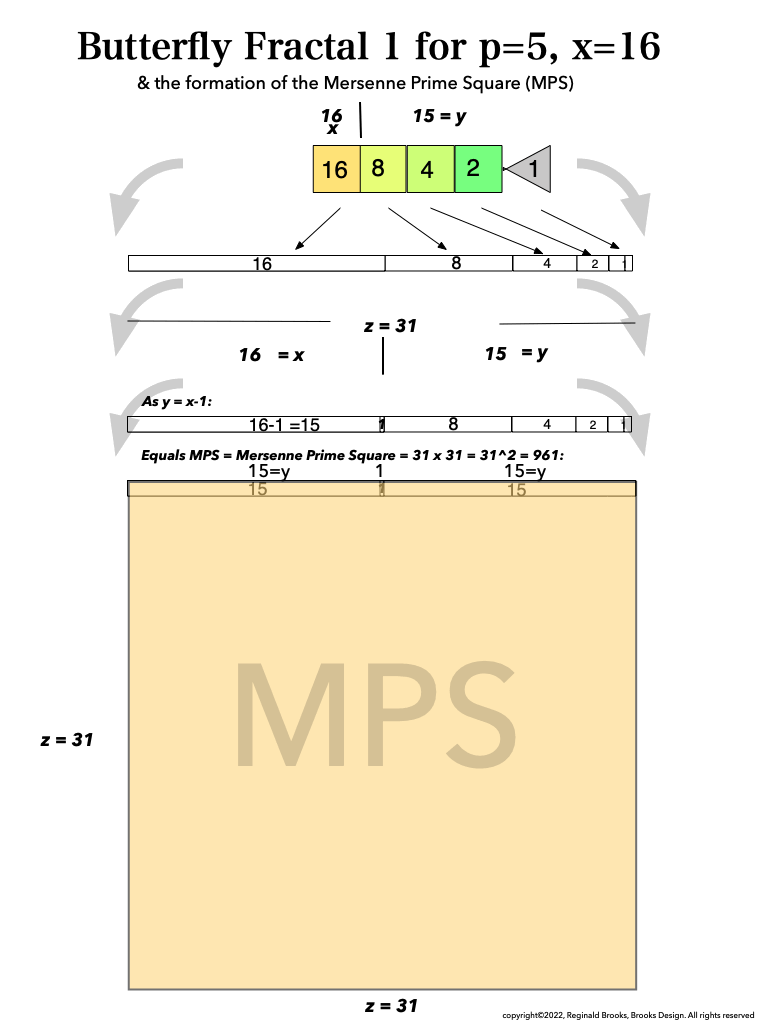
BFsums-x=16_p=5MPS-6
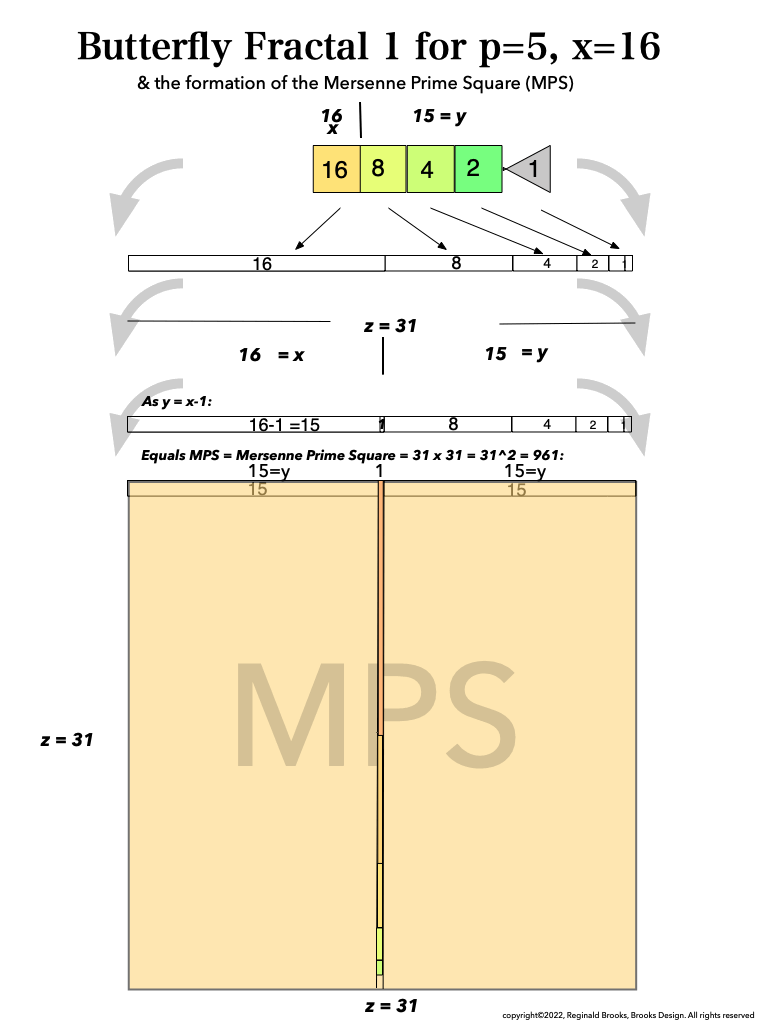
BFsums-x=16_p=5MPS-7
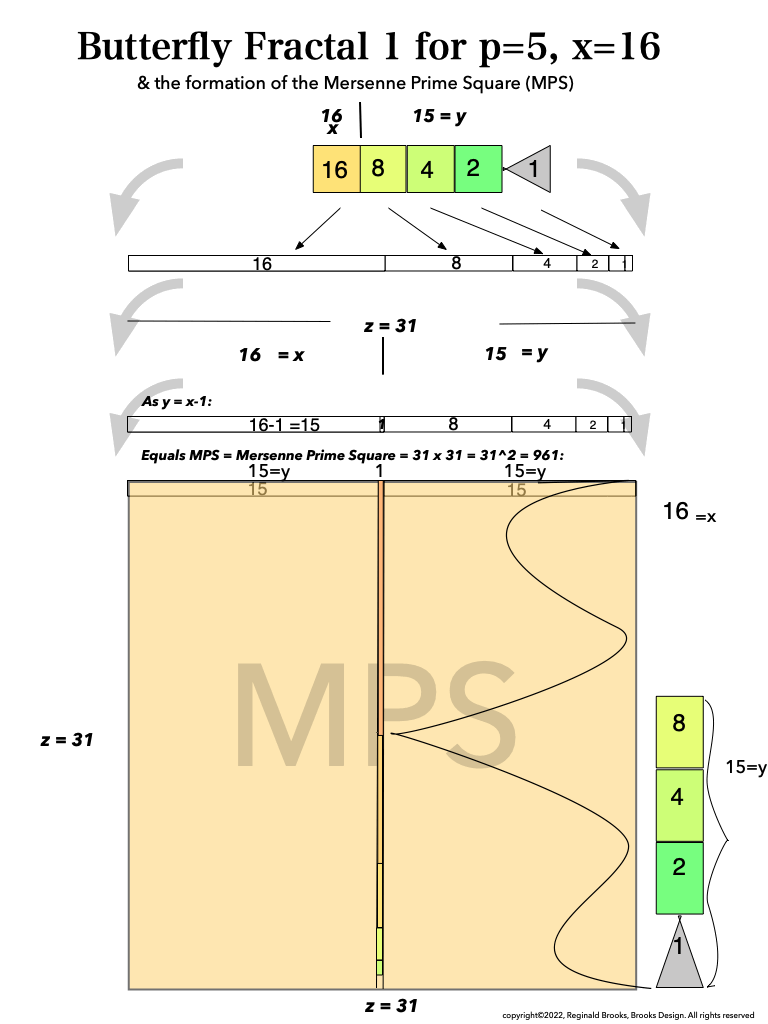
BFsums-x=16_p=5MPS-8
BFsums-x=16_p=5MPS-9
BFsums-x=16_p=5MPS-10
BFsums-x=16_p=5MPS-11
BFsums-x=16_p=5MPS-12
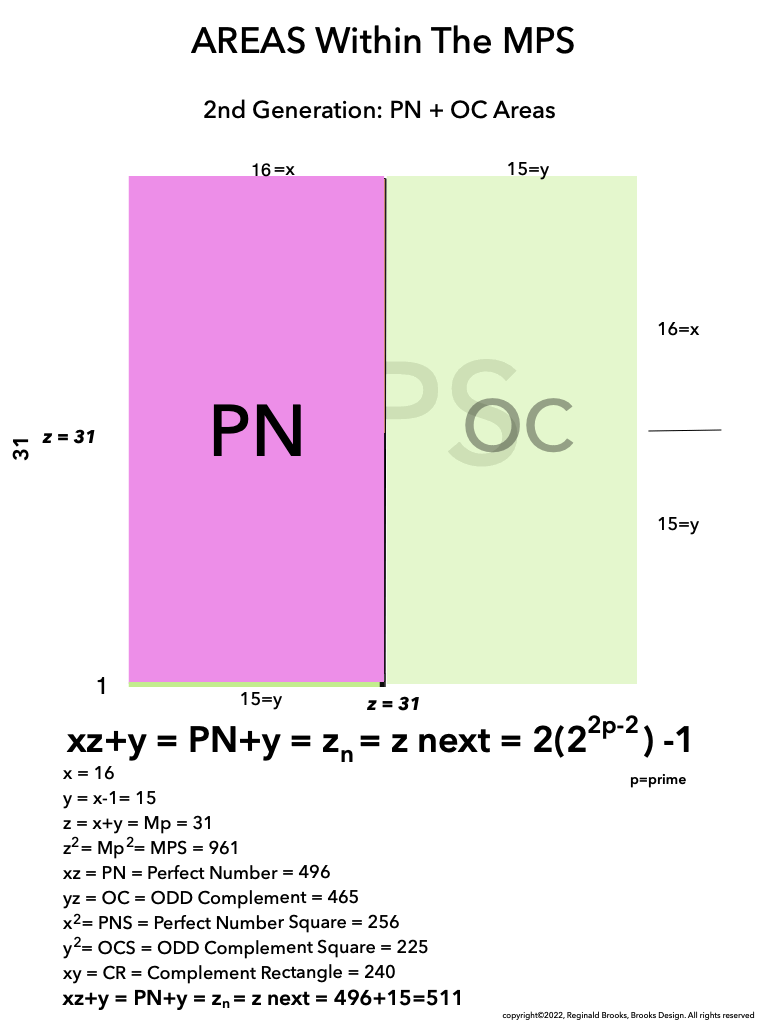
BFsums-x=16_p=5MPS-13
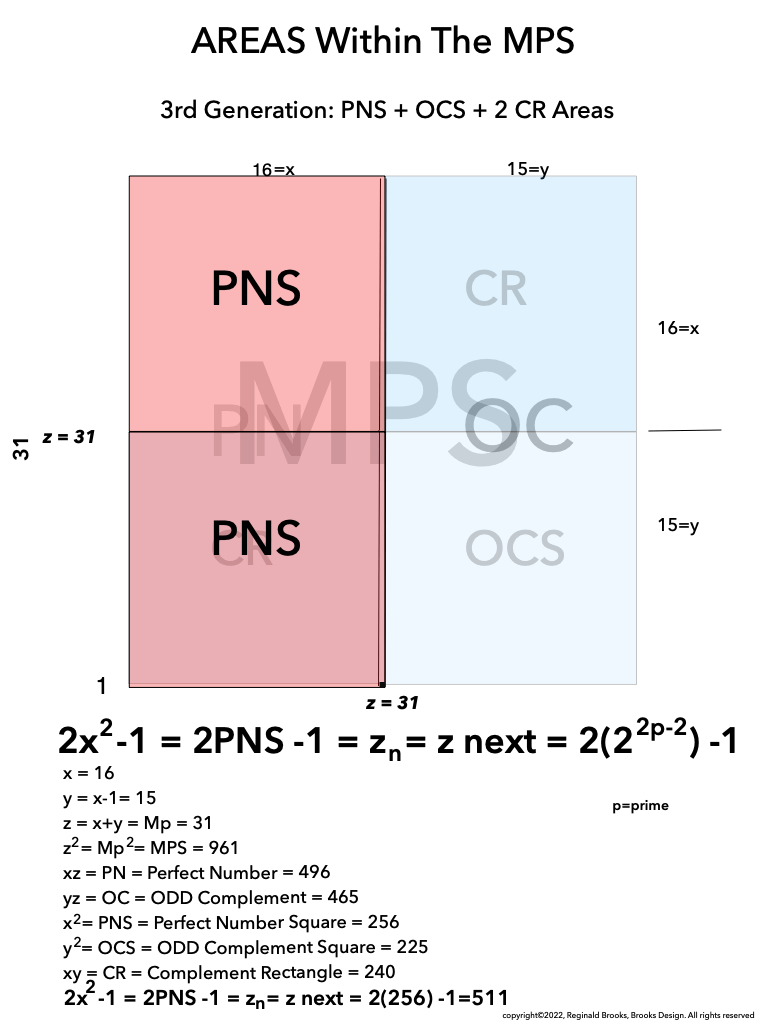
BFsums-x=16_p=5MPS-14
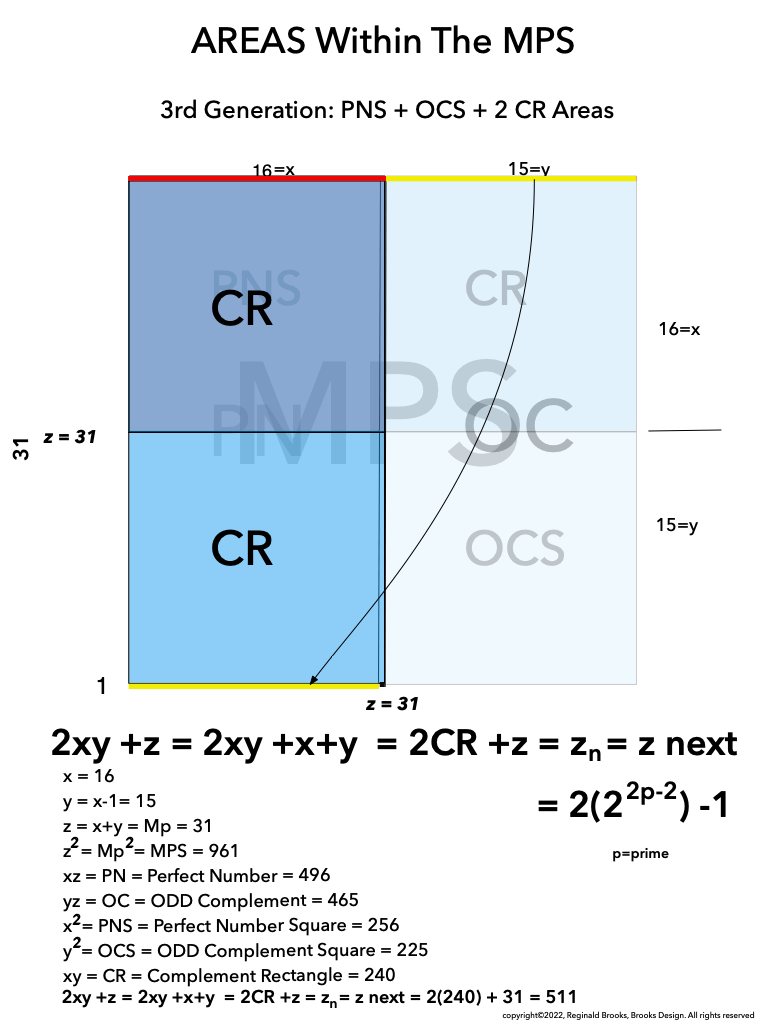
BFsums-x=16_p=5MPS-15

BFsums-x=16_p=5MPS-16
BFsums-x=16_p=5MPS-17
BFsums-x=16_p=5MPS-18
BFsums-x=16_p=5MPS-19
BFsums-x=16_p=5MPS-20
BFsums-x=16_p=5MPS-21
BFsums-x=16_p=5MPS-22
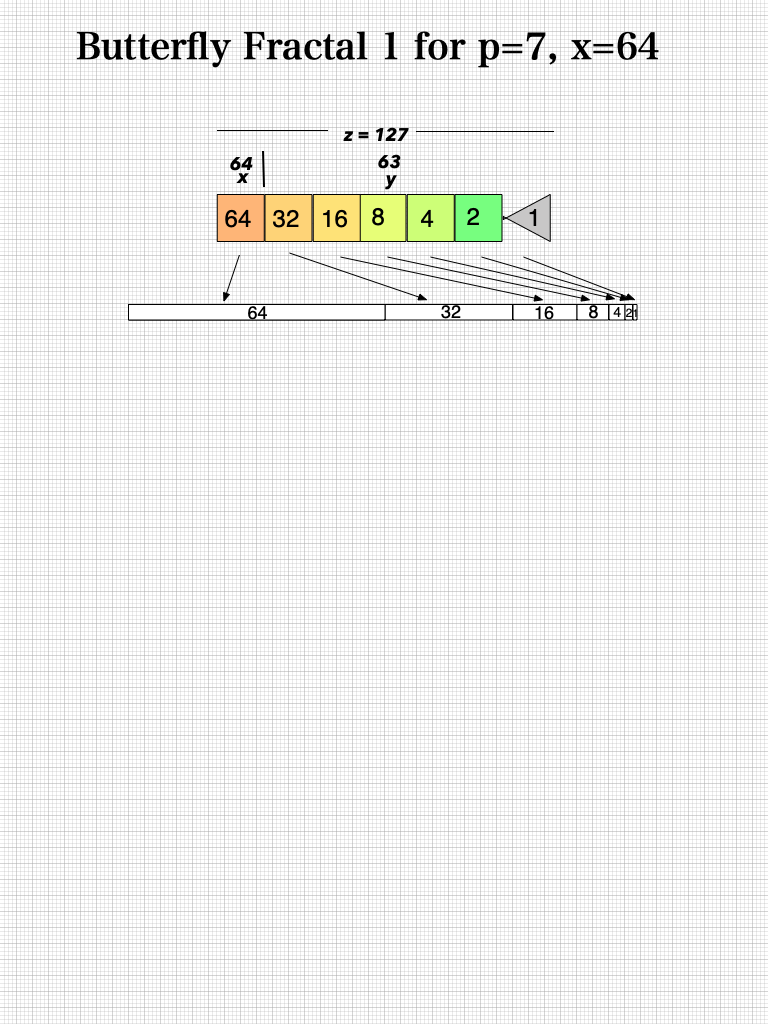
And finally, looking atBFsums-x=64_p=7MPS-0-22 in detail:

MPS-0-22/BFsums-x=64_p=7_0
MPS-0-22/BFsums-x=64_p=7_1
MPS-0-22/BFsums-x=64_p=7_2

MPS-0-22/BFsums-x=64_p=7_3
MPS-0-22/BFsums-x=64_p=7_4
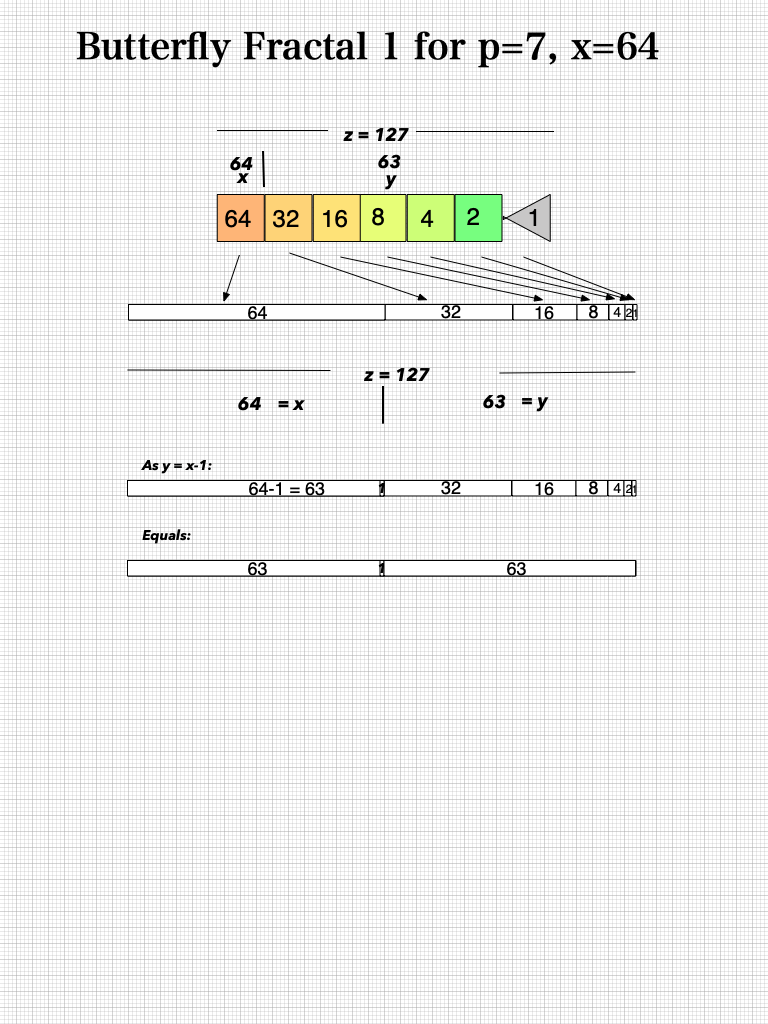
MPS-0-22/BFsums-x=64_p=7_5
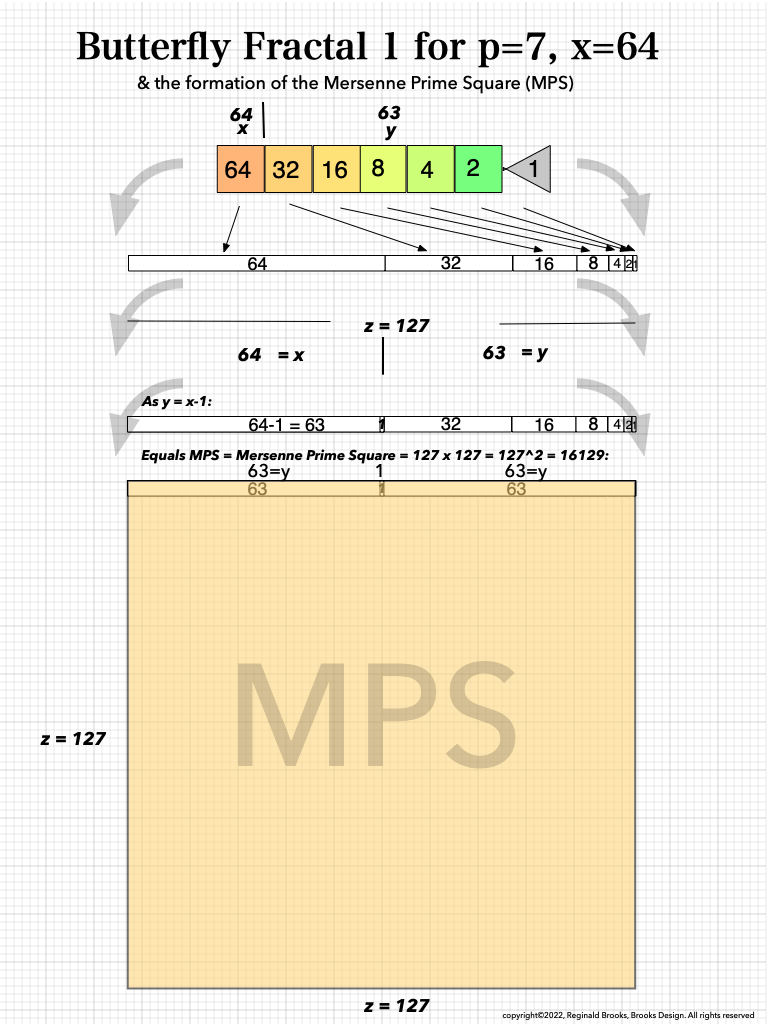
MPS-0-22/BFsums-x=64_p=7_6
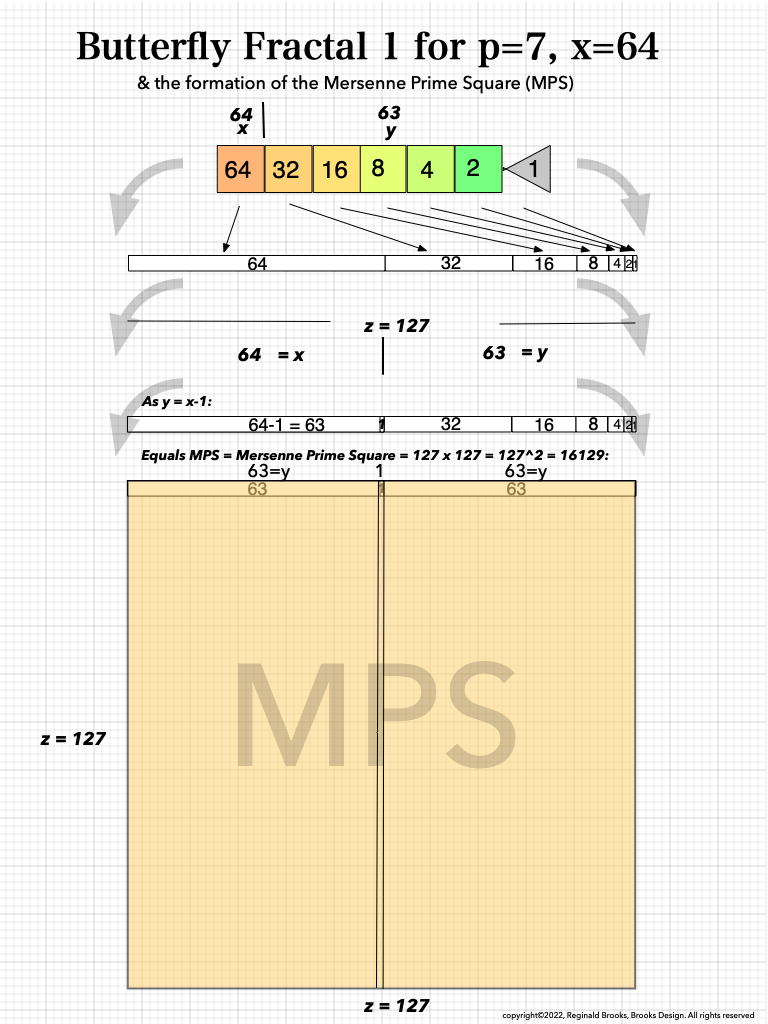
MPS-0-22/BFsums-x=64_p=7_7
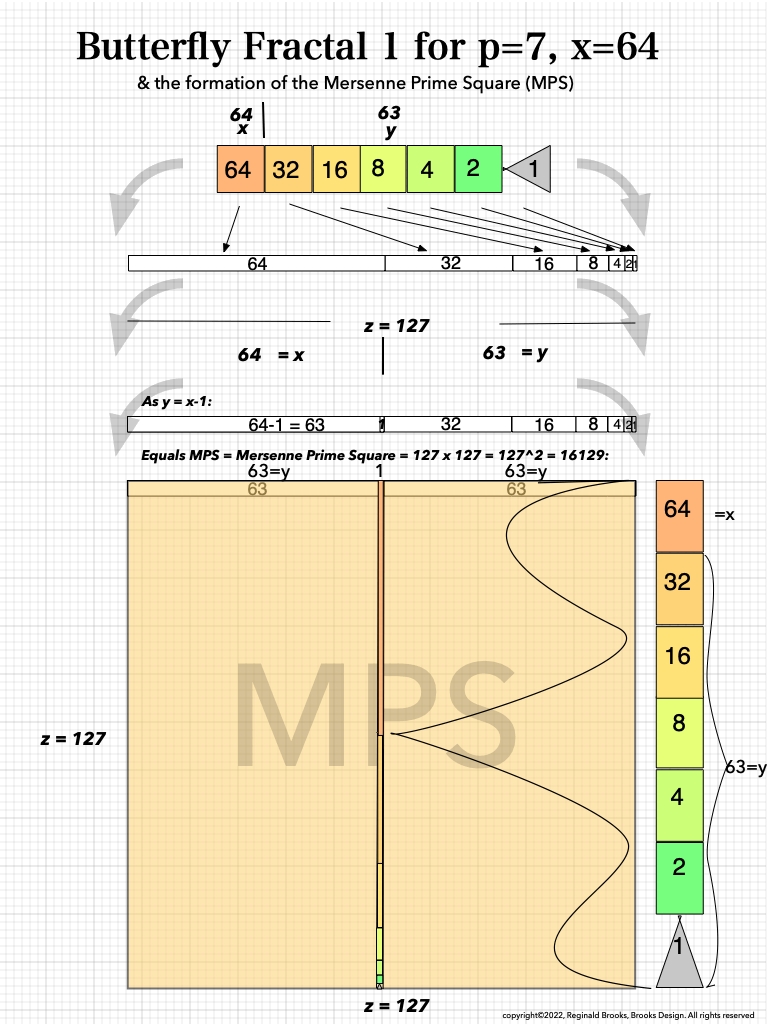
MPS-0-22/BFsums-x=64_p=7_8
MPS-0-22/BFsums-x=64_p=7_9
MPS-0-22/BFsums-x=64_p=7_10
MPS-0-22/BFsums-x=64_p=7_11
MPS-0-22/BFsums-x=64_p=7_12
MPS-0-22/BFsums-x=64_p=7_13
MPS-0-22/BFsums-x=64_p=7_14
MPS-0-22/BFsums-x=64_p=7_15

MPS-0-22/BFsums-x=64_p=7_16
MPS-0-22/BFsums-x=64_p=7_17
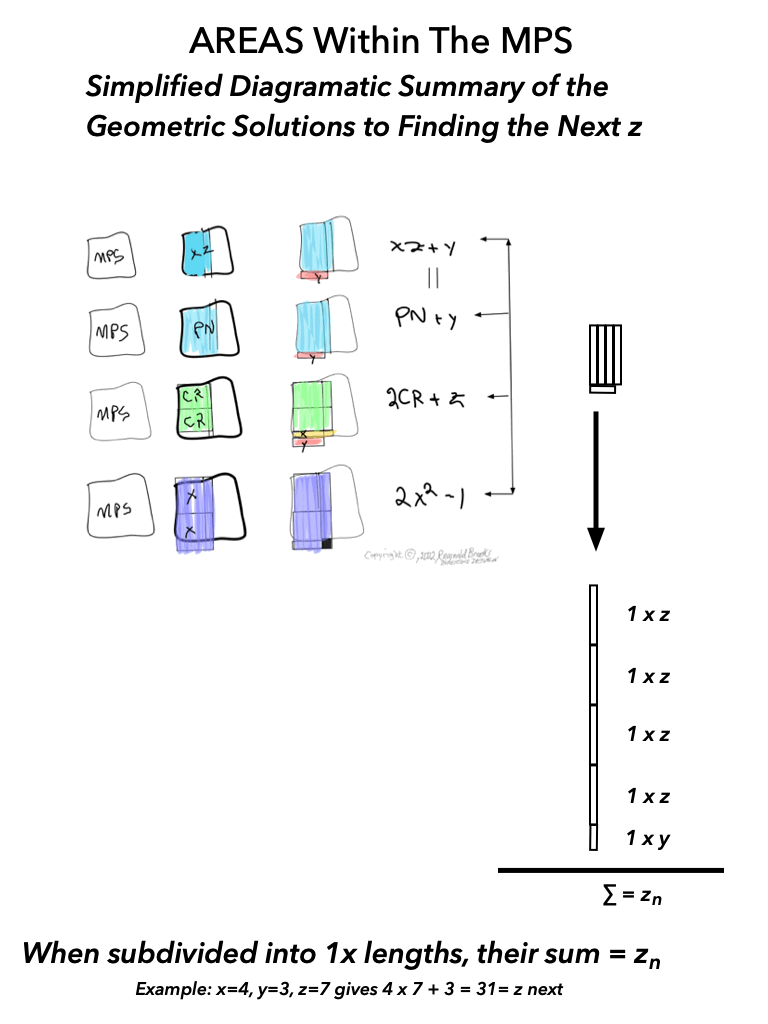
MPS-0-22/BFsums-x=64_p=7_18
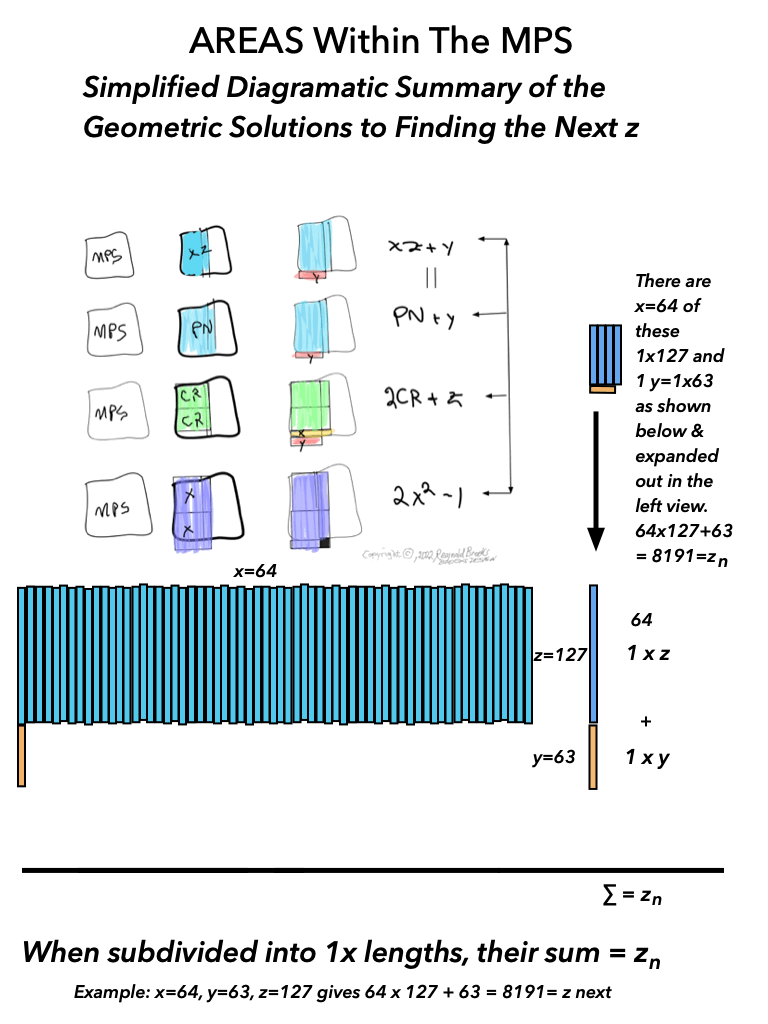
MPS-0-22/BFsums-x=64_p=7_19
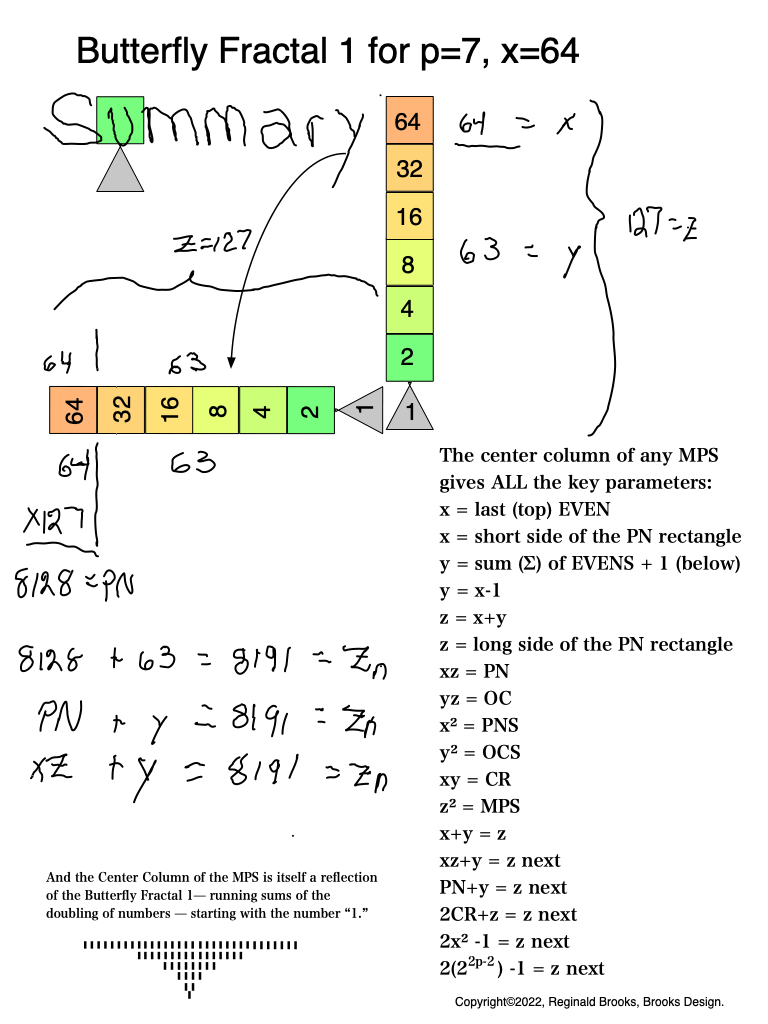
MPS-0-22/BFsums-x=64_p=7_20
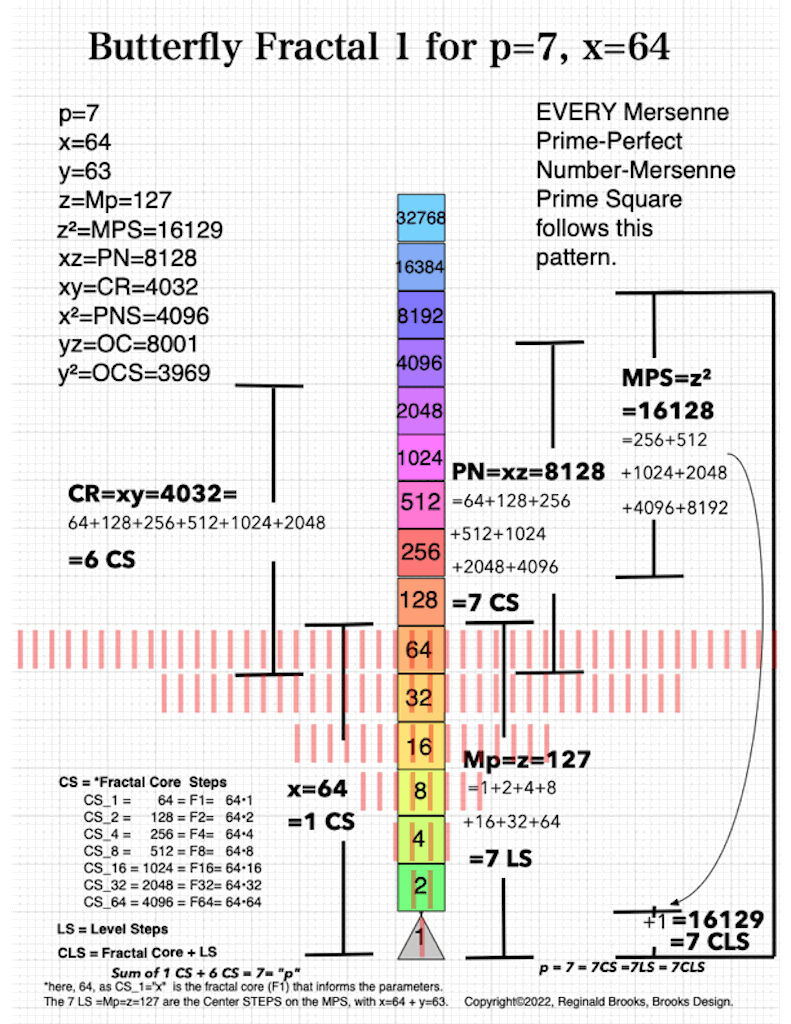
MPS-0-22/BFsums-x=64_p=7_21
MPS-0-22/BFsums-x=64_p=7_22
Yet another advanced section. And it will be addressed in the Appendix I in Book VI. Here is just a little bit.
The MPS on the BIM (BIMMPS)Bringing it all together: Parts I - II - III - IV
Let's repeat a key concept covered in Part II and III:
The Perfect Numbers may be expressed as the sequential running sums (∑) of the cubes of the sequential ODD numbers as 1³ + 3³ + 5³ ... and we have the genesis of the Butterfly Fractal~3~.
In the Butterfly Fractal~1~ and Butterfly Fractal~2~, we find the MPS parameters based around the EVEN numbers, especially within the exponential power of 2. When we look at their summations, we find it delivers the ODDs we are looking for that inform the MPS directly.
This gave the x and z=Mp directly and the y, xz=PN and xy=CR indirectly by calculation.
Now, in the Butterfly Fractal~3~, we find the MPS parameters based around the ODD numbers, especially the Running Sums (∑) of the ODD numbers sequence of 1,3,5,… giving the MPS and the ODD³ sequence of 1³, 3³, 5³,… giving the PN!
of Numbers (Part I)
NEXT: BOOK III: An Artist, Mathematician and Choreographer...Oceans of Numbers (Part II)
~~~~~~~~
~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~
LINKS:
Mersenne Prime Squares (Part I) the Introductory white paper.
Mersenne Prime Squares (Part II) 3 Simple Intros.
Mersenne Prime Squares (Part III) the Advanced white paper.
The MPS Project The Mersenne Prime Squares Project.
LINKS:MathspeedST: TPISC Media Center
MathspeedST: eBook (free)
Apple Books
Artist Link in iTunes Apple Books Store:
Reginald Brooks
 KEYWORDS TAGS:
BMP, BIM-MersenneSquare-PerfectNumber, Mersenne Primes, Mersenne Prime Square, Perfect Number, Perfect Square, MPS, Mp, PTOP, Periodic Table Of PRIMES, PRIMES vs NO-PRIMES, algebraic geometry, BIM, TPISC, The Pythagorean - Inverse Square Connections, Pythagorean Triangles, DNA, Zika virus, pentagon, decagon, double pentagon, composite axial DNA double-helix, Pythagorean Triples, primitive Pythagorean Triples, non-primitive Pythagorean Triples, Pythagorean Theorem, Pythagorus Theorem, The Dickson Method, BBS-ISL Matrix, Expanded Dickson Method, r-sets, s-set, t-sets, Pair-sets, geometric proofs, MathspeedST, leapfrogging LightspeedST FASTER than the speed of light, Brooks (Base) Square- Inverse Square Law (ISL), BBS-ISL Matrix grid, The Architecture Of SpaceTime (TAOST), The Conspicuous Absence Of Primes (TCAOP), A Fresh Piece Of Pi(e), AFPOP, Numbers of Inevitability, LightspeedST, Teachers, Educators and Students (TES), number theory, ubiquitous information, FASTER than the speed of light, primes, prime numbers, fractals, mathematics, Universe, cosmos, patterns in number, DSEQEC, Double-Slit Experiment-Quantum Entanglement Conjecture, CaCost, Creation and Conservation of SpaceTime.
KEYWORDS TAGS:
BMP, BIM-MersenneSquare-PerfectNumber, Mersenne Primes, Mersenne Prime Square, Perfect Number, Perfect Square, MPS, Mp, PTOP, Periodic Table Of PRIMES, PRIMES vs NO-PRIMES, algebraic geometry, BIM, TPISC, The Pythagorean - Inverse Square Connections, Pythagorean Triangles, DNA, Zika virus, pentagon, decagon, double pentagon, composite axial DNA double-helix, Pythagorean Triples, primitive Pythagorean Triples, non-primitive Pythagorean Triples, Pythagorean Theorem, Pythagorus Theorem, The Dickson Method, BBS-ISL Matrix, Expanded Dickson Method, r-sets, s-set, t-sets, Pair-sets, geometric proofs, MathspeedST, leapfrogging LightspeedST FASTER than the speed of light, Brooks (Base) Square- Inverse Square Law (ISL), BBS-ISL Matrix grid, The Architecture Of SpaceTime (TAOST), The Conspicuous Absence Of Primes (TCAOP), A Fresh Piece Of Pi(e), AFPOP, Numbers of Inevitability, LightspeedST, Teachers, Educators and Students (TES), number theory, ubiquitous information, FASTER than the speed of light, primes, prime numbers, fractals, mathematics, Universe, cosmos, patterns in number, DSEQEC, Double-Slit Experiment-Quantum Entanglement Conjecture, CaCost, Creation and Conservation of SpaceTime.
| PIN: Pattern in Number...from primes to DNA. | PIN: Butterfly Primes...let the beauty seep in. | PIN: Butterfly Prime Directive...metamorphosis. | PIN: Butterfly Prime Determinant Number Array (DNA) ~conspicuous abstinence~. | GoDNA: the Geometry of DNA (axial view) revealed. | SCoDNA: the Structure and Chemistry of DNA (axial view). | The LUFE Matrix | The LUFE Matrix Supplement | The LUFE Matrix: Infinite Dimensions | The LUFE Matrix: E=mc2 | Dark Matter=Dark Energy | The History of the Universe in Scalar Graphics | The History of the Universe_update: The Big Void | Quantum Gravity ...by the book | The Conservation of SpaceTime | LUFE: The Layman's Unified Field Expose` | GoMAS: The Geometry of Music, Art and Structure ...linking science, art and esthetics. Part I | Brooks (Base) Square (BBS): The Architecture of Space-Time (TAOST) and The Conspicuous Absence of Primes (TCAOP) - a brief introduction to the series | more White Papers...
|
|
|
| net.art index | netart01: RealSurReal...aClone, 2001 | netart02: Hey!Ufunk'n with my DNA? | netart03: 9-11_remembered | netart04: Naughty Physics (a.k.a. The LUFE Matrix) | netart05: Your sFace or Mine? | netart06: Butterfly Primes | netart07: Music-Color-ISL | netart08: BBS-ISL matrix | netart09: BBS-interactive (I) | netart10: Sunspots and Solar Flares | netart11: Music-Color-ISL (II-III) | Art Theory 101: PIN, DNA, LUFE Matrix, GoMAS, BBS index | home
| Art Theory 101 / White Papers Index
|
Copyright 2021-23, Reginald Brooks, Brooks Design. All rights reserved.
|
|
iTunes, iTunes Store, Apple Books, iBooks, iBooks Store, iBooks Author, Mac OS are registered® trademarks of Apple Inc. and their use on this webpage does not reflect endorsement by Apple Inc.
|
TOP























































