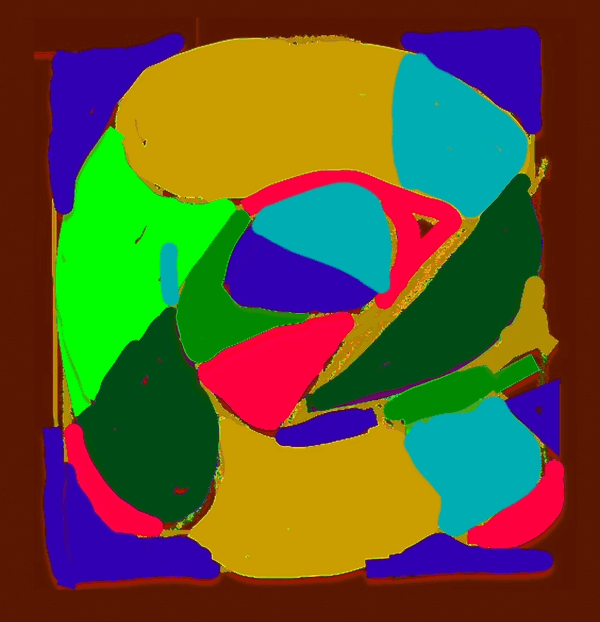BIM-MPS: Details, Part I
The Geometry of the PN and OC within the MPS as informed by the Exponential Power of 2.
Three-part video introduction:
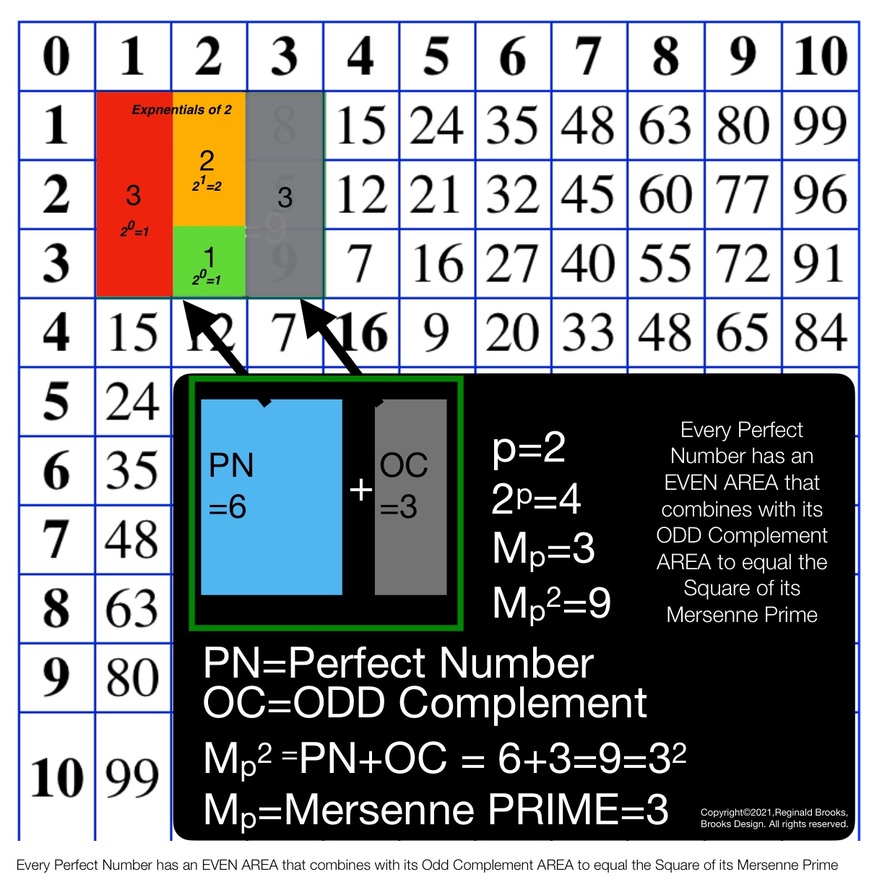
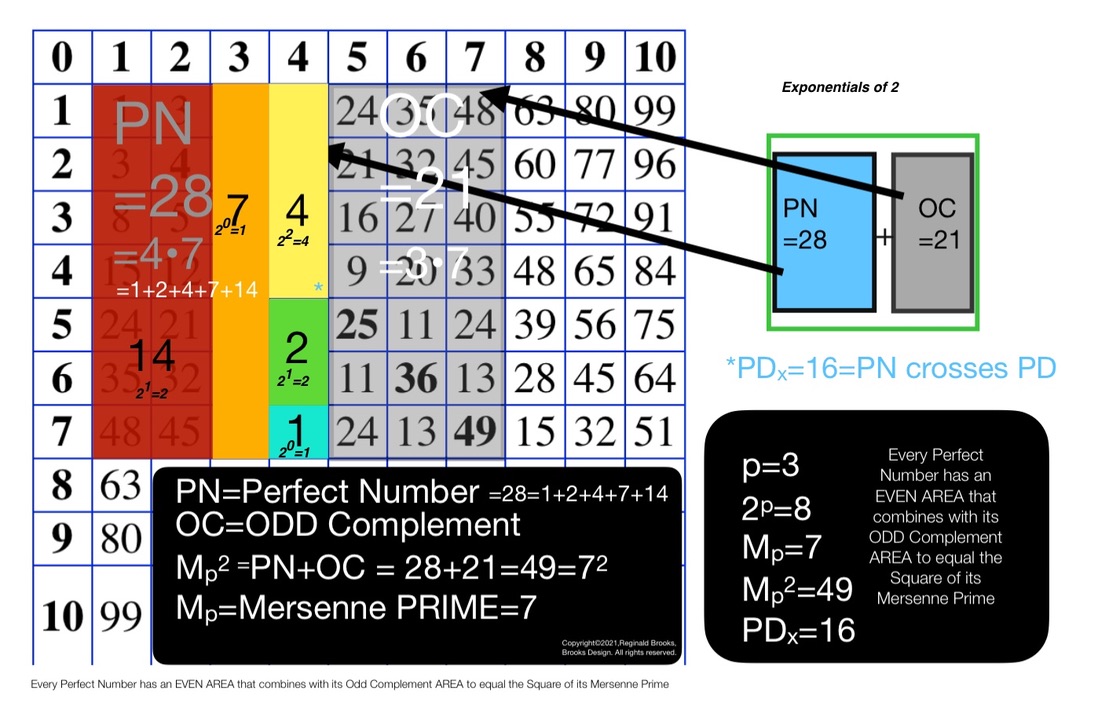
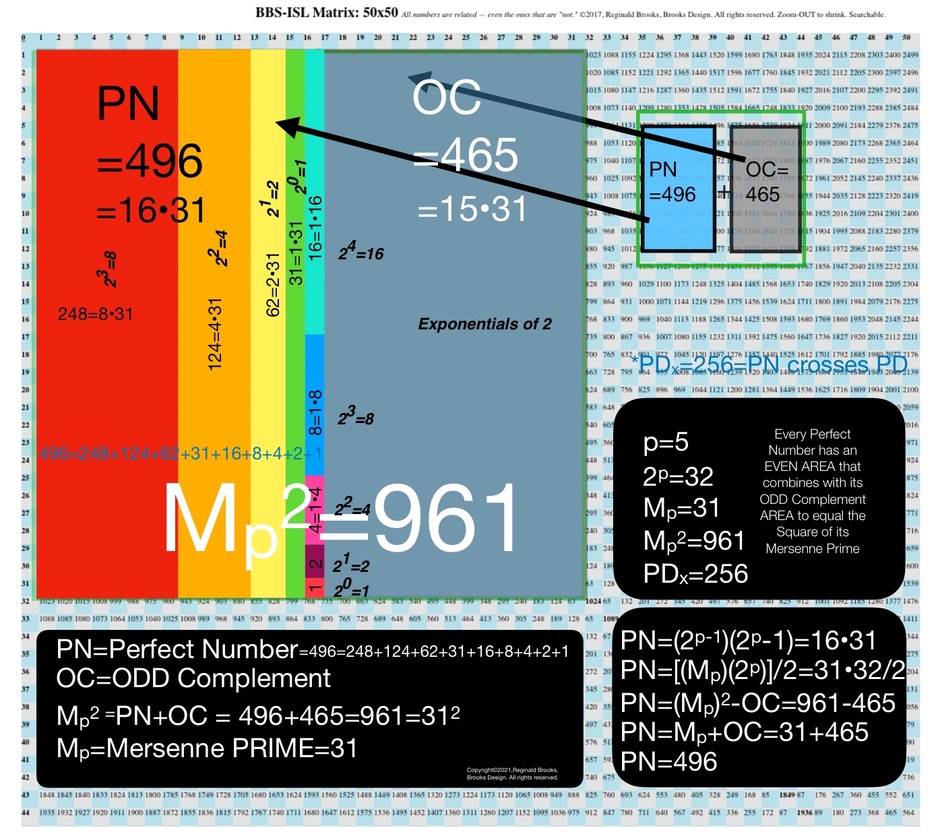
Is not the number one (1) the ultimate "fractal?"
While not technically a prime, it is only divisible by itself and 1.
If we loosen our definition of what a fractal is to include that which forms a larger whole simply by doubling itself and each sum/product thereafter: 1--2--4--8--16--32--64--....
We can also write that as exponentials of 2:
2^0^--21--22--23--24--25--26--..., respectively.
A careful look at the four images above of the first four MPS reveals that just such a simple definition of fractal is in play here.
Once you can see how the "big" forms of the MPS are formed from the smaller forms by this simple fractal of one, you will have one of the keys that unlock how ALL the forms of the MPS are formed! And it is quite amazing!
While these simple fractal forms that become the AREAS that define the three generations of AREAS that make up each and every MPS, as can be seen on any common grid layout, it is not until one reveals the same on the BIM that the true details can be seen!
Our method will be to put each MPS on the BIM and then highlight their individual details -- profiles, really -- and then proceed to show how such a Number Pattern Sequence (NPS) is fractal repeated in each successive MPS.
We will start with the simpler universal grid and then proceed to the details as seen in the MPS on the BIM (BIM + MPS = BIMMPS).
Before we get started, let's just get an overview by looking again at the four images above. The comments below will apply as a NPS across to ALL MPS.
The MPS on the universal grid
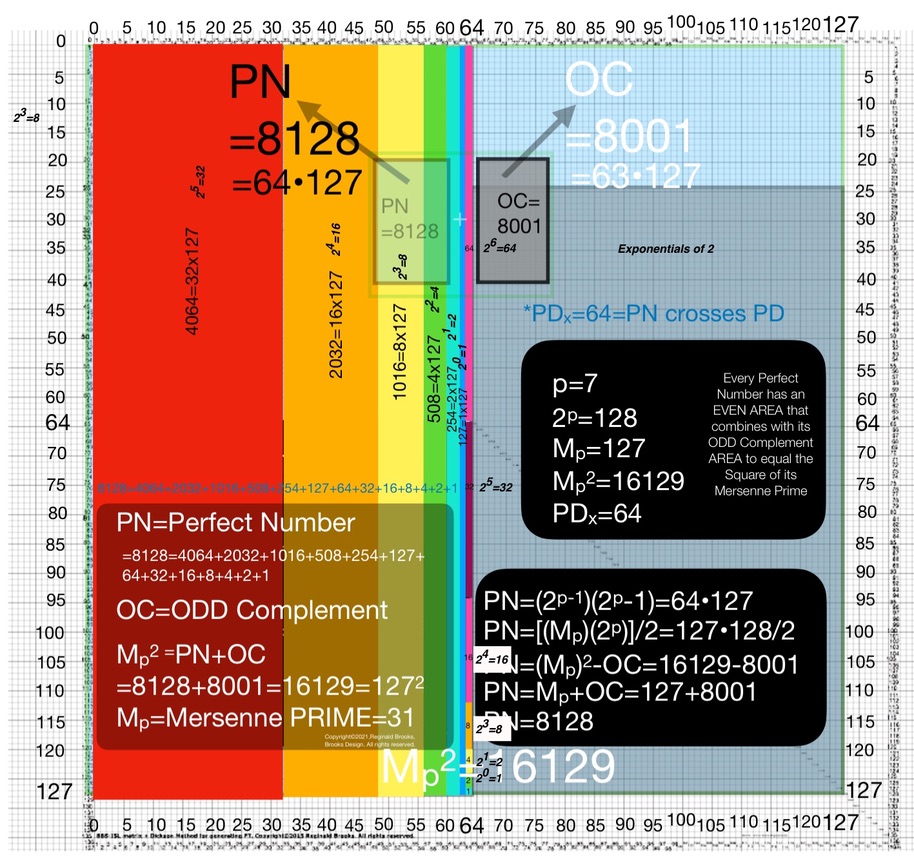
The MPS Square Area is divided into two parts - rectangles - one that is EVEN (colors) and slightly larger, the other ODD (gray).
The EVEN is the Perfect Number (PN) and the ODD is the ODD Complement (OC).
The PN has rectangular bands of a single color that meets up with the last multi-colored band.
This last, polychromatic band sits right on the center line of the MPS.
The large rectangles on either side are equal. That's right, the colorful rectangle to the left = the gray rectangle to the right.
This central, polychromatic band is ALWAYS composed of a sequence of 1-2-4-... fractals and it ALWAYS ends with an EVEN.
Because it has ALL EVENS + the ODD #1, it sums (∑) up to an ODD that = Mp = z.
The ∑ of ALL the fractals, up to but not including the last ending EVEN, = y, as the last, ending EVEN itself = x, and x+y=z. Mp=z.
So the difference (∆) between the PN and OC is this Mp=z.
The number of fractals in this central, vertical band = p, where p = prime.
The total number of the colorful vertical bands, with the central band counted as one, within the PN also = p.
Not counting the central band, the remaining bands are exponential powers of 2 fractals that multiply with the z=Mp to give the remaining AREAS of the PN, each one successively doubling its predecessor.
The ∑ of these AREAS = the OC, and, when added to the AREA of the central band = PN.
That's it -- for now! Every MPS follows this NPS!
Let's go over some of the MPS in detail using the above NPS overview as a starting point.

- The MPS Square Area is divided into two parts - rectangles - one that is EVEN (colors) and slightly larger, the other ODD (gray).
- The EVEN is the Perfect Number (PN) and the ODD is the ODD Complement (OC).
- The PN has rectangular bands of a single color that meets up with the last multi-colored band.
- This last, polychromatic band sits right on the center line of the MPS.
- The large rectangles on either side are equal. That's right, the colorful rectangle to the left = the gray rectangle to the right.
- This central, polychromatic band is ALWAYS composed of a sequence of 1-2-4-... fractals and it ALWAYS ends with an EVEN.
- Because it has ALL EVENS + the ODD #1, it sums (∑) up to an ODD that = Mp = z.
- The ∑ of ALL the fractals, up to but not including the last ending EVEN, = y, as the last, ending EVEN itself = x, and x+y=z.
- The ∑ of ALL the fractals, up to but not including the last ending EVEN, = y, as the last, ending EVEN itself = x, and x+y=z.
- So the difference (∆) between the PN and OC is this Mp=z.
- The total number of the colorful vertical bands, with the central band counted as one, within the PN, also = p.
- The total number of the colorful vertical bands, with the central band counted as one, within the PN, also = p.
- Not counting the central band, the remaining bands are exponential powers of 2 fractals that multiply with the z=Mp to give the remaining AREAS of the PN, each one successively doubling its predecessor.
- The ∑ of these AREAS = the OC, and, when added to the AREA of the central band = PN.
- The MPS Square Area is divided into two parts - rectangles - one that is EVEN (colors) and slightly larger, the other ODD (gray).
- The EVEN is the Perfect Number (PN) and the ODD is the ODD Complement (OC).
- The PN has rectangular bands of a single color that meets up with the last multi-colored band.
- This last, polychromatic band sits right on the center line of the MPS.
- The large rectangles on either side are equal. That's right, the colorful rectangle to the left = the gray rectangle to the right.
- This central, polychromatic band is ALWAYS composed of a sequence of 1-2-4-... fractals and it ALWAYS ends with an EVEN.
- Because it has ALL EVENS + the ODD #1, it sums (∑) up to an ODD that = Mp = z.
- The ∑ of ALL the fractals, up to but not including the last ending EVEN, = y, as the last, ending EVEN itself = x, and x+y=z. Mp=z.
- So the difference (∆) between the PN and OC is this Mp=z.
- The number of fractals in this central, vertical band = p, where p = prime.
- The total number of the colorful vertical bands, with the central band counted as one, within the PN also = p.
- Not counting the central band, the remaining bands are exponential powers of 2 fractals that multiply with the z=Mp to give the remaining AREAS of the PN, each one successively doubling its predecessor.
- The ∑ of these AREAS = the OC, and, when added to the AREA of the central band = PN.
As described earlier, there are three generations -- grandparent-parent-grandchild-- that inform each MPS. The "grandparent" is of course the MPS itself. The "parent" is the generation layered below. Most of the above #1-13 NPSs above describe this generation.
Below the "parent" is the "grandchild" generation. The PN and OC Rectangles of the "parent" generation are simply further divided into the Perfect Number Square (PNS) and remaining Complement Rectangle (CR) of the PN, and, the ODD Complement Square (OCS) and the identical CR of the OC. The next three (#14, 15, and 16) NPS describe the PNS, OCS and CR.
- The Complement Rectangle (CR) =xy, appears twice in the “grandchild” generation as 2CR=2xy=OC+y=yz+y= gray(OC)+all the central bands except the last EVEN=PN - the central band last EVEN, e.i., 24=21+3=28-4.
- While the Perfect Number Square (PNS) = x² appears just once and as double its value as 2PNS=2x² =2(x*x) = PN + x = xz+x = color(PN)+central band last EVEN, e.i., 32=28+4.
- While the ODD Complement Square (OCS) = y² appears just once and as double its value as 2OCS=2y² =2(y*y)=OC-y=yz-y=gray(OC) - all the central bands except the last EVEN, e.i., 18=21-3.
The #17 NPS describes something special: the sum (∑) of the PNS + OCS Areas.
- The sum (∑) of the PNS + OCS Areas = ∑(x² + y² )= PN-y = color(PN) - all central bands except the last EVEN = gray(OC)+x, e.i., 16 + 9 =25 =28-3=21+4.
(See next size up for images and examples.)
xxxxxxxxxx

- The MPS Square Area is divided into two parts - rectangles - one that is EVEN (colors) and slightly larger, the other ODD (gray).
- The EVEN is the Perfect Number (PN) and the ODD is the ODD Complement (OC).
- The PN has rectangular bands of a single color that meets up with the last multi-colored band.
- This last, polychromatic band sits right on the center line of the MPS.
- The large rectangles on either side are equal. That's right, the colorful rectangle to the left = the gray rectangle to the right.
- This central, polychromatic band is ALWAYS composed of a sequence of 1-2-4-... fractals and it ALWAYS ends with an EVEN.
- Because it has ALL EVENS + the ODD #1, it sums (∑) up to an ODD that = Mp = z.
- The ∑ of ALL the fractals, up to but not including the last ending EVEN, = y, as the last, ending EVEN itself = x, and x+y=z.
- The ∑ of ALL the fractals, up to but not including the last ending EVEN, = y, as the last, ending EVEN itself = x, and x+y=z.
- So the difference (∆) between the PN and OC is this Mp=z.
- The total number of the colorful vertical bands, with the central band counted as one, within the PN, also = p.
- The total number of the colorful vertical bands, with the central band counted as one, within the PN, also = p.
- Not counting the central band, the remaining bands are exponential powers of 2 fractals that multiply with the z=Mp to give the remaining AREAS of the PN, each one successively doubling its predecessor.
- The ∑ of these AREAS = the OC, and, when added to the AREA of the central band = PN.
- The MPS Square Area is divided into two parts - rectangles - one that is EVEN (colors) and slightly larger, the other ODD (gray).
- The EVEN is the Perfect Number (PN) and the ODD is the ODD Complement (OC).
- The PN has rectangular bands of a single color that meets up with the last multi-colored band.
- This last, polychromatic band sits right on the center line of the MPS Square.
- The large rectangles on either side are equal. That's right, the colorful rectangle to the left = the gray rectangle to the right.
- This central, polychromatic band is ALWAYS composed of a sequence of 1-2-4-... fractals and it ALWAYS ends with an EVEN.
- Because it has ALL EVENS + the ODD #1, it sums (∑) up to an ODD that = Mp = z.
- The ∑ of ALL the fractals, up to but not including the last ending EVEN, = y, as the last, ending EVEN itself = x, and x+y=z. Mp=z.
- So the difference (∆) between the PN and OC is this Mp=z.
- The number of fractals in this central, vertical band = p, where p = prime.
- The total number of the colorful vertical bands, with the central band counted as one, within the PN also = p.
- Not counting the central band, the remaining bands are exponential powers of 2 fractals that multiply with the z=Mp to give the remaining AREAS of the PN, each one successively doubling its predecessor.
- The ∑ of these AREAS = the OC, and, when added to the AREA of the central band = PN.
As described earlier, there are three generations -- grandparent-parent-grandchild-- that inform each MPS. The "grandparent" is of course the MPS itself. The "parent" is the generation layered below. Most of the above #1-13 NPSs above describe this generation.
Below the "parent" is the "grandchild" generation. The PN and OC Rectangles of the "parent" generation are simply further divided into the Perfect Number Square (PNS) and remaining Complement Rectangle (CR) of the PN, and, the ODD Complement Square (OCS) and the identical CR of the OC. The next three (#14, 15, and 16) NPS describe the PNS, OCS and CR.
- The Complement Rectangle (CR) =xy, appears twice in the “grandchild” generation as 2CR=2xy=OC+y=yz+y= gray(OC)+all the central bands except the last EVEN=PN - the central band last EVEN, e.i., 24=21+3=28-4.
- While the Perfect Number Square (PNS) = x² appears just once and as double its value as 2PNS=2x² =2(x*x) = PN + x = xz+x = color(PN)+central band last EVEN, e.i., 32=28+4.
- While the ODD Complement Square (OCS) = y² appears just once and as double its value as 2OCS=2y² =2(y*y)=OC-y=yz-y=gray(OC) - all the central bands except the last EVEN, e.i., 18=21-3.
- The Complement Rectangle (CR) =xy, appears twice in the “grandchild” generation as 2CR=2xy=OC+y=yz+y= gray(OC)+all the central bands except the last EVEN=PN - the central band last EVEN, e.i., 24=21+3=28-4.
- While the Perfect Number Square (PNS) = x² appears just once and as double its value as 2PNS=2x² =2(x*x) = PN + x = xz+x = color(PN)+central band last EVEN, e.i., 32=28+4.
- While the ODD Complement Square (OCS) = y² appears just once and as double its value as 2OCS=2y² =2(y*y)=OC-y=yz-y=gray(OC) - all the central bands except the last EVEN, e.i., 18=21-3.
The #17 NPS describes something special: the sum (∑) of the PNS + OCS Areas.
- The sum (∑) of the PNS + OCS Areas = ∑(x² + y²)= PN-y = color(PN) - all central bands except the last EVEN = gray(OC)+x, e.i., 16 + 9 =25 =28-3=21+4.
- The sum (∑) of the PNS + OCS Areas = ∑(x² + y² )= PN-y = color(PN) - all central bands except the last EVEN = gray(OC)+x, e.i., 16 + 9 =25 =28-3=21+4.
x

- The MPS Square Area is divided into two parts - rectangles - one that is EVEN (colors) and slightly larger, the other ODD (gray).
- The EVEN is the Perfect Number (PN) and the ODD is the ODD Complement (OC).
- The PN has rectangular bands of a single color that meets up with the last multi-colored band.
- This last, polychromatic band sits right on the center line of the MPS.
- The large rectangles on either side are equal. That's right, the colorful rectangle to the left = the gray rectangle to the right.
- This central, polychromatic band is ALWAYS composed of a sequence of 1-2-4-... fractals and it ALWAYS ends with an EVEN.
- Because it has ALL EVENS + the ODD #1, it sums (∑) up to an ODD that = Mp = z.
- The ∑ of ALL the fractals, up to but not including the last ending EVEN, = y, as the last, ending EVEN itself = x, and x+y=z.
- The ∑ of ALL the fractals, up to but not including the last ending EVEN, = y, as the last, ending EVEN itself = x, and x+y=z.
- So the difference (∆) between the PN and OC is this Mp=z.
- The total number of the colorful vertical bands, with the central band counted as one, within the PN also = p.
- The total number of the colorful vertical bands, with the central band counted as one, within the PN also = p.
- Not counting the central band, the remaining bands are exponential powers of 2 fractals that multiply with the z=Mp to give the remaining AREAS of the PN, each one successively doubling its predecessor.
- The ∑ of these AREAS = the OC, and, when added to the AREA of the central band = PN.
- The MPS Square Area is divided into two parts - rectangles - one that is EVEN (colors) and slightly larger, the other ODD (gray).
- The EVEN is the Perfect Number (PN) and the ODD is the ODD Complement (OC).
- The PN has rectangular bands of a single color that meets up with the last multi-colored band.
- This last, polychromatic band sits right on the center line of the MPS Square.
- The large rectangles on either side are equal. That's right, the colorful rectangle to the left = the gray rectangle to the right.
- This central, polychromatic band is ALWAYS composed of a sequence of 1-2-4-... fractals and it ALWAYS ends with an EVEN.
- Because it has ALL EVENS + the ODD #1, it sums (∑) up to an ODD that = Mp = z.
- The ∑ of ALL the fractals, up to but not including the last ending EVEN, = y, as the last, ending EVEN itself = x, and x+y=z. Mp=z.
- So the difference (∆) between the PN and OC is this Mp=z.
- The number of fractals in this central, vertical band = p, where p = prime.
- The total number of the colorful vertical bands, with the central band counted as one, within the PN also = p.
- Not counting the central band, the remaining bands are exponential powers of 2 fractals that multiply with the z=Mp to give the remaining AREAS of the PN, each one successively doubling its predecessor.
- The ∑ of these AREAS = the OC, and, when added to the AREA of the central band = PN.
As described earlier, there are three generations -- grandparent-parent-grandchild-- that inform each MPS. The "grandparent" is of course the MPS itself. The "parent" is the generation layered below. Most of the above #1-13 NPSs above describe this generation.
Below the "parent" is the "grandchild" generation. The PN and OC Rectangles of the "parent" generation are simply further divided into the Perfect Number Square (PNS) and remaining Complement Rectangle (CR) of the PN, and, the ODD Complement Square (OCS) and the identical CR of the OC. The next three (#14, 15, and 16) NPS describe the PNS, OCS and CR.
- The Complement Rectangle (CR) =xy, appears twice in the “grandchild” generation as 2CR=2xy=OC+y=yz+y= gray(OC)+all the central bands except the last EVEN=PN - the central band last EVEN, e.i., 24=21+3=28-4.
- While the Perfect Number Square (PNS) = x² appears just once and as double its value as 2PNS=2x² =2(x*x) = PN + x = xz+x = color(PN)+central band last EVEN, e.i., 32=28+4.
- While the ODD Complement Square (OCS) = y² appears just once and as double its value as 2OCS=2y² =2(y*y)=OC-y=yz-y=gray(OC) - all the central bands except the last EVEN, e.i., 18=21-3.
- The Complement Rectangle (CR) =xy, appears twice in the “grandchild” generation as 2CR=2xy=OC+y=yz+y= gray(OC)+all the central bands except the last EVEN=PN - the central band last EVEN, e.i., 24=21+3=28-4.
- While the Perfect Number Square (PNS) = x² appears just once and as double its value as 2PNS=2x² =2(x*x) = PN + x = xz+x = color(PN)+central band last EVEN, e.i., 32=28+4.
- While the ODD Complement Square (OCS) = y² appears just once and as double its value as 2OCS=2y² =2(y*y)=OC-y=yz-y=gray(OC) - all the central bands except the last EVEN, e.i., 18=21-3.
The #17 NPS describes something special: the sum (∑) of the PNS + OCS Areas.
- The sum (∑) of the PNS + OCS Areas = ∑(x² + y²)= PN-y = color(PN) - all central bands except the last EVEN = gray(OC)+x, e.i., 16 + 9 =25 =28-3=21+4.
- The sum (∑) of the PNS + OCS Areas = ∑(x² + y²) = PN-y = color(PN) - all central bands except the last EVEN = gray(OC)+x, e.i., 16 + 9 =25 =28-3=21+4.
xxxxxxxxxx

- The MPS Square Area is divided into two parts - rectangles - one that is EVEN (colors) and slightly larger, the other ODD (gray).
- The EVEN is the Perfect Number (PN) and the ODD is the ODD Complement (OC).
- The PN has rectangular bands of a single color that meets up with the last multi-colored band.
- This last, polychromatic band sits right on the center line of the MPS.
- The large rectangles on either side are equal. That's right, the colorful rectangle to the left = the gray rectangle to the right.
- This central, polychromatic band is ALWAYS composed of a sequence of 1-2-4-... fractals and it ALWAYS ends with an EVEN.
- Because it has ALL EVENS + the ODD #1, it sums (∑) up to an ODD that = Mp = z.
- The ∑ of ALL the fractals, up to but not including the last ending EVEN, = y, as the last, ending EVEN itself = x, and x+y=z.
- The ∑ of ALL the fractals, up to but not including the last ending EVEN, = y, as the last, ending EVEN itself = x, and x+y=z.
- So the difference (∆) between the PN and OC is this Mp=z.
- The total number of the colorful vertical bands, with the central band counted as one, within the PN also = p.
- The total number of the colorful vertical bands, with the central band counted as one, within the PN also = p.
- Not counting the central band, the remaining bands are exponential powers of 2 fractals that multiply with the z=Mp to give the remaining AREAS of the PN, each one successively doubling its predecessor.
- The ∑ of these AREAS = the OC, and, when added to the AREA of the central band = PN.
- The MPS Square Area is divided into two parts - rectangles - one that is EVEN (colors) and slightly larger, the other ODD (gray).
- The EVEN is the Perfect Number (PN) and the ODD is the ODD Complement (OC).
- The PN has rectangular bands of a single color that meets up with the last multi-colored band.
- This last, polychromatic band sits right on the center line of the MPS Square.
- The large rectangles on either side are equal. That's right, the colorful rectangle to the left = the gray rectangle to the right.
- This central, polychromatic band is ALWAYS composed of a sequence of 1-2-4-... fractals and it ALWAYS ends with an EVEN.
- Because it has ALL EVENS + the ODD #1, it sums (∑) up to an ODD that = Mp = z.
- The ∑ of ALL the fractals, up to but not including the last ending EVEN, = y, as the last, ending EVEN itself = x, and x+y=z. Mp=z.
- So the difference (∆) between the PN and OC is this Mp=z.
- The number of fractals in this central, vertical band = p, where p = prime.
- The total number of the colorful vertical bands, with the central band counted as one, within the PN also = p.
- Not counting the central band, the remaining bands are exponential powers of 2 fractals that multiply with the z=Mp to give the remaining AREAS of the PN, each one successively doubling its predecessor.
- The ∑ of these AREAS = the OC, and, when added to the AREA of the central band = PN.
As described earlier, there are three generations -- grandparent-parent-grandchild-- that inform each MPS. The "grandparent" is of course the MPS itself. The "parent" is the generation layered below. Most of the above #1-13 NPSs above describe this generation.
Below the "parent" is the "grandchild" generation. The PN and OC Rectangles of the "parent" generation are simply further divided into the Perfect Number Square (PNS) and remaining Complement Rectangle (CR) of the PN, and, the ODD Complement Square (OCS) and the identical CR of the OC. The next three (#14, 15, and 16) NPS describe the PNS, OCS and CR.
- The Complement Rectangle (CR) =xy, appears twice in the “grandchild” generation as 2CR=2xy=OC+y=yz+y= gray(OC)+all the central bands except the last EVEN=PN - the central band last EVEN, e.i., 24=21+3=28-4.
- While the Perfect Number Square (PNS) = x² appears just once and as double its value as 2PNS=2x² =2(x*x) = PN + x = xz+x = color(PN)+central band last EVEN, e.i., 32=28+4.
- While the ODD Complement Square (OCS) = y² appears just once and as double its value as 2OCS=2y² =2(y*y)=OC-y=yz-y=gray(OC) - all the central bands except the last EVEN, e.i., 18=21-3.
- The Complement Rectangle (CR) =xy, appears twice in the “grandchild” generation as 2CR=2xy=OC+y=yz+y= gray(OC)+all the central bands except the last EVEN=PN - the central band last EVEN, e.i., 24=21+3=28-4.
- While the Perfect Number Square (PNS) = x² appears just once as double its value as 2PNS=2x² =2(x*x) = PN + x = xz+x = color(PN)+central band last EVEN, e.i., 32=28+4.
- While the ODD Complement Square (OCS) = y² appears just once as double its value as 2OCS=2y² =2(y*y)=OC-y=yz-y=gray(OC) - all the central bands except the last EVEN, e.i., 18=21-3.
The #17 NPS describes something special: the sum (∑) of the PNS + OCS Areas.
- The sum (∑) of the PNS + OCS Areas = ∑(x² + y²) = PN-y = color(PN) - all central bands except the last EVEN = gray(OC)+x, e.i., 16 + 9 =25 =28-3=21+4.
- The sum (∑) of the PNS + OCS Areas = ∑(x² + y²) = PN-y = color(PN) - all central bands except the last EVEN = gray(OC)+x, e.i., 16 + 9 =25 =28-3=21+4.
xxxxxxxxxx
As one can see, the color bands that make up the PN can form all three "generations" withing the MPS space. They do so in a completely fractal manner, based on the exponential power of 2. They do so in a repeating NPS template that is exactly the same for each MPS, with only the relative numbers being different.
BIM-MPS-PN-1--1.mp4

BIM-MPS-PN-1--1.gif
Now let's go back and look at the opening statement:
Is not the number one (1) the ultimate "fractal?"
While not technically a prime, it is only divisible by itself and 1.
If we loosen our definition of what a fractal is to include that which forms a larger whole simply by doubling itself and each sum/product thereafter: 1--2--4--8--16--32--64--....
We can also write that as exponentials of 2:
20--21--22--23--24--25--26--..., respectively.
Letting the Fractal "1" (F~1~) simply double itself and then let the result double itself, and that result double itself -- a successive doubling -- generates a bi-lateral mirror-symmetric fractal pattern whose mirrored sides exactly repeat the pattern of the "whole!" The resulting image is aptly called the "Butterfly Fractal~1~" and not only does it more than suggest the patterns of butterflies and moths, it also generates the key values within the MPS Table as the running sum (∑) of each doubling and the exponential value of each doubling level are considered. This will be considered next in Part II.
NEXT: MPS Master Tables
Reginald Brooks
Brooks Design
Portland, OR
brooksdesign-ps.net
~~~~~~~~
~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~
NEXT: MPS Master Tables
LINKS:
Mersenne Prime Squares (Part I) the Introductory white paper.
Mersenne Prime Squares (Part II) 3 Simple Intros.
Mersenne Prime Squares (Part III) the Advanced white paper.
The MPS Project The Mersenne Prime Squares Project.