BIMMPS = BIM - MPS = BBS-ISL Matrix - Mersenne Prime Square:
a.k.a. "Serendipity: Oceans of Numbers At Your Door (SONAYD)
MPS-OUTLINE
BOOK I: Two Dots: The MPS
Intro
Abstract—minimalist
Simple basics
- BIM-MPS_SimpleAnimations-videos-Intro.html Geometry -simple animations and videos
- MPS_3.html 3 Simple Intros
- MPS_Project.html The MPS Project
Advanced basics
- MPS.html The Geometry of the Mersenne Prime-Perfect Number Relationship
- MPS_2.html The MPS: Advanced
Details—maximalist
- BIM-MPS_Details-I.html The Geometry of the PN and OC within the MPS
- MPS_Master_Tables.html MPS Master Tables
BOOK II: An ODD Tale: Ocean of Numbers (Part I)
An_ODD_Tale.html The Butterfly Fractal 1
BIM-MPS_Details-II.html The Exponential Power of 2 and the Butterfly Fractal 1, 2
Ocean_of_Numbers.html Ocean of Numbers (Part I)
*
BIM-MPS_Details-IV.html The MPS on the BIM (BIMMPS)
*
- {{note}} BIM-MPS_Details-III.html The Exponential Power of 3 and the Butterfly Fractal~3~this, plus BIMMPScubed, along with BIMMPScoordinates and BIMMPNTables, goes in the APPENDIX I.
- BIMMPS_coordinates.html
- BIMMPNTables.html end note}}}
BOOK III: An Artist, Mathematician and Choregrapher ... : Oceans of Numbers (Part II)
- BIM-MPS_Details-V.html The MPS on the BIM (BIMMPS): Bringing it all together
- Ocean_of_Numbers(Part_II).html Oceans of Numbers (Part II): An Artist, Mathematician and Choreographer...
BOOK IV: Not to be outdone-the Artist-Geometer: MPSnext & 10 Common Parameters
MPS_next-next-z_10-parametersMPS.html MPS next - 10 Parameters ALL MPS Follow.
BOOK V: PTOFBMPPN: A Mathematicians Table
PTOFBMPPN.html Periodic Table of Fractal-Based Mersenne Prime-Perfect Numbers
BOOK VI: Summary-Conclusion-References-Appendix I
- BIM-MPS_Conclusion.html Summary-Conclusion-References-Appendix I
BOOK VII: Appendix II: A researchers delight: Tables+
- BIM-MPS_Appendix-II.html Appendix II: Tables 70-132+
- BIM-MPS_Media-Tables.html
- BIM-MPS_Media.html Figures, tables, animations and videos
BOOK VIII: Appendix III: Do the math: Equations
BOOK IX: Appendix IV: Butterfly Fractal Expansion
BOOK X: Appendix V: MPS_PN_Factors(Divisors)
Some helpful "Ground Rules" -- if you will -- to keep in mind throughout.
The BIM (BBS-ISL Matrix)
Background
The BIM is a matrix grid of natural, whole integer numbers (WINs) describing the very universal Inverse Square Law (ISL) discovered and developed by the author since first published online in December of 2009. (See page 15 of Art Theory 101 White Papers. Mathspeed refers to early works that collectively reveal the inner workings of the BIM.
The BIM has been found to be an incredible resource for discovering basic number connections (Number Theory), mostly focused on:
Pythagorean Triples
Pythagorean Triples
Pythagoran Tree
Primes
Primes vs Non-Primes
Goldbach Conjecture
Periodic Table of Primes (PTOP)
Mersenne Primes-Perfect Numbers
Mersenne Prime Squares (MPS)
Butterfly Fractal 1
Butterfly Fractal Matrix (BFM)
Periodic Table of Fractal-Based Mersenne Primes - Perfect Numbers (PTOFBMPPN)
All of the works up to this point, under the banner of Math-Art-Physics (MAP) are indexed here.
Operational "Rules"
Some 200 "Rules" are laid out in the early published papers and ebooks found here.
These include text, animations and videos on some 20 ways to make the BIM, finding the Pythagorean Triples, PTOPs, MPS, and more. Another 100 "Rules" -- or close to it -- are sprinkled throughout the Art Theory 101 White Papers beginning with Page 15 (linked above).
In every case, the following simple "Rules" should be kept in mind:
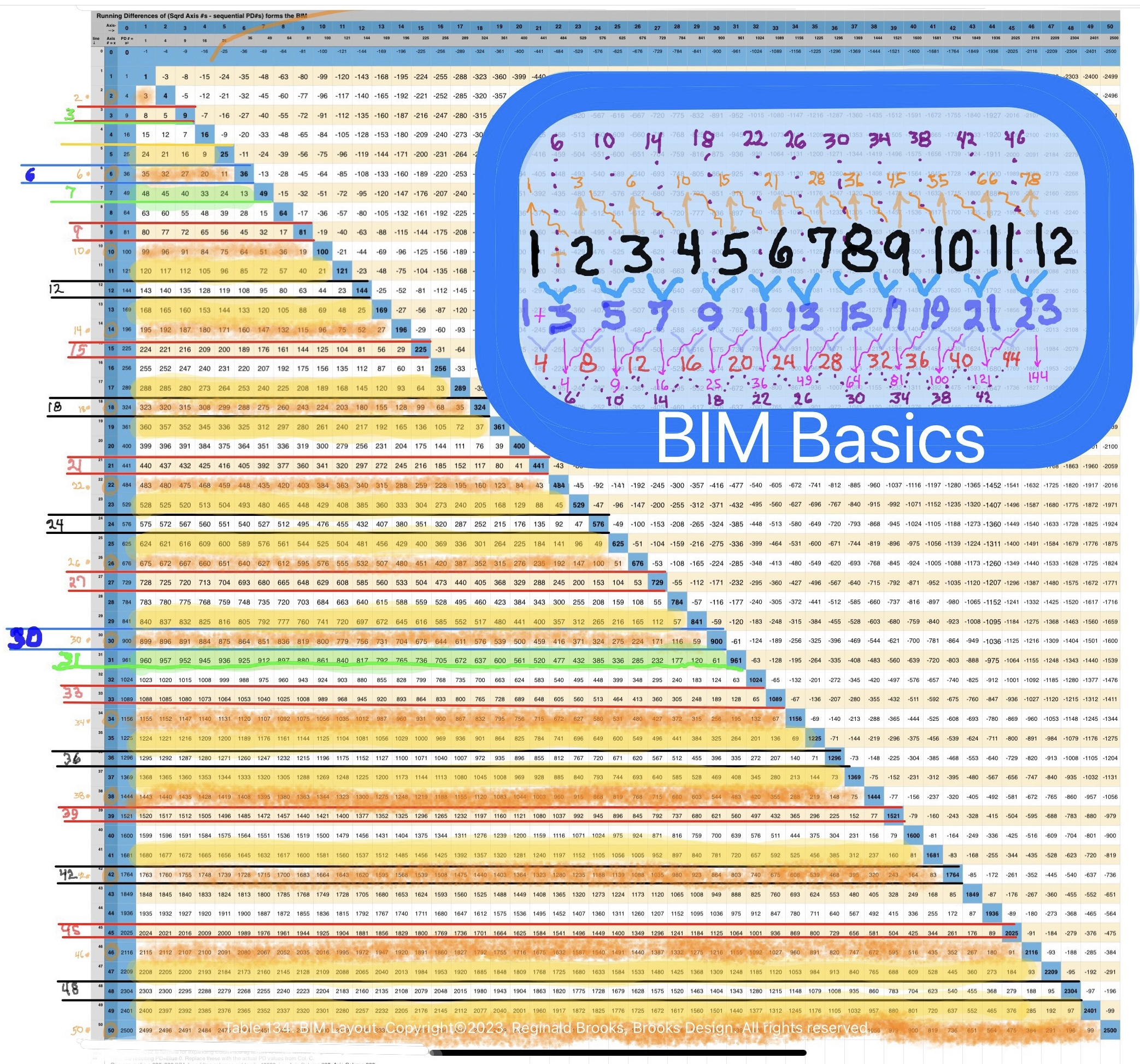
The Horizontal and Vertical Axis contain all the WINs 0,1,2,3,..
The downward Diagonal -- early on referred to as the Prime Diagonal (PD), not because it contains any PRIMES, but rather to distinguish it from the 1st, 2nd, 3rd,.. Parallel Diagonals -- also consists of the Running Sums of the ODD 1st Parallel Diagonal.
The PD bilaterally divideds the BIM into two, mirror symmetric halves.
The PD -- and only the PD -- consists of Squares of the Axis members (1-4-9...)
The Inner Grid (IG) consists of ALL the cells inside of the PD and Axis.
The Strict Inner Grid (SIG) = IG - 1st Parallel Diagonal.
The cells within the IG alternate between ODD and EVEN numbers.
The Parallel Diagonals also alternate between ODD and EVEN.
The 1st Parallel Diagonal consists of the fundamental ODD number series 1-3-5-... and thus also contains -- other than PRIME number 2 -- ALL the PRIMES.
ALL other Parallel Diagonals contain NO PRIMES and ALL EVENS are ÷4
All IG cells consist of the Difference (∆) between Horizontal and Vertical intercepting PD values. This is can be seen as just a restatement of No.2 above.
Going Down a Column or Across a Row: the ∆ between adjacent cell values = the sum of its two Axis values, while the difference down a Parallel Diagonal is a consistent value that = Axis value x2. A very handy tip!
The product of the Diagonals of any two same Axis values intercept on the IG.
It is the nature of WINs that every third number, starting with 3, is ÷3, All others are NOT. Thus every 3rd Row Axis number is ÷3 and is designated as a Non-Active Row (NAR) and never contains a PRIME nor a Pythagorean Triple.
Below the BIM lies the original fundamental "Sub-Matrix 0" -- found by a dividing every IG by the sum of its coordinates -- that lays out simply as 1-2-3-... down each Column from the PD! Example: From PD =16, Column values below in the Sub-Matrix 0 are: 9÷(Row Axis 5+Column Axis 4 ) = 1, 20÷(Row Axis 6+Column Axis 4 ) = 2, 33÷(Row Axis 7+Column Axis 4 ) = 3,... for values 1-2-3.
ALL PRIMES and ALL Pythagorean Triples are found exclusively on Axis Row numbers that strattle either side of an EVEN number that is ÷6 (The rule of 24 = Sub-Matrix 1) as an Active Row (AR).
Dropping down from ANY PD until it intercepts with a Squared WIN on a Row, reveals that Row as containing ALL three sides of a Pythagorean Triple -- with the hypotenuse on the ending PD.
The EVEN numbers NOT ÷4 -- 2-6-10-14-18-22-26-30-34-38-42-46-50-... and NOT on the IG -- nevertheless, like the PRIMES, occupy strategic values within the connection of ALL numbers.
Likewise, the PRIMES -- while only visible on the Axis and 1st Parallel Diagonal -- are present throughout the IG in the form of PRIME PAIR (PP) Sets that symmetrically strattle ALL Axial EVENS, accounting for the sum values of said EVENS. Together these PP Sets, collated as Axial Coordinates (Sub-Matrix 2) , form the Periodic Table of PRIMES (PTOP), revealing a geometric proof of Euler's Strong Form of the Goldbach Conjecture (Every EVEN is made of two PRIMES.).
At this point, it appears that ALL Mersenne Primes exclusively occupy only the higher UPPER AR.
The LARGER VIEW:
One can not over-emphasize enough: The BIM and its subsets of Pythagorean Triples and PRIMES consists simply of the most fundamental additions, subtractions, multiplications and divisions of simple WINs. The Inverse Square Law (ISL) that universally defines the dissipation of an energy expression with distance, does so by:
Forming Fractal and/or Fractal-like Number Pattern Sequences (NPS) that it scales throughout the SpaceTime (ST) continuum from a Singularity to an Infinity.
The basis of these Fractal NPS is to relate simple quantities (expressed as WINs)-- starting with the smallest -- as subsequent, sequential iterations of simple direct additions (or multiplications) of the one and the following, and/or, the Running Sum (∑) of the same + the next in line. Or, by the difference (subtraction or division) of the same such sequence. Yet this simplicity gives rise to richness beyond the imagination!
It is the inherent "quantum" nature of the quantities expressed as WINs that this fractal expression is particulate, i.e. each fractal iteration is both self-similar and redundant, and is also fully expressed -- or contained, if you will --as an entity that nevertheless is fully dependent on its past and future iteration(s), forming as such a wave! The wave-particle duality is built in.
So be it that the Fractal NPS forms an expressive "container" that is built upon and holds all that that resonating form has to give, NOT every subset expression -- e.i. the Pythagorean Triples or PRIMES (especially the Mersenne Primes) resonances -- will necessarily present or "fill" within such "containers." Some to most times, blanks are shot! The larger set (BIM) presents the larger set of resonances within which the various smaller subsets (PT, PRIMES) resonances are expressed. A most important finding that without its appreciation, the Fractal NPS of such subsets would not be evident!
If one invests in the study of simple WIN relationships with the freshness of a child, one gains a lifetime of rewards!
~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~
BIM-MPS-Outline-LINKS.html Outline -- LINKS to the BIM-MPS Series

Portfolio of Reginald Brooks

Copyright©2023-25, Reginald Brooks, Brooks Design. All rights reserved.

