The Butterfly Fractal 1; copyright©2022, Reginald Brooks, Brooks Design. All rights reserved.

An ODD Tale.

So, this ODD fellow, all by himself, walks into a bar. A bar you might remember?

“So, what’ll you have?” says the bartender.

“What I want is just a double — of me!” replies the ODD with a little smirk on his face.

“Come on, give me a break, fella!” barks the drink sloshier. “A double of what?”

“A double of me! Look, I am simply a one. Quantity one. I want you to double me. Duplicate me. Replicate me. Reiterate me. Just make two self-similar, identical ones to make a double. An EVEN!” scratched out the lonely one. “And can you serve them up on the table just behind me?”

“Double it is — coming up! Two identical ones — a pair — and right over there!” beeps the bartend. “And what, might I dare ask, are the two ones — better known as the first EVENS — going to have?”

ODD one leans over the bar, kicks back his hat, and wanes, “Well now, I don’t suppose you would wage a guess, now would you? How about this: each of the replicate ones naturally wants to order up duplicates — doubles — of themselves, and wouldn’t you know it, they would like you to serve them at the table behind them!”

“Well, I’ll be dipped!” exclaims the barkeep, choking back the tears of astonishment. You see, he had been through this number journey before and found then — and apparently now once again — that the simplest arrangement of numbers — of quantities — can lead to profound, unimaginable richness. Such was the case with the Mersenne Primes and Perfect Numbers culminating in the Mersenne Prime Squares (MPS).

“So each successive table will have duplicates — doubles — of each of the ones from the table before?” he sobbed.

“That’s right,” said the ODD one, “a whole sea of identical ones grouped into successive groups of EVENS!

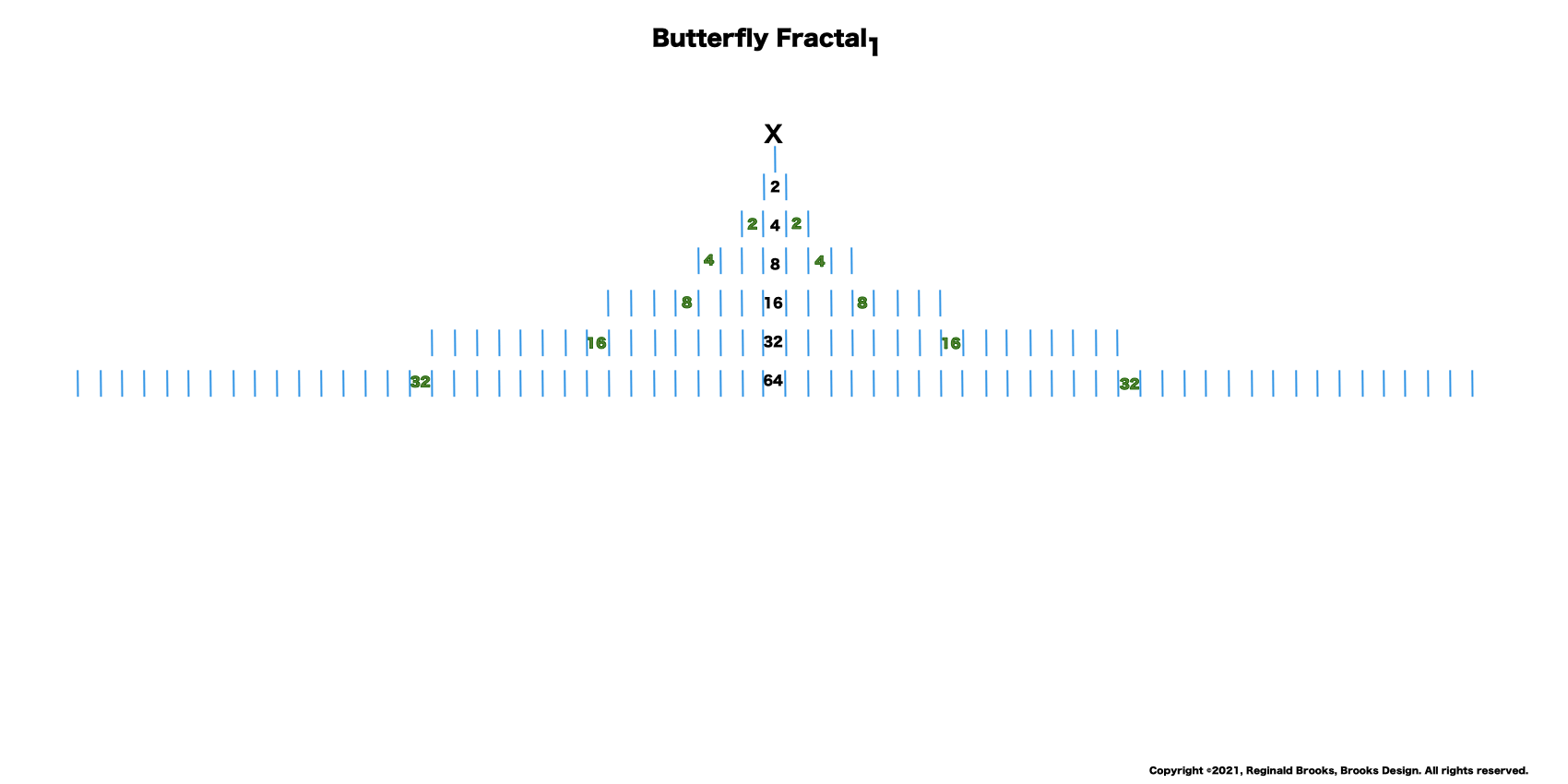
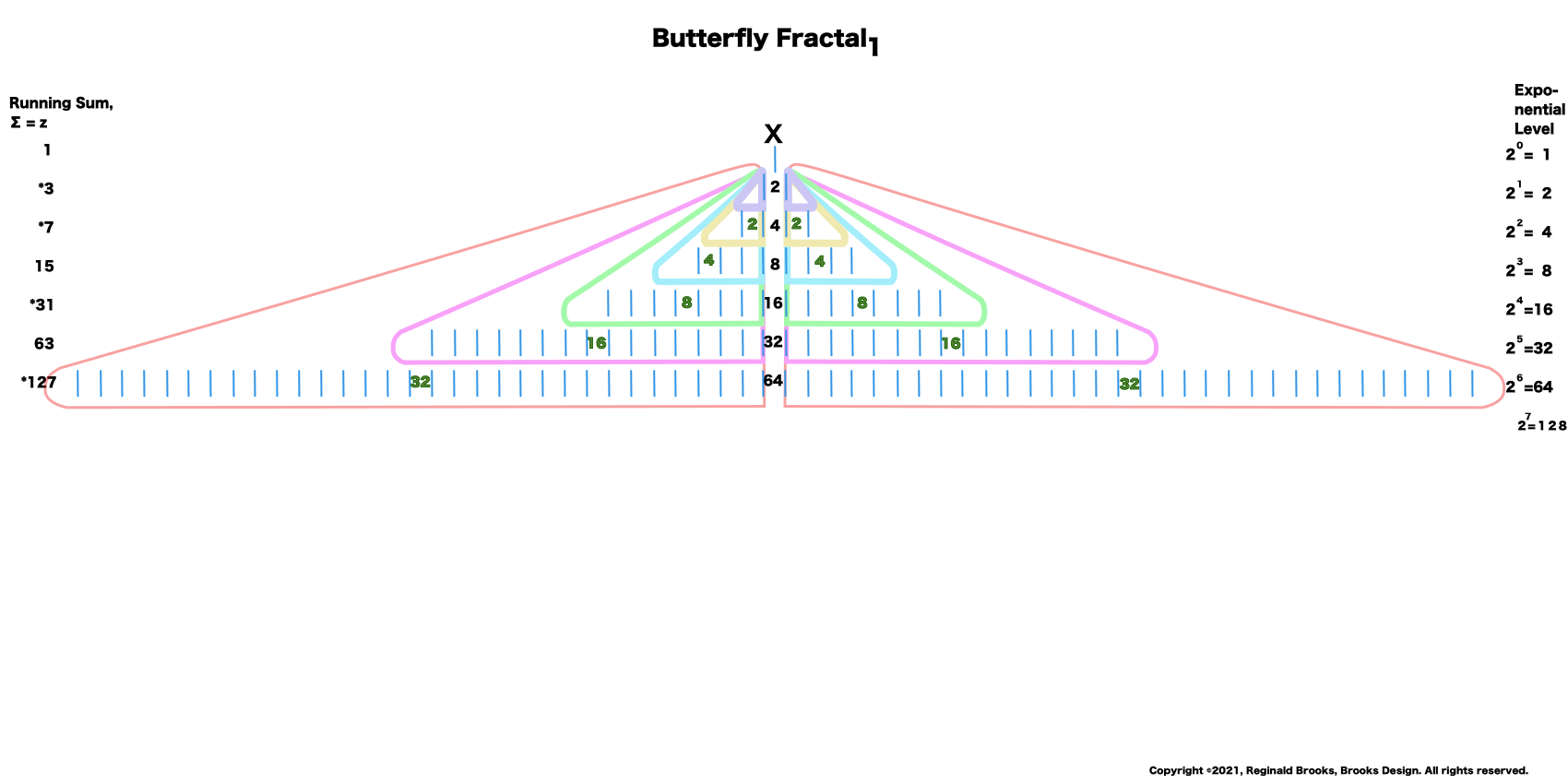
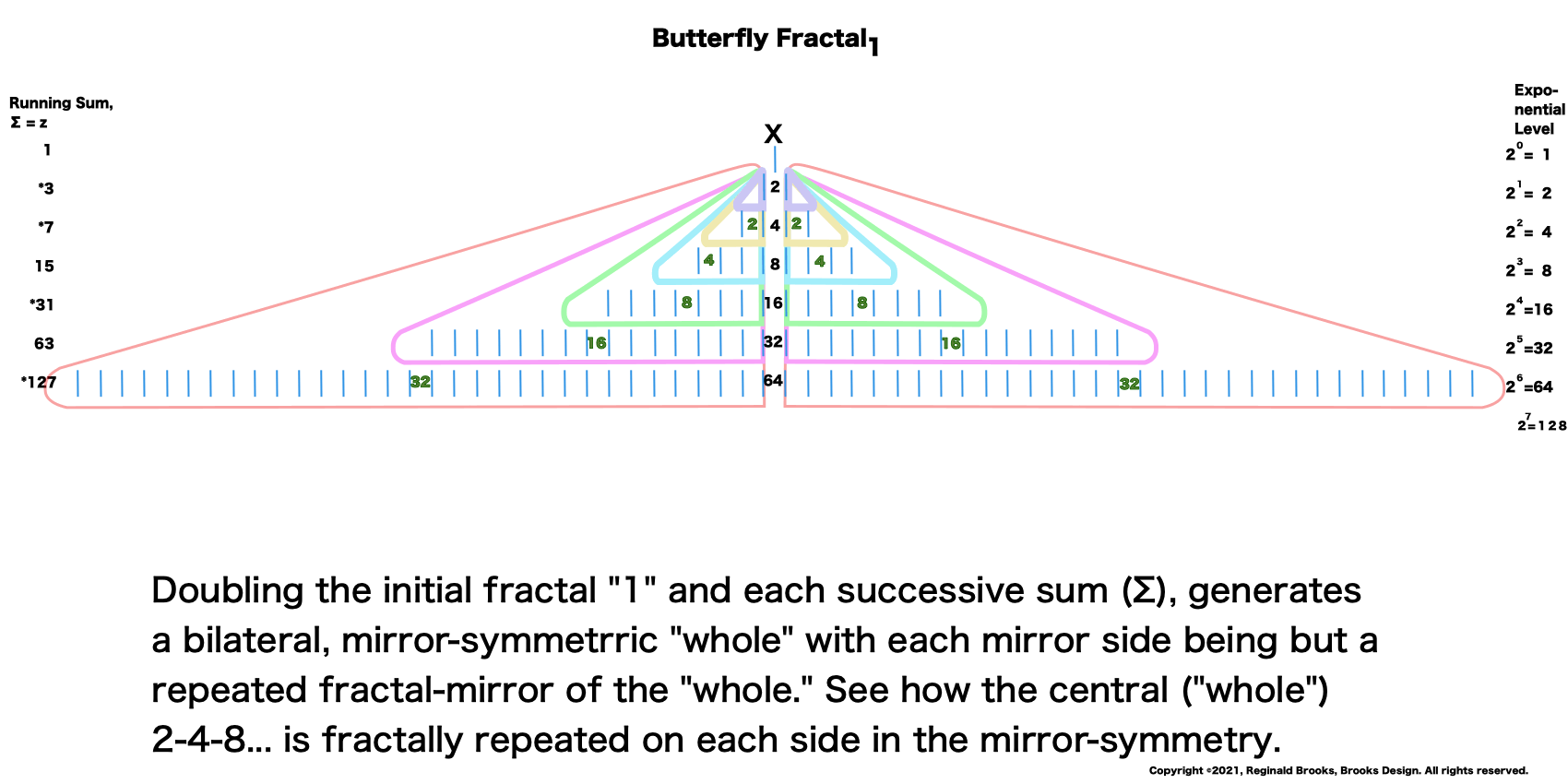
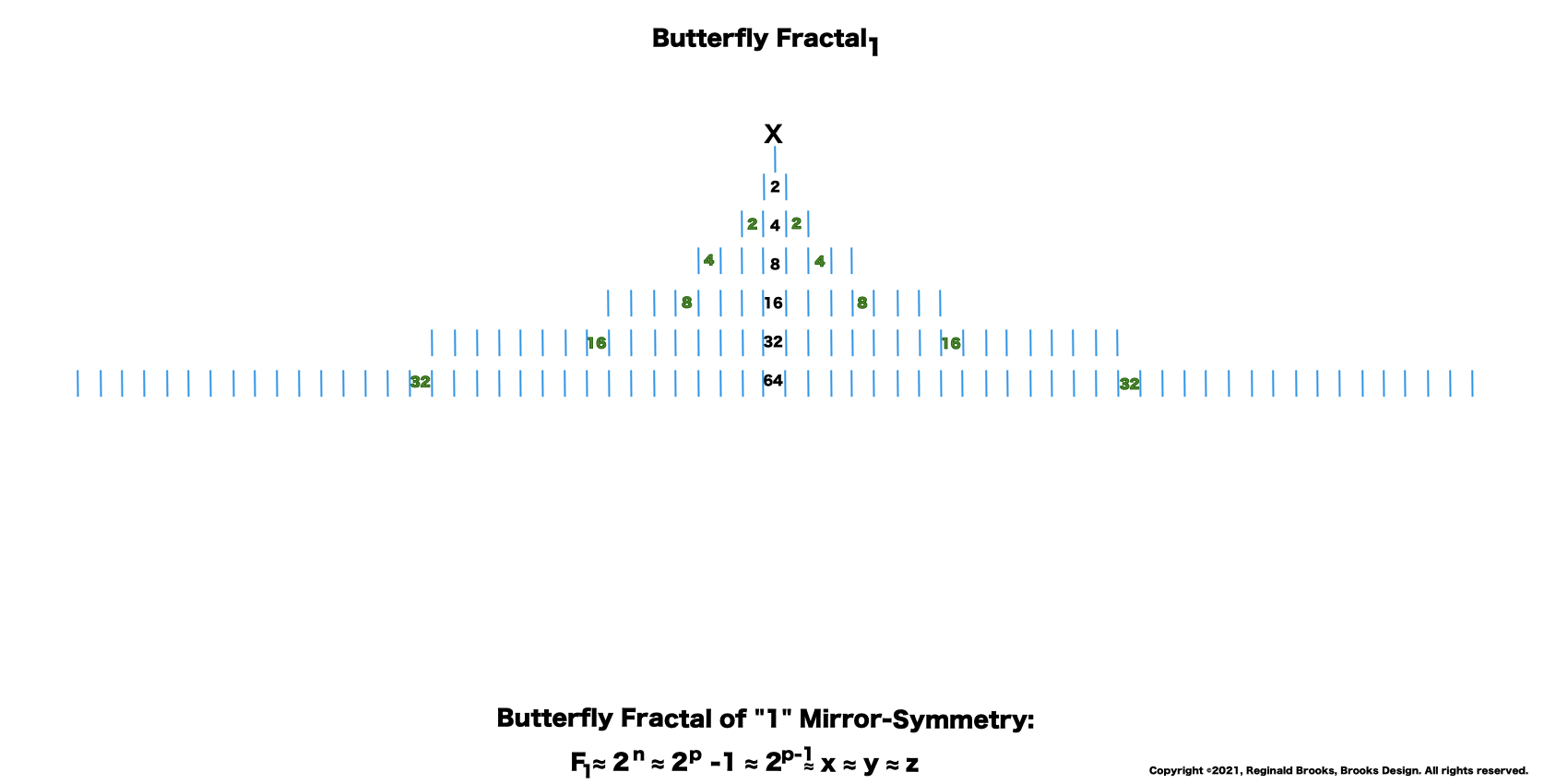
“I get it! I get it!” shrieked the bartend. “Its a fractal. Indeed, a whole series of self-similar, redundant, reiterative ones doubling to twos and the twos double to fours, the fours to eights, the eights to sixteens, and on and on! This must go on to infinity! And right here in my own bar!”

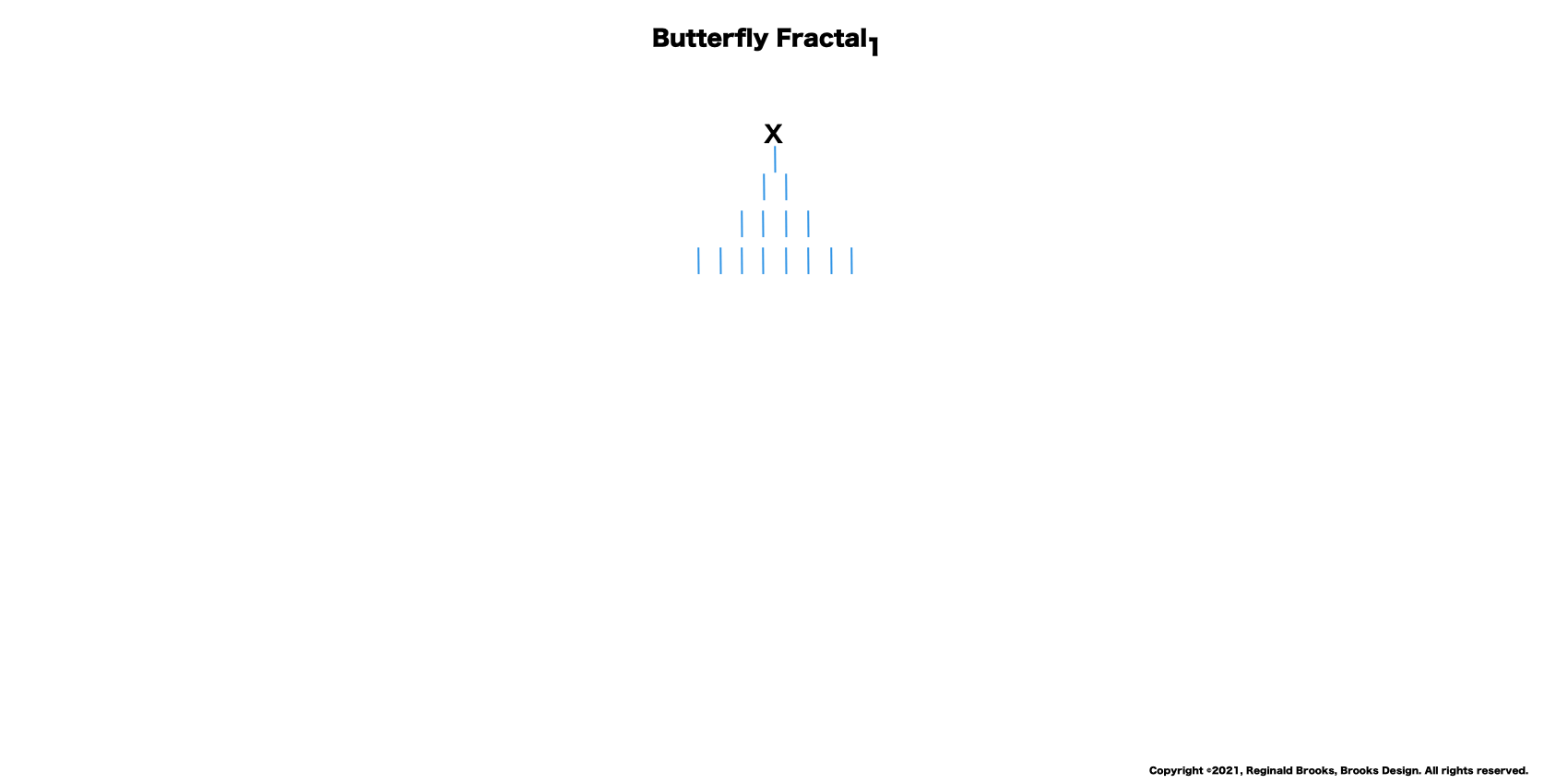
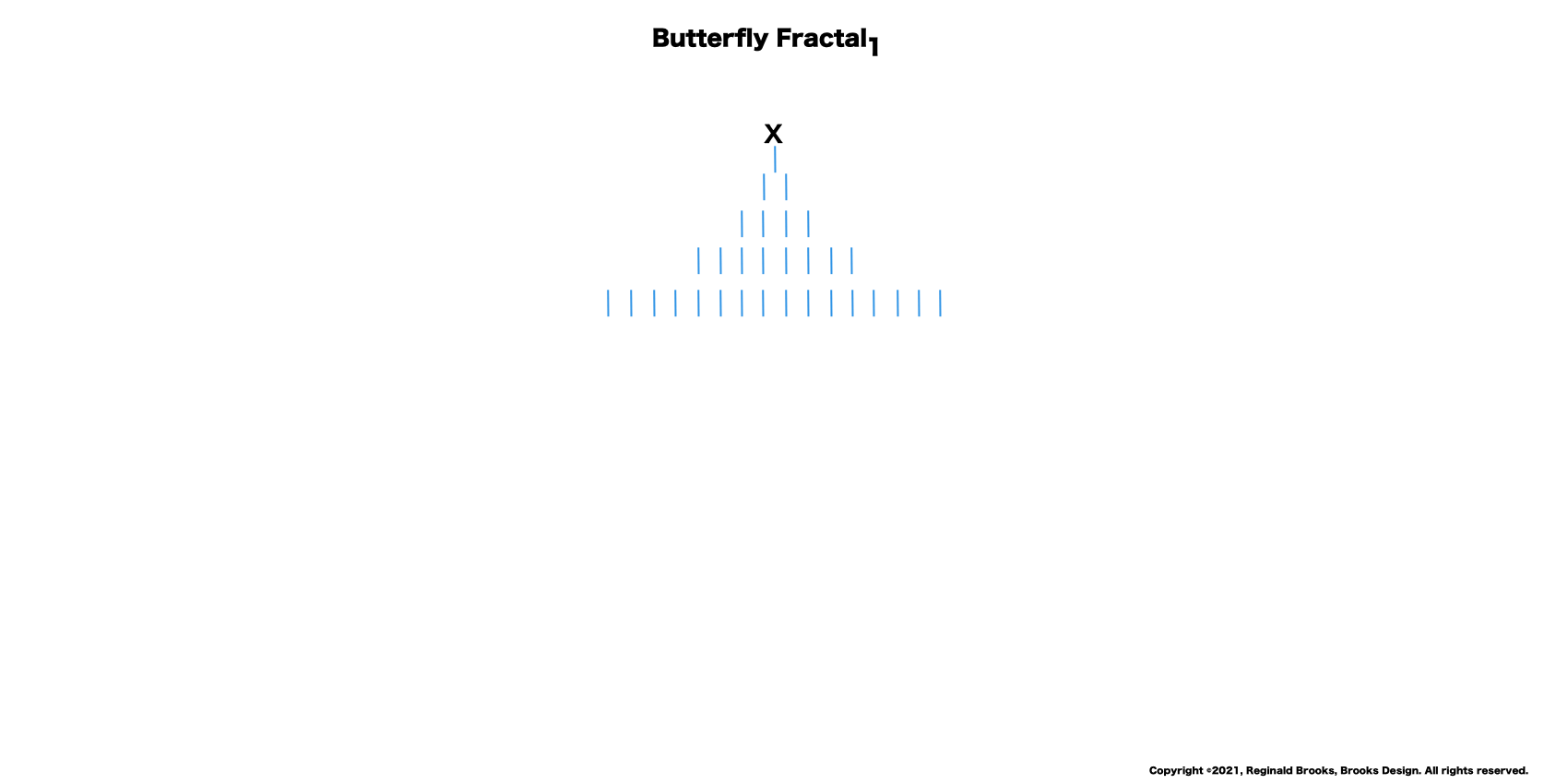
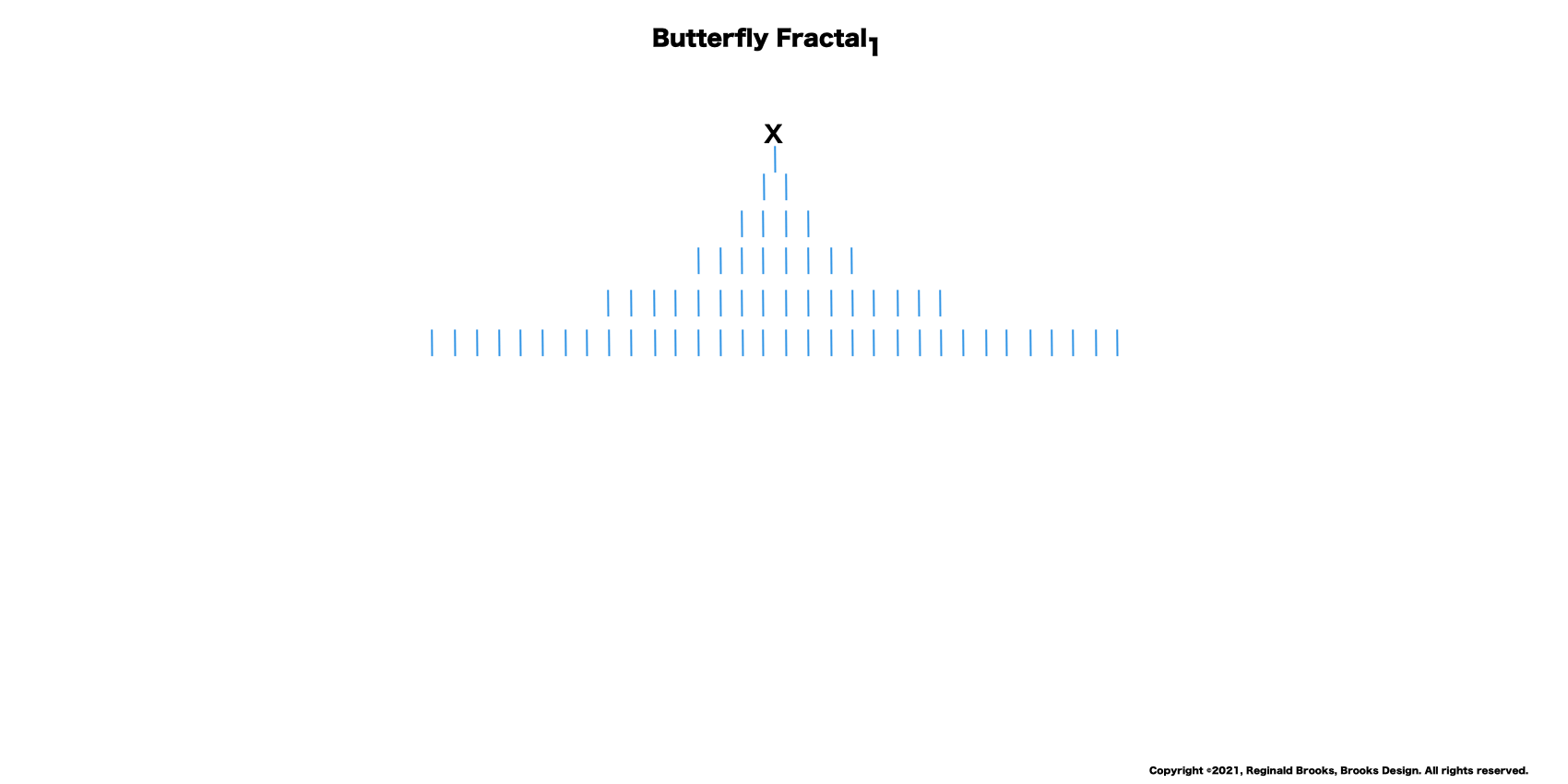
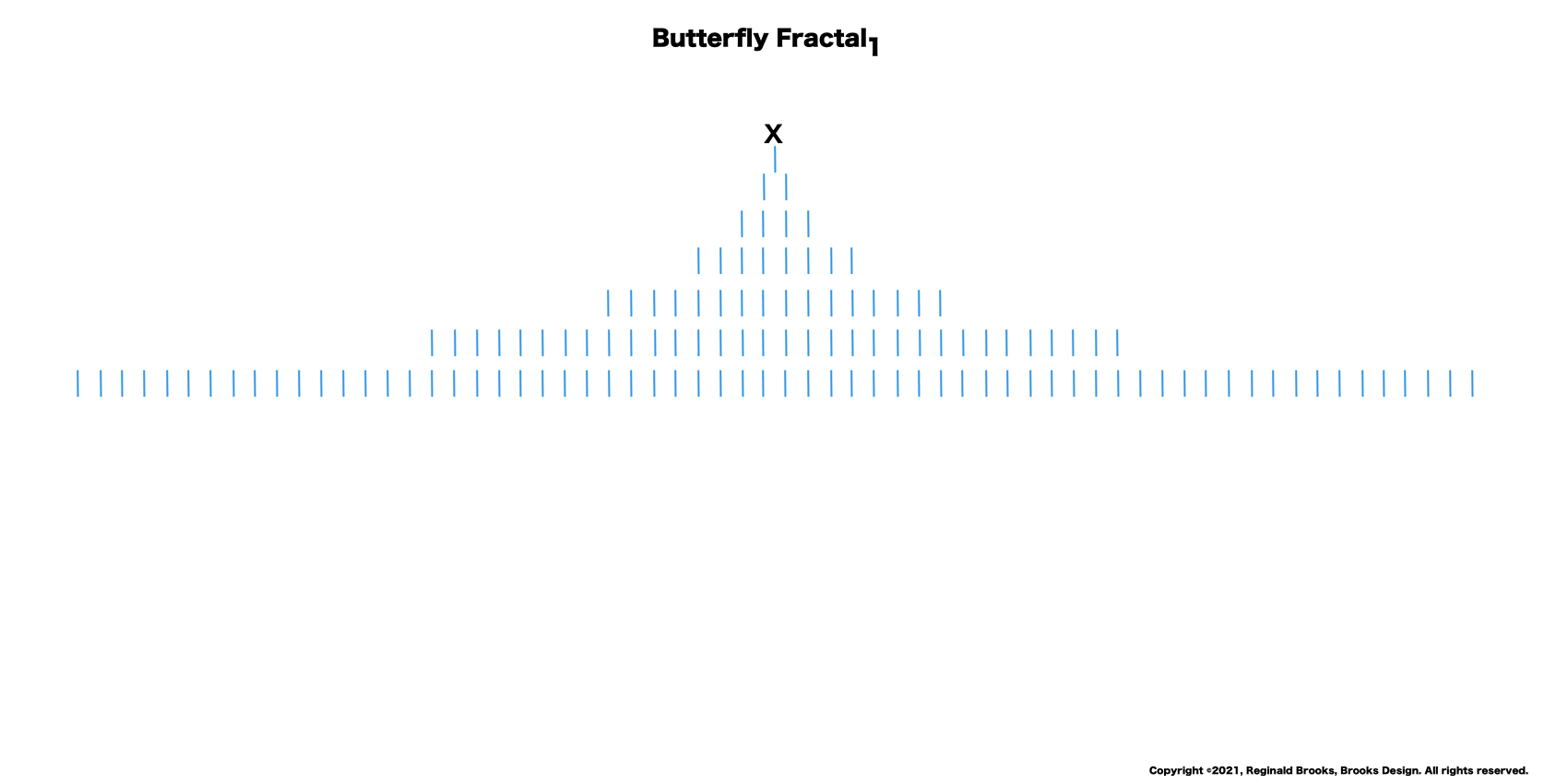
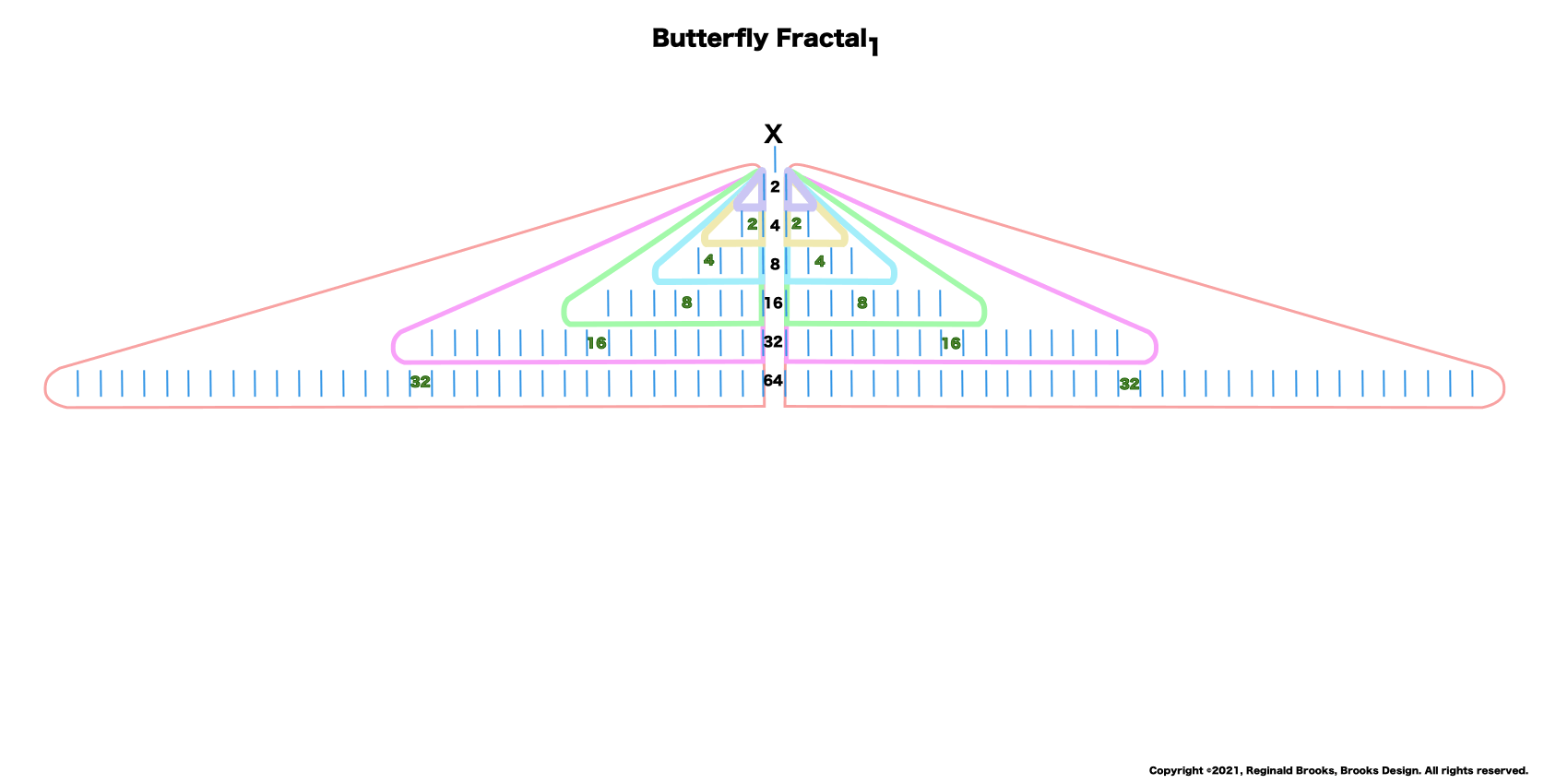
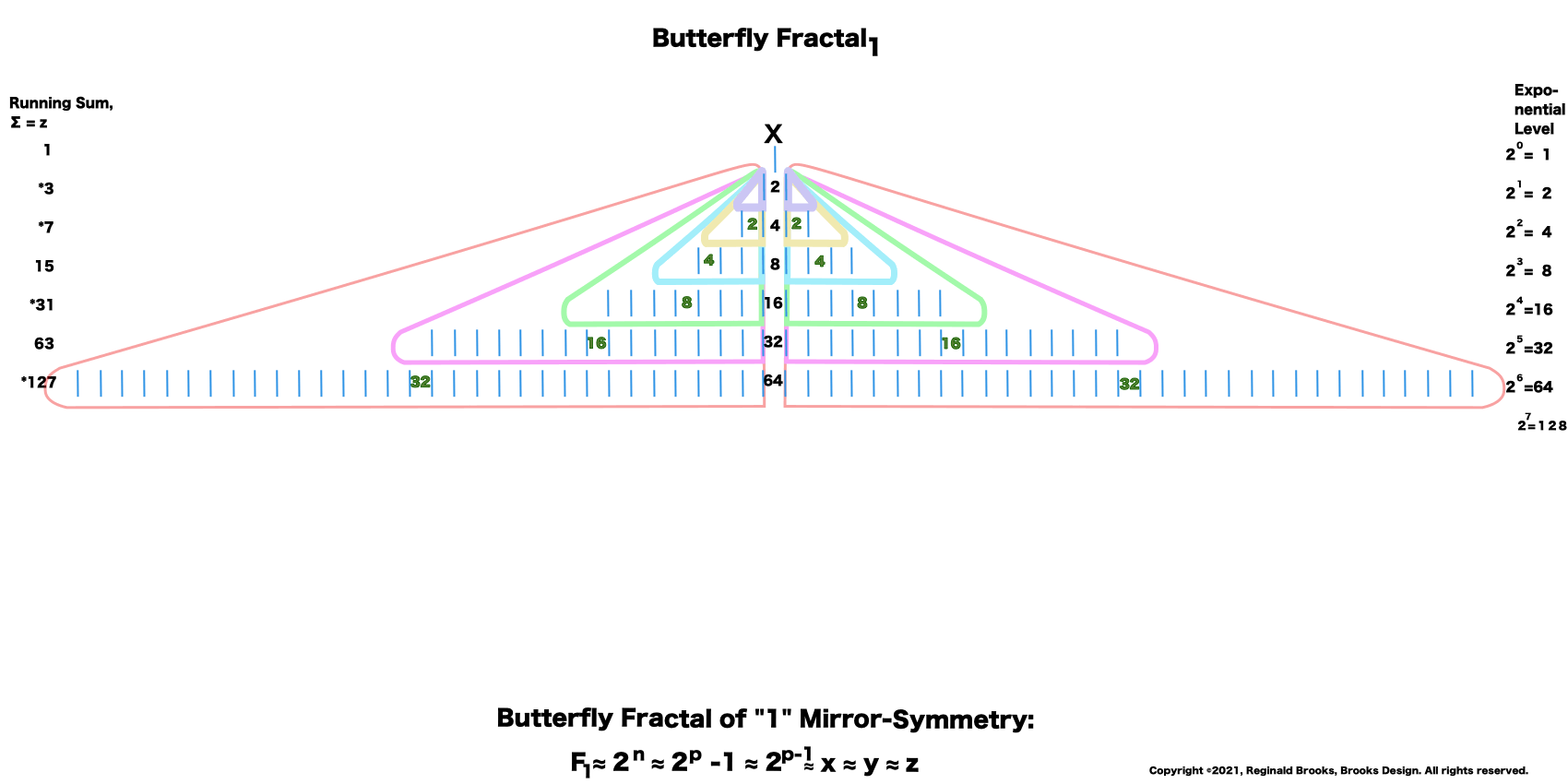
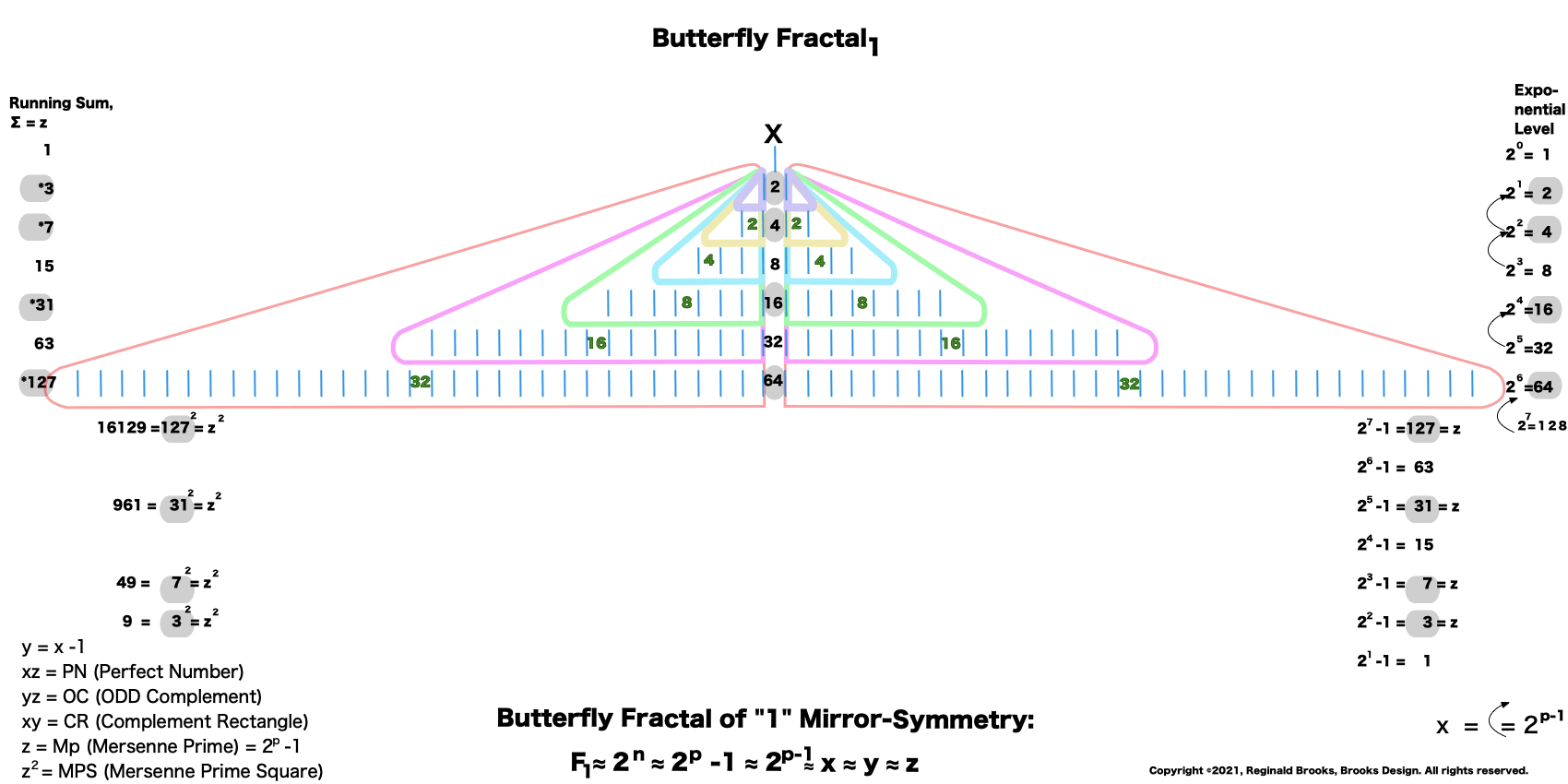
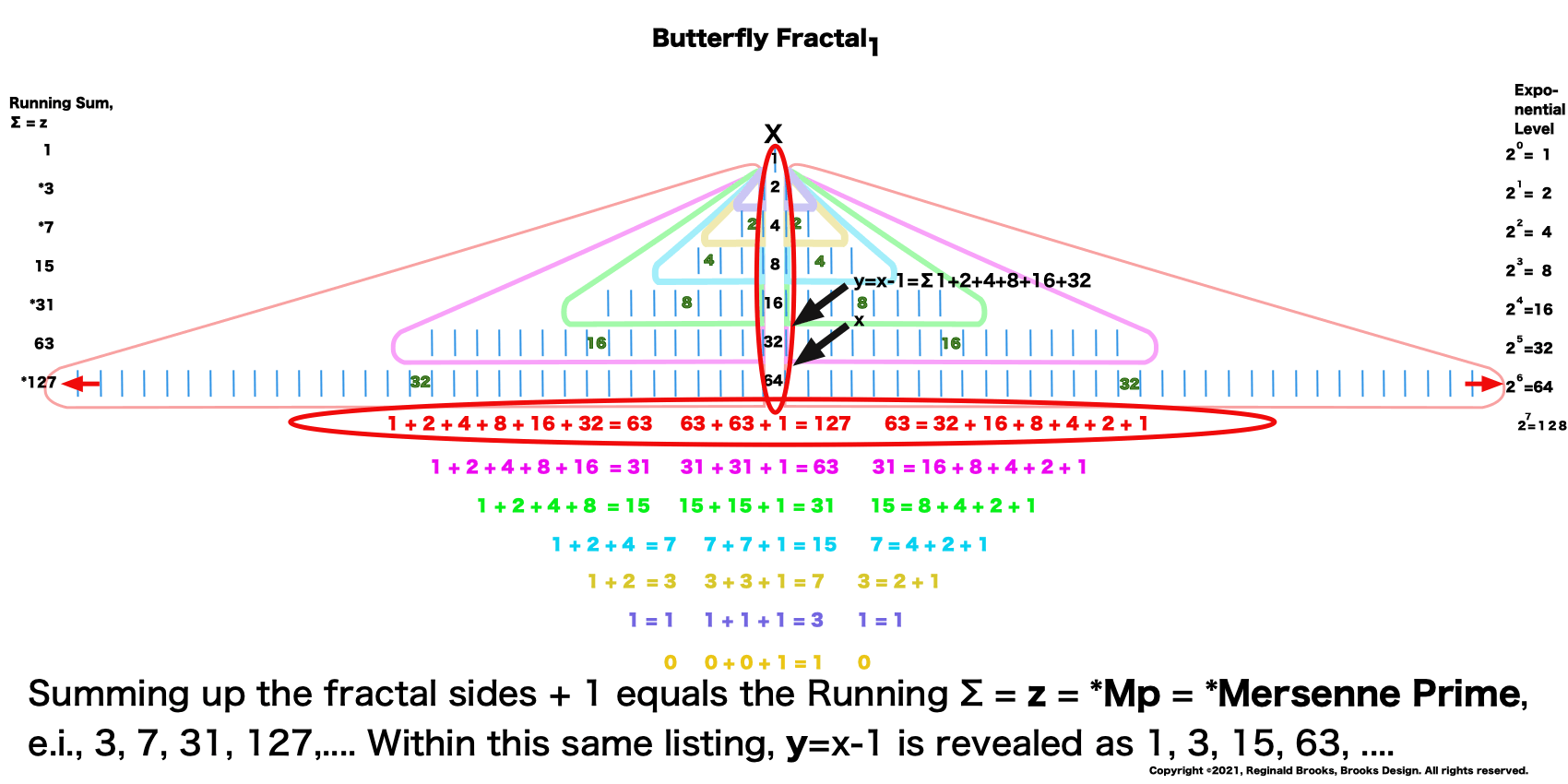
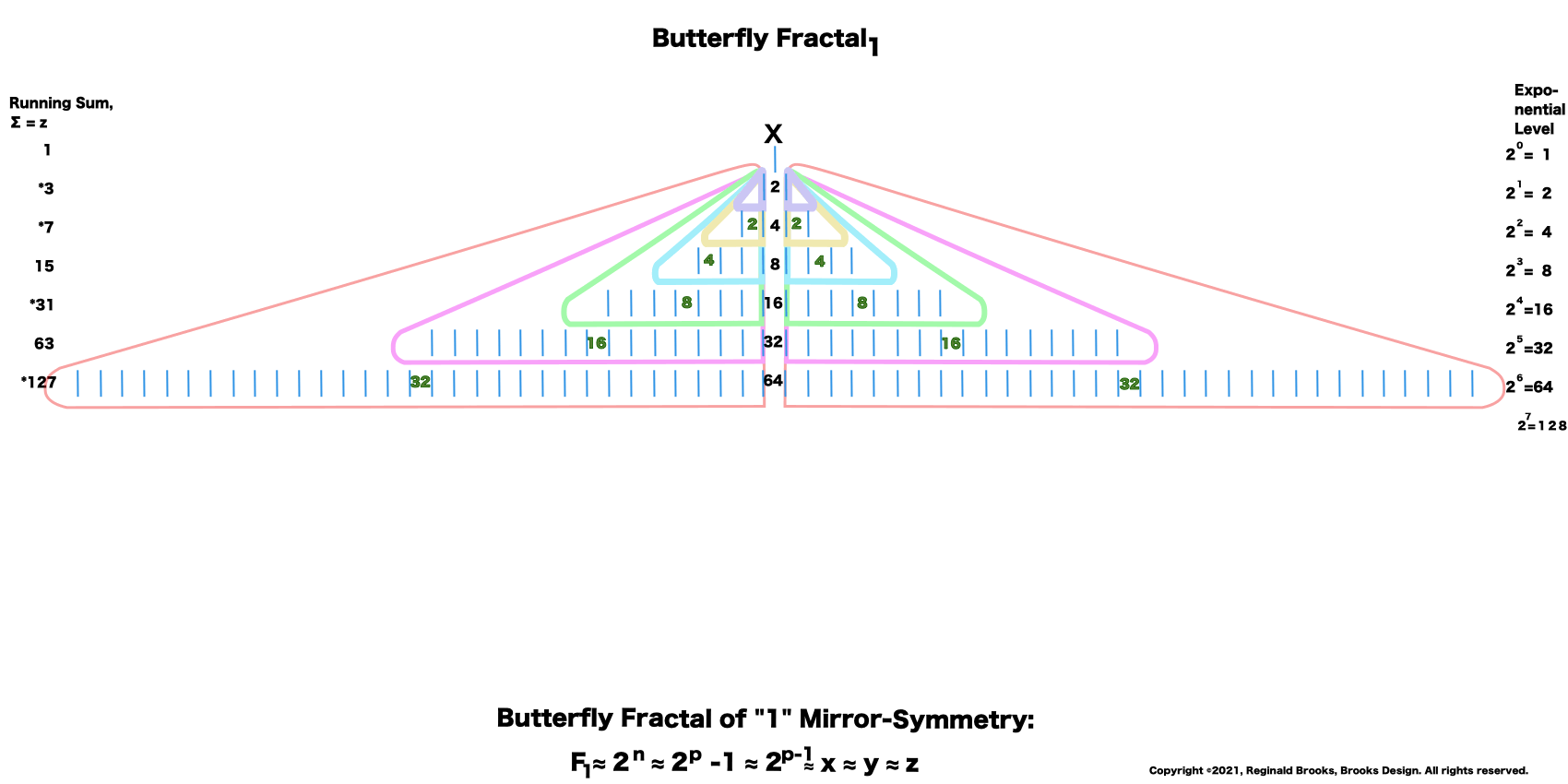
“Well, my friend, hold on to your hat, because we are just getting started. That’s just the half of it. Just as every EVEN two is made up of two identical ODD ones (me) as they expand out forming a butterfly-like pattern — The Butterfly Fractal 1 — when we add them all up at each table, we find that every successive table is simple double the total EVENS from the table before: (1)—2–4–8–16–32–64–128–256–512–1024–…” says ODD.

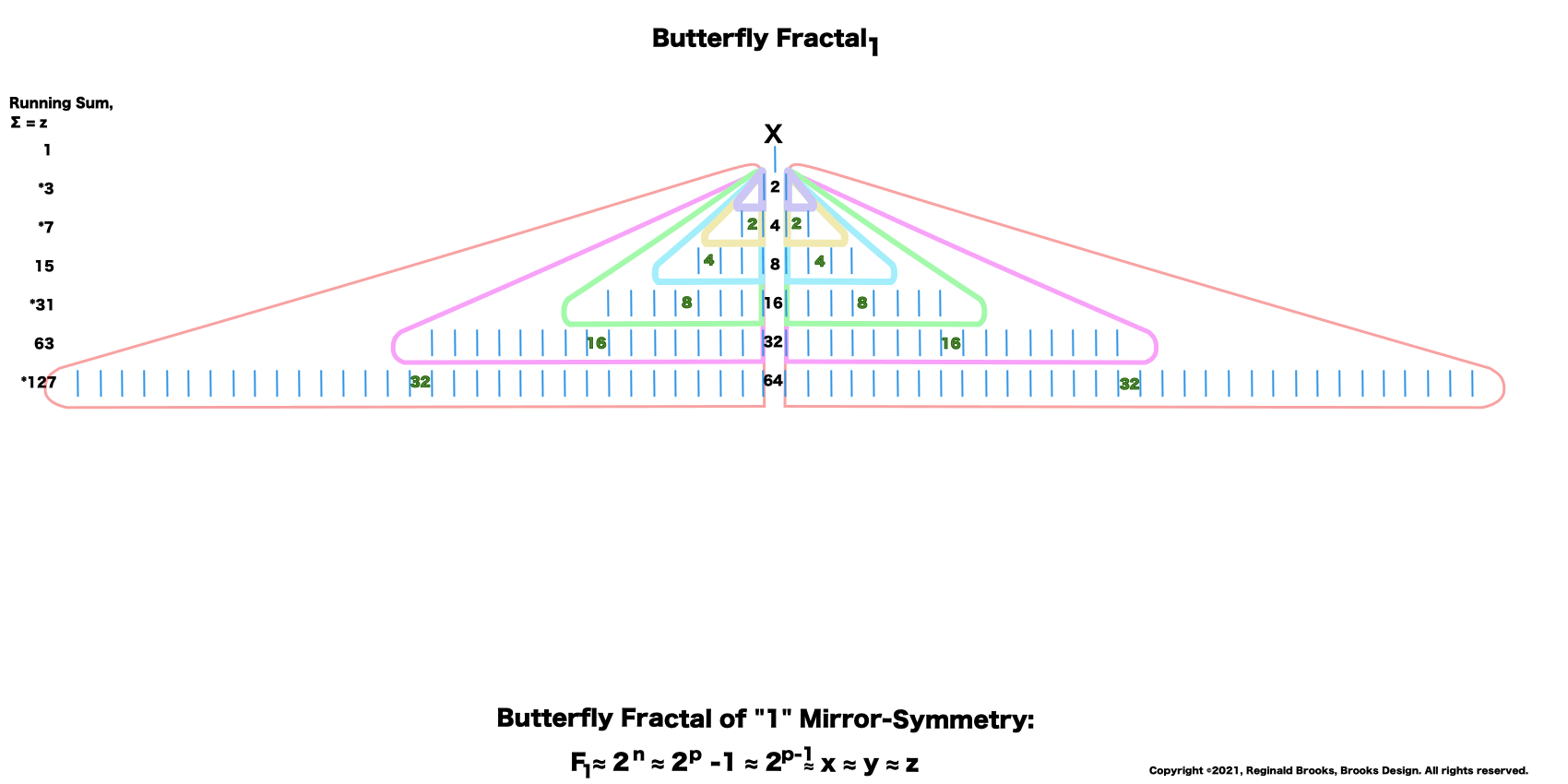
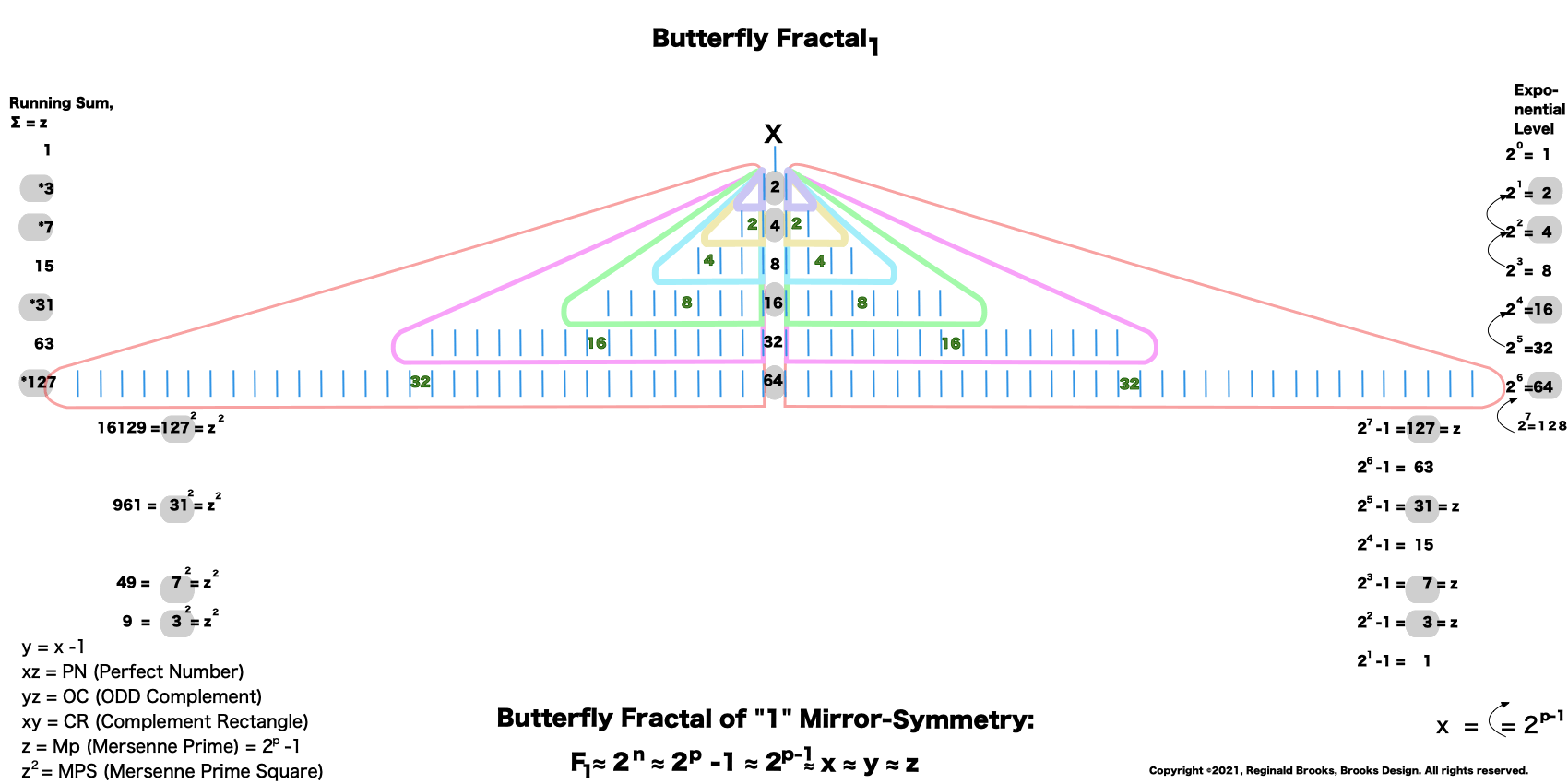
“And now for some of that magic! If you add me (1) to the first table( of 2) you get 3, then add that total to the next table (of 4) to get 7, that total to the next table (of 8) you get 15, and that to the next (of 16) to get 31, and so on. This is called a “running sum, ∑” and gives us that richness we want. You see, the 3–7–31 are the first 3 Mersenne Primes!”

“Holy Rollie, Mother of God, down on your knees,… what’s next, the Perfect Numbers?” howled the barkeep.

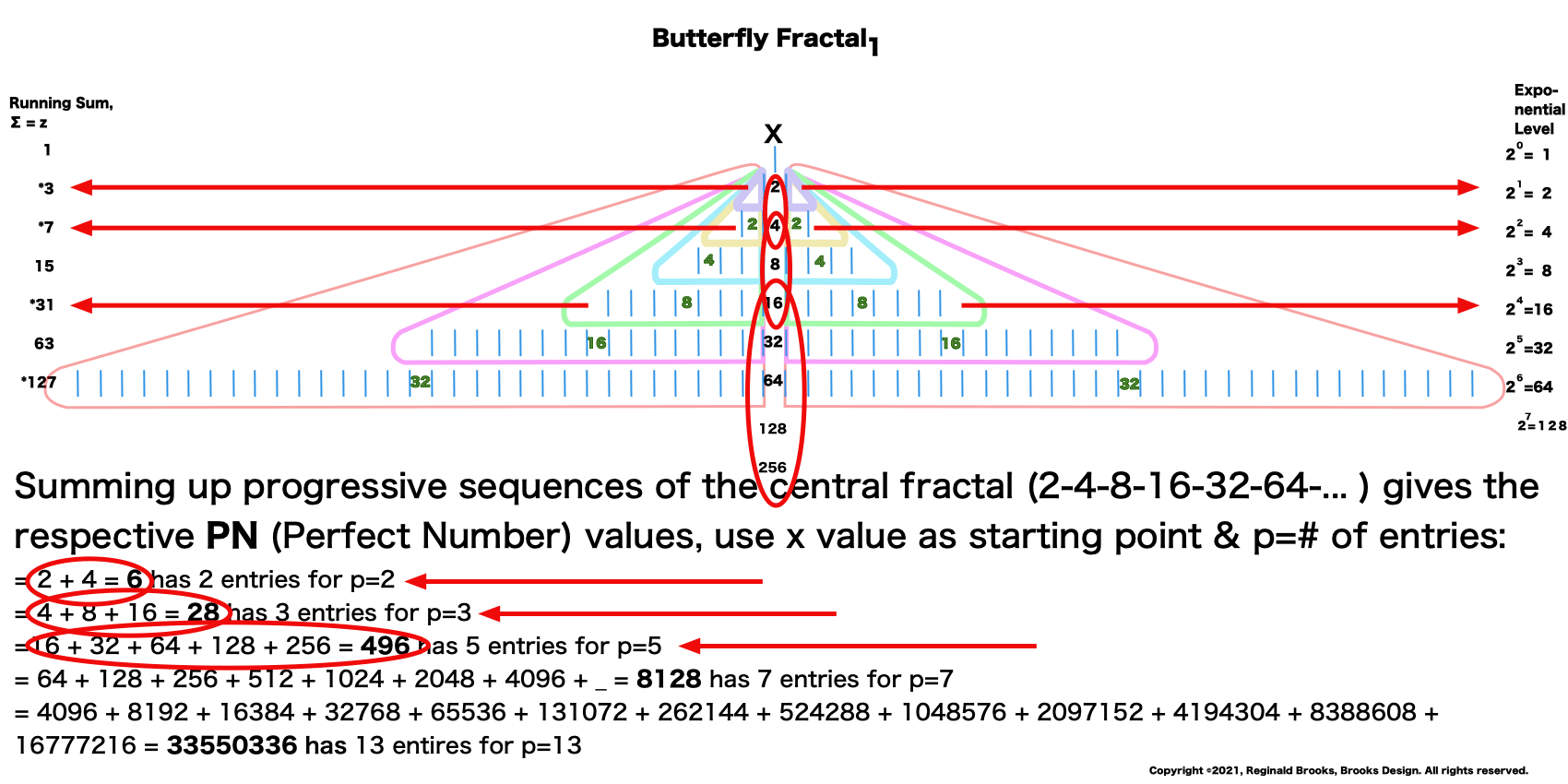
“Well, a simple “cool” would do, but now that you mentioned it, yes we also can get the Perfect Numbers (PN) that go with each of the 51 known Mersenne Primes (Mp)!” one replied.

“Cool,” replied the barkeep nonchalantly.

“If you do a limited running sum (∑) of the table sums of EVENS, it equals the Perfect Number. A couple of examples: 1. ∑ 2–4 = 6 the PN of Mp 3; and 2. ∑ 4-8-16 = 28 the PN of Mp 7.

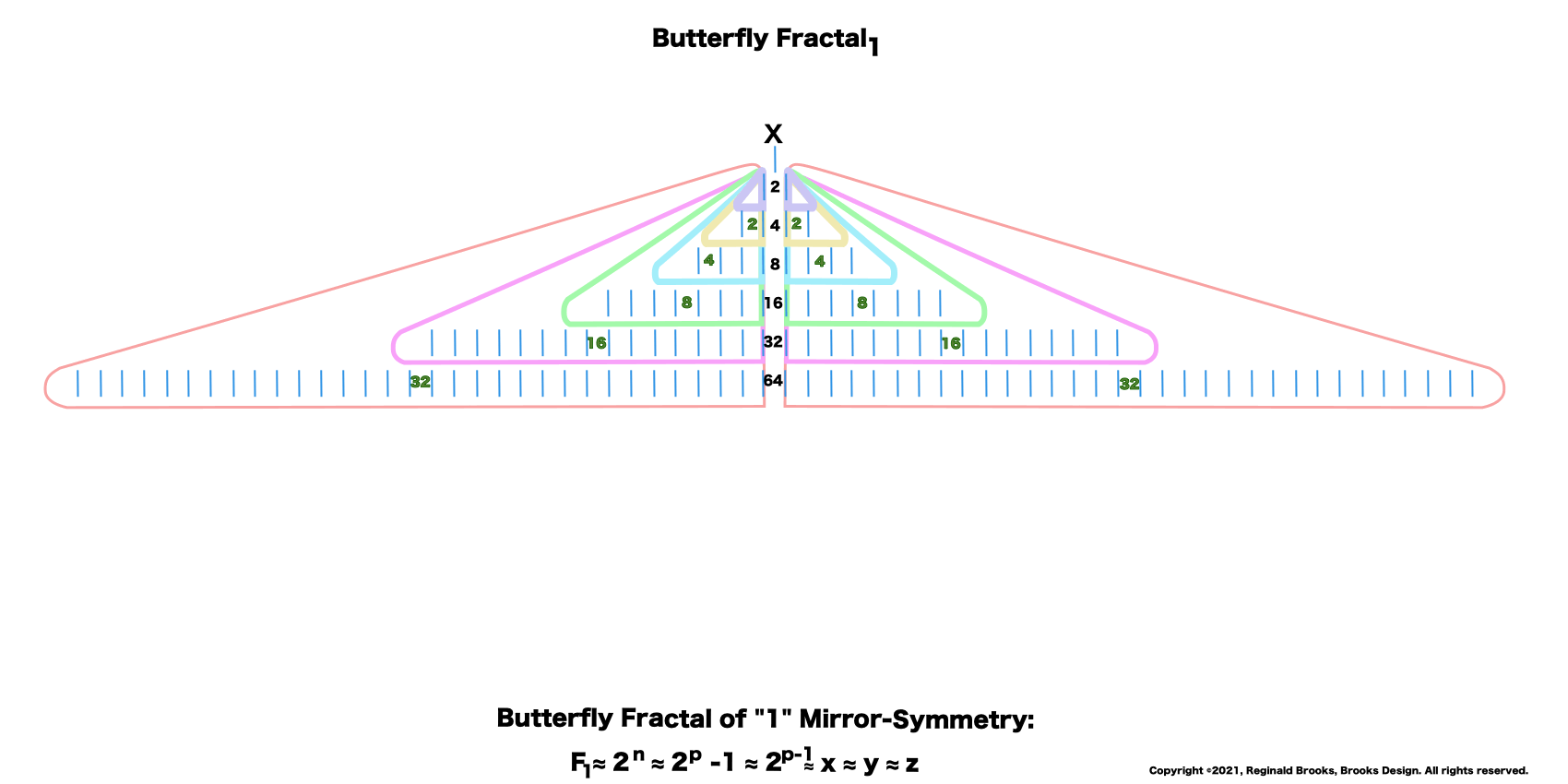
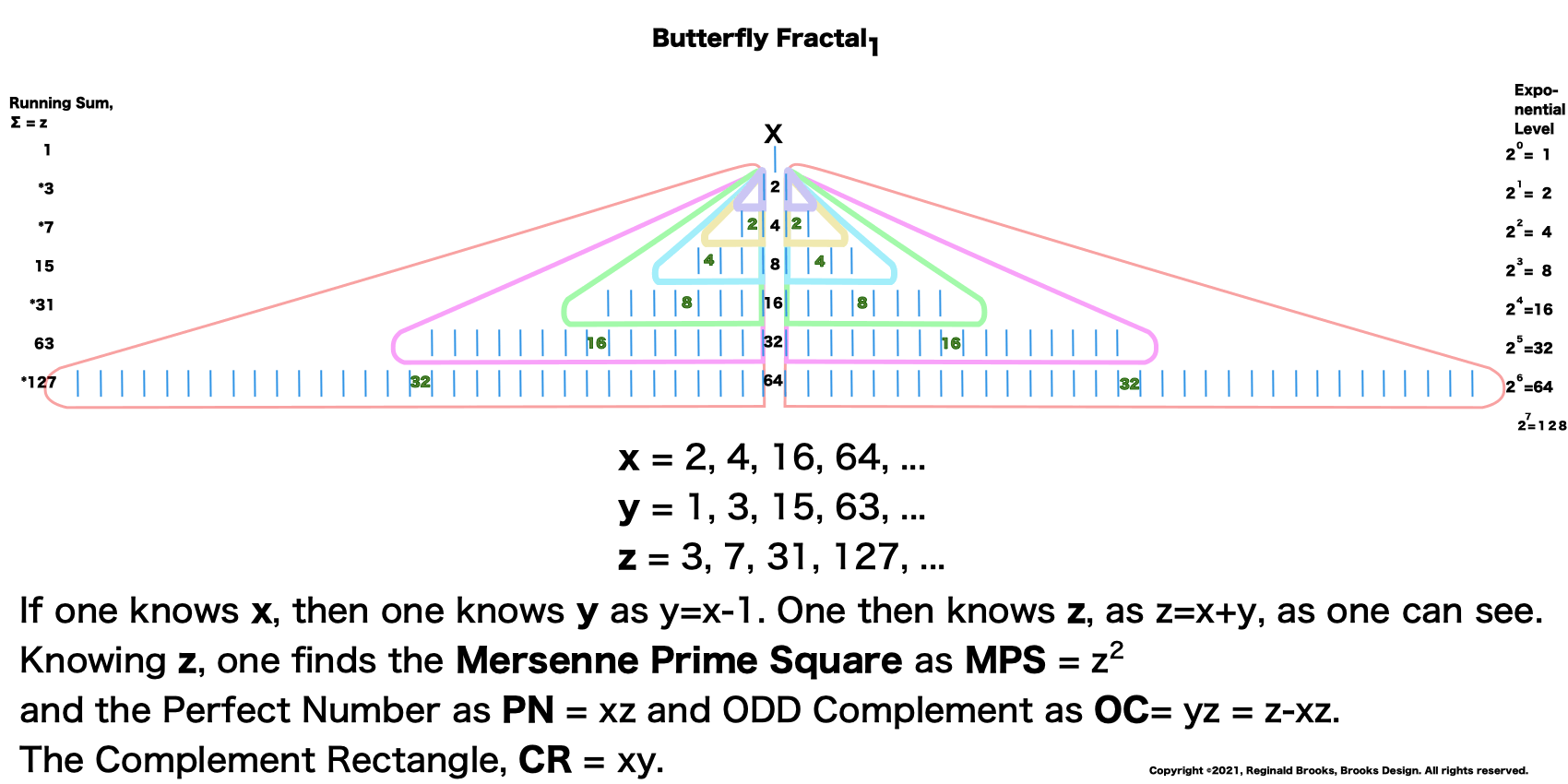
“And,” continued the ODD one, “All the parameters of the MPS — x—x² —y—y² —z—z² —xz—yz—xy — can be found by similarly simple means directly from this very simple doubling of the quantity one! Now that is simply amazing!”

“Phew!” exhaled the bartend, “and we haven’t even left the 2Dimensional plane!”

“Well, hold on to your pants!” said the ODD one. “The running sum (∑) of the cube of the ODDs will give each and every Perfect Number (>6), too! 1³ + 3³ = 1 + 27 = PN 28 and 1³ + 3³ + 5³ + 7³ = PN 496, yet each of these 3D versions can be simply rotated back into the 2D plane, confirming the priority of the simple plane geometry in establishing the structural backbone, itself tied to the linear, 1D form of the line.”

To wit the bartend added, “It seems, quite simply, that every ONE counts!”

IMAGES

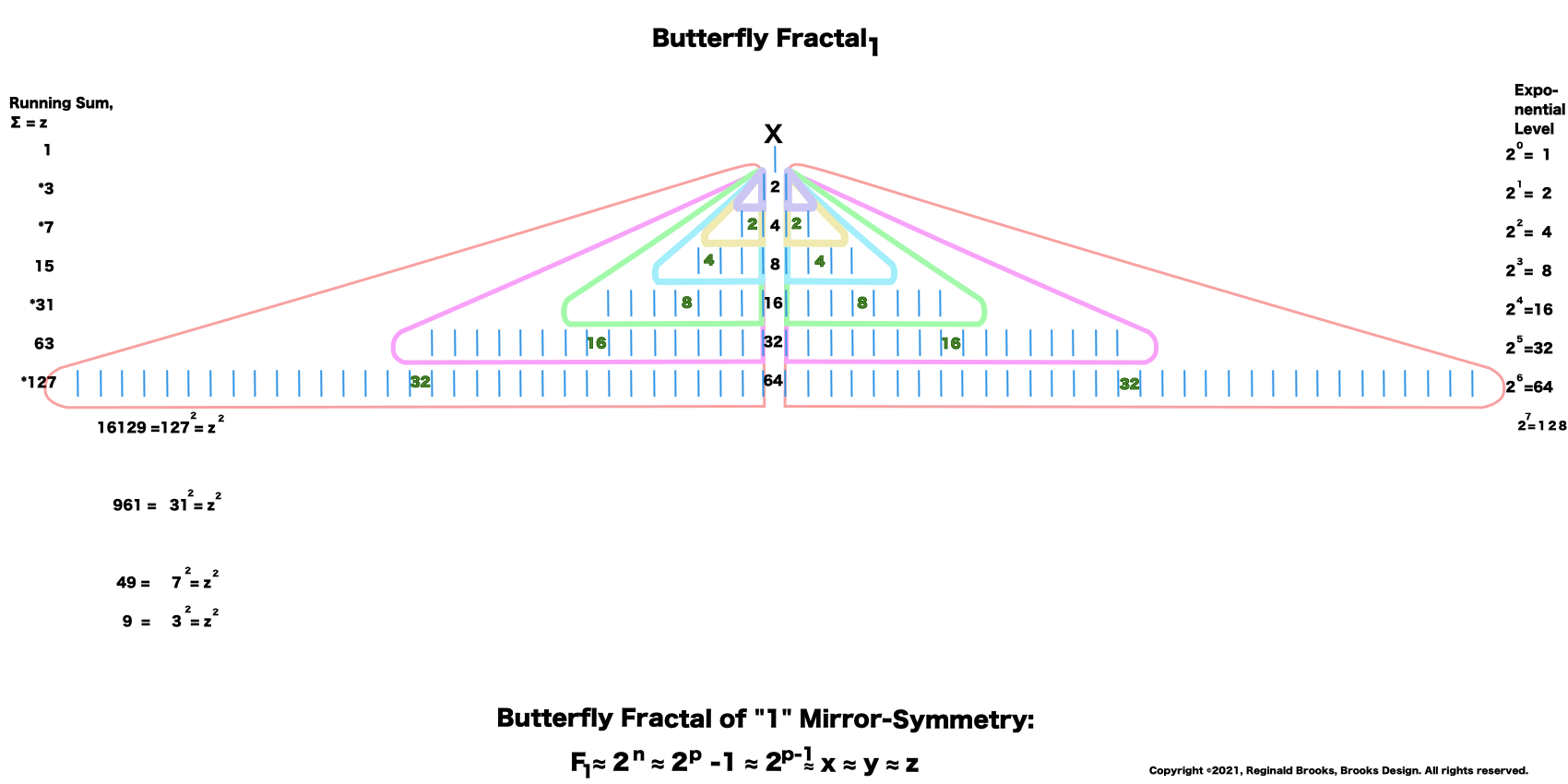
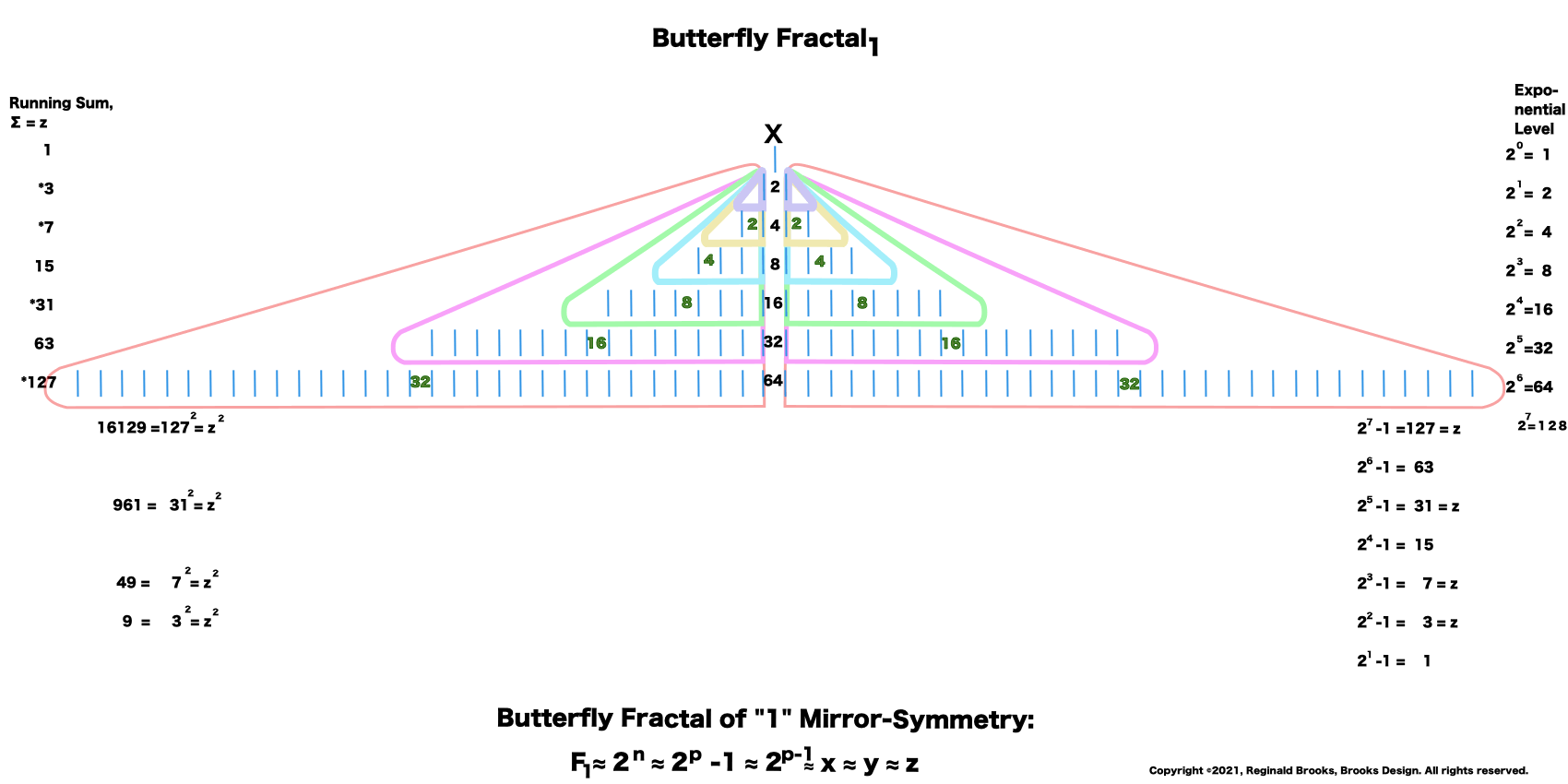
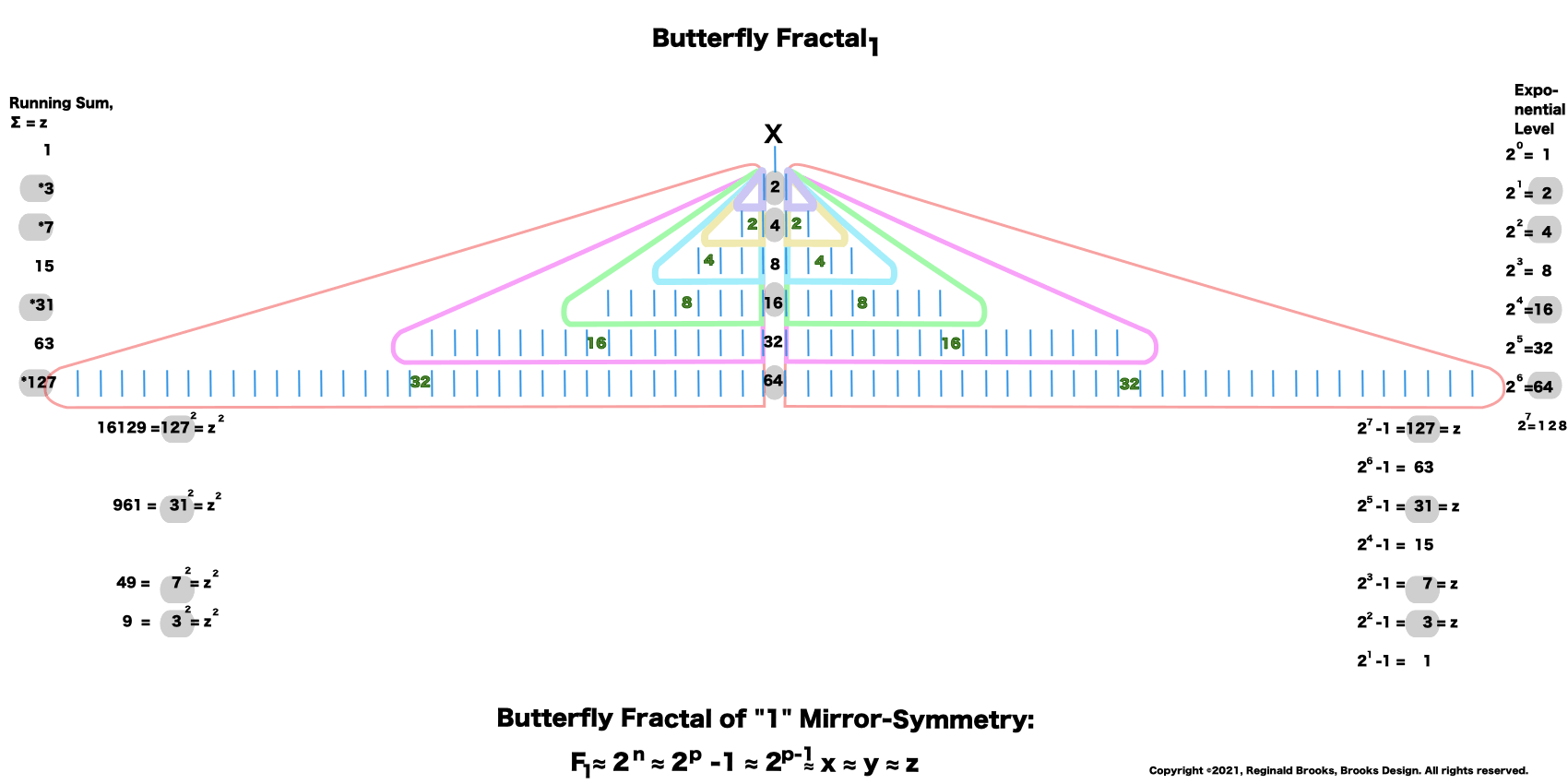
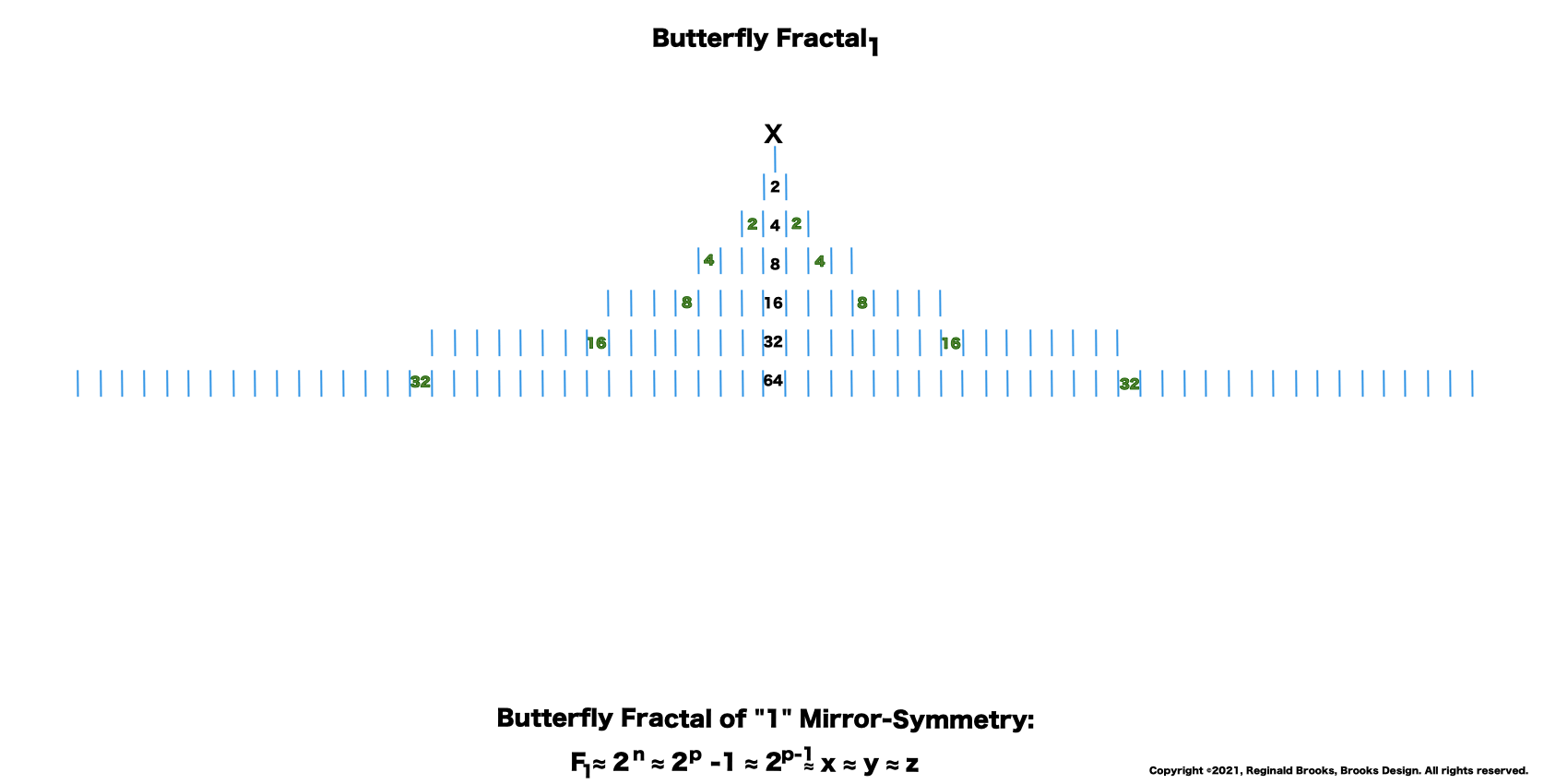
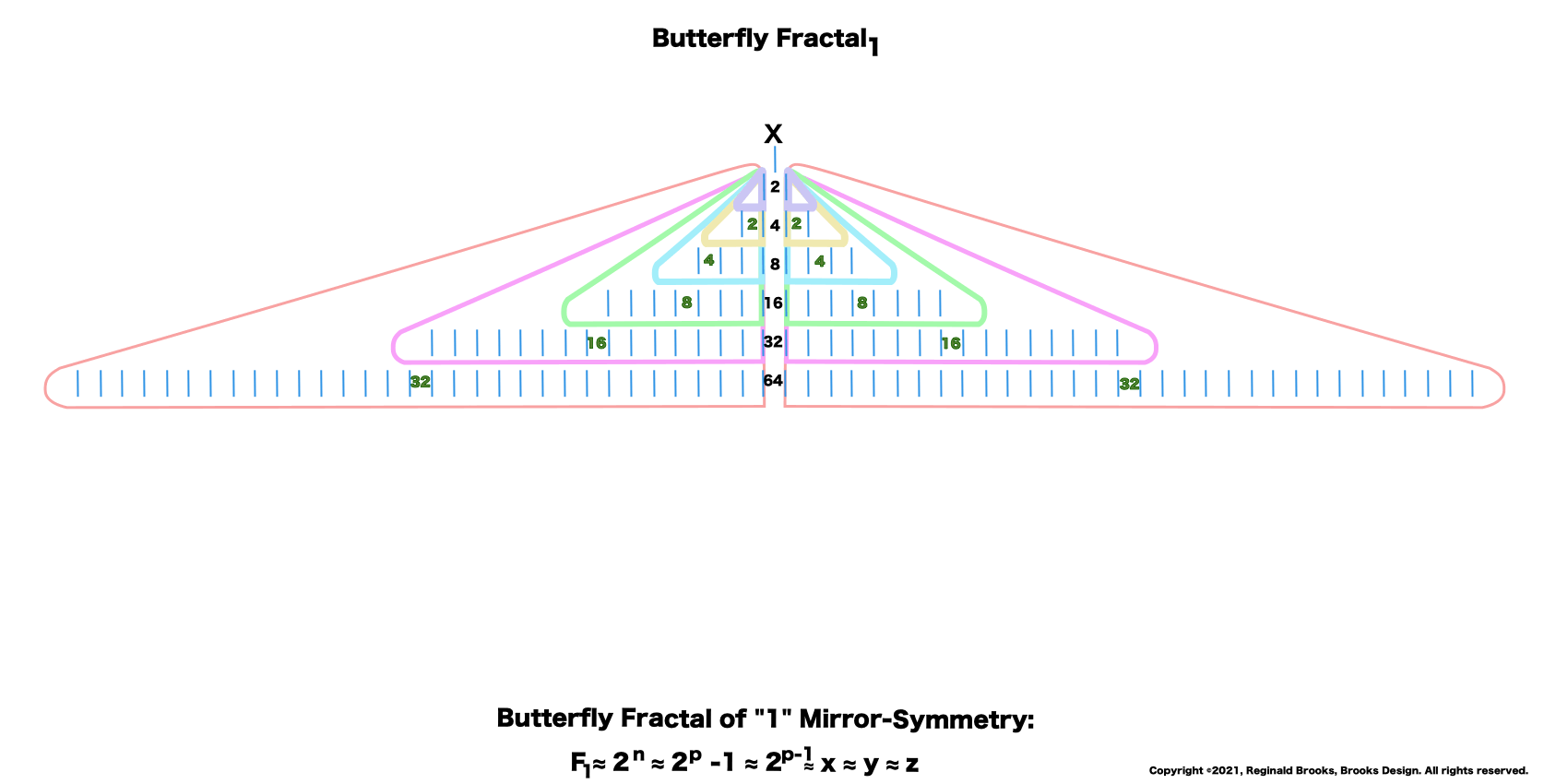
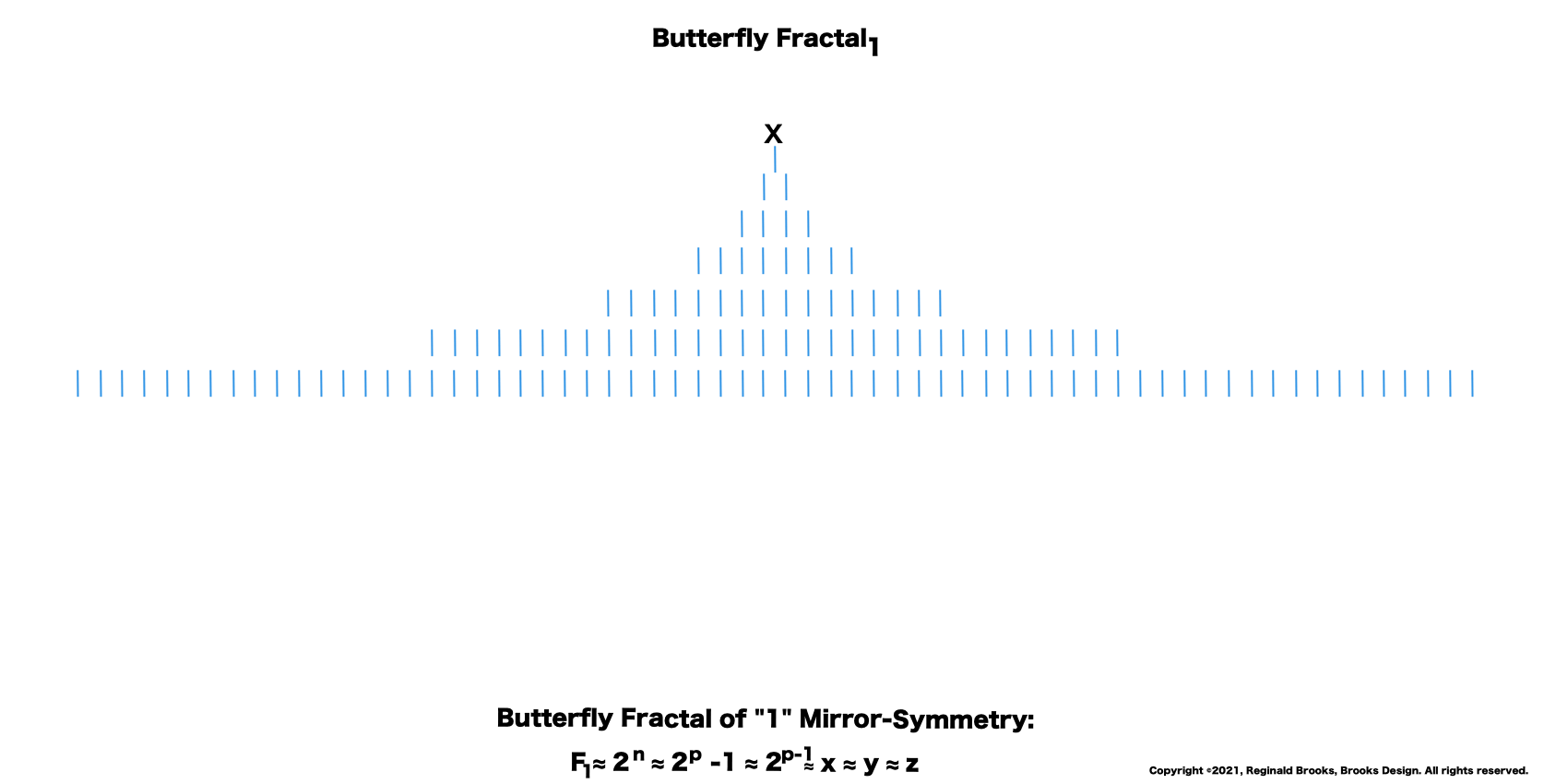
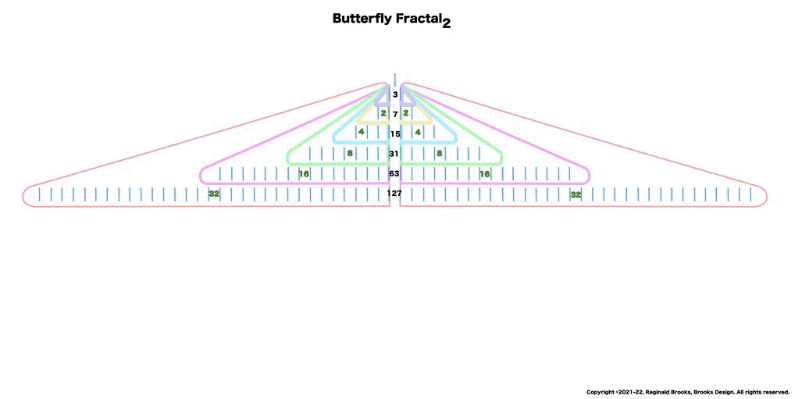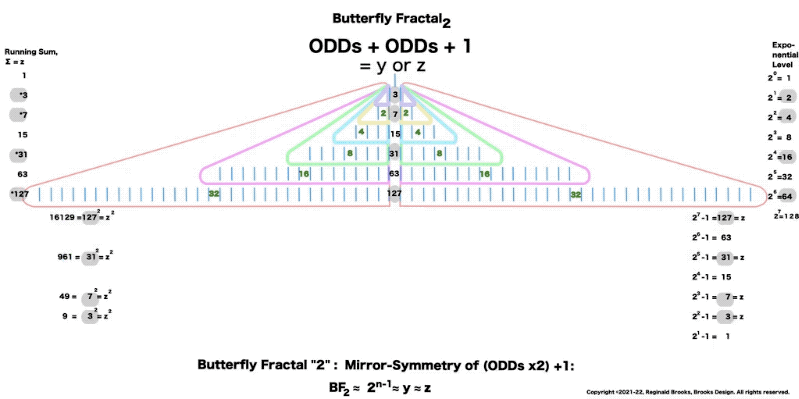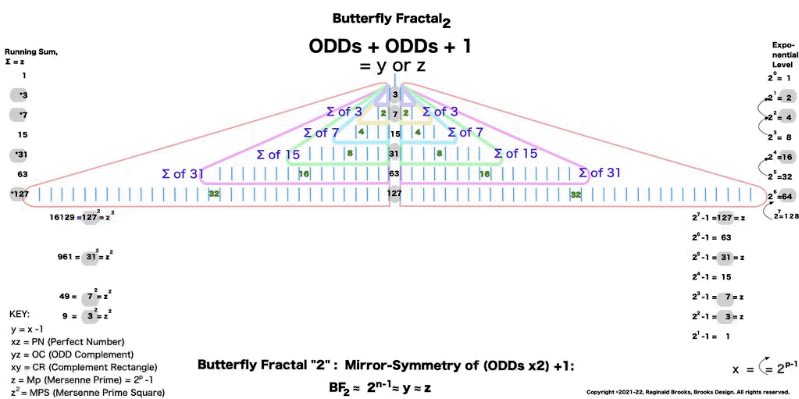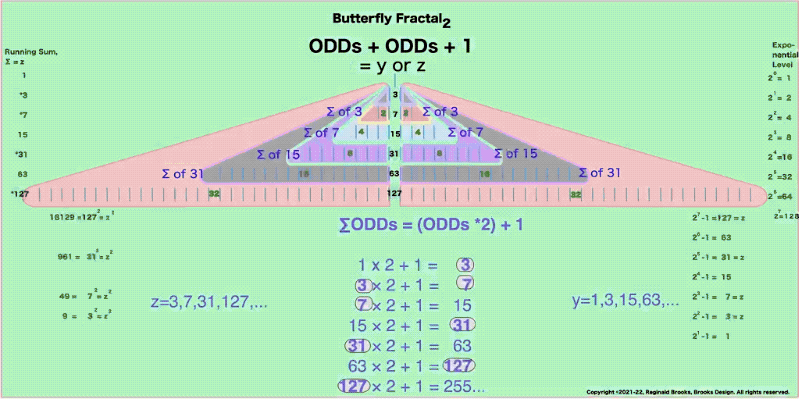Butterfly Fractal 2 is simply BF1 with the ODD sums inserted. It takes time to load.

SUMMARY

For centuries, Mersenne Primes were considered from the perspective of simple, plain number — number without dimension. When, instead, one treats the number value in a linear manner, as in the side “length” of a square, the Mersenne Prime Square is born.

As we have also known for many years, every Mersenne Prime has an associated Perfect Number — a number that is always EVEN.

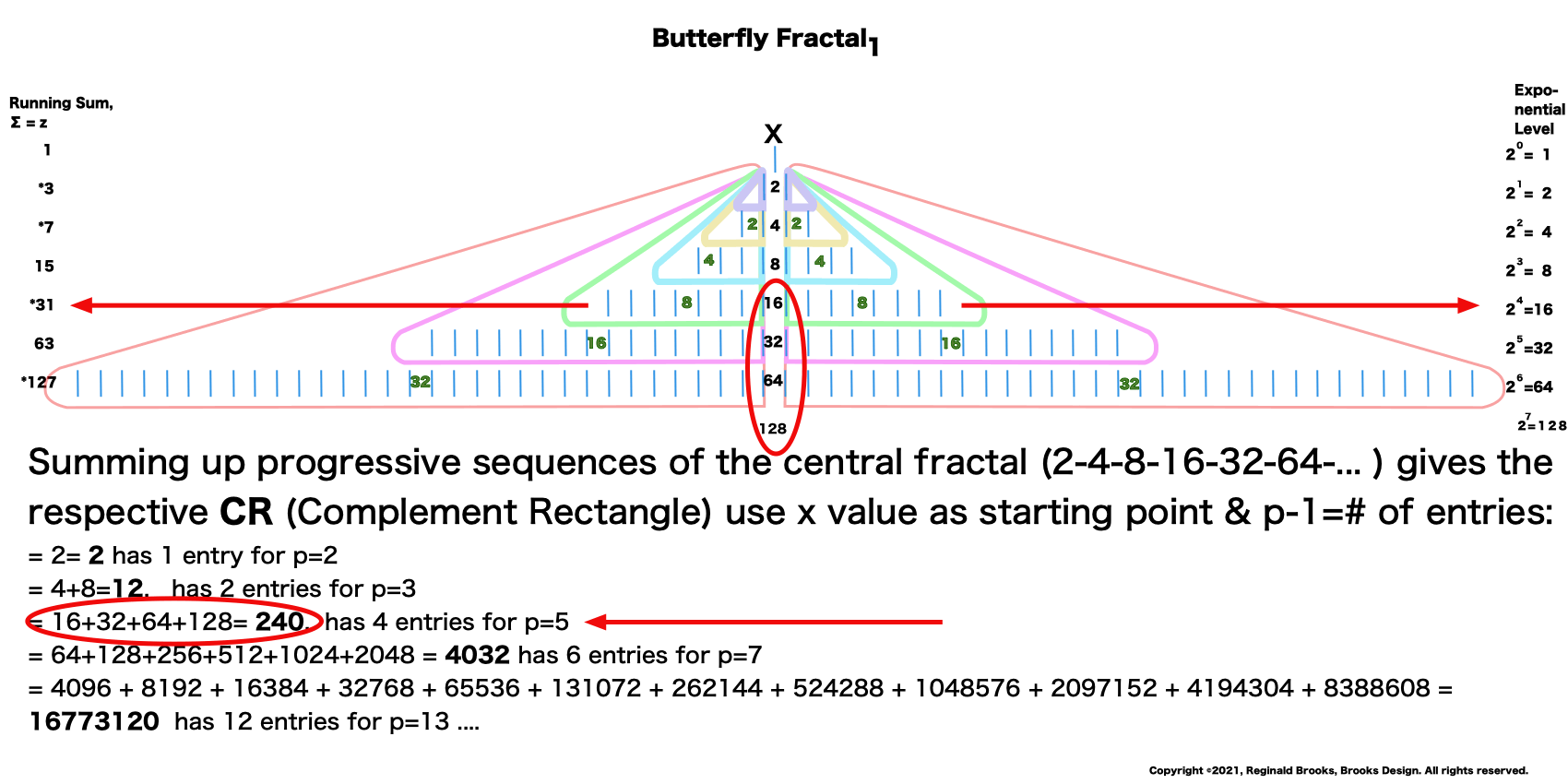
Therefore, in our ODD MPS, there must be an EVEN PN — and there is. It is found by asymmetrically dividing the MPS into two rectangles with the EVEN rectangle being the slightly larger of the two. It is the PN.

As the short side of each rectangle — when squared — becomes the embedded Perfect Square of that rectangle, with the remaining complement being the Complement Rectangle, CR. Thus the PN has its EVEN Perfect Number Square (PNS) and the OC has its ODD Complement Square (OCS).

A perfectly logical expression of EVEN-ODD interactions gives a natural Number Pattern Sequence (NPS) to each and every MPS.

CONCLUSION

The relationship between Mersenne Primes and Perfect Numbers is clarified as a natural consequence of their inherent geometric profile as revealed on the BIM.

Of perhaps greater significance is the actual play-out of the ODDS and EVENS, or is it the EVENS and ODDS. In this special case, the powers of 2 give the EVENS a very high profile presence in determining and defining a relationship to the normally more dominating ODD PRIMES.

Is it not interesting that sequentially dividing the EVEN PN by 2 will continue for the same number of times equal to its p-1 value before reaching an ODD. That ODD, of course, is z = Mp, i.e. PN/x = Mp, which is not surprising as PN = xMp = 2ᵖ⁻¹(2ᵖ-1) = Euclid-Euler Theorem.

But there is also a new window. Much as with the *PTOP* on the BIM, if one takes any EVEN and ÷ by 2, one finds symmetrically to either side, two members of a PRIME Pair set (PPset) that sum up to said EVEN; now, something new.

If one takes the approach, but now with the EVENS: to either side of EVEN PNS on the BIM Axis, symmetrically there are two EVENS that sum up to said PN, and these two EVENS are in fact the PNS and CR, e.i. PN = 28 when located as PN/2 = 28/2 = 14 on the BIM Axis, symmetrically 2 STEPS to either side are 12 and 16, the CR and PNS, respectively.

Another, example: PN = 496, 496/2 = 248, and 240 and 256 lie symmetrically 8 STEPS to either side of 248 on the BIM Axis, with CR = 240 and 256 = PNS for the 496 PN.

One more example: PN = 8128, 8128/2 = 4064, and PNS = 4096 and CR = 4032 lie symmetrical 32 STEPS to 4064, summing up to PN = 8128.

In every case, the STEPS are an EVEN, being a power of 2, 2ⁿ, specifically 2ᵖ-2 = 2ᵖ/4 = x/2.

We have much to learn on this relationship between ODD and EVEN numbers. The BIM-Mersenne Prime - Perfect Number is, perhaps, just the portal we need to see this vista that lies just beyond!

<~~

REFERENCES

LINKS:

Back to Part I of the BIM-Goldbach_Conjecture.

Back to Part III of the BIM-Goldbach_Conjecture.

BACK: ---> PRIMES Index on a separate White Paper

BACK: ---> Periodic Table Of PRIMES (PTOP) and the Goldbach Conjecture on a separate White Paper (REFERENCES found here.)

BACK: ---> Periodic Table Of PRIMES (PTOP) - Goldbach Conjecture ebook on a separate White Paper

BACK: ---> Simple Path BIM to PRIMES on a separate White Paper

BACK: ---> PRIMES vs NO-PRIMES on a separate White Paper

BACK: ---> TPISC_IV: Details_BIM+PTs+PRIMES on a separate White Paper

BACK: ---> PRIME GAPS on a separate White Paper

Reginald Brooks

Brooks Design

Portland, OR

brooksdesign-ps.net

KEYWORDS TAGS: BMP, BIM-MersenneSquare-PerfectNumber, Mersenne Primes, Mersenne Prime Square, Perfect Number, Perfect Square, MPS, Mp, PTOP, Periodic Table Of PRIMES, PRIMES vs NO-PRIMES, algebraic geometry, BIM, TPISC, The Pythagorean - Inverse Square Connections, Pythagorean Triangles, DNA, Zika virus, pentagon, decagon, double pentagon, composite axial DNA double-helix, Pythagorean Triples, primitive Pythagorean Triples, non-primitive Pythagorean Triples, Pythagorean Theorem, Pythagorus Theorem, The Dickson Method, BBS-ISL Matrix, Expanded Dickson Method, r-sets, s-set, t-sets, Pair-sets, geometric proofs, MathspeedST, leapfrogging LightspeedST FASTER than the speed of light, Brooks (Base) Square- Inverse Square Law (ISL), BBS-ISL Matrix grid, The Architecture Of SpaceTime (TAOST), The Conspicuous Absence Of Primes (TCAOP), A Fresh Piece Of Pi(e), AFPOP, Numbers of Inevitability, LightspeedST, Teachers, Educators and Students (TES), number theory, ubiquitous information, FASTER than the speed of light, primes, prime numbers, fractals, mathematics, Universe, cosmos, patterns in number, DSEQEC, Double-Slit Experiment-Quantum Entanglement Conjecture, CaCost, Creation and Conservation of SpaceTime.

Art Theory 101 / White Papers Index

PIN: Pattern in Number...from primes to DNA. | PIN: Butterfly Primes...let the beauty seep in. | PIN: Butterfly Prime Directive...metamorphosis. | PIN: Butterfly Prime Determinant Number Array (DNA) ~conspicuous abstinence~. | GoDNA: the Geometry of DNA (axial view) revealed. | SCoDNA: the Structure and Chemistry of DNA (axial view). | The LUFE Matrix | The LUFE Matrix Supplement | The LUFE Matrix: Infinite Dimensions | The LUFE Matrix: E=mc² | Dark Matter=Dark Energy | The History of the Universe in Scalar Graphics | The History of the Universe_update: The Big Void | Quantum Gravity ...by the book | The Conservation of SpaceTime | LUFE: The Layman's Unified Field Expose` | GoMAS: The Geometry of Music, Art and Structure ...linking science, art and esthetics. Part I | Brooks (Base) Square (BBS): The Architecture of Space-Time (TAOST) and The Conspicuous Absence of Primes (TCAOP) - a brief introduction to the series | more White Papers...

iTunes, iTunes Store, Apple Books, iBooks, iBooks Store, iBooks Author, Mac OS are registered® trademarks of Apple Inc. and their use on this webpage does not reflect endorsement by Apple Inc.

IMAGES

SUMMARY

CONCLUSION

<~~ REFERENCES

~~LINKS:

Back to Part I of the BIM-Goldbach_Conjecture.

Back to Part III of the BIM-Goldbach_Conjecture.

<~~

REFERENCES

~~
LINKS: