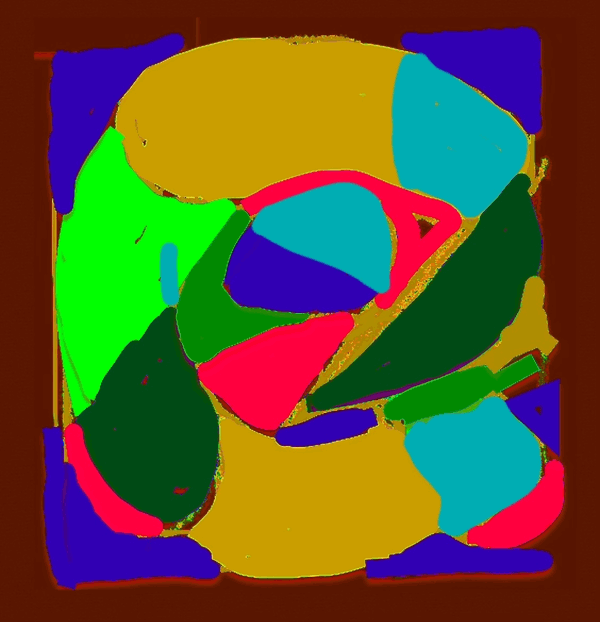
CLICK for LINKS
©2021,Reginald Brooks, Brooks Design, Portland, OR. All rights reserved.

A Mersenne Prime Square:
Mersenne Prime-Perfect Number
And two Perfect Squares
~~~
What was once a dot
• Mersenne Prime
has become a line
____ Mersenne Prime
and lines become areas
▢ Mersenne Prime Square
…the story follows.
~~~
ABSTRACT:
UNIVERSAL:
SPECIFIC:
EXAMPLE: let *z*=*Mp*=7
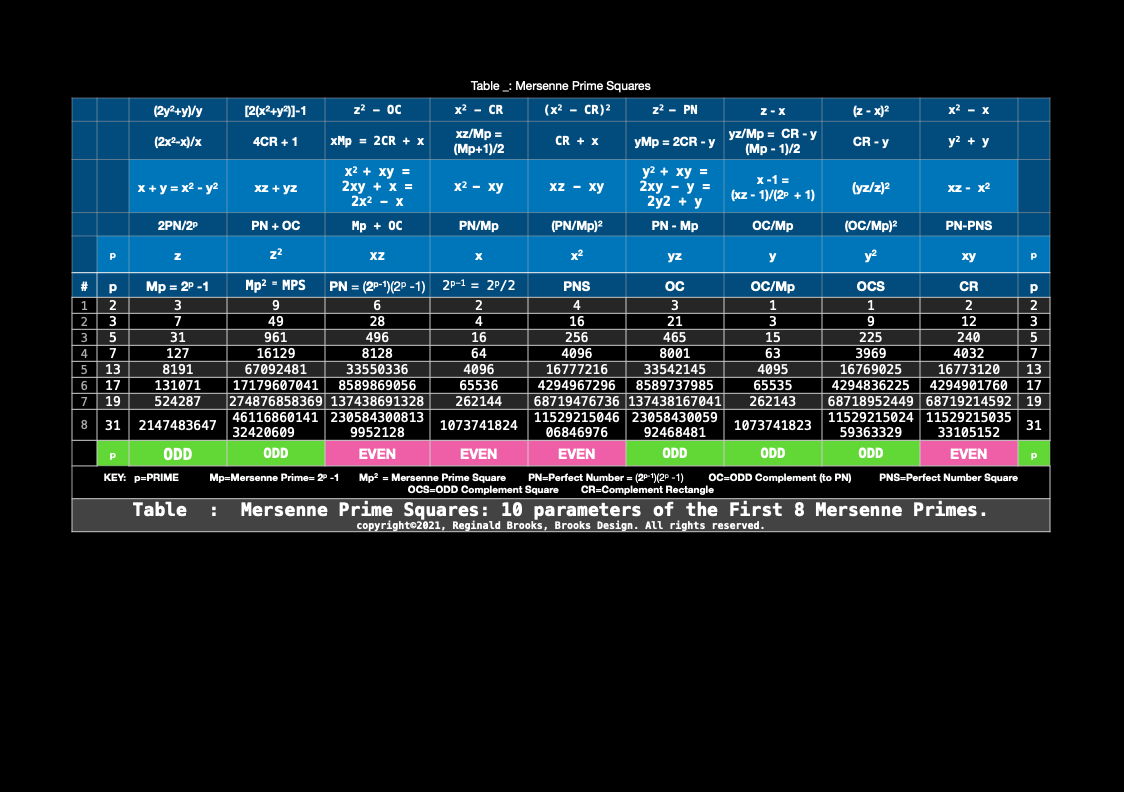
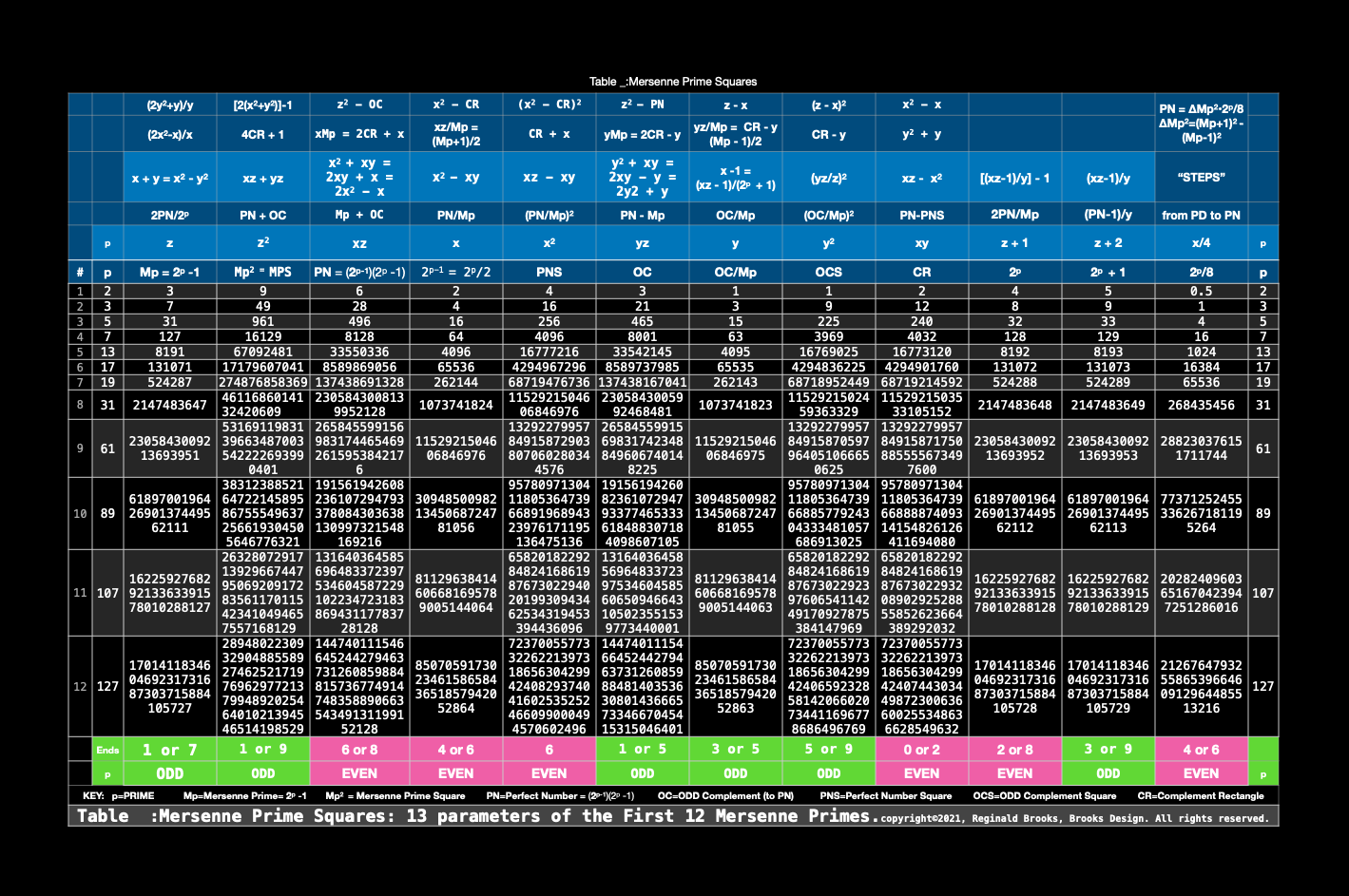
KEY: Mp = Mersenne Prime, Mp² = MPS = Mersenne Prime Square, PN = Perfect Number, PNS = Perfect Number Square, OC = ODD Complement, OCS = ODD Complement Square, CR = Complement Rectangle, Brooks (Base) Square - Inverse Square Law Matrix = BBS-ISL Matrix (BIM), BMP, BIM-MersenneSquare-PerfectNumber. NOTE: ALL NUMBERS = natural whole integer numbers (WIN).
~~~~~~~~~
From Euclid’s proof of Perfect Numbers to Euler’s connecting them to Mersenne Primes, the universal and ongoing mystery remains to this day. Why is there this connection? What is it trying to tell us about the fundamental relationship between EVEN (all known Perfect Numbers are EVEN) and ODD (all primes >2 are ODD) numbers — at least in regards to the Mersenne Prime - Perfect Number pairing? Is there a new approach? Yes!
A brief reference:
In mathematics, a Mersenne prime is a prime number that is one less than a power of two.That is, it is a prime number of the form Mn =2n −1 for some integer n. They are named after Marin Mersenne, a French Minim friar, who studied them in the early 17th century. If n is a composite number then so is 2n − 1. Therefore, an equivalent definition of the Mersenne primes is that they are the prime numbers of the form Mp = 2p − 1 for some prime p.
Reference: Wikipedia: Mersenne Prime
Mersenne primes Mp are closely connected to perfect numbers. In the 4th century BC, Euclid proved that if 2p − 1 is prime, then 2p−1(2p − 1) is a perfect number. In the 18th century, Leonhard Euler proved that, conversely, all even perfect numbers have this form.[4] This is known as the Euclid–Euler theorem. It is unknown whether there are any odd perfect numbers.
Reference: Wikipedia: Mersenne Prime
In number theory, a perfect number is a positive integer that is equal to the sum of its positive divisors, excluding the number itself. For instance, 6 has divisors 1, 2 and 3 (excluding itself), and 1 + 2 + 3 = 6, so 6 is a perfect number.
Reference: Wikipedia: Perfect number
The Euclid–Euler theorem is a theorem in mathematics that relates perfect numbers to Mersenne primes. It states that an even number is perfect if and only if it has the form 2p−1(2p − 1), where 2p − 1 is a prime number. The theorem is named after Euclid and Leonhard Euler.
It has been conjectured that there are infinitely many Mersenne primes. Although the truth of this conjecture remains unknown, it is equivalent, by the Euclid–Euler theorem, to the conjecture that there are infinitely many even perfect numbers. However, it is also unknown whether there exists even a single odd perfect number.[1]
Reference: Wikipedia: Euclid-Euler theorem
~~~~~~~~
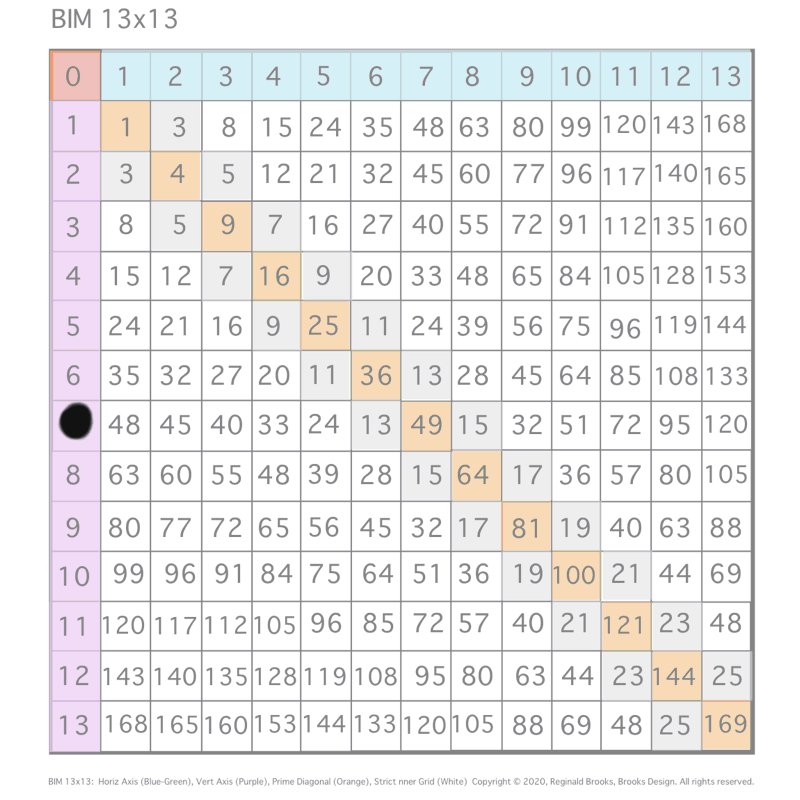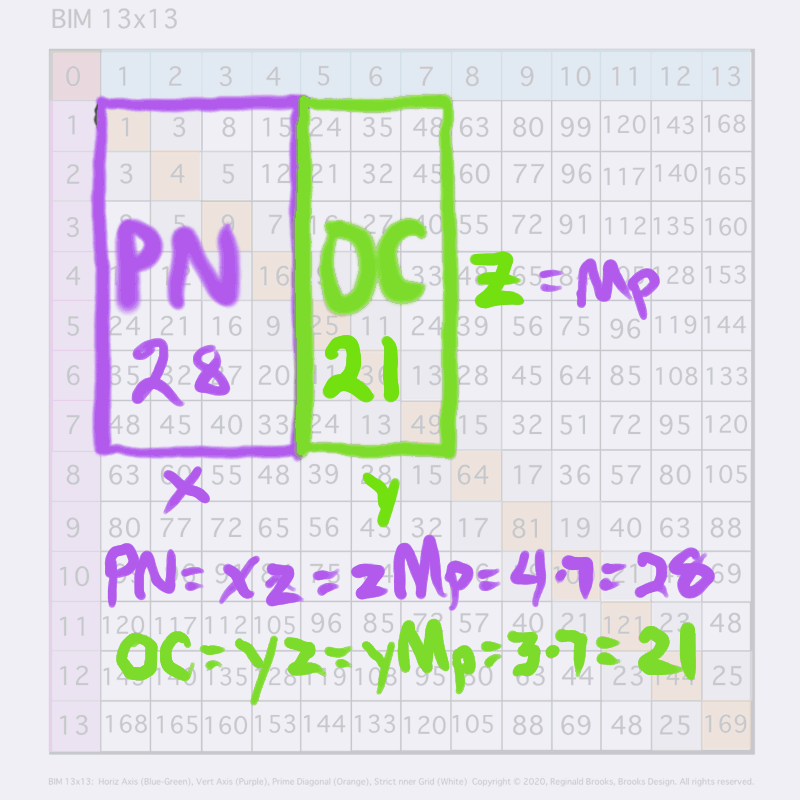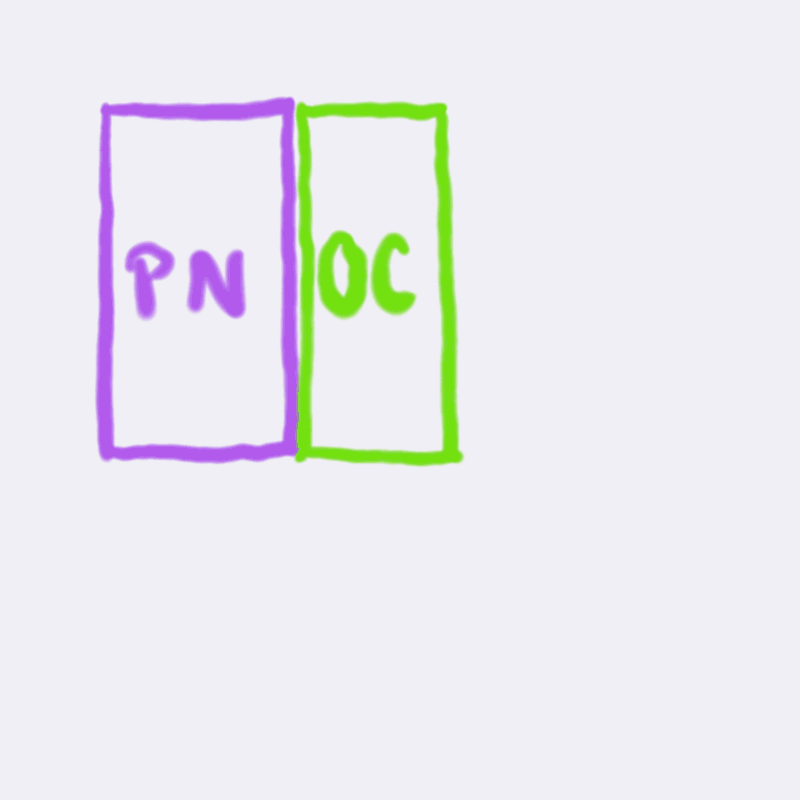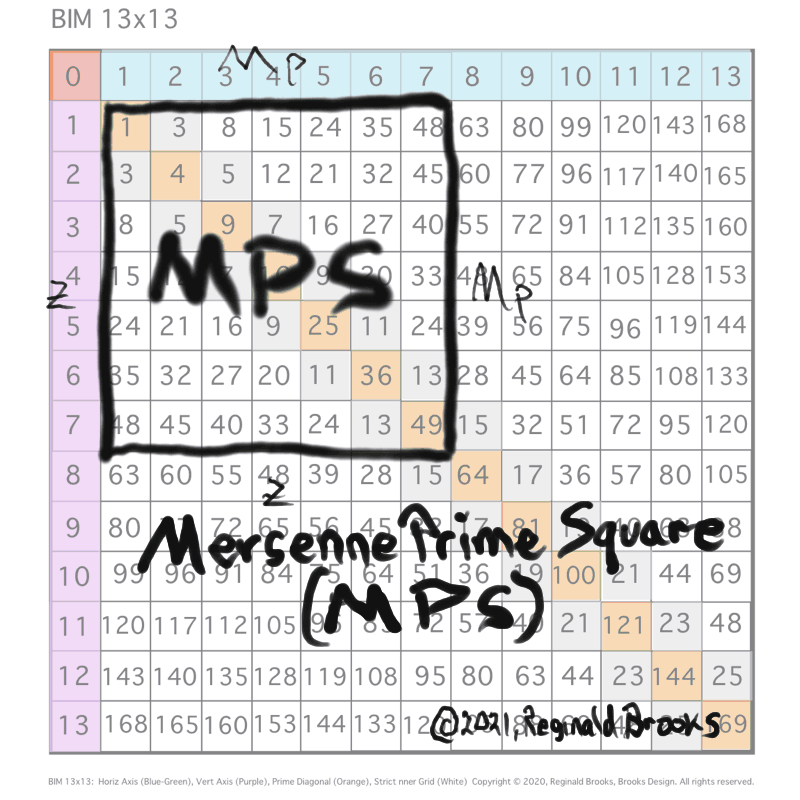
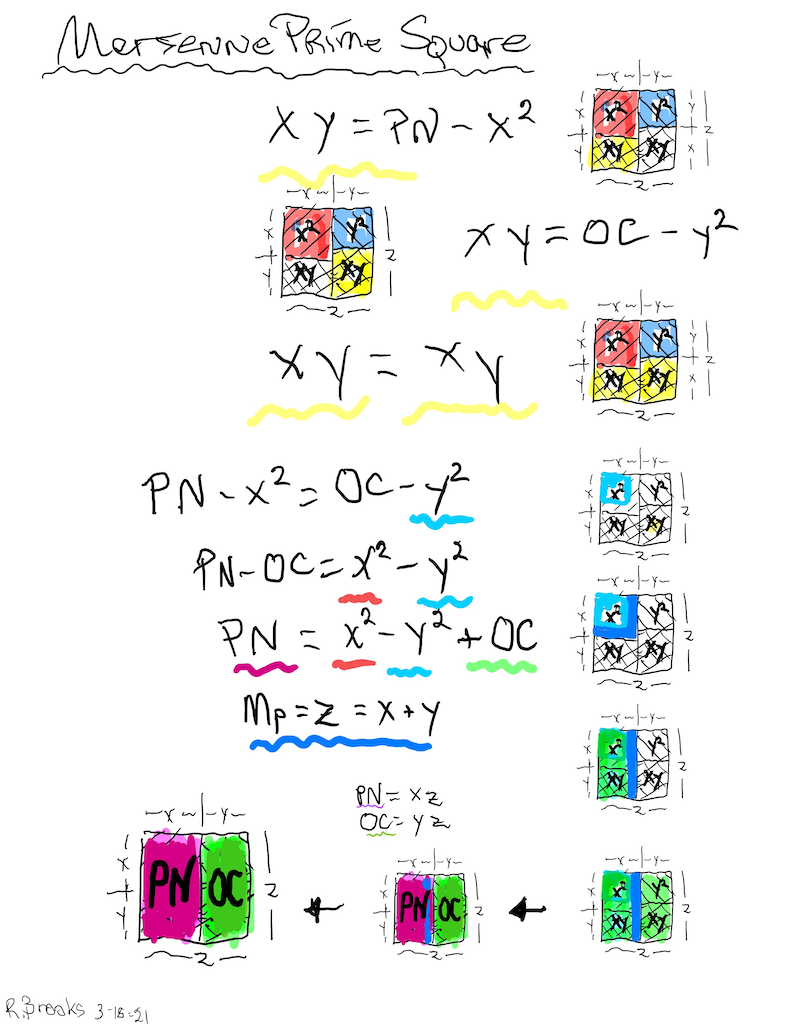
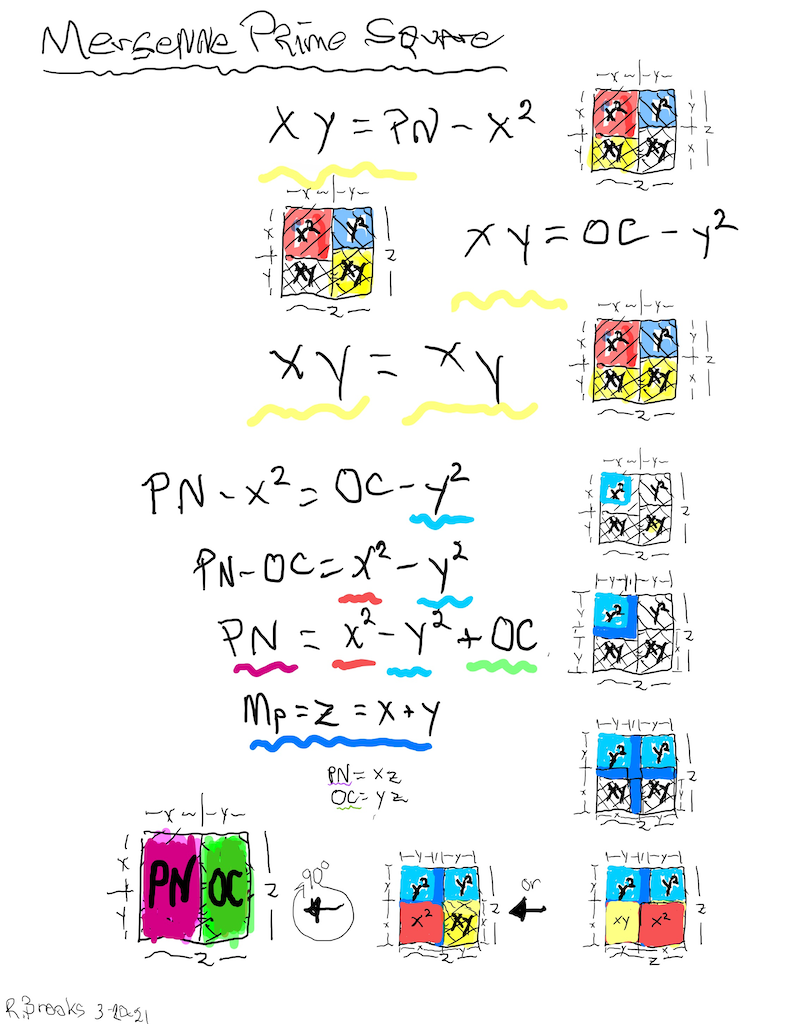
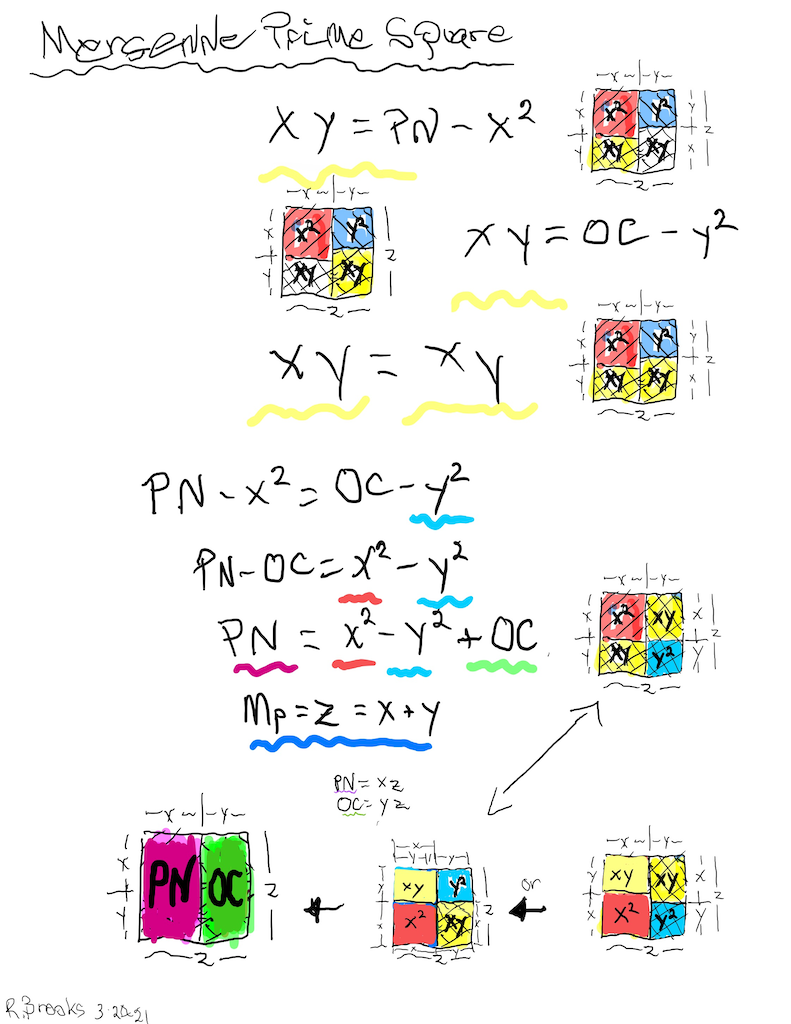
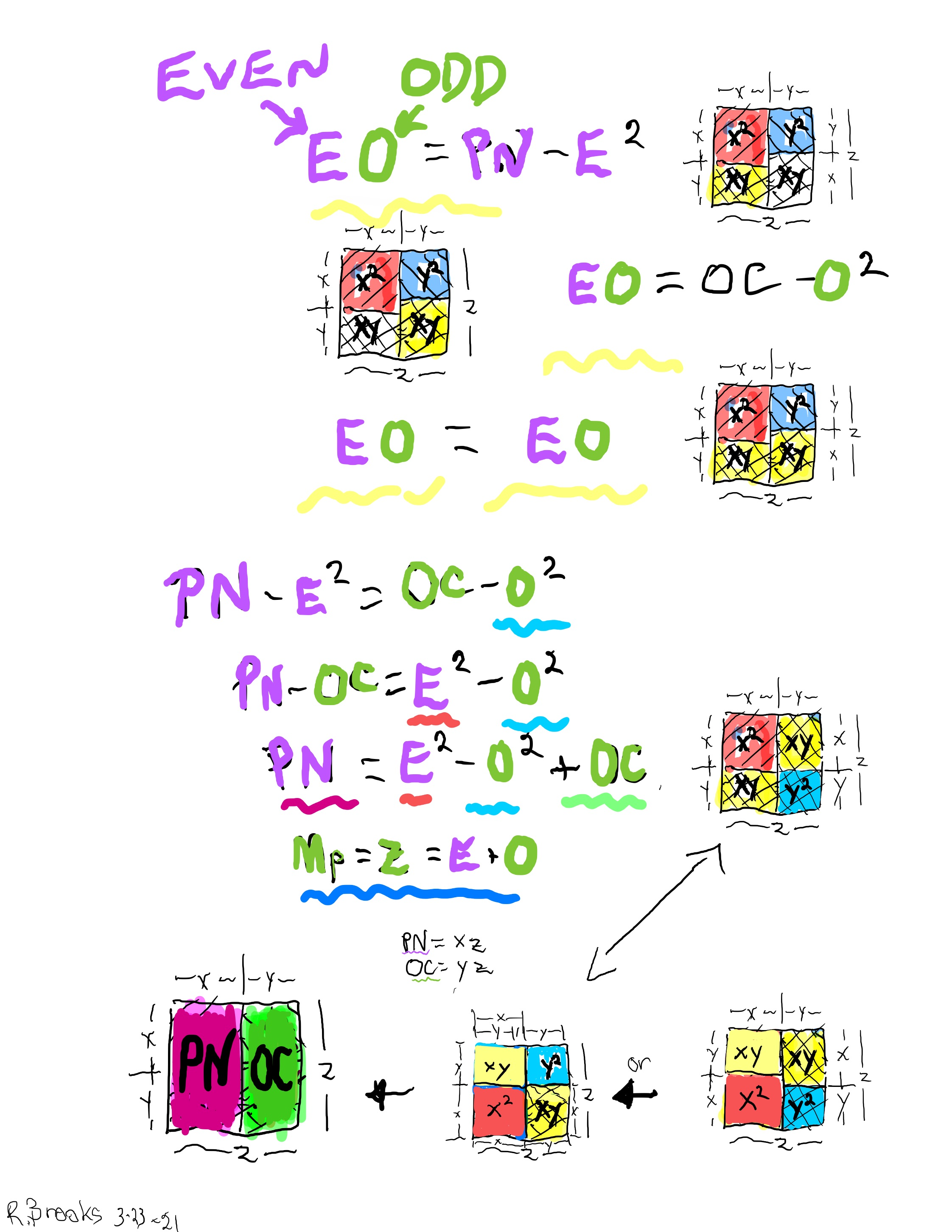
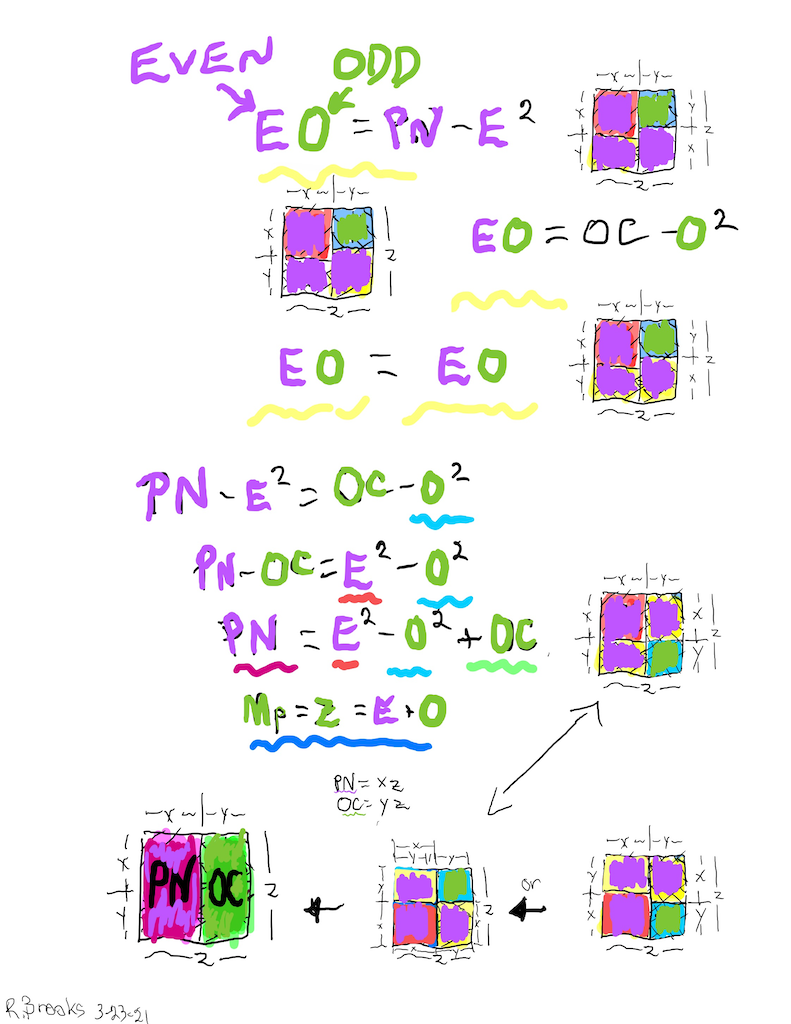
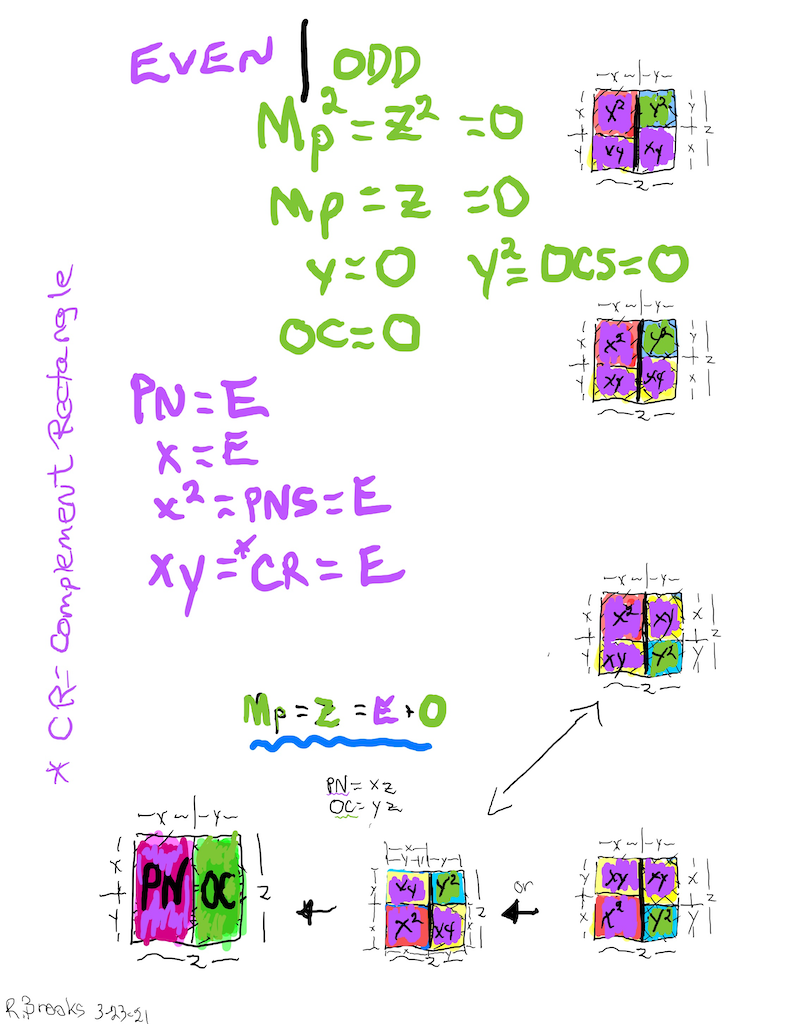
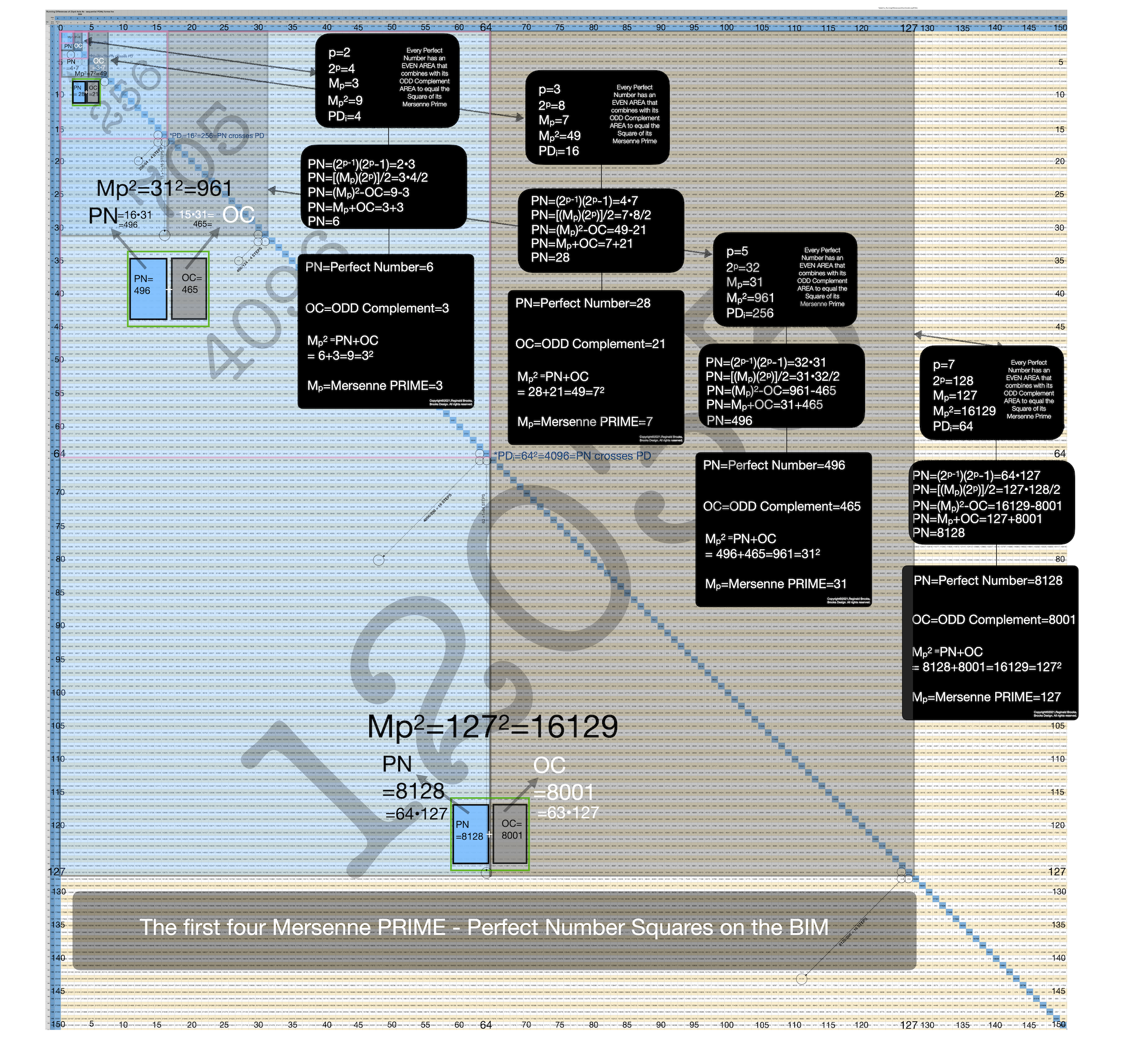
Letting a Mersenne Prime (Mp=z) be one side of a square, we end up with a Mersenne Prime Square (Mp²=z²).
Asymmetrically subdividing z² into 2 rectangles such the short sides are (z+1)/2 = x and (z-1)/2 = y, giving an EVEN Perfect Number = xz rectangle and an ODD Complement = yz rectangle.
A further subdivision of each PN and OC rectangle, with the short side x and y, respectively, will form 2 Perfect Squares.
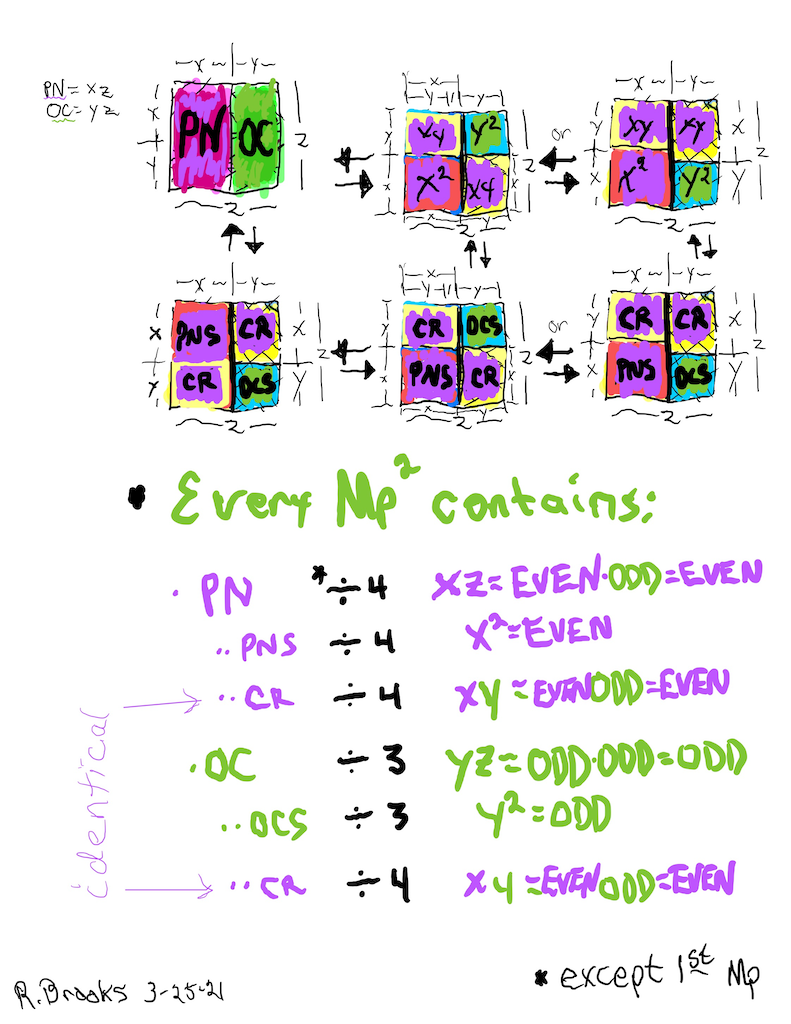
The Complement Rectangle (CR = xy) left over from each subdivision is identical.
Every Mp is ODD, as too, is its square area, Mp²=z².
The Mp²=z² is always asymmetrically divided into an EVEN PN rectangle and and ODD Complement (OC) rectangle.
The EVEN PN rectangle is subdivided into a Perfect Number Square (PNS) and Complement Rectangle (CR), both being EVENS.
The OC rectangle is subdivided into an ODD Complement Square (OCS) and a similar, identical CR.

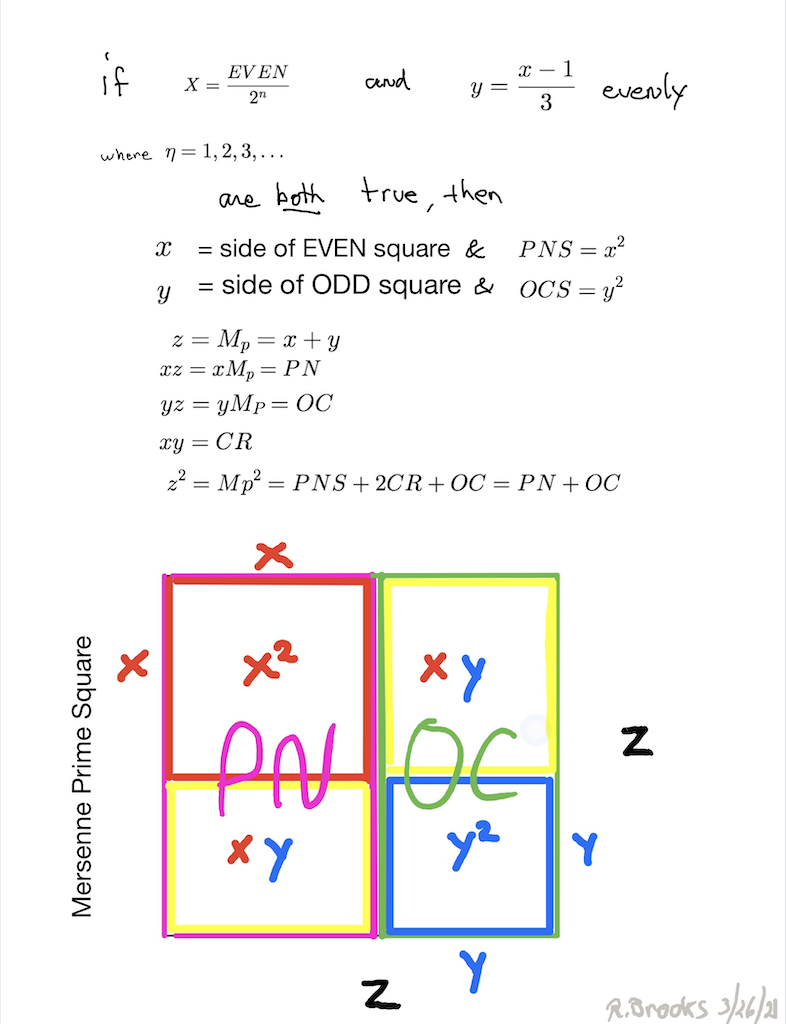
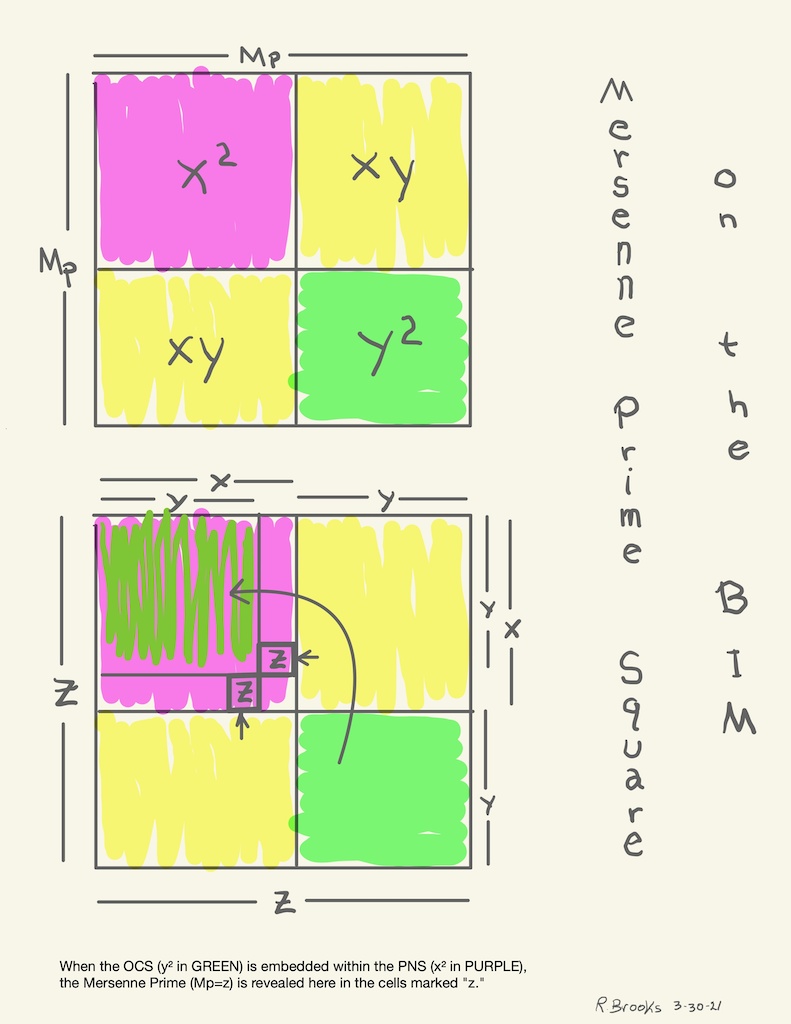
Simply overlaying the GREEN y² = OCS on to the larger PURPLE x² = PNS on the BIM, always reveals the Mersenne Prime = Mp = z at the cells immediately below and to the right of the OCS lower corner — as shown in the cells marked “z.”
~~~~~~~~
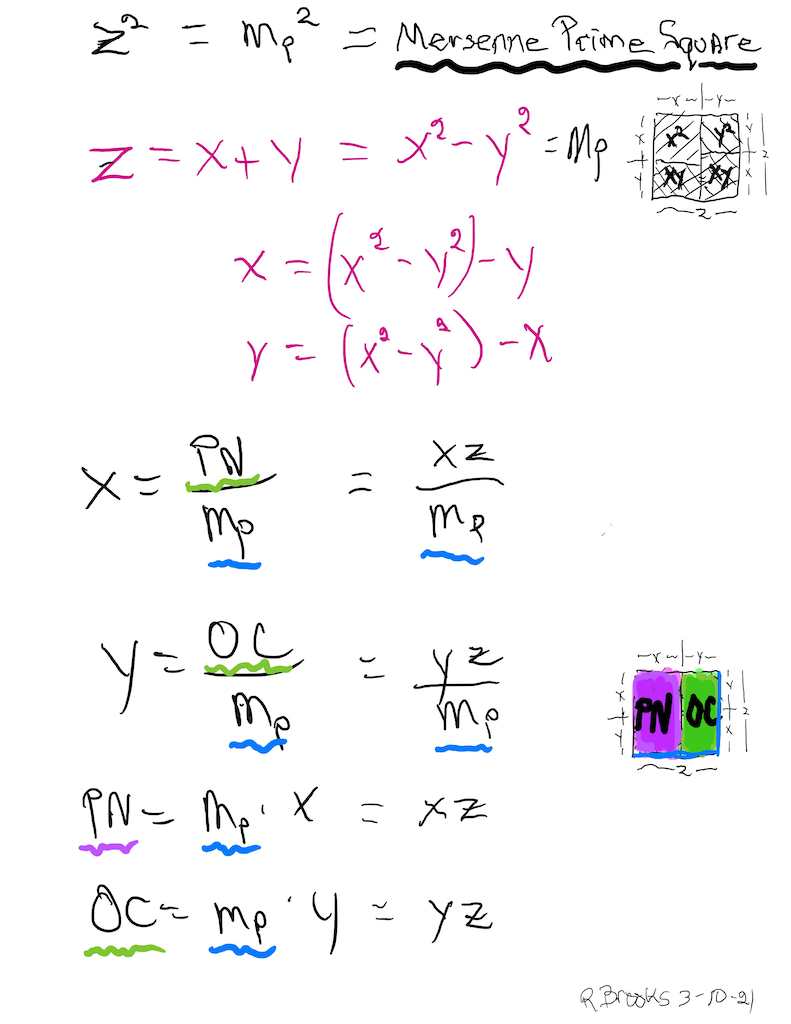
Let’s follow the example given in the intro.
EXAMPLE: let *z*=*Mp*=7
SPECIFIC:
UNIVERSAL:

EXAMPLE: let *z*=*Mp*=7
SPECIFIC:
UNIVERSAL:
EXAMPLE: let *z*=*Mp*=7
SPECIFIC:
UNIVERSAL:
EXAMPLE: let *z*=*Mp*=7
SPECIFIC:
UNIVERSAL:
EXAMPLE: let *z*=*Mp*=7
SPECIFIC:
UNIVERSAL:
EXAMPLE: let *z*=*Mp*=7
SPECIFIC:
UNIVERSAL:
ABSTRACT:
UNIVERSAL:
SPECIFIC:
EXAMPLE: let *z*=*Mp*=7
ABSTRACT:
UNIVERSAL:
:
EXAMPLE: let *z*=*Mp*=7

ABSTRACT:
UNIVERSAL:
SPECIFIC:
EXAMPLE: let *z*=*Mp*=7
ABSTRACT:
UNIVERSAL:
SPECIFIC:
EXAMPLE: let *z*=*Mp*=7

ABSTRACT:
UNIVERSAL:
SPECIFIC:
EXAMPLE: let *z*=*Mp*=7

ABSTRACT:
UNIVERSAL:
SPECIFIC:
EXAMPLE: let z=Mp=7

Simply overlaying the GREEN y² = OCS on to the larger PURPLE x² = PNS on the BIM, always reveals the Mersenne Prime = Mp = z at the cells immediately below and to the right of the OCS lower corner — as shown in the cells marked “z.”
~~~~~~~~
FIGURES and TABLES:
~~~~~~~
SUMMARY
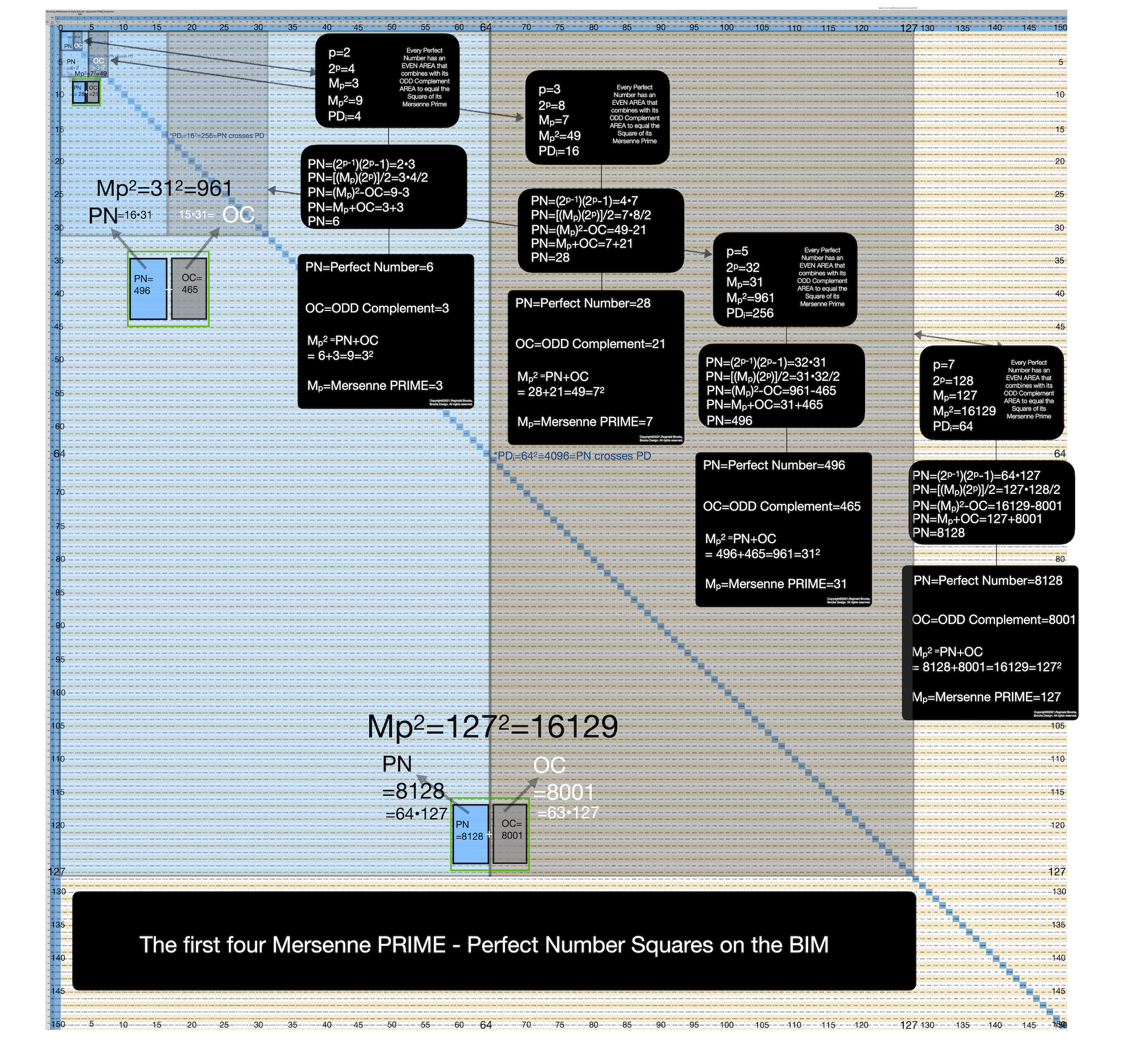
For centuries, Mersenne Primes were considered from the perspective of simple, plain number — number without dimension. When, instead, one treats the number value in a linear manner, as in the side “length” of a square, the Mersenne Prime Square is born.
As we have also known for many years, every Mersenne Prime has an associated Perfect Number — a number that is always EVEN.
Therefore, in our ODD MPS, there must be an EVEN PN — and there is. It is found by asymmetrically dividing the MPS into two rectangles with the EVEN rectangle being the slightly larger of the two. It is the PN.
The ODD rectangle is the complement to it, thus being the OC.
As the short side of each rectangle — when squared — becomes the embedded Perfect Square of that rectangle, with the remaining complement being the Complement Rectangle, CR. Thus the PN has its EVEN Perfect Number Square (PNS) and the OC has its ODD Complement Square (OCS).
The CRs are identical and always EVEN.
The PNS is always EVEN, while the OCS always ODD.
A perfectly logical expression of EVEN-ODD interactions gives a natural Number Pattern Sequence (NPS) to each and every MPS.
~~~~~~~~
CONCLUSION
The relationship between Mersenne Primes and Perfect Numbers is clarified as a natural consequence of their inherent geometric profile as revealed on the BIM.
Of perhaps greater significance is the actual play-out of the ODDS and EVENS, or is it the EVENS and ODDS. In this special case, the powers of 2 give the EVENS a very high profile presence in determining and defining a relationship to the normally more dominating ODD PRIMES.
Is it not interesting that sequentially dividing the EVEN PN by 2 will continue for the same number of times equal to its p-1 value before reaching and ODD. That ODD, of course, is z = Mp, i.e. PN/x = Mp, which is not surprising as PN = xMp = 2ᵖ⁻¹(2ᵖ-1) = Euclid-Euler Theorem.
But there is also a new window. Much as with the *PTOP* on the BIM, if one takes any EVEN and ÷ by 2, one finds symmetrically to either side, two members of a PRIME Pair set (PPset) that sum up to said EVEN; now, something new.
If one takes the approach, but now with the EVENS: to either side of EVEN PNS on the BIM Axis, symmetrically there are two EVENS that sum up to said PN, and these two EVENS are in fact the PNS and CR, e.i. PN = 28 when located as PN/2 = 28/2 = 14 on the BIM Axis, symmetrically 2 STEPS to either side are 12 and 16, the CR and PNS, respectively.
Another, example: PN = 496, 496/2 = 248, and 240 and 256 lie symmetrically 8 STEPS to either side of 248 on the BIM Axis, with CR = 240 and 256 = PNS for the 496 PN.
One more example: PN = 8128, 8128/2 = 4064, and PNS = 4096 and CR = 4032 lie symmetrical 32 STEPS to 4064, summing up to PN = 8128.
In every case, the STEPS are an EVEN, being a power of 2, 2ⁿ, specifically 2ᵖ-2 = 2ᵖ/4 = x/2.
We have much to learn on this relationship between ODD and EVEN numbers. The BIM-Mersenne Prime - Perfect Number is, perhaps, just the portal we need to see this vista that lies just beyond!
~~~~~~~~
REFERENCES
Wikipedia: Mersenne Prime
Wikipedia: Perfect number
Wikipedia: Euclid-Euler theorem
~~~~~~~~
APPENDIX
+
(images notes from BMPNt_images go here)
~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~
NEXT: Details 1: Review of Advanced Basics of the MPS from Part I
LINKS:
Mersenne Prime Squares (Part I) the Introductory white paper.
Mersenne Prime Squares (Part II) 3 Simple Intros.
Mersenne Prime Squares (Part III) the Advanced white paper.
The MPS Project The Mersenne Prime Squares Project.
LINKS:
MathspeedST: TPISC Media Center
Artist Link in iTunes Apple Books Store: Reginald Brooks

Back to Part I of the BIM-Goldbach_Conjecture.
Back to Part III of the BIM-Goldbach_Conjecture.
BACK: ---> PRIMES Index on a separate White Paper BACK: ---> Periodic Table Of PRIMES (PTOP) and the Goldbach Conjecture on a separate White Paper (REFERENCES found here.) BACK: ---> Periodic Table Of PRIMES (PTOP) - Goldbach Conjecture ebook on a separate White Paper BACK: ---> Simple Path BIM to PRIMES on a separate White Paper BACK: ---> PRIMES vs NO-PRIMES on a separate White Paper BACK: ---> TPISC_IV: Details_BIM+PTs+PRIMES on a separate White Paper BACK: ---> PRIME GAPS on a separate White PaperReginald Brooks
Brooks Design
Portland, OR
brooksdesign-ps.net