BIM-MPS Details, Part II

The Exponential Power of 2 and the Butterfly Fractal~1~

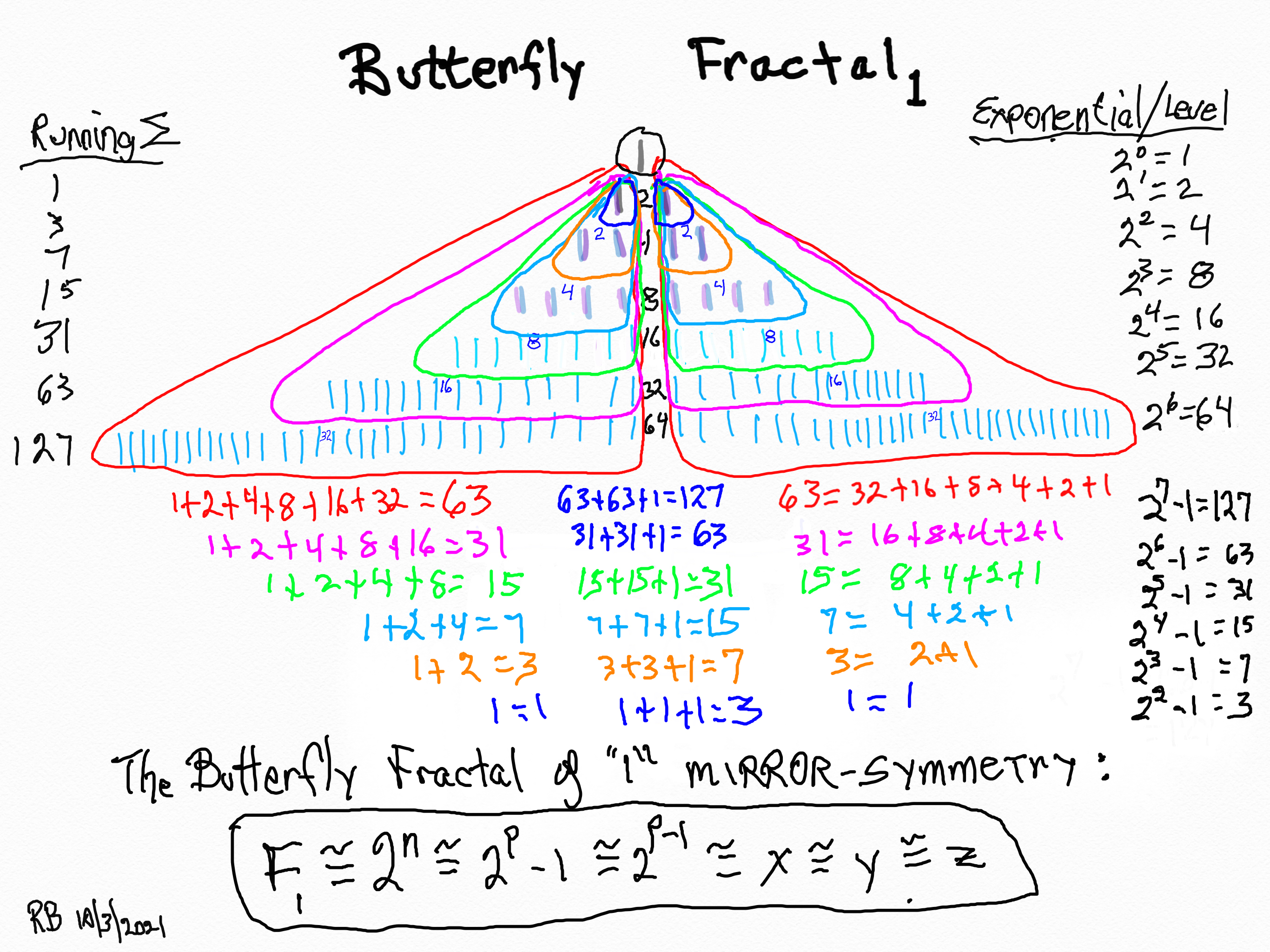
Butterfly Fractal~1~

Now let's go back and look at the opening statement:

Is not the number one (1) the ultimate "fractal?"

While not technically a prime, it is only divisible by itself and 1.

If we loosen our definition of what a fractal is to include that which forms a larger whole simply by doubling itself and each sum/product thereafter: 1--2--4--8--16--32--64--....

We can also write that as exponentials of 2:

2⁰--2¹--2²--2³--2⁴--2⁵--2⁶--..., respectively.

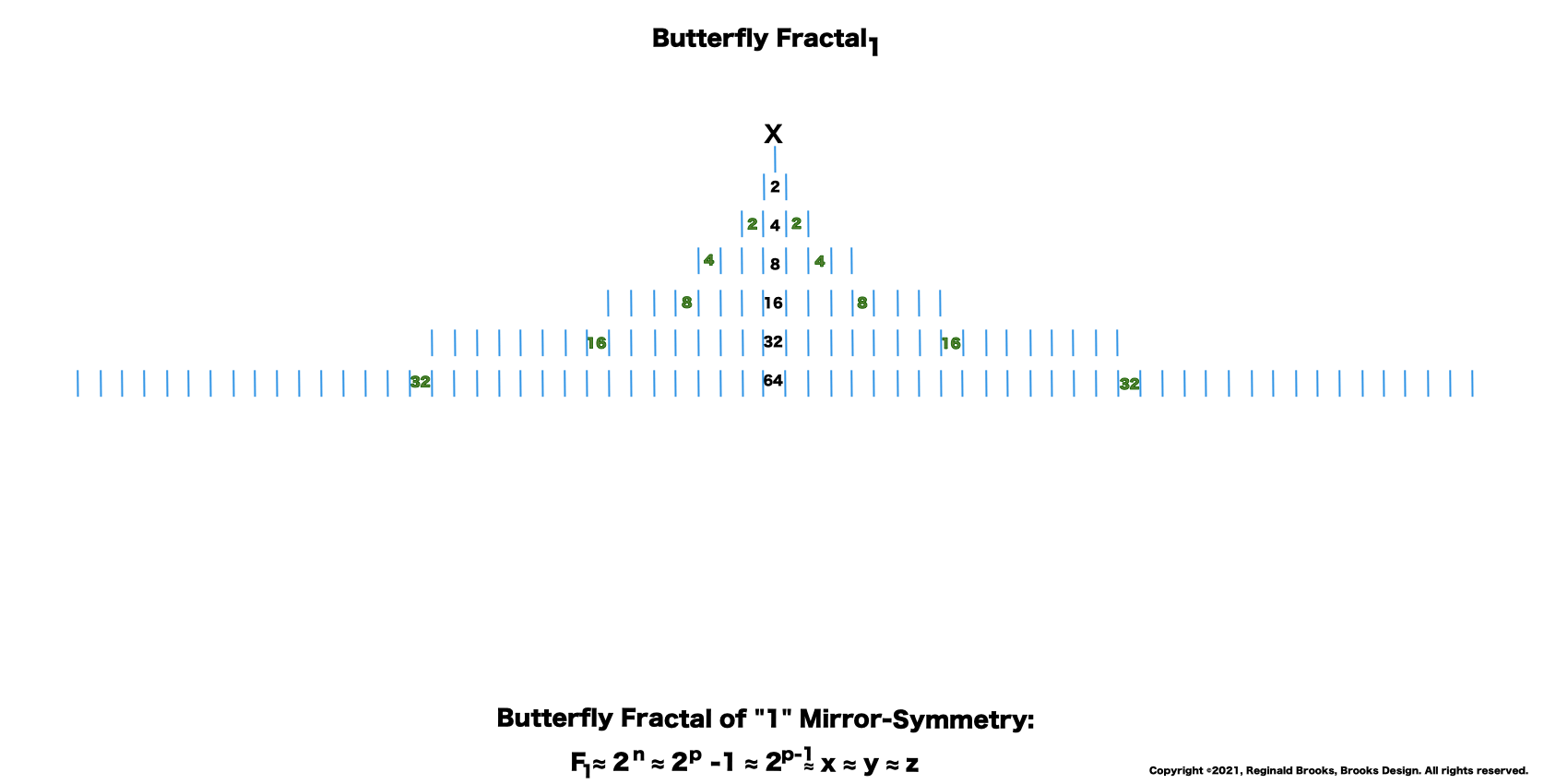
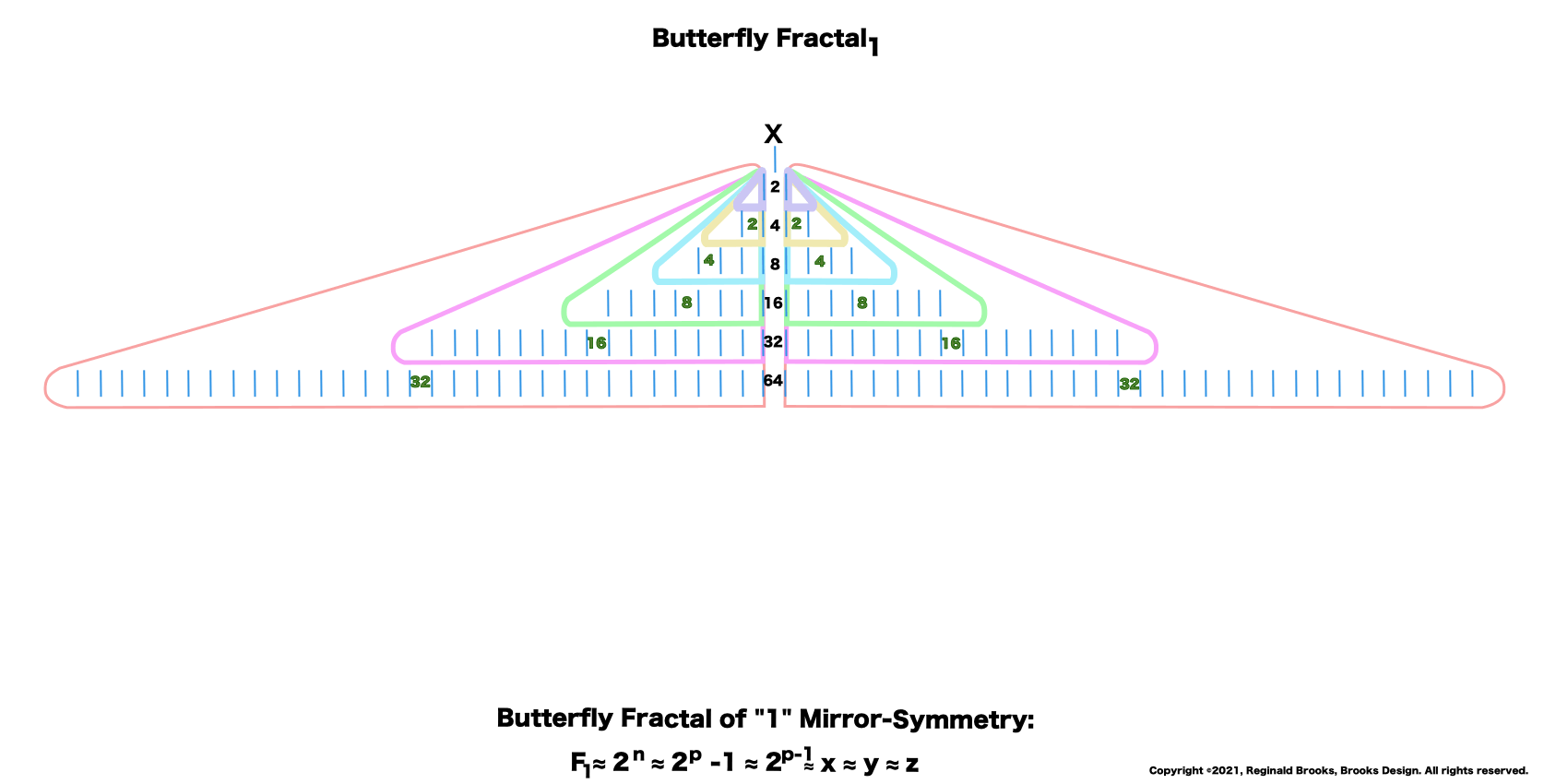
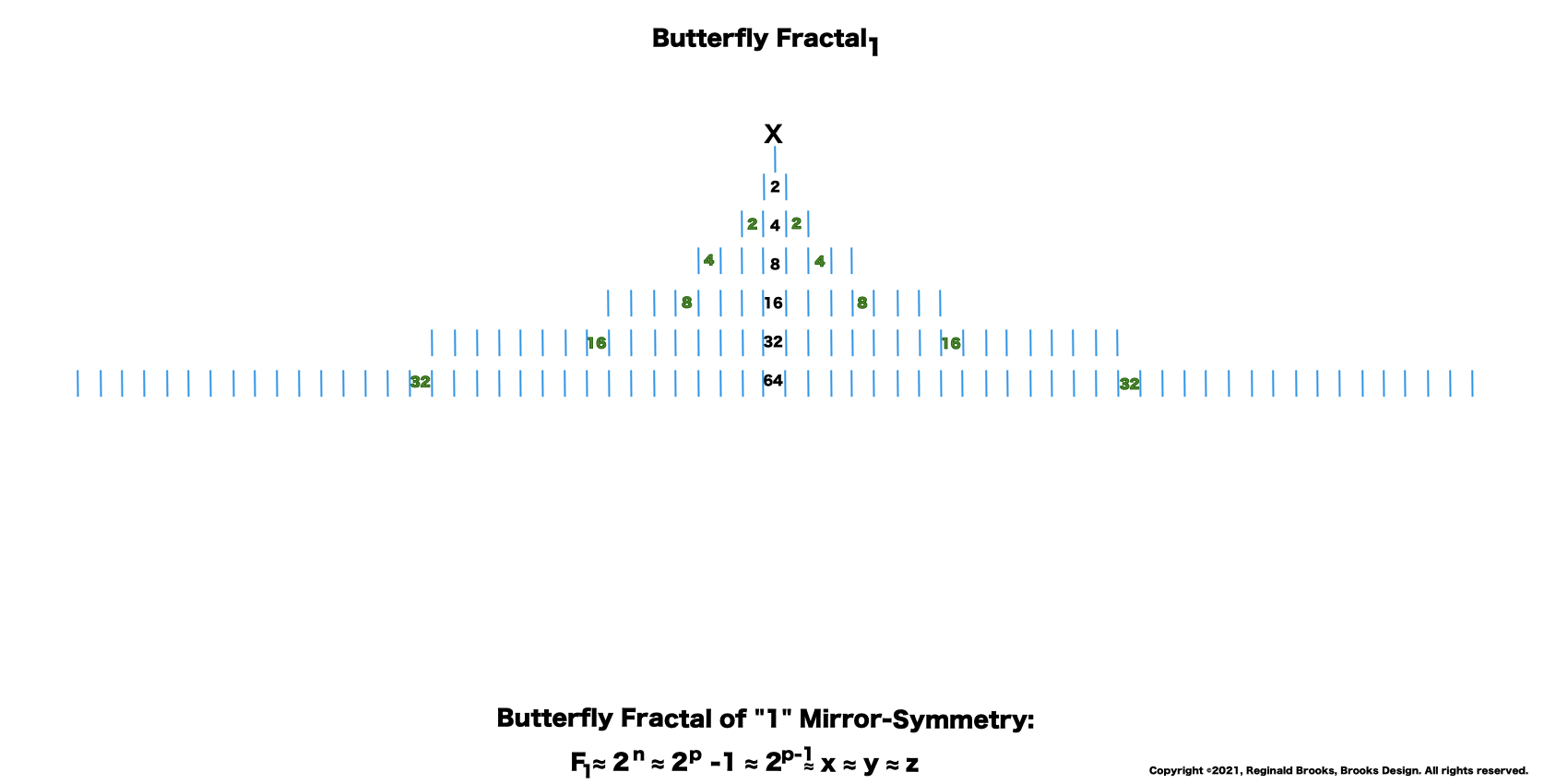
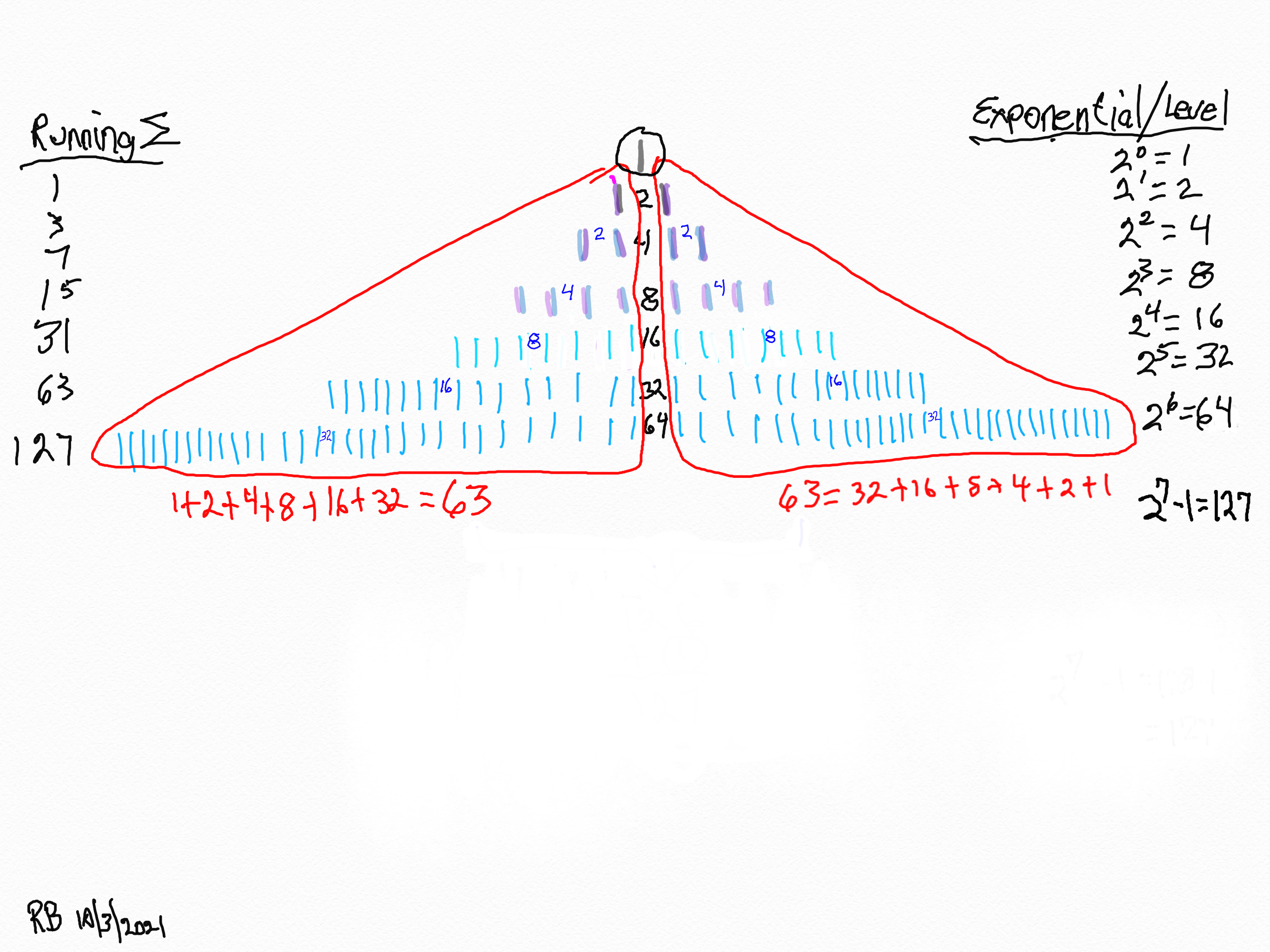
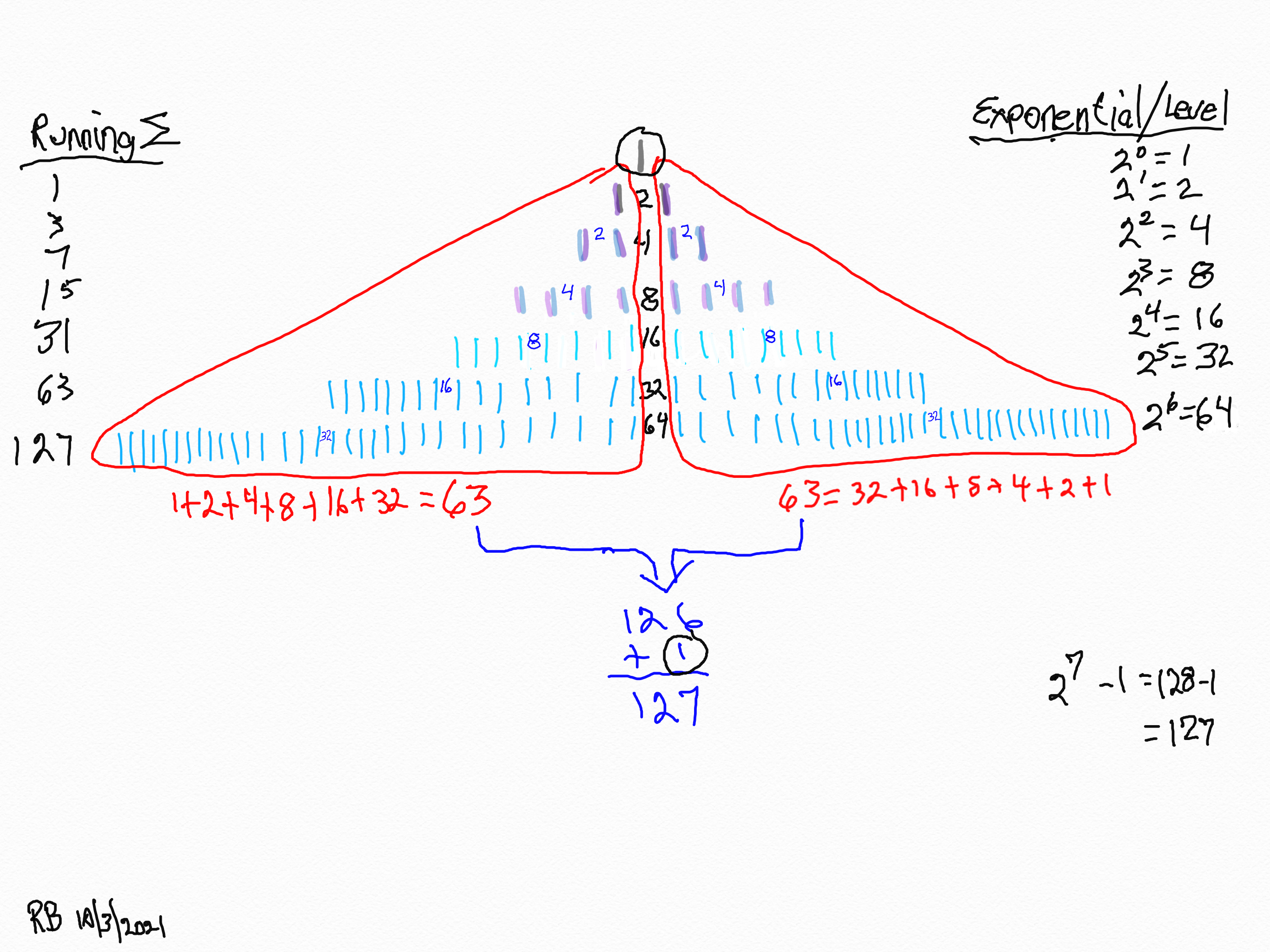
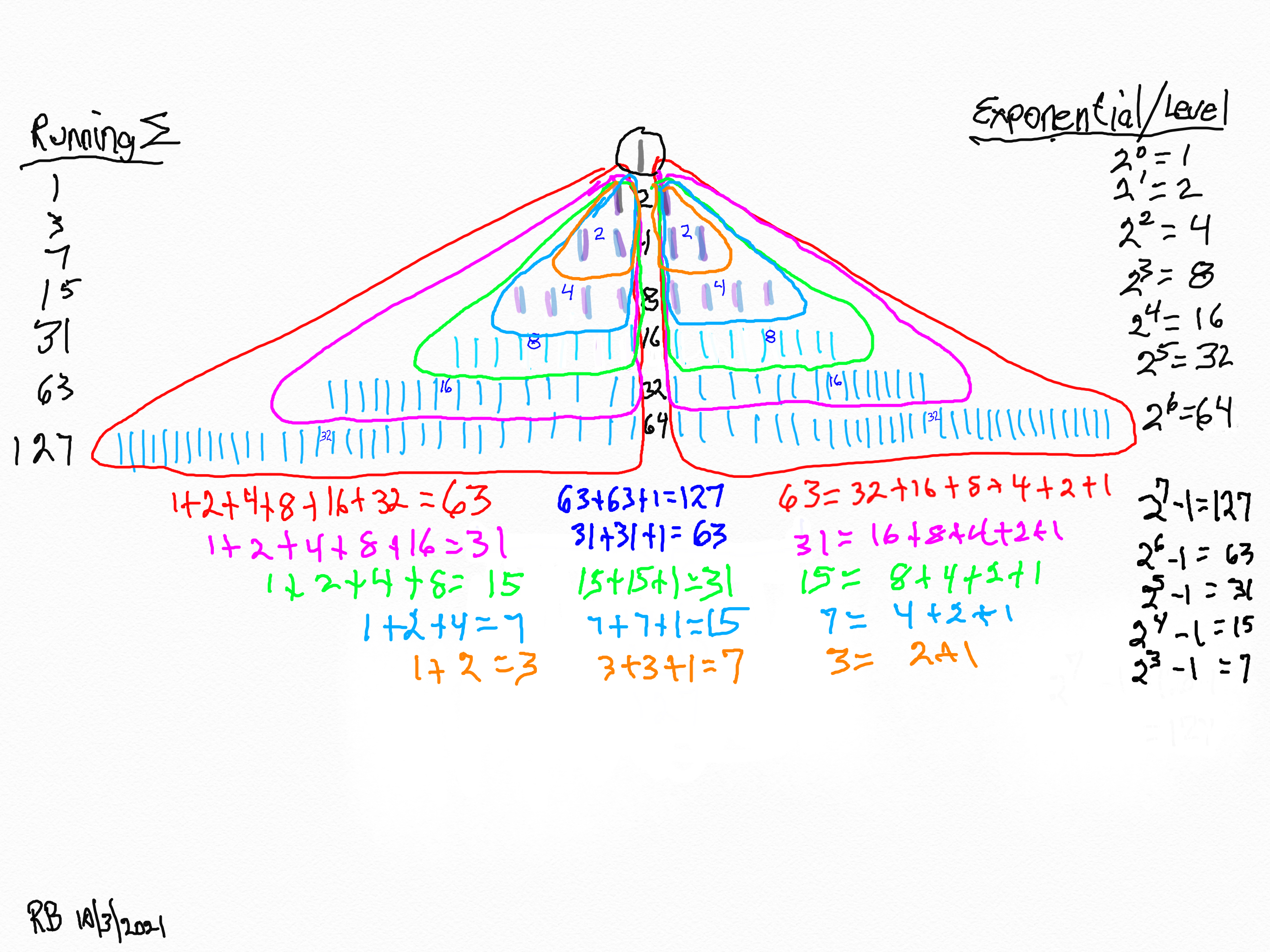
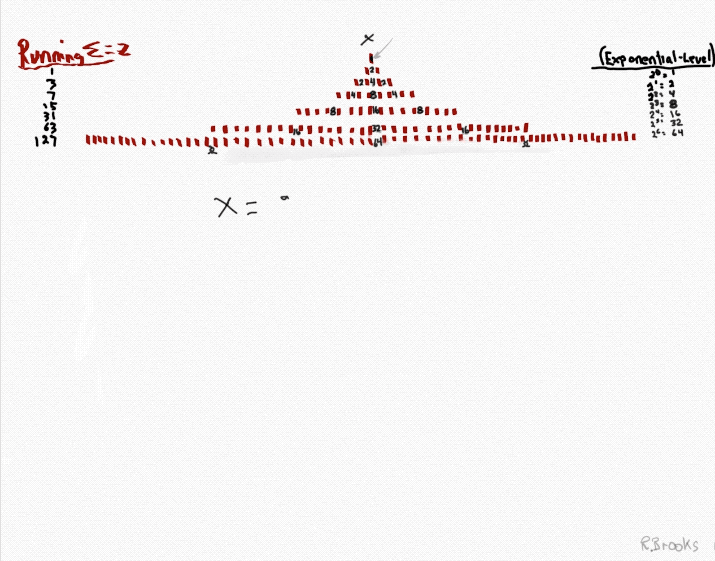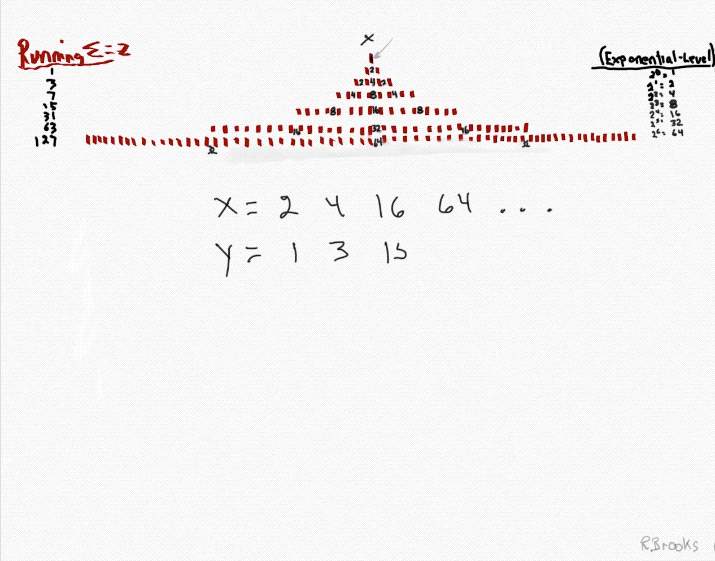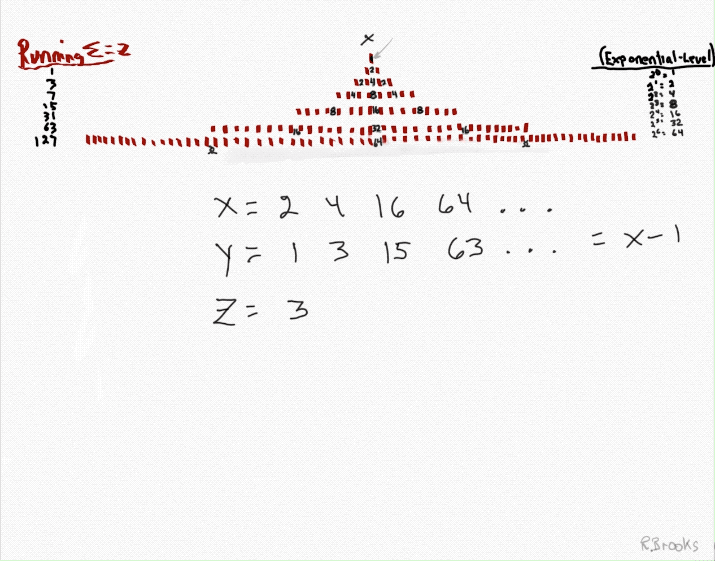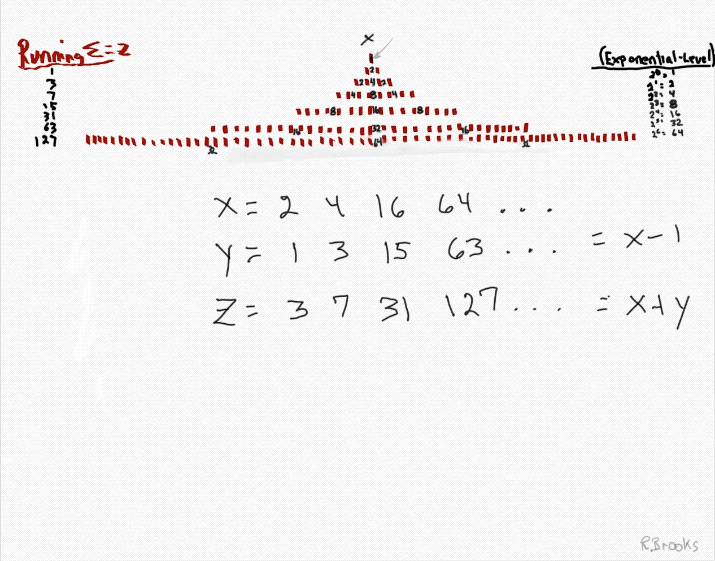
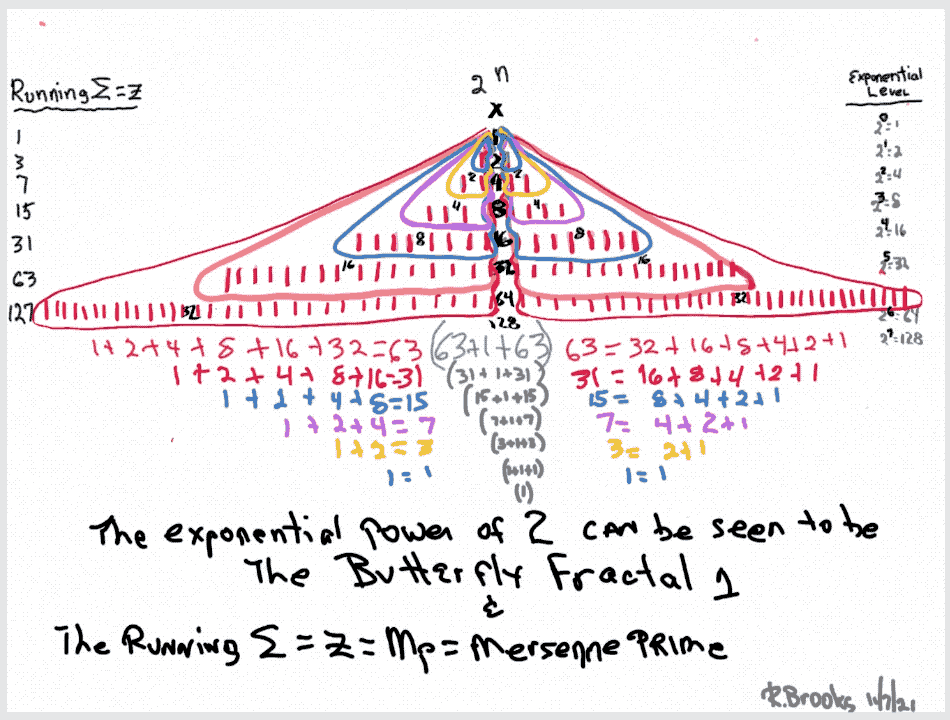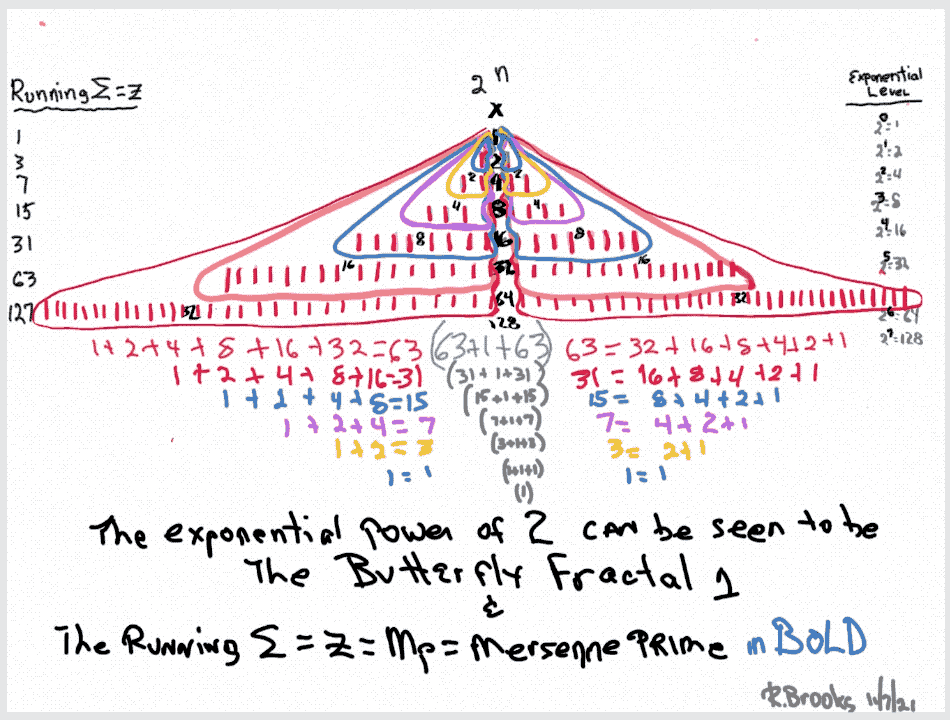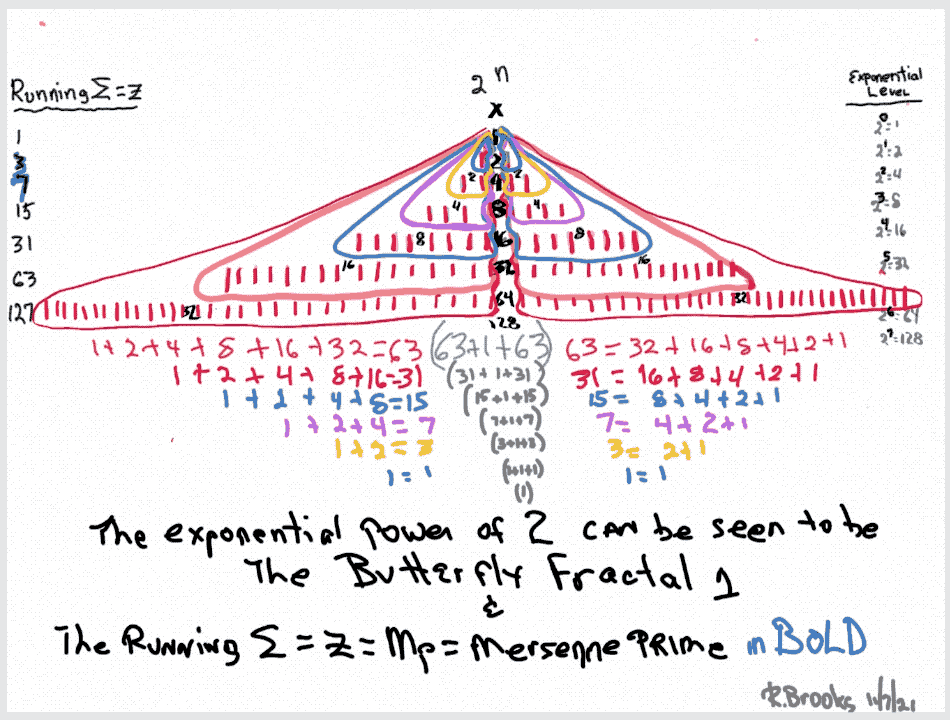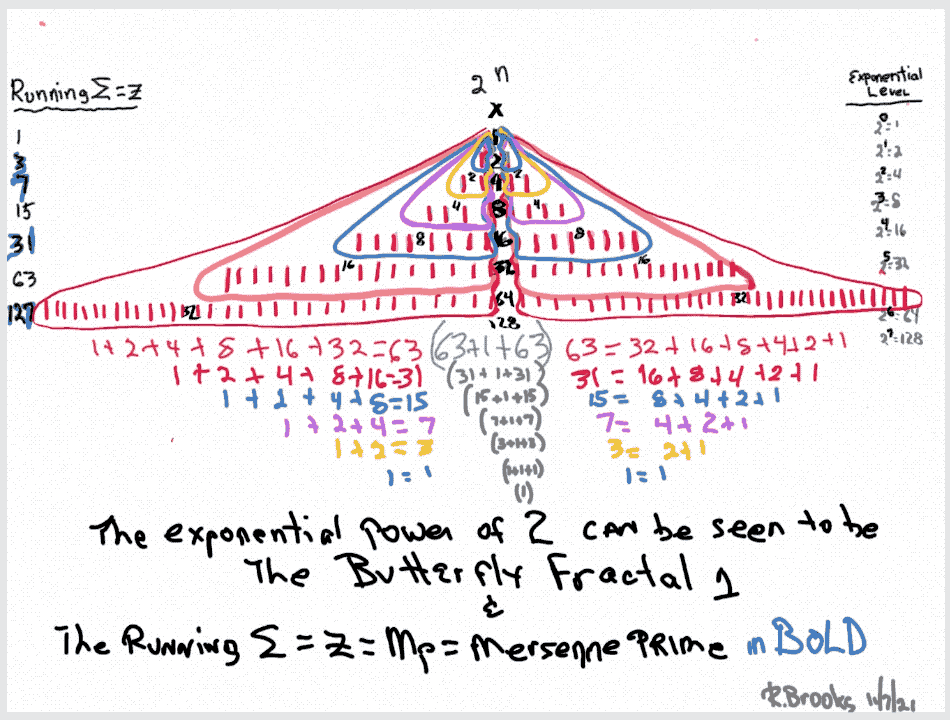
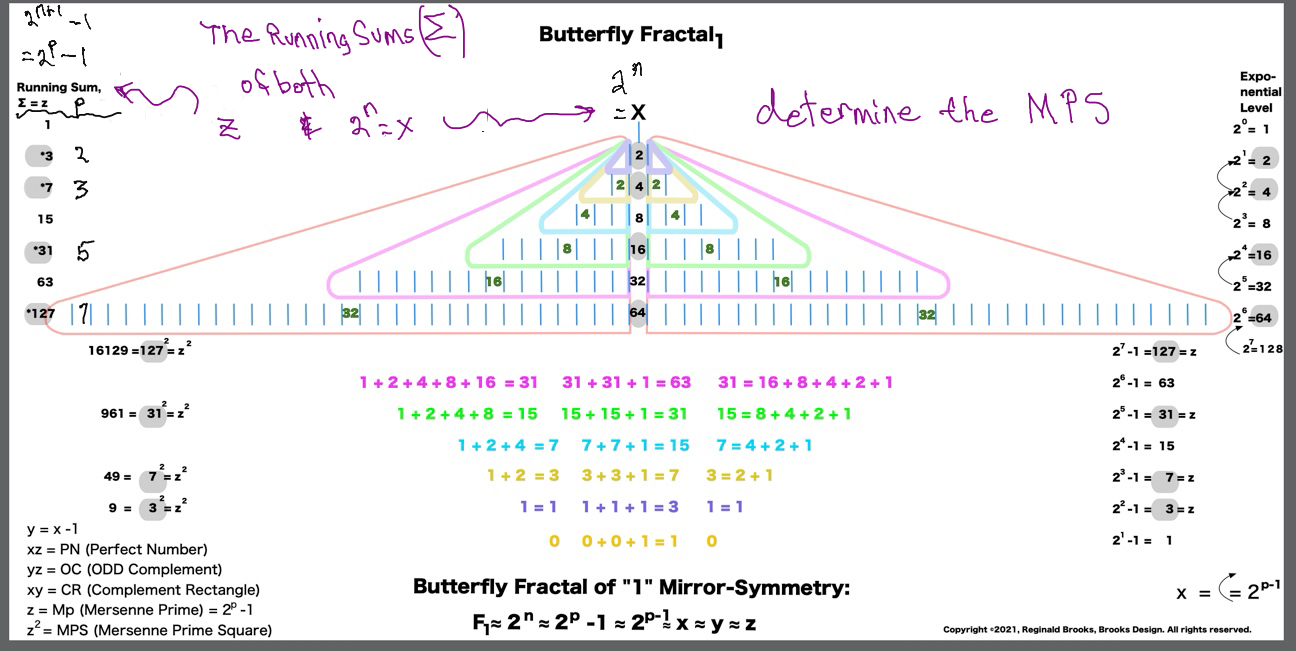
Letting the Fractal "1" (F~1~) simply double itself and then let the result double itself, and that result double itself -- a successive doubling -- generates a bi-lateral mirror-symmetric fractal pattern whose mirrored sides exactly repeat the pattern of the "whole!" The resulting image is aptly called the "Butterfly Fractal~1~" and not only does it more than suggest the patterns of butterflies and moths, it also generates the key values within the MPS Table as the *running sum (∑) of each doubling and the exponential value of each doubling level are considered.

The following literal, step-by-step doubling of F~1~ in graphical form will explicitly reveal these properties as inherent NPSs to the process itself. They are also directly translatable to the MPS on the universal grid above. Every step of the way. In fact, one could say this F~1~ NPS is the very basis of the Perfect Number - Mersenne Prime theorem (Eulic-Euler Theorem ), and, the discovery shown within this work -- the MPS -- that the Mersenne Primes are directly related to the AREAS they form and the component AREAS of the PN, OC, PNS, OCS and CR.

*running sum (∑): The summation of a series/sequence is presented mathematically as

$\sum{j=m}^{n}{a{j}\; }=\; a{m}\; +\; a{m+1\; +\; ...\; +\; a_{n}}$

where m=lower limit, n=upper limit and j = index of summation. Another example is

$\sum_{i=1}^{n}{i³\; }$

for the running sum of integers cubed starting with 1, with to be defined n=1,2,3,...

Throughout this work, we will simply the mathematical expressions for taking the progressive sum of a series/sequence of numbers by referring to it as the "Running Sum (∑)."

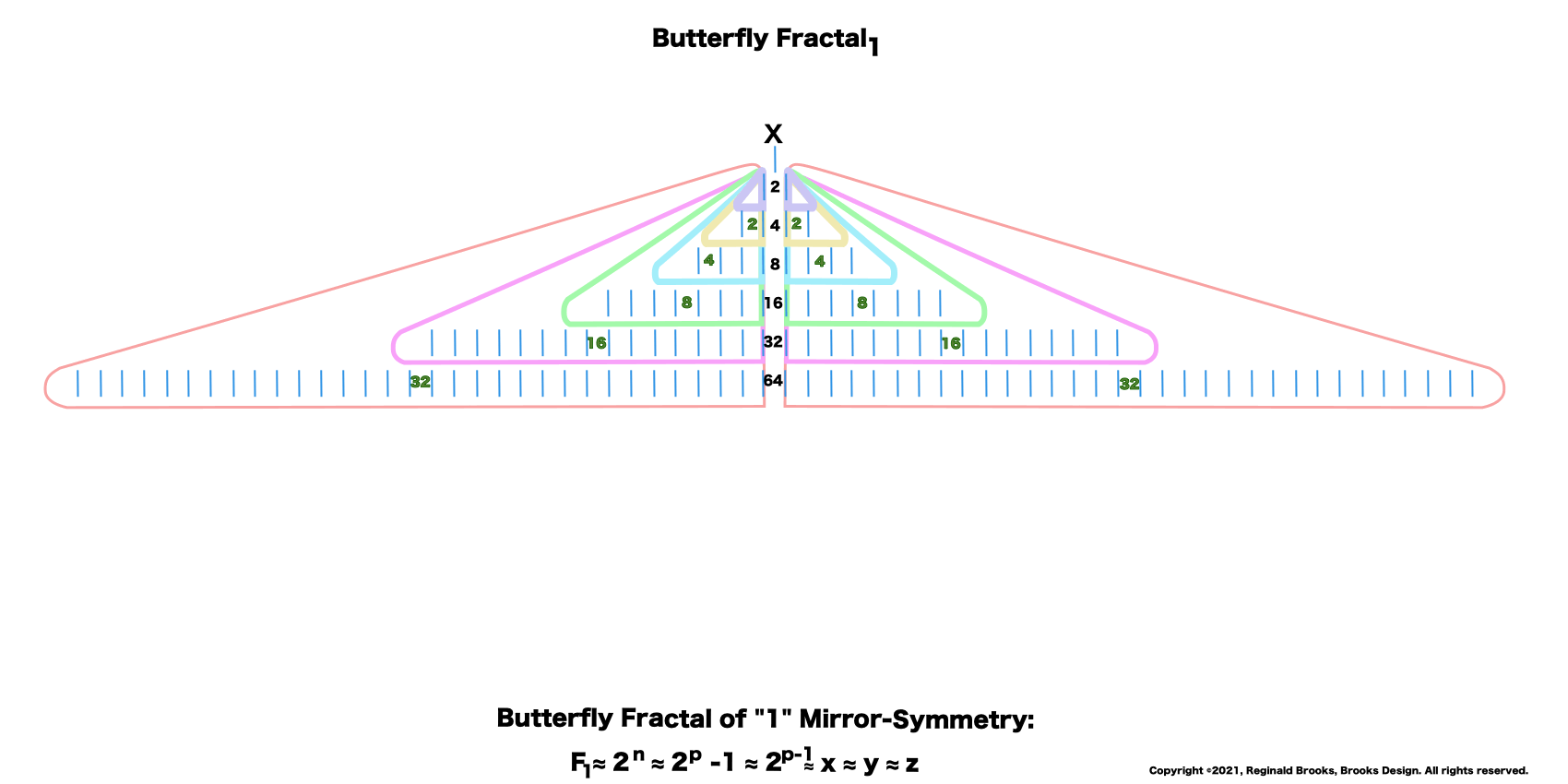
The Butterfly Fractal of "1" Mirror-Symmetry: F~1~≈2ⁿ≈2^p -1≈2^p-1≈x≈y≈z.

BIM-MPS_Exp2-1.mp4

BIM-MPS_Exp2-1.gif

BIMMPS_Fractal-1-30seq.mp4

BIMMPS_Fractal-1-30seq.gif

BIMMPS_Fractal-1-30 IMAGE SEQUENCE is presented below.

1. We start with "1."

2. x = the short side of the PN rectangle, and y = x-1, the short side of the OC rectangle, together sum ∑ to = z = Mp = the long side of the PN and OC rectangles and the basis of the MPS=z². Here, the "x" is the number value of each of the rows of the exponential power of 2. The first row, x = 1.

3. The second row, x = 2.

4. The third row, x = 4.

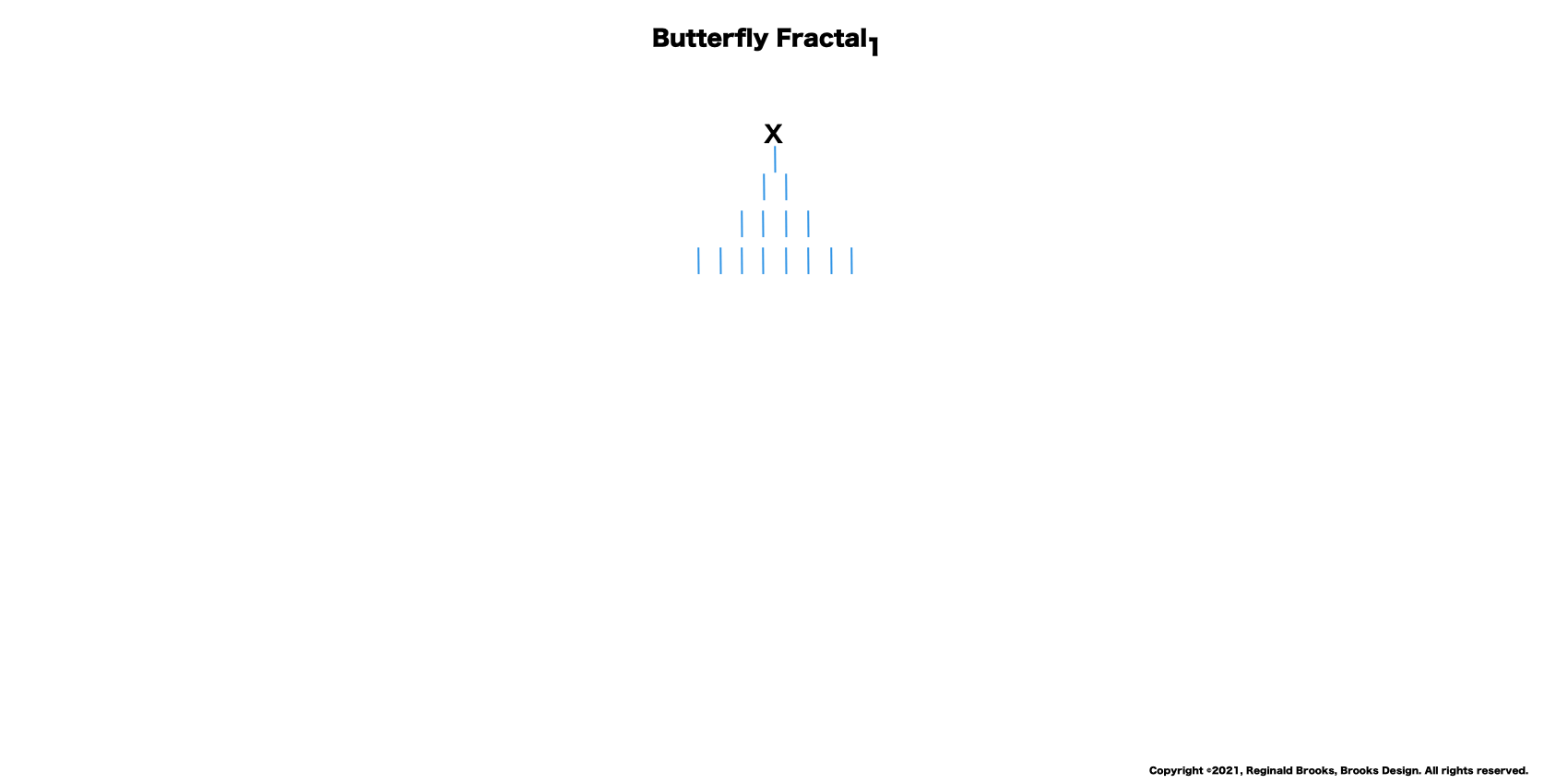5. The fourth row, x = 8.

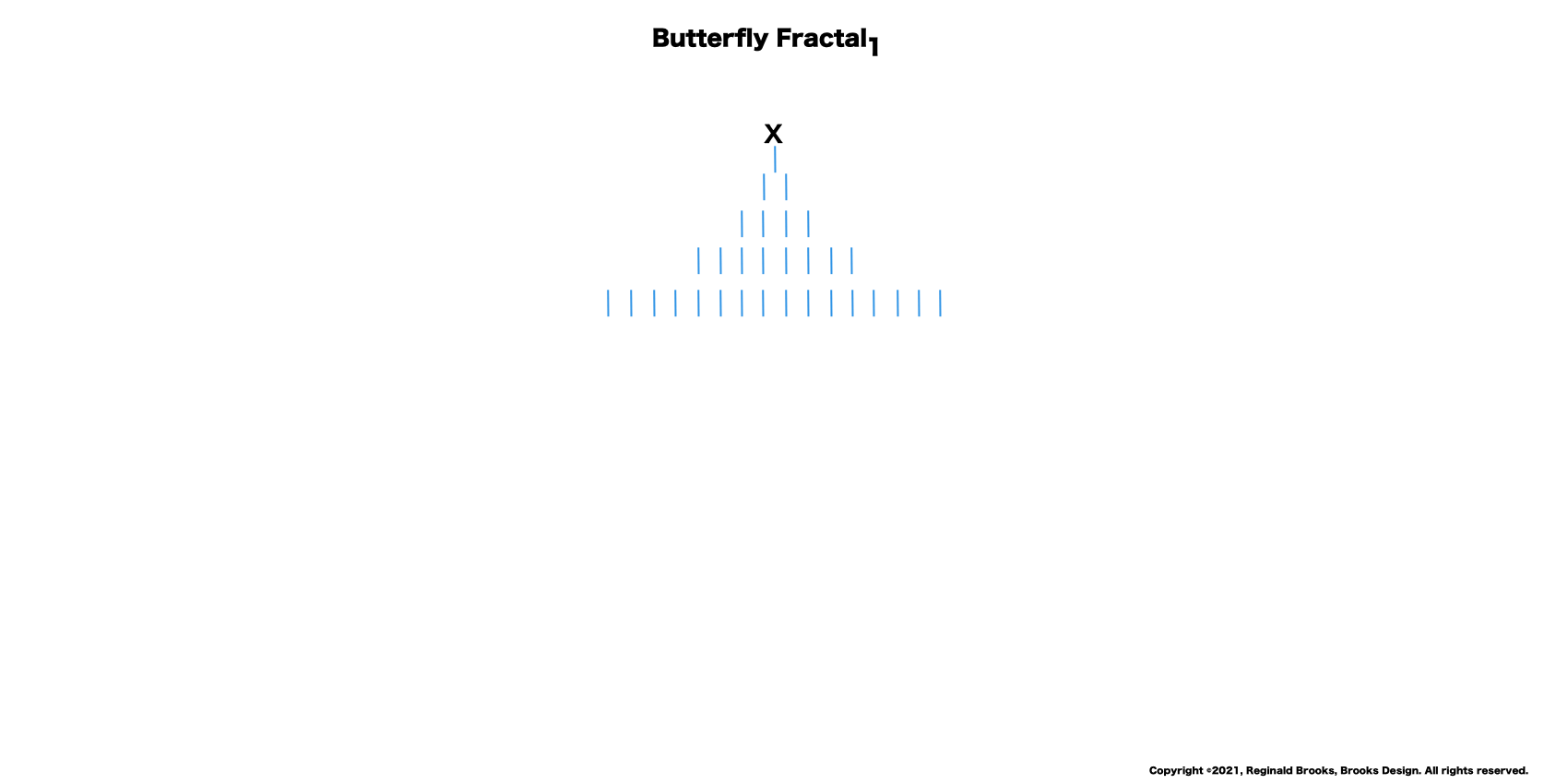6. The fifth row, x = 16.

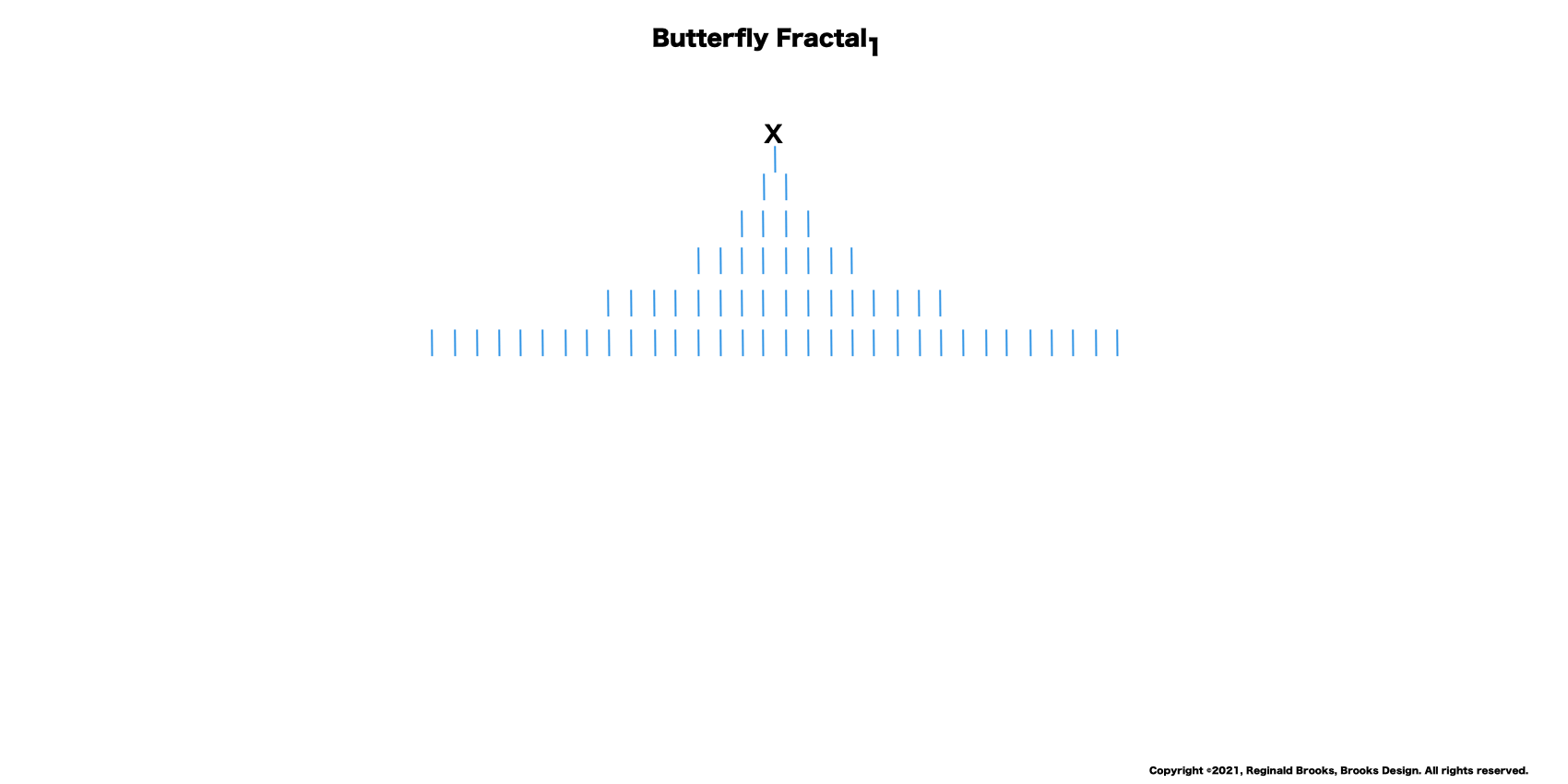7. The sixth row, x = 32.

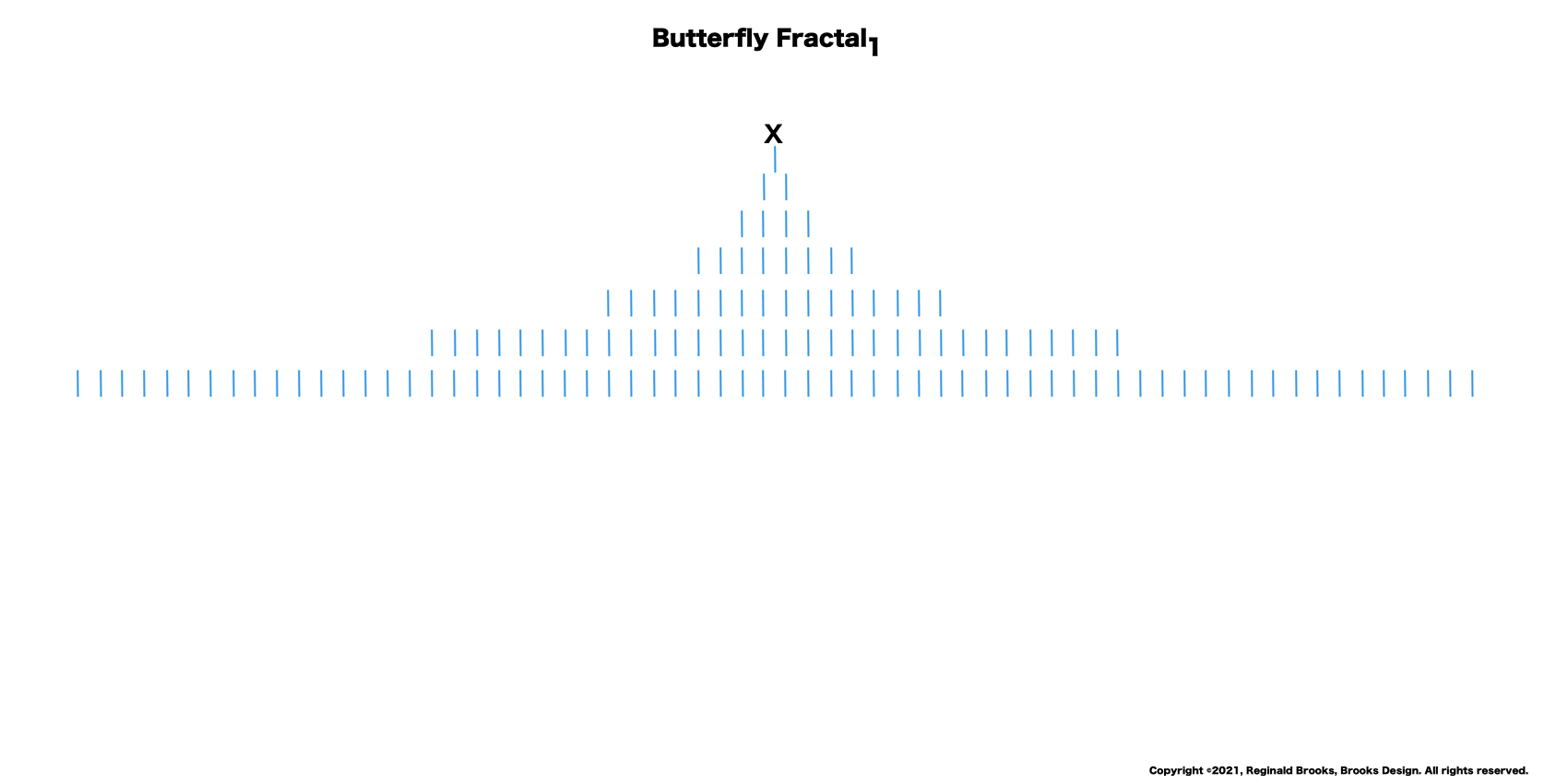8. The seventh row, x = 64.

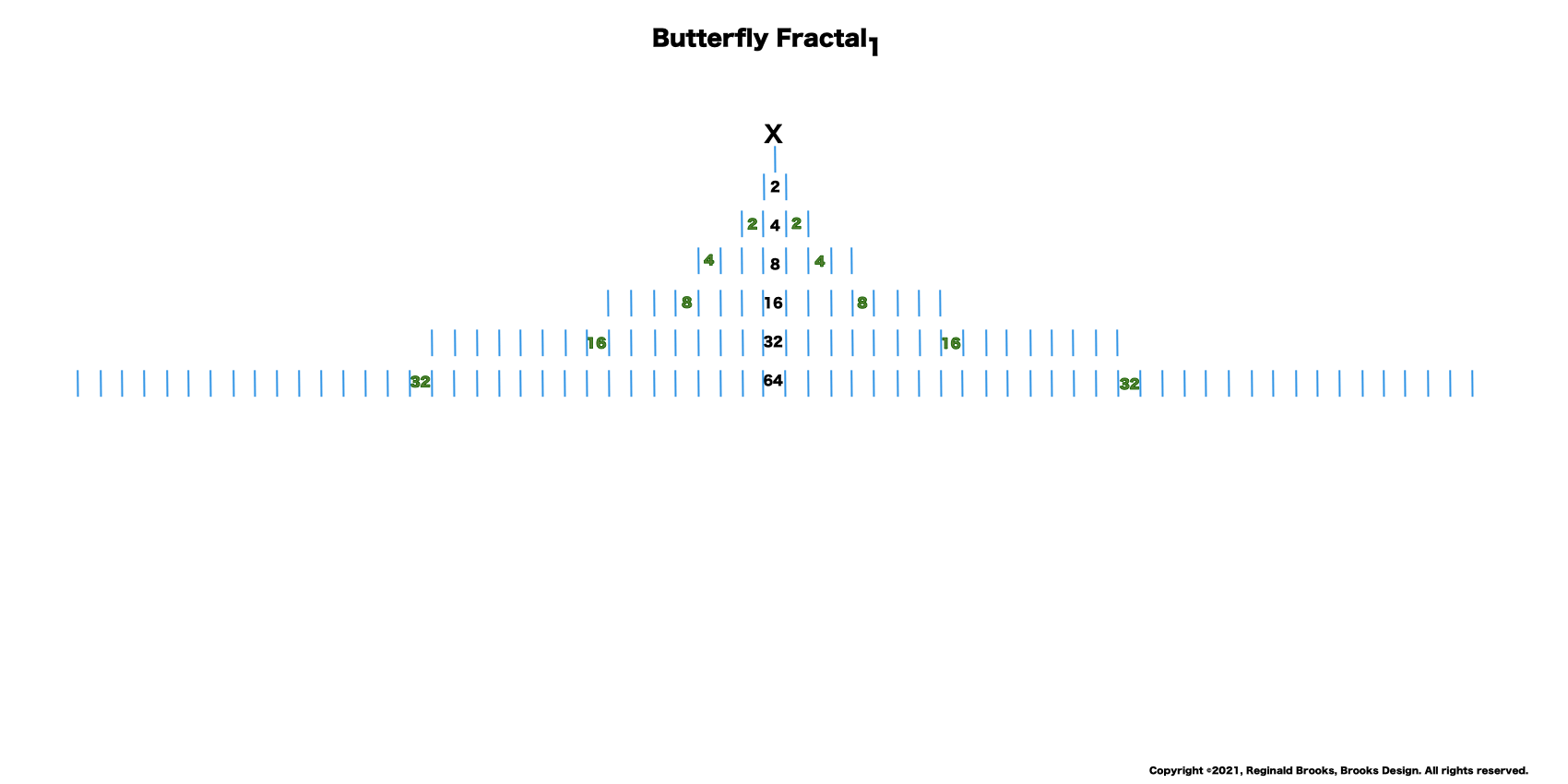9. Notice how the same identical NPS of the central column of the exponential power of two is fractally

repeated as the mirror-symmetry sides of the central column -- 2-4-8-16-32-...

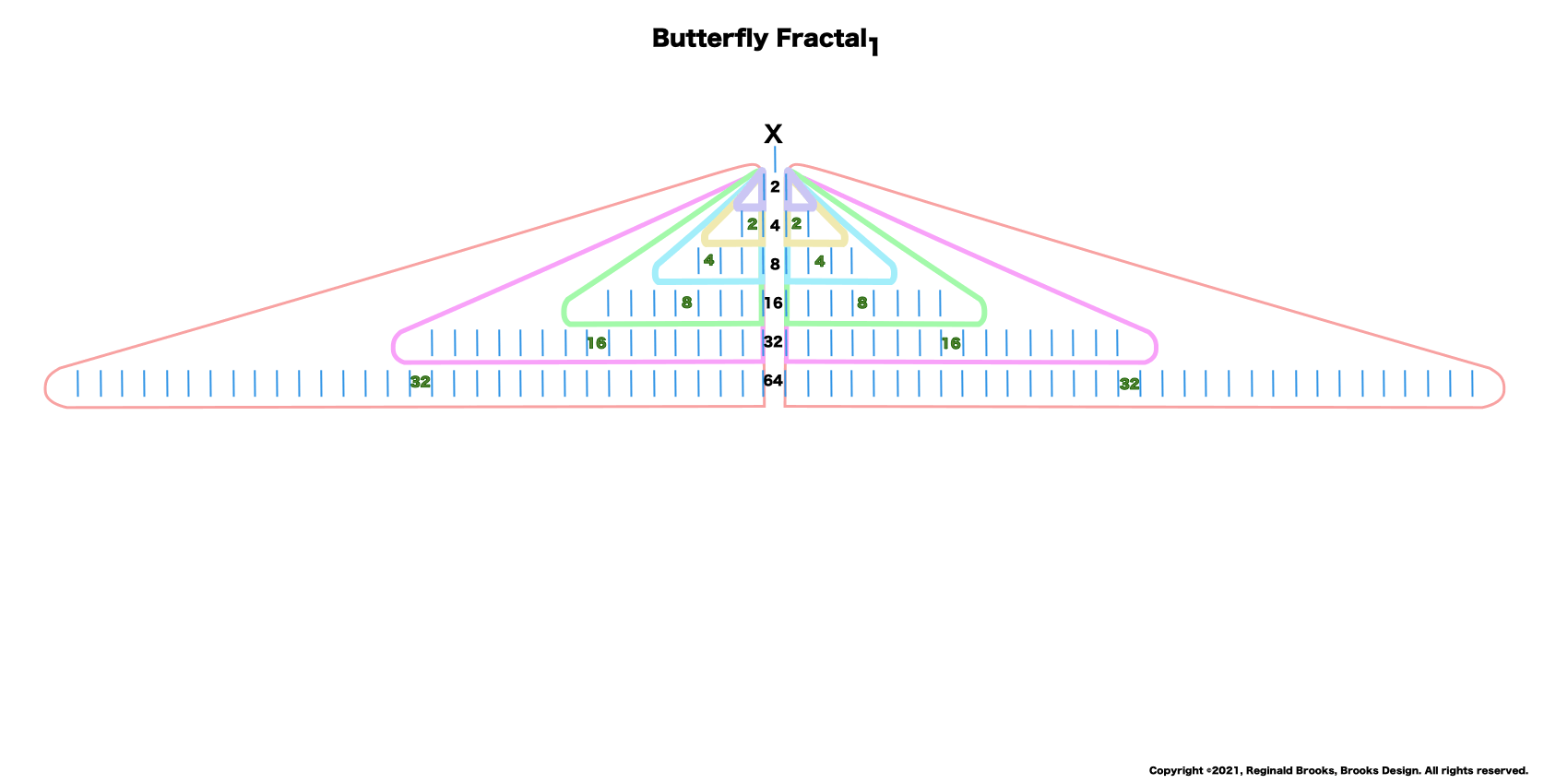10. Encompassing each row as a set, we now have formed the Butterfly Fractal~1~.

11. Sometimes directly -- sometimes indirectly -- the Butterfly Fractal of "1" Mirror-Symmetry can account for all the forms of the MPS.

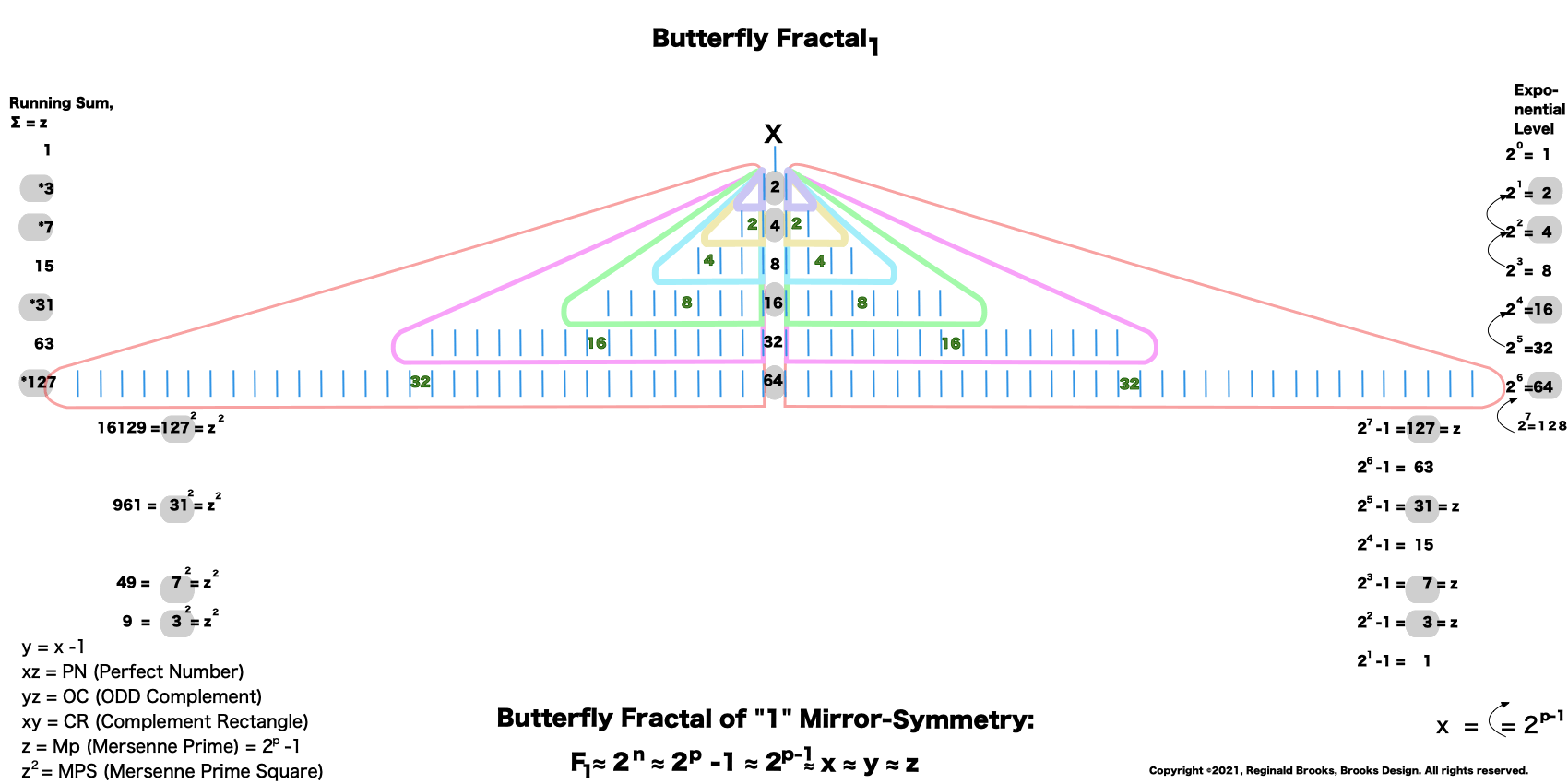
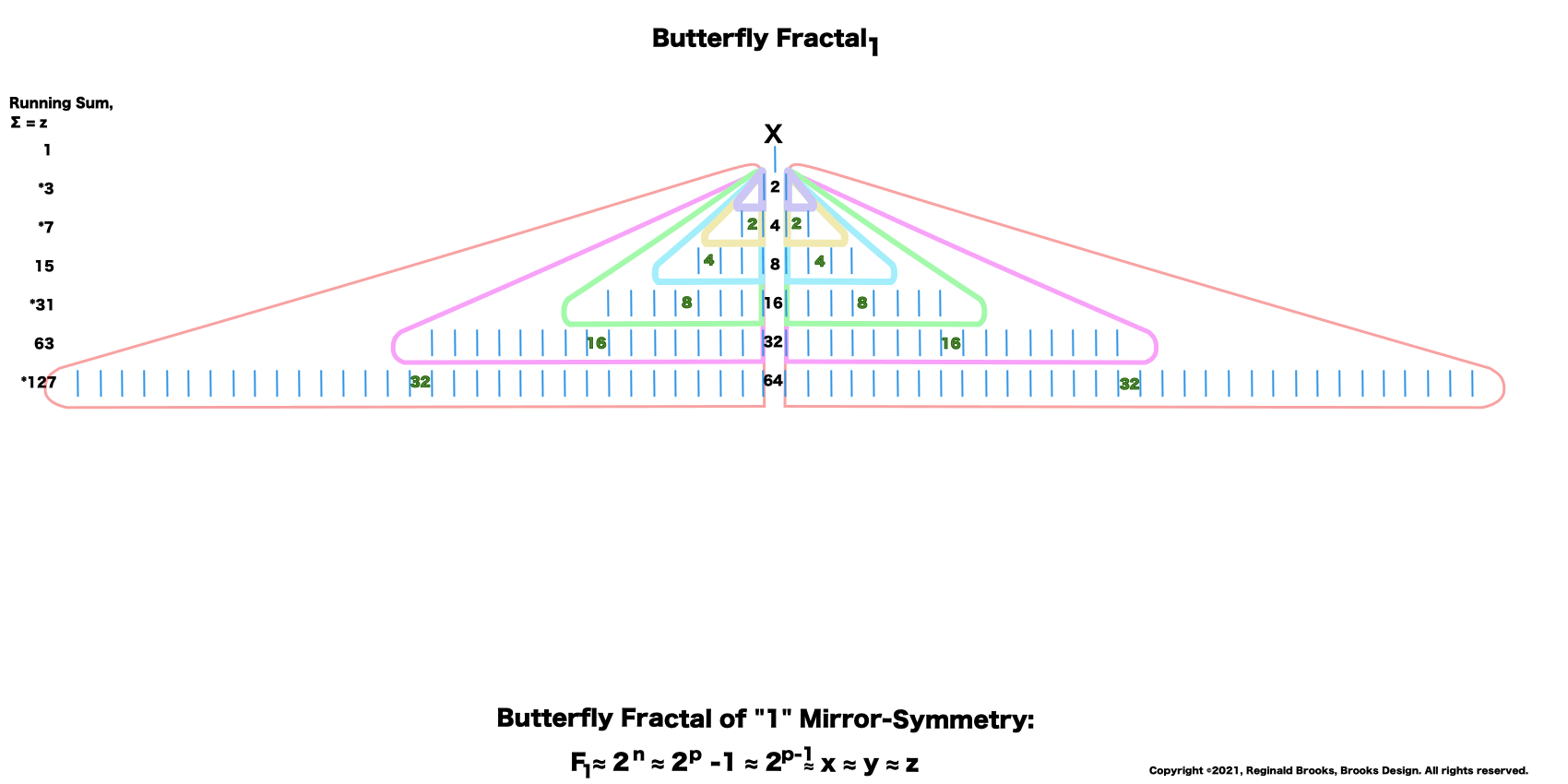12. On the left, the Running Sum, ∑ = z = Mersenne Prime = Mp is found by adding up a given row and all the rows preceding. The * refer to these being values of the MPS.

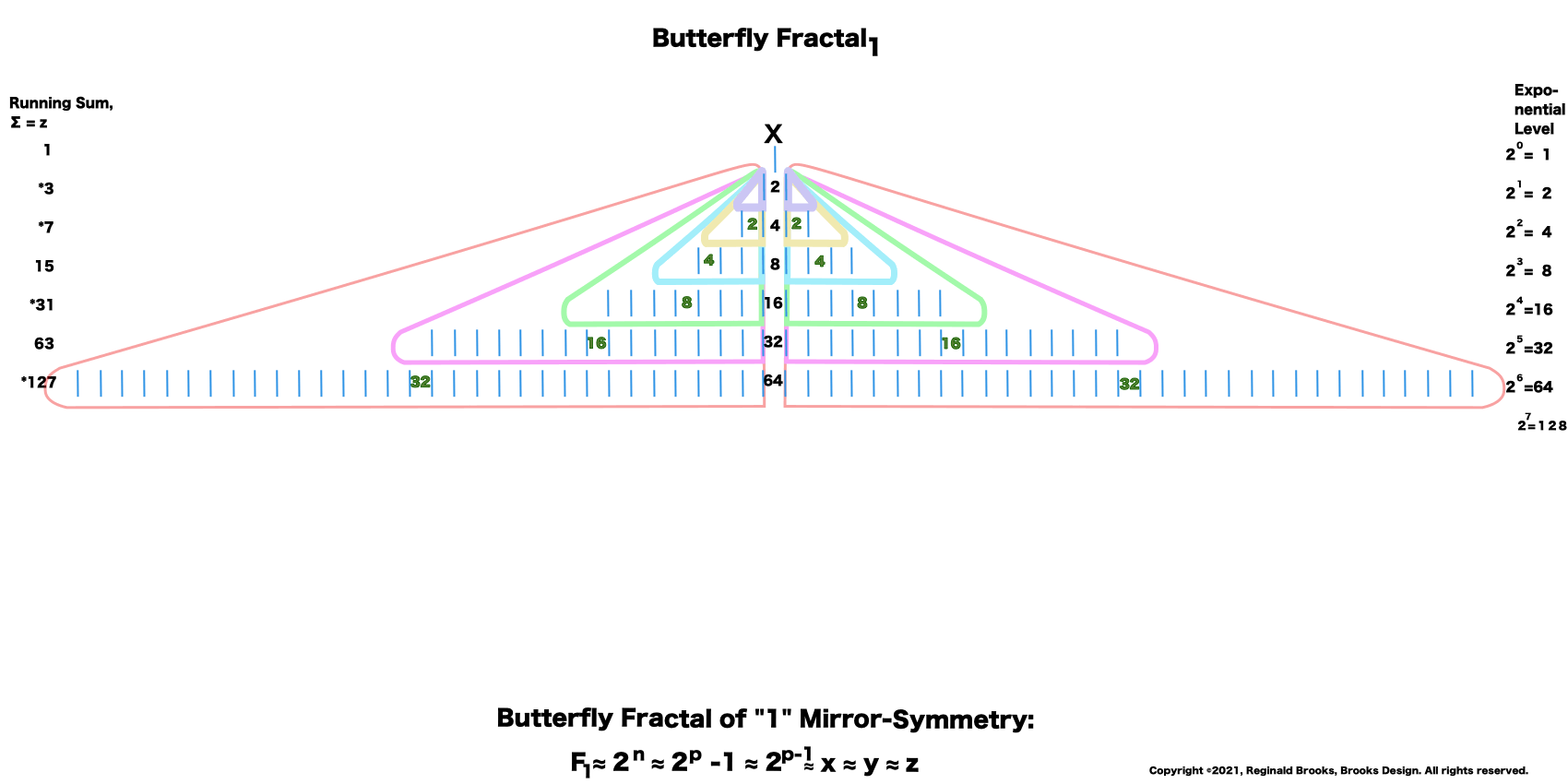13. The right column list is the Exponential Level or value of each row.

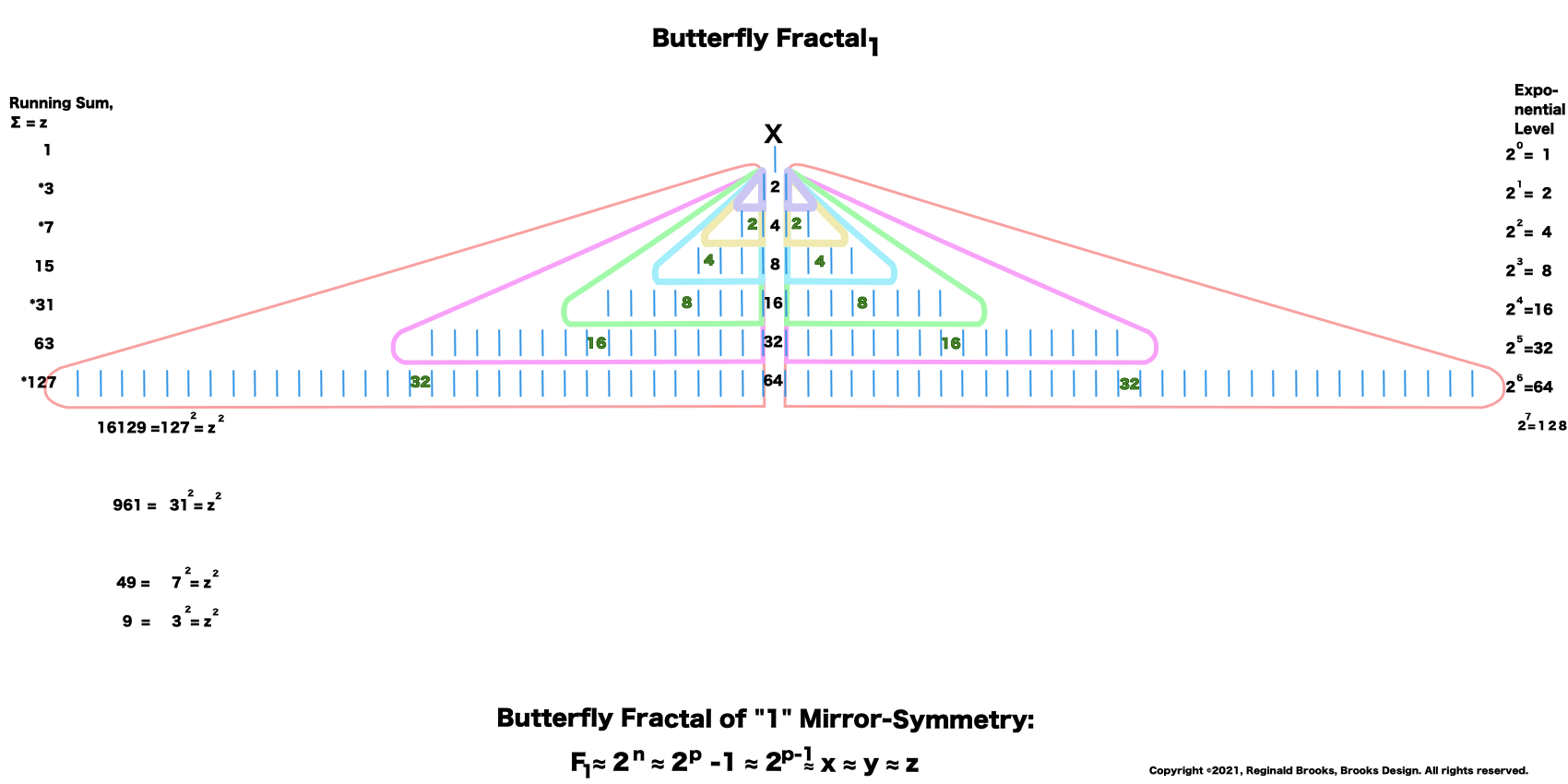14. The lower left column lists the square of z = z².

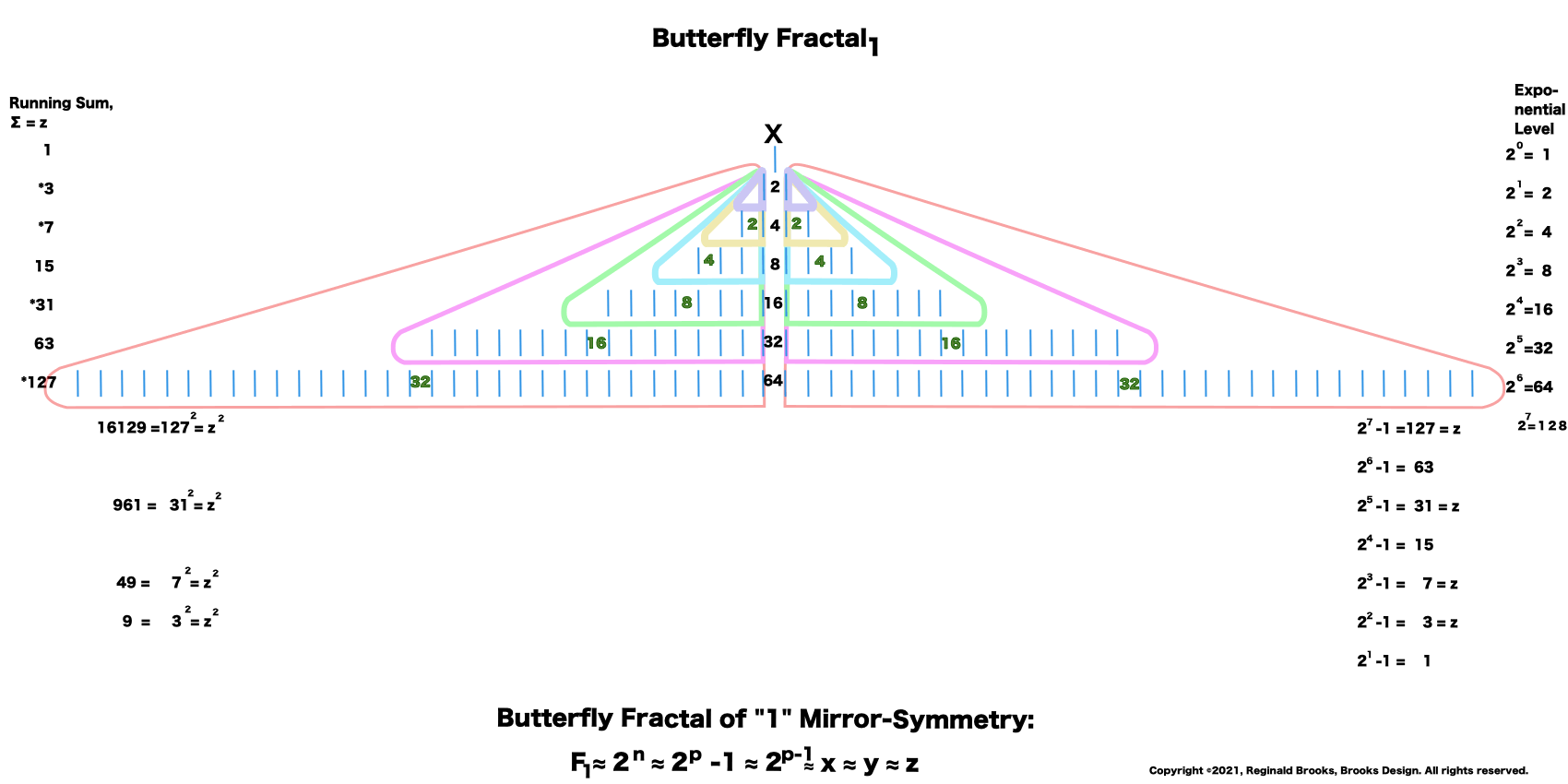15. The lower right column lists the Exponential Level -1. This is part of the Euclid-Euler Theorem as PN = (2ᵖ⁻¹)(2ᵖ -1), where p=prime.

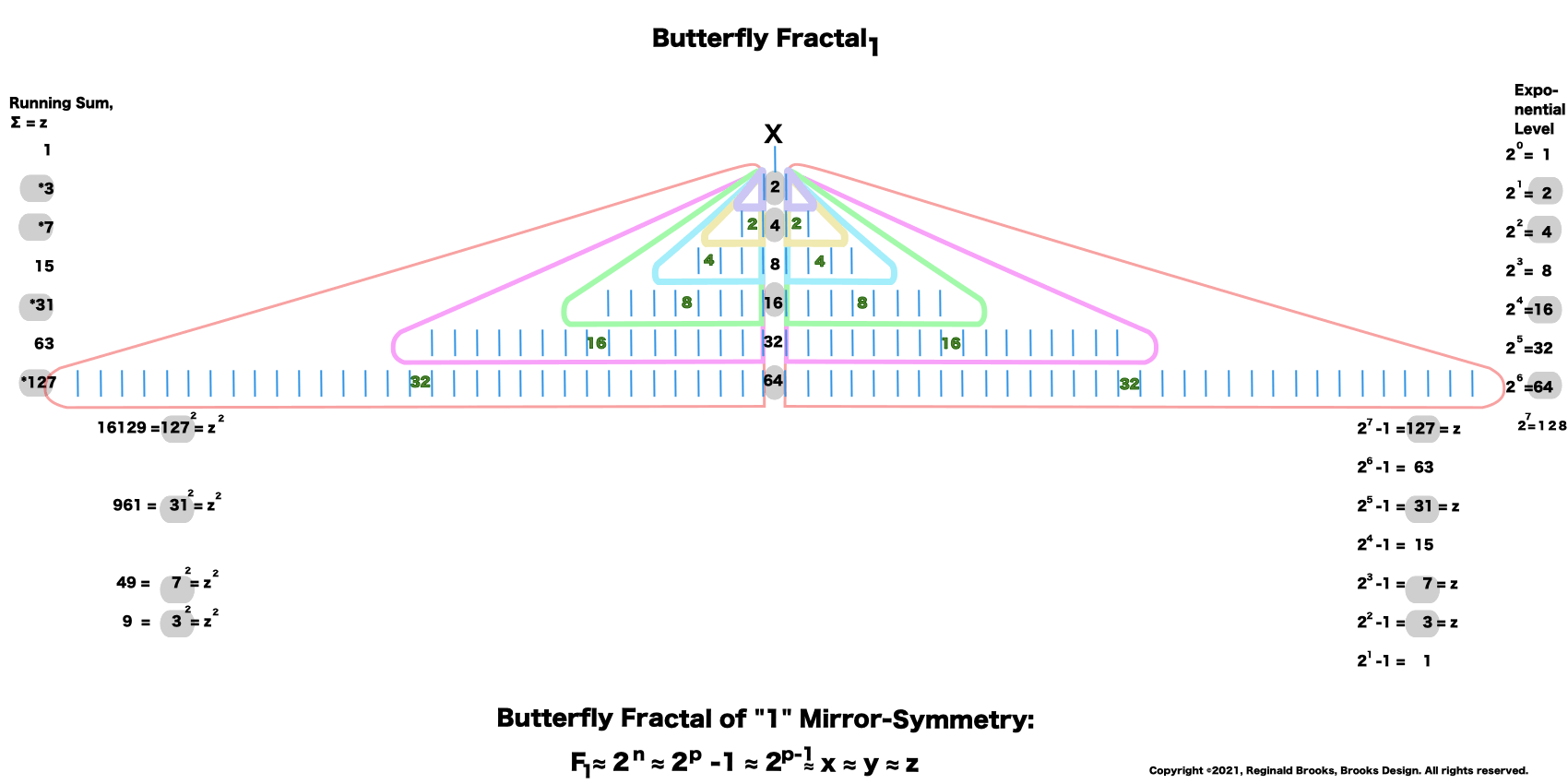16. The gray ovals = the * and refer to these being values of the MPS.

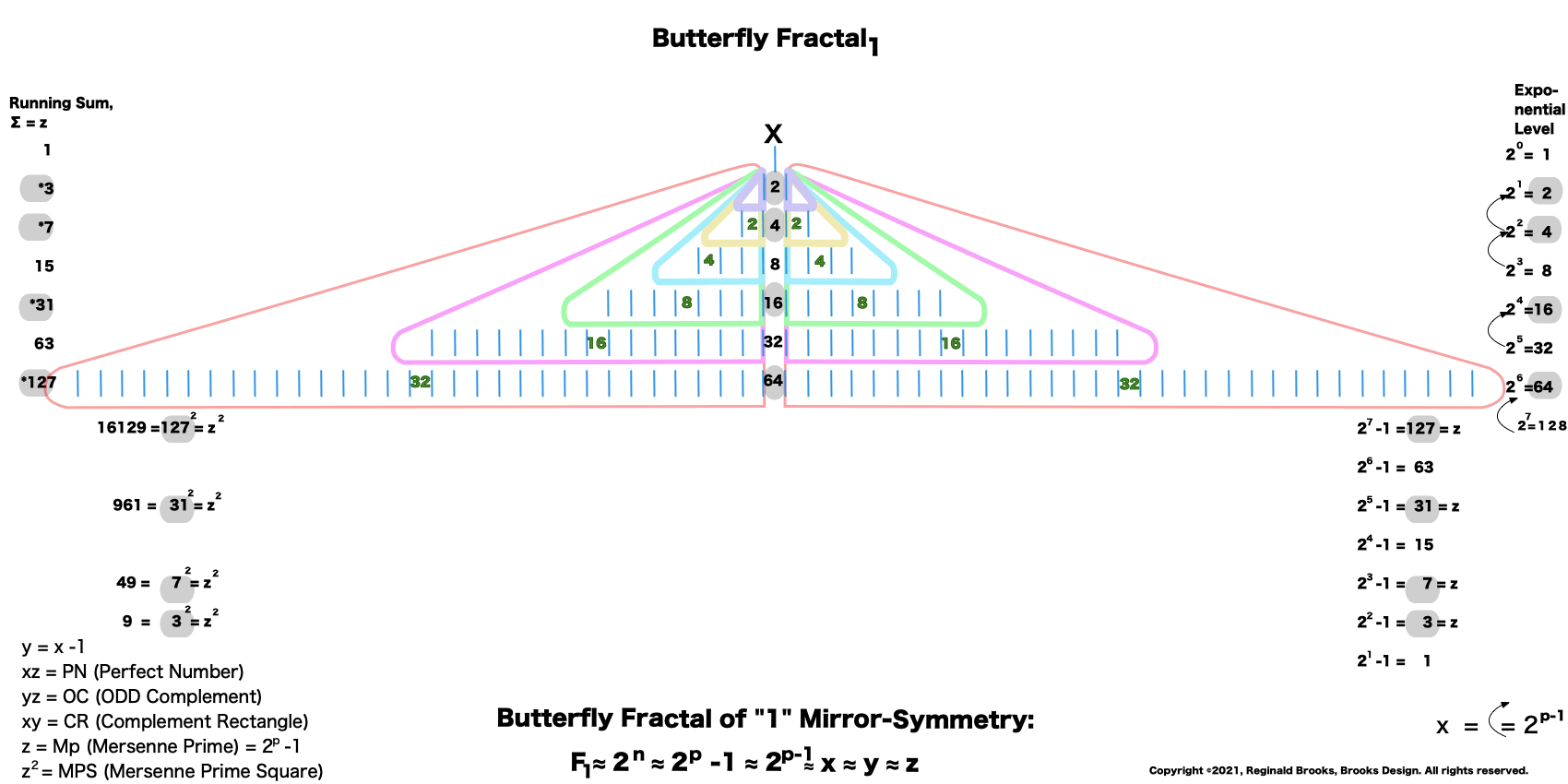17. The bottom left is the KEY to the MPS forms, and the arrows in the far right refer to the other part of the Euclid-Euler Theorem as x = 2ᵖ⁻¹.

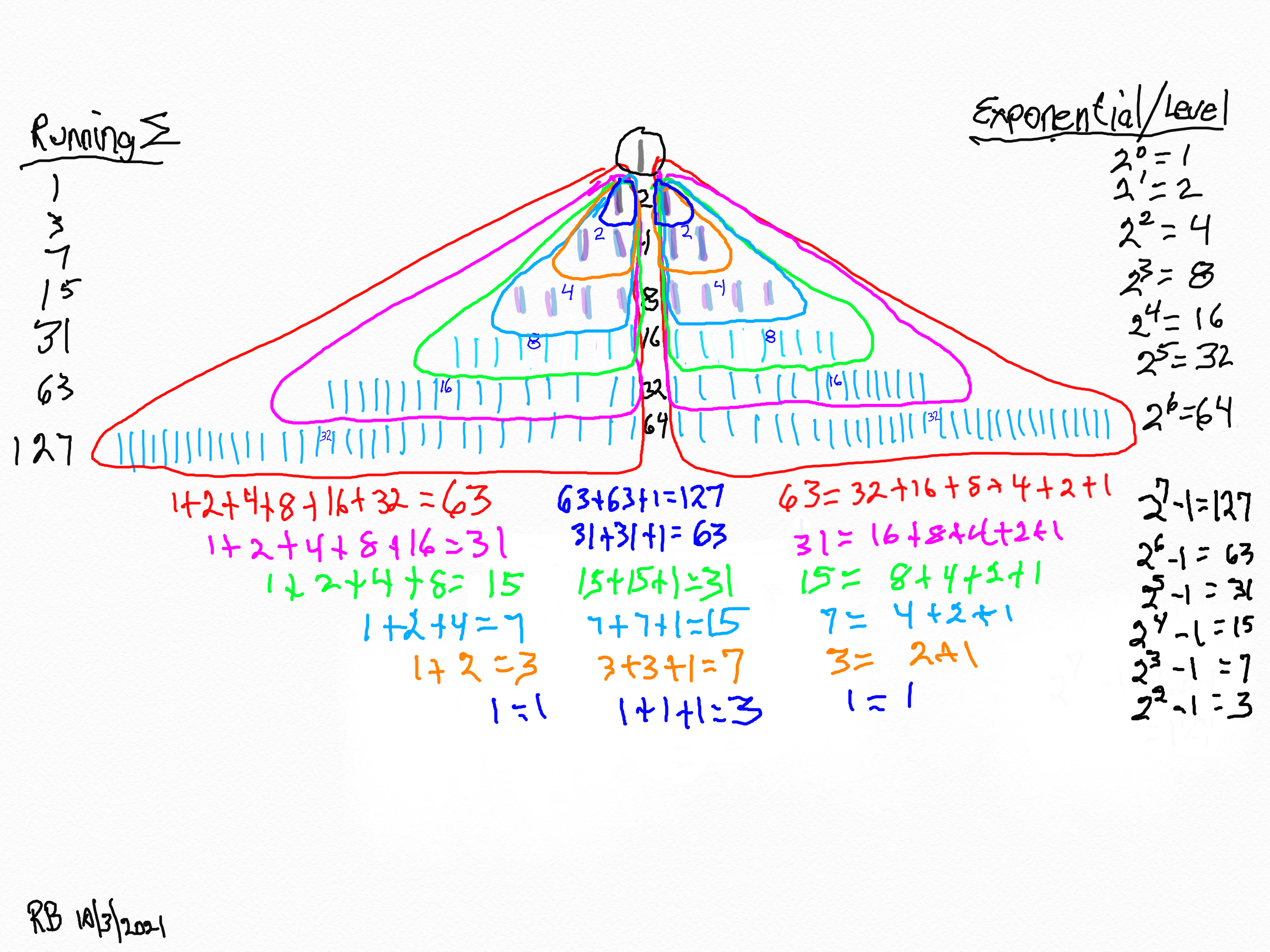
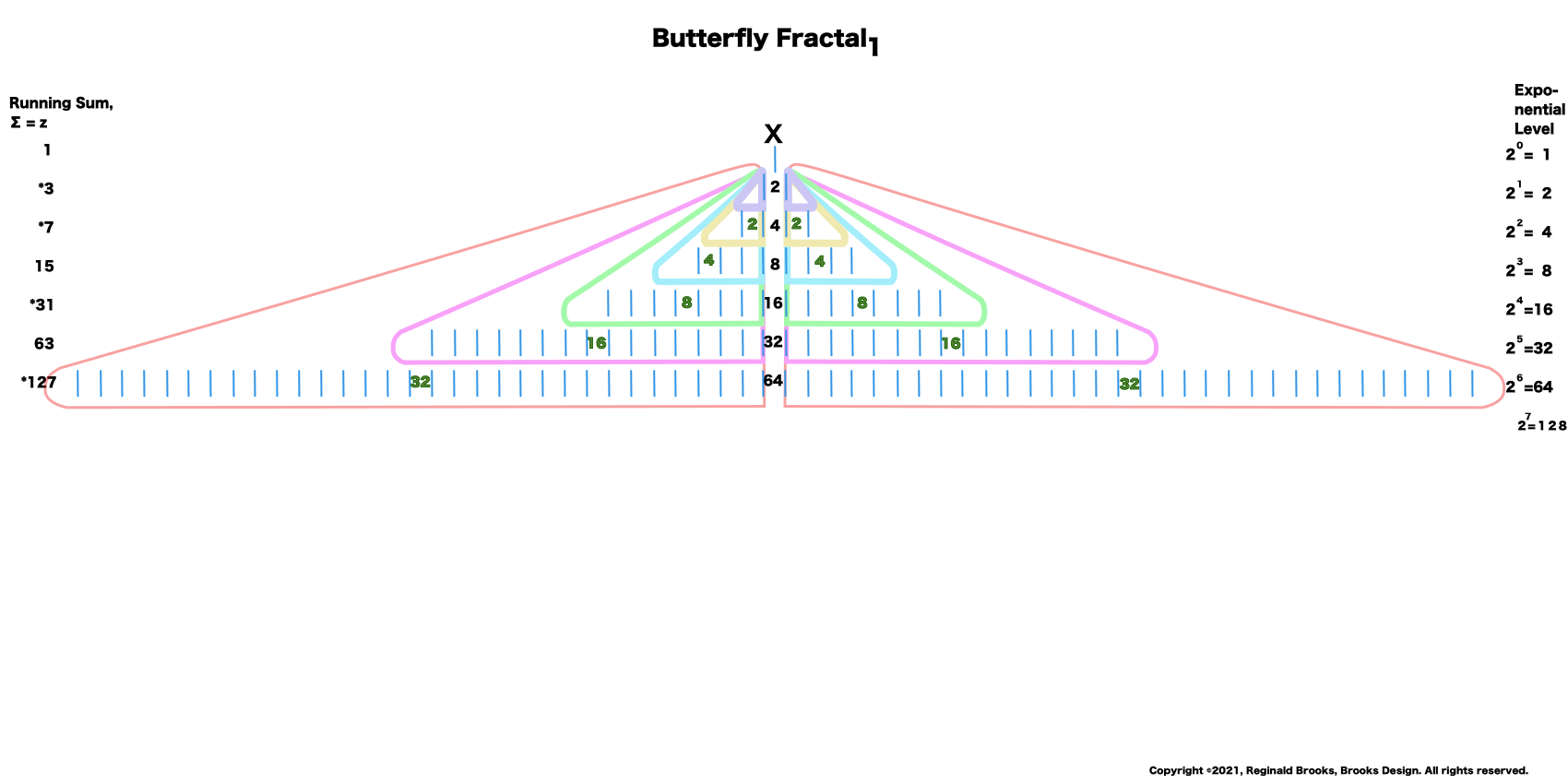18. Take a breather -- take it all in. Here is the simple Butterfly Fractal~1~.

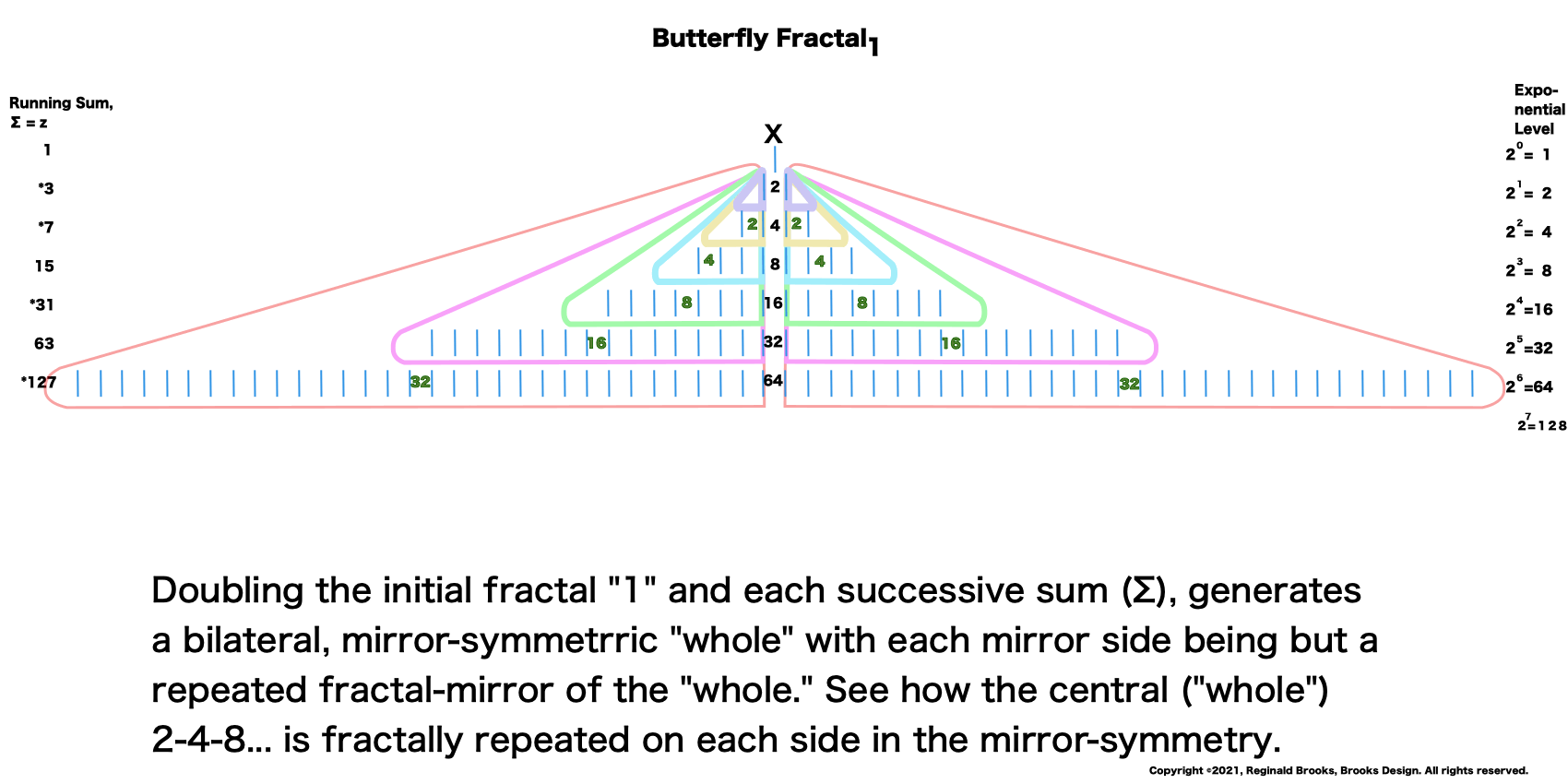19. Let's dig in!

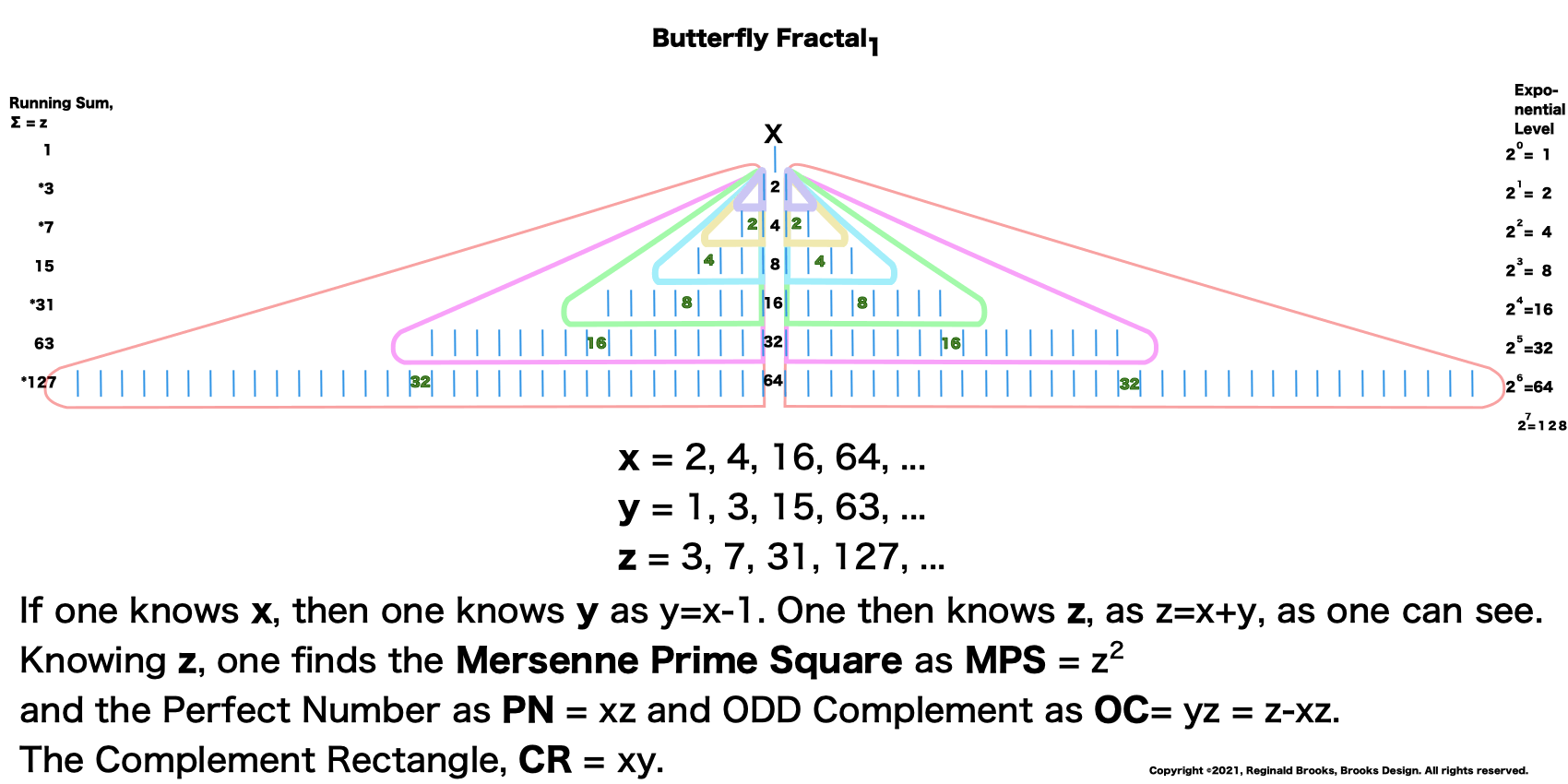20. It's all right here. Assigning x, y and z to the MPS generational forms helps simply the math, notation and visualization.

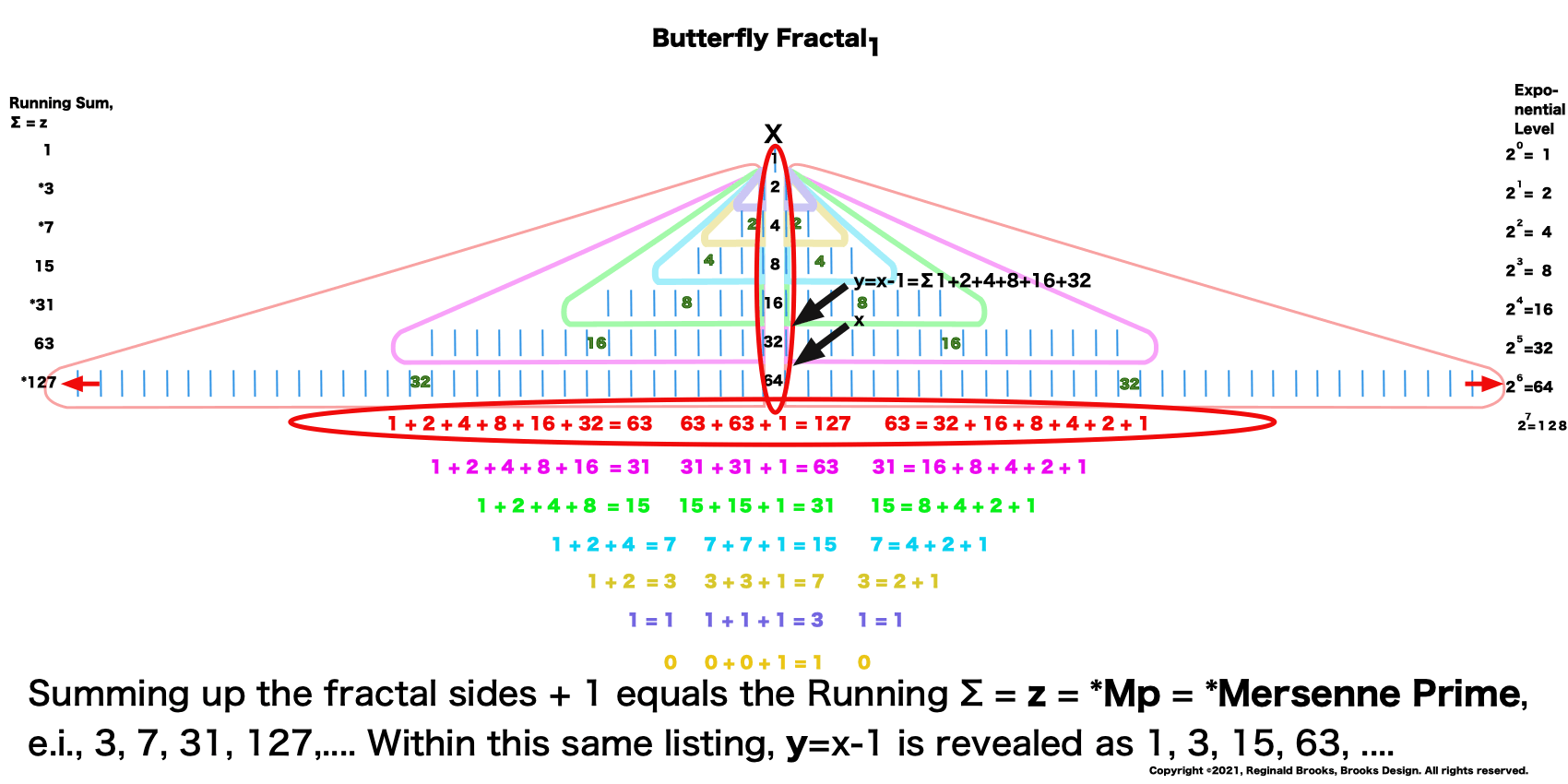21. For example, take the third (yellow-orange) row: 1+ 2 = 3 on one side, plus 1+2=3 on the other, plus "1" in the center=7.

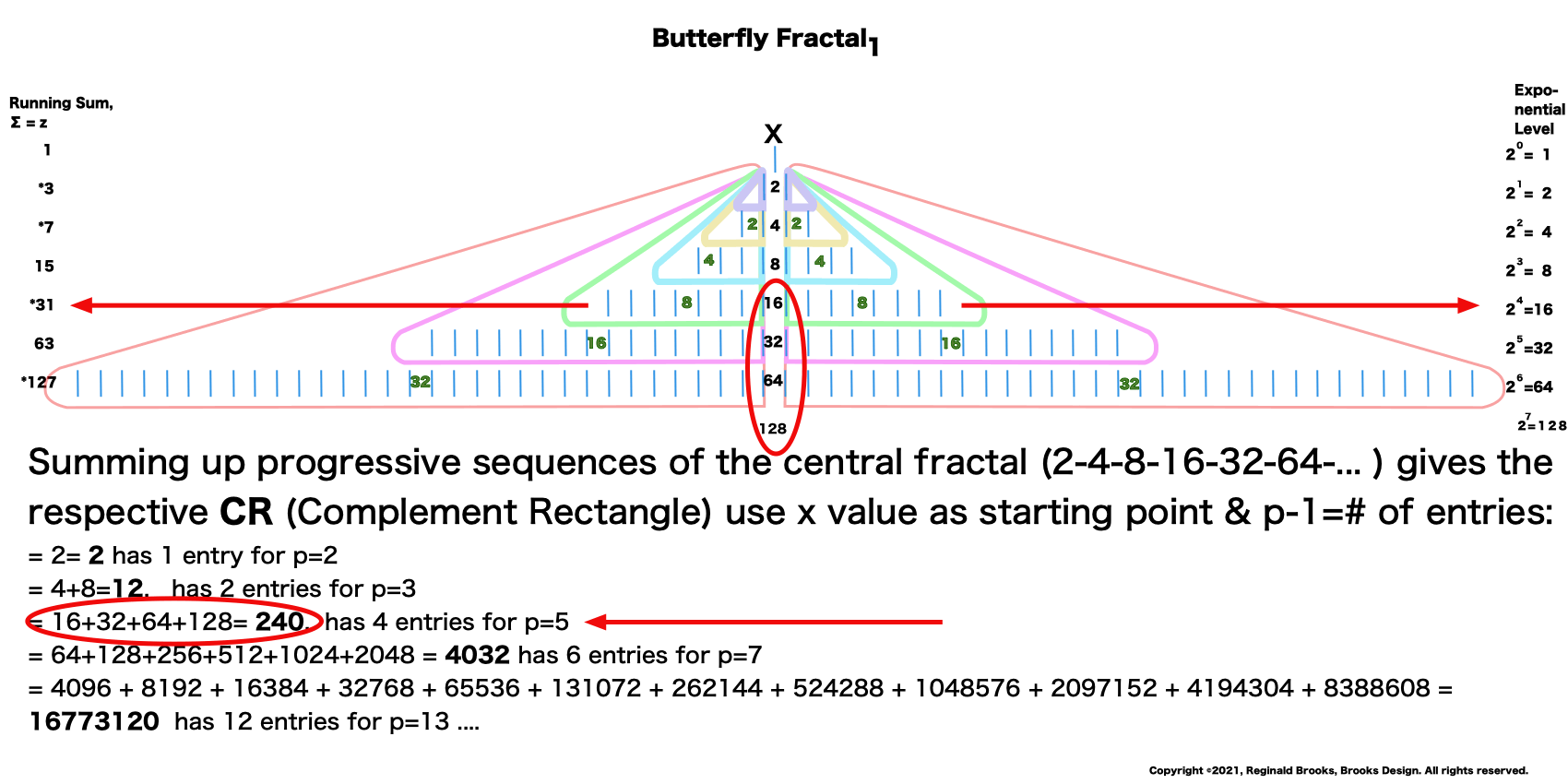22. This is simpler than it looks. We are just going to grab and ∑ up part of the center column values to give its respective CR = xy values. The "rules" say to use the "x" value as the starting point and take p-1 = the actual number of entries in that ∑. Remember, that p=prime and the entire Euclid-Euler Theorem rests on the p values. The encircled example ∑s up 16+32+64+128=240. It has 4 entries because p=5, so 5-1=4 entries. It helps to have the MPS Master Table for reference. The p values go as 2-3-5-7-13-17-19-31-61-89... The actual Mp start with row 2, the first exponential power of 2 as the * shows. So the left arrow points to *31 as it is the third Mp and is based on p=5 (2ᵖ -1 = 2⁵ -1= 32-1=31). The right arrow points across to 2⁴ =16 = the exponential power of 2 at this row level.

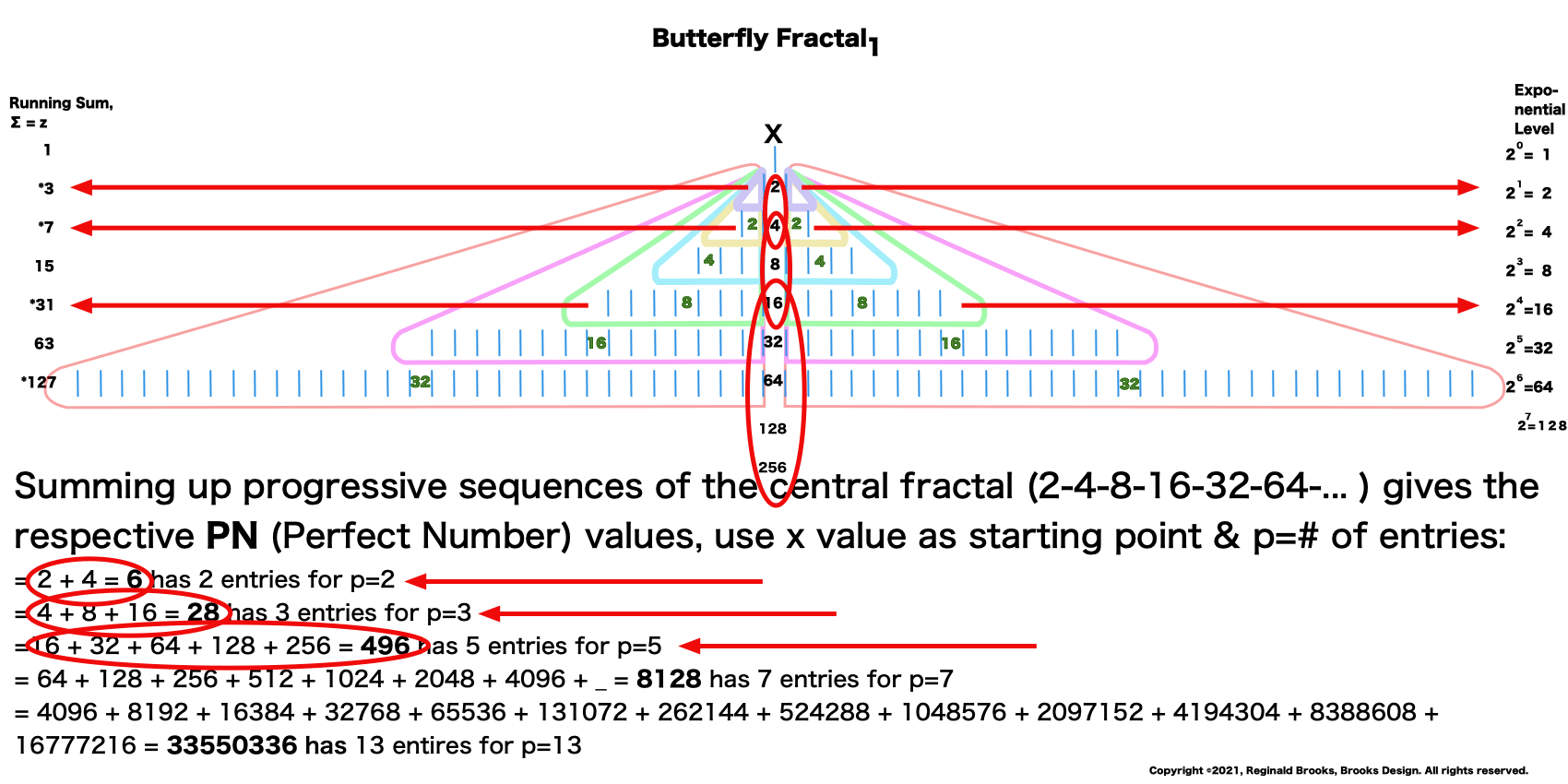23. This is similar to #22 above: the starting point is at the "x" level value, but now the # of entries = p. The third entry down has 16+32+64+128+256=496 = PN = xz and the # of entries = p = 5.

24. That's it for now. You've got it!

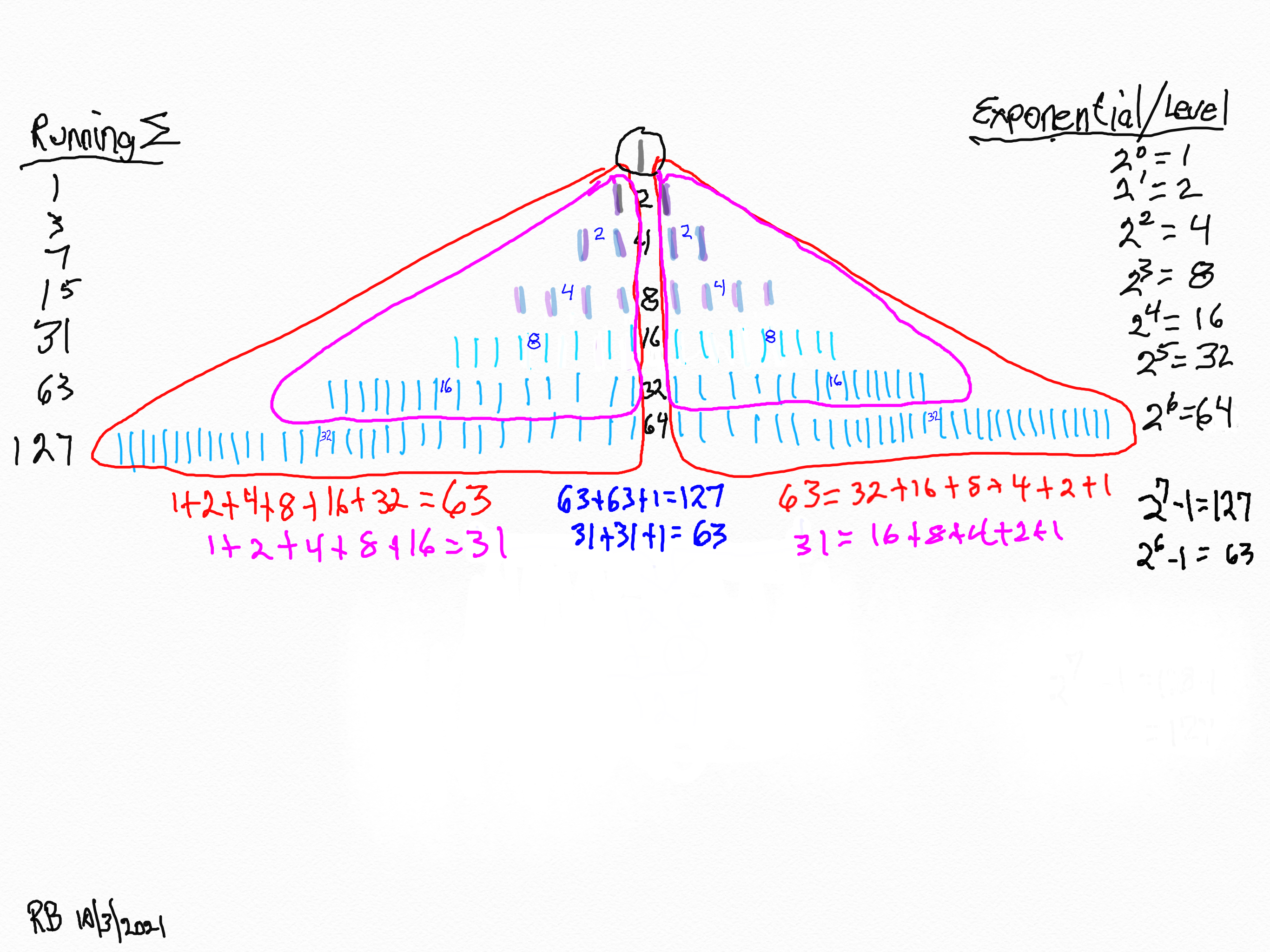
25. Review the pure fractalness of the exponential power of 2!

26. Review the pure fractalness of the exponential power of 2!

27. Review the pure fractalness of the exponential power of 2 and the beautiful Butterfly Fractal~1~~ it produces!

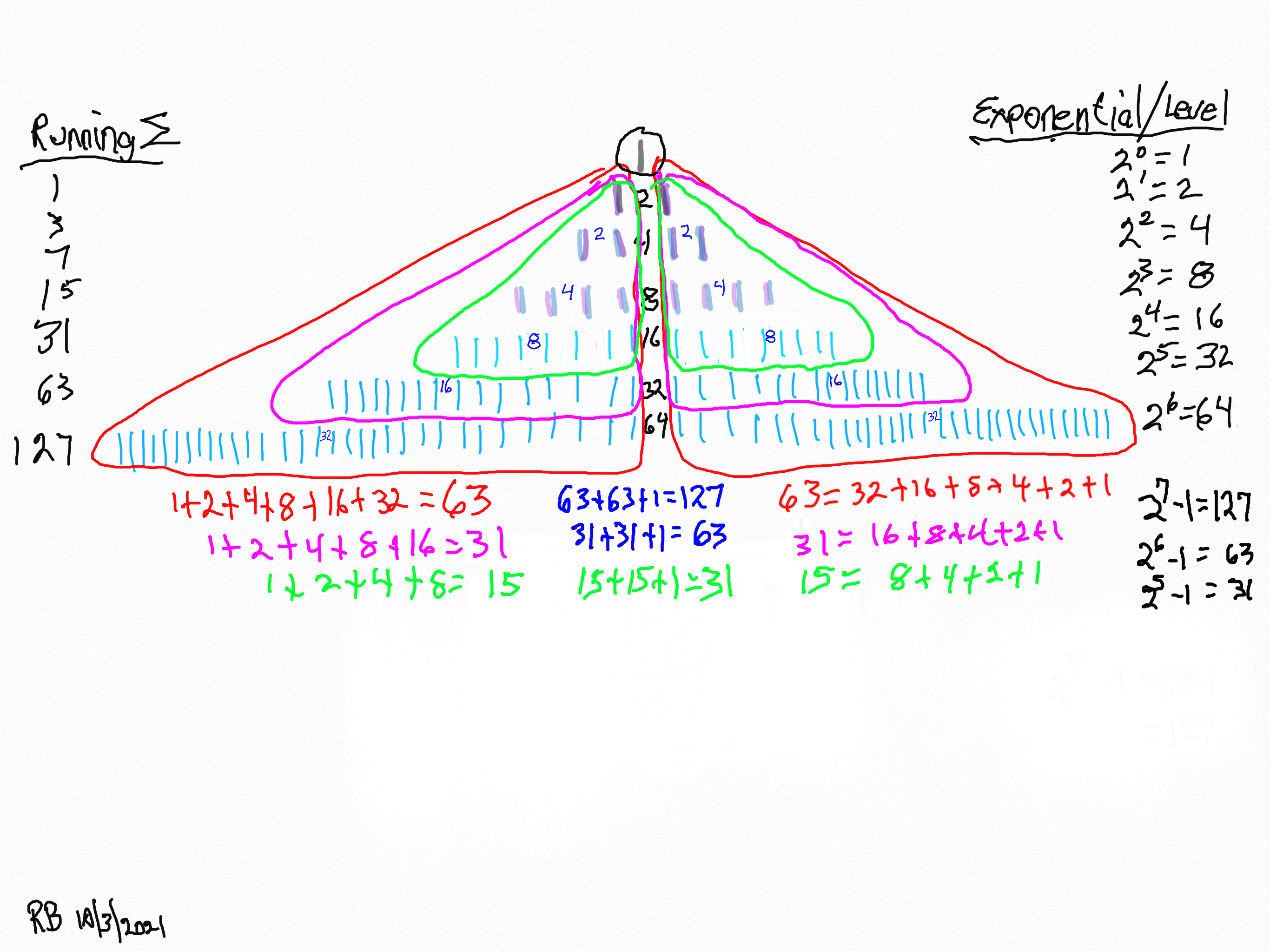
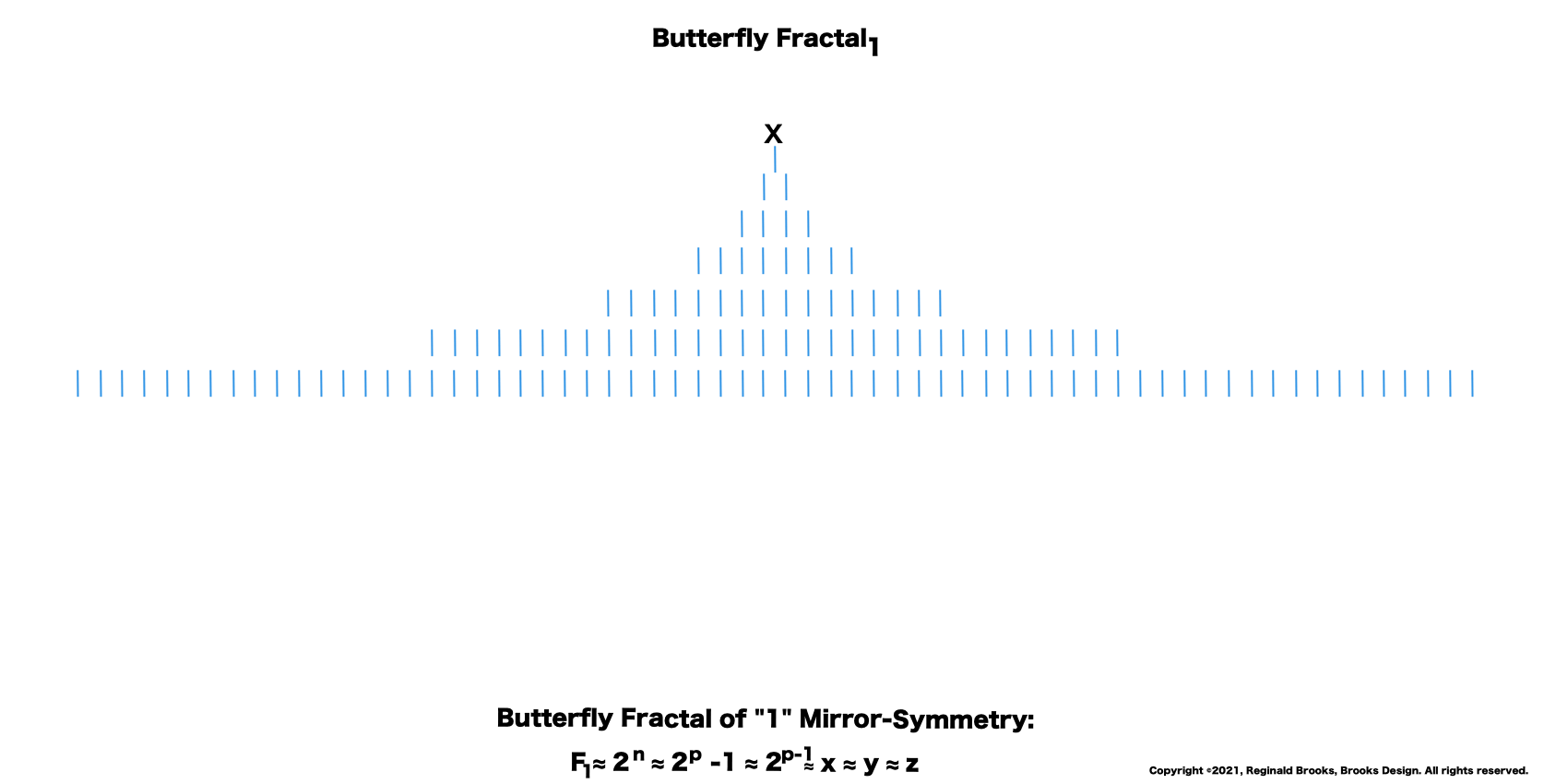28. Review the pure fractalness of the exponential power of 2!

29. Review the pure fractalness of the exponential power of 2!

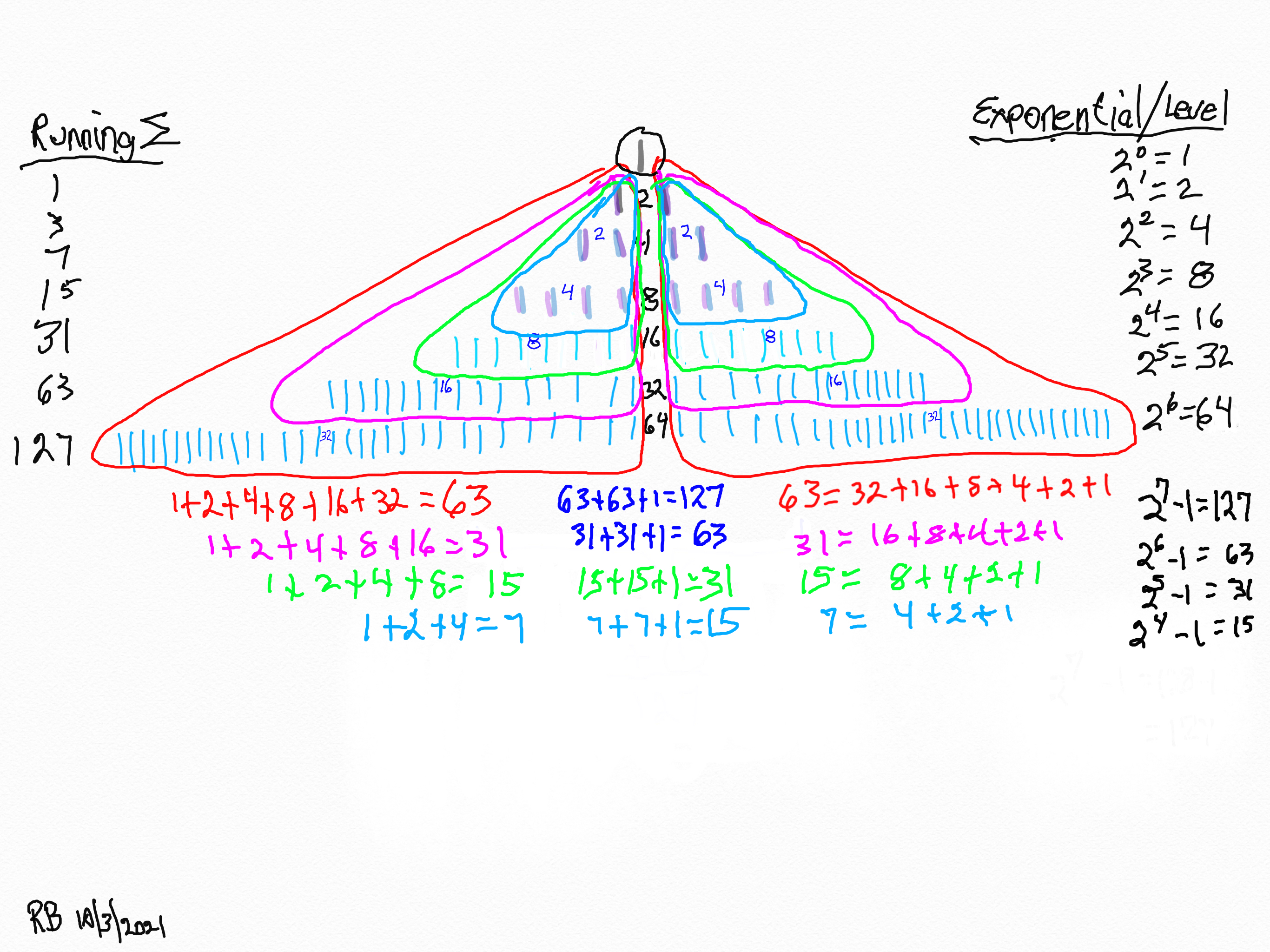
30. Review the pure fractalness of the exponential power of 2 and the Butterfly Fractal~1~.

MPS Master Table. The headers for each column are in BLUE.

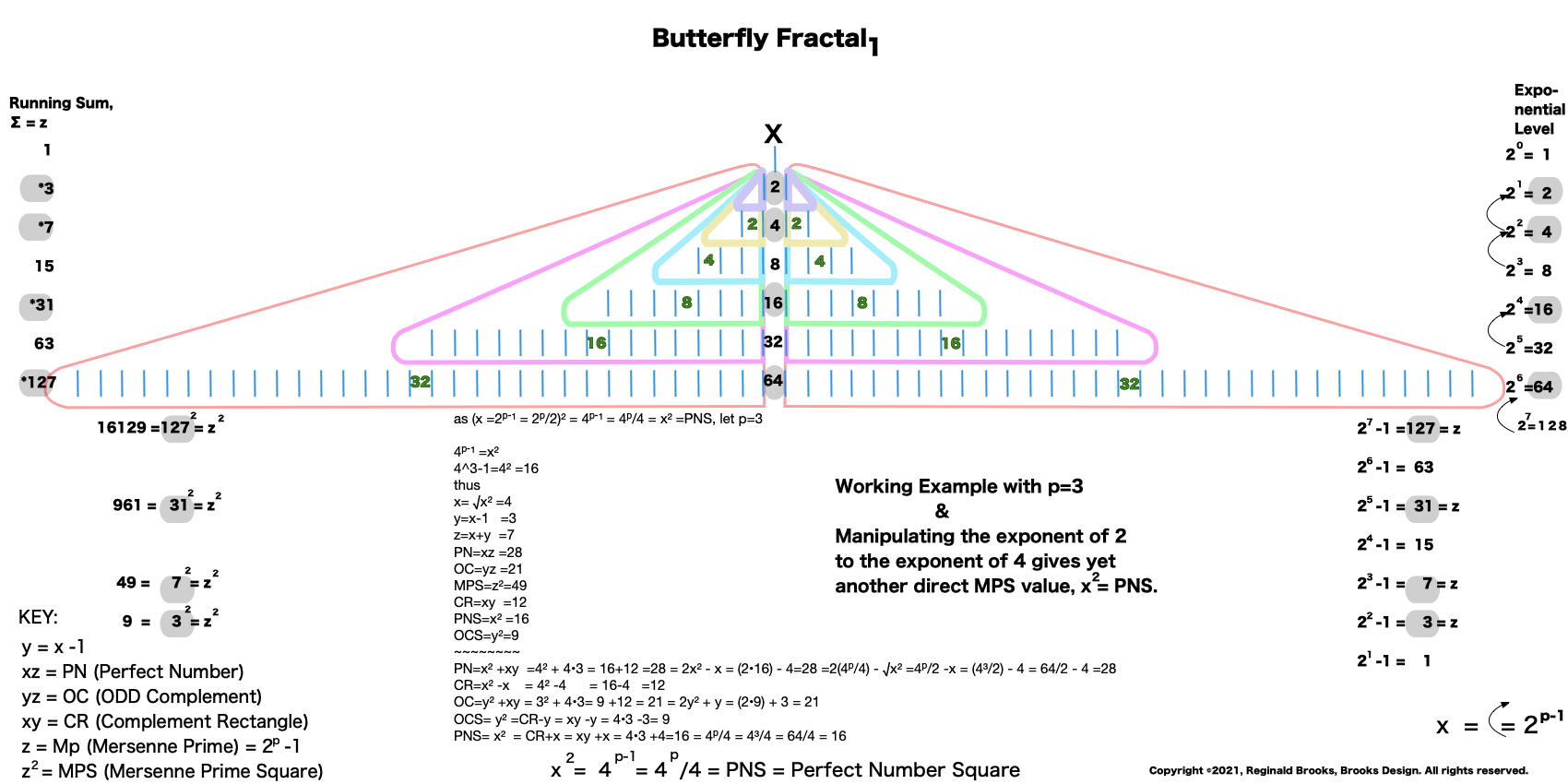31. Manipulating the exponential power of 2 -- squaring it to the exponential power of 4 -- gives x² = PNS.

Now that we have a roadmap revealing how the waveform of the Butterfly Fractal~1~ exponential power of 2 informs the MPS by its very interactive interference, let us now just see how easy it is to calculate this.

It is all based on the exponential power of 2. Through it, one may immediately ascertain key parameters such as x, p and z (Mp). Once x is known -- and as shown x is simply the value of 2ⁿ -- one immediately knows p as (2•n)+1. That's right, p = 2n+1. One simple takes the product of the power of 2 times its exponent value "n" and adds 1, e.i. p = 5 = (2•2) + 1. (Note: exception for when n=1, as 2 • 1 =2, as 2¹=2, and in order to get to a value of n=1, we must use 2⁰=1). And as y=x-1, we have everything to calculate the rest:

If you know x you can quickly calculate the rest.

x = 2ⁿ and,

x = 2ᵖ⁻¹ = 2ᵖ/2

where p = PRIME

y = x-1

z = Mp = x + y

x • y = CR = x² - x

x • y = CR = y² + y

x • z = PN = x² + xy

y • z = OC = y² + xy

x² = PNS = CR + x

y² = OCS = CR - y

z² = MPS = Mp²

Here are three shortcut calculation methods that will generate key parameters of the MPS starting with nothing else but 2ⁿ.

It will be helpful to reference this updated BIM_MPS_Master Table with the Butterfly Fractal1 Exponential Power of 2.

MPS Master Table with Butterfly Fractal~1~

Butterfly Fractal~1~ Shortcut Calculation Method 1: Gives the x, CR, PN and MPS.

Viewing the right side of the table, we find the Columns p---n---2ⁿ=x. Notice that while 2ⁿ goes as 2-4-8-16-... only the 2ⁿ values matching the Mp = z entries are shown. We will need to add up (∑) ALL the sequential 2ⁿ values in these calculations.

1. Using the x = 2ⁿ starting value, sum up (∑) the 2ⁿ values for the number of entry values = n, and that = CR as ∑2ⁿ = xy = CR.
2. Continue the ∑ by adding the next 2ⁿ value -- that makes the total number of entry values = n + 1 when starting from the same initial x value, and that = PN as ∑2ⁿ⁺¹ = xz = PN.32
3. Continue adding to the ∑ by adding the next 2ⁿ value -- that makes the total number of entry values = n + 2 when starting from the same initial x value, and that = ∑2ⁿ⁺².
4. Subtract 3x from this last ∑.
5. Add + 1 = MPS = z².

Example: let n=2:

1. x=4, as 2ⁿ=2^²^=4 with n=2 entry. ∑=CR as ∑2ⁿ=xy=4•3=12=CR as y=x-1.
2. ∑=PN as ∑2ⁿ⁺¹=xz=PN as n+1=3 entry values of , 2ⁿ=2²=4, 2ⁿ=2³=8, and 2ⁿ=2⁴=16, and 4+8+16=28 = xy=PN.
3. ∑=4+8+16=28 as n+2=4 entry values of 2ⁿ=2²=4, 2ⁿ=2³=8, 2ⁿ=2⁴=16, and 2ⁿ=2⁵=32, and 4+8+16+32=60.
4. Substract 3x from 60: 60-3•4=60-12=48.
5. Add + 1. 48+1=49=MPS=z².

Notice the emphasis on "when starting from the same initial x value" above. One is really just adding the next 2ⁿ on top of the previous, but for clarity, it also specifies the actual path as when starting from x.

See the MPS Master Table with Butterfly Fractal~1~ above.

(∑2ⁿ - 3x) +1 = MPS = z²

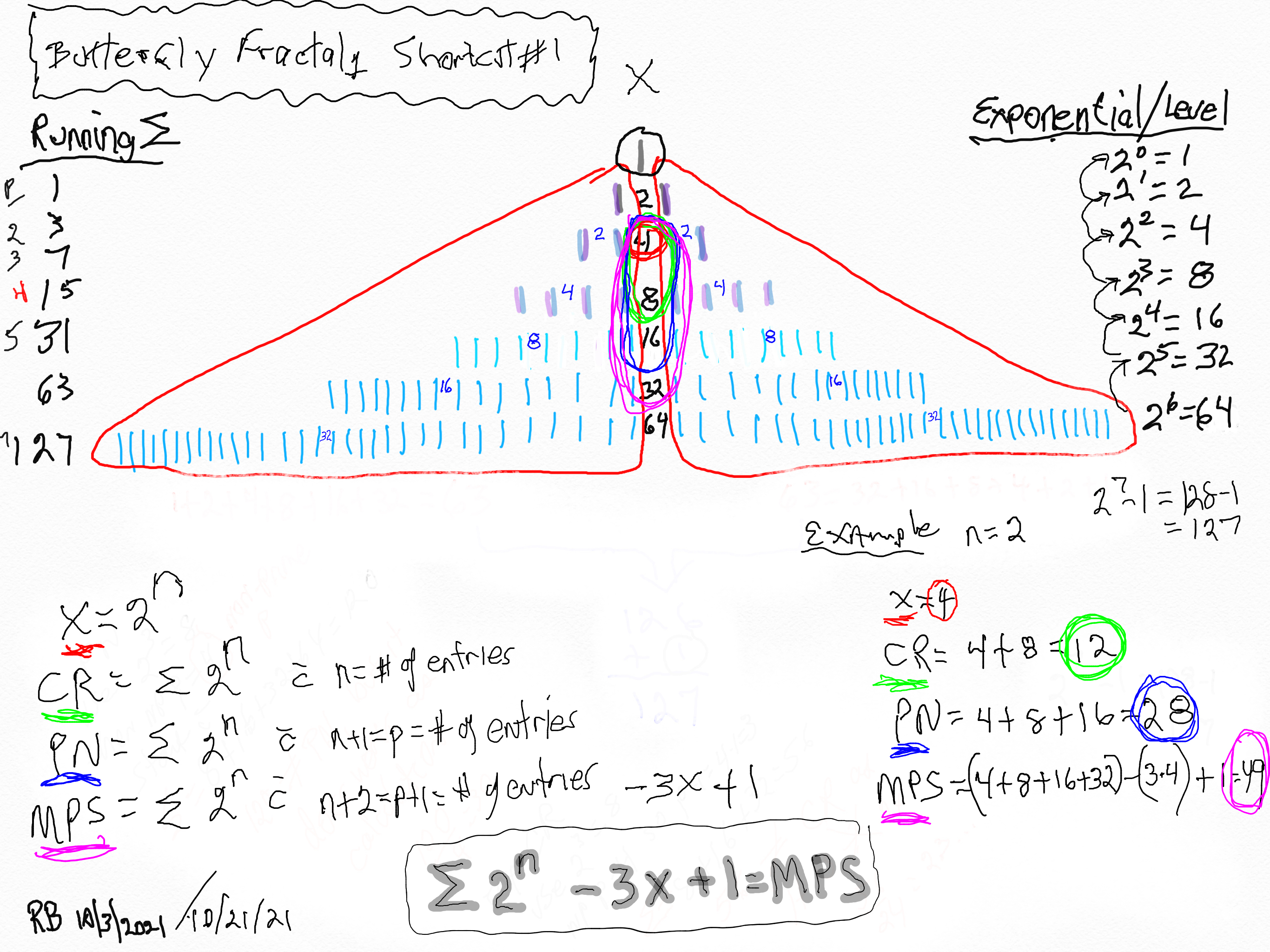Butterfly Fractal~1~ Shortcut Method 1. x=4.

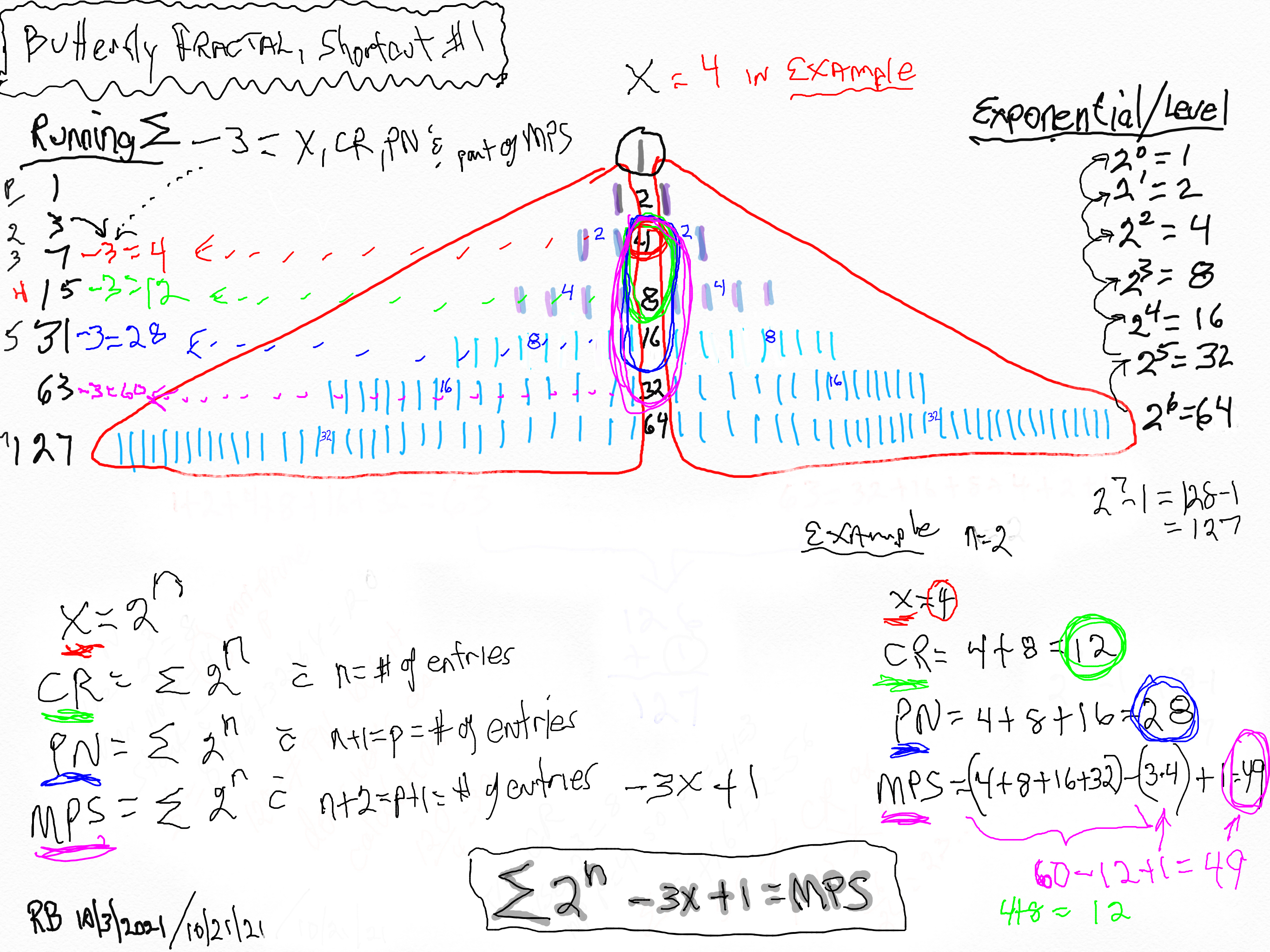Butterfly Fractal~1~ Shortcut Method 1. x=4.

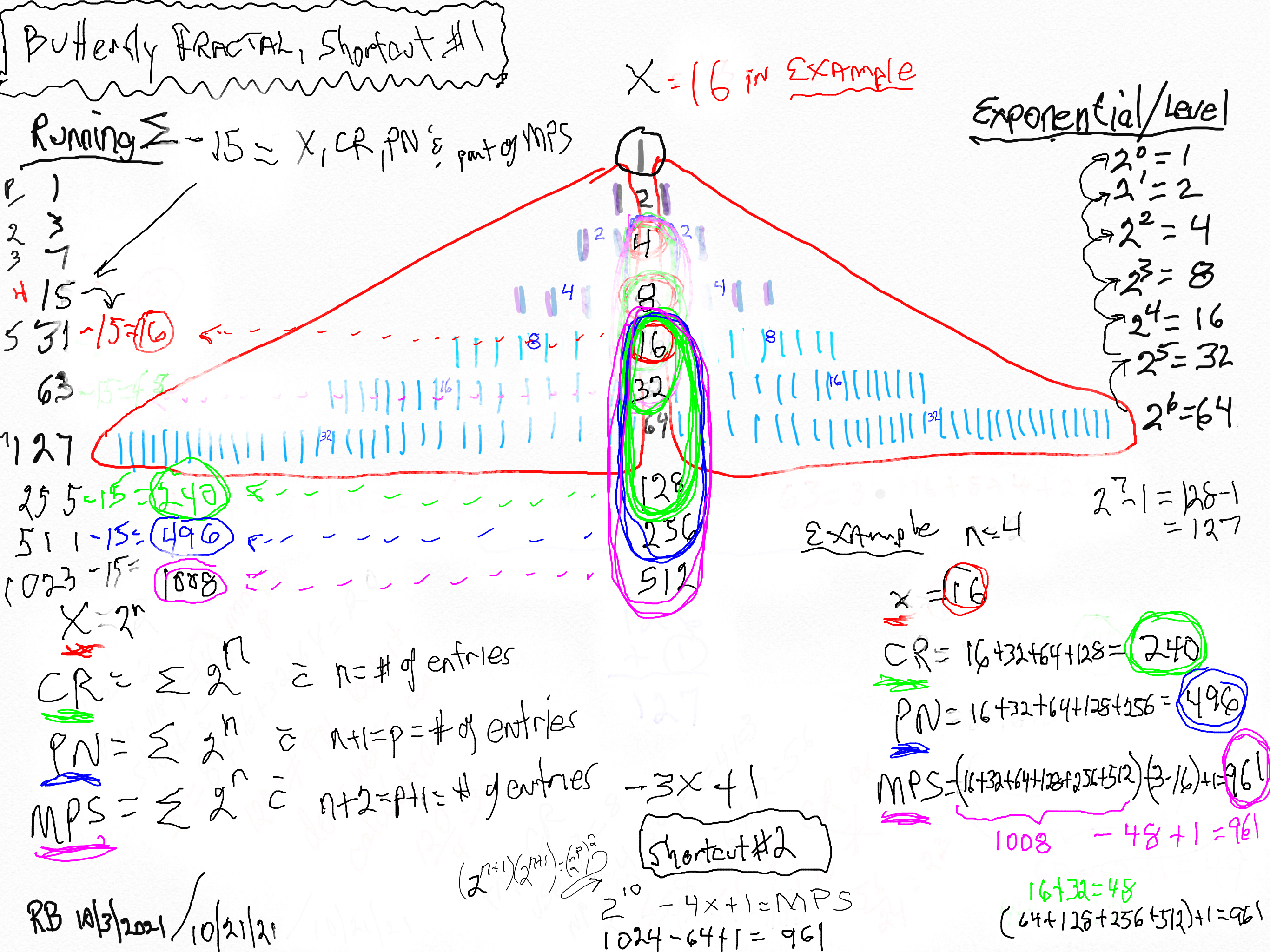Butterfly Fractal~1~ Shortcut Method 1. x=16.

Butterfly Fractal~1~ Shortcut Calculation Method 2: Gives the x and MPS.

Wouldn't you know it. You can simplify the process even further in Method 2:

1. Take the 2ⁿ and add + 1 to the n value -- n+1 -- and then double it. Since (2•n) + 1 = p, then 2ⁿ⁺¹= 2ᵖ and doubling it gives (2ᵖ)².
2. Subtract 4x from this last.
3. Add + 1 = MPS = z².

Example: let n=1: (note: for n=1 only, p=n+1. For all n>1, p=((2•n)+1))

1. 2ⁿ⁺¹=2ᵖ and doubling it gives (2ᵖ)², so n+1=1+1=2=p and (2²)²=16.
2. 16-4x=16-4•2= 8.
3. Add + 1. 8+1=9=MPS=z².

In this latter shortcut, one can see that the MPS can be calculated, without any prior knowledge of the p value, in three simple steps. That's because knowing x you really know everything else and x = 2ⁿ!

MPS = z² = (2ⁿ⁺¹)(2ⁿ⁺¹) = (2ᵖ)(2ᵖ) = ((2ᵖ)² - 4x)+ 1

Here are the first 10 MPS: (only the MPS are shown)

(2² × 2²) - (4 × 2) + 1 = 9 (2³ × 2³) - (4 × 4) + 1 = 49 (2⁵ × 2⁵) - (4 × 16) + 1 = 961 (2⁷ × 2⁷) - (4 × 64) + 1 = 16129 (2¹³ × 2¹³) - (4 × 4096) + 1 = 67092481 (2¹⁷ × 2¹⁷) - (4 × 65536) + 1 = 17179607041 (2¹⁹ × 2¹⁹) - (4 × 262144) + 1 = 274876858369 (2^31^ × 2^31^) - (4 × 1073741824) + 1 = 4611686014132420609 (2^61^ × 2^61^) - (4 × 1152921504606846976) + 1 = 5316911983139663487003542222693990401 (2^89^ × 2^89^) - (4 × 309485009821345068724781056) + 1 = 383123885216472214589586755549637256619304505646776321

See the MPS Master Table with Butterfly Fractal~1~ above.

Butterfly Fractal~1~ Shortcut Calculation Method 3 (starting with 2ⁿ=2²): Gives the x and MPS.

Essentially: double the 2ⁿ as the starting point, but only use n-2 = number of entries for the tally, then add + 1.

1. MPS = z² = ∑(2ⁿ)² + 1 with ∑(2ⁿ)² as the starting point, and the number of entries = final n-2.

Example: let n=2

1. MPS = z² = ∑(2ⁿ)² + 1 =∑(2²)² + 1 =∑2⁴ + 1 = 16 + 32 + 1 = 49 with 16 as the starting point, and n-2 = 4 - 2 = 2 entries.

MPS = z² = ∑(2ⁿ)² + 1

Here are the first 5 MPS:

∑(2¹)² = 2² = 4 for n-2=2-2=0 entries starting with 4: (NOTE: Shortcut Method 3 starts with *2ⁿ=2².)

MPS = z² = 4 + 1 = 5 and not 9 = MPS for Mp=z=3 at p=2. Does not work for this method.

If the starting point was 2³ = 8, then 8 + 1 = 9 would work above. The PN=6 is also atypical in that it is the only PN not found within the BIM as it is not ÷4.

*∑(2²)² = 2⁴ = 16 for n-2=4-2=2 entries starting with 16:

MPS = z² = 16 + 32 + 1 = 49 = MPS for Mp=z=7 at p=3.

∑(2³)² = 2⁶ = 64 for n-2=6-2=4 entries starting with 64:

MPS = z² = 64 + 128 + 256 + 512 + 1 = 961 = MPS for Mp=z=31 at p=5.

∑(2⁴)² = 2⁸ = 256 for n-2=8-2=6 entries starting with 256:

MPS = z² = 256 + 512 + 1024 + 2048 + 4096 + 8192 + 1 = 16129 = MPS for Mp=z=127 at p=7.

∑(2⁵)² = 2¹⁰ = 1024 for n-2=10-2=8 entries starting with 1024:

MPS = z² = 1024 + 2048 + 4096 + 8192 + 16384 + 32768 + 65536 + 131072 + 1 = 261121 is not a MPS.

∑(2⁶)² = 2¹² = 4096 for n-2=12-2=10 entries starting with 4096:

MPS = z² = 4096 + 8192 + 16384 + 32768 + 65536 + 131072 + 262144 + 524288 + 1048576 +1= 2093057 is not a MPS.

∑(2⁷)² = 2¹⁴ = 16384 for n-2=14-2=12 entries starting with 16384:

MPS = z² = 16384 + 32768 + 65536 + 131072 + 262144 + 524288 + 1048576 + 2097152 + 4194304 + 8388608 + 16777216 + 33554432 +1 = 67092481= MPS for Mp=z=8191 at p=13.

∑(2⁸)² = 2¹⁶ = 65536 for n-2=16-2=14 entries starting with 65536:

MPS = z² = 65536 + 131072 + 262144 + 524288 + 1048576 + 2097152 + 4194304 + 8388608 + 16777216 + 33554432 + 67108864 + 134217728 + 268435456 + 536870912 +1 =1073676289 is not a MPS.

∑(2⁹)² = 2¹⁸ = 262144 for n-2=18-2=16 entries starting with 262144:

MPS = z² = 262144 + 524288 + 1048576 + 2097152 + 4194304 + 8388608 + 16777216 + 33554432 + 67108864 + 134217728 + 268435456 + 536870912 + 1073741824 + 2147483648 + 4294967296 + 8589934592 +1 = 17179607041= MPS for Mp=z=131071 at p=17.

See the MPS Master Table with Butterfly Fractal~1~ above.

There is little doubt in the importance of the PRIMES in the formation of all the natural numbers. Yet here we see that the simple repeated doubling of the number "1" -- as Fractal~1~ (F~1~) -- and all its progeny, gives rise to the exponential power of 2 as visualized in the Butterfly Fractal~1~ images and table above. The EVEN multiple numbers of "2" -- with the simple addition or subtraction of "1" from their ∑ tally totals gives rise to the very, very exclusive ODD numbers of the Mersenne Primes and its square the MPS!

Two seemlingly independent number waveforms interfere to produce that magic!

And you only need the power of 2!

Nature once again humbles us in the exquisite beauty of simplicity!

The the connection between the exponential power of 2 -- as revealed in the Butterfly Fractal~1~ -- and the Mersenne Prime Square is summarized in Tables 81 and 82 below.

Table 81: Mersenne Prime Squares and the Butterfly Fractal~1~. The "n" column represents the value of "n."

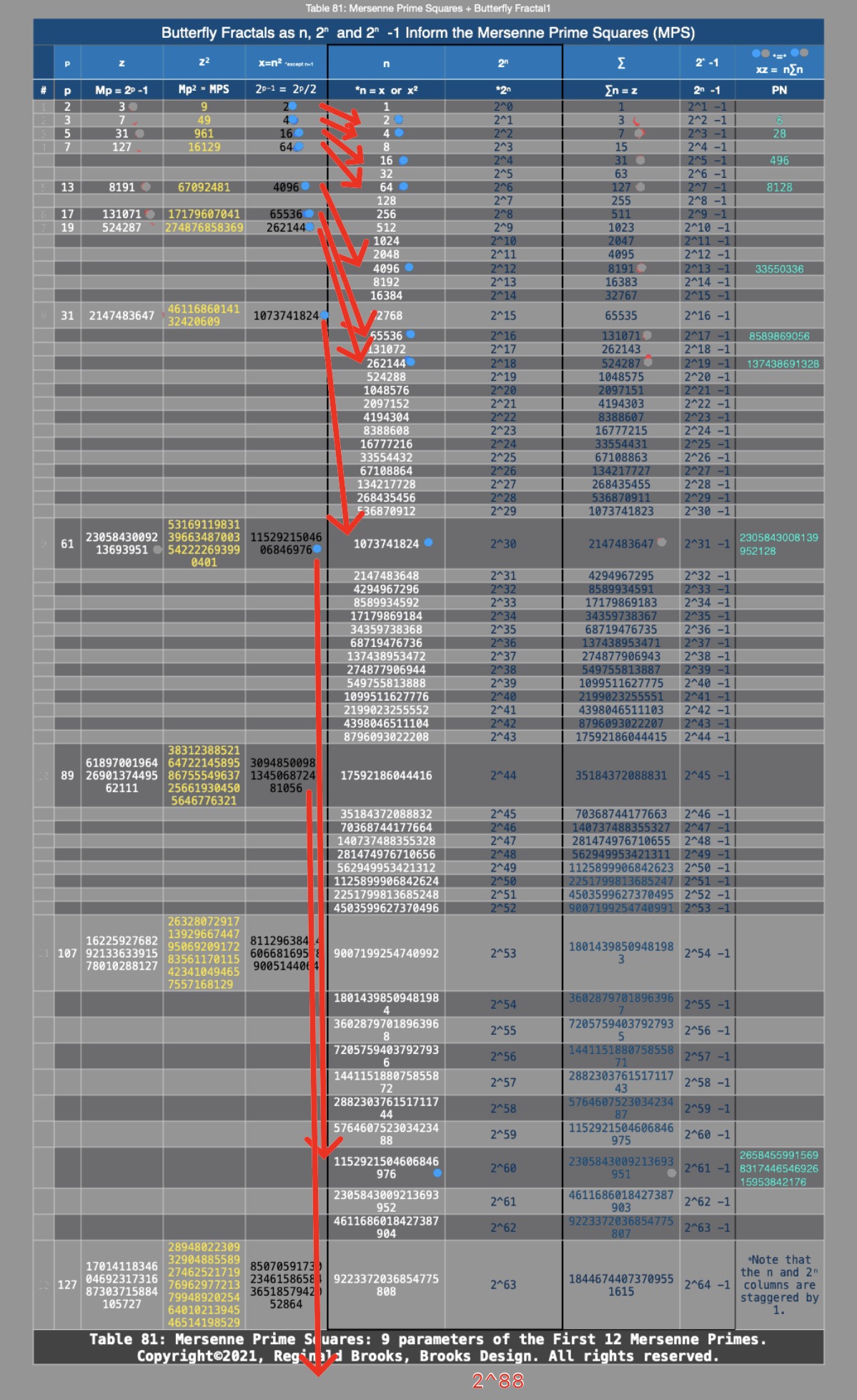
Table 81: Mersenne Prime Squares and the Butterfly Fractal~1 annotation showing x = n².

Table 82: Exponential Power of 2 + Butterfly Fractal~1~ + Mersenne Prime Squares

Summary:

• n and 2ⁿ play a fundamental role in defining the Mp and its square, the MPS. Lines 1-3 are there for completeness. Easier to start with Line 4.

• All parameters of the MPS defined. All n = EVEN numbers (except Lines 1 & 3).

• The exponential power of 2 itself generates a bilateral, mirror-symmetric fractal of itself (Butterfly Fractal1), directly informing x — and x², following with y = x - 1 = 2ⁿ - 1.

• Added together, x + y = z = Mp, and of course, z² = Mp² = MPS.

• Here, we show that z = (2ⁿ⁻¹) - 1 which is the same as 2ᵖ - 1, reveals how, without knowing any of the PRIMES (p)— especially the Mersenne Primes (Mp) — one can fully define the entire MPS and all of its generations including the PN = xz, the OC = yz, and the CR = xy.

• The remaining PNS = x², OCS = y² and the MPS = z².

• Notice that p falls half way between the n values, naturally as one would expect, being that it represents the special case where 2ᵖ - 1 (as shown in Dark BLUE) = Mp = z, and, 2ᵖ⁻¹ (as shown in Dark BLUE) = 2ⁿ = x.

• Together, xz = 2ᵖ⁻¹ (2ᵖ -1) = PN is the Euclid-Euler Theorem.

• Below the Euclid-Euler Theorem lies the more fundamental exponential power of 2 as the Butterfly Fractal~1~ primary wave, that, when interfering with the larger PRIMES wave, reveals the very special — and quite specific — relationship between the Mersenne Primes and Perfect Numbers. n

(2ⁿ⁻¹) -1 = z = Mp where 2ⁿ⁻¹ = x, such that xz = 2ⁿ⁻¹ [(2ⁿ⁻¹) -1] = (2ᵖ⁻¹)(2ᵖ -1) = PN is the Euclid-Euler Theorem.

I can not emphasize this enough: the historic approach to the Mersenne Primes and Perfect Number relationship -- as detailed in the Euclid-Euler Theorem -- is based on exponential power of 2 having ODD number exponents (p) -- specifically an ODD Mersenne Prime number -- while the very new BIMMPS approach detailed herein is based on the underlying exponential power of 2 having EVEN number exponents (initially) as presented as "n" in the also new Butterfly Fractal~1~. (Exception being the very first p=2, Mp=3 and PN=6.)

In the former one must start out with knowing the Mersenne Prime, in the latter, one gets the generic layout of the number relationships as defined by the exponential power of 2, and thereafter one picks out the Mersenne Prime, et al, from this matrix by elimination. There are many clues along the way!

The Butterfly Fractal~1~ as a representation of the exponential power of 2 is like one grand, primary wave that selectively interferes with another even grander, primary wave -- the wave of all PRIMES -- generating at the crossover nodes the very, very specific Mersenne Prime - Perfect Number phenomena that we have now seen is really just part of the Mersenne Prime Squares geometry!

Before we go to Part III, we have just a few more things to add. Some very new and interesting findings!

As proof that the exponential power of 2 underlies and resolves -- in the very special case of the Euclid-Euler Theorem -- to p = n + 1 as 2ⁿ⁺¹ = 2^p and (2ⁿ⁺¹) -1 = 2^p - 1 = z as x = 2ⁿ = 2^p-1 as xz = 2^p-1 (2^p -1) only validates its importance.

In Table 83 we walk through the exponential power of 2 as it forms the x, y and z parameters of the MPS.

In Table 84 we have consolidated the 51 Mersenne Primes, and their PN, p and x values along with the # of digits.

What unfolds is yet another amazing NPS!

• The sum (∑) of the z + PN # of digits approaches a constant value of ≈90% of p;
• The sum (∑) of z + z # of digits approaches a constant value of ≈100% of PN;
• The sum (∑) of z + z + z # of digits approaches a constant value of ≈90% of p;
• The # of digits for z is nearly identical to that of x (or y) -- differing only occassionally by 1;

Table 85: Specifically compares the p value with that of the combined number (#) of digits for the x-, y- and z-values.

Visual Recap and Summary

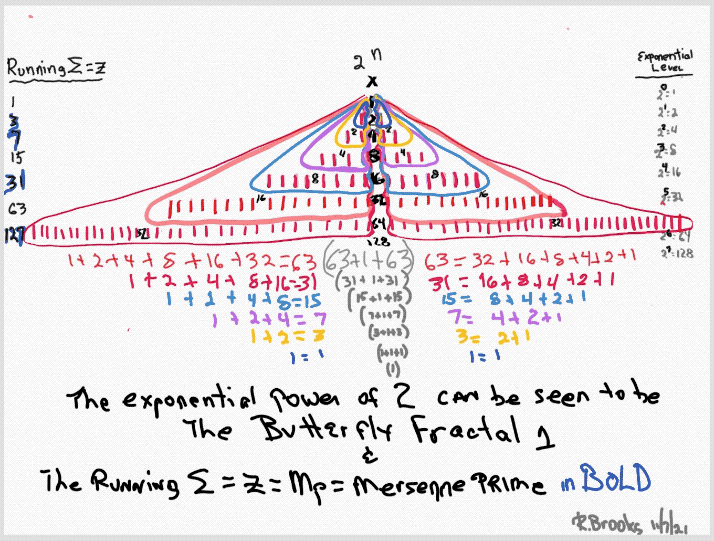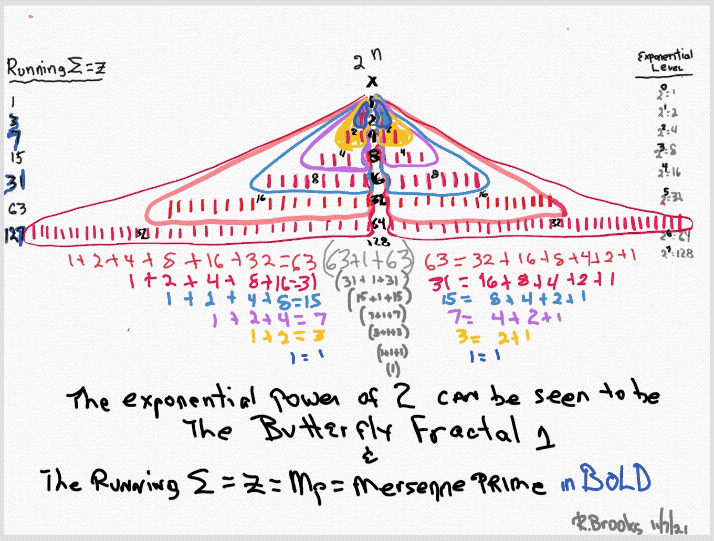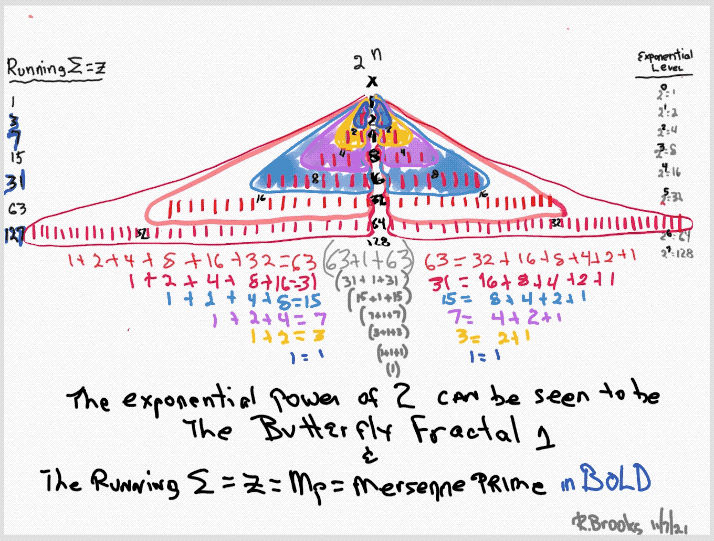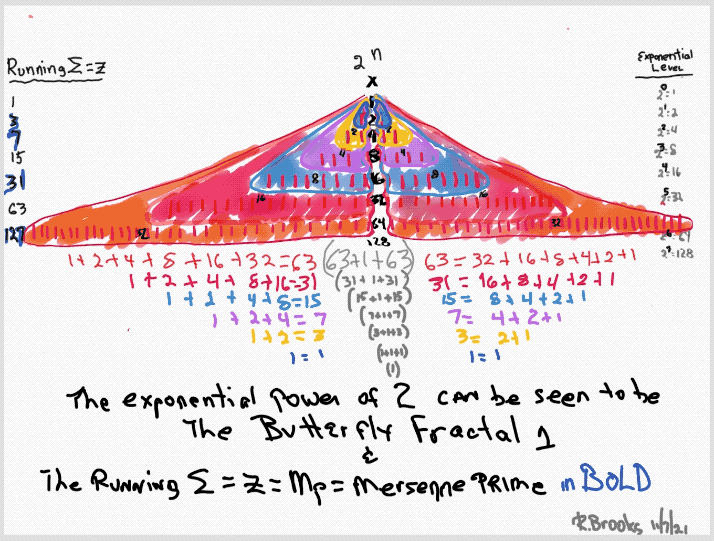
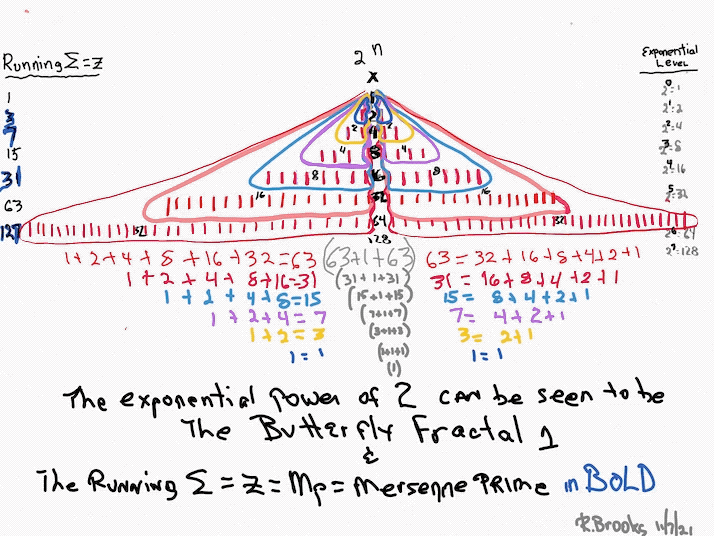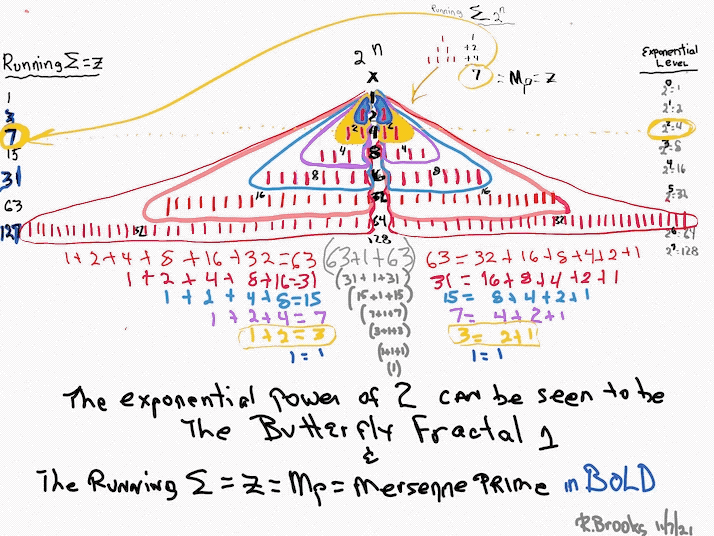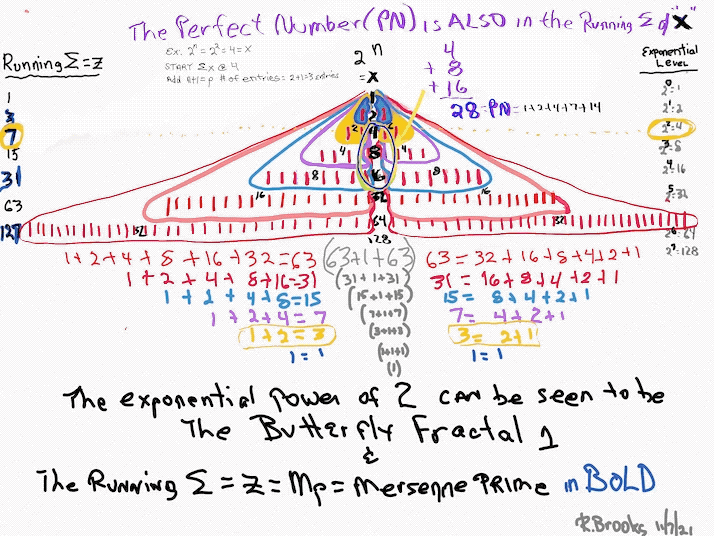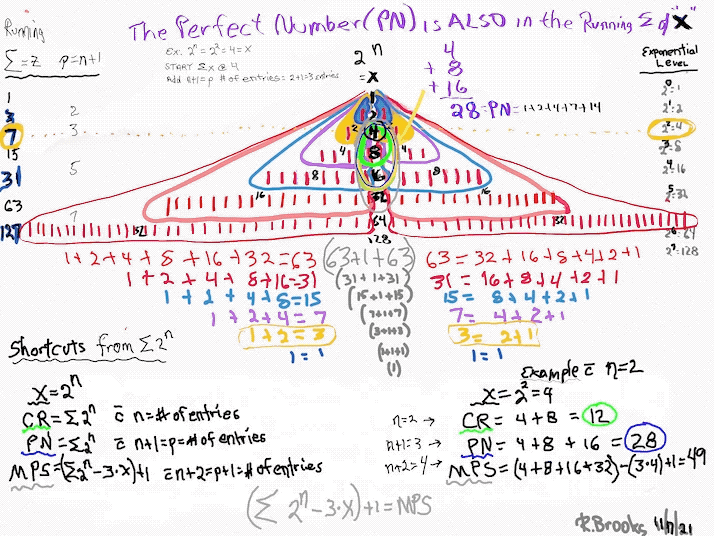
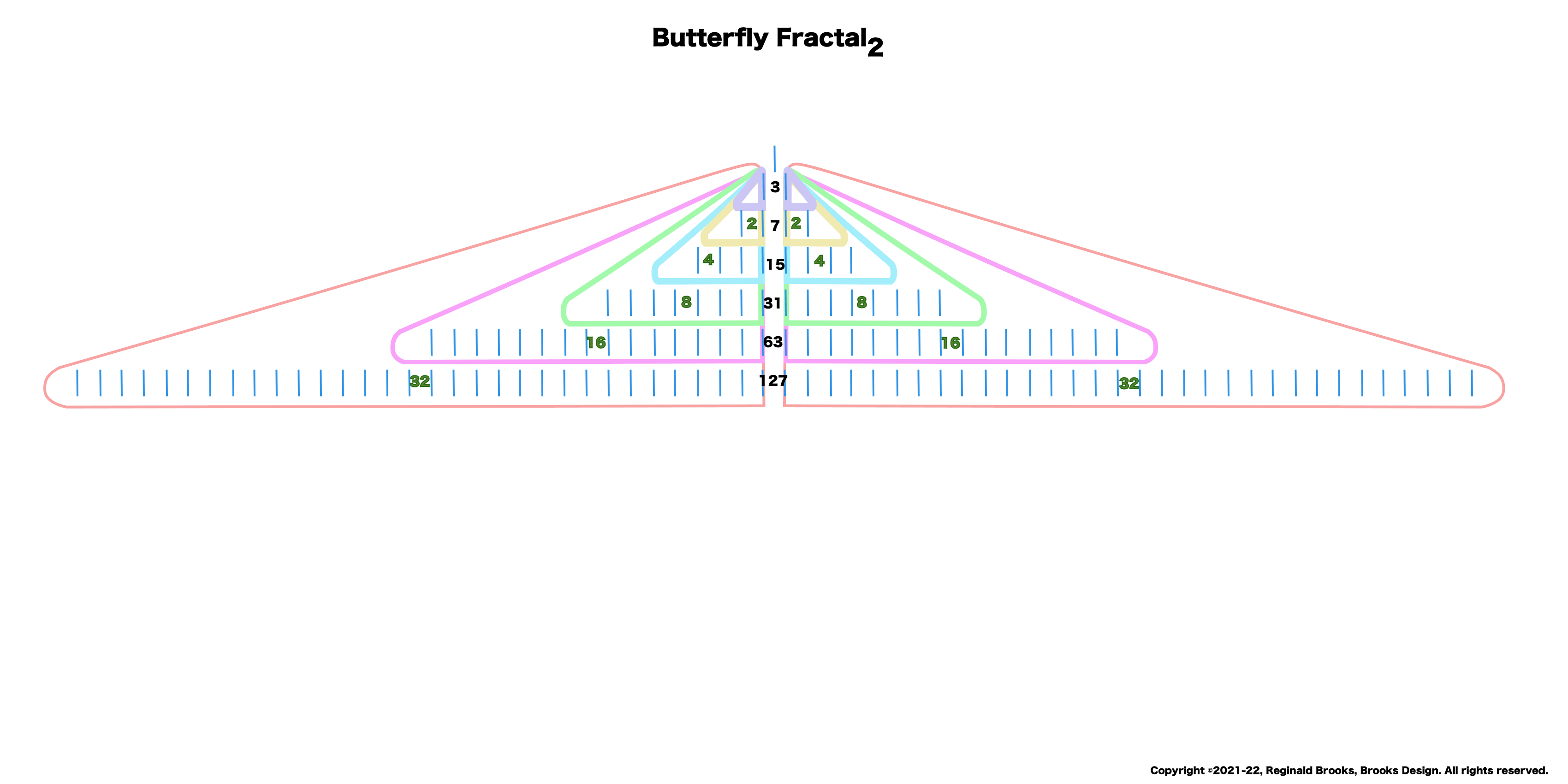
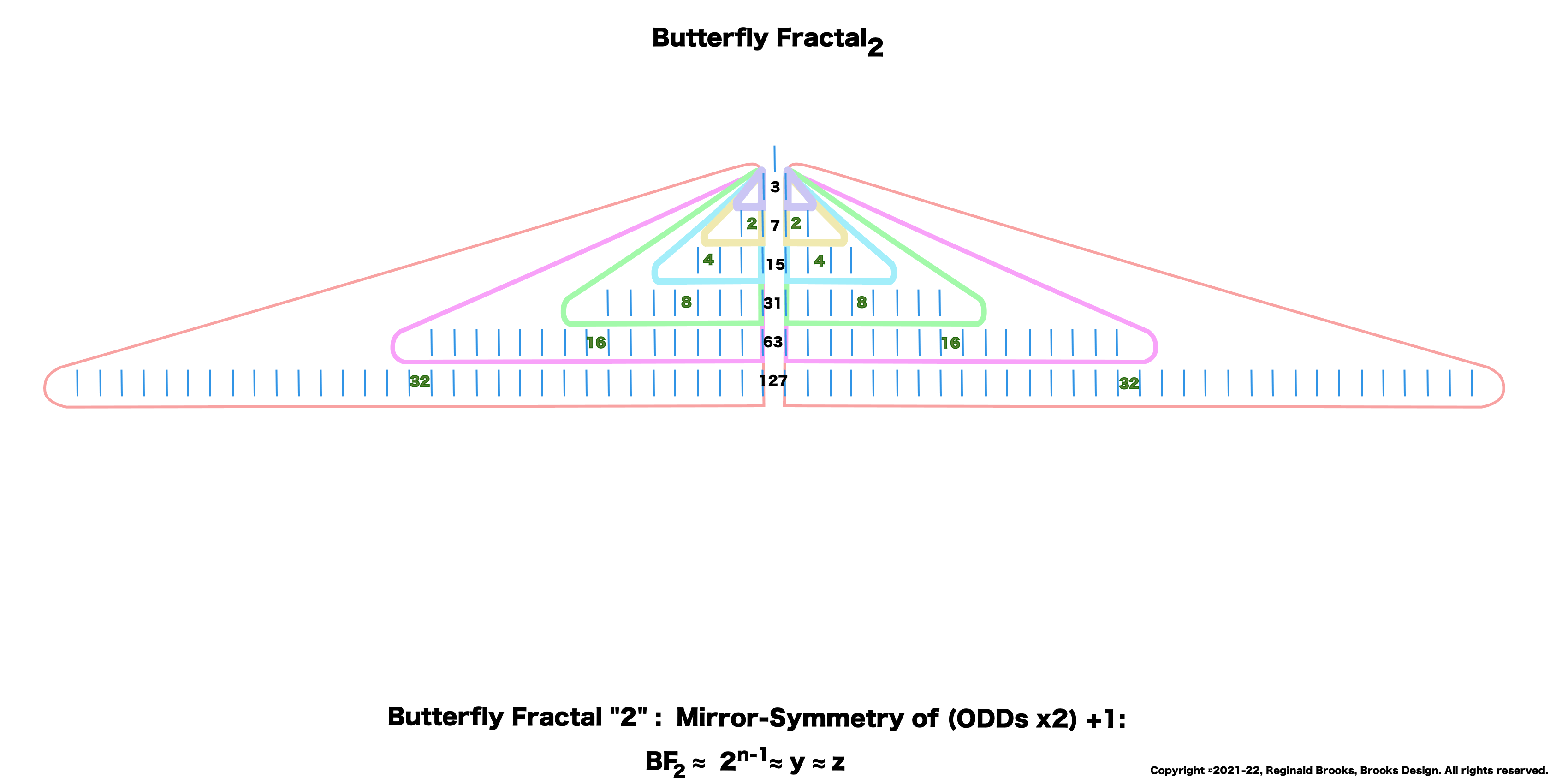
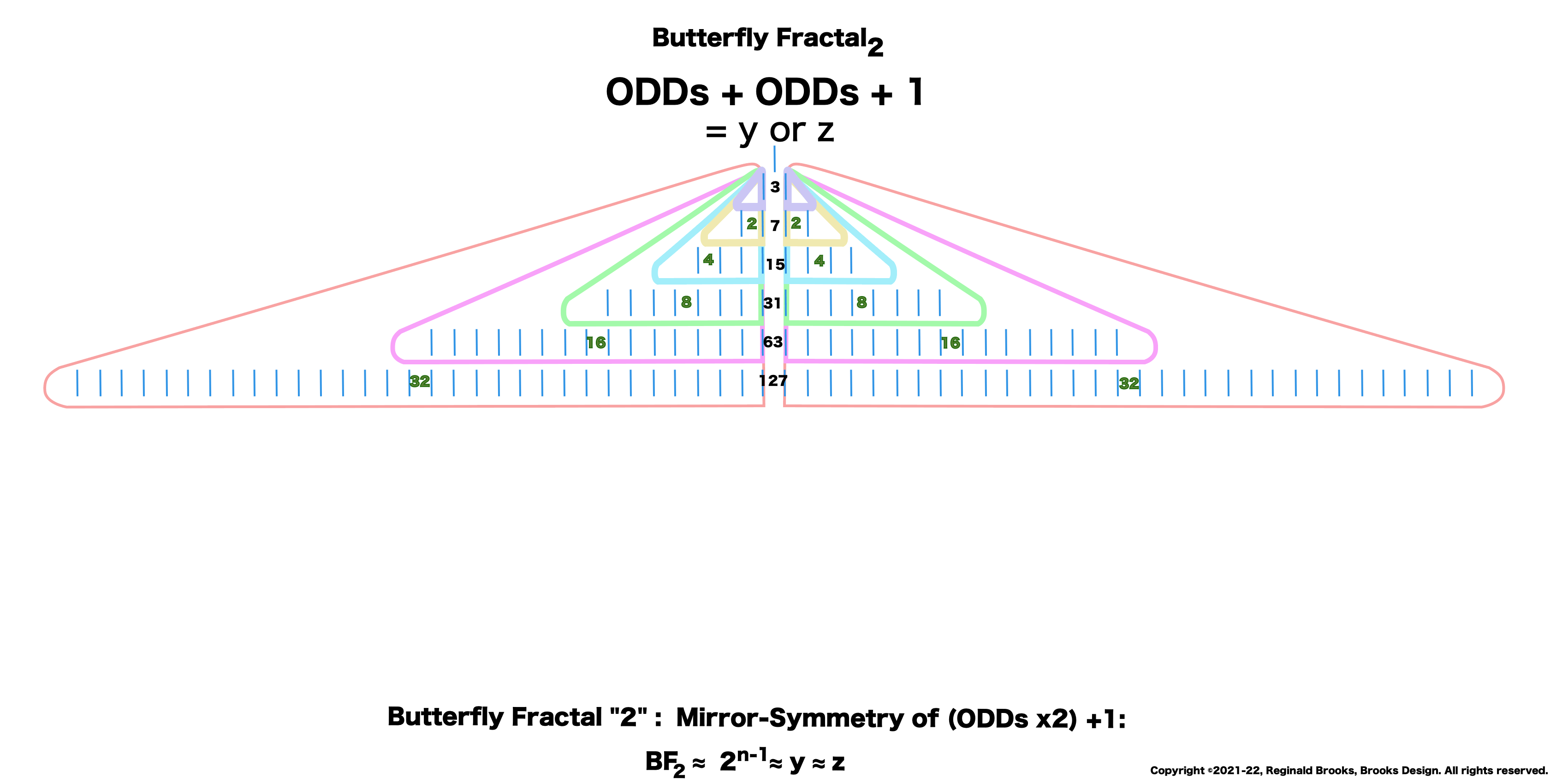
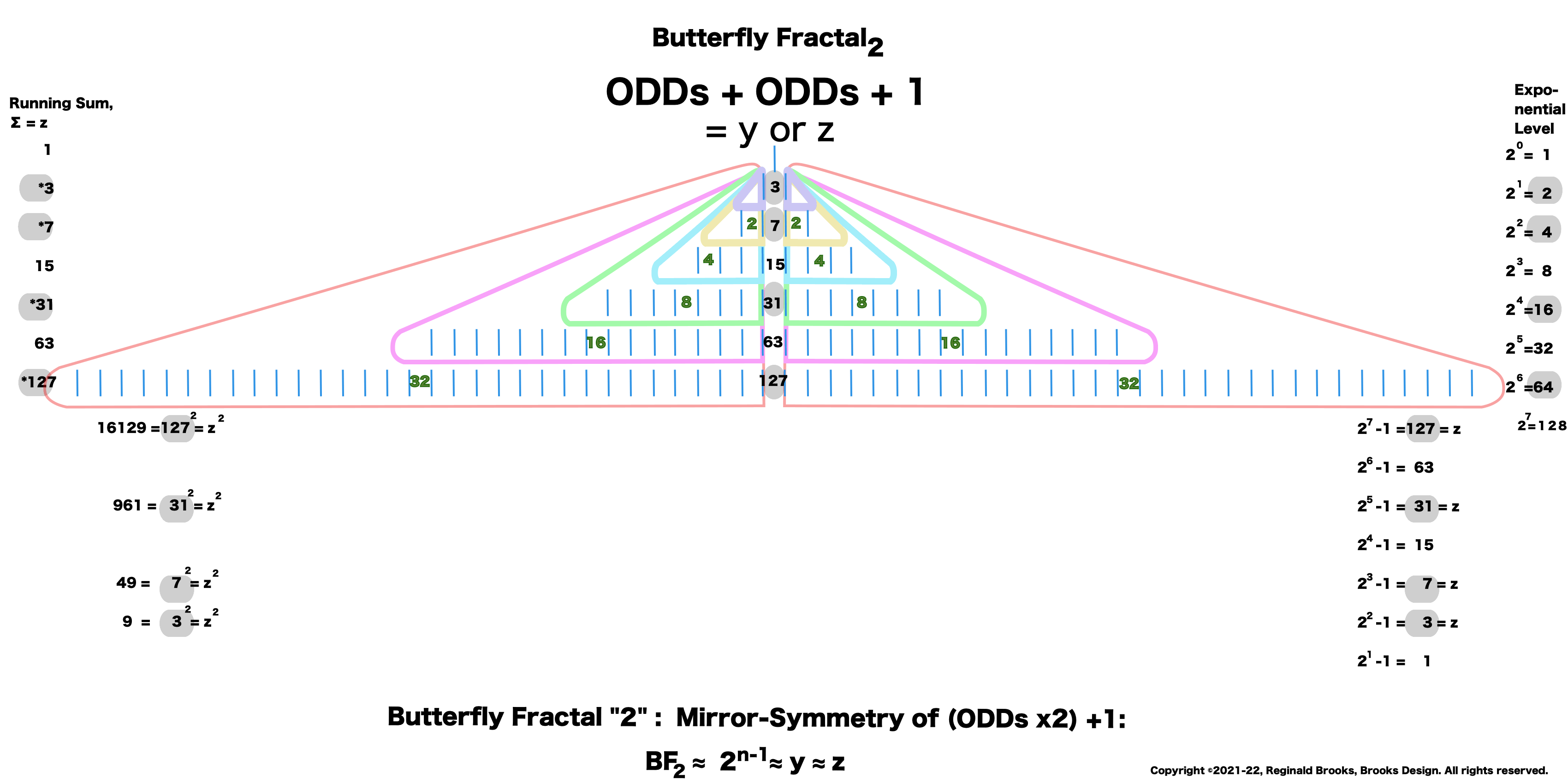
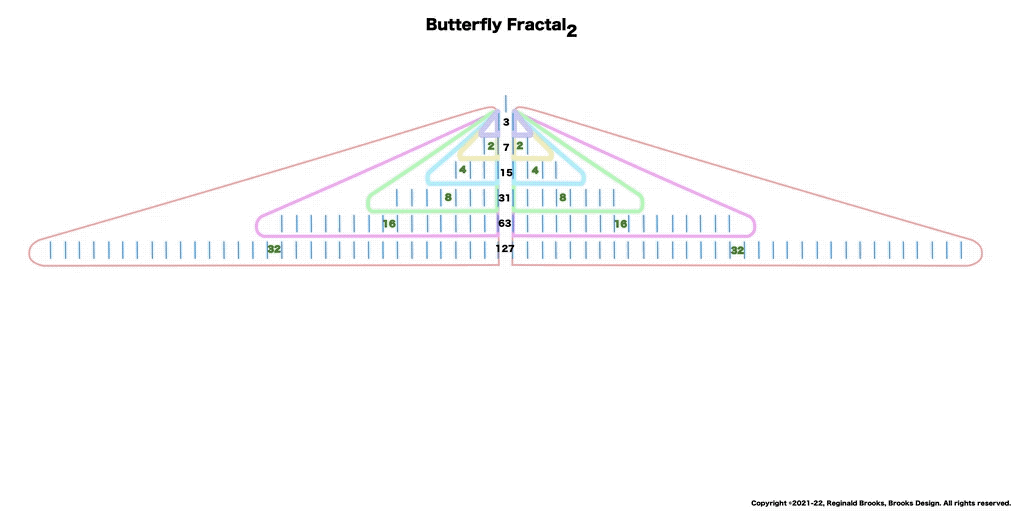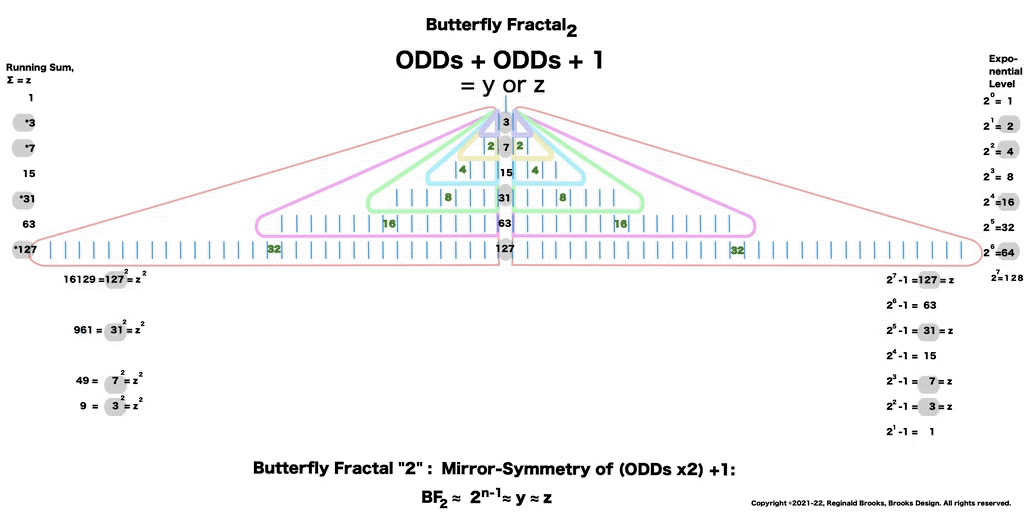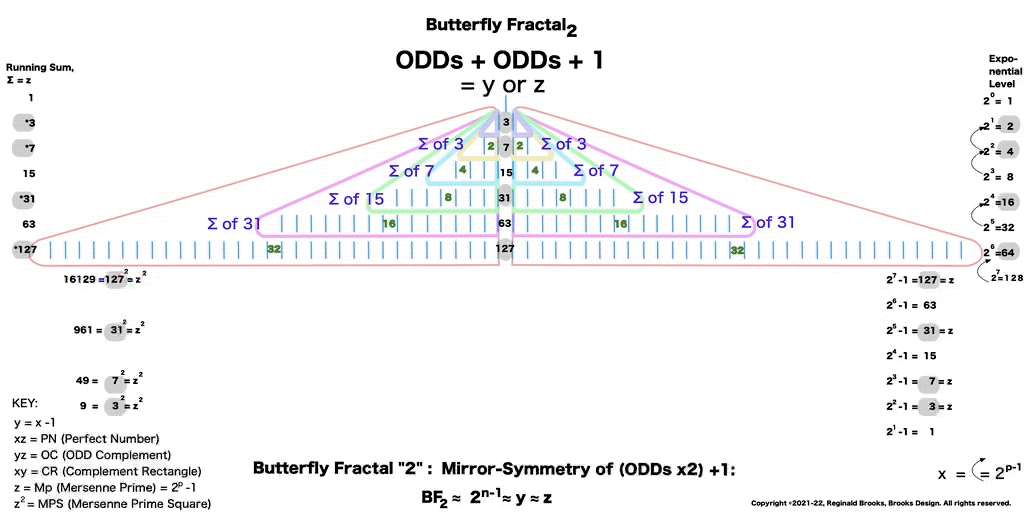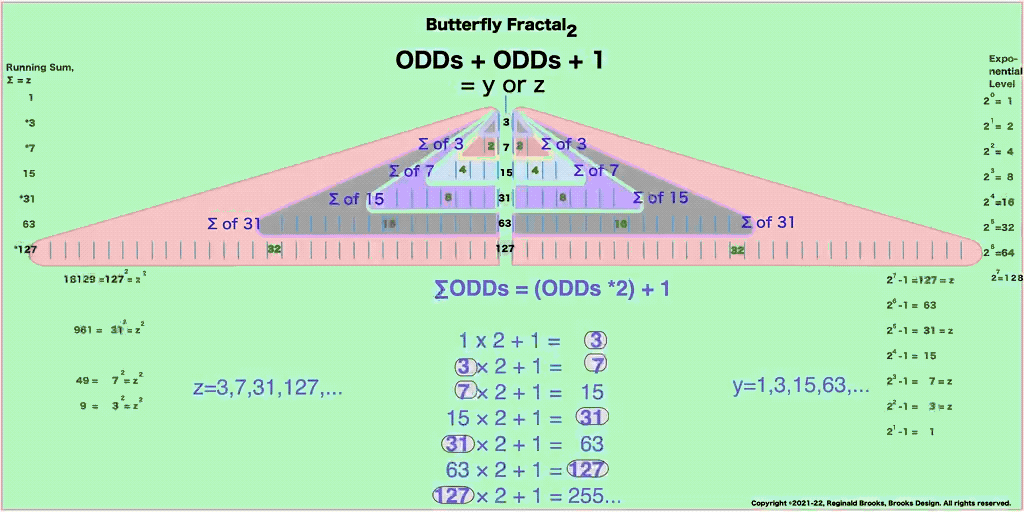
Butterfly Fractal~2~

The F~2~~ fractal -- which is really just F~1~ fractal re-imaged with the sums (∑) from the exponentiation of the power of 2 now shown in the center (body) of the Butterfly Fractal -- is there to really emphasize how this summation informs the MPS. This becomes important, at least to this author, in that visualizing the same material from various viewports locks in the underlying fundamentals.

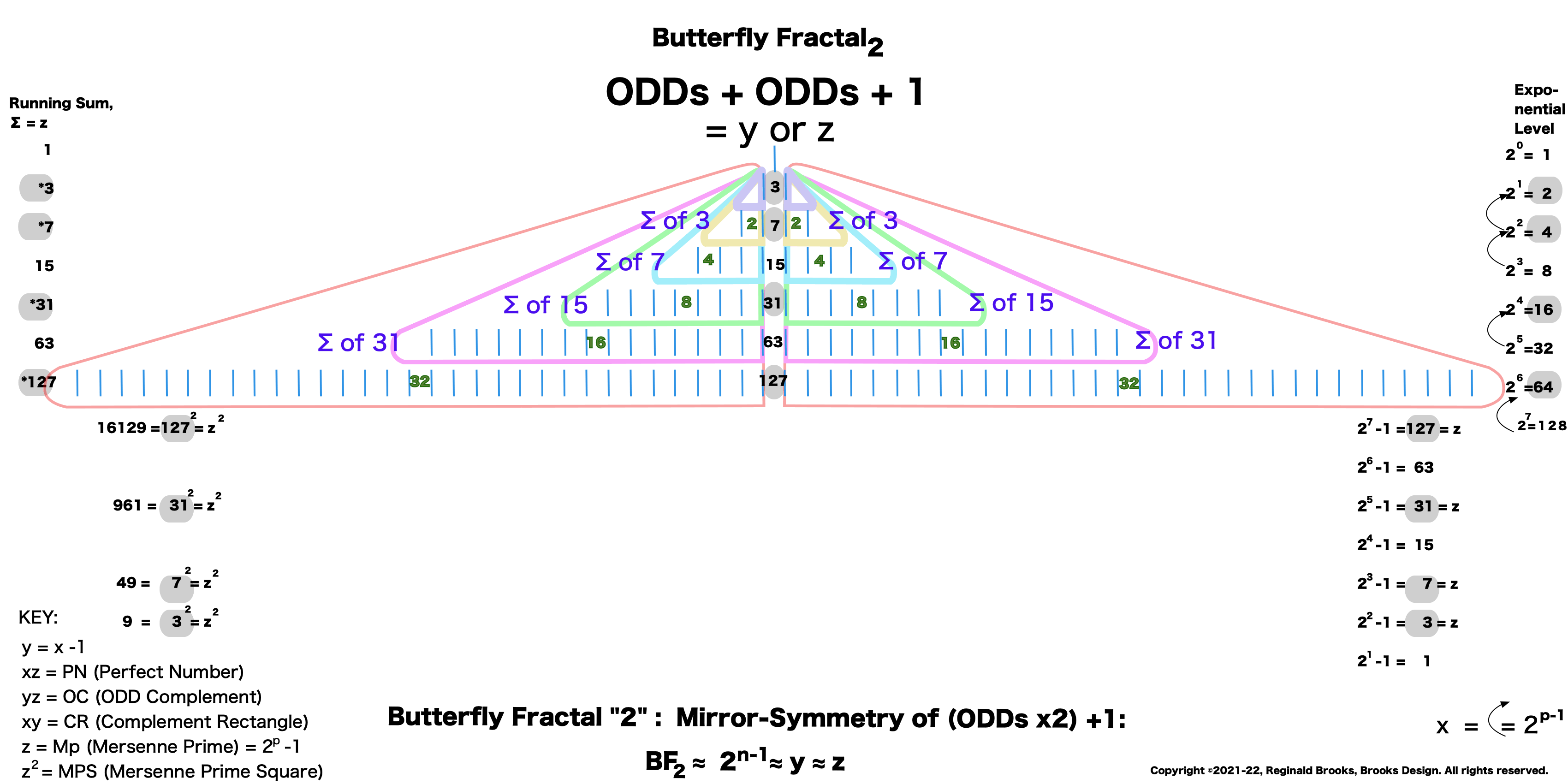
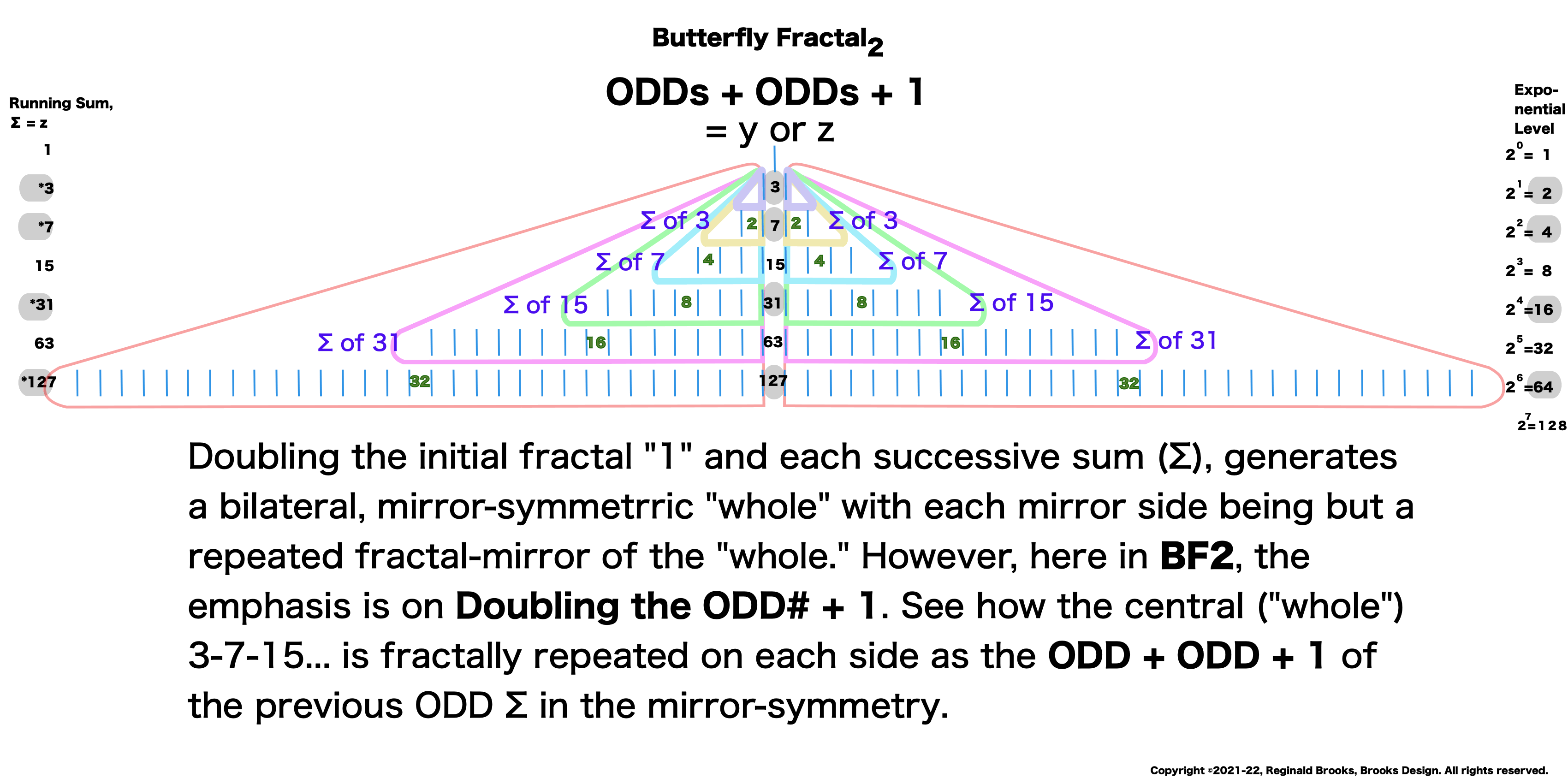
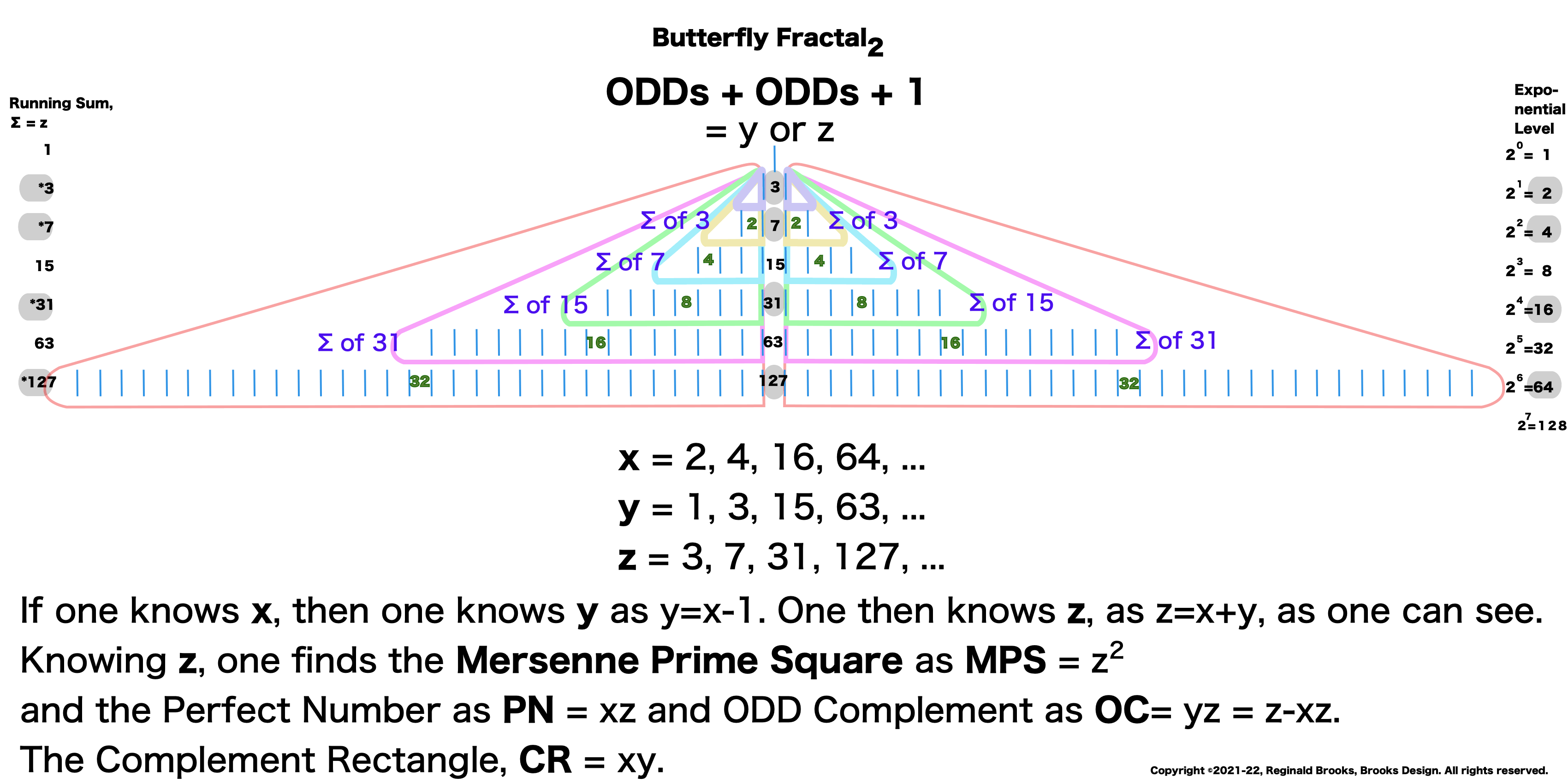
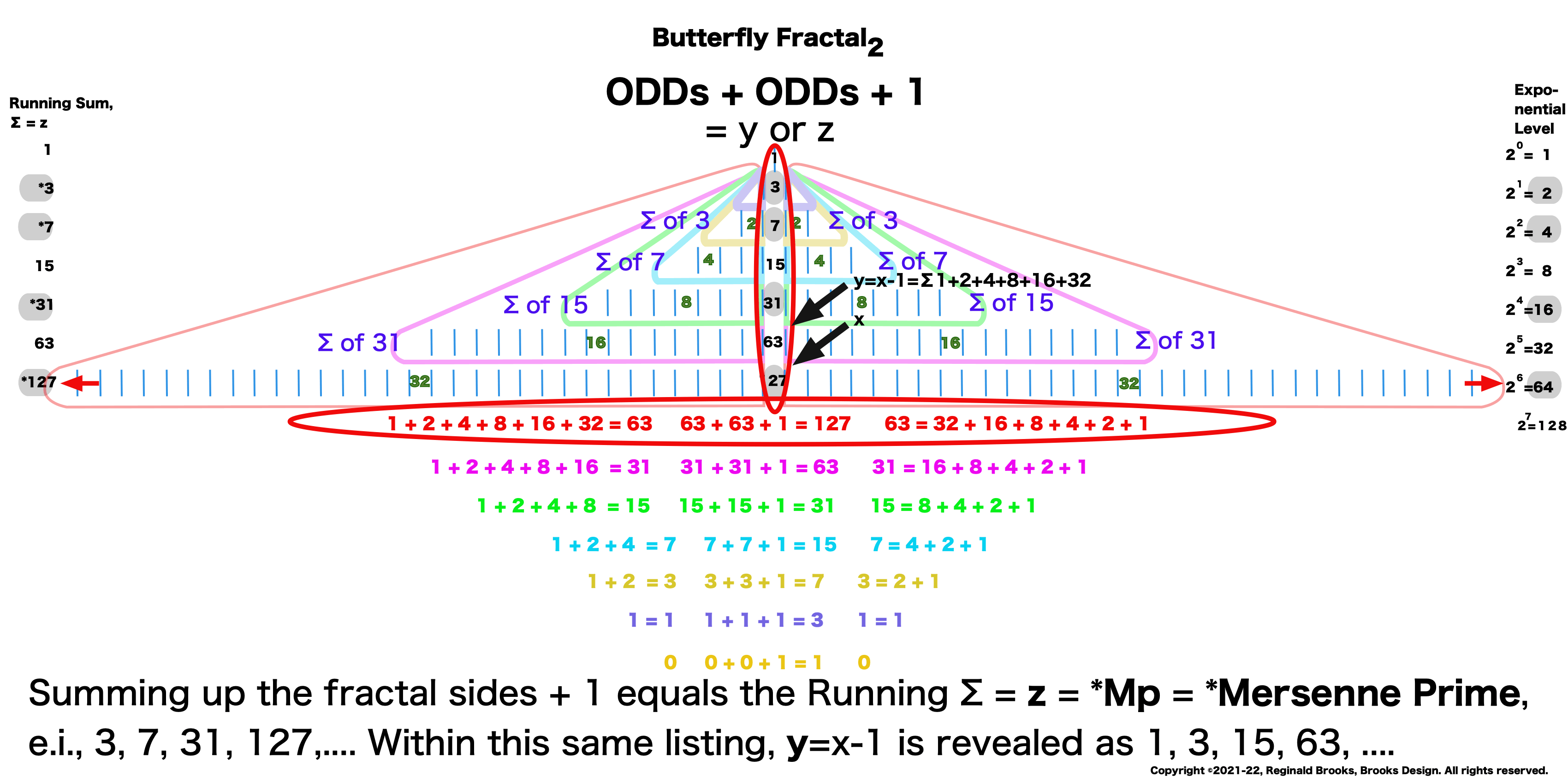
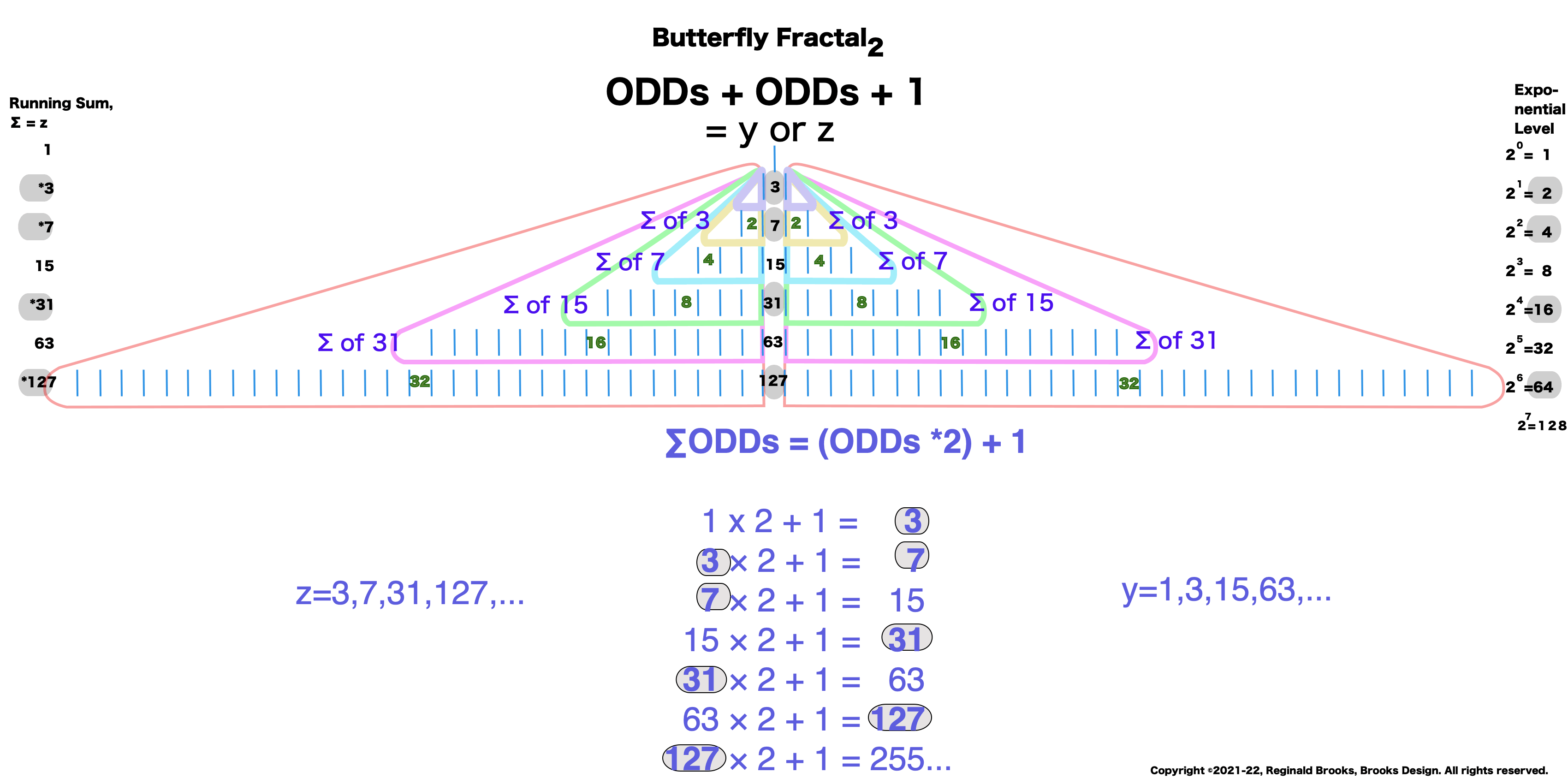
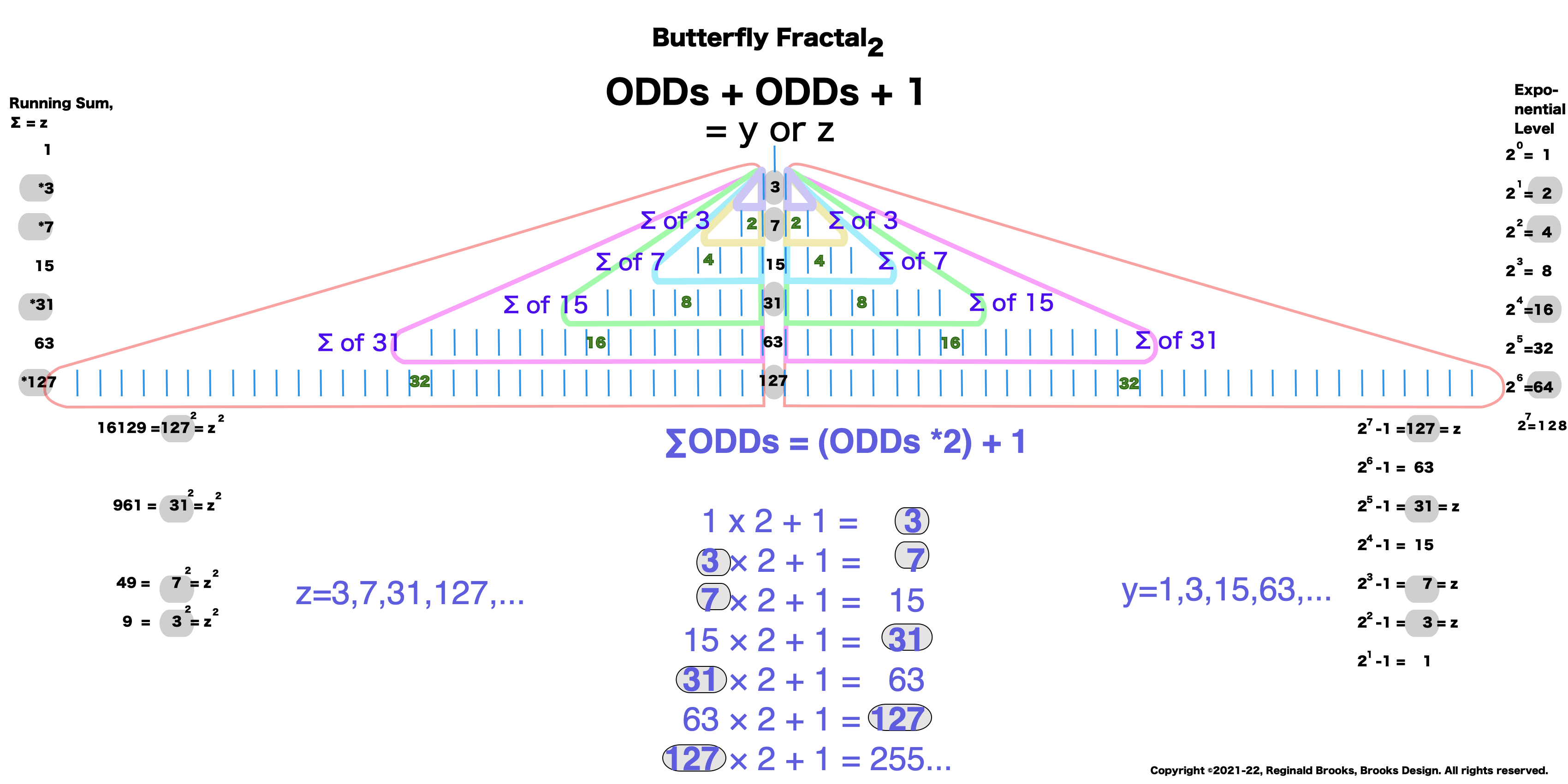
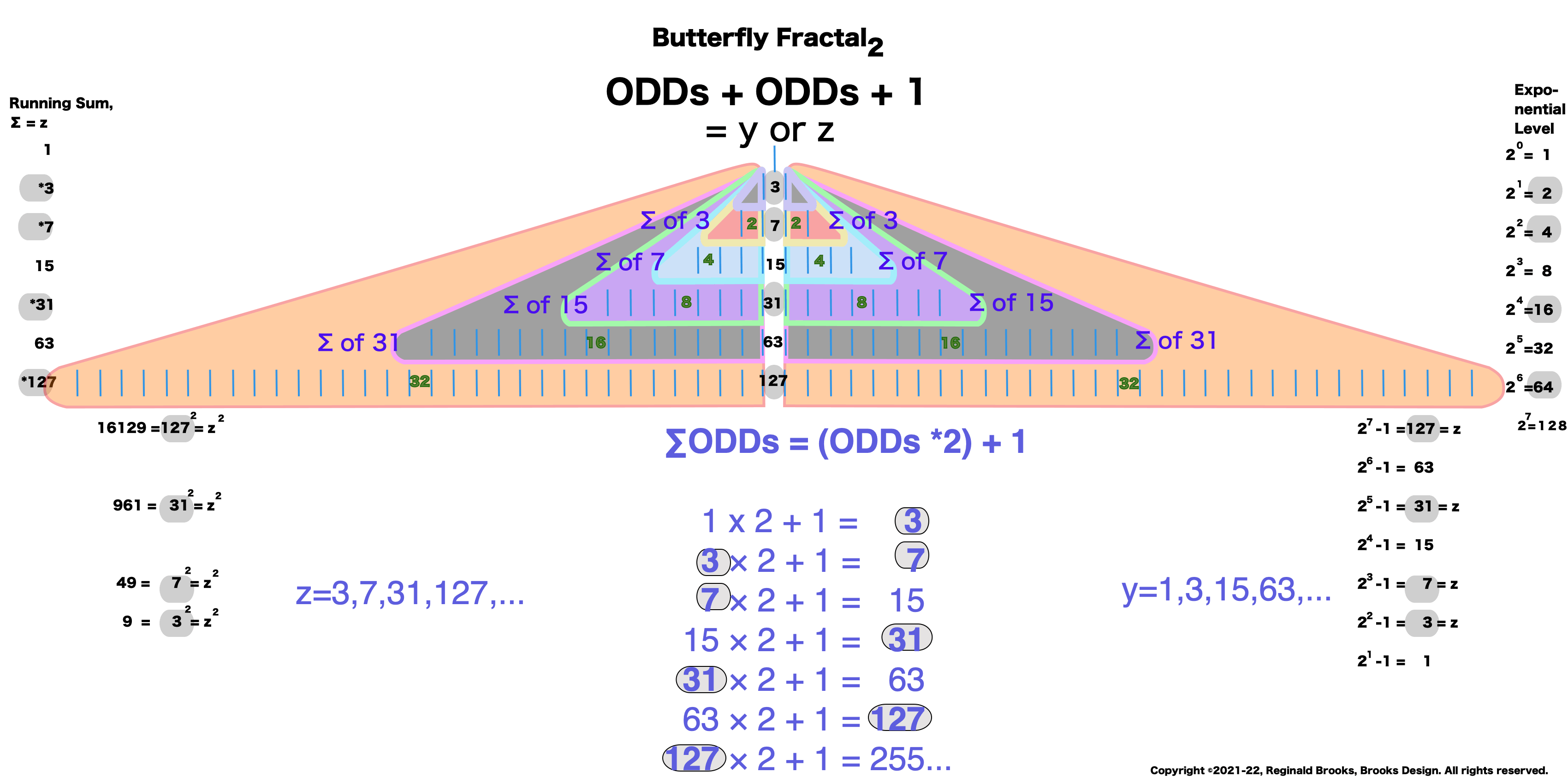
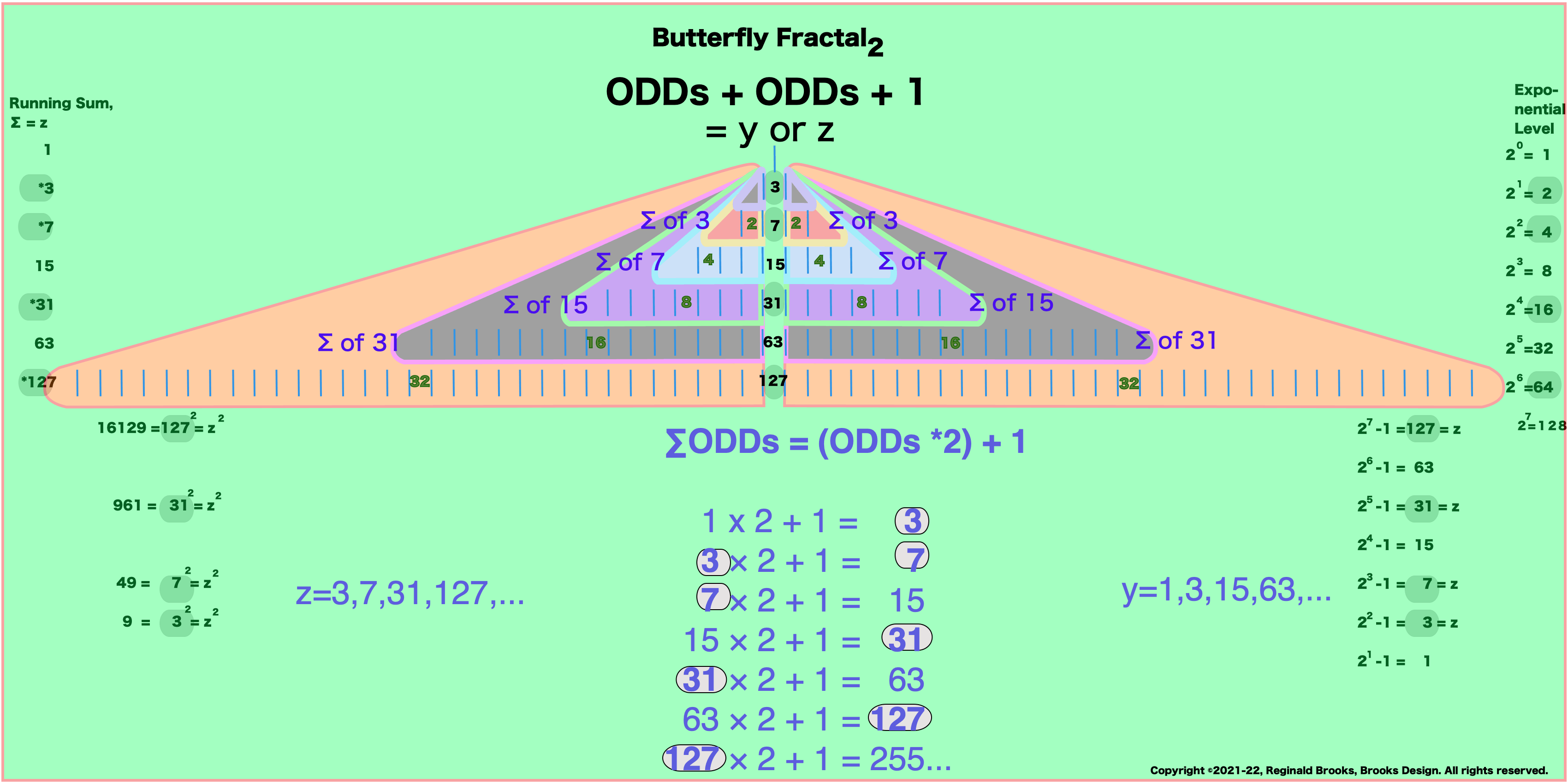
Animated Gif

Video

Oceans of Numbers (Part I) is next.

NEXT: Ocean of Numbers (Part I)~

~~~~~~~~

~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~

LINKS:

Mersenne Prime Squares (Part I) the Introductory white paper.

Mersenne Prime Squares (Part II) 3 Simple Intros.

Mersenne Prime Squares (Part III) the Advanced white paper.

The MPS Project The Mersenne Prime Squares Project.