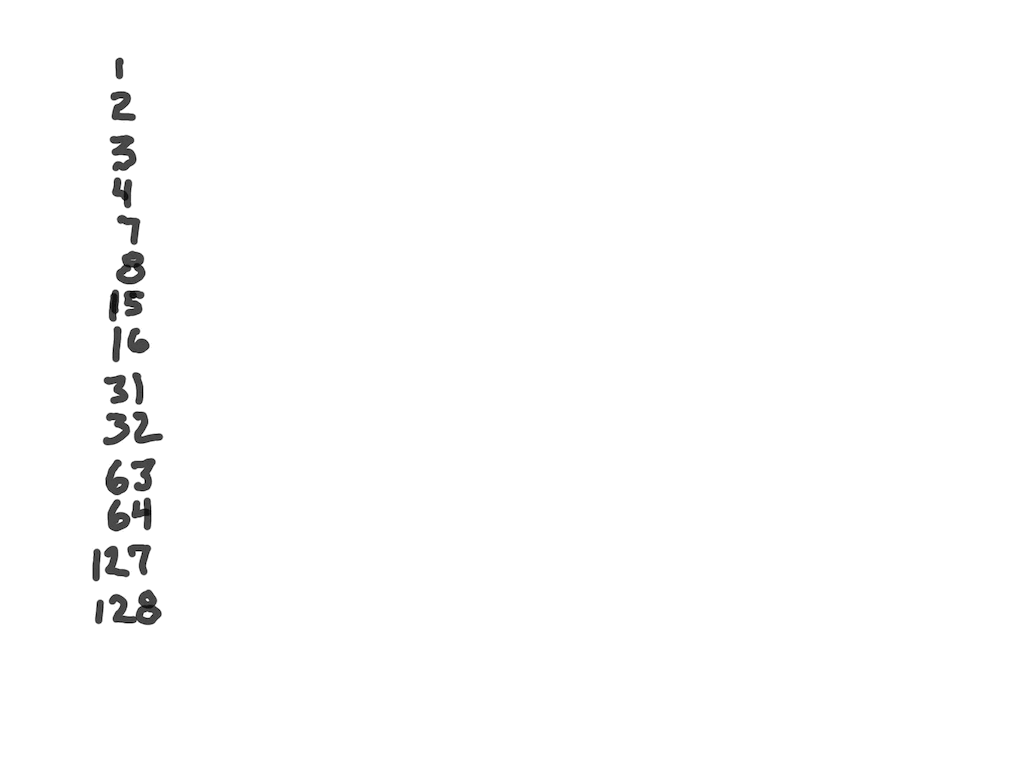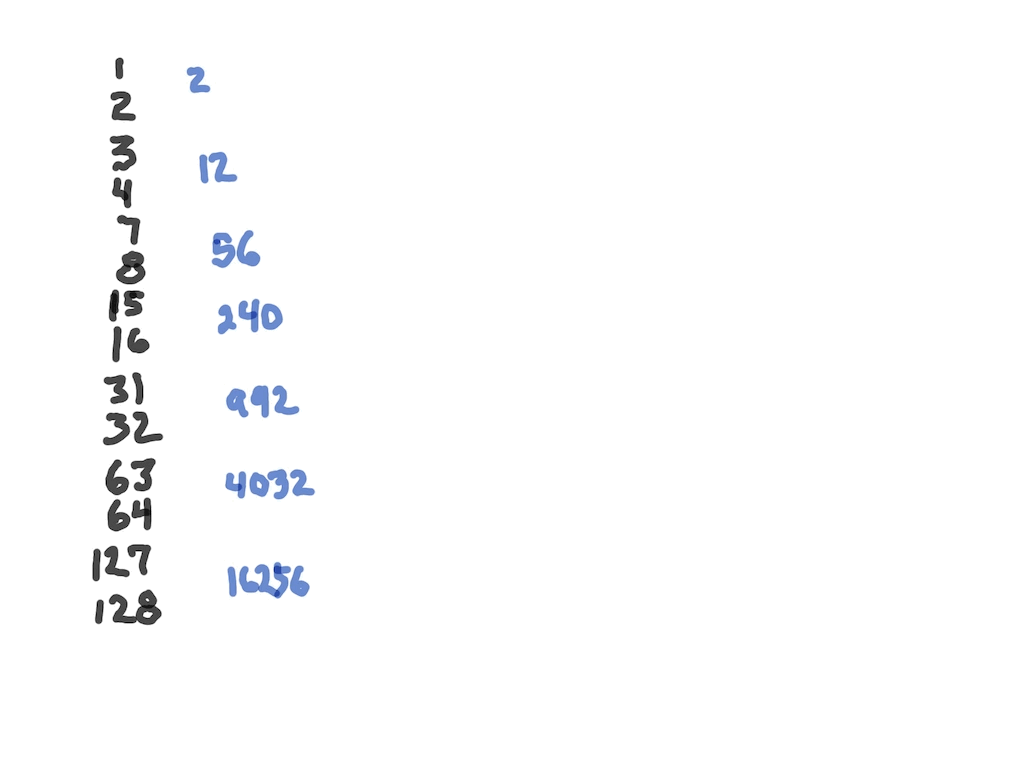BIM-MPS Details, Part V
The MPS on the BIM (BIMMPS)
Bringing it all together: Parts I - II - III - IV - V.
Sidenote: before we get started, and in an attempt to stay on track, we briefly glance at some Appendix material. It's one of those little excursions where the deeper you look the further and further away you go, and yet the irony is, if you go far enough you return to where you started! Fitting for the Appendix, but not to be ignored.
Let's repeat a key concept covered in Part II and III:
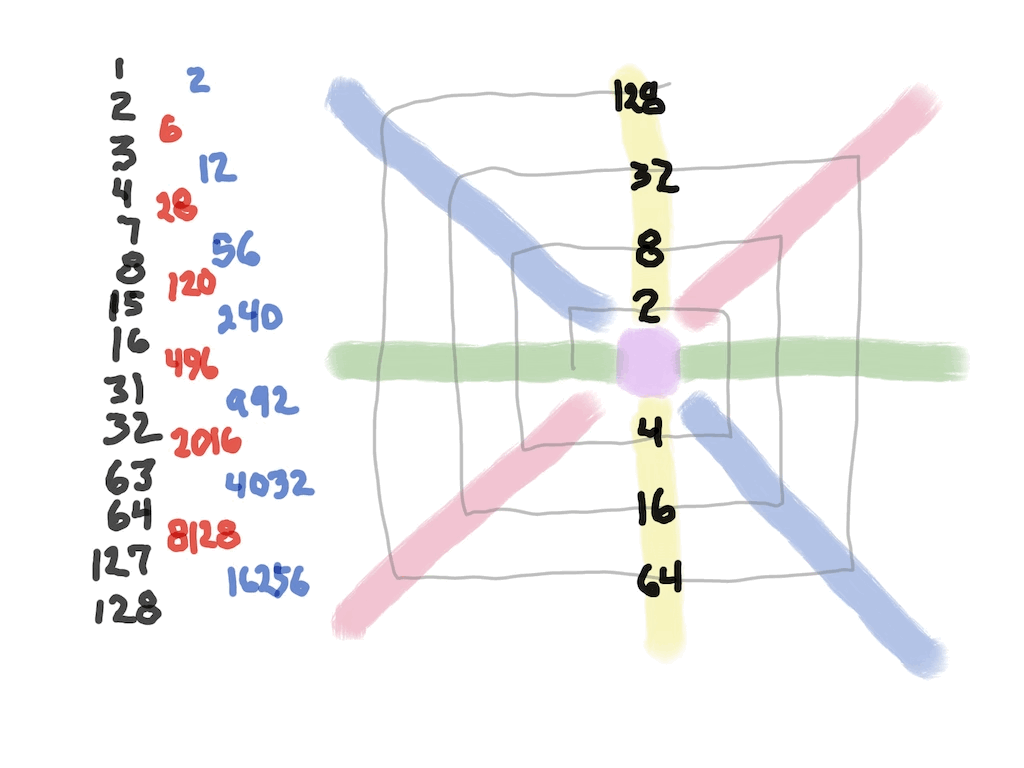
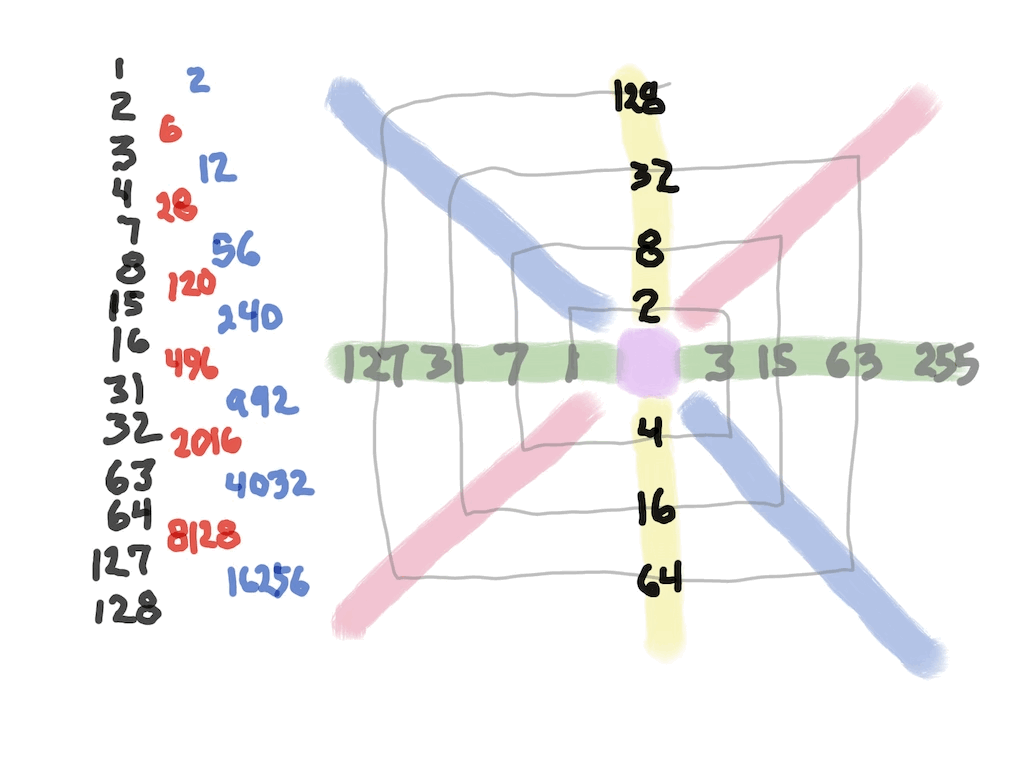
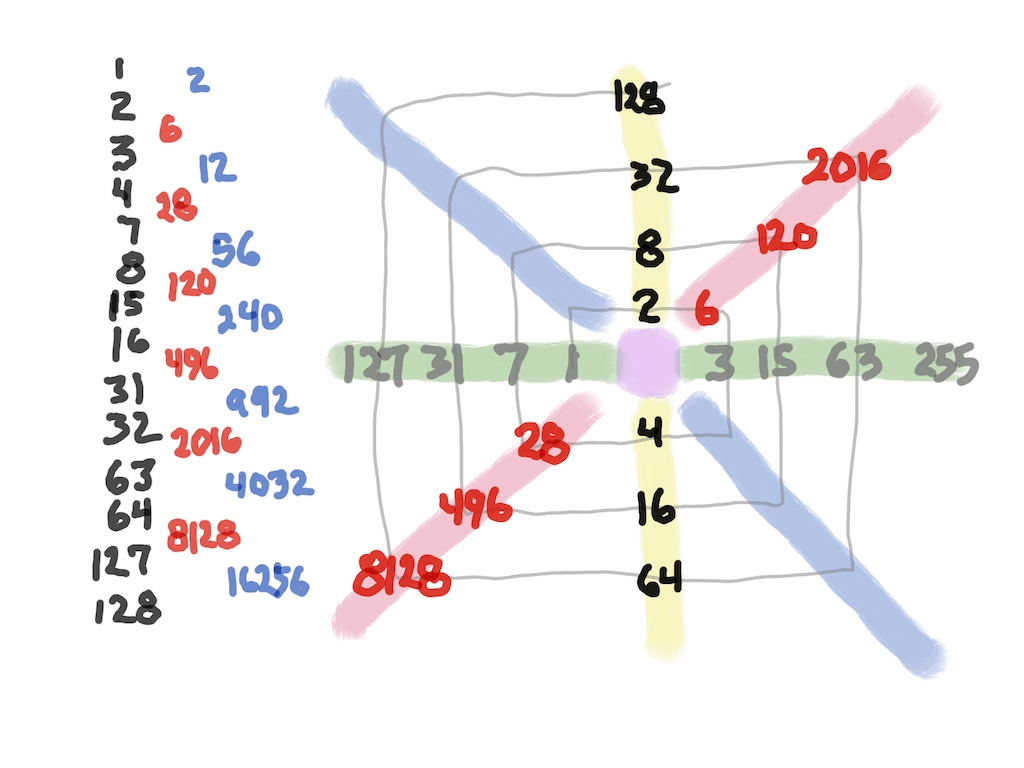
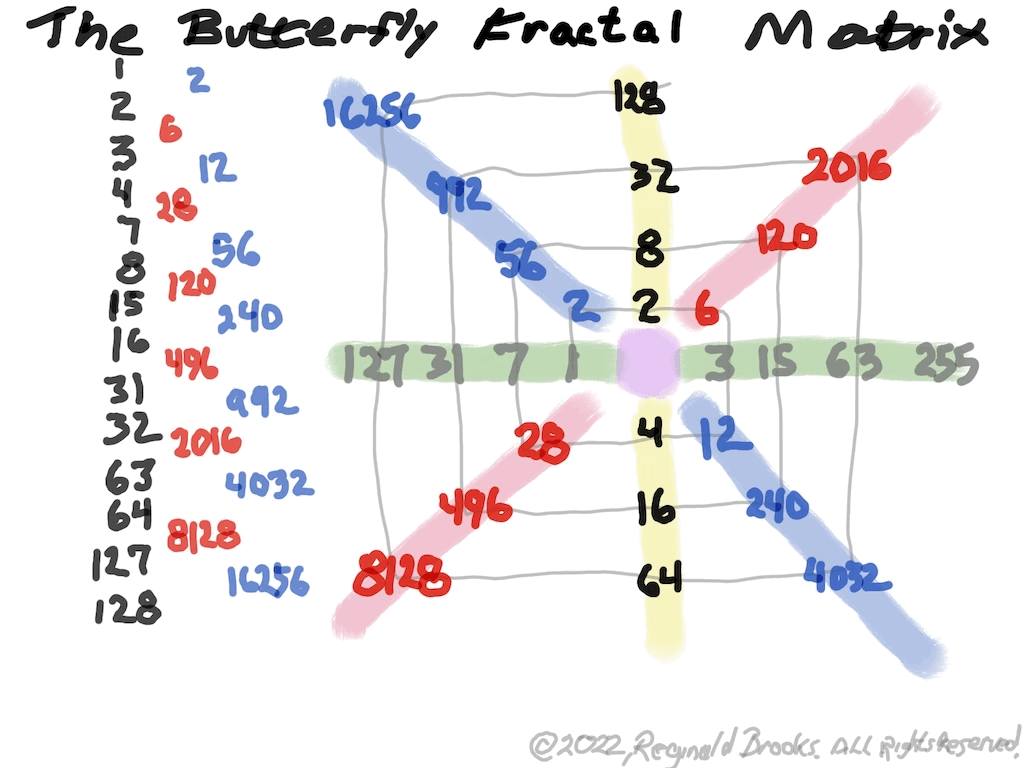
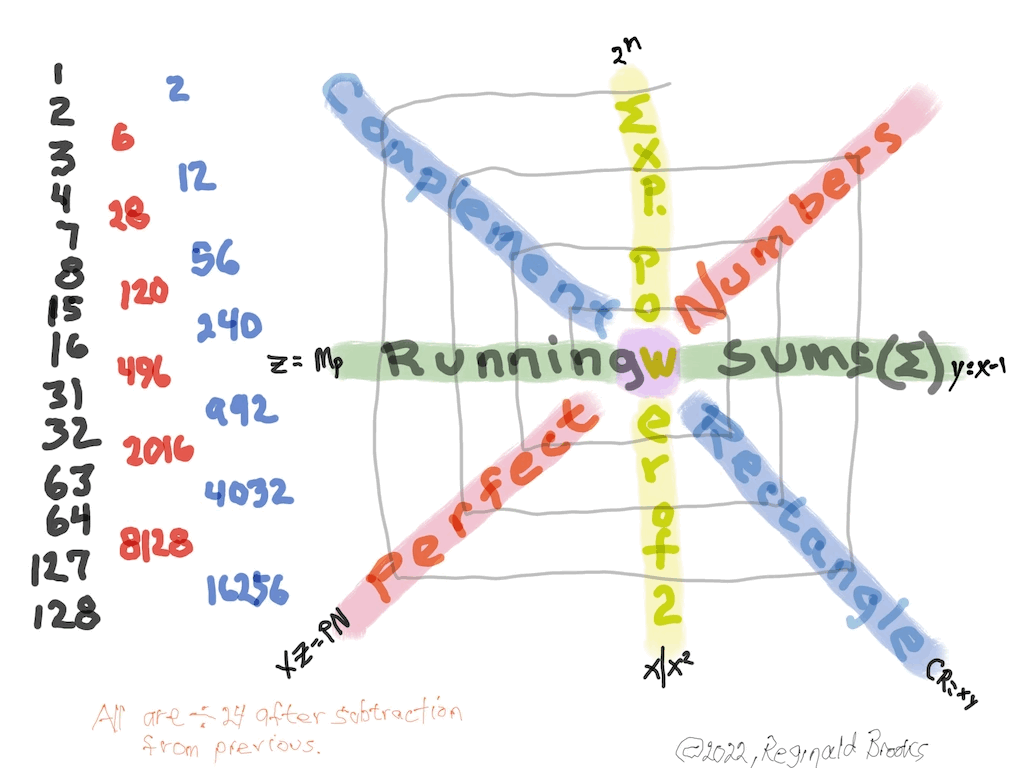
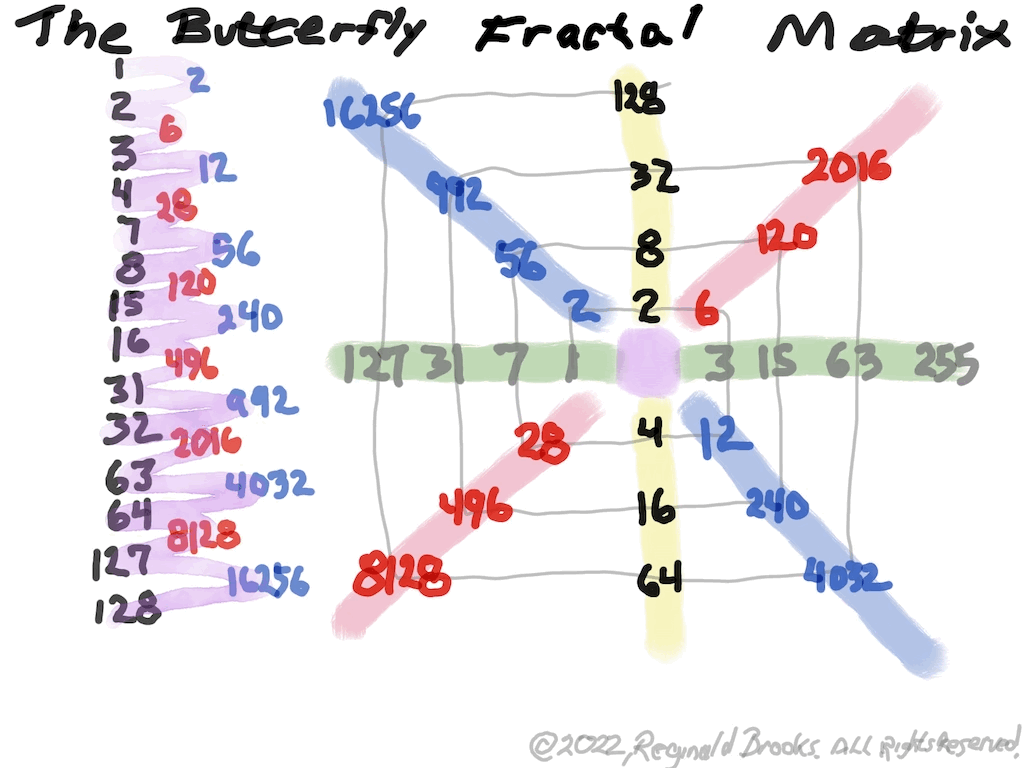
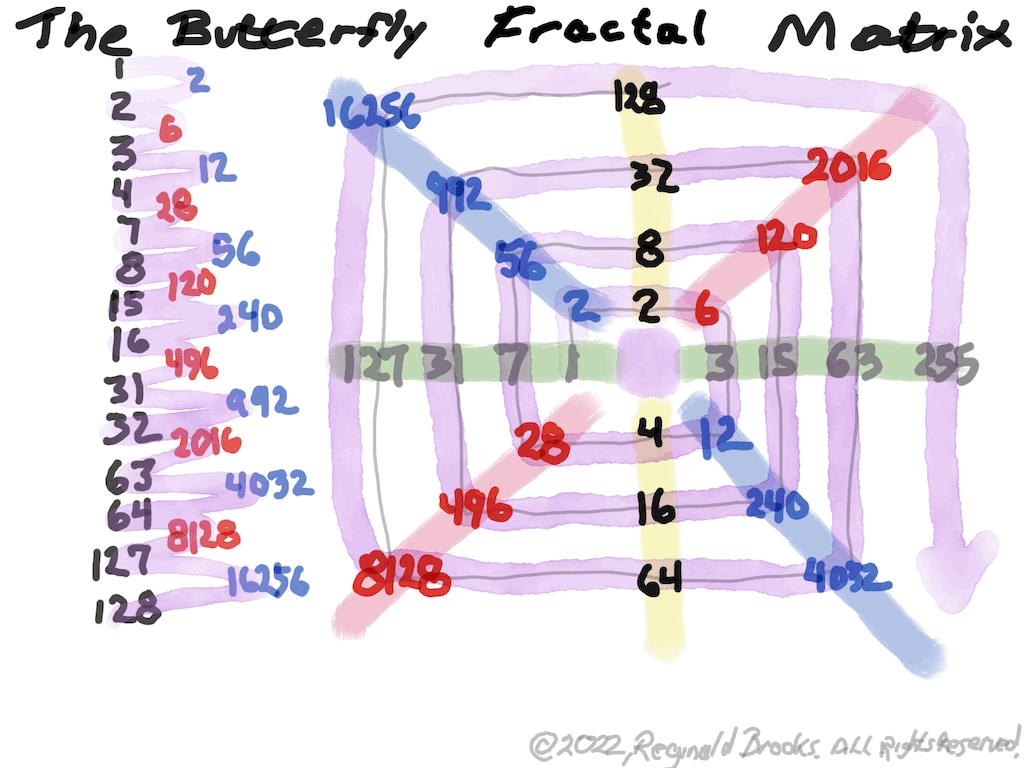
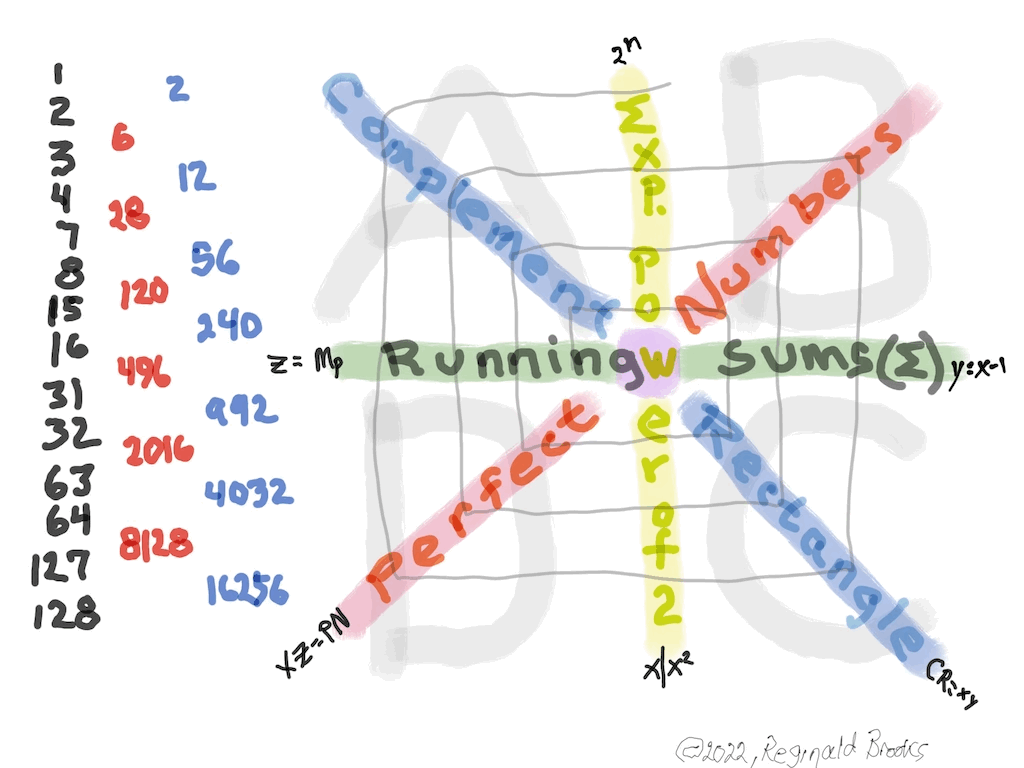
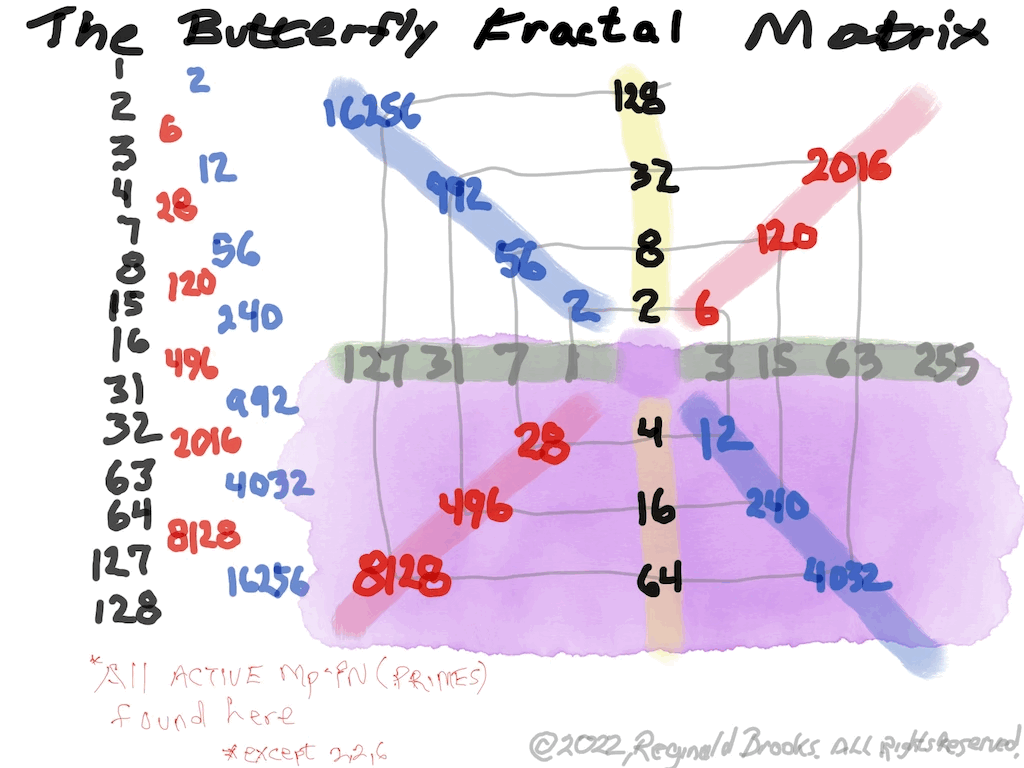
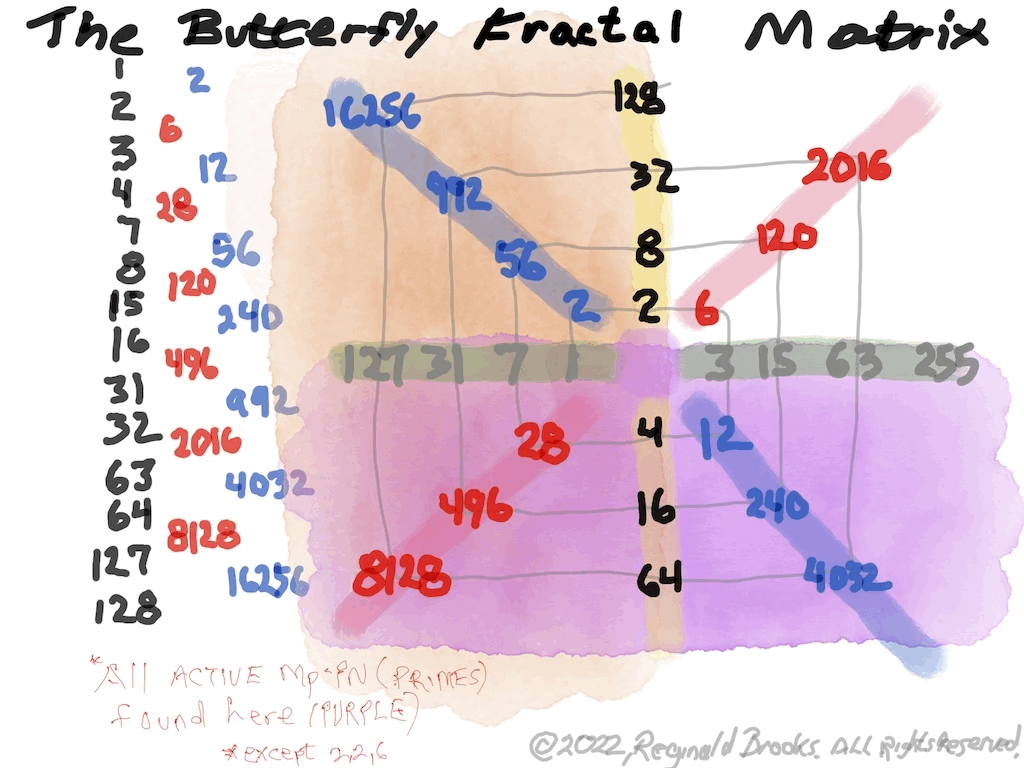
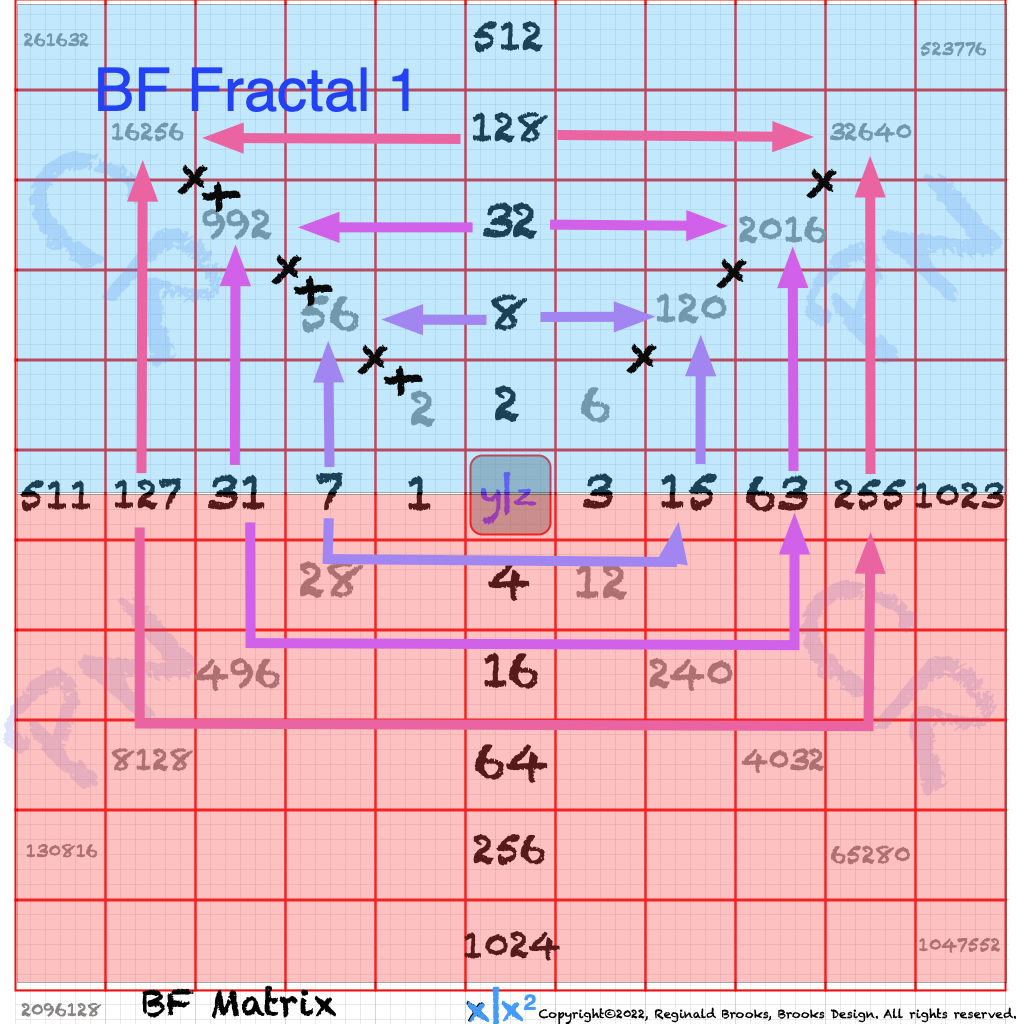
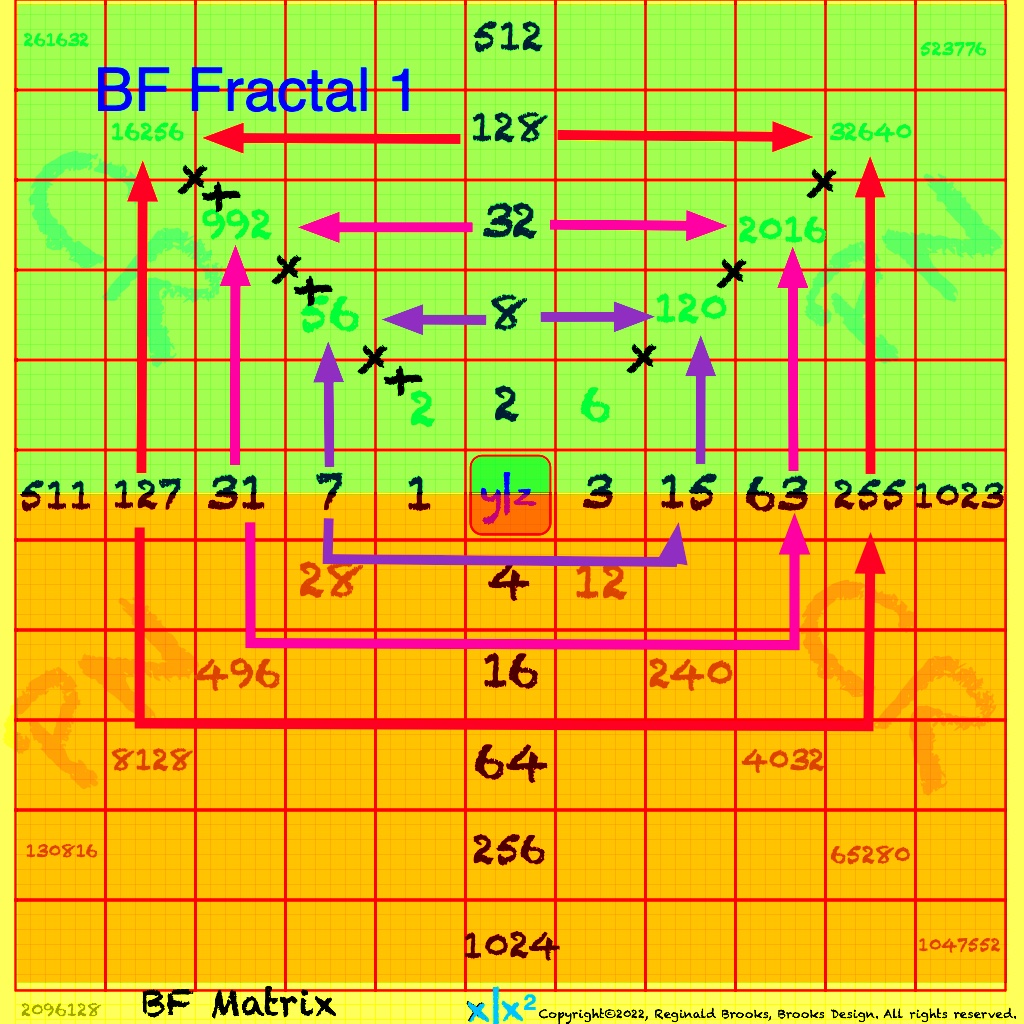
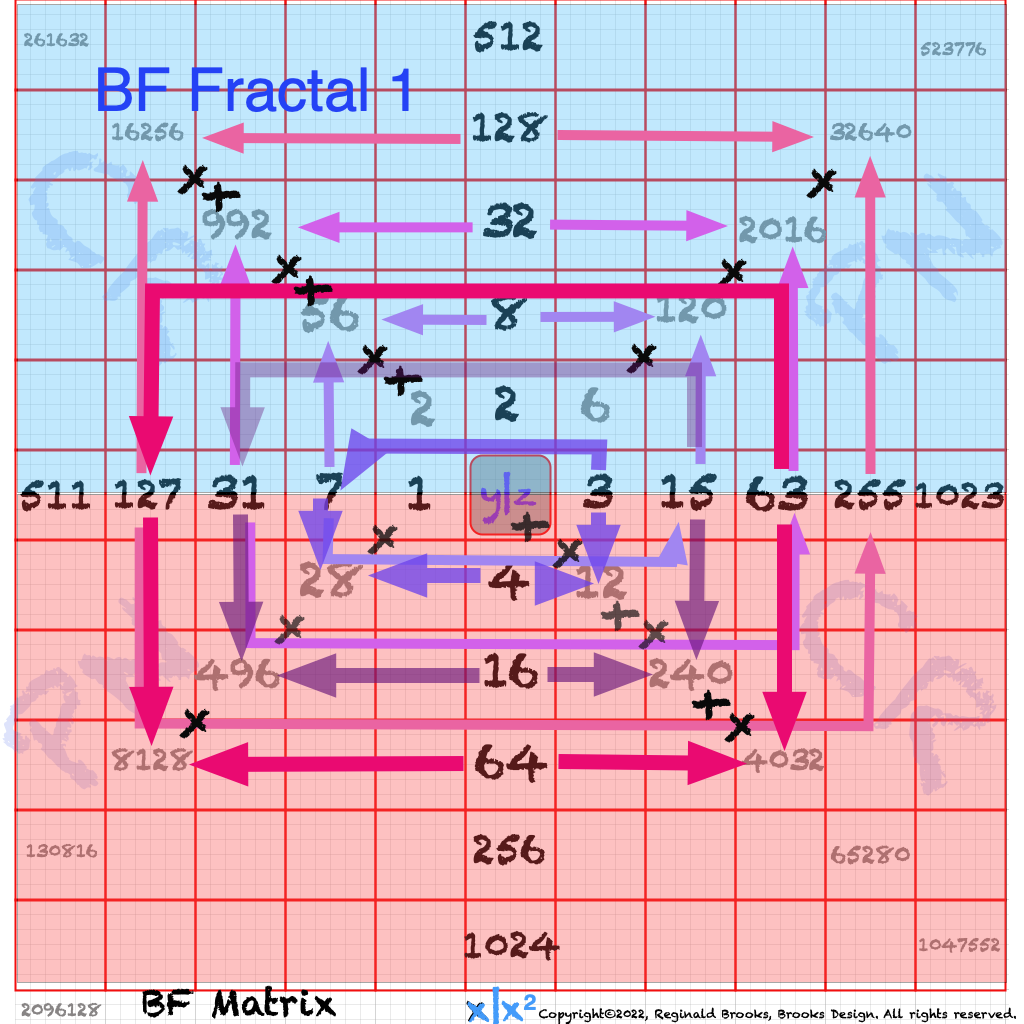
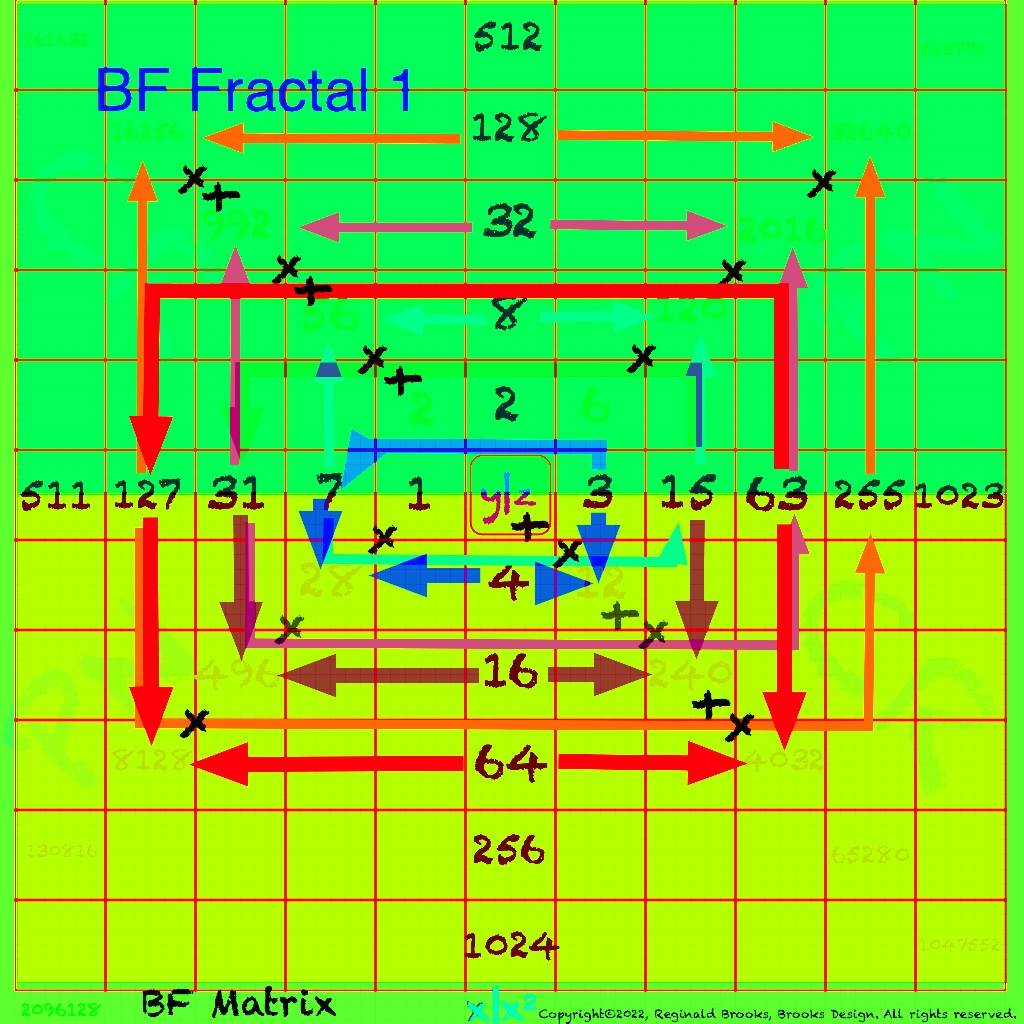
The Perfect Numbers may be expressed as the sequential running sums (∑) of the cubes of the sequential ODD numbers as 1³ + 3³ + 5³ ... and we have the genesis of the Butterfly Fractal~3~ (see Appendix).
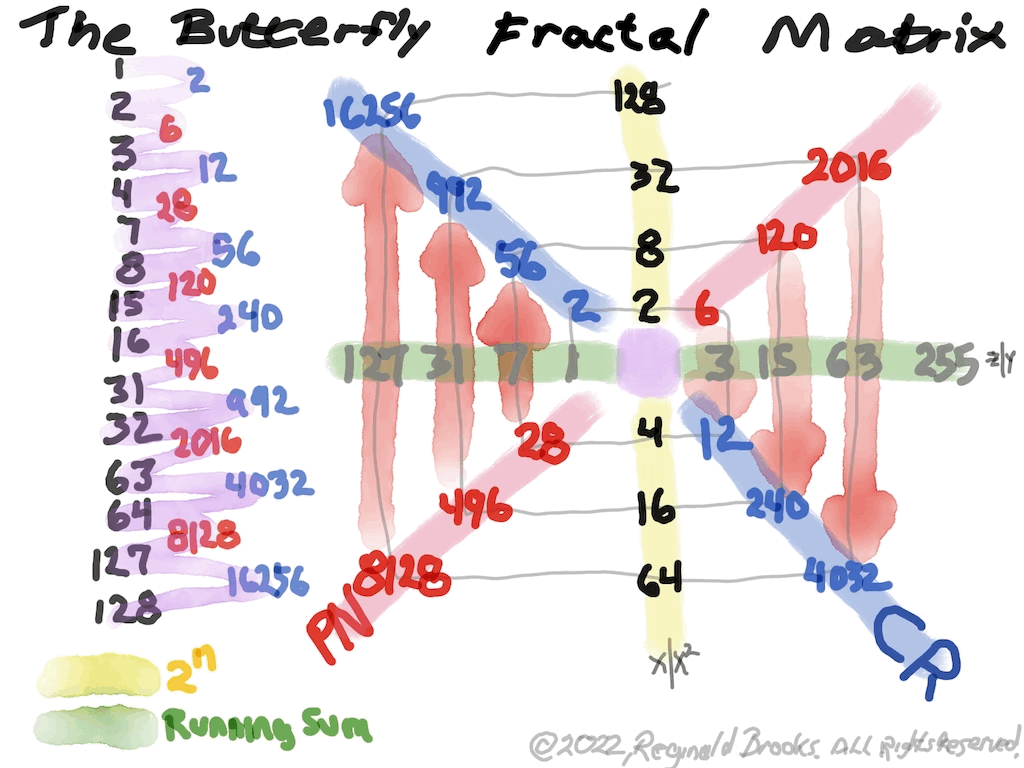
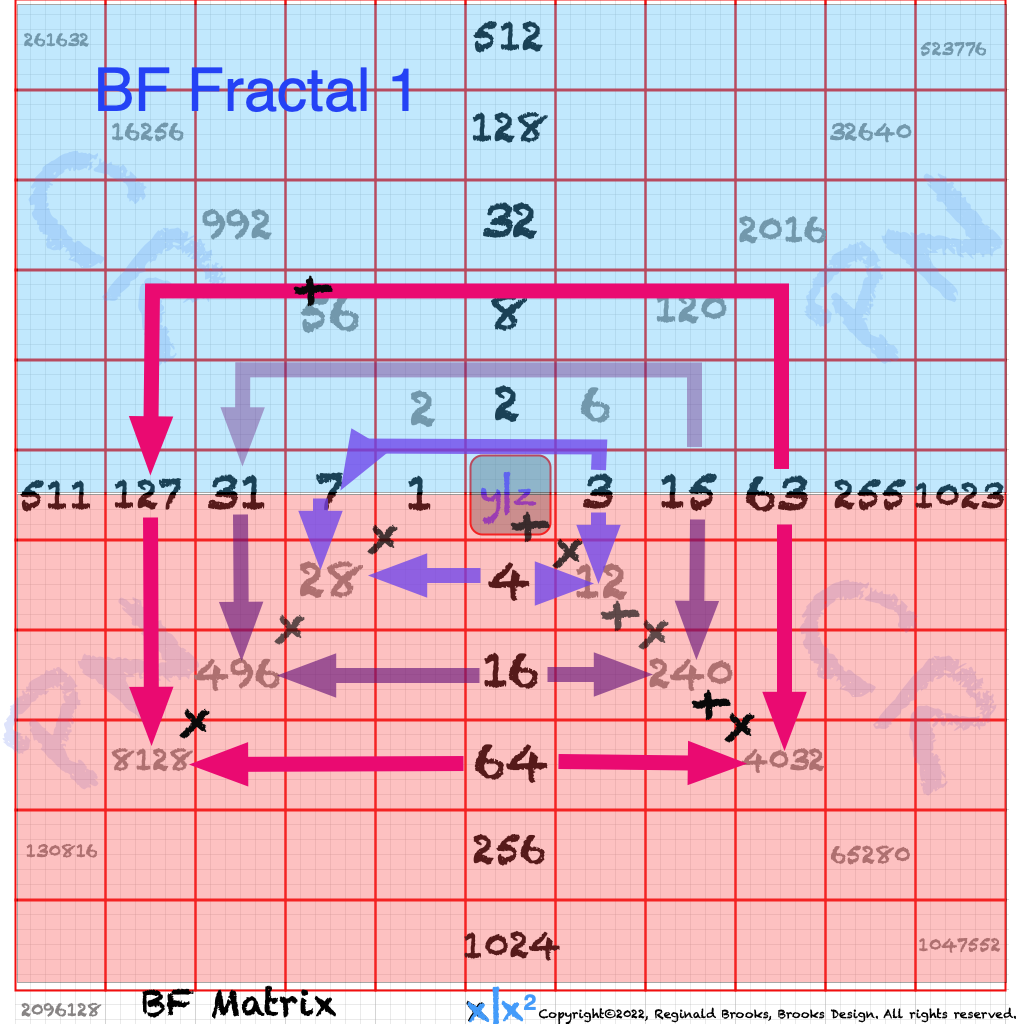
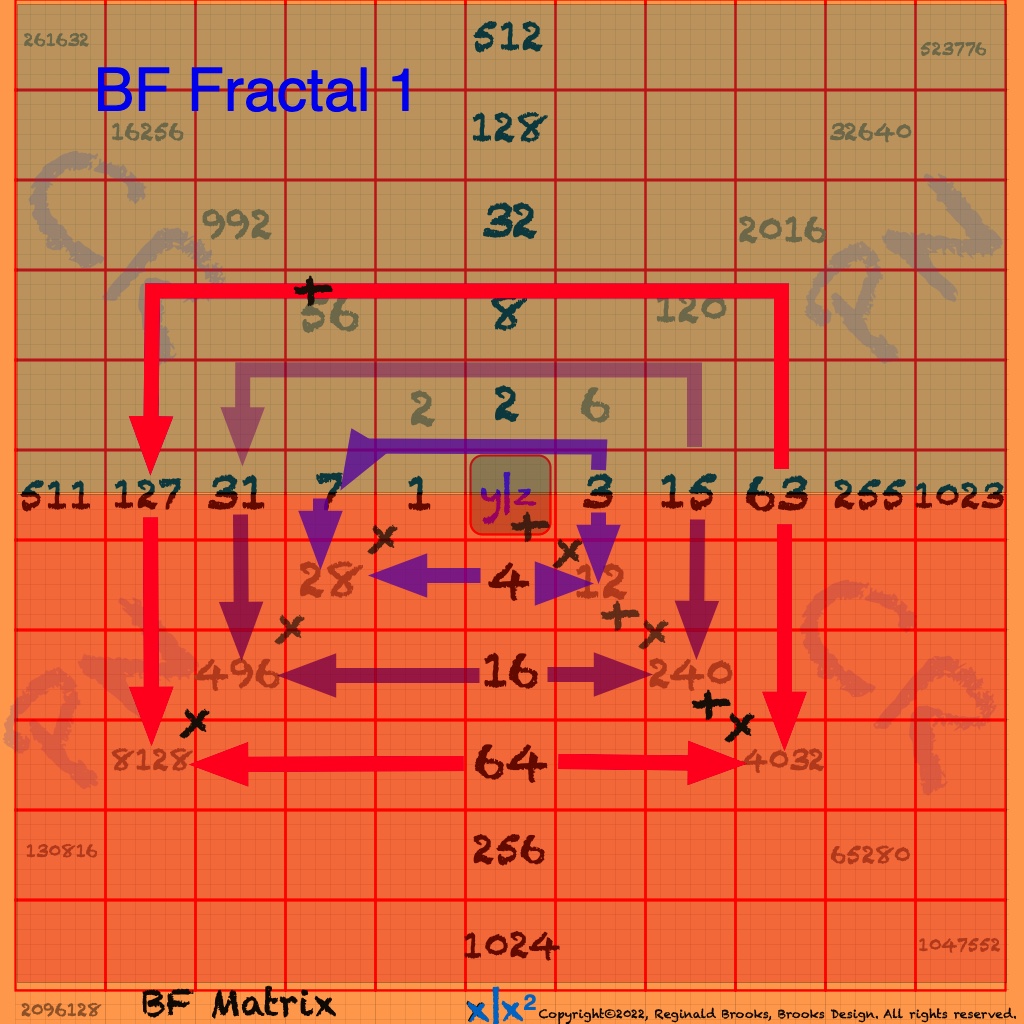
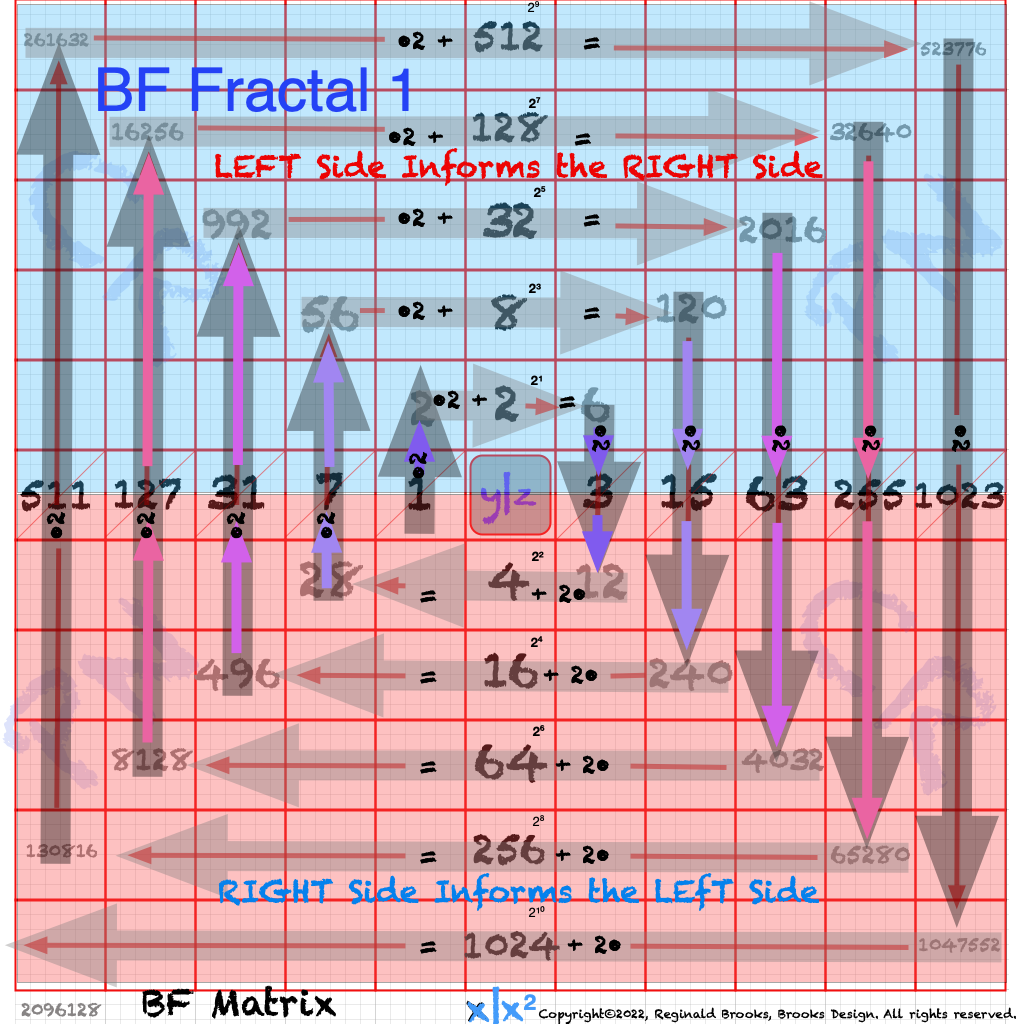
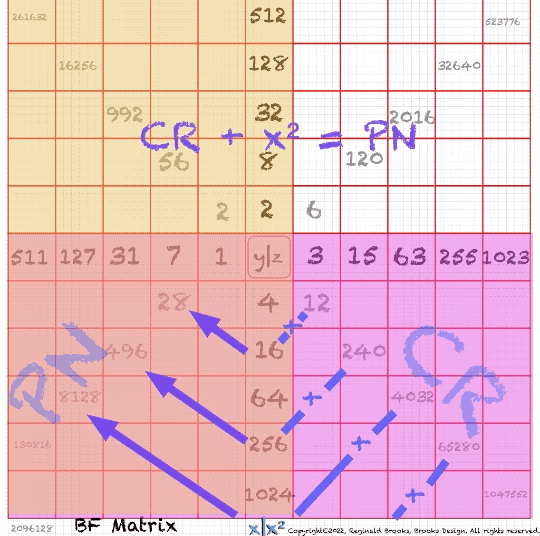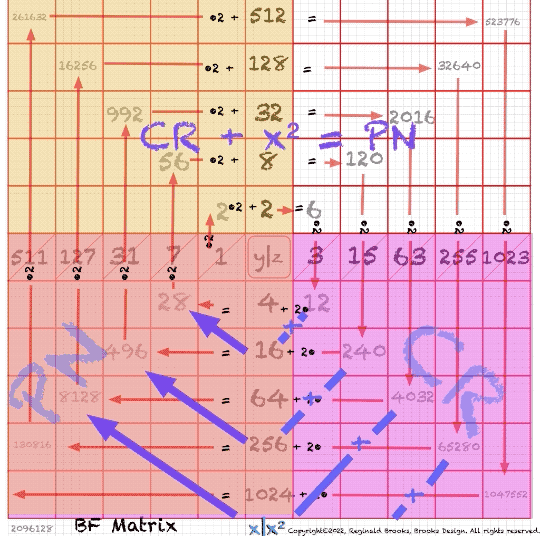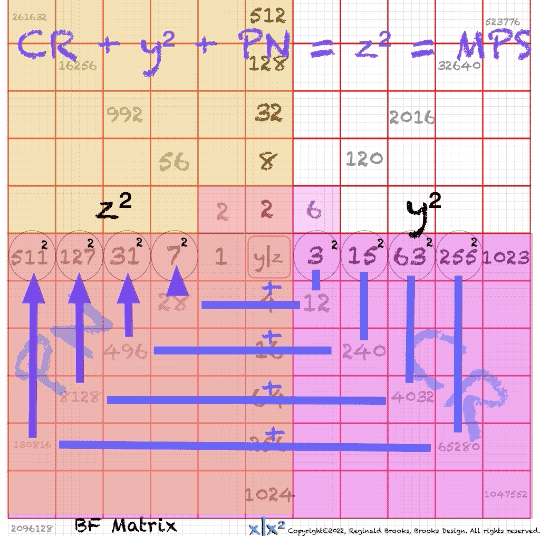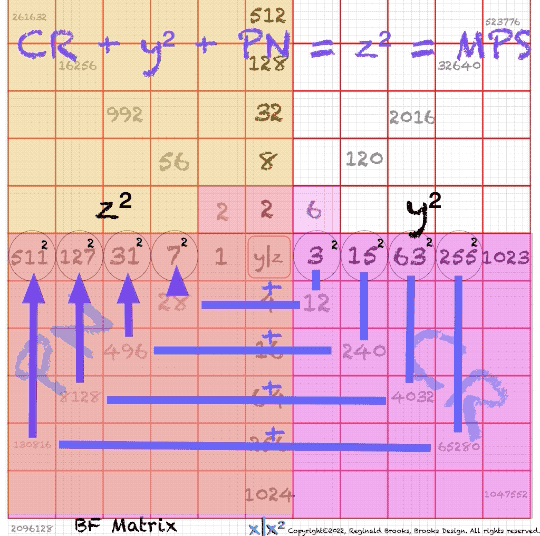
In the Butterfly Fractal~1~ and Butterfly Fractal~2~, we find the MPS parameters based around the EVEN numbers, especially within the exponential power of 2. When we look at their summations, we find it delivers the ODDs we are looking for that inform the MPS directly.
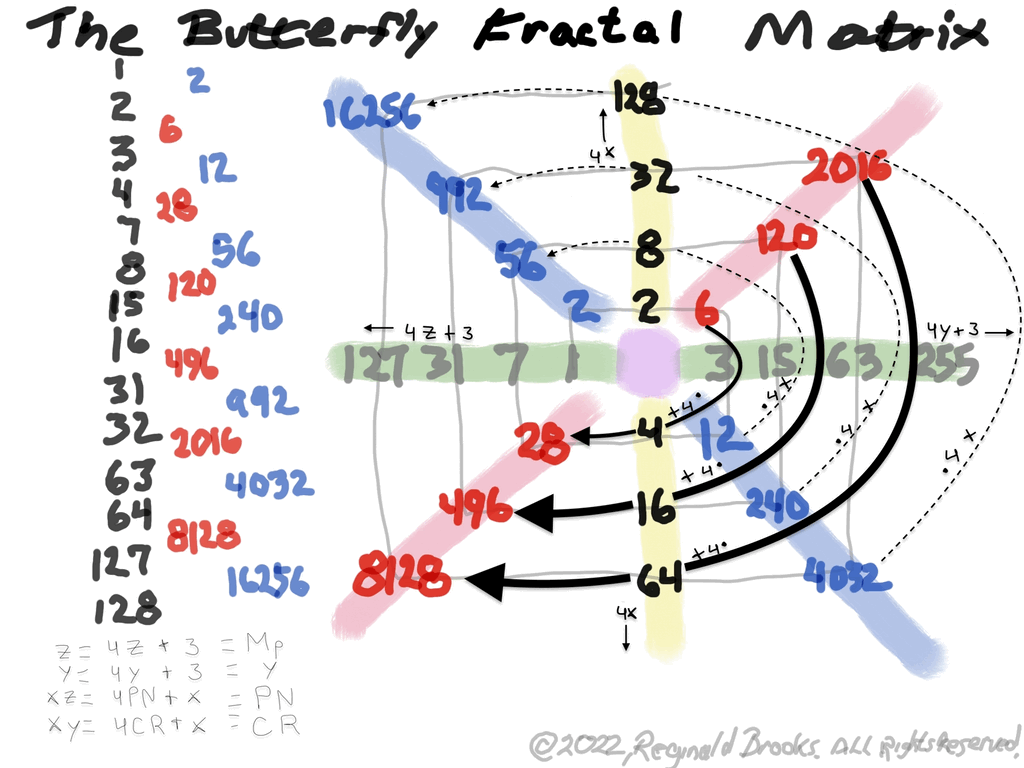
This gave the x and z=Mp directly and the y, xz=PN and xy=CR indirectly by calculation.
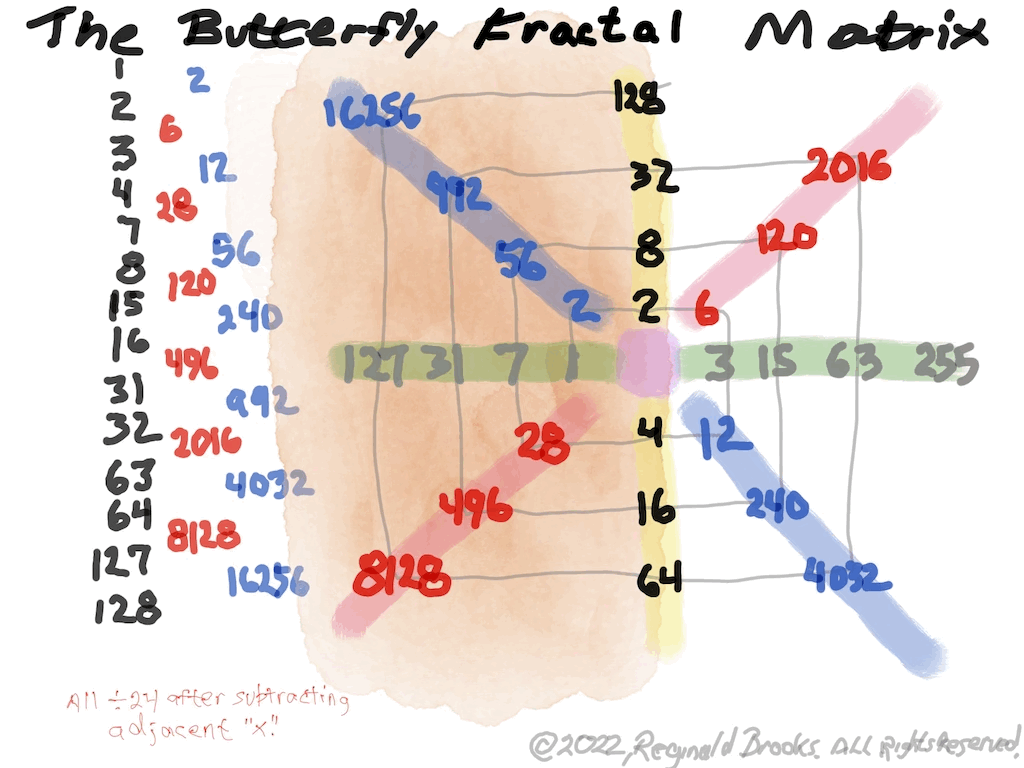
Now, in the Butterfly Fractal~3~ (see Appendix), we find the MPS parameters based around the ODD numbers, especially the Running Sums (∑) of the ODD numbers sequence of 1,3,5,… giving the MPS and the ODD³ sequence of 1³, 3³, 5³,… giving the PN!
The Butterfly Fractal~4~, based on the ∑ of the ODDs, is of course the basis of the BIM.
In talking about the Butterfly Fractal~1~, Butterfly Fractal~2~, Butterfly Fractal~3~ and Butterfly Fractal~4~, it begs the question: how are these all related? How can the ∑ of the exponential power of 2, of the cubed ODDs and even simply the ODDs by themselves, all be related to each other and, especially, to the Butterfly Fractal~4~ = BIM?
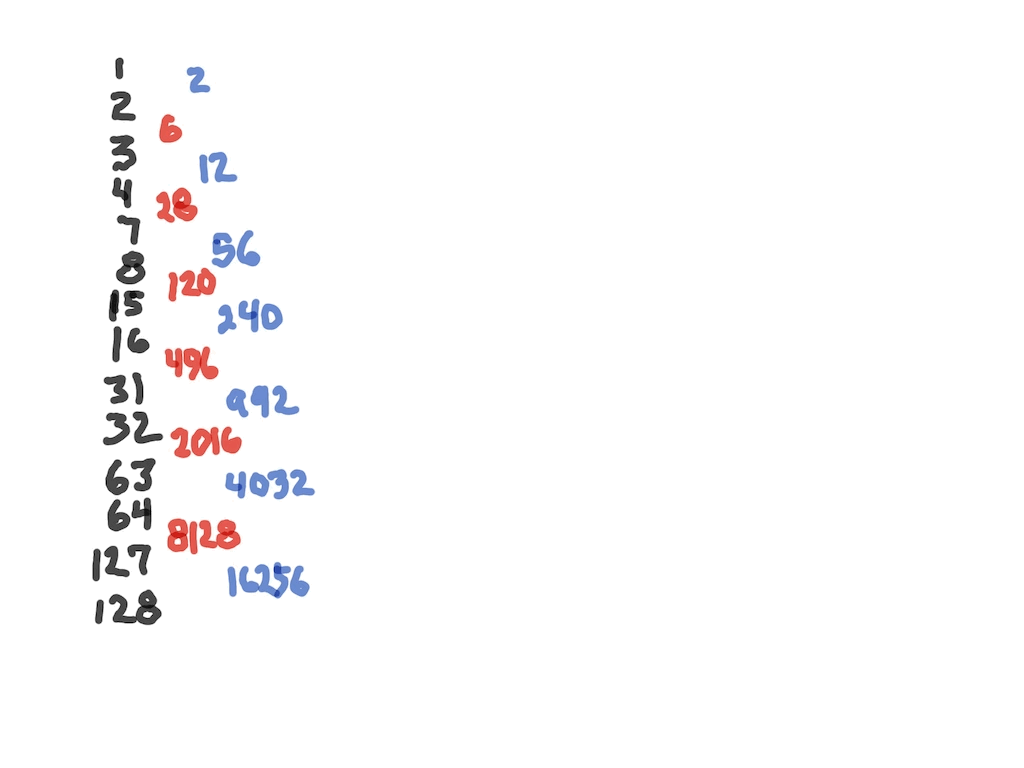
On the PD:
All “x”
All “x²”
All “y²”
All “z²”
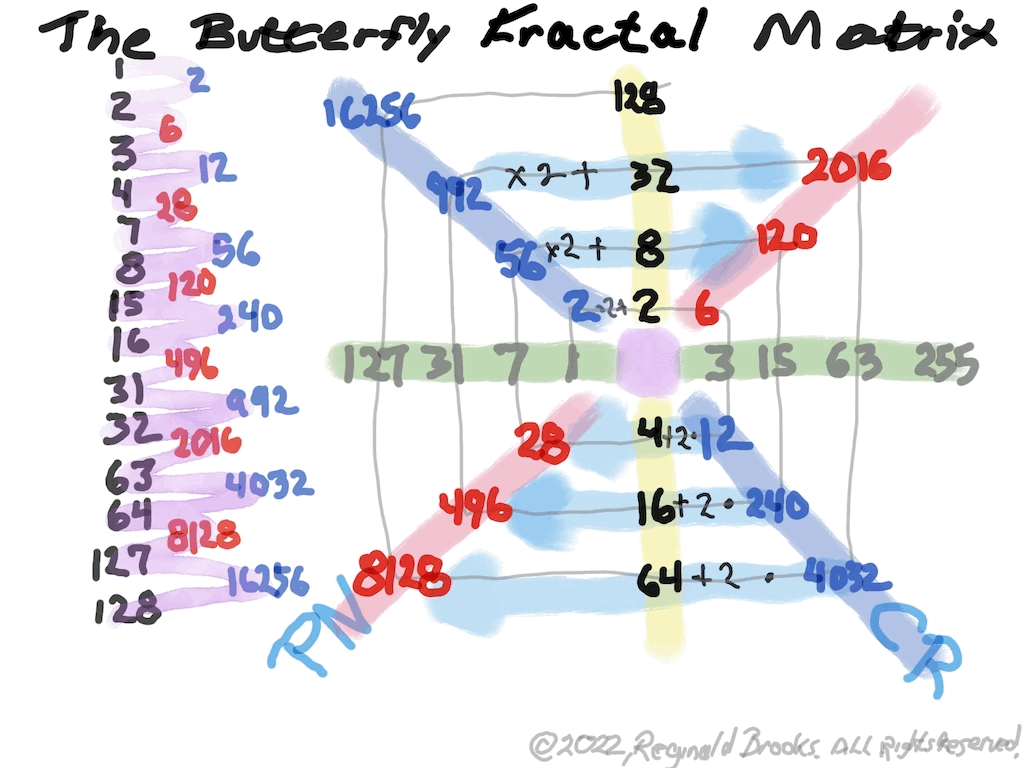
Rule: On PD, the square of any PD value — (2ⁿ)² — is found at the exponent value, the # of STEPS:
e.i. 16² = (2⁴)² = 2⁸ =256 = 4 STEPS down PD 16–>256
e.i. 1024² = (2¹⁰)² = 2²⁰ =1048576 = 10 STEPS down PD 1024–>1048576
e.i. 2048² = (2¹¹ )² = 2²² = 4194304 = 11 STEPS down PD 2048–>4194304
Note that while the PD does not contain ALL the 2ⁿ values — e.i. 2³ = 8 — it does contain ALL the 2ⁿ values that are “Active (BLUE Dot above)” — relevant — to the Mps as well as those “Inactive (I)” values that act like placeholders for the Mp sequence, i.e. multiples of 4x (ALL “x” values can be found by sequential multiplication by 4), like 256. These “I” are present as the PD contains every “other” 2ⁿ value starting with 2² — 2² - 2⁴ - 2⁶ - 2⁸ - 2¹⁰ -2¹² …in other words, only those exponential powers of 2 with EVEN exponents. Naturally, the square of any ODD exponent 2ⁿ — like (2⁷)² = an EVEN and will be on the PD, as 2¹⁴.
As stated above, this makes the PD the container for all MPS. ...
Sidenote end.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~