Copyright ©2021, Reginald Brooks, Brooks Design. All rights reserved.

~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~

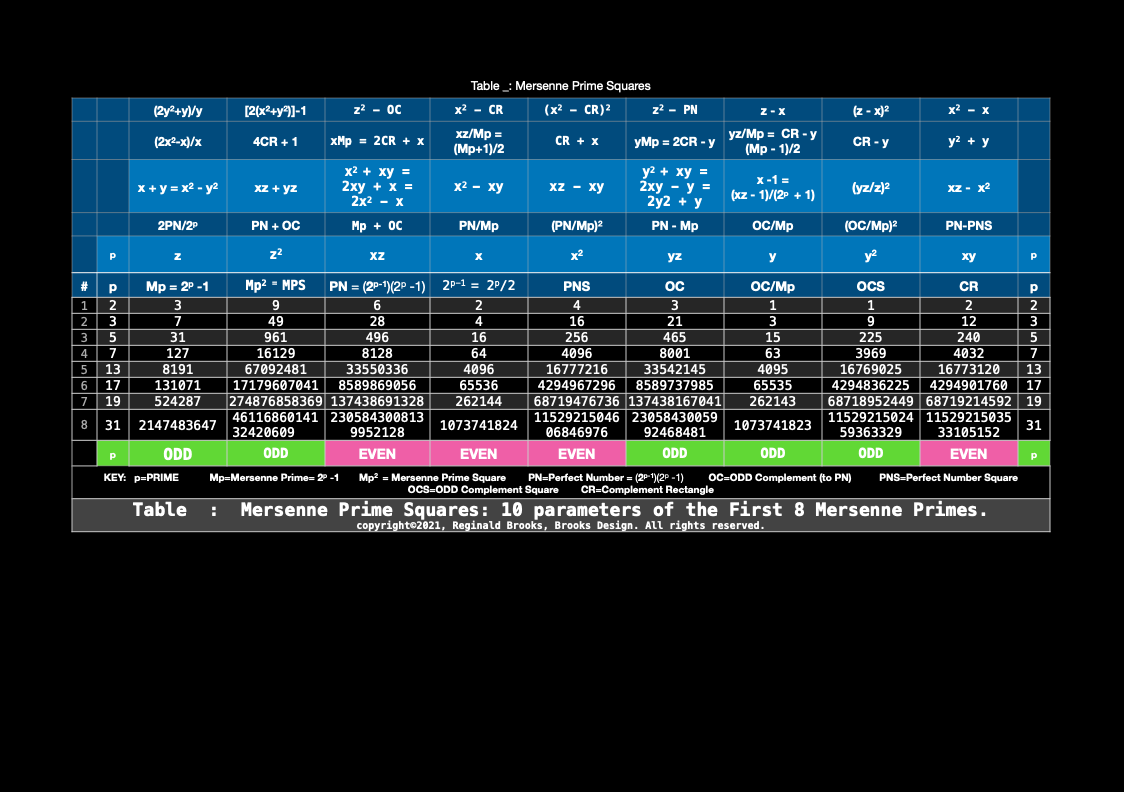
Mersenne Prime Squares:
3 Simple Intros

Part I: Basics

There once were two dots — numbers, really. One was ODD, but very special. The other was EVEN, but also very special. At least that is what everyone told them! But they were just dots — numbers, really — and they thought they were part of something bigger!

The really crazy thing about this special ODD and special EVEN number is that they are related! Like family! They are part of a larger family! How so?

First, the ODD dot:

The ODD dot says, “I am only a point, a simple number. People know I exist as a number — even as a special PRIME number — but that’s it. It seems I am almost invisible!”

Well, let’s fix that! Get out your pens, pencils, crayons, brushes, or whatever you like to make some drawings and paintings.

A line is nothing more than a series of dots, so just make a pretty straight line of your dots. That line is now a side of a SQUARE, so draw in the other sides with lines that make up a SQUARE. Any size you like is just fine, for now.

Wow, the little ODD dot is now an AREA!!!!

WELCOME TO THE VISIBLE WORLD. EVERYONE CAN SEE YOU NOW.

Let’s give you a name, how about MPS (decoded as Mersenne Prime Square).

And guess what MPS? You are actually the grandparent(s) in this big family! Think of yourself as the TOP LAYER!

Second, the EVEN dot:

The EVEN dot also says, “I am only a point, a simple number. People know I exist as a number — even as a special EVEN Perfect Number — but that’s it. It seems I am almost invisible!”

Well, let’s fix that, but along the way you will see that you have another brother/sister that is actually an ODD number. That’s OK because we equally like both ODD and EVEN numbers!

In fact, you the EVEN dot and your ODD complement dot will, like the children of your grandparents, together form 2 AREAS that exactly match your grandparents MPS Layer!

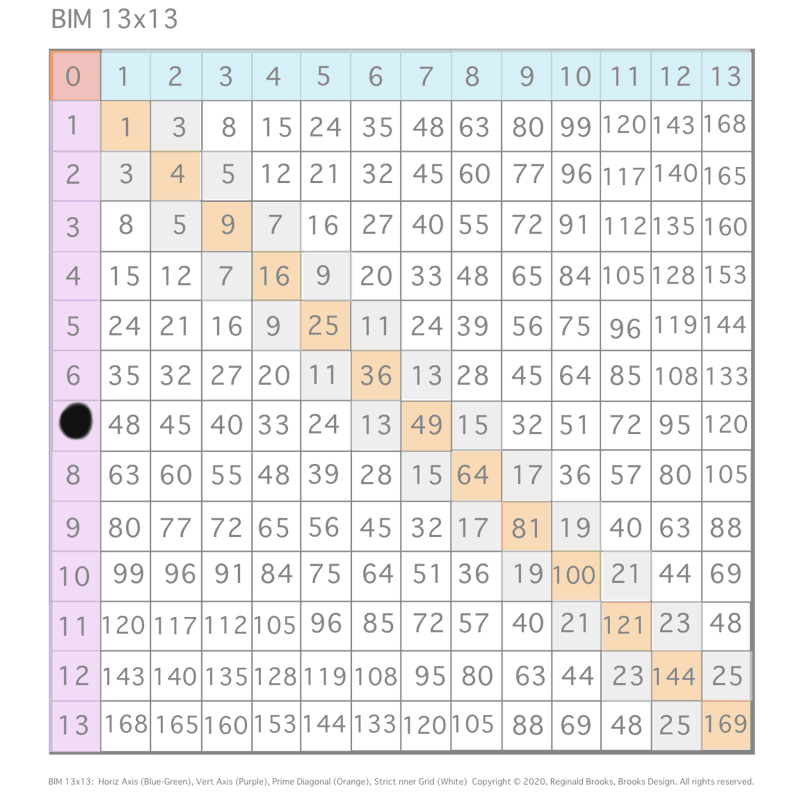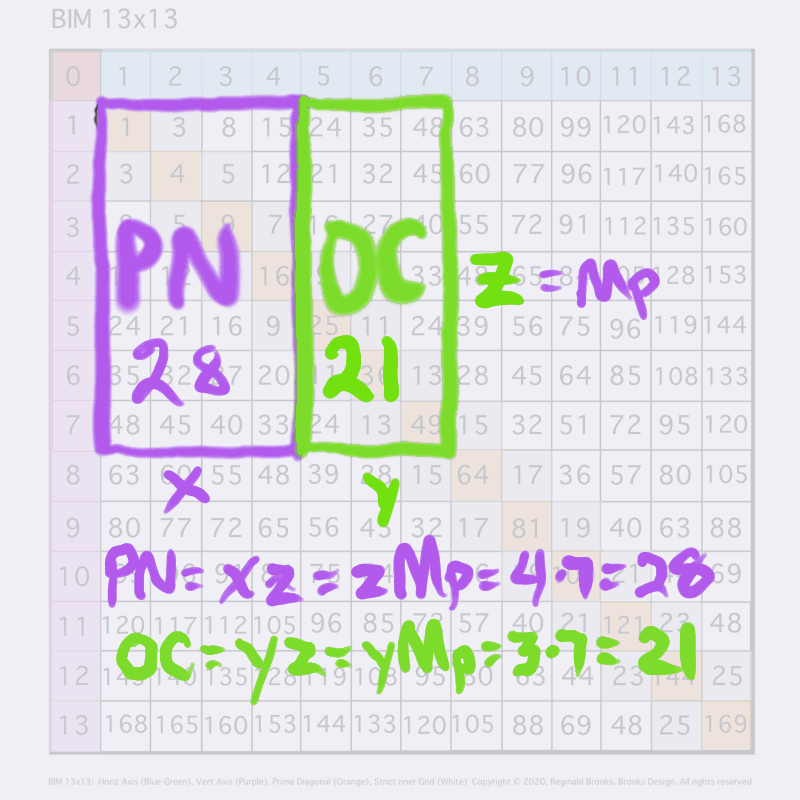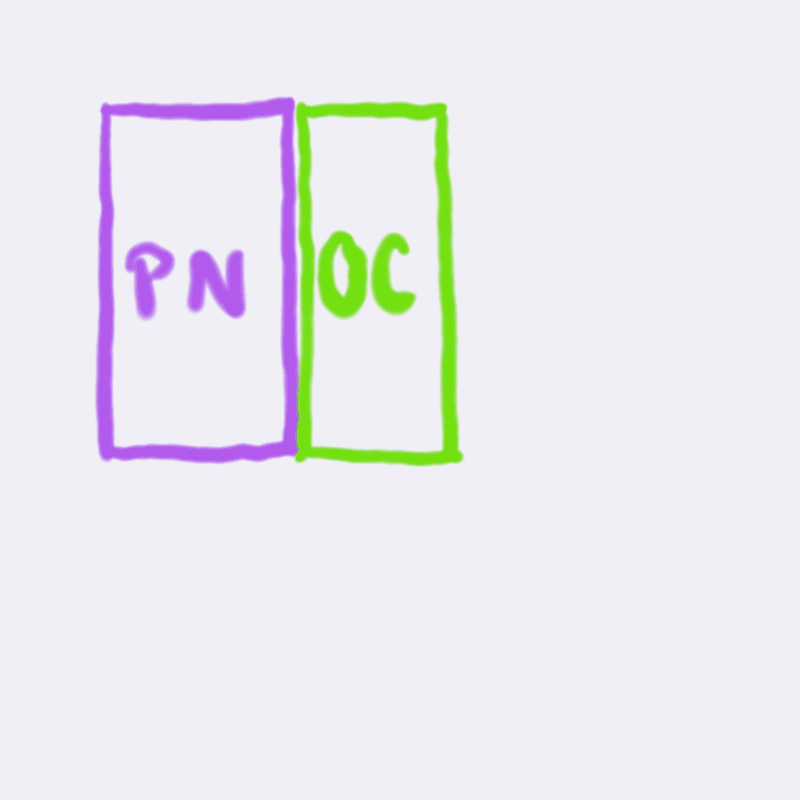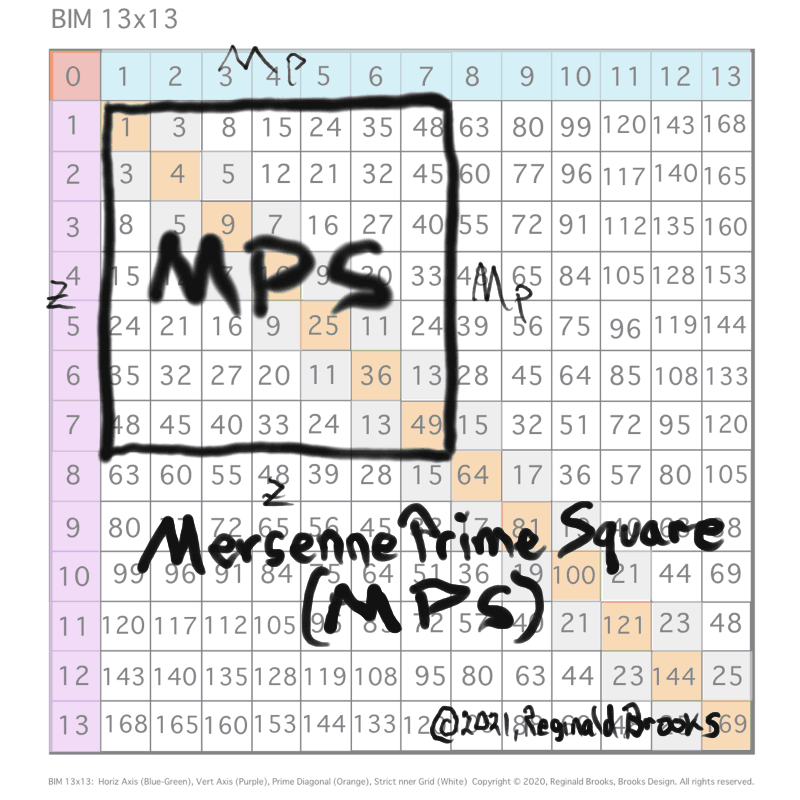
And what should we call you two? How about PN and OC (decoded as PN=Perfect Number and OC=ODD Complement)?

While we are here looking at the MIDDLE Layer of PN + OC, just what is so special about being an EVEN Perfect Number? A PN is a number whose “factors” add up to equal the number itself. (Just don’t include the number itself as one of the factors.) For example: the PN 6 = 1+ 2+ 3 The next PN = 28 = 1 + 2 + 4 + 7 + 14.

So, if we look below the TOP MPS Layer, we see our 2nd, MIDDLE Layer of the PN + OC.

And now, for the 3rd, BOTTOM Layer:

You might have guessed it! Yes, the children of the MIDDLE Layer have given rise — NOW AS PARENTS — to their own children of the BOTTOM Layer.

Making a SQUARE out of the short sides of the PN and OC RECTANGULAR AREAS above, we know have 2 new little SQUARES + 2 new smaller, left-over RECTANGLES that exactly fill out the same AREA as their parents and their grandparents!

Their names are the Perfect Number Square (PNS), ODD Complement Square (OCS) and the two identical Complement Rectangles (CR).

You might ask, “Does this BOTTOM Layer of PNS+OCS+CR+CR give rise to yet another layer? Yes, and on and on! What a family tree!

And in this great and wonderful family tree we have an assortment of ODD and EVEN AREAS that all came from ODD and EVEN little dots!

Every dot counts!

MPS Project-Intro video

~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~

 

MPS Project-Intro video

 

~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~

Part II: Intermediate

The PRIME Numbers, or PRIMES for short, are those special numbers that make up ALL the other numbers. The PRIMES can only be divided by 1 and themselves, e.i. 2-3-5-7-11-13-17-19, Except for the #2, ALL PRIMES are ODDs. p=PRIME

A Mersenne Prime is a special type of PRIME based on multiplies of the number 2. There are only 51 known Mersenne Primes! And, of course, being PRIMES, they are ALWAYS ODD. Mp = Mersenne Prime.

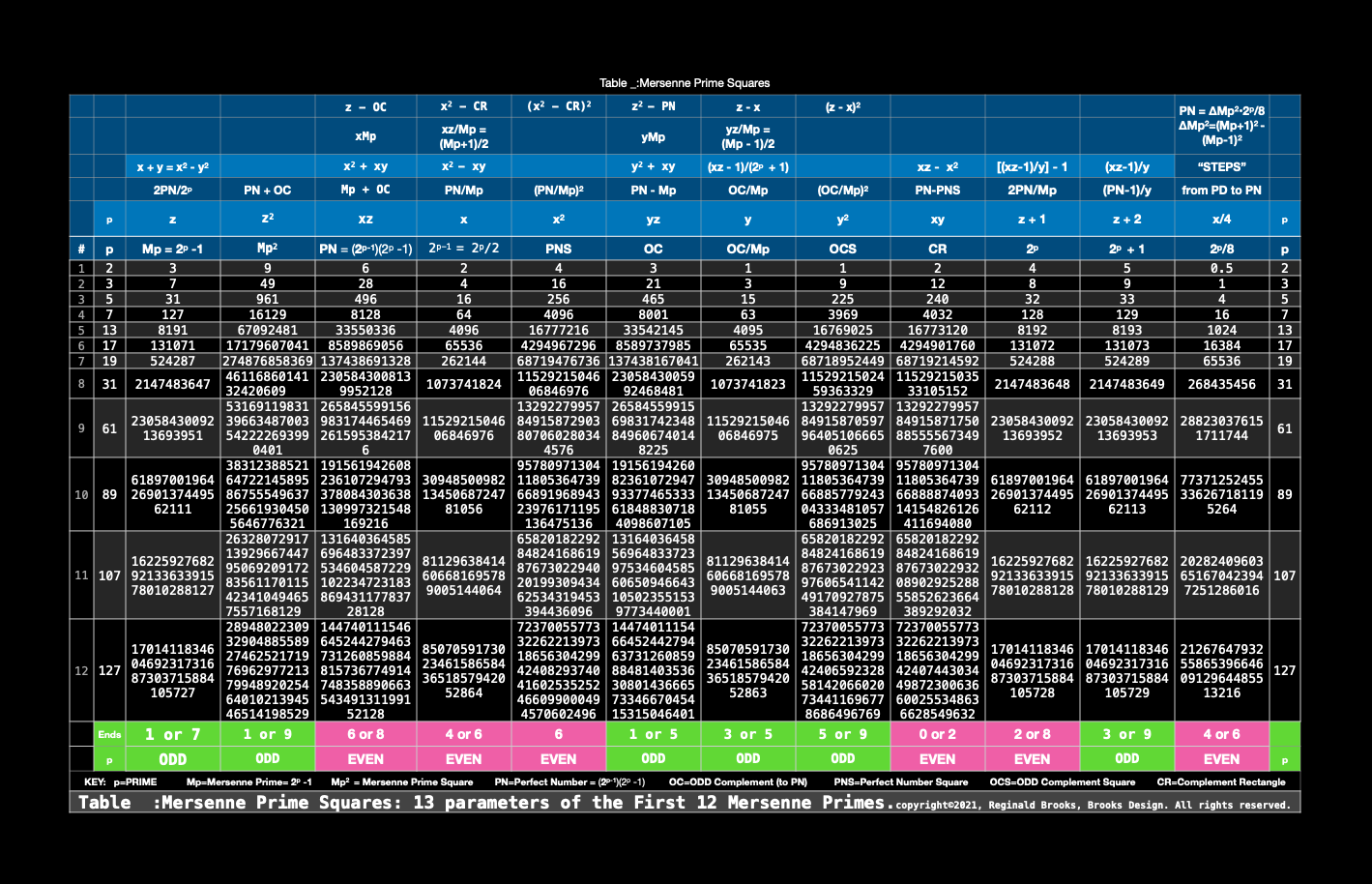
Over 2000 years ago, Euclid — that famous Greek mathematician — discovered an equation that produced Perfect Numbers (PN). Now what is amazing about Perfect Numbers — PNs — is that the factors that make up the number — when added together — equal the number itself, e.i. the PN = 6 = 1+2+3. Another example: PN = 28 = 1+2+4+7+14.

It was later proved by Euler that Euclid’s equation produced ALL the Perfect Numbers and that they are ALL EVEN numbers! He also proved that every PN is paired with a Mersenne Prime. That’s right, there are also only 51 known PNs. This is called the Euclid-Euler Theorem.

So for every ODD Mersenne Prime we have a corresponding EVEN Perfect Number!

The Euclid-Euler Theorem is simply an algebraic equation that, given a Mp, solves for its PN.

But how do you see this! They are just numbers! How do we see that tight, close perpetual relationship between each Mp and its PN?

Well, what if we let the Mp be a line — instead of just a point. And if we let the line be the side of a SQUARE we can get the AREA of the SQUARE by simple multiplying side x side. For example: let the Mp = side = 7 then 7x7 = 49

We call the SQUARE AREA the MPS. MPS = Mersenne Prime Square

Wow, that was easy! We just make a SQUARE by multiplying the Mp side x Mp side = MPS.

So where is that Perfect Number (PN)?

Well, the short answer is that — kind of like the way Russian Dolls are nested inside — they are inside the Mersenne Prime Square (MPS). The big difference is that they — along with their remaining area — fit EXACTLY inside the MPS.

 

The PN is an EVEN AREA RECTANGLE that fits inside the MPS. It takes up just over half of the MPS AREA. The remaining area is called the ODD Complement RECTANGLE. It’s called ODD because it is ALWAYS ODD and Complement because it complements — or fills out — the MPS AREA once the PN AREA is laid out. It is abbreviated as OC.

So now the MPS is divided into two RECTANGLES as:

​x
      MPS = PN + OC
​
      MPS = 49 = 28 + 21

And, if you look closely, you will find that the PN AREA contains the sum of ALL the little AREAS of its factors just like the example we gave before, e.i, PN = 28 = 1+2+4+7+14.

So now we can really see how the Mersenne Prime always has a Perfect Number because the MPS AREA contains the PN AREA, with a left-over OC AREA!

You might be asking, “Is there anything more?” Of course, the beauty of math is that there is always MORE!

What if we were to sub-divide the PN and OC RECTANGLES?

YES! EXACTLY! If we take the short side of each RECTANGLE and make it a new side, we can multiply the side x side = SQUARE. The PN — being an EVEN — will give an EVEN SQUARE that we call the PNS = Perfect Number Square. The OC — being an ODD — will give an ODD SQUARE that we call the OCS = ODD Complement Square. Each RECTANGLE will have a left-over AREA that we call the Complement Rectangle (CR). The CR is the same for both and ALWAYS an EVEN as it is made by multiplying the EVEN short side of the PN x the ODD short side of the OC.

And that’s it! We have taken the Mp point, turned it into a side to make the MPS AREA and then divided this MPS AREA into two overlapping layers of AREAS as:

xxxxxxxxxx
    Mp x Mp = MPS = PN + OC = (PNS + CR) + (OCS + CR)
​
    as MPS = the 1st or UPPER Layer
        PN + OC = the 2nd or MIDDLE Layer
          (PNS + CR) + (OCS + CR) is the LOWER Layer   

In this example of the absolute beauty of mathematics, it is not so important that one remembers the exact name of each AREA within the layers. Those names can change. What is important is the exact nesting of each of the AREAS within its larger Layer and that larger Layer within its larger PARENT Layer.

The role of the ODD and EVEN numbers is particularly fascinating! The next time you find a number, you might just look at it a little more to try and “see” if it holds its own special relationship with other ODD and EVEN numbers! I’ll bet it will!

 

MPS Project-simple animation gif

~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~

Part III: Advanced

Bottom UP!

Take an odd number that is ÷ by 3 and square it, (one exception) Now, add +1 to that original number to give an even number that is ÷4. Square it. Make a rectangle with the ODD and EVEN number. It must be an EVEN number ÷4.

 

So now we have two squares — and ODD and an EVEN — and an EVEN rectangle. Make a second identical rectangle.

 

Add one rectangle to the ODD square. This will give a larger ODD rectangle. It, too, must be ÷3. Add the other similar rectangle to the EVEN square. This will give a larger EVEN rectangle. It, too, must be ÷4.

 

Adding these two larger rectangles — one ODD and one EVEN — together will form a new, larger square that is NOT ÷3 and NOT ÷4. In fact, it is only ÷ by its side number and one. That’s because it is a PRIME Number square — its side number is a PRIME Number and as such, is only divisible by itself and one. This particular PRIME Square is called the newly discovered Mersenne Prime Square, MPS. Its PRIME number is a special type of PRIME called a Mersenne Prime (2p -1).

 

*caveats: the first Mp-PN (Mp=3, PN=6) doesn not follow this exactly -- it is the inverse, and, in order for this Bottom Up sequence to work, some pre-filtering is required, i.e. the x-value must be an exponential power of two, and, the sum of the x+y = z, must result in z = Mp = Mersenne Prime. Naturally, x>y by 1.

 

Now for some magic. Remember that larger EVEN rectangle ÷4 that is part of this MPS? Well, it is what is called a Perfect Number (PN)! What is a Perfect Number? A PN is a number whose factors that make it up — not counting itself — add up to a sum that equals itself. For example: the number 6 is a PN as 1+2+3=6.

What is truly amazing is that so far, there are only 51 PNs out of all the numbers.

What is also truly amazing is that every PN is matched with a Mersenne Prime number! That’s right! There are so far also only 51 known Mersenne Prime numbers and every one of them is matched with one of the 51 known PNs!

And, as we have shown here today, we can see why. That BIG MPS that we made ALWAYS contains a BIG EVEN PN rectangle!

 

Furthermore, that PN rectangle contains a SMALLER square — a Perfect Number Square (PNS). All ÷4.

 

And, the slightly smaller ODD Complement (OC) rectangle — the other rectangle that, along with the PN rectangle, adds up to make the MPS, well, it too, has a SMALLER square — an ODD Complement Square (ODS) within. All ÷3.

 

For completeness, the two similar Complement Rectangles (CR) that are made up of one side from each of the PNS and OCS, are found in each BIG rectangle. Which only makes sense, as each BIG rectangle is the sum of its PNS + CR and OCS + CR, respectively.

 

Thousands of years ago, Euclid discovered a formula — mathematical equation — that would generate a PN. Some 1500+ years later Euler improved upon the formula to prove that it generates ALL the EVEN PNs and that each is associated with a Mersenne Prime number. This is known as the Euclid-Euler Theorem: PN = (2p−1)(2p -1). It stills stand today only NOW we have a NEW Geometry — the MPS — that gives a clear visualization of how the PN is embedded within the Mp based Mp² . There are NO known ODD PNs.

 

1. Now let’s try an example. ODD #: 1. Square it: 1x1=1 (one exception is this first smallest ODD number 1) Add +1: 1+1=2. Square it: 2x2=4 Make rectangle: 1x2=2 (one exception) Make similar, identical rectangle: 1x2=2. Add ODD square + rectangle: 1+2=3 Add EVEN square + rectangle: 4+2=6 and 6 is a PN as 1+2+3=6 Add these two BIG rectangles (one ODD and one EVEN): 3+6=9 and 9 is the Mp2 = 32 = MPS!
2. Now let’s try an example. ODD #: 3. Square it: 3x3=9 Add +1: 3+1=4. Square it: 4x4=16 Make rectangle: 3x4=12 Make similar, identical rectangle: 3x4=12. Add ODD square + rectangle: 9+12=21 and it is ÷3 Add EVEN square + rectangle: 16+12=28 and 28 is a PN as 1+2+4+7+14=28 Add these two BIG rectangles (one ODD and one EVEN): 21+28=49 and 49 is the Mp2 = 72 = MPS!!

 

This latter example is the one that the MPS Project is showing. If you look carefully you will see that the larger MPS containts two BIG rectangles (PN & OC). The PN contains a SMALLER square and rectangle (PNS + CR), and, the OC contains a SMALLER square and rectangle (OCS + CR). The sides of the SMALLER squares are the EVEN and ODD numbers we started with! If you know either of these, you can build the entire MPS!

 

 

~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~

Retake

Two dots (numbers, really), one ODD one EVEN, walk into a bar.

The bartender says, “Haven’t I seen you two before?”

“Not likely,” says the ODD dot as he plops on a stool, “there are only 51 of us known in the entire Universe — and that makes us kind of special!”

To which the bartender snidely replies to the other dot, “Special? So what makes you two so special?”

“He/she is an ODD Prime number, while I am simply an EVEN,” smirked the EVEN number. “And, we are always together as pairs. Like ODD said, there are currently only 51 pairs: ODD PRIME—EVEN Perfect Number and we like it that way!”

Now grimacing with disbelief, the bartender barks out, “A Perfect Number! Alright, what makes you such a damn Perfect Number — and though you say you are EVEN I am pretty sure you both are odd?”

“Well, since you asked, EVEN Perfect Number replied, “The sum of my factors — not counting myself — equals myself, a Perfect Number! And there are only 51 known Perfect Numbers! I’d say that is pretty special! For example: take the PN 6 = 1+2+3!”

Looking askance at the ODD PRIME, the bartender then leans over and asks, “And you?”

“Hey, you might get more than you bargained for! But here goes. Not only am I a PRIME number and all PRIMES — except 2 — are ODD, I am a very special type of PRIME number called a Mersenne Prime. Technically, that is Mp=2ᵖ -1, where p=PRIME. For you earthlings, that translates to a PRIME that is an exponential power of 2, subtract 1. For example, let p=2, then Mp=2² -1 = 4 - 1 = 3 and 3 is a Mersenne Prime. And , of course, you have met my partner, Perfect Number(PN) 6. We are a pair!”

“Cool! So what can I get you?” the bartender grins. It is, after all, nice to start your day with a little elevated mathematics!

“Well, what we really want is to be seen!” said the ODD “Though we have always been here, at least since the Big Bang, for the last 2000+ years we have only been known as dots — numbers, really — but never seen. We want our land! We want our AREA!”

“Whoa, fella!” exclaims the bartender, “are you talking about going from algebra to geometry? What do you want me to do?”

To which in unison both the ODD and EVEN pair respond, “Connect the dots! Makes some lines”

“Hear me out,” says the ODD. “Here is how you can see us, and, how we are related. You see, my little EVEN PN is really more like one of my children! Yeah, I know, it looks bad, but that is not how it is. You have never before had the opportunity to see what our relationship is and how it naturally forms from the geometry.”

“If you run my dots out to a line, or side, and now square it, you get an actual geometric shape, a SQUARE. Since it is made from my Mersenne Prime (Mp), it is called a Mersenne Prime Square (MPS). Now think of it as the TOP layer.”

“That MPS can be divided into 2 RECTANGLES. Best seen on the MIDDLE layer. The EVEN Perfect Number is one of those RECTANGLES, the other is an ODD RECTANGLE.”

“So right from the start, one can ‘see’ that the PN is actually a child AREA of its parent MPS! This occurs in all 51 of the ODD PRIME — EVEN Perfect Number pair sets!”

“In the BOTTOM layer below, the 2 RECTANGLES within the MPS can each be subdivided in to a Perfect Square and a common, remaining RECTANGLE — grandchildren of the MPS!’

“From the MPS we have 2 generational subdivisions giving rise to a total of 6 geometric AREAS, or 7 total AREAS when the MPS AREA is included! And you can ‘see’ every one of them! Not only that, but if you know the number value of the shortest side, you can calculate and draw out the geometry all the way back up to the MPS!”

 

“So, I’ll have what she/he is having! Thank you, thank you —- thank you very much!”

 

“Whew!” exclaimed the bartender with a bit of relief, “I think I might have just created a new drink! We’ll call it the ‘MPS’ for Mersenne Prime Square. Take the bottle of Mersenne Primes and pour it out on to a stack of sieves. It will first form an AREA, then filter down to smaller AREAS that thereafter filter down to even smaller AREAS. Pour the AREAS back into a tall glass, layer by layer. Enjoy!”

~~ ~~ ~~

Later on after the bar had closed, he sat down to enjoy a nightcap with his new concoction. He couldn’t help but to reflect on all that math he had sucked up that day. Wiping his brow, he threw the bar towel back over his shoulder, took another big draw, and zoned out. Didn’t it seem like there was this constant and never-ending exchange between the EVENS and the ODDS? First the ODDS are ahead, but then the EVENS splurge. Yes, every EVEN is composed of two ODD PRIMES (Goldbach Conjecture, as he recalled!). But the mix changes with different arithmetics. He drew out a little chart. Isn’t math beautiful he thought?

And it’s just like people!

 

http://www.brooksdesign-ps.net/Reginald_Brooks/Code/Html/MSST/TPISC/TPISC_V/MPS.html

 

 

When he/she got home that night he/she kissed her/his spouse who she/he missed each and every day. Yeah, she/he thought, work is work, but these two little dots — areas, really — made him/her think about things differently. Maybe they were on to something. It wasn’t that he/she didn’t like his/her job, he/she really did, especially the people! The characters! But the daily onslaught of — call it slant, ax to grind, bigotry, misogamy this, -phobic that — old-fashioned, never ending prejudice was getting tiresome. Differences are the joy!

 

“Honey,” she/he cried out, “get your ODD or EVEN butt to bed!”

 

“Be right in! Just got this little family tree chart to fill in.”

 

 

~~~

Counting is as old as your fingers (and toes). So is drawing. What’s the difference?

 

Less than you might think.

 

The arithmetic of simple counting — adding,subtracting, including the efficiency upgrades of multiplying,dividing — is basic to most all human activity. Much the same for all life forms. How so?

 

Every biological process is contingent on quantity. Too much or the lack of pushes evolution. We are but an expression of the universalness of quantity.

 

So how does counting relate to drawing or painting or any other art form, or any form of expression for that matter? What line, how many lines, how thick are the lines, what tone or color lies within, how much, how intense, what are the proportions, how does the weight of one side balance with the other,… There’s no getting away from it. We all use math everyday and in thousands of ways.

 

So why study and express your art through pure math — you know simple natural whole numbers?

 

Because they reveal anything and everything about you, yourself, your family, your group or tribe, your Universe. Yes, indeed, you are but a speck of dust in the cosmos of billions and billions of stars, but you still count!

 

I invite you to come count with me, even if it is just for a little quantity of time!

 

 

White Paper: Mersenne Prime Squares

~~

 

REFERENCES

 

Wikipedia: Mersenne Prime

Wikipedia: Perfect number

Wikipedia: Euclid-Euler theorem

 

~~~~~~~~

 

~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~

LINKS:

Mersenne Prime Squares (Part I) the Introductory white paper.

 

Mersenne Prime Squares (Part II) 3 Simple Intros.

 

Mersenne Prime Squares (Part III) the Advanced white paper.

 

The MPS Project The Mersenne Prime Squares Project.

 

The Butterfly Fractal 1 Introduction.

 

Ocean of Numbers Overview of it alls.