>Mersenne Prime Squares: Advanced

The MPS: Advanced

A step-by-step look at the details in the formation of the Mersenne Prime Square (MPS)


xxxxxxxxxx

INTRODUCTION

A Mersenne Number is a number that is formed from

2ᵖ -1 where p = prime number.

If the resulting Mersenne number is itself prime, it is called a Mersenne Prime (Mp). Let it = z.

Every Mersenne prime has an associated Perfect Number (PN).

A PN is a number whose factors (other than itself) sum up to equal itself, e.i. 28 = I+2+4+7+14. Let PN = xz.

Euclid discovered that

PN = (2ᵖ⁻¹)(2ᵖ -1 )

always gives an EVEN Perfect Number.

Euler proofed that the above gives ALL the PNs. The above is the Euclid-Euler Theorem. No ODD PN has been found.

DEVELOPMENT

So we have

Mp = z = 2ᵖ -1

PN = xz

x = PN/Mp = xz/z

If z = Mp represents a number value on a line, then let it represent a length, z, such that a square equals

Mp² = z² = Mersenne Prime Square ( MPS)

ODD X ODD = EVEN

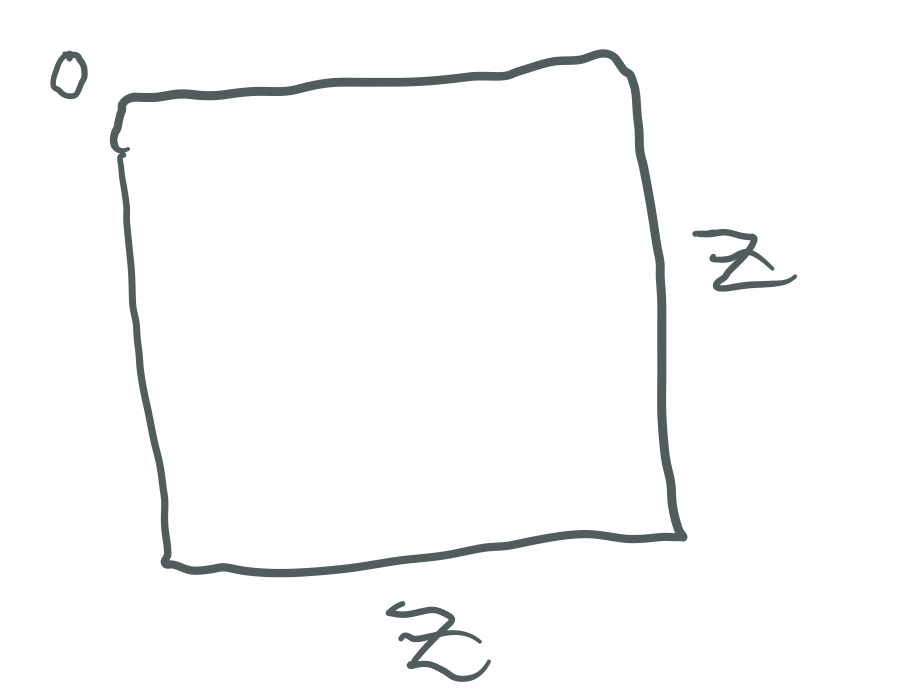
Example: let Mp = z = 7

PN = xz and x = PN/Mp = xz/z

then

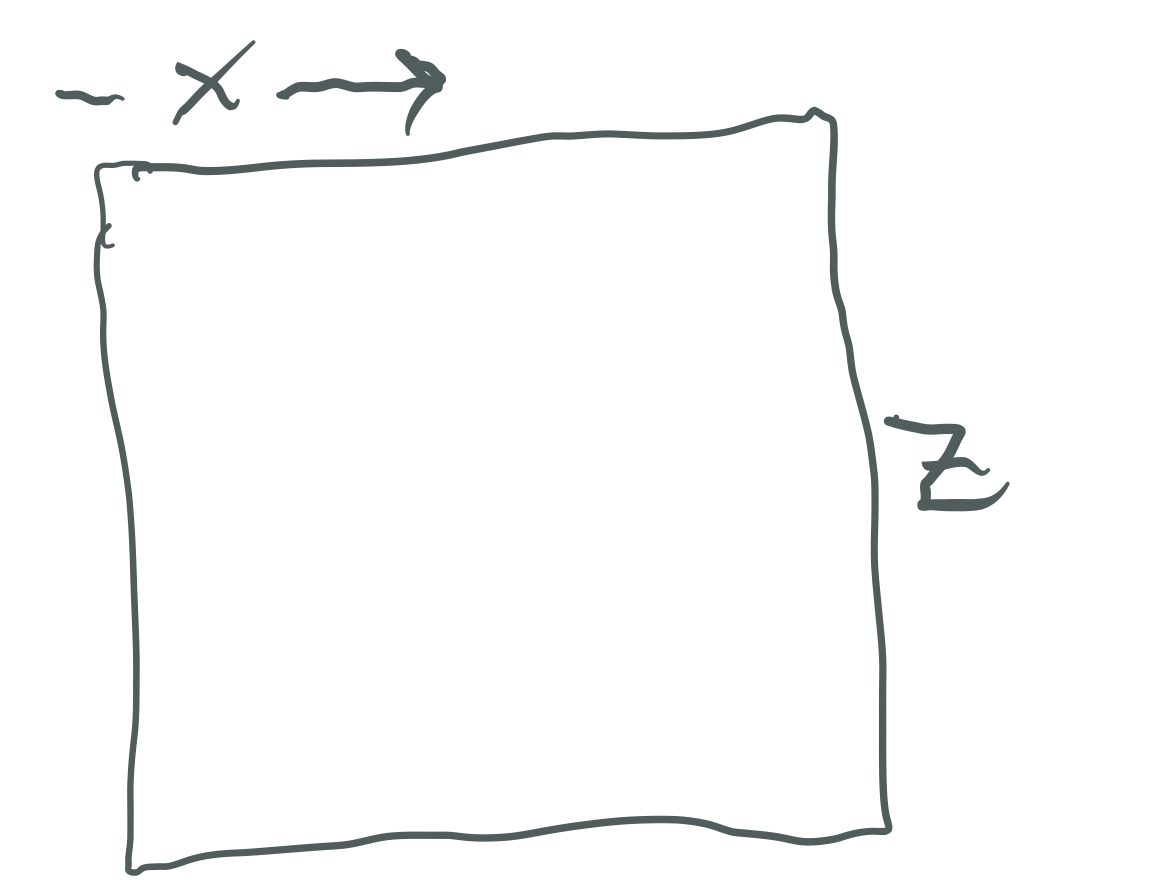
Some portion of length Mp = z is equal to x.

Let

x = (Mp +1)/2 and y = (Mp -1)/2

as the PN is always EVEN, so the complement is always ODD.

Example:

x = 4 = (7 + 1)/2 and y = 3 = (7-1)/2

It follows that x = y + 1.

Squaring y gives a somewhat similar pattern on the OC

OCS = y² = ODD

leaving the same CR value as a remainder. The CR value is always EVEN as ODD x EVEN = EVEN.

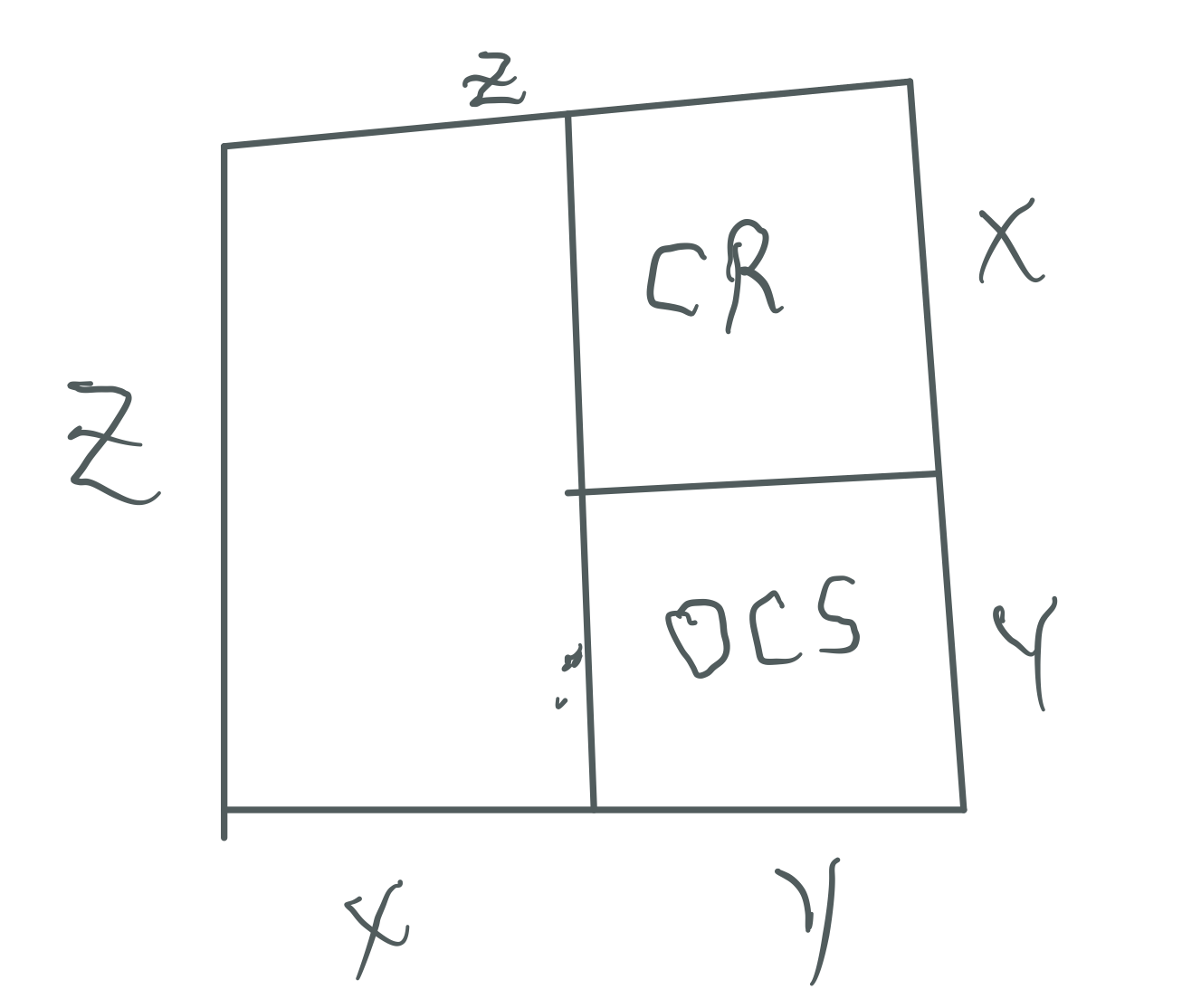
Let:

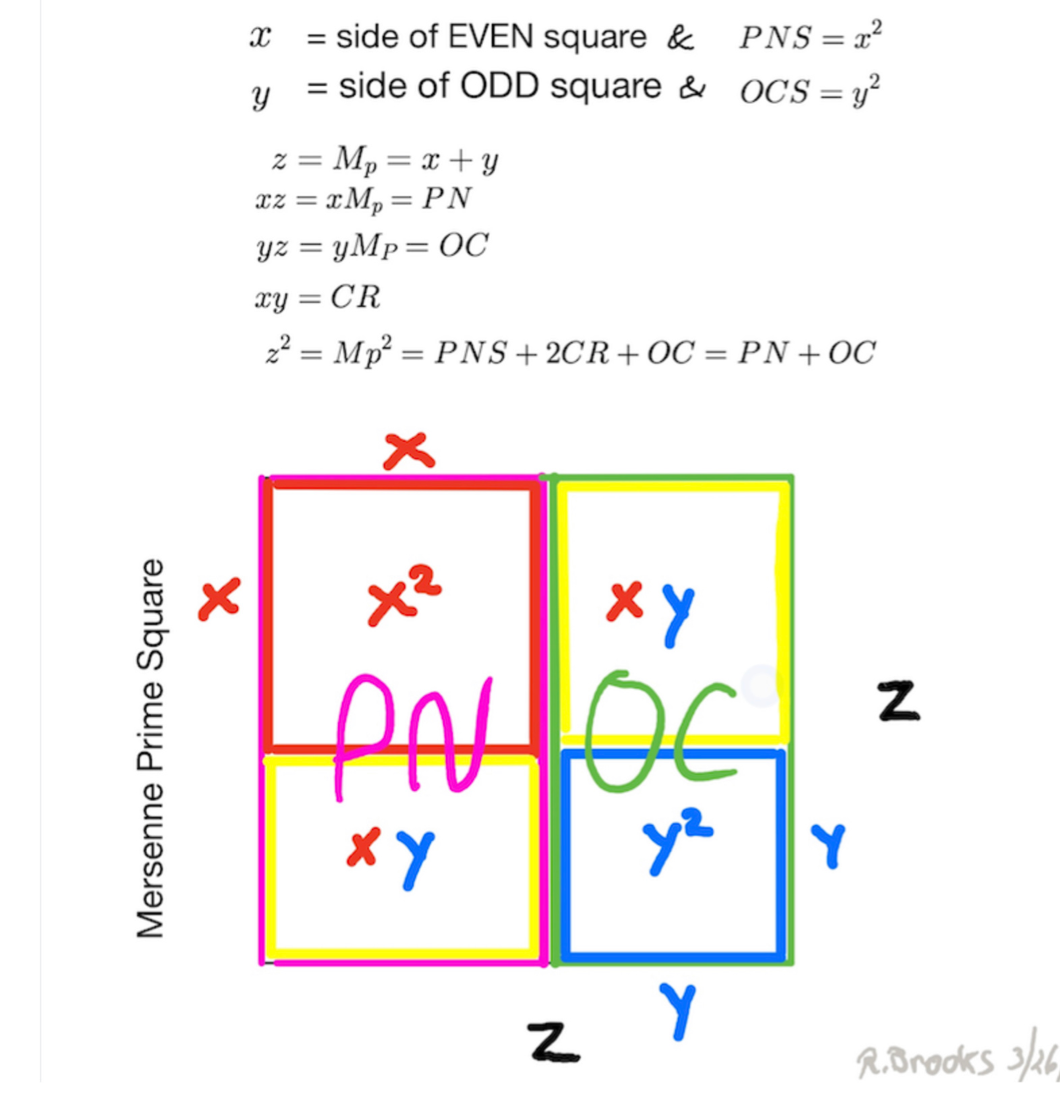
INTERIM SUMMARY

Thus we can say:

Every Mersenne Prime is ODD, as is its square area, Mp² = z²
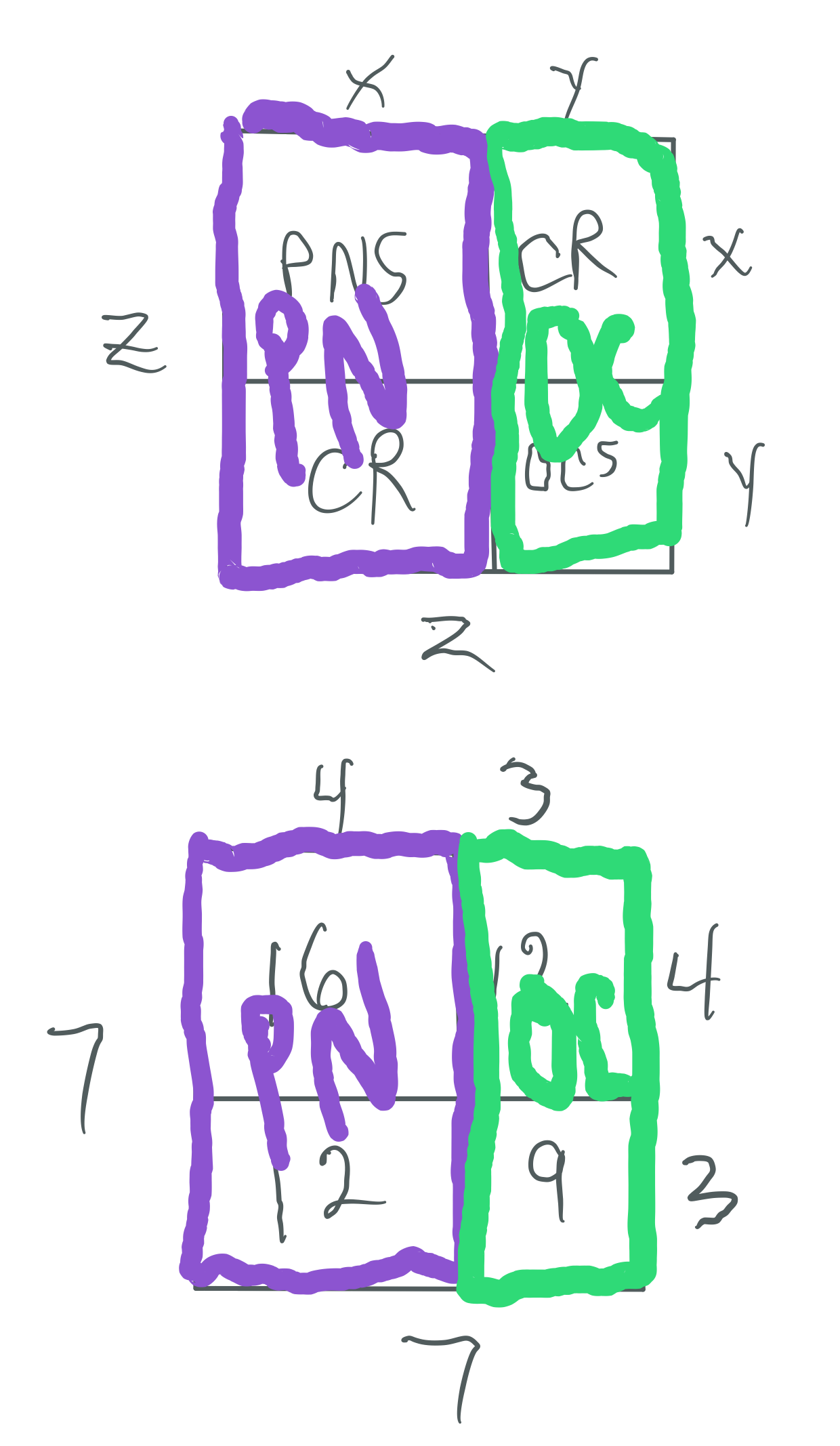
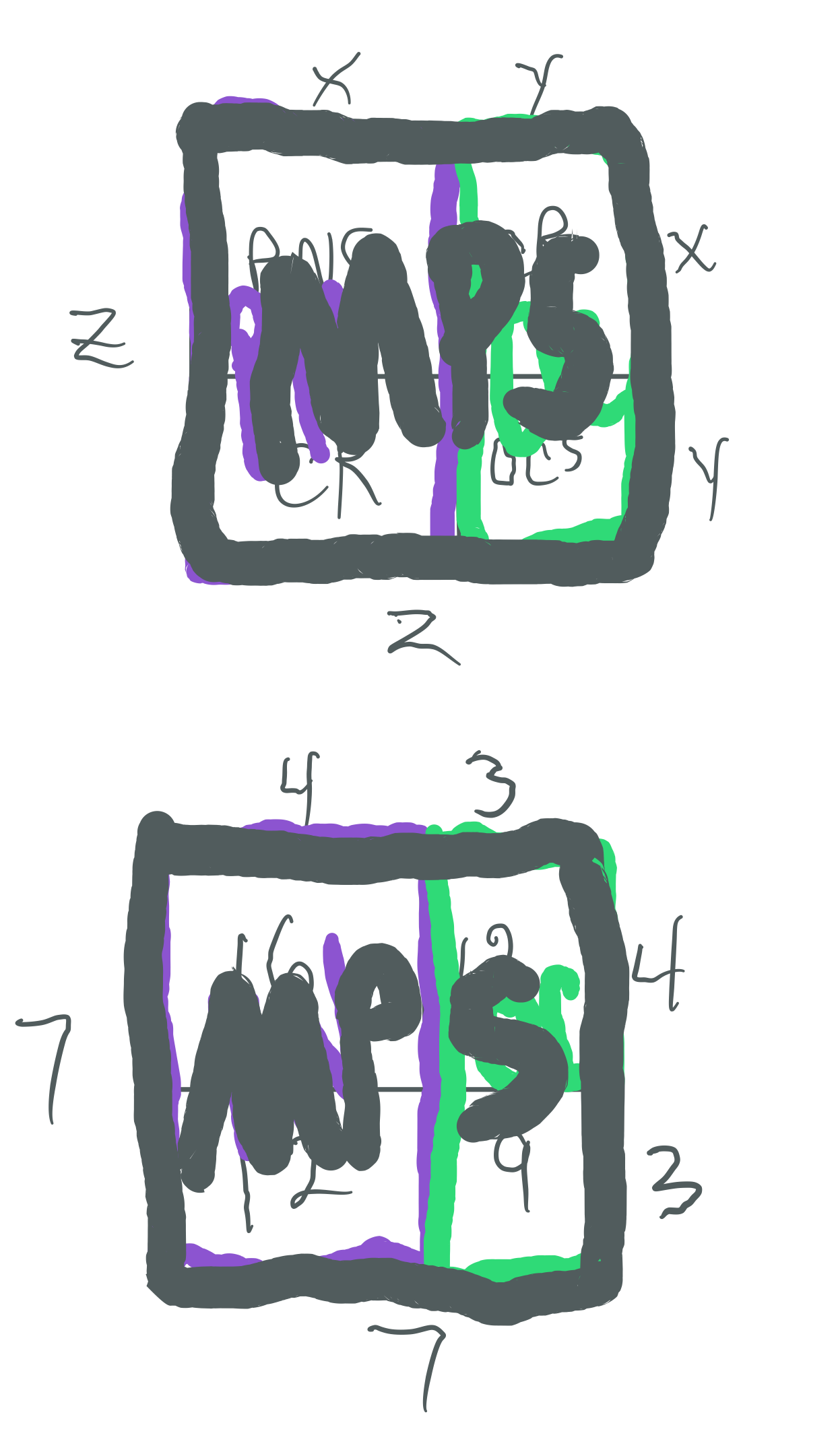
The Mp² is always asymmetrically divided into an EVEN Perfect Number Rectangle and an ODD Complement Rectangle (OC)
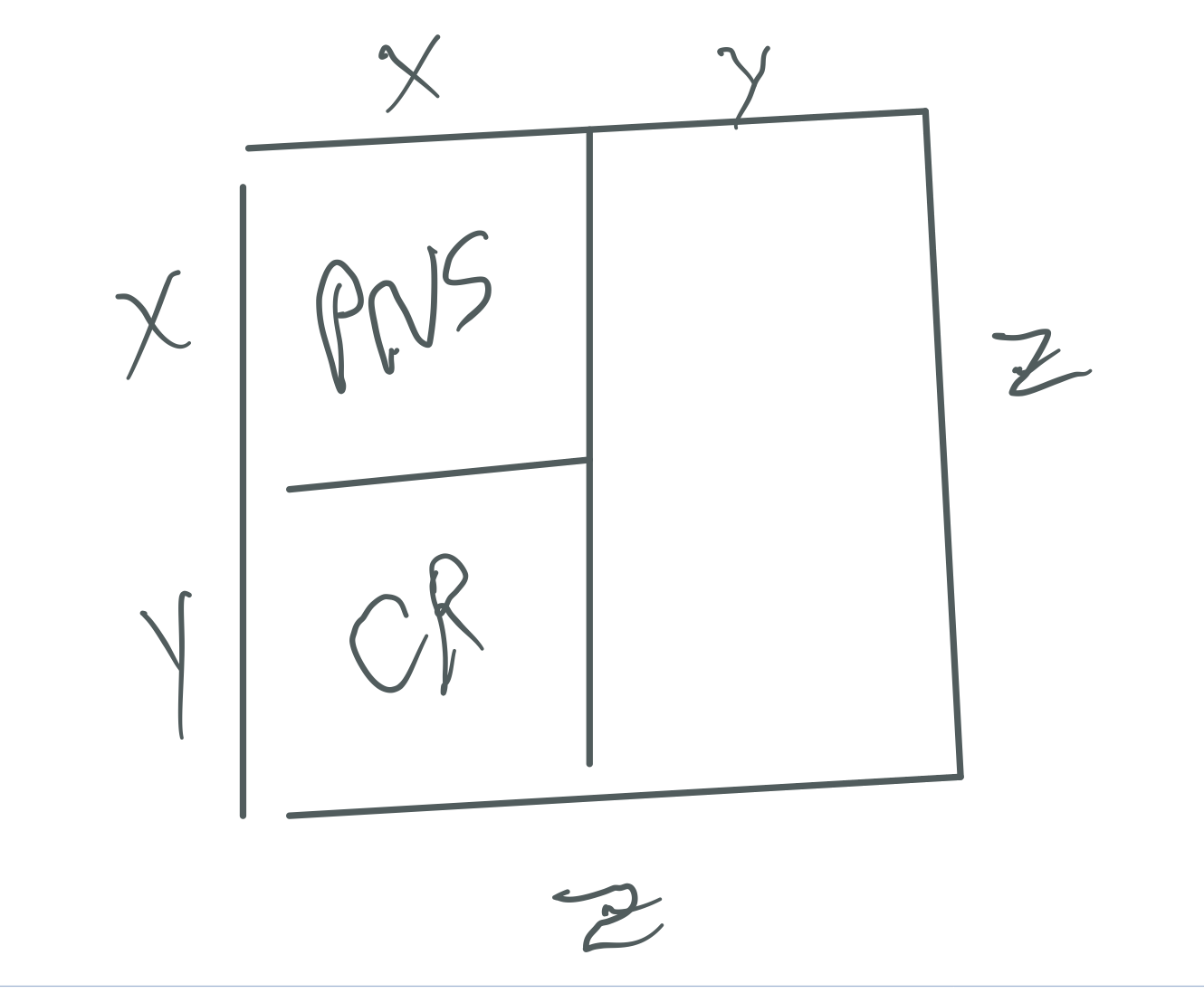
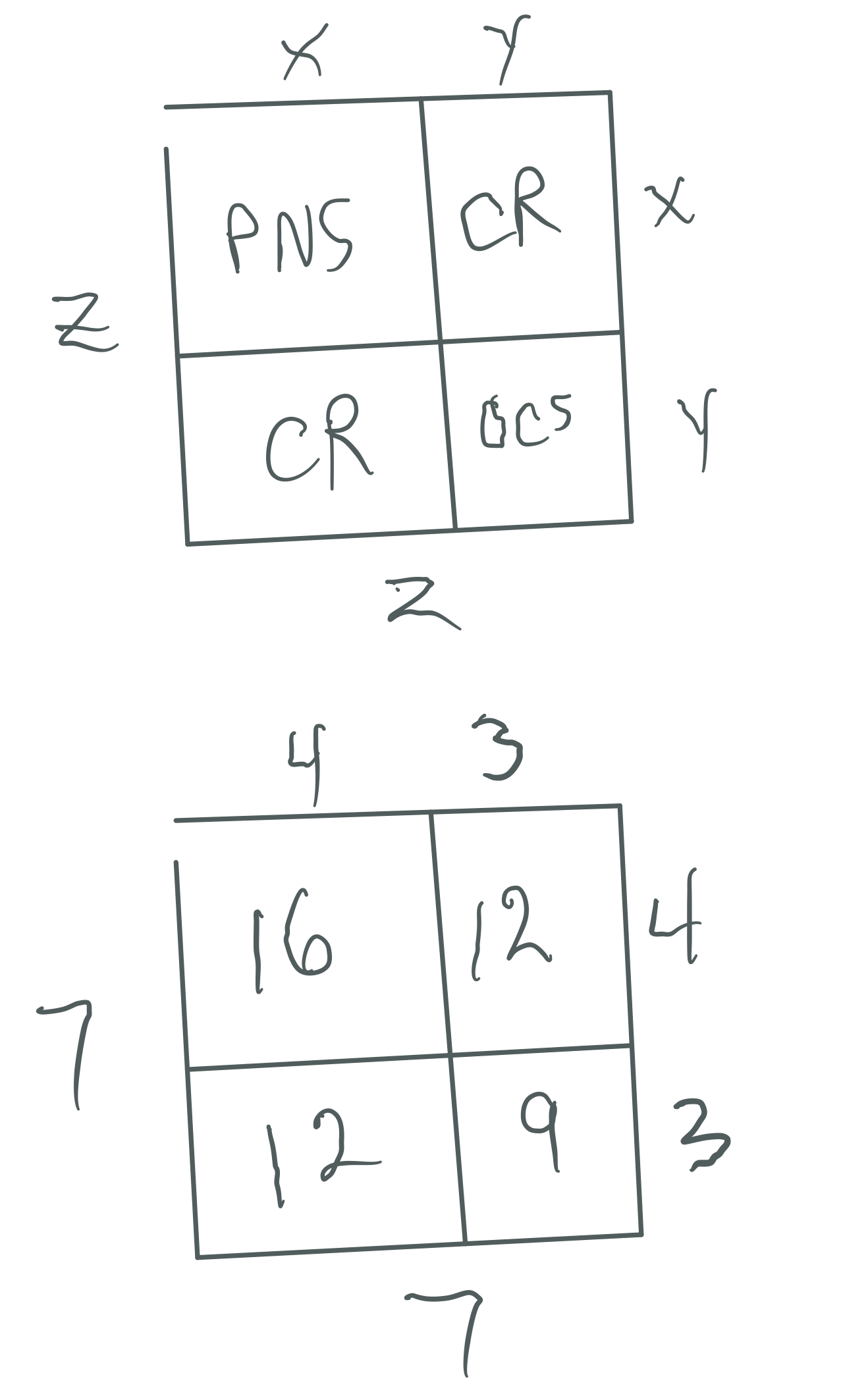
The Even PN Rectangle is subdivided into a Perfect Number Square (PNS) and a Complement Rectangle (CR), and both are always EVEN
The OC Rectangle is subdivided into an ODD Complement Square (OCS) and a similar matching CR (EVEN)
Every Mp² contains:
- PN *that is ÷4 = xz = EVEN •ODD = EVEN
  - PNS is ÷4 = x² = EVEN
  - CR is ÷4 = xy = EVEN •ODD = EVEN
- OC that is ÷3 = yz = ODD •ODD = ODD
  - OCS is ÷3 = y² = ODD
  - CR is ÷4 = xy = EVEN •ODD = EVEN

EVEN + EVEN + EVEN + ODD = ODD

x² + xy + xy + y² = z²

PNS + CR + CR + OCS = Mp²

*except PN = 6.

EXAMPLES

A Perfect Number represents the maximum EVEN-Number-Rectangular-Area—with the long side equal to the Mersenne Prime—within a Mersenne Prime Square, itself made by squaring said Mersenne Prime.

The ODD complement is the remaining ODD-Number- Rectangular-Area within the Mersenne Prime Square. Both the PN & OC contain perfect squares equal to the short sides of their respective rectangles.

Subtracting the Perfect Squares leaves an identical Complement Rectangle within both PN & 0C rectangles.

Mp² = PN + OC = (PNS + CR) + (OCS + CR)

z² = xz + yz = (x² + xy) + (y² + xy)

z² = x² + 2xy = y²

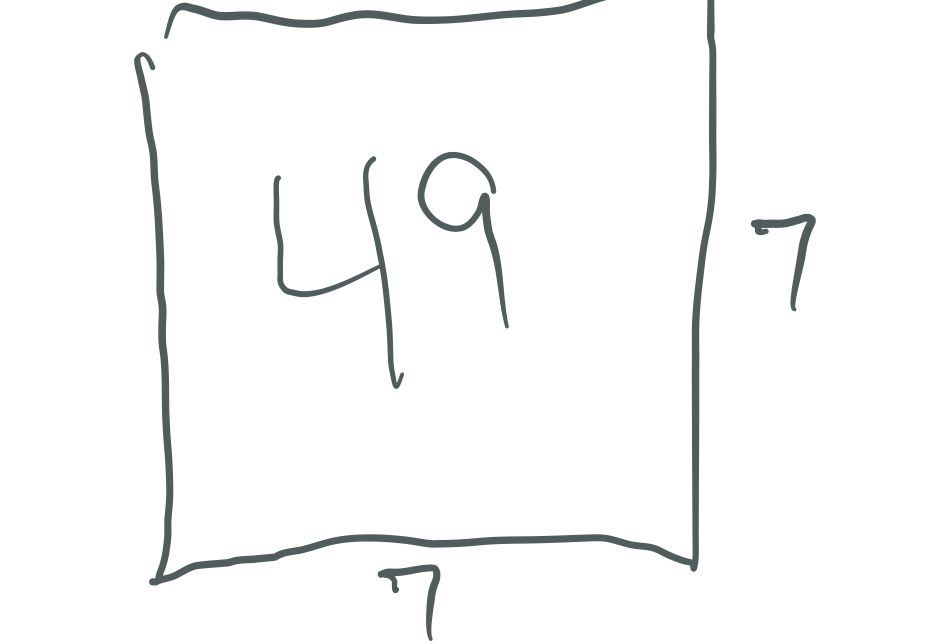
Example:

Mp = z = 7

7² = (4•7) + (3•7) = 28 + 21 = 49

7² = 4² + 2(3•4) + 3² = 16 + 24 + 9 = 49

Example:

Mp² = 2PN - Mp

7² = (2•28) - 7 =49

Example:

PN = (Mp + Mp²)/2

28 = (7 + 49)/2

Example:

Mp² = 2OC + Mp

7² = (2•21) + 7 = 49

Example:

OC = (Mp + Mp²)/2

21 = (49 - 7)/2

~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~

FURTHER DEVELOPMENT

Let x be a power of two, then x² = EVEN number.

Example:

let

x = 2, then x² = 4

If we double x² and subtract x we get another AREA, call it xz:

2x² - x = xz

2(2²) - 2 = 6

Solving for z, we get:

z = (2x² -x)/x

3 = (8-2)/2

And z is always both >x and an ODD number.

Thus far we have:

x = side = EVEN

x² = AREA (Square) = EVEN

xz = AREA (Rectangle) = EVEN

z = side of Rectangle = ODD

z² = AREA (Square) = ODD.

If the EVEN x² Square AREA is embedded in the EVEN xz Rectangle AREA, then the remaining, complement AREA must be a Rectangle as the sides:

z - x = y

ODD - EVEN = ODD

3 - 2 = 1

and:

xy = AREA (Rectangle) = EVEN.

It follows that if the EVEN Square AREA (x²) + the EVEN Rectangle AREA (xy) entirely compose the larger Rectangle AREA (xz), then it must be EVEN, too:

x² + xy = xz

EVEN + EVEN = EVEN

2² + (2•1) = 6.

It also follows that if the EVEN Rectangle AREA (xz) is embedded in the larger ODD Square AREA (z²), then there must be a remainder, complement ODD AREA (yz):

yz = z² - xz

ODD = ODD - EVEN

3 = 3² - (2•3).

If y = short side and z = long side of the ODD Complement Rectangle (yz), then y² = AREA (Square) = ODD, and, the remaining, complement AREA is an EVEN Rectangle, identical in value to that before:

yz = y² + xy = ODD Complement (OC)

ODD = ODD + EVEN

1•3 = 1² + (2•1).

It follows that if the ODD Square AREA (y²) + the EVEN Rectangle AREA (xy) entirely compose the larger Rectangle AREA (yz), then it must be ODD, too:

y² + xy = yz

ODD + EVEN = ODD

1² + (2•1) = 3.

It also follows that if the two larger Rectangles -- the EVEN AREA (xz) and the ODD AREA (yz) comprise the total AREA (z²), then it must be ODD:

z² = xz + yz = ODD

ODD = EVEN + ODD

3² = (2•3) + (1•3).

NEXT SUMMARY

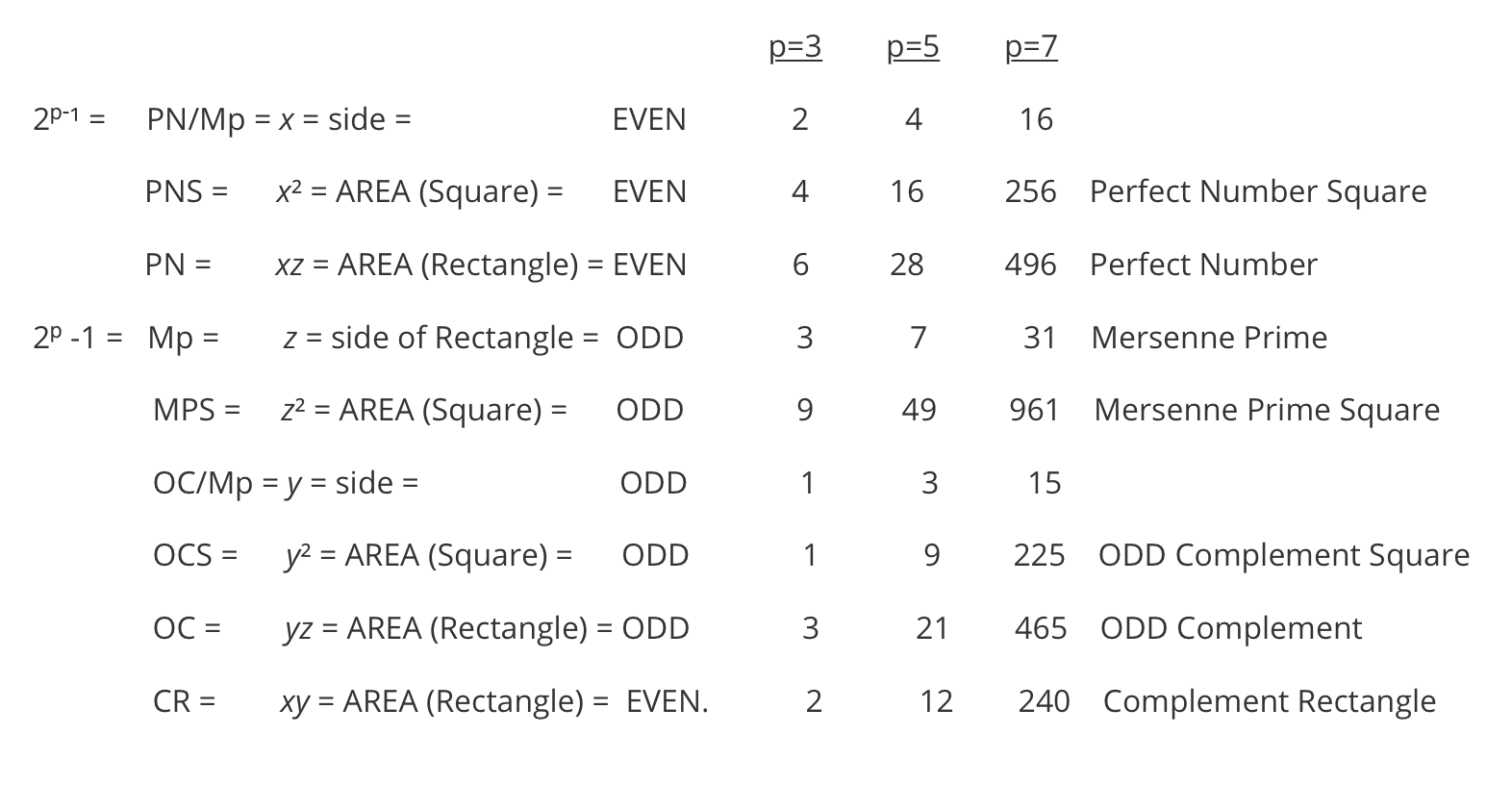
In summary:

x = side = EVEN
x² = AREA (Square) = EVEN
xz = AREA (Rectangle) = EVEN
z = side of Rectangle = ODD
z² = AREA (Square) = ODD
y = side = ODD
y² = AREA (Square) = ODD
yz = AREA (Rectangle) = ODD
xy = AREA (Rectangle) = EVEN

FURTHERMORE

Furthermore:

OC = 2y² + y

ODD = EVEN + ODD

3 = 2(1²) + 1

and:

Mp² = [2 (x² + y²)] - 1

ODD = [EVEN (EVEN + ODD)] - ODD

ODD = EVEN - ODD

9 = [2 (2² + 1²)] - 1.

From earlier:

2x² - x = 2CR + x

2x² = 2CR + 2x

x² = CR + x

CR = x² - x

x = x² - CR.

Likewise:

2y² + y = 2CR - y

2y² = 2CR - 2y

y² = (2CR - 2y)/2

y² = CR - y

CR = y² + y

y = CR - y² .

On the MPS, the point where the PN Rectangle crosses the Prime Diagonal, referred to as PDx or PDi, is equal to x²:

PN = 28 crosses the PDi at 16 = 4² = x².

Pretty much ALL parts of the MPS:

MPS
- PN
  - PNS
  - CR
- OC
  - OCS
  - CR

can be found once x or y is known as:

x = 2ᵖ⁻¹ , y = 2ᵖ⁻¹ -1

as x is just one-half of the Euclid-Euler Theorem:

xy = (2ᵖ⁻¹)(2ᵖ⁻¹ -1)

12 = (2ᵖ⁻¹)(2ᵖ⁻¹ -1) = (2³^-1)(2³^-1 -1) = 4•3

If one knows either x or y, then one can calculate PN, Mp and MPS.

If one know either PN or Mp, then one can calculate x and y.

PN = 2CR + x

PN = xz = 2xy + x

28 = 4•7 = (2•4•3) + 4

OC = 2CR - y

OC = yz = 2xy - y

21 = 3•7 = (2•4•3) - 3

MPS = Mp² = 4CR + 1

MPS = z² = 4xy + 1

49 = 7² = (4•4•3) +1

xz = 2x² - x

z = (2x² - x)/x = Mp

7 = (2•4² - 4)/4.

The simplification -- and subsequent visualization -- of the geometry behind the Euclid-Euler Theorem provides a clearer understanding -- and new insights -- into the relationship(s) between the PRIMES -- as ODDs -- and the EVENS, that they make, witness the Goldbach Conjecture.

Deconstructing the Mersenne Prime Squares (MPS) into their constituent elements -- geometric lengths and AREAS -- and/or reconstructing them back up to their composite geometry of the MPS, provides new information -- and filters -- for parsing out the PRIMES from their offsprings!

Any grant, prize, or otherwise monetary reward resulting from this work, directly or indirectly, should -- from the author's position -- donated and/or set in trust to aid in the education and advancement of disadvantaged youth.

SUMMARY

The Perfect Number (PN) and ODD Complement (OC) are the two Rectangles formed on the Middle (parent) layer. They result from the asymmetrical division of the TOP MPS (Mersenne Prime Square) layer. The PN coordinates are x•z and the OC coordinates are y•z, where z = Mp = Mersenne Prime.

x + y = z

z² = Mp² = Mersenne Prime Square.

The “x” and “y” — that are the short sides of the respective PN and OC rectangles — are key to the whole MPS. The asymmetry results from x = y + 1, and as the PN is always an EVEN, then x = EVEN and y=ODD.

Example:

x = 4, y = 3, z = 7

x = y + 1 = 3 + 1 =4

z = x + y = 3 + 4 = 7

PN = xz = 4•7 = 28

OC = yz = 3•7 = 21

MPS = PN + OC = 28 + 21 = 49.

z² = Mp² = Mersenne Prime Square = 7² = 49.

In the Euclid-Euler Theorem — PN= (2ᵖ⁻¹ ) (2ᵖ -1), as p=prime. Substituting x=(2ᵖ⁻¹ ) and z = (2ᵖ-1), we see that

PN = (2ᵖ⁻¹ ) (2ᵖ -1) = xz.

The MPS presents a number of NEW insights into the Euclid-Euler Theorem:

The MPS AREA is formed by simply squaring the Mp.
The pairing of the Mp and PN is actually the result of the PN being a subdivision AREA of the MPS AREA.
The remaining difference AREA — MPS-PN=OC — is the ODD Complement AREA. It is always ODD as the MPS is always ODD.
With the MPS as the TOP layer, one can see that the PN + OC are the two RECTANGULAR AREAS in the MIDDLE layer below, formed by subdividing the MPS.
This MIDDLE layer is also subdivided into smaller AREAS in the BOTTOM layer: the PN is subdivided into a SQUARE AREA (PNS = Perfect Number Square) and a remaining RECTANGLE AREA (CR = Complement Rectangle), while the OC is also divided into a smaller SQUARE AREA (OCS=ODD Complement Square) and a similar remaining RECTANGLE AREA (CR).

Thus MPS = PN + OC = (PNS + CR) + (OCS + CR) or Grandparent (TOP) layer = Parent (MIDDLE) layer = Child (BOTTOM) layer.

One can decode the family tree by working from the TOP down or the BOTTOM up!

A new vision of the intimate relationship between the ODD PRIMES — specifically the Mersenne Primes — and the EVENS — specifically the Perfect Numbers — gives yet another piece of the puzzle as to how the “reality” of quantity — that very, very so profoundly simple notion of so much of this versus so much of that, as represented by simple, natural whole numbers — informs the spacetime that builds it all!