Butterfly Fractal Expansions
Simple as can be
Simple as can be:
1-2-3 gives y-x-z
Next y comes from z
You hopefully will recall that re-assigning the terms in the Euclid-Euler Theorem to x, y and z values greatly simplifies both their geometric visualizations -- as in the Mersenne Prime Square (MPS) -- and their algebraic expressions:
Euclid-Euler Theorem: PN=2ᵖ⁻¹ (2ᵖ -1)
PN = xz =Perfect Number
z = Mersenne Prime = Mp = 2x-1 = long side of the PN Rectangle
x = (z+1)/2 = 2ᵖ⁻¹ = short side of the PN Rectangle
y= (z-1)/2 = x-1 = the other, shorter side of the OC Rectangle -- that when combined with the PN = MPS = z².
*Please do remember that these relationships describe a larger body of numbers taken from the Exponential Power of 2 -- a.k.a. The Butterfly Fractal 1 (BF1) -- that we refer to as "containers" in that they have all the defining parameters of the Active and True Mersenne Prime - Perfect Numbers, but are not "TRUE," in that one or more of their paramaters are not based on actual Mersenne Primes -- they function as necessary, place holding, pattern-revealing "containers." Most often, the TRUE Mp-PN are shown in BOLD.
That said, let us continue:
Simple as can be:
1-2-3 gives y-x-z
Next y comes from z
1-2-3 y-x-z
3-4-7 y-x-z
7-8-15 y-x-z
15-16-31 y-x-z
31-32-63 y-x-z
63-64-127 y-x-z
127-128-255 y-x-z
255-256-511 y-x-z
511-512-1023 y-x-z
1023-1024-2047 y-x-z
2047-2048-4095 y-x-z
4095-4096-8191 y-x-z
y-x-z ∑ ∆
1-2-3 6
3-4-7 14 8 = 2³
7-8-15 30 16 = 2⁴
15-16-31 62 32 = 2⁵
31-32-63 126 64 = 2⁶
63-64-127 254 128 = 2⁷
127-128-255 510 256 = 2⁸
255-256-511 1022 512 = 2⁹
511-512-1023 2046 1024 = 2¹⁰
1023-1024-2047 4094 2048 = 2¹¹
2047-2048-4095 8190 4096 = 2¹²
4095-4096-8191 16382 8192 = 2¹³
~~
A Little More Work:
PN as Perimeter
Is a Surprise Perk!
~~
There are lots of tables at the end (Tables 146-159) with all the details. The gist of the Butterfly Fractal Expansion can be seen here in these simple examples, summarized in the images that follow. A somewhat similar area within an area was found in the Pythagorean Triples works (TPISC I-IV). Once you accept that the fractal-like concept of similar, re-iterative expansion of initial conditions/parameters as an underlying organizing principle of Nature, you might well be rewarded by taking this expansion notion out through several or more larger iterations!
The PN divided by 4 = sides of the Area (A) of Multiple Mersenne Prime Squares (MMPS).
PN/4 = s and s² = A.
That A will hold N² number of MPS.
Dividing A by N² = MPS = z².
A/N² = 16A/x² = z² = MPS.
N² = x²/16 as N = x/4.
A = N² z² = (x² z² )/16 = PN²/16.
PN² =16A.
Some examples:
If you divide the PN/4 it gives the p sides=s of a larger area, A, of Multiple MPS (MMPS).
28/4 = 7 7² = 49 = A. PN/4 = s s² = A
If you divide the Area, A, by N² = x²/16 as A/N² or 16A/x² = MPS = z².
49/1 = 49 = MPS = 7² = 16•49/16 A/N² =16A/x² = z² = MPS
N² = x²/16 as N = x/4
If you square the PN to PN² = 16A.
PN² = x² PN + xy PN = PNS • PN + CR•PN PN² = 16A = (PNS+CR)PN
28² = 784 =16A =16•49 = (16•28)+(12•28)
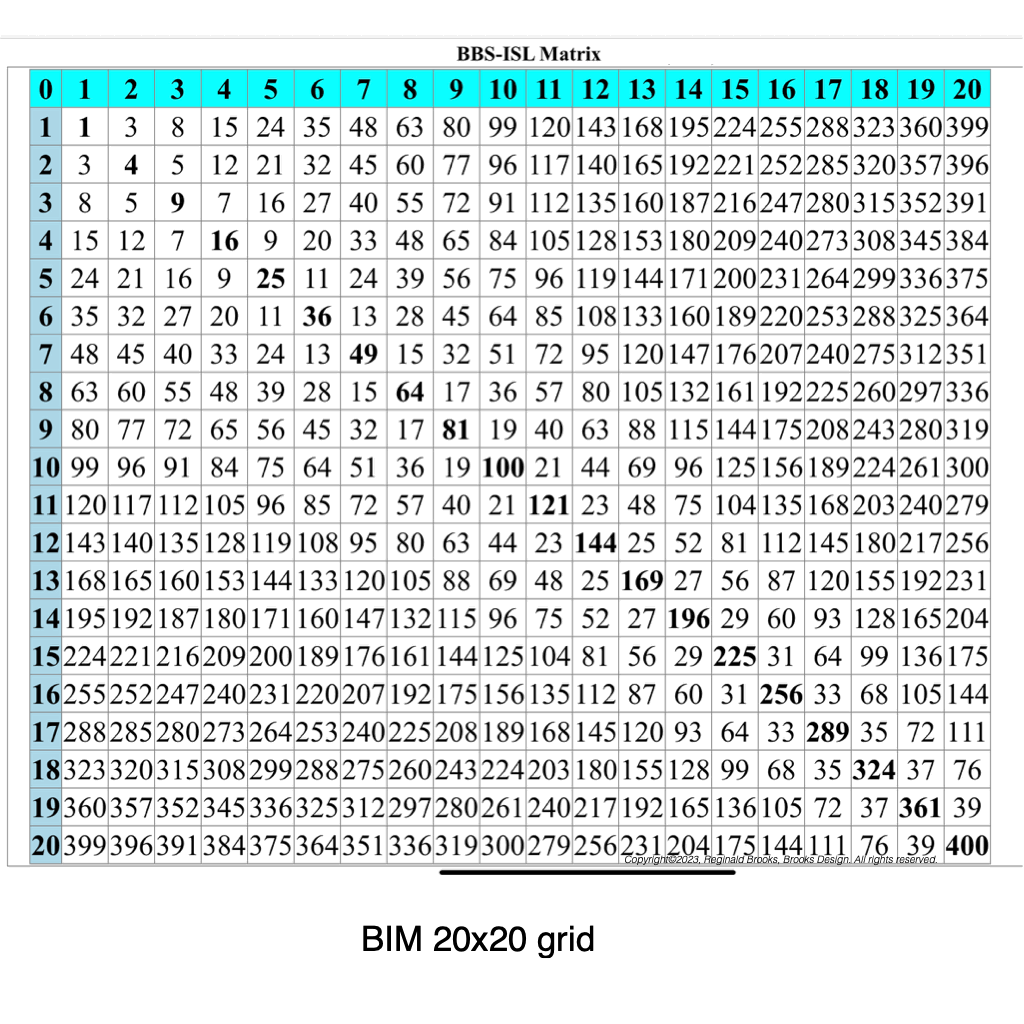
On the BIM, the *perpendicular value from PN² = 4PN. PN² - ->PPD = 4PN
28•4 = 112
On the BIM, the *perpendicular value from A = PN. A - ->PPD = PN
A = 49 ppd value = 28 = PN
*perpendicular value diagonally from...(PPD or simply ppd) on the BIM (BBS-ISL Matrix)
~~
If you divide the PN/4 it gives the p sides=s of a larger area, A, of Multiple MPS (MMPS).
120/4 = 30 30² = 900 = A.
If you divide the Area, A, by N² = x²/16 as A/N² or 16A/x² = MPS = z²
900/4 = 225 = MPS = 15² = 16•900/64
If you square the PN to PN² = 16A
120² = 14400 = 16A = 16•900
On the BIM, the perpendicular value from PN² = 4PN
120•4 = 480
On the BIM, the perpendicular value from A = PN
A = 900 ppd value = 120 = PN
~~
If you divide the PN/4 it gives the p sides = s of a larger area, A, of Multiple MPS.
496/4 = 124 124² = 15376 = A. 15376/4 = 961 = MPS = 31²
If you divide the Area, A, by N² = x²/16 as A/N² or 16A/x² = MPS = z²
15376/16 = 961= MPS = 31² = 16•15376/256
If you square the PN to PN² = 16A
496² = 246016 = 16A = 16•15376
On the BIM, the perpendicular value from PN² = 4PN
496•4 = 1984
On the BIM, the perpendicular value from A = PN
A = 15376 ppd value = 496 = PN
~~
If you divide the PN/4 it gives the p sides = s of a larger area, A, of Multiple MPS.
2016/4 = 504 504² = 254016 = A. 15376/4 = 961 = MPS = 31²
If you divide the Area, A, by N² = x²/16 as A/N² or 16A/x² = MPS = z²
254016/64 = 3969 = MPS = 63² = 16•254016/32²
If you square the PN to PN² = 16A
2016² = 4064256 = 16A = 16•254016
On the BIM, the perpendicular value from PN² = 4PN
2016•4 = 8064
On the BIM, the perpendicular value from A = PN
A = 254016 ppd value = 2016 = PN
A=Area
MMPS=Multiple MPS
N=number of
PN=Perfect Number
z=Mp=x+y
z² =MPS

Movie
Here are some background images covered in previous sections:

~~
Here is peak at the next section, Book X: MPS_PN Factors/Divisors:
PN = xz
Here are two examples showing the “next” PN. TRUE, Actives in BOLD. The first example shows Sets 1 and 2, but requires the “x” value of the “next” PN. The second part shows the same Sets 1 and 2, but uses the known “x” value of the current PN.
16xz+3x=PN>next
(4•6+2•2)=28 p=3
16•28+3•16=496 p=5
16•496+3•64=8128 p=7
16•8128+3•256=130816
16•130816+3•1024=2096128
16•2096128+3•4096=33550336 p=13
16•33550336+3•16384=536854528
16•536854528+3•65536=8589869056 p=17
16•8589869056+3•262144=137438691328 p=19
16•137438691328+3•1048576= 2199022206976
16•2199022206976 +3•4194304= 35184367894528
16•35184367894528 +3•16777216= 562949936644096
16•562949936644096 +3•67108864= 9.0071991876E15
16•9.0071991876E15 +3•268435456= 1.4411518781E17
16•1.4411518781E17 +3•1073741824= 2.3058430082E18 p=31
=
(4•6+2•2)=28 p=3
16•28+12•4=496 p=5
16•496+12•16=8128 p=7
16•8128+12•64=130816
16•130816+12•256=2096128
16•2096128+12•1024=33550336 p=13
16•33550336+12•4096=536854528
16•536854528+12•16384=8589869056 p=17
16•8589869056+12•65536=137438691328 p=19
16•137438691328+12•262144=2199022206976
16•2199022206976 +12•1048576= 35184367894528
16•35184367894528 +12•4194304= 562949936644096
16•562949936644096 +12•16777216= 9.0071991876E15
16•9.0071991876E15 +12•67108864 = 1.4411518781E17
16•1.4411518781E17 +12•268435456 = 2.3058430081E18 p=31
The latter (16xz+12x) uses x=current "x" associated with xz while the former (16xz+3x) uses x=new (next) associated with solution, x•4. The both use the same x sequence, only the starting point differs. Note that in the latter, shortcut method, "x" is often not BOLD.
This, again, shows the importance of the inActive Set 2 & 3 “containers” in the NPS.
4PN+2x=PNn gives the intermediary (p=EVENS, like p=4, PN=120) in Set 3, between those above.
~~ ~~ ~~
Table105_Mersenne Prime Squares Master Table.pdf
Tables 146-159
Table146_perimeters.pdf
Table147_Square-perimeters.pdf
Table148_Square_Perimeters-3.pdf
Table149_Square-perimeters-4.pdf
Table150_Square-perimeters-5.pdf
Table151_Square-perimeters-6.pdf
Table152_p+xSqd+ySqd-x+1=xz.pdf
Table153pSetsOf4.pdf
Table154_Square-perimeters-7.pdf
Table155_PNdivide2tilODD-2.pdf
Table156_ExpandingFractals.pdf
Table157_ExpandingFractals_Calculate.pdf
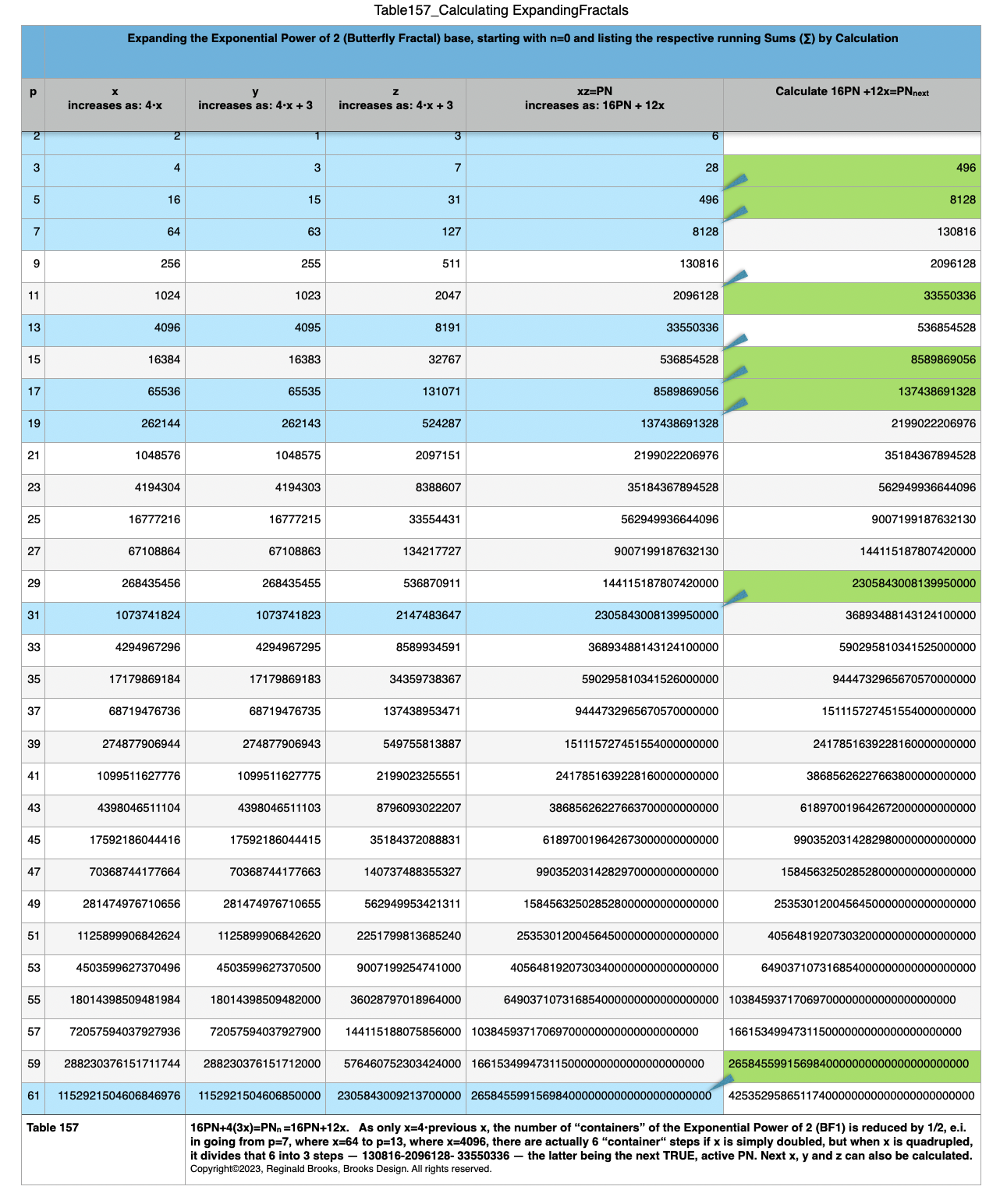
Table157_ExpandingFractals_Calculate.png
Table159_PN_factors_divisors_Colors.pdf

Table159_PN_factors_divisors_Colors.png
~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~
BACK: BOOK VIII: Appendix III: Equations
NEXT: BOOK X: Appendix V: MPS_PN_Factors(Divisors)
LINKS:
Mersenne Prime Squares (Part I) the Introductory white paper.
Mersenne Prime Squares (Part II) 3 Simple Intros.
Mersenne Prime Squares (Part III) the Advanced white paper.
The MPS Project The Mersenne Prime Squares Project.
















