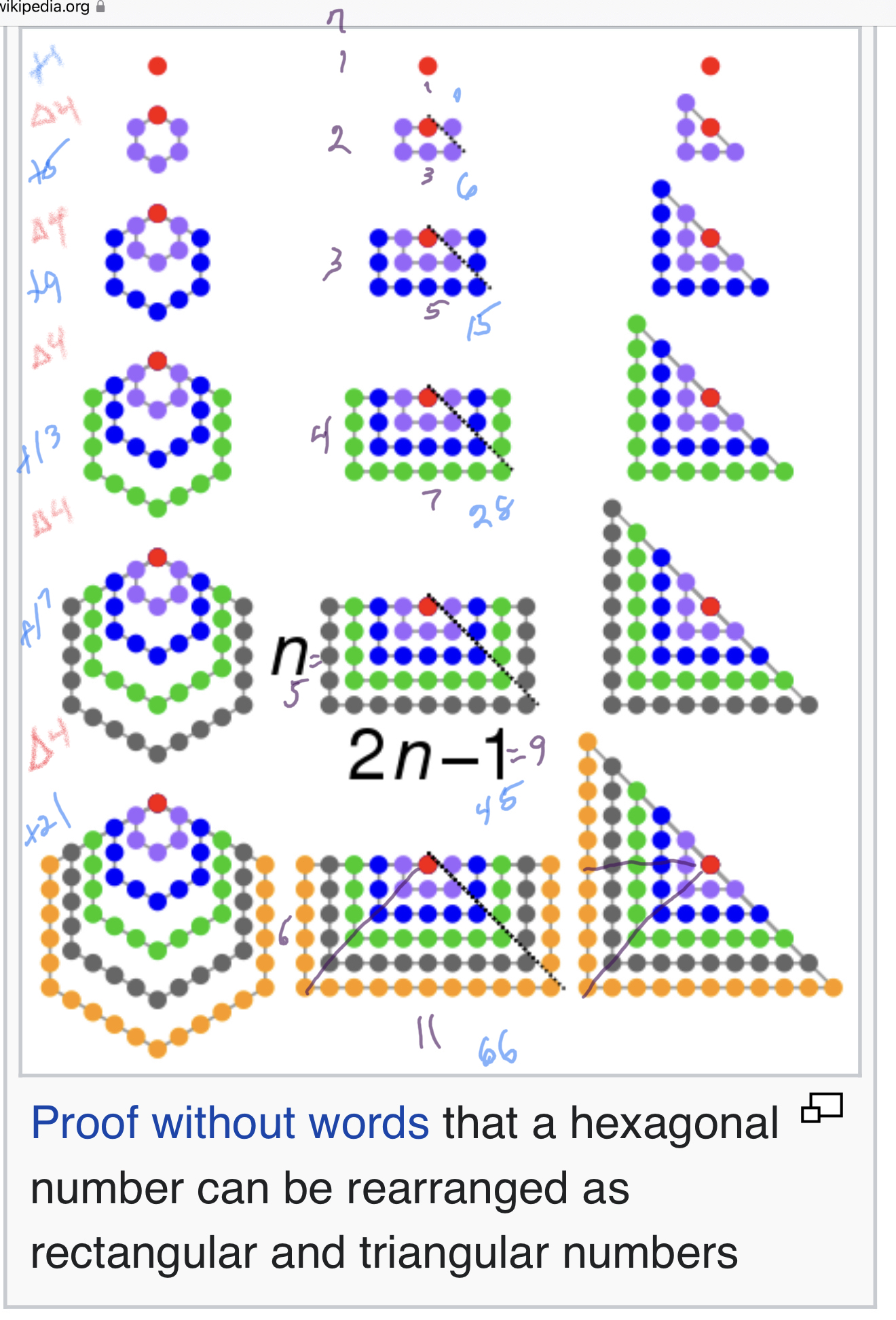
Appendix I: Cubed, Coordinates
About the Appendix: Although it would have been natural to place this Appendix I in a separate section, the decision to place it here at the end of the Summary-Discovery-Conclusion-References section was to give it the notice it deserves! Hidden in the research were a few -- and only a few -- references to the Mersenne Prime-Perfect Number pairings when cubed, versus the normal squaring methods. Well, a whole new MP-PN Universe is opened up upon the sequential running sums (∑) of the CUBES of the sequential ODD numbers series. A very rich vein of discovery (by others) has not been given a thorough enough evaluation. Yes it is being spotlighted here in Appendix I, referred to as the Butterfly Fractal-3, and placed on hold while the Squared 2D version of BIMMPS-MPPN is panned out.
Butterfly Fractal 1 (BF1): original, base fractal based on the Exponential Power of 2.
Butterfly Fractal 2 (BF2): original, base fractal based on the Exponential Power of 2, but with the Running Sums (R∑) emphasized.
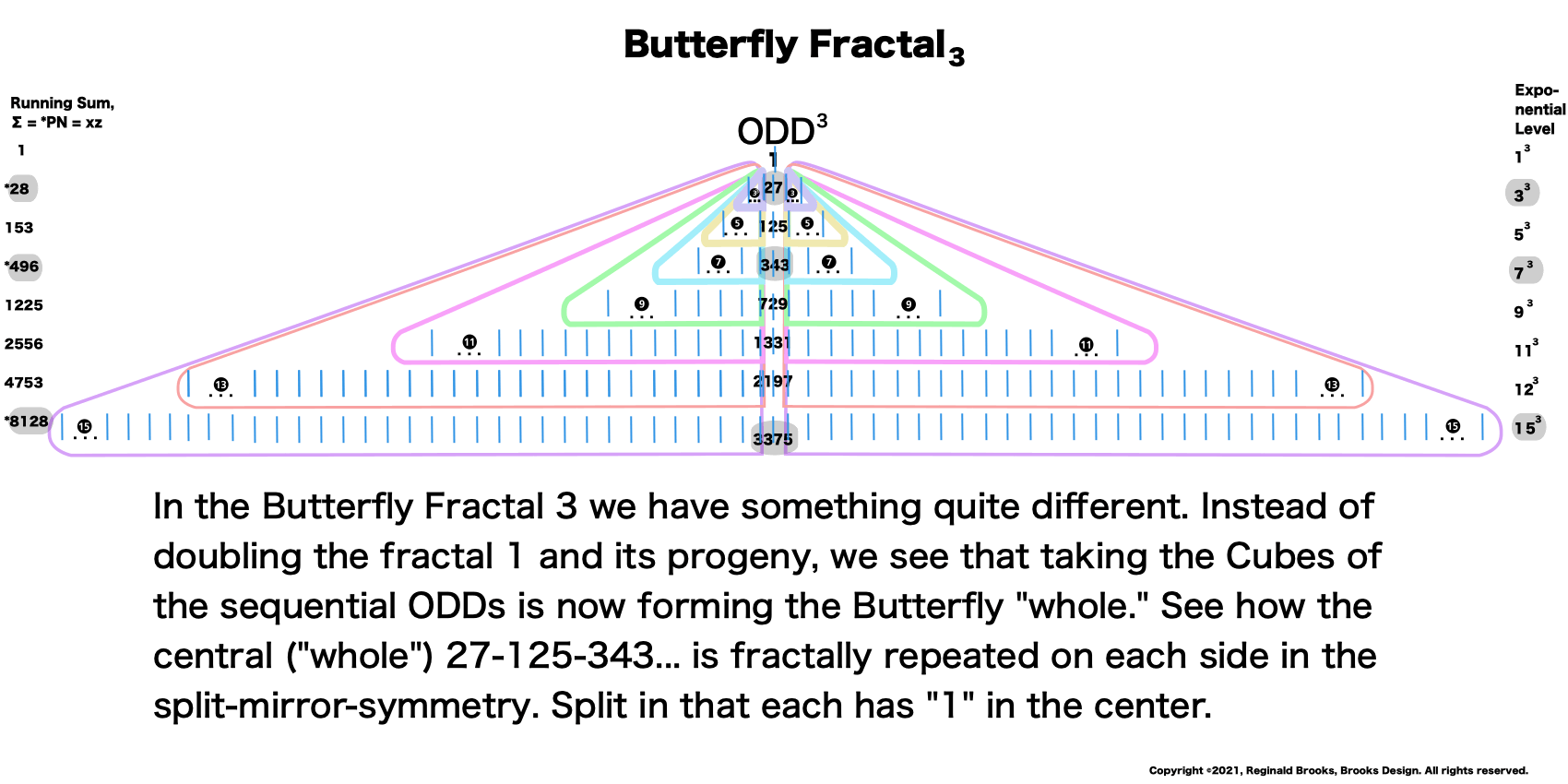
Butterfly Fractal 3 (BF3): based on cubing the exponents.
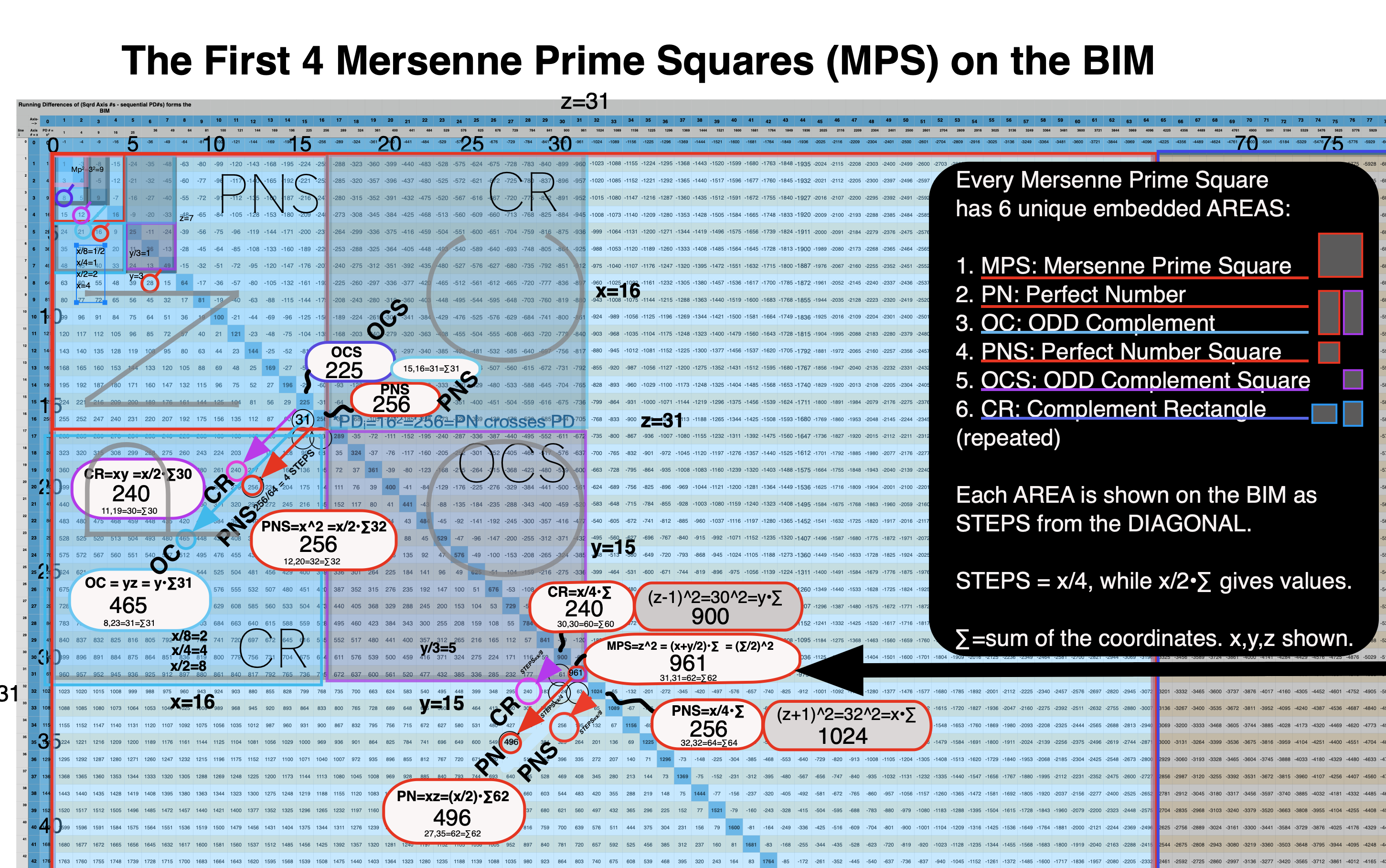
Butterfly Fractal 4 (BF4): the 10 fundamental parameters of every Mersenne Prime Square (MPS) are revealed by SAME fractal-pattern of BF1, only using the x, y and z values of a given MPS.
Similarly, for the mini-topic of "coordinates!" Although an approach to looking at the basic BIMMPS-MPPN via the "coordinate approach" -- as was done in the work on the Goldbach Conjecture -- seemed quite fruitful awhile back, it was considered quite challenging to follow and it, too, was placed on the "back burner." Then very recently two new Coordinate-Based Rectangles (CBR) were discovered and presented in the Summary-Discovery pages. Something special is going on here where the Axial coordinates of the BIM provide keen and unique insights into the BIMMPS-MPPN. To note is that the NEW CBR involve the BIM Axial coordinates while the "Coordinates" being brought to light in this Appendix 1 have a more intricate relationship to the PD in their expression. Again, so very much going on here and it serves a much deeper look!
What about Appendix II: Tables and Appendix III: Equations? Aren't they of enough importance to be placed into the body of this work? Answer: yes, indeed! The Tables Appendix is best viewed in its own section and an Appendix makes sense as you will find out. There are decades worth of data consolidated with the tables. Much of it is quite pertinent and needs to be upfront and some is just so interesting and question-asking that it needs to be documented and referenced, but will nevertheless be best kept behind the scenes so as not to obfuscate the basic results presented. The Equations will present the basic story -- and then some -- in pure math form.
Cubed
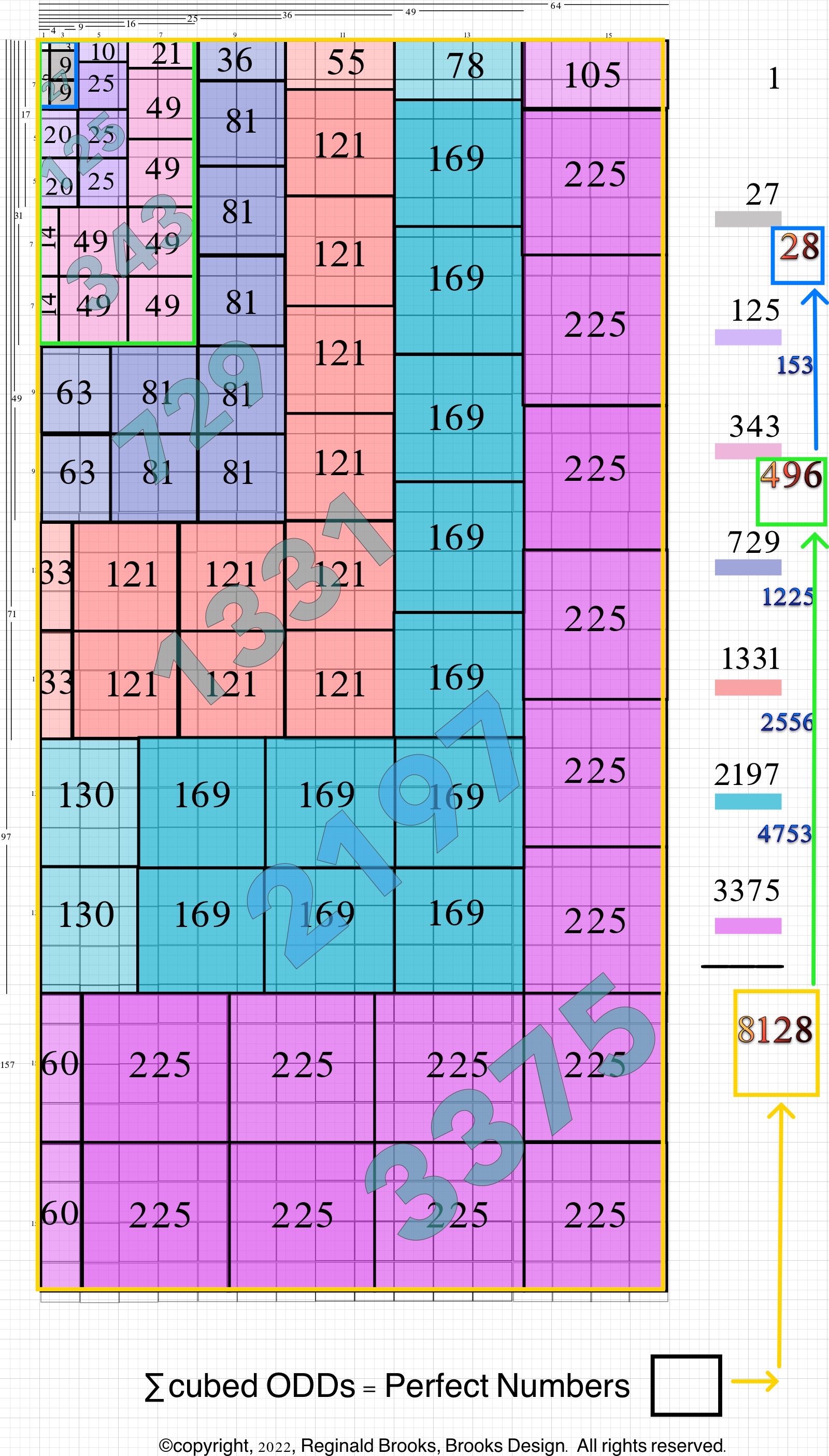
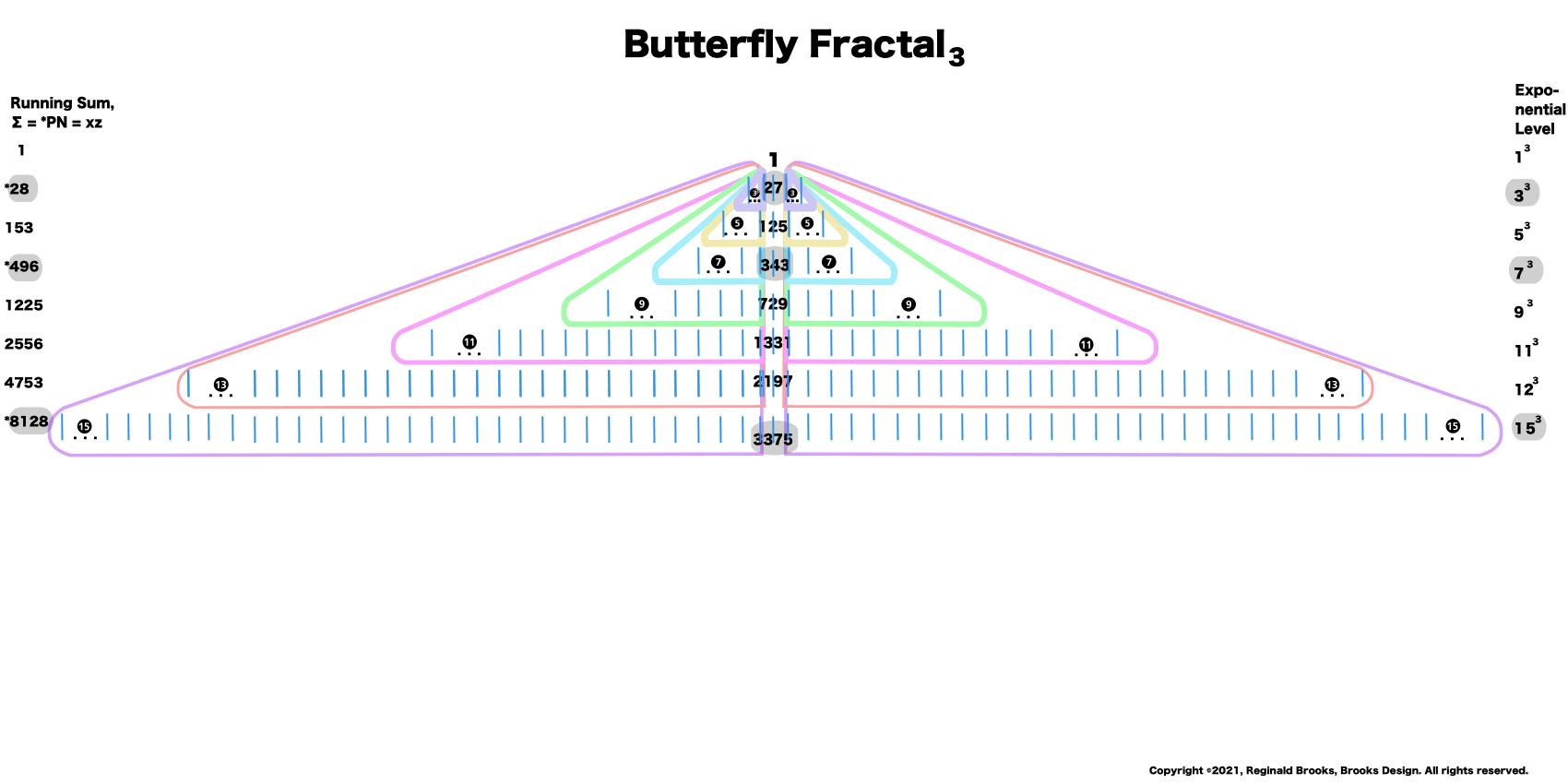
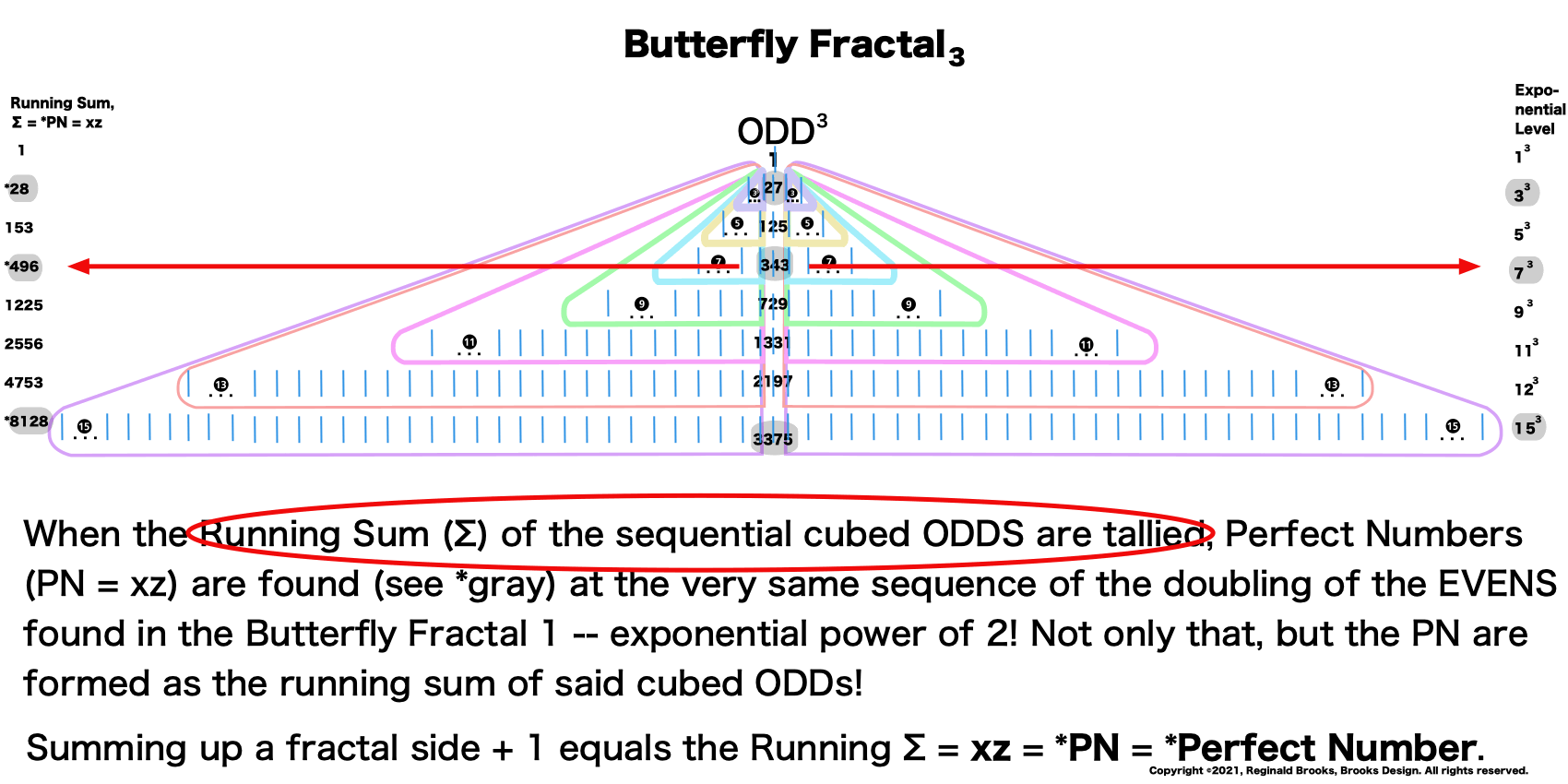
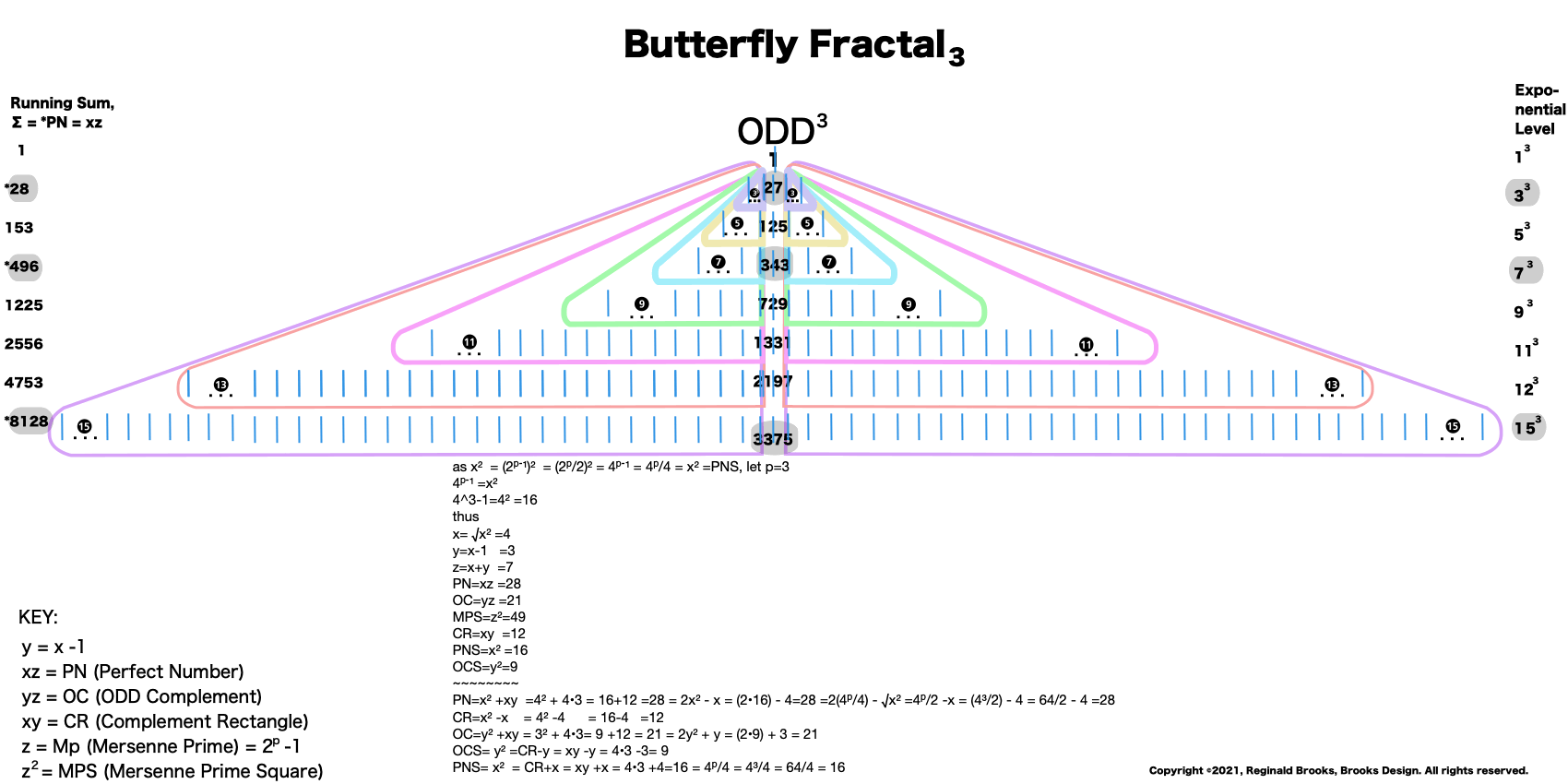
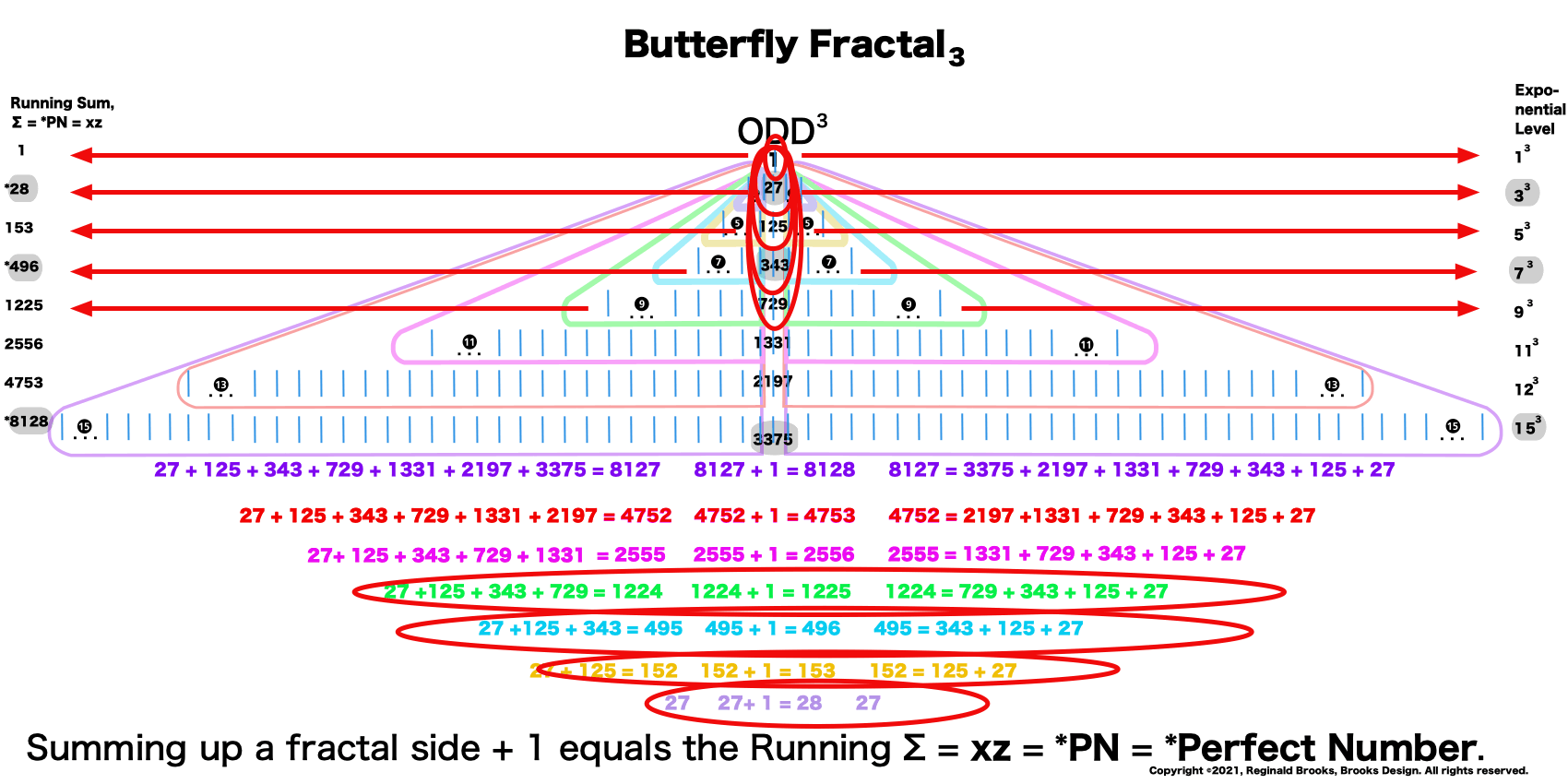
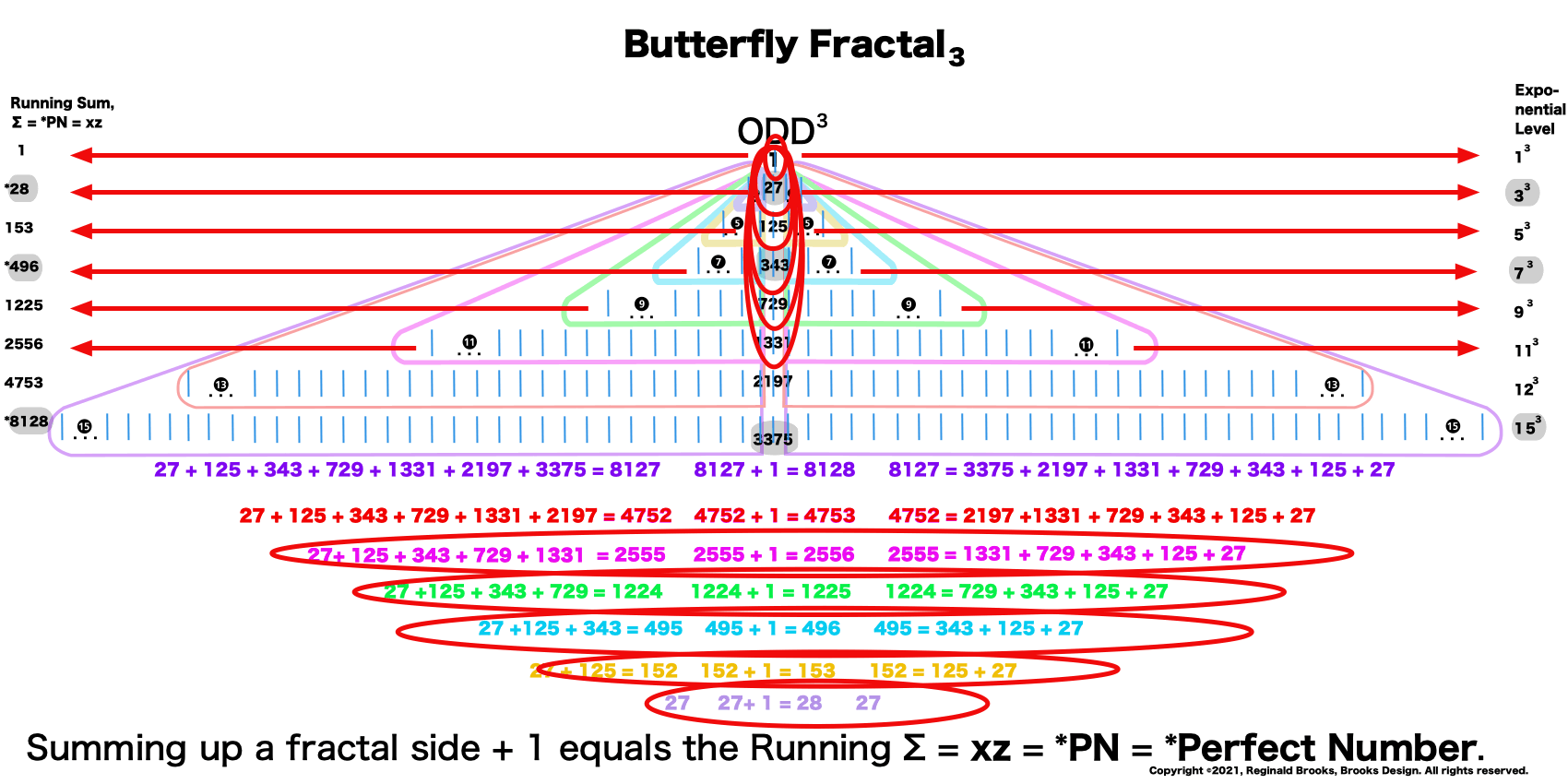
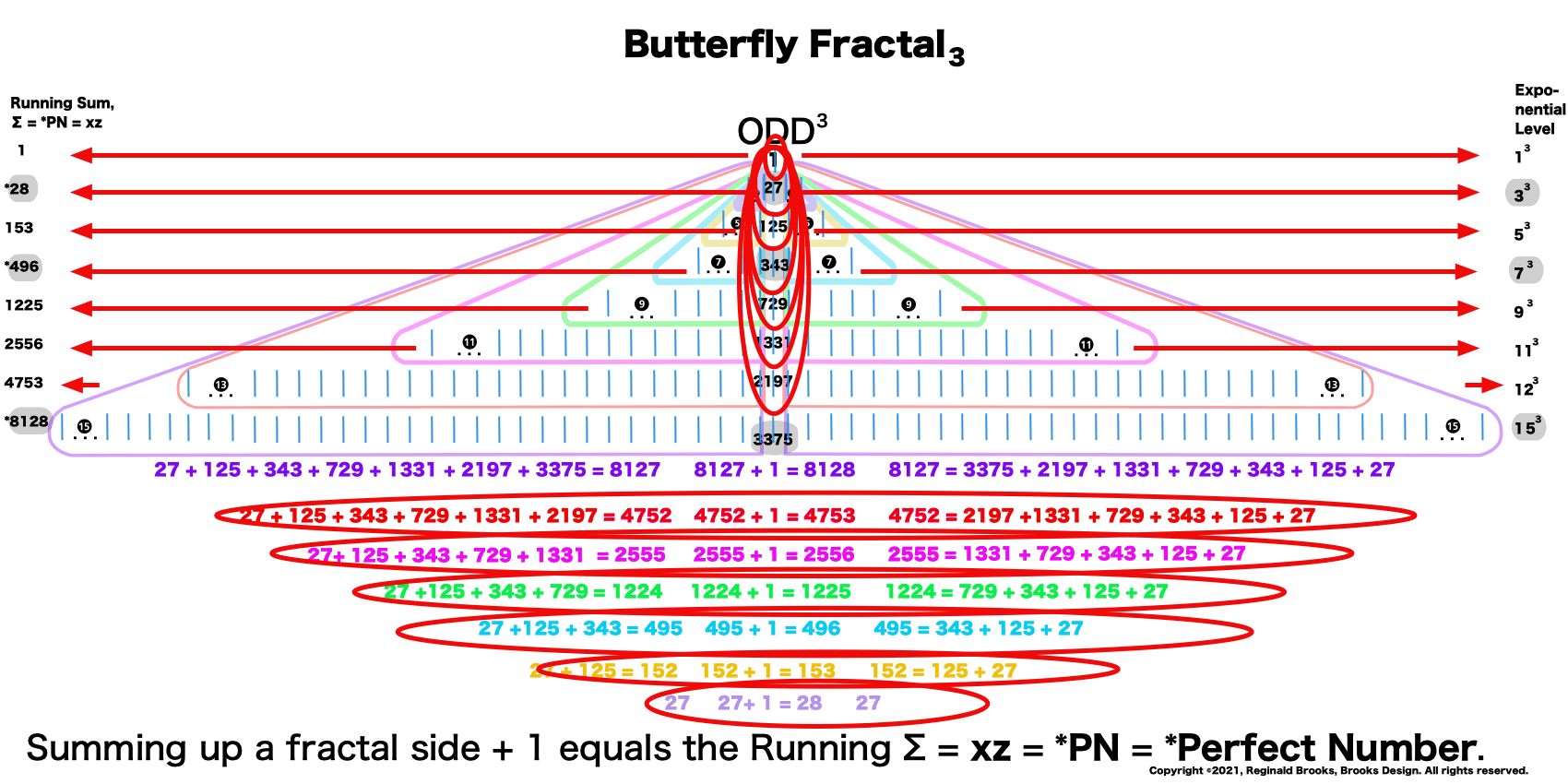
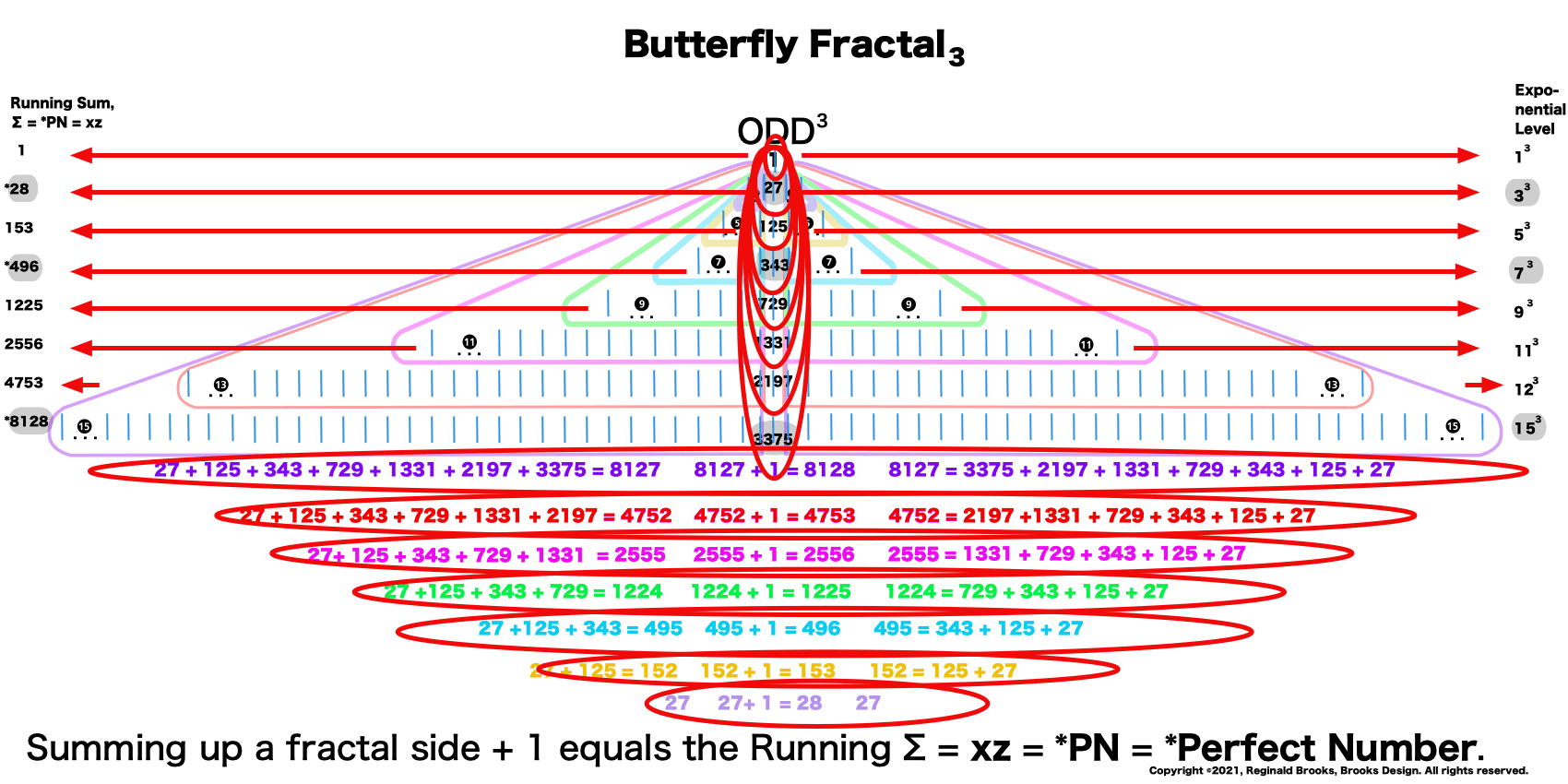
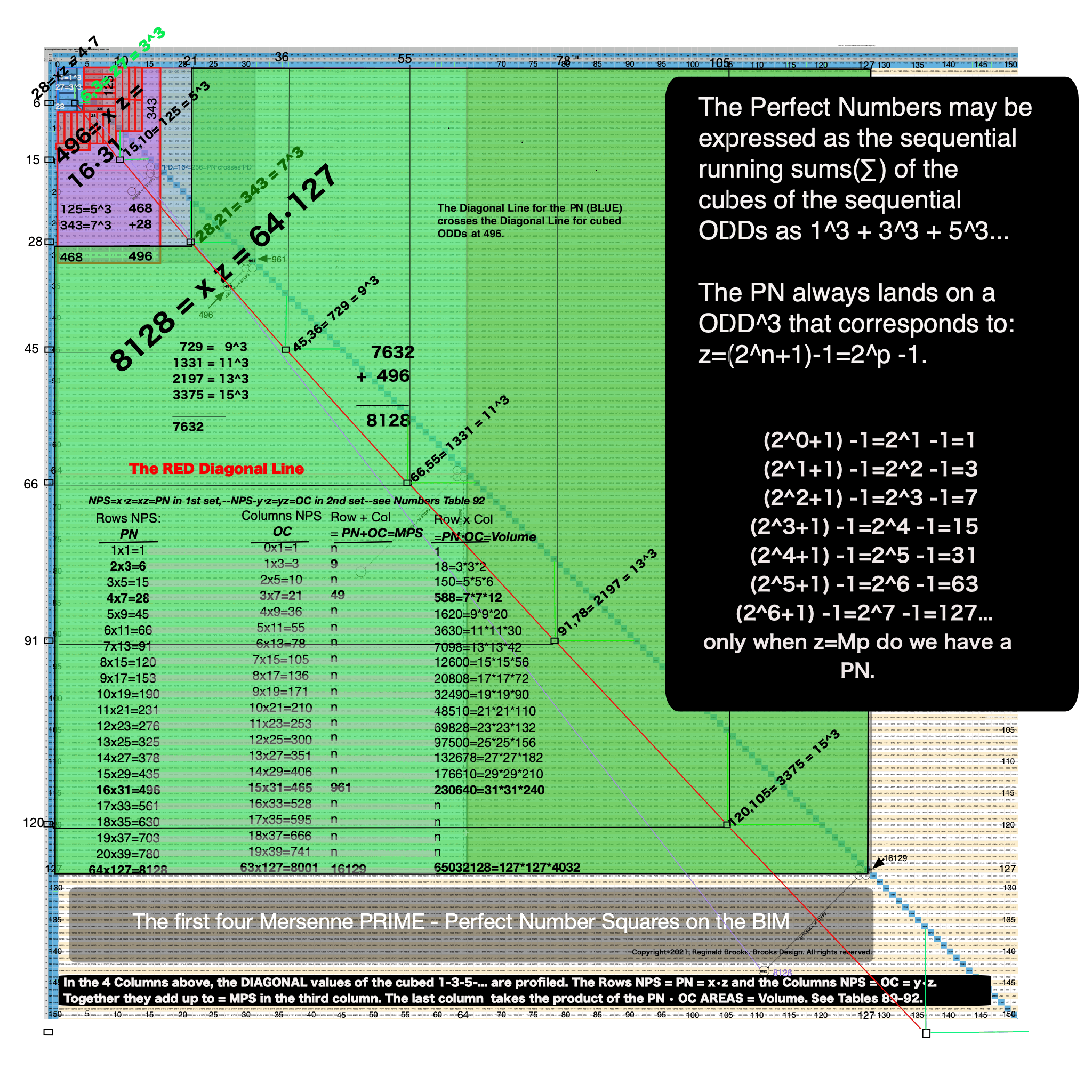
The Perfect Numbers may be expressed as the sequential running sums (∑) of the cubes of the sequential ODD numbers as 1³ + 3³ + 5³ ... and we have the genesis of the Butterfly Fractal~3~.
References:
Garcia, Arturo, "On Perfect Numbers."Saint Mary's College Of California, Department of Mathematics and Computer Science, May 17, 2016. Print.
"Theorem 5. Every even perfect number greater that 6 can be expressed as the sum of the cubes of consecutive odd integers.
Proof. Recall that $\sum_{i=1}^{n}{i³\; }\; =\; \frac{\; \; \; n²\left( n+1 \right)²\; }{4}$
Let m = 2^(p−1)/2^ where p is prime. We want to rewrite the sum of the cubes of consecutive odd integers so that it is of the form 2^p−1^(2^p^ − 1). That is to say, we claim that:
1^3^ +3^3^ +···+(2m−1)^3^ =2^p−1^(2^p^ −1)..." (Direct reference to 2. below.)
Voight, John. 1998. Perfect Numbers: An Elementary Introduction. Department of Mathematics, University of California, Berkeley. California.
"We can also write any perfect number as the sum of cubes:
Proposition 11 ([1]). If N = 2ⁿ⁻¹(2ⁿ − 1) is perfect then n = 1³ + 3³ + ··· + $\left( 2^{\frac{\left( n−1 \right)}{2}}−\; 1 \right)^{3}$.
Proof. Recall the formula
$\sum_{i=1}^{n}{i³\; }\; =\; \frac{\; \; \; n²\left( n+1 \right)²\; }{4}$
a fact which can be proved by induction..." (Direct reference to 3. below.)
Syed Asadulla, Even perfect numbers and their Euler’s function, Internat. J. Math. Math. Sci. 10 (1987), 409–412. (Direct reference to 4. below.)
SHOCKL, J.E., Introduction to Number Theory, Holt, Rinehart and Winston, New
York, N.Y. 1967.
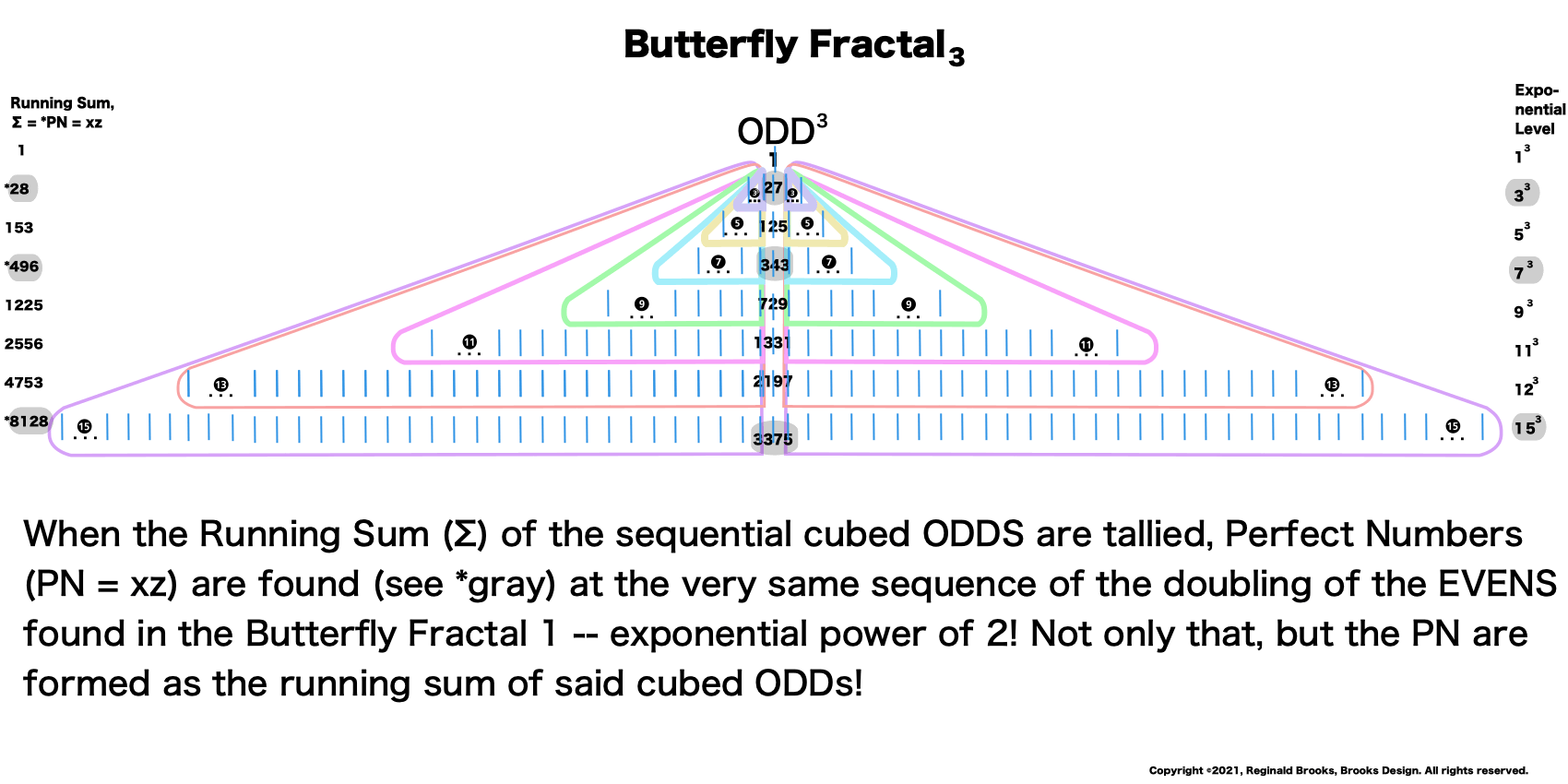
In the Butterfly Fractal~1~ and Butterfly Fractal~2~, we find the MPS parameters based around the EVEN numbers, especially within the exponential power of 2. When we look at their summations, we find it delivers the ODDs we are looking for that inform the MPS directly.
This gave the x and z=Mp directly and the y, xz=PN and xy=CR indirectly by calculation.
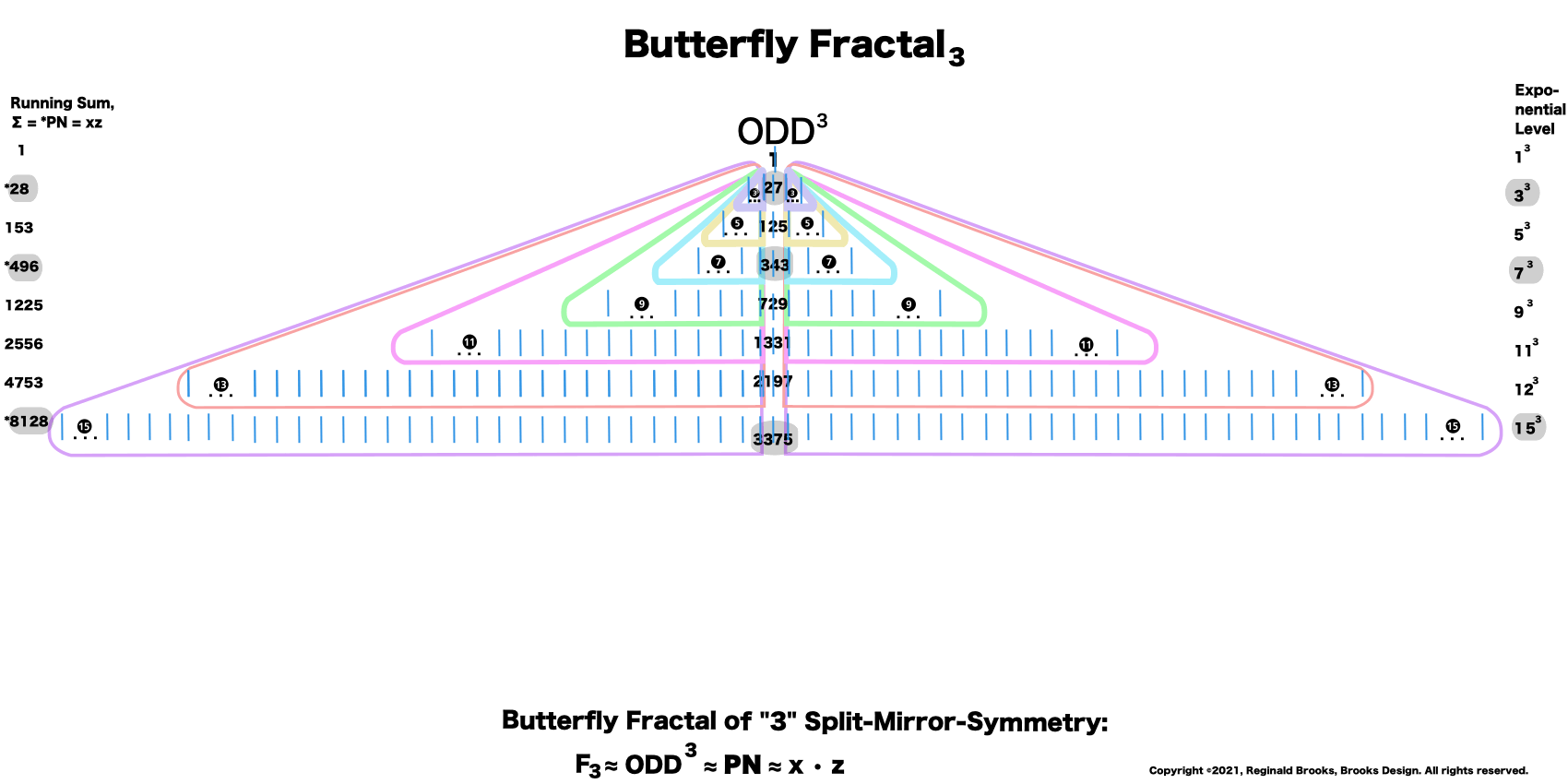
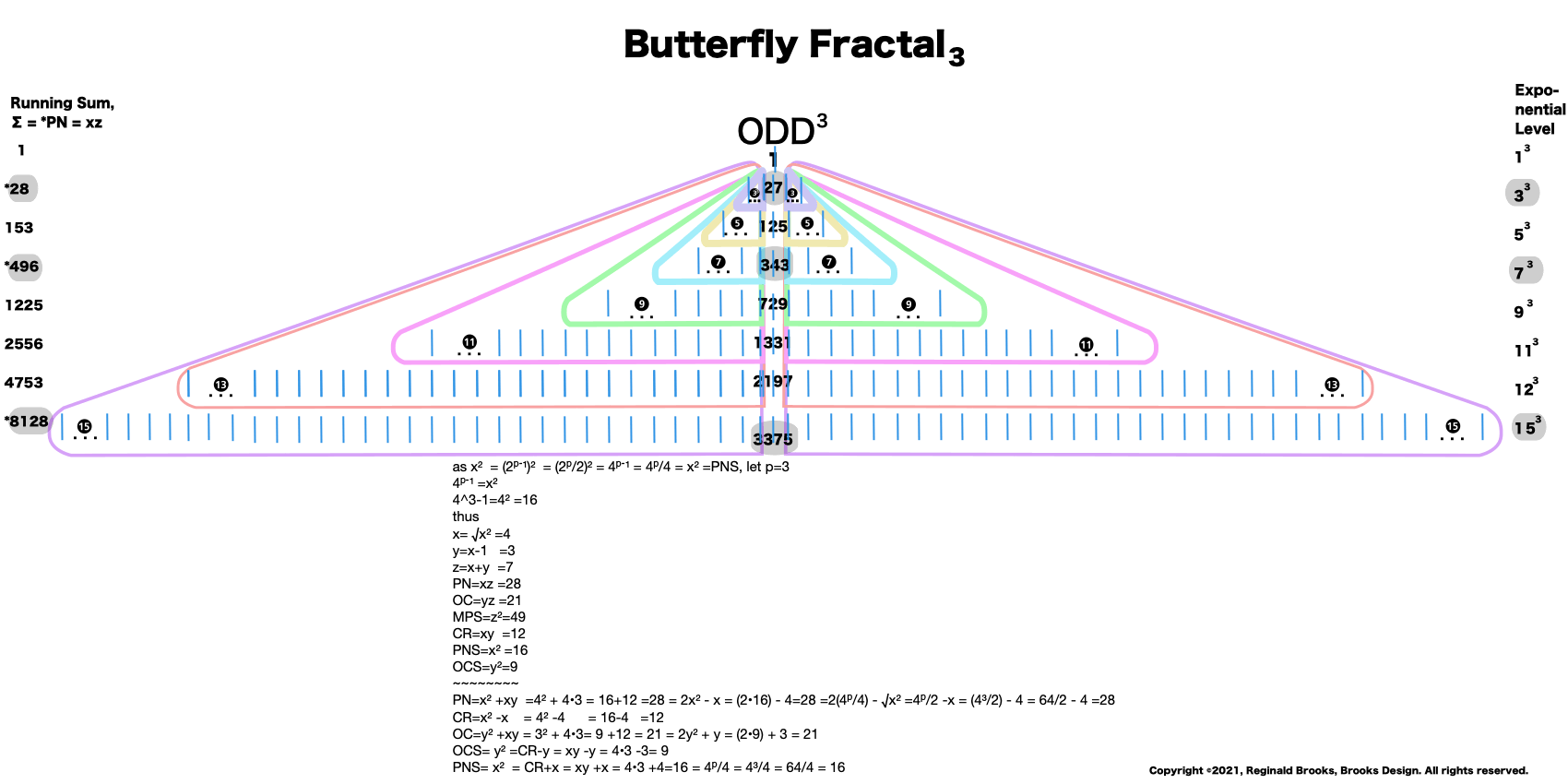
Now, in the Butterfly Fractal~3~, we find the MPS parameters based around the ODD numbers, especially the Running Sums (∑) of the ODD numbers sequence of 1,3,5,… giving the MPS and the ODD³ sequence of 1³, 3³, 5³,… giving the PN!
Butterfly Fractals that start with the ODDs:
Butterfly Fractal~3~
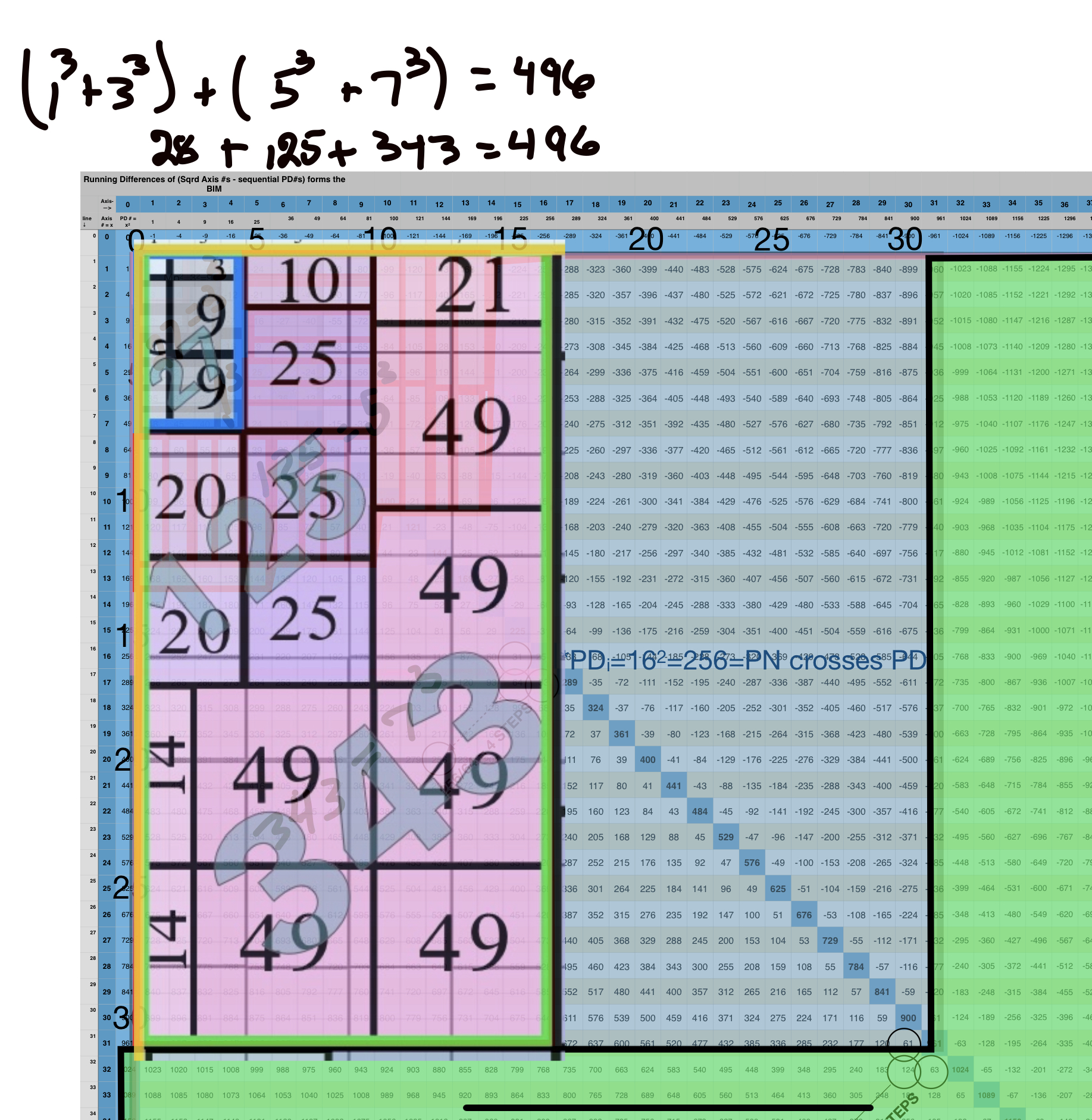
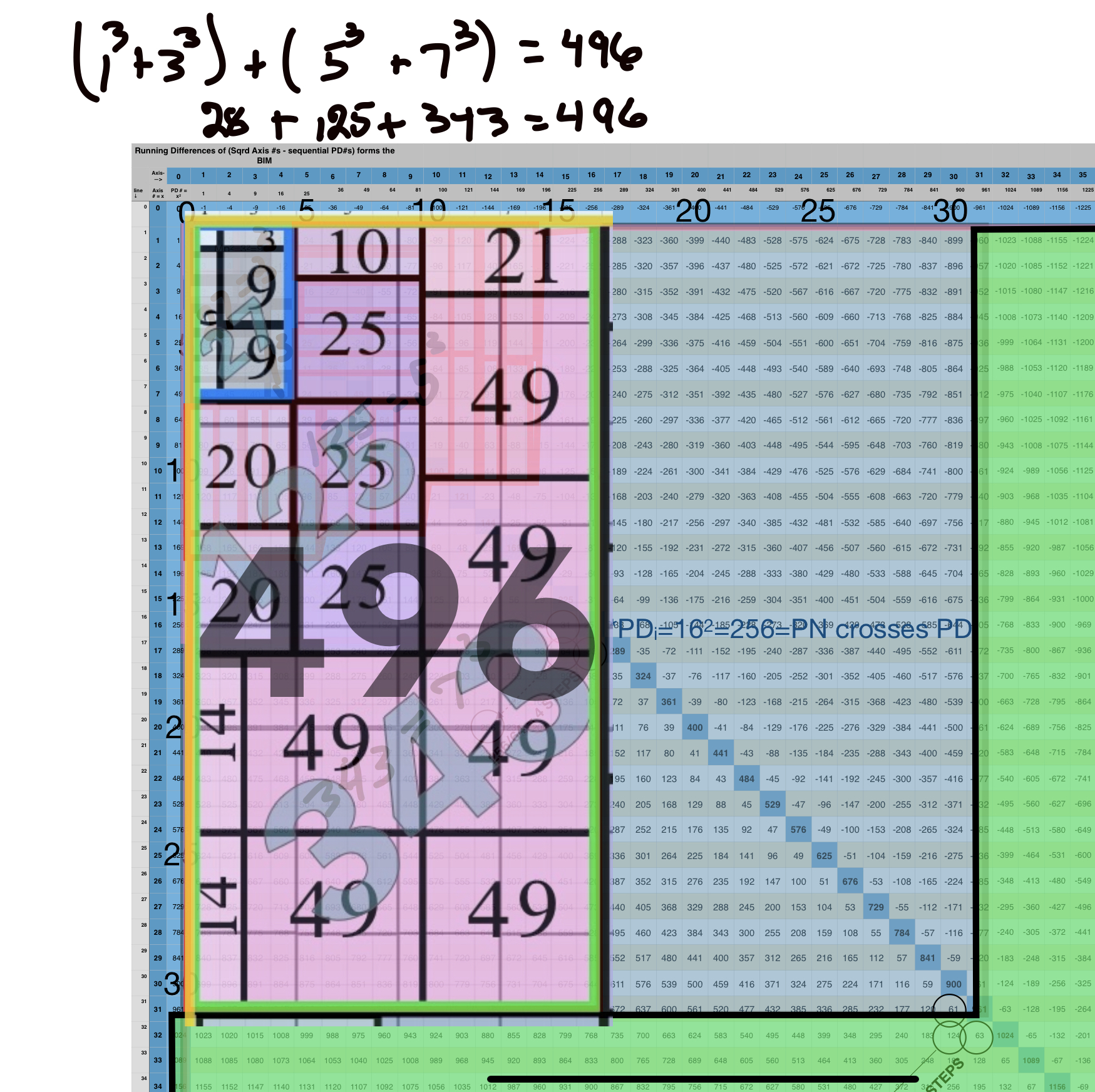
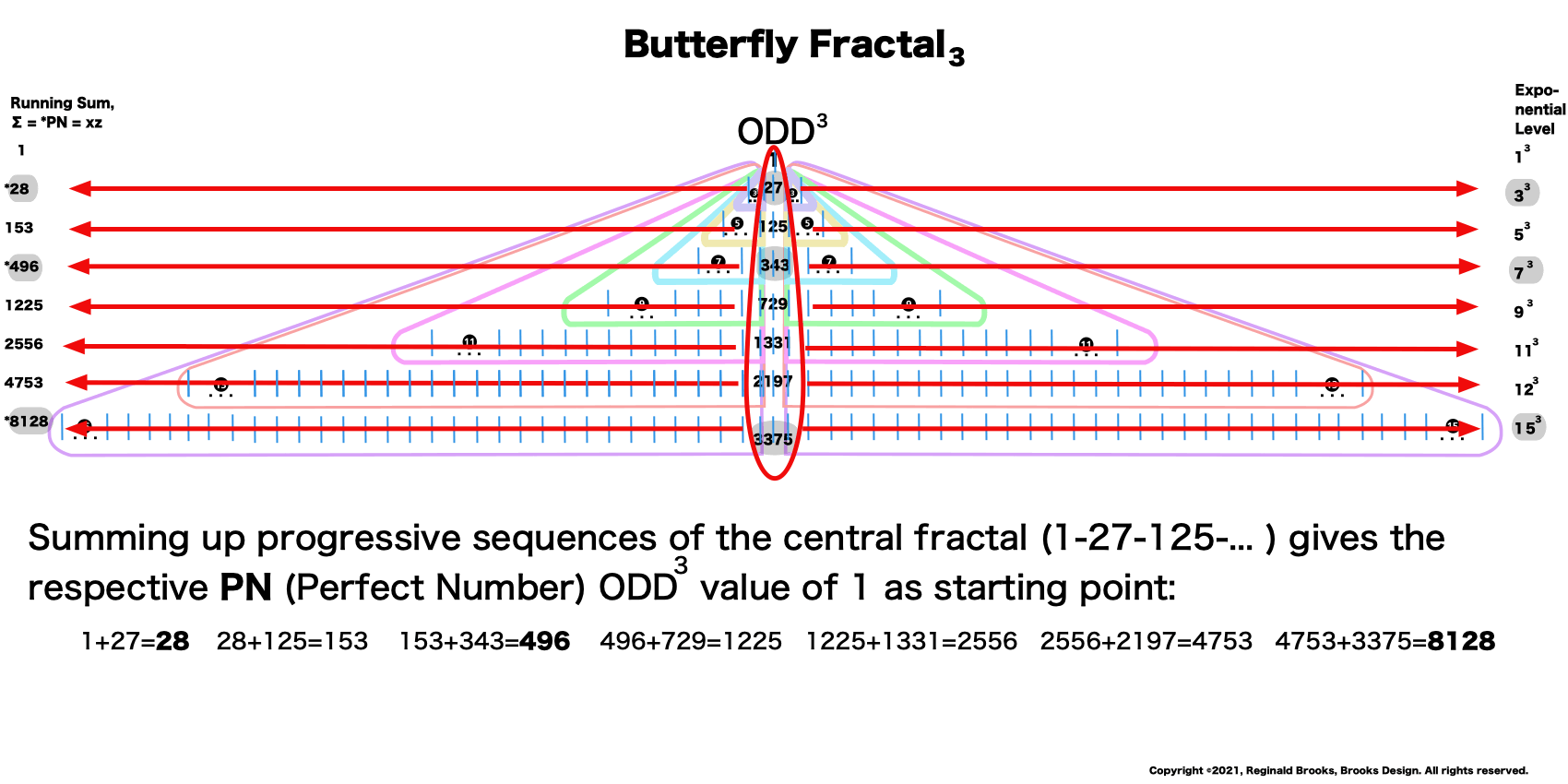
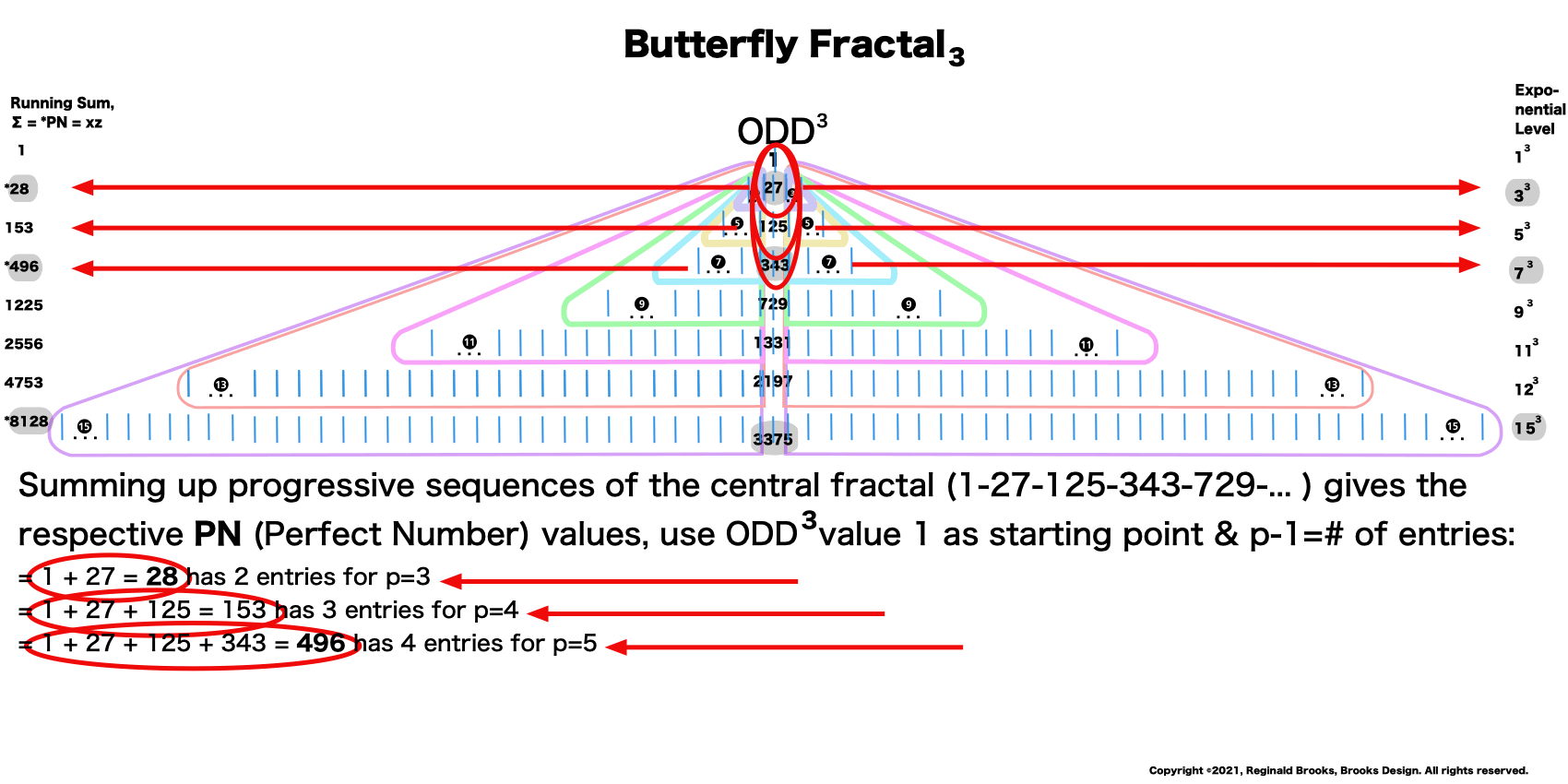
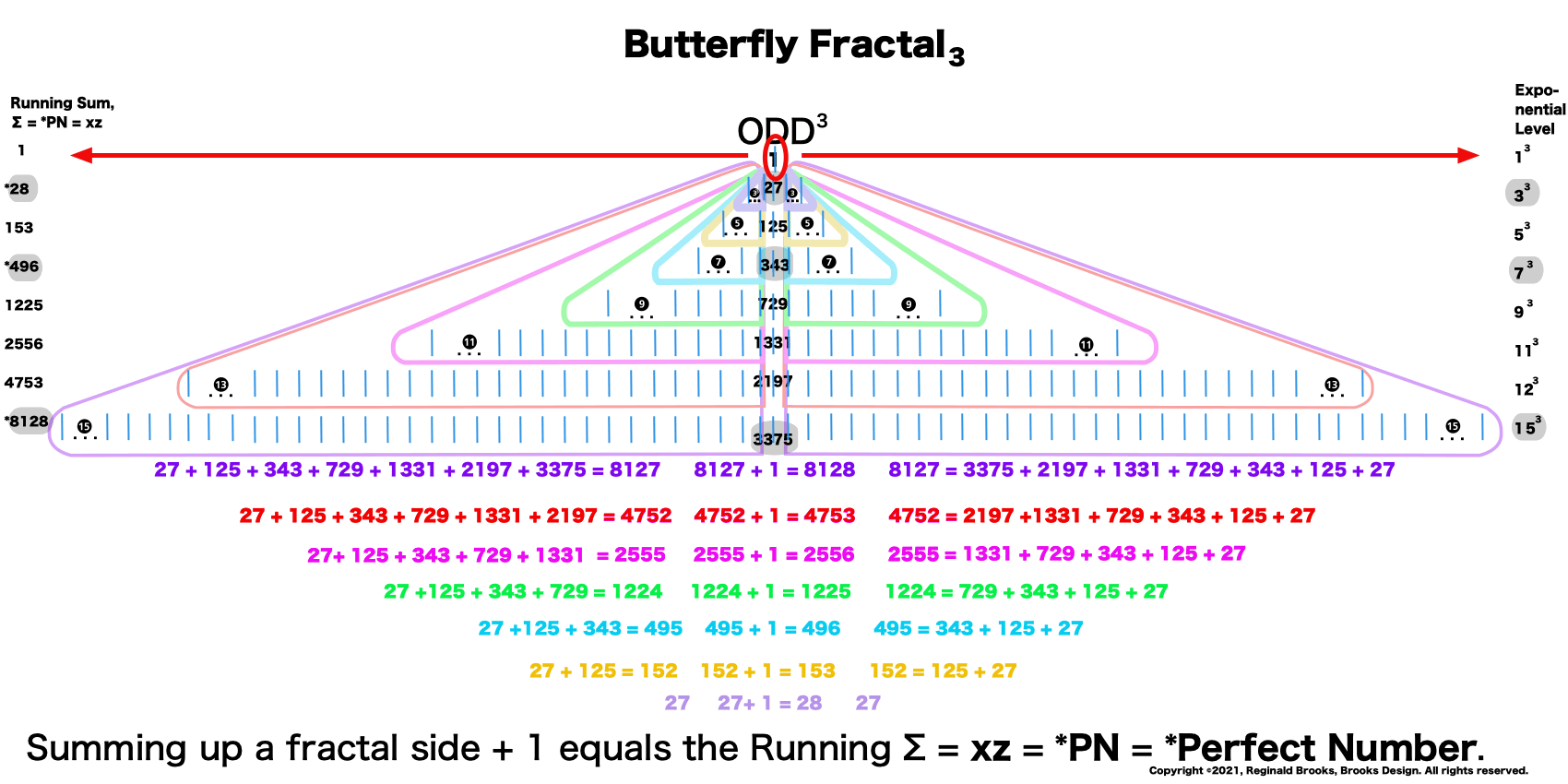
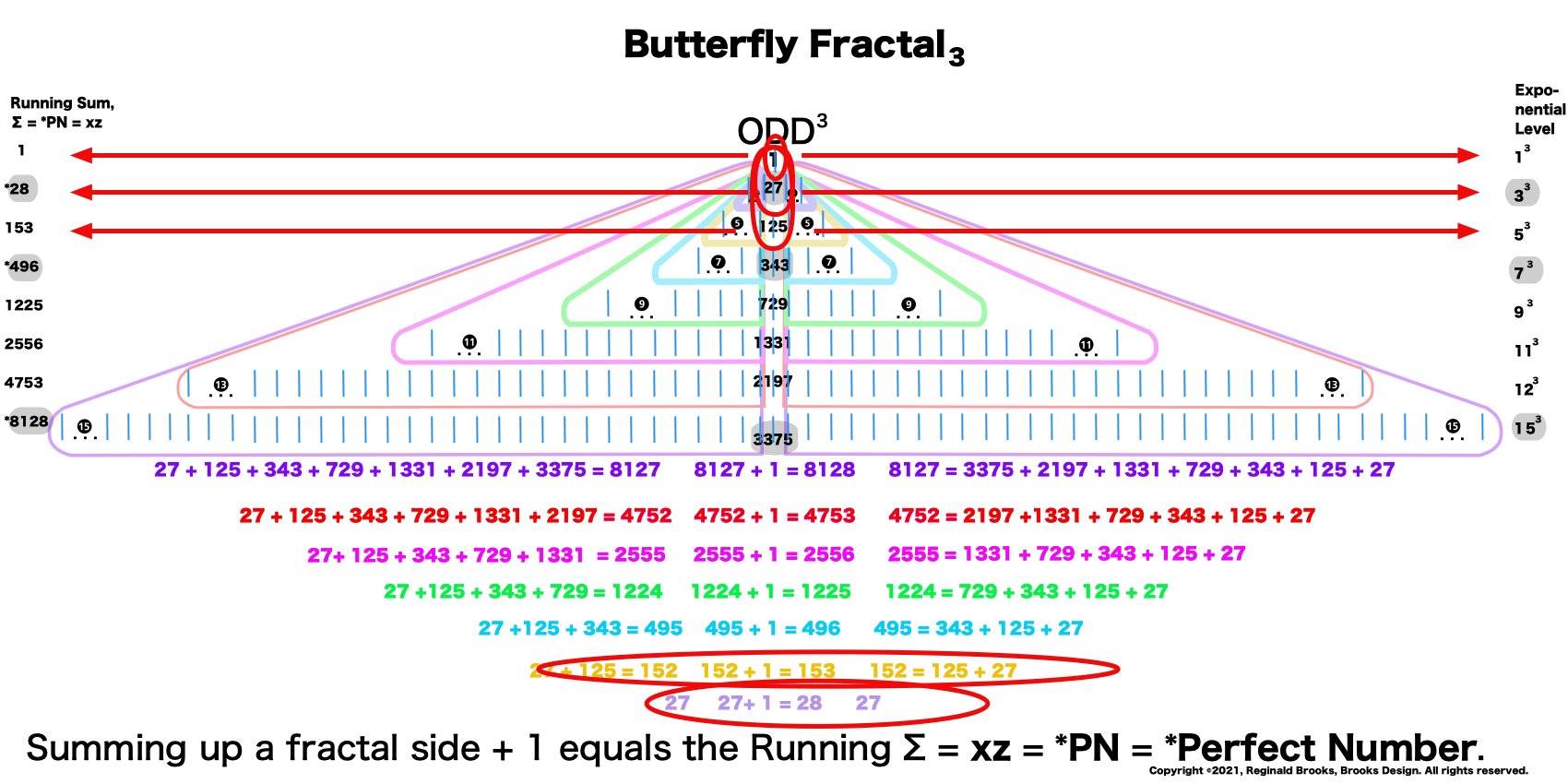
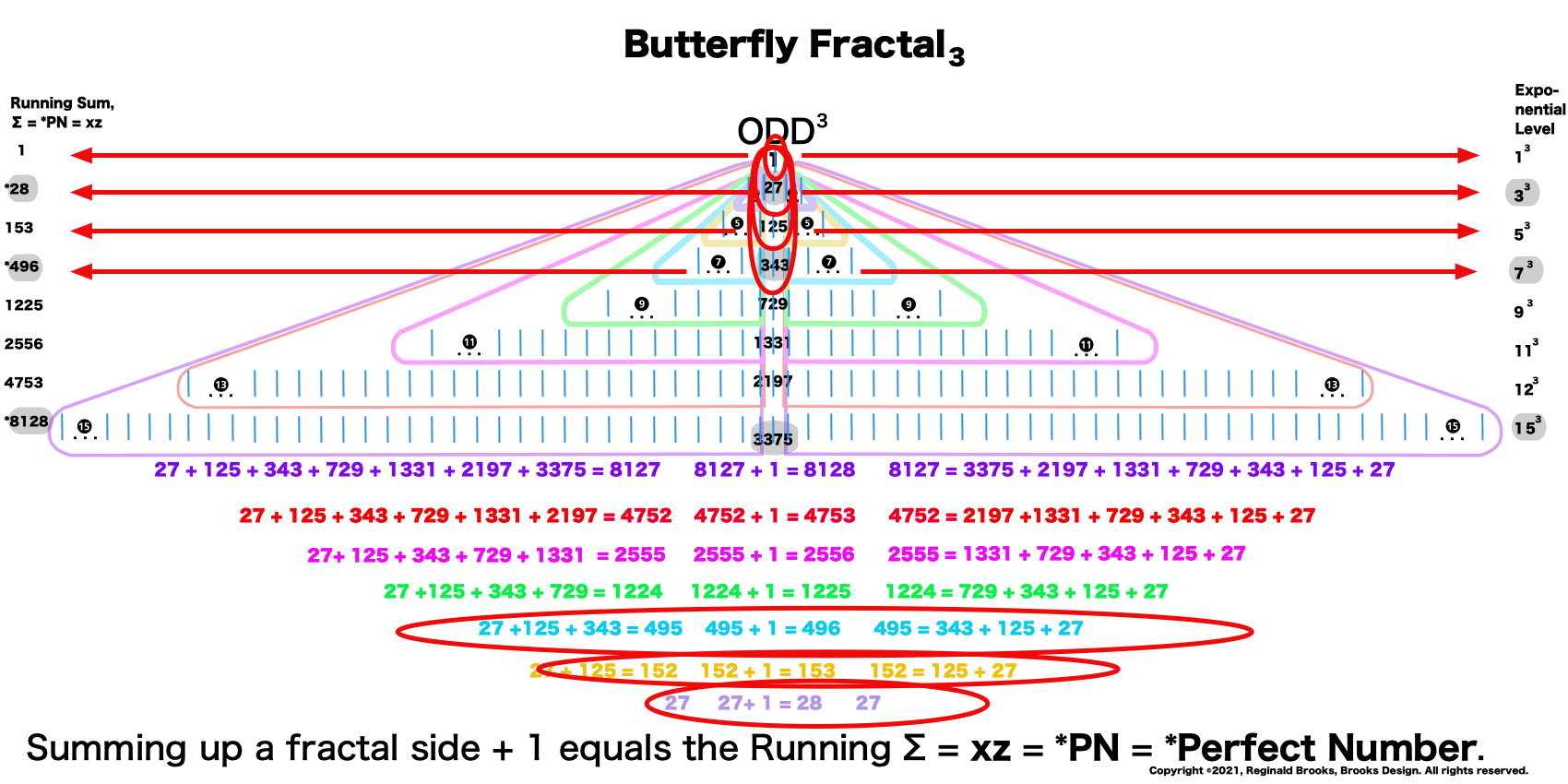
1³+ 3³ = 1+27 = 28 = PN = xz with 2 entries.
1³ + 3³ + 5³ + 7³ =496 = PN = xz = 16•31 with 4 entries.
1³ + 3³ + 5³ + 7³ + 9³ + 11³ + 13³ + 15³ =8128 = PN = xz = 64 •127 with 8 entries.
This gives the Perfect Numbers (PN = xz) as the running sum (∑) of the cubed ODDs.
Butterfly Fractal~4~
1+3+5+7+9+11+13 = 49 = MPS = z² = PN + OC with 7 = z = Mp #of entries.
1+3+5+7+9+11+13 …+61 = 961 = MPS = z² = PN + OC with 31 = z = Mp #of entries.
1+3+5+7+9+11+13…+253 = 16129 = MPS = z² = PN + OC with 127 = z = Mp #of entries.
Interestingly enough, the running sum (∑) of the ODDs is exactly that which informs the BIM!
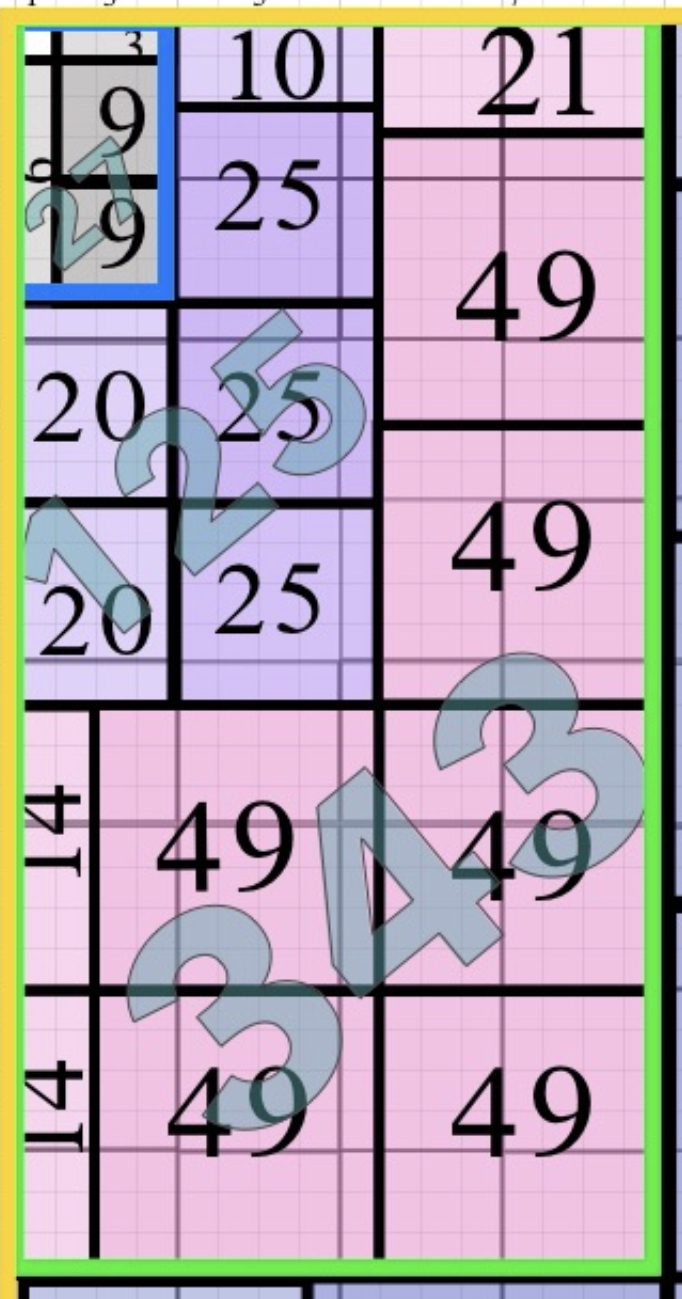
Those ∑ are quite simply the square of the Axis values on the BIM: 1² -- 2² -- 3² -- 4² -- 5² --... equals 1--4--9--16--25--..., respectively. These, of course, make up the main Primary, or Prime, Diagonal (PD) that is the mainstay of the BIM. In fact, every Inner Grid (IG) value on the BIM is simply the difference between its two PD values of horizontal and vertical intersect. e.i. IG = 16 is PD 25 - PD 9.
Naturally, as the Mersenne Prime Square (MPS = Mp² = z²) is the square of the Mersenne Prime, it will appear on this ODD-Number-Summation-Series (ONSS): 1+3+5+7+9+11+13 …
Starting with 3, this ONSS -- that may also be referenced as ∑~ODDs~ -- is the 1^st^ Parallel Diagonal on the BIM.
The relationship between the ODDs and EVENs that is the hallmark of the Inverse Square Law (ISL) as depicted on the BIM is so fundamental that it deserves it own Butterfly Fractal reference: Butterfly Fractal~4~!
Butterfly Fractal~3~

BIMMPS_Fractalidraw3-1.gif"
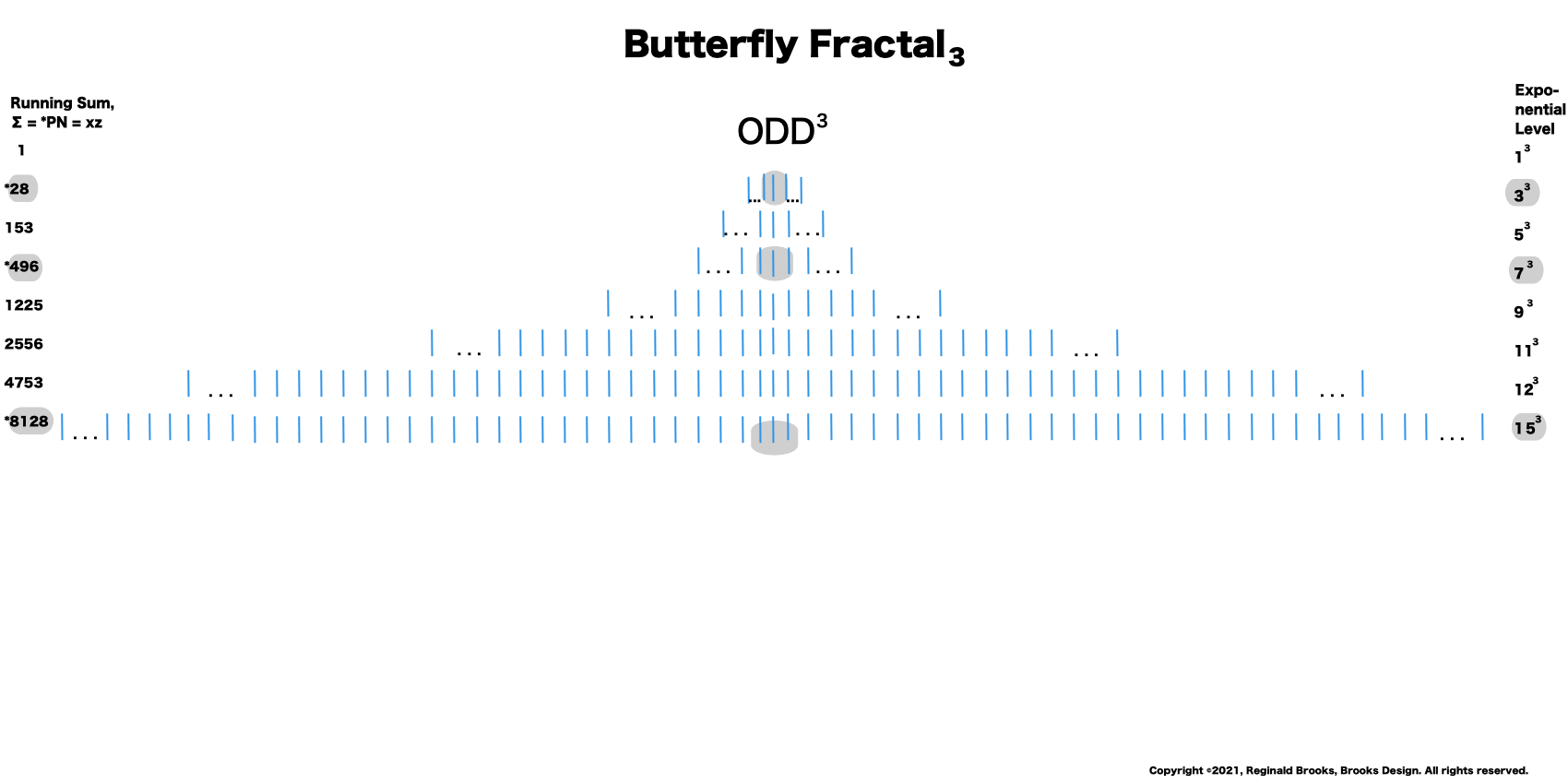
BIMMPS_Fractalidraw3-2.gif"
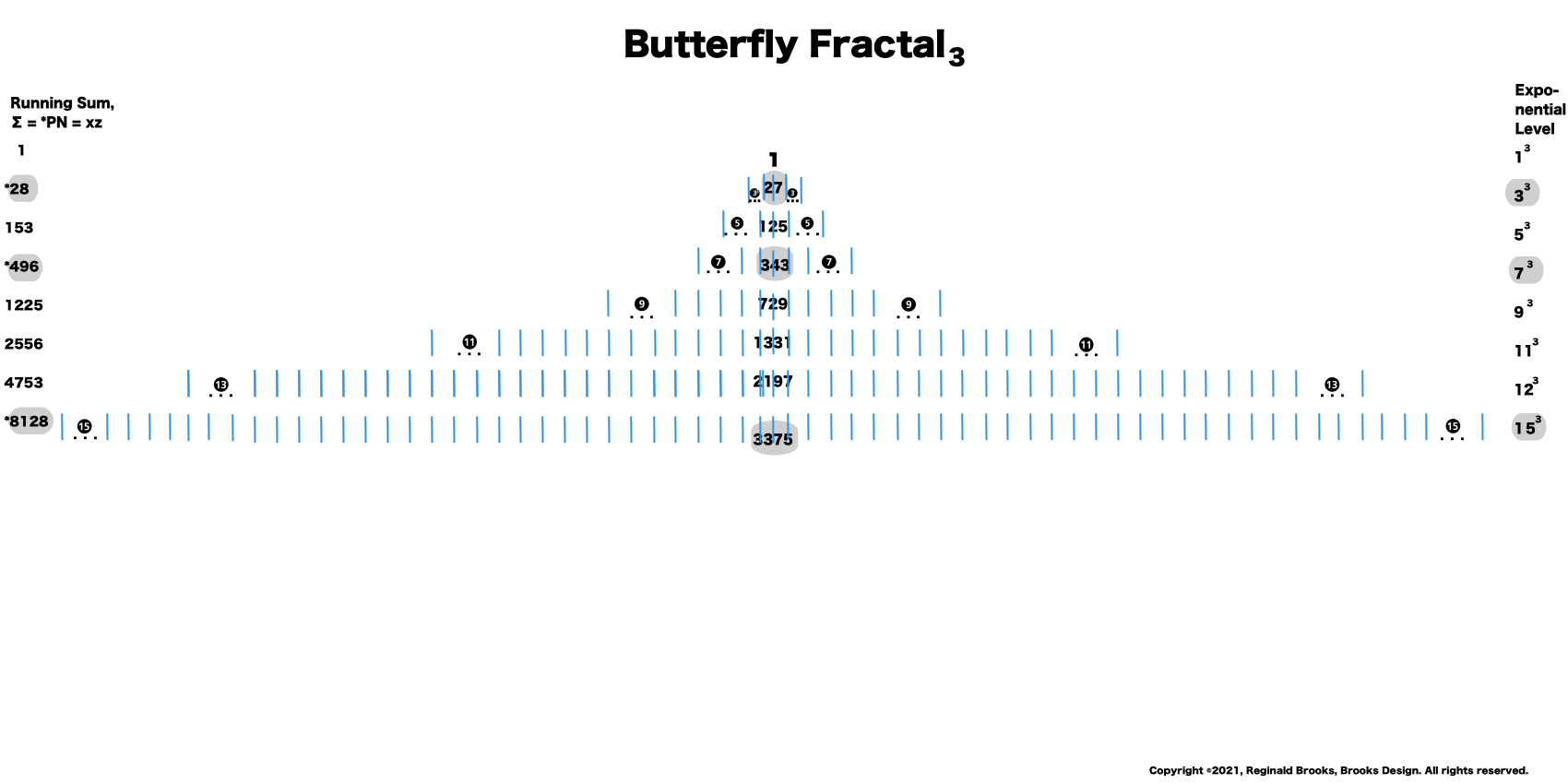
BIMMPS_Fractalidraw3-3.gif"
BIMMPS_Fractalidraw3-4.gif"
BIMMPS_Fractalidraw3-5.gif"
BIMMPS_Fractalidraw3-6.gif"
BIMMPS_Fractalidraw3-7.gif"
BIMMPS_Fractalidraw3-8.gif"
BIMMPS_Fractalidraw3-9.gif"
BIMMPS_Fractalidraw3-10.gif"
BIMMPS_Fractalidraw3-11.gif"
BIMMPS_Fractalidraw3-12.gif"
BIMMPS_Fractalidraw3-13.gif"
BIMMPS_Fractalidraw3-14.gif"
BIMMPS_Fractalidraw3-15.gif"
BIMMPS_Fractalidraw3-16.gif"
BIMMPS_Fractalidraw3-17.gif"
BIMMPS_Fractalidraw3-18.gif"
BIMMPS_Fractalidraw3-19.gif"

BIMMPS_Fractalidraw3-20.gif"

BIMMPS_Fractal3.gif"
Animated gif.

BIMMPS_Fractal3.mp4"
Video
BIM150-MPS-cubed-1-2-3.gif"