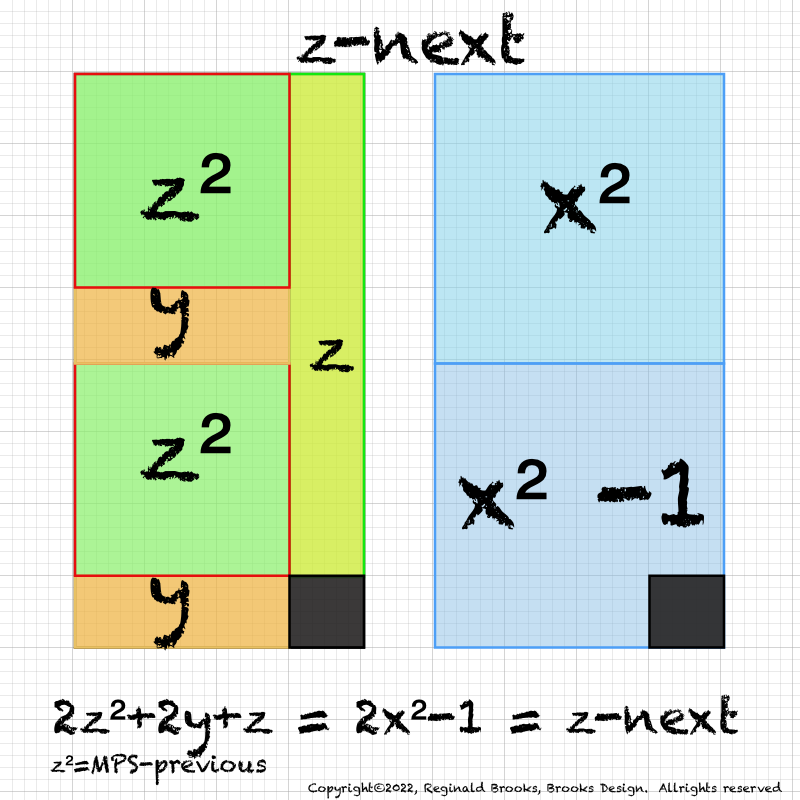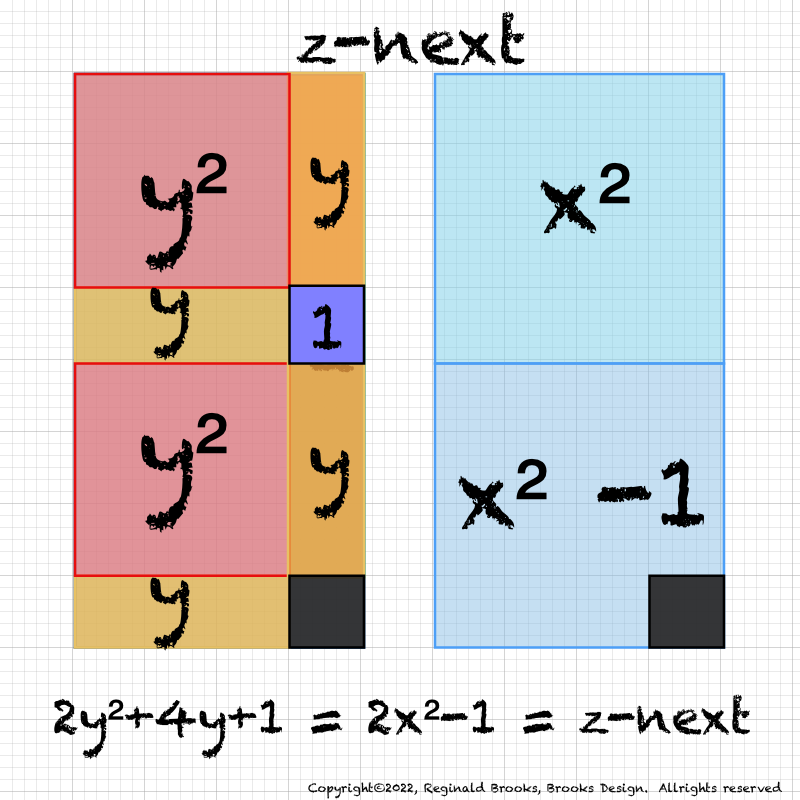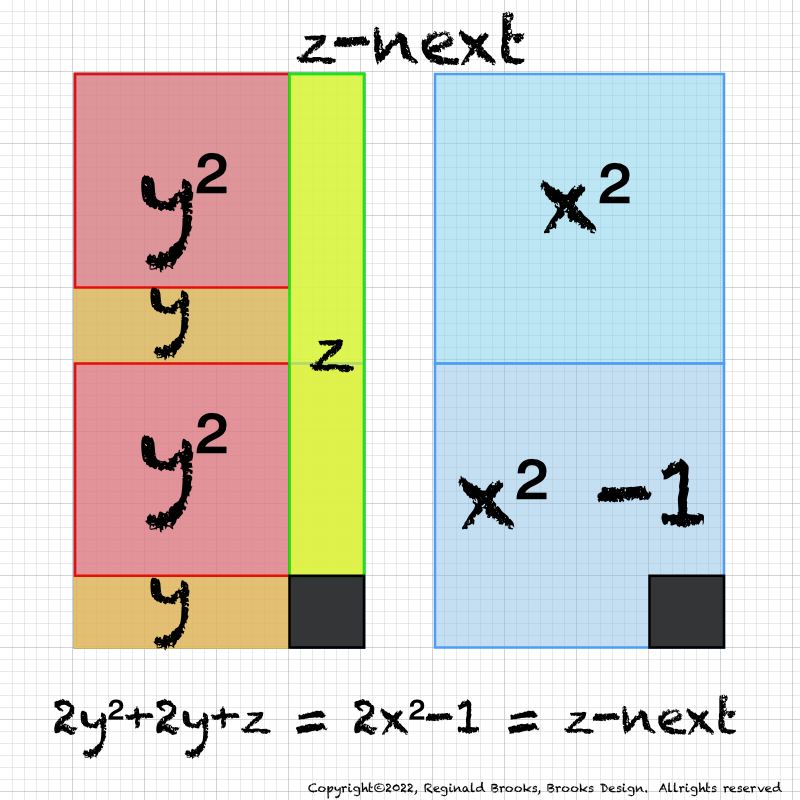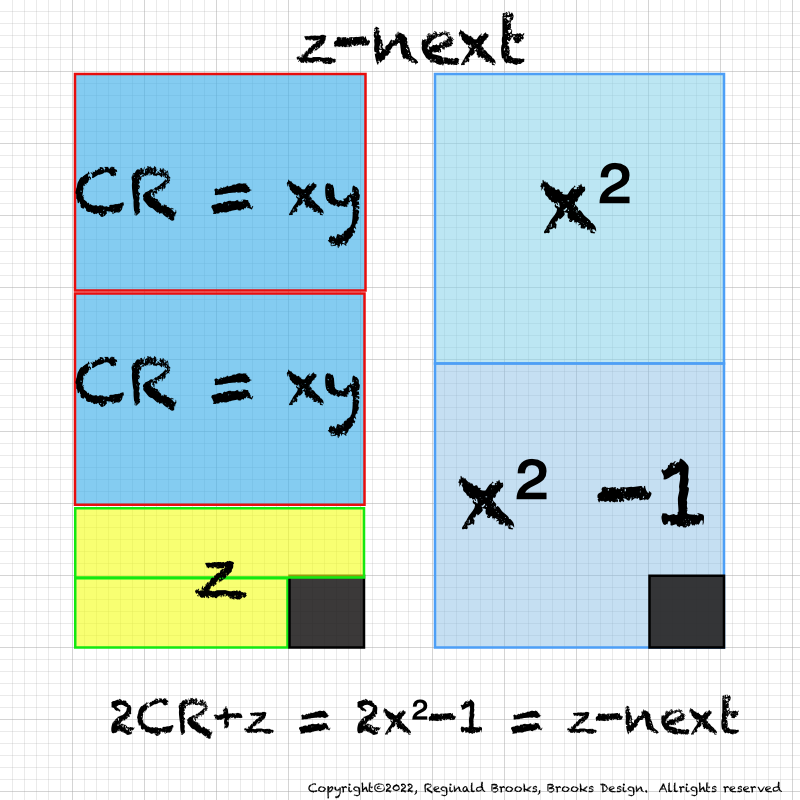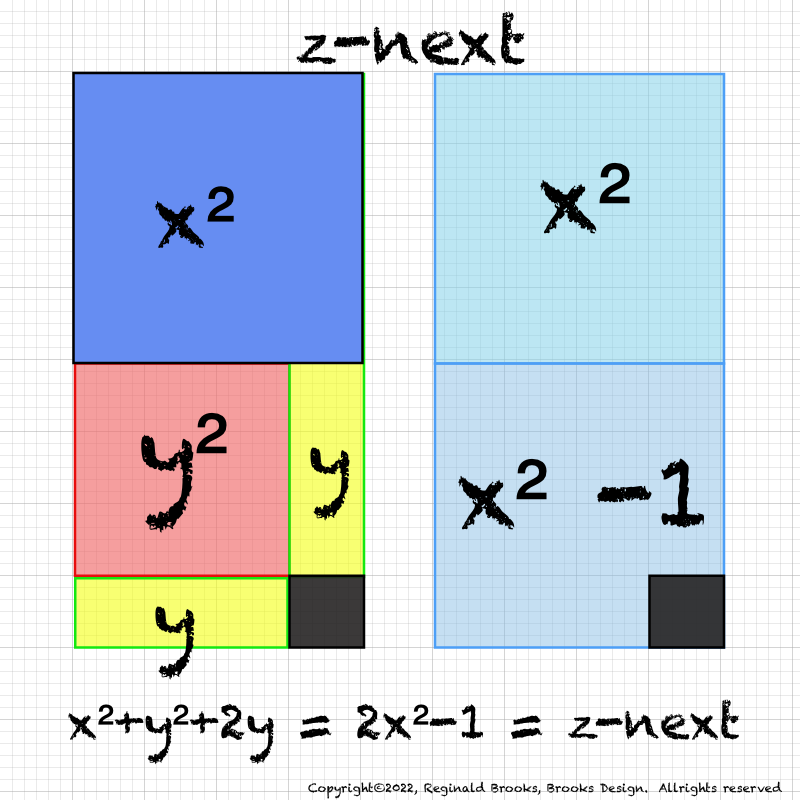CLICK for LINKS
The 10-Parameters section is an exciting finding! It means there are 10(+) common parameters on every "Diamond-shaped MPS that ALL the individual MPS follow.
It was not exactly a linear, straight-line discovery -- more of some visualizations on the BIM combined with some simple doodling while checking the numerous tables that related different parameters between various MPS and their containers.
We are going to present just a little of that early discovery before quickly diving right in to the 10(+) parameters.
We will be going from simple to advanced.
Like we often do, sometimes the exact same information will be presented in different forms.
A picture is worth a thousand words:
1-2-3-simple.gif
BIM50_AR-NAR-4-6.gif. BIM. BLACK=÷6; GREEN=z=Mersenne Prime; YELLOW=Active Row; RED=Non-Active Row=÷3; ORANGE=EVENS not÷4. ALL Pythagorean Triples and ALL PRIMES are found -- and only found -- on Active YELLOW Rows. Mersenne Primes appear to be found only on the larger of any YELLOW Active Row pair.
A subset of the Butterfly Matrix occurs in the whirling squares of the MPS.
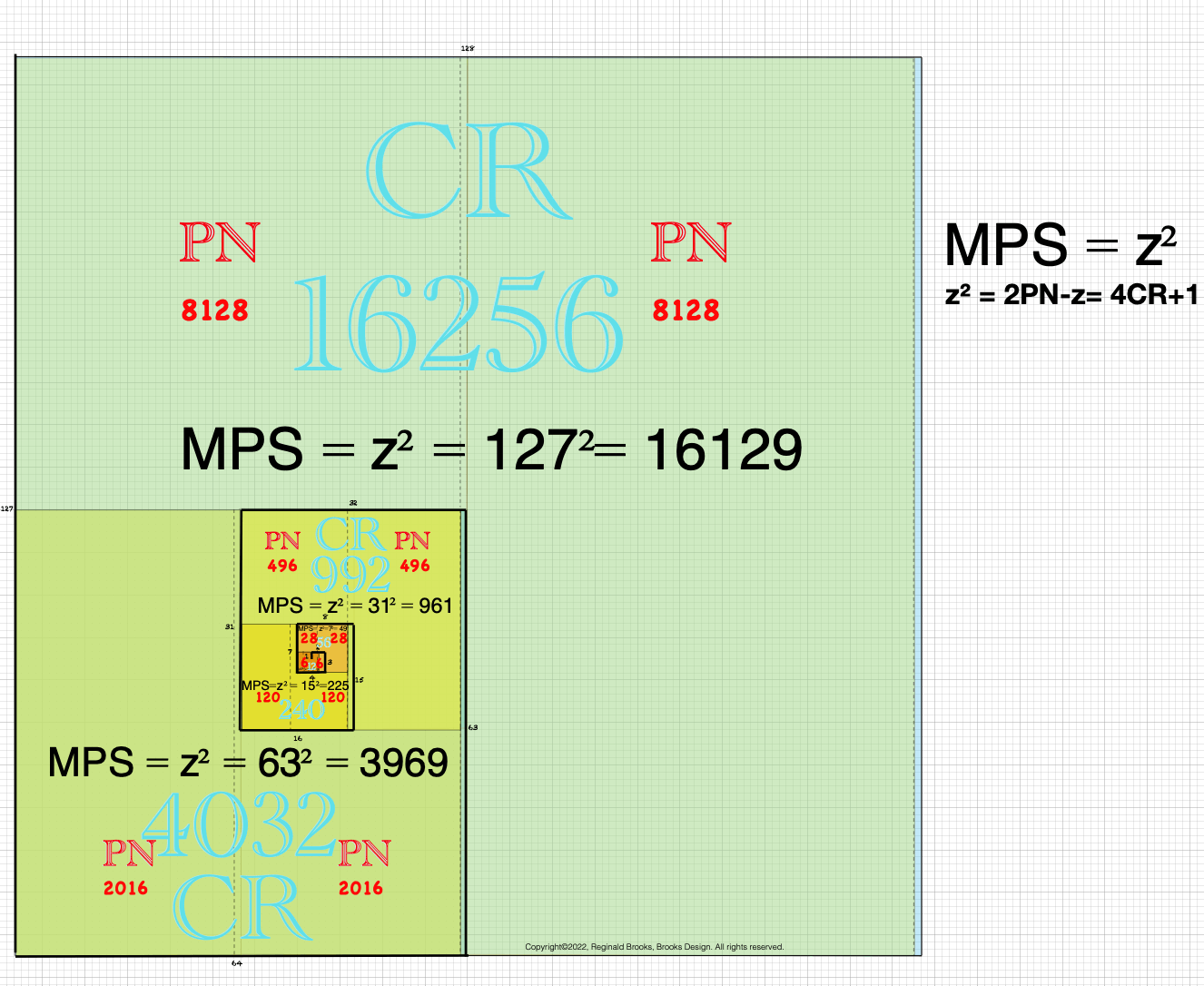
The Mersenne Prime Square (z2) equals 2PN-z.
It also equals 4CR+1.
This happens as every CR=2PN.
Other interesting connections between the MPS and its parts will be shown later on in the advanced sections of BIMMPS.
A picture is worth a thousand words:
BFMatrix.gif

Make_BFM-19.pdf. With the doubling of the EVENS alternating on the Vertical Axis, place the Running Sums (∑) of ODDS alternating on the Horizontal Axis. Start with "1" then 1+2=3, 3+4=7, 7+8=15,... On the diagonals, place the product of the corresponding Axis cells. Label one diagonal CR, the other PN.

BIMMPS9.pdf

BIMMPS10.pdf

BIMMPS11.pdf.
The Exponential Power of 2 as it interferes with the MPS on the BIM:plotting 2n on the BIM picks out all the Mp-PN "containers" by subtracting out "1" (moving back one Row). Within these "containers" will be found ALL the actual, true Mp=z and their paired PN=xz, as well as the rest of the 10 parameters that define the profile of each and every MPS. This includes the MPS-"container-only" profiles, as well. It is both highly visual and highly informative.

BIM-MPS_3DIAGONAL_Layout.pdf
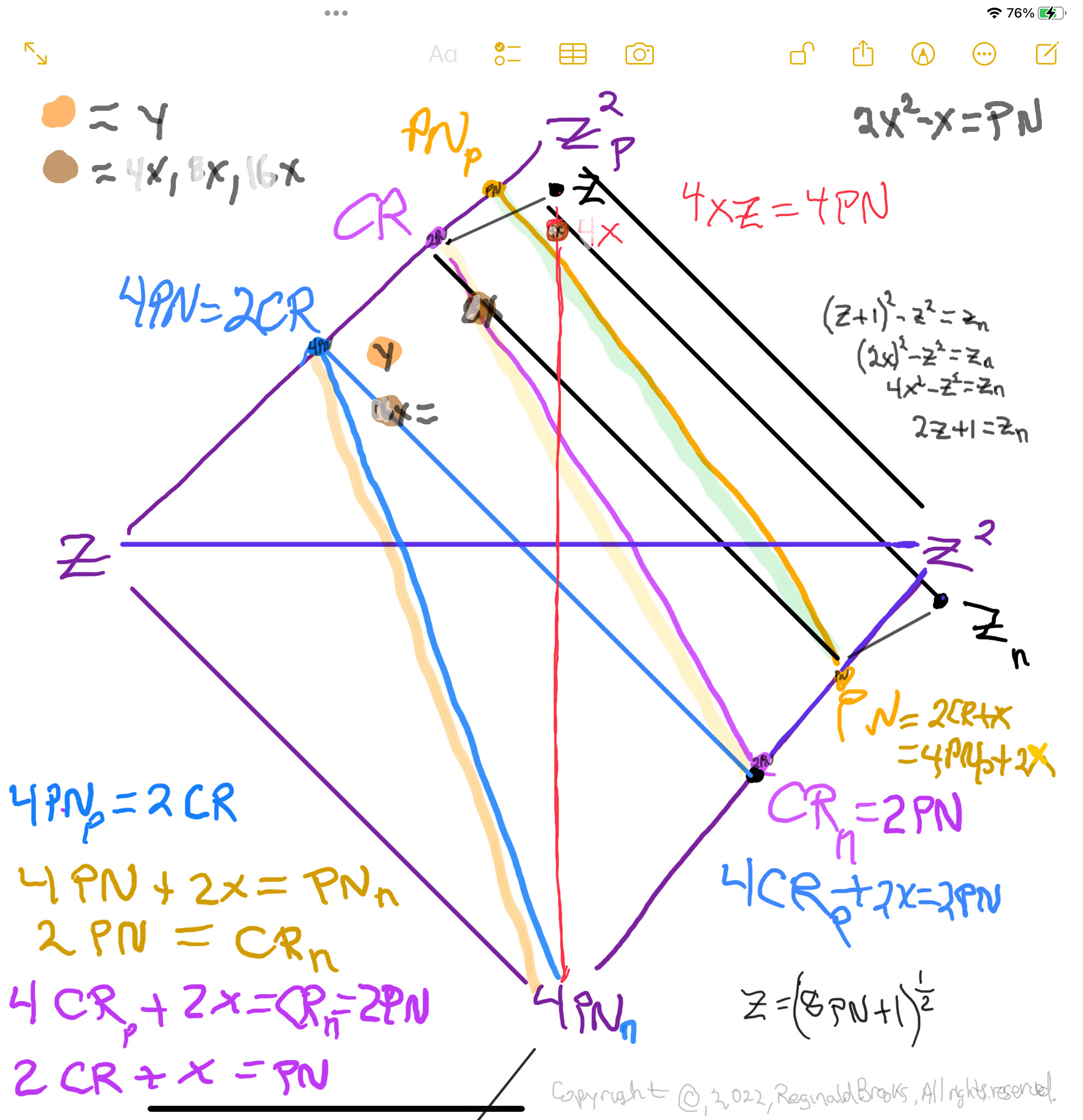
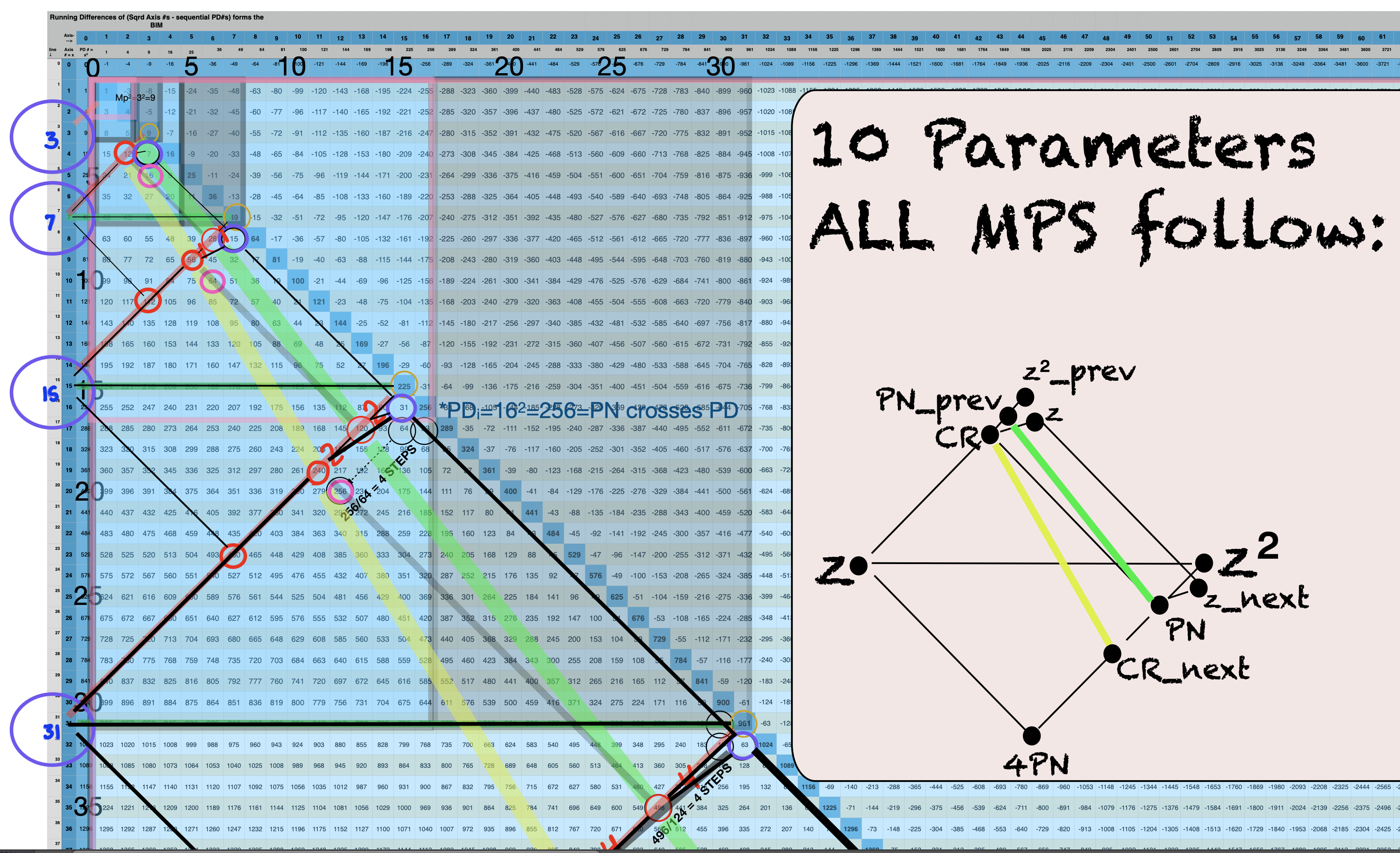
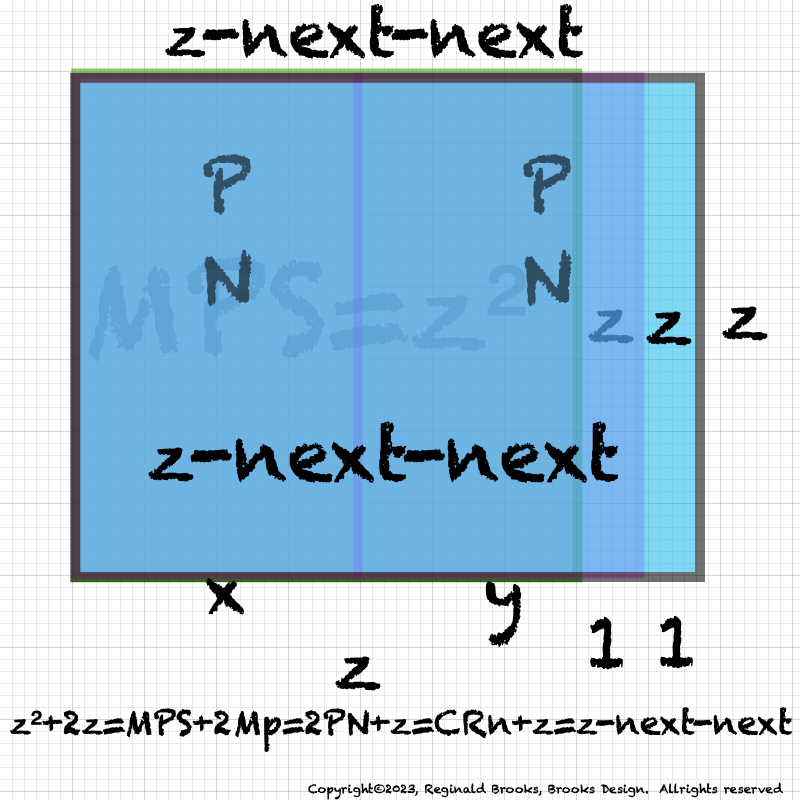
BIM150-MPS-10parametersAnnotate.jpg. Schematic of the 10-parameters within the Diamond-shaped MPS.
Transposing the Mersenne Prime Square (MPS) to a Diamond-shaped MPS (DMPS) on the BBS-ISL Matrix (BIM) reveals a whole new set of connections between the Mersenne Primes (Mp=z), Perfect Numbers (PN=x=2ᵖ⁻¹), Complement Rectangles (CR=xy, where y=x-1)… and their respective DMPS.
Every Mersenne Prime Square (MPS) when transposed to a Diamond shape (DMPS) on the BIM (BBS-ISL Matrix) will have this geometric configuration. While the numbers at the ends of each line may change (scale), they do so in a strictly fractal-ordered basis. The back edge informs the front edge — and — that front edge become the new back edge of the next larger DMPS, and so on.
Each subsequent DMPS is simply a larger fractal-based clone of its smaller (past) DMPS and informs its yet larger DMPS that follows (future). But they do this as Exponential Power of 2 — The Butterfly Fractal — “containers” as a necessary, but not sufficient, profile of a Mersenne Prime-Perfect Number, i.e. they are “containers” that hold all possible MPS, but only certain “containers” are actual Mersenne Prime-Perfect Number containers. The larger wave set is selectively interfered with the smaller wave set giving us the 51 known MP-PN.
Now here is something to scramble your mind — like Dylan’s lyric (Idiot Wind): “You’ll find out when you reach the top, you’re on the bottom.” — if the primes are the number atoms that all other composite numbers are made of, is not the above larger wave set that of the primes, the smaller set being the Exponential Power of 2?
Regardless, the fractal-based, relative relationship remains in tack — the one becomes the many.
The beauty of the numbers is that they give us all!
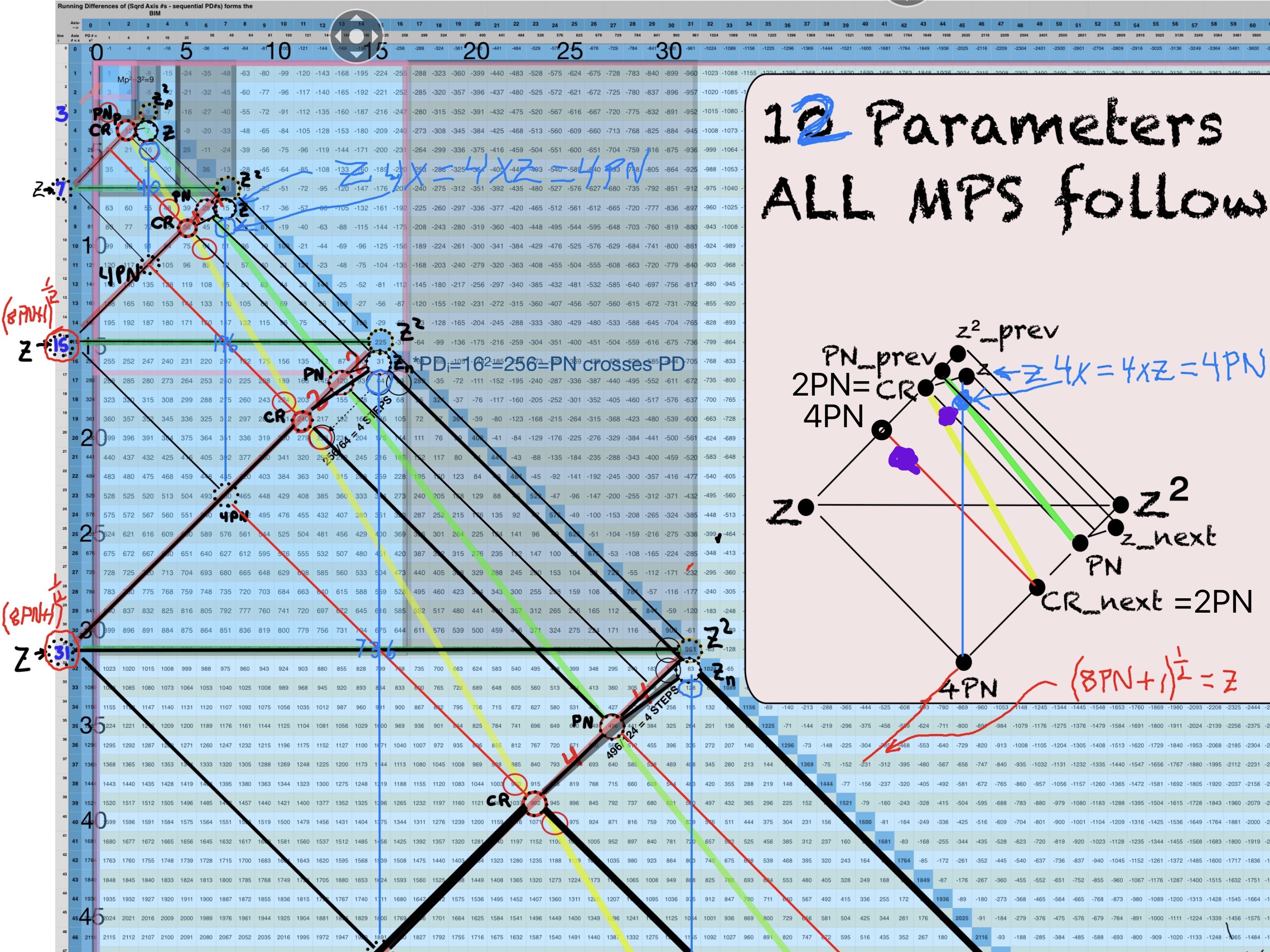
IMG_7457.jpg. Yes, there are actually more than 10 parameters, but it does get a bit busy!
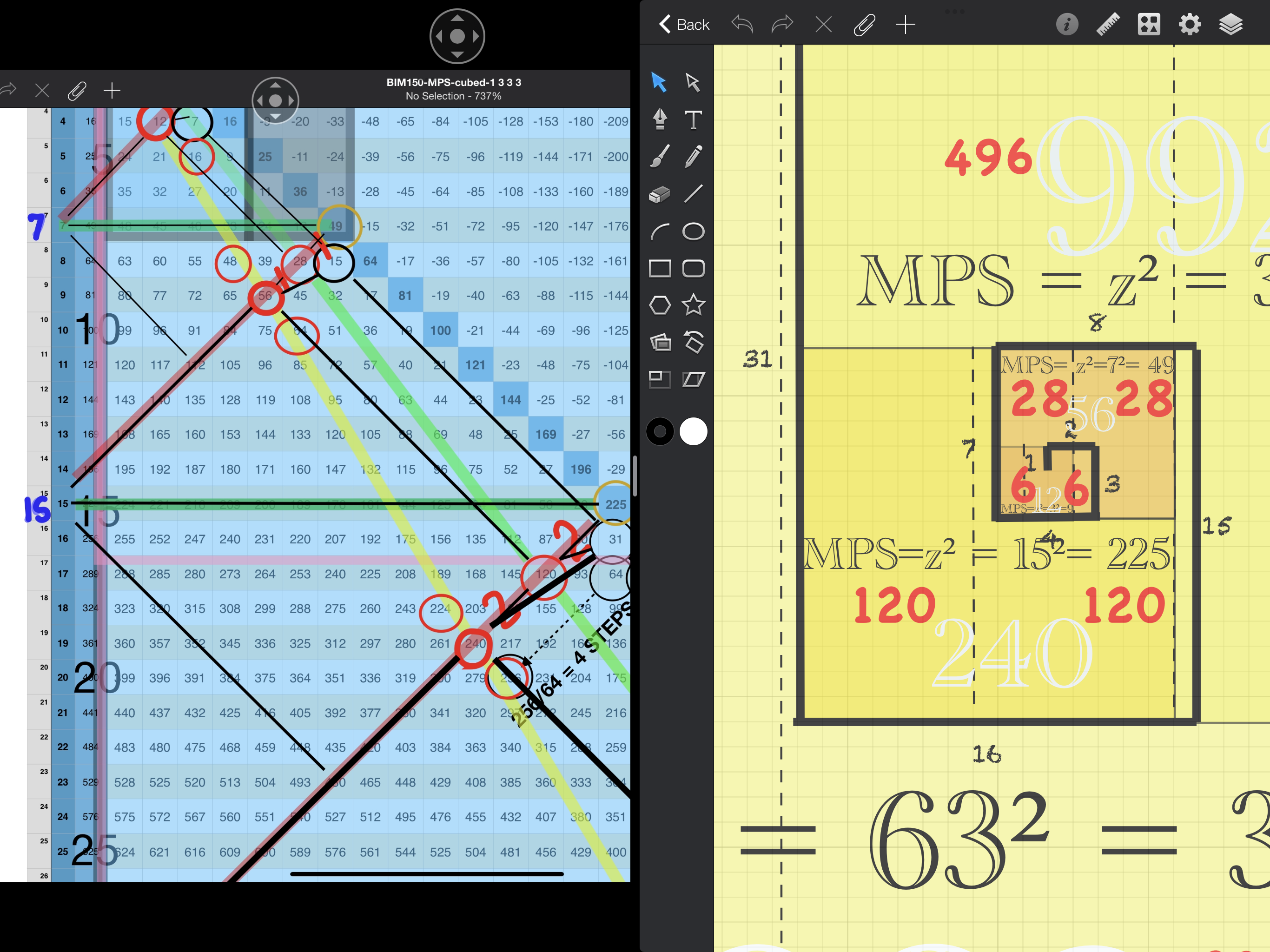 IMG_7271.png. Juxtaposing the BF Matrix next to the BIM shows how the former maps out on the BIM. Remember, every CR equals the doubling of the previous PN.
IMG_7271.png. Juxtaposing the BF Matrix next to the BIM shows how the former maps out on the BIM. Remember, every CR equals the doubling of the previous PN.
IMG_7271.png
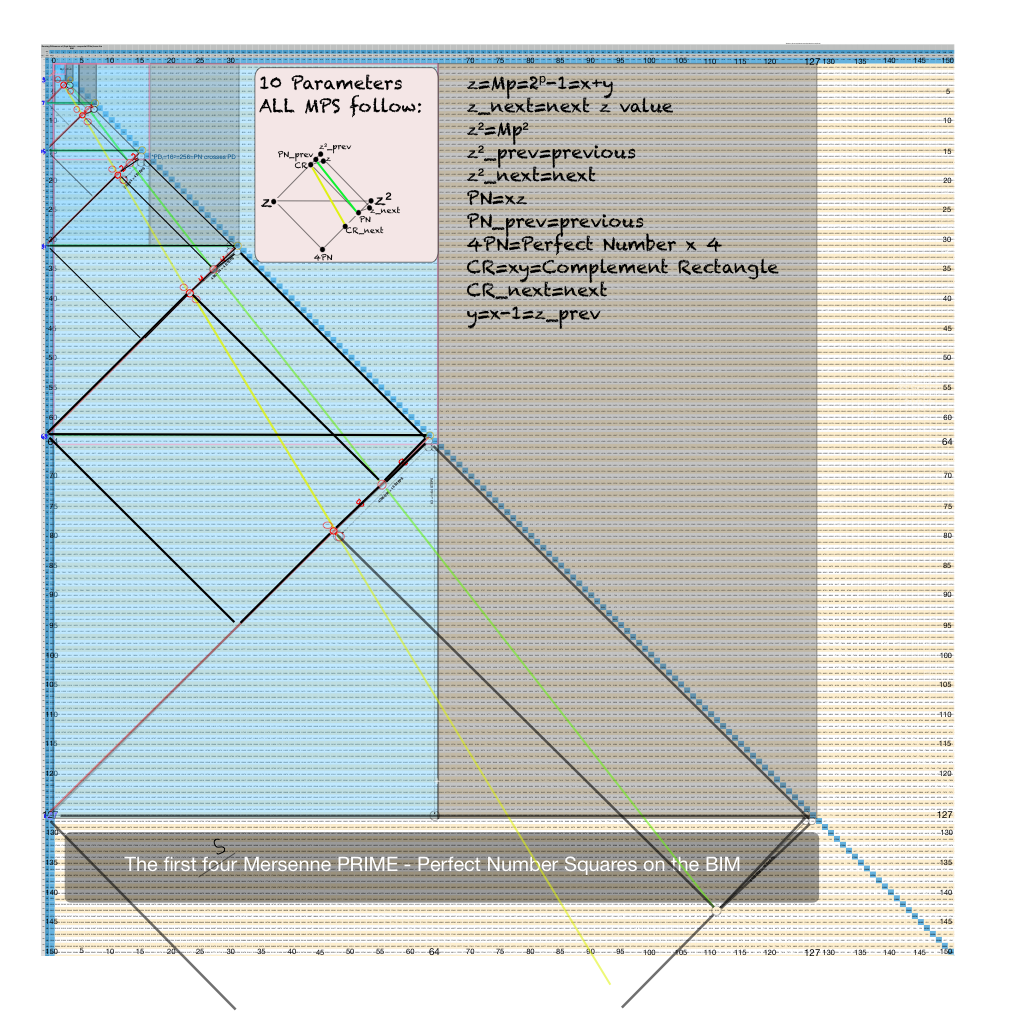
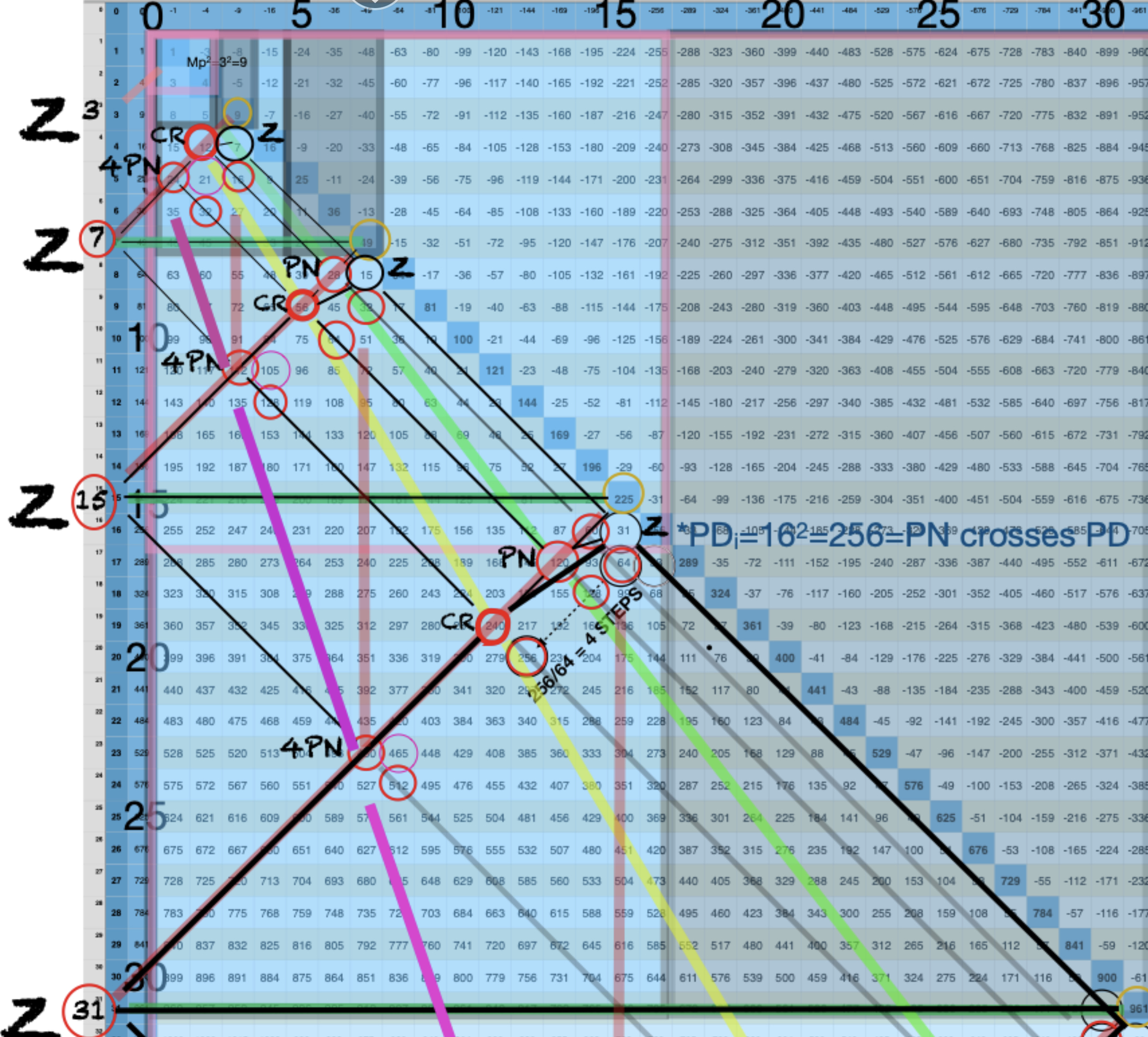
IMG_7266.png. Follow the pattern as each Diagonal that ends the previous (smaller) D-MPS becomes the start of the next (larger) one. The Number Pattern Sequence (NPS) remains the same for all D-MPS profiles.
10parametersMPS_detail.png

10parametersMPS.pdf
BIM150_10parameters0.jpg

BIM150-MPS-BF1_2.pdf

BIM150-MPS-10parameters+.pdf. Follow the pattern as each Diagonal that ends the previous (smaller) D-MPS becomes the start of the next (larger) one. The Number Pattern Sequence (NPS) remains the same for all D-MPS profiles.

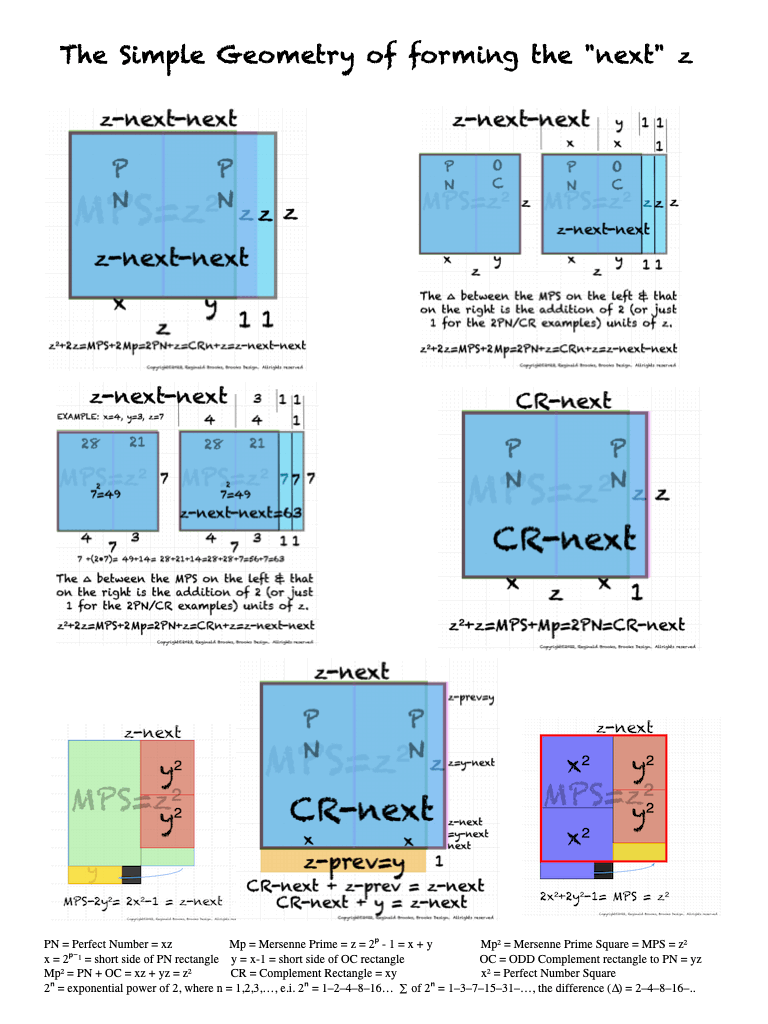
BIM150-MPS-CRnext.pdf. The GREEN and YELLOW Diagonal lines show the NPS connection between subsequent D-MPS "containers," some that will be actual, true MPS. The "containers" are required in the sense that in their absence, the NPS of the actual, true MPS becomes increasingly vague and ultimately lost as the size grows.

BIM150_10parametersSchematic 2.pdf

BIM150-MPS-BF1.pdf
IMG_1451 2.jpg
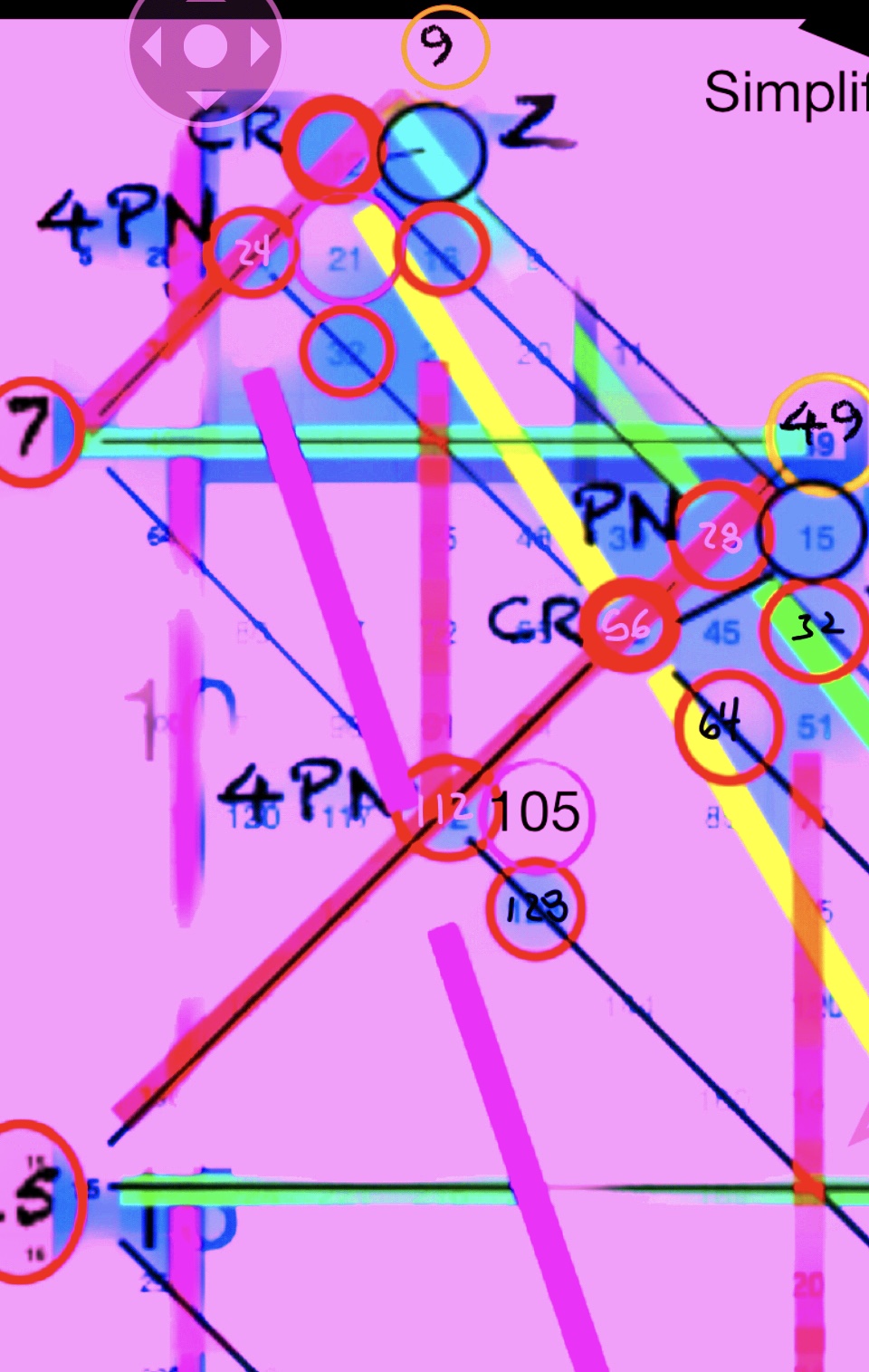
IMG_1451 2.jpg
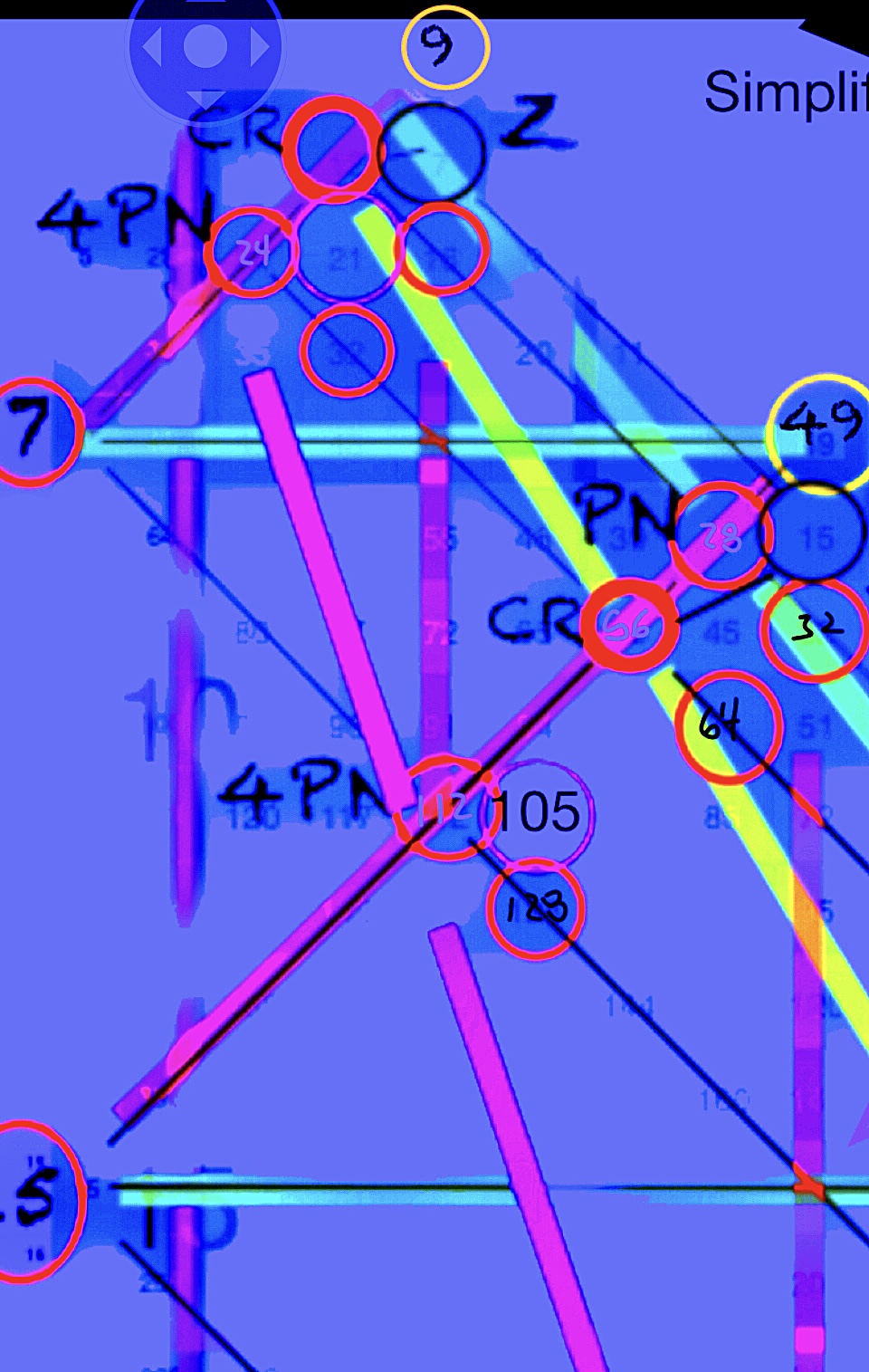
IMG_1451 3.jpg
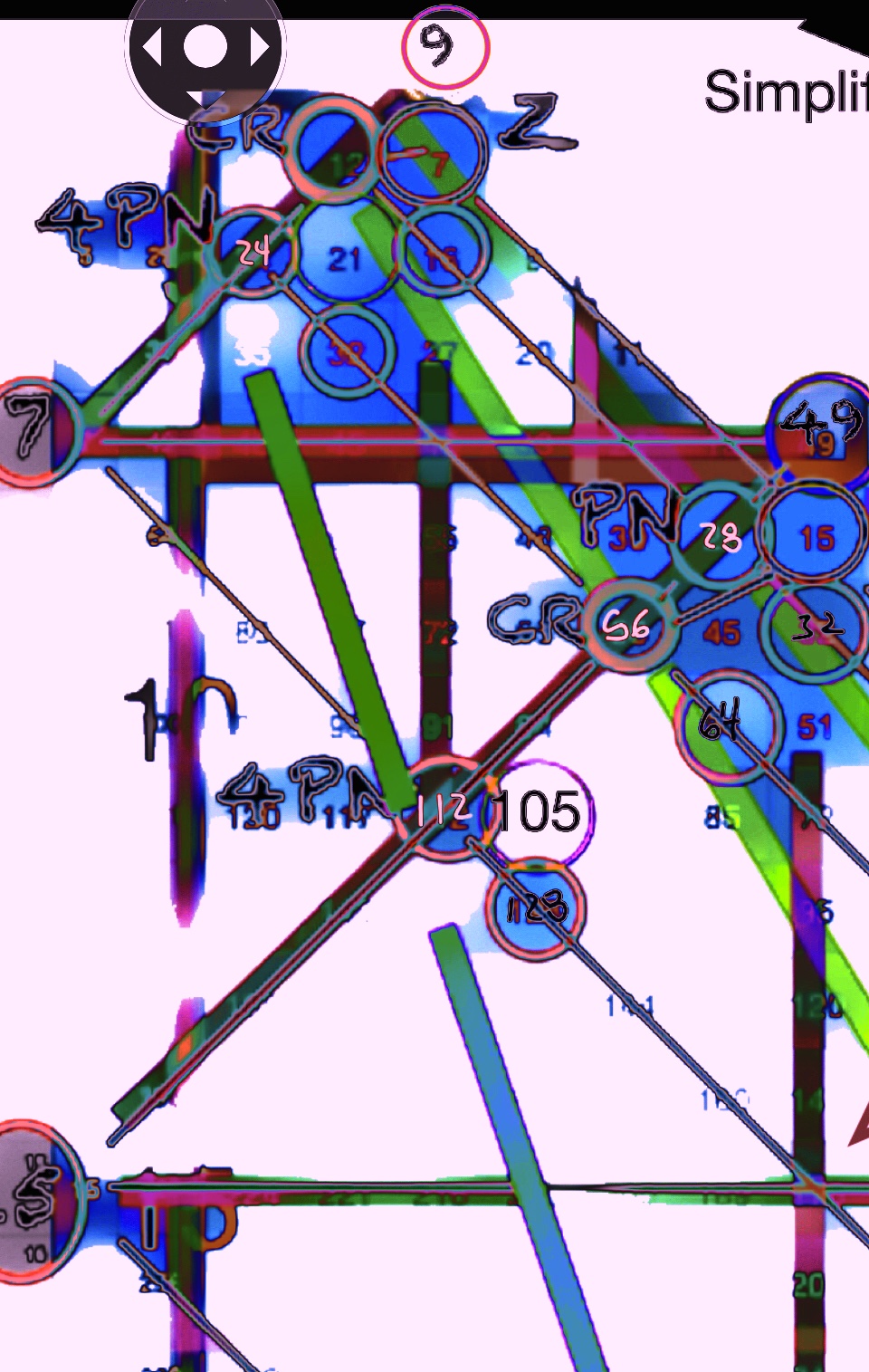
IMG_1451.jpg

BIM150x150_PTOFBMPPN-DMPS.pdf. Preview of the details to follow in the next section: PTOFBMPPN.
~~~ ~~~ ~~~ ~~~ ~~~ ~~~ ~~~ ~~~ ~~~ ~~~ ~~~ ~~~ ~~~ ~~~ ~~~ ~~~ ~~~ ~~~ ~~~ ~~~ ~~~ ~~~ ~~~ ~~~ ~~~ ~~~ ~~~ ~~~ ~~~ ~~~ ~~~ ~~~
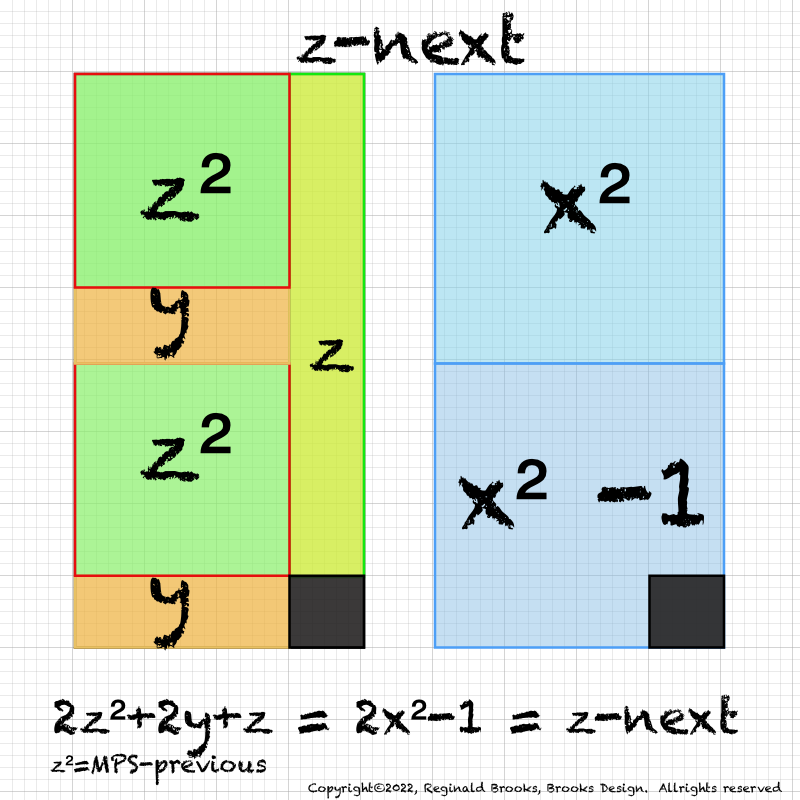
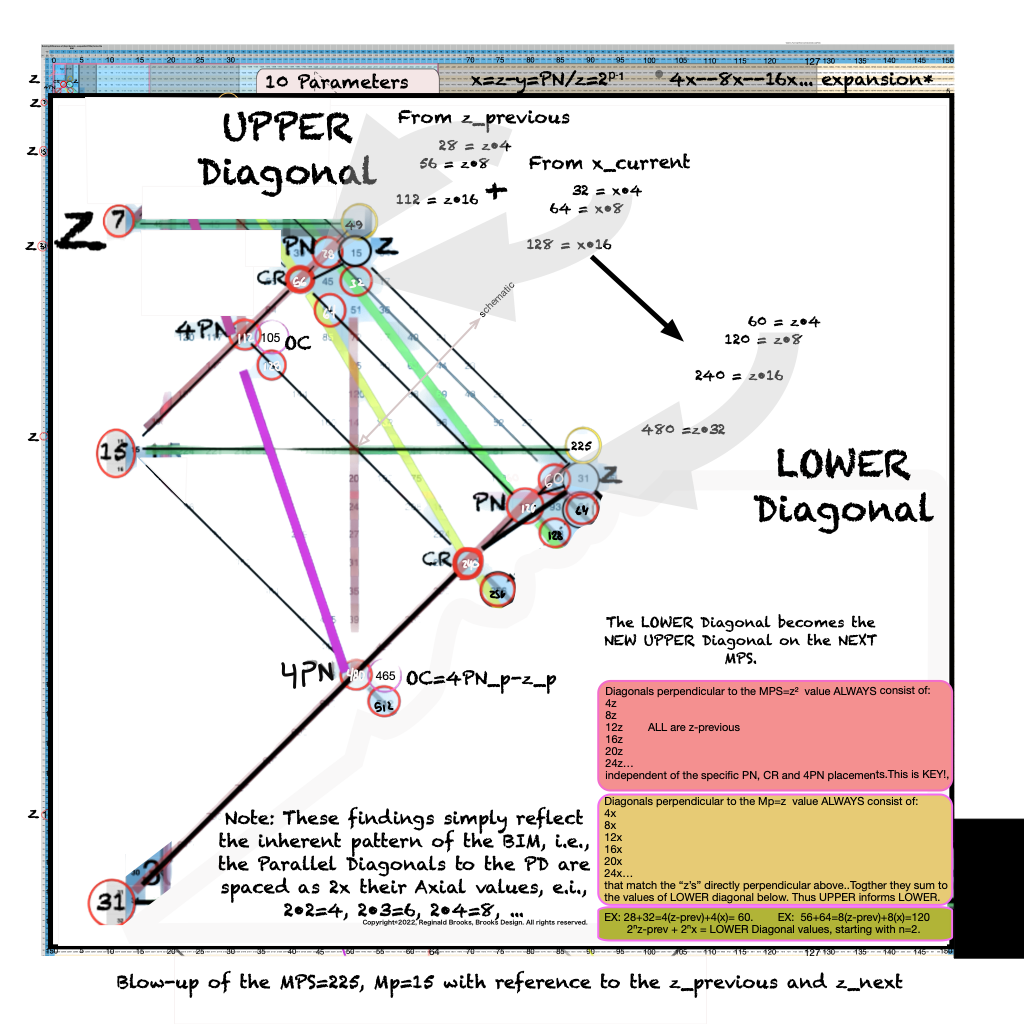
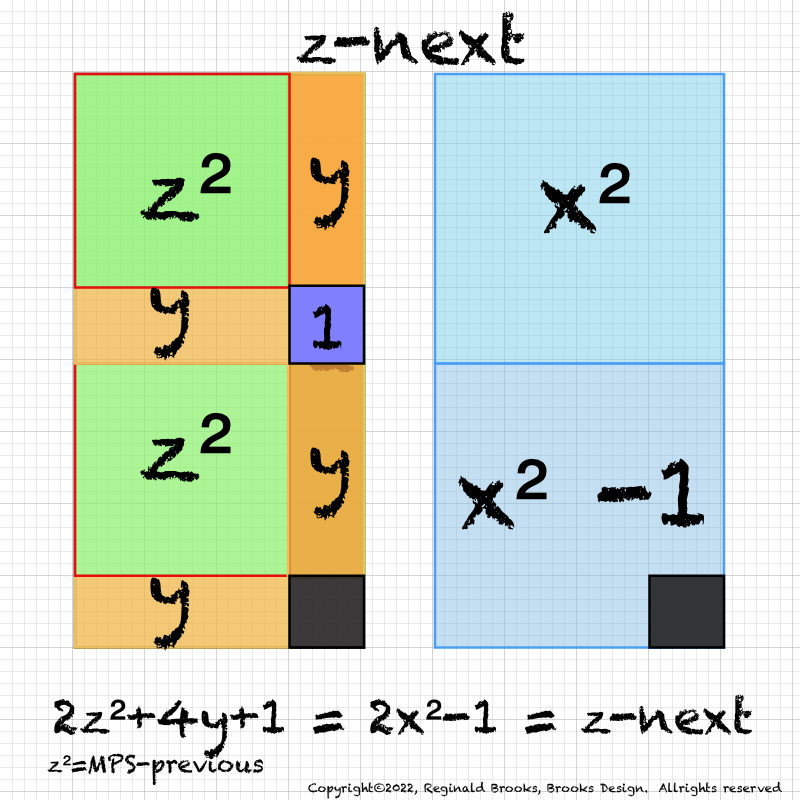
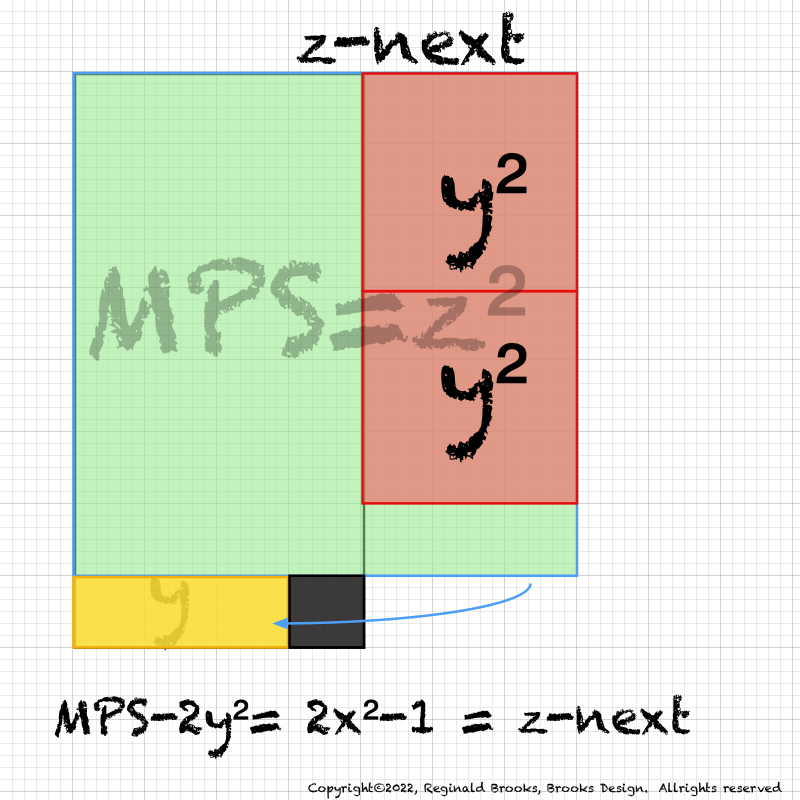
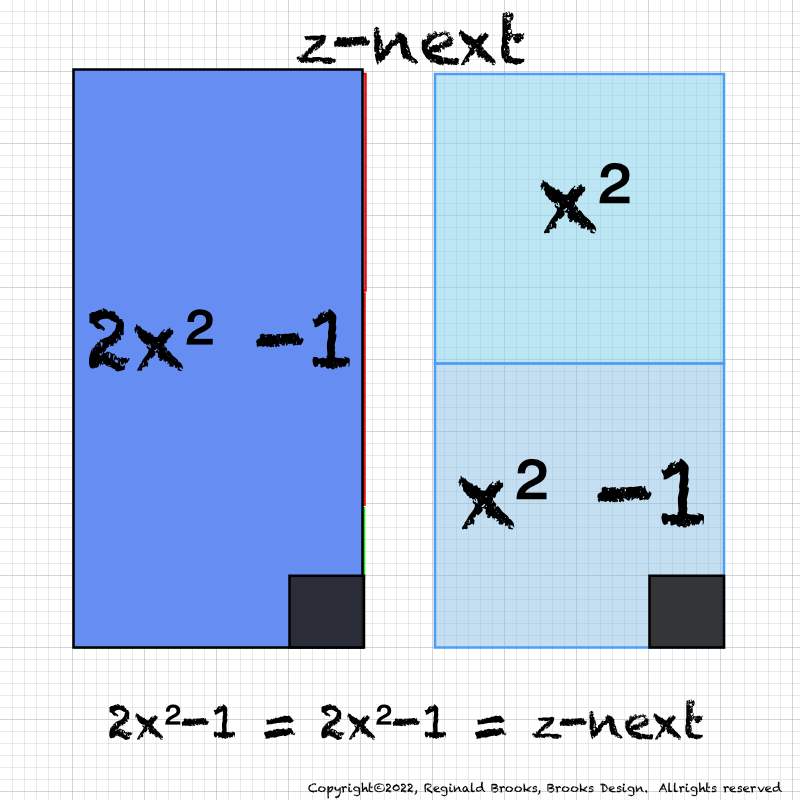
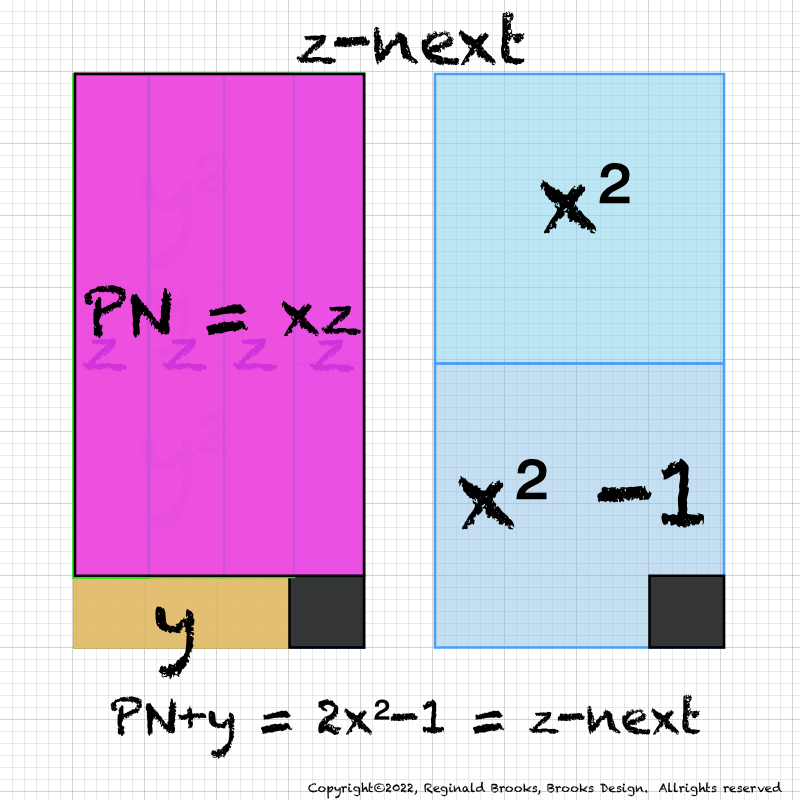
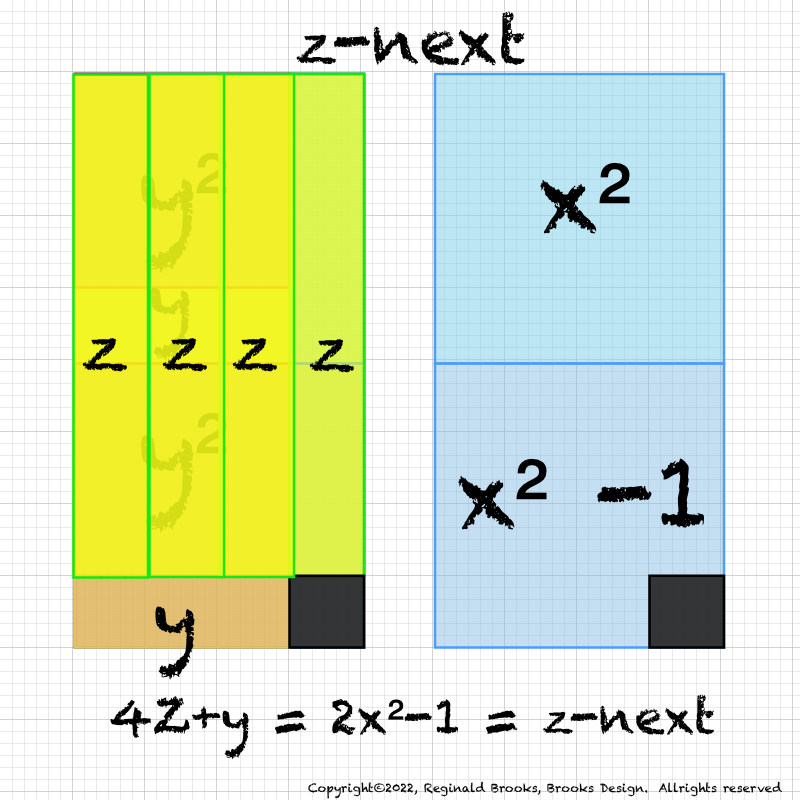
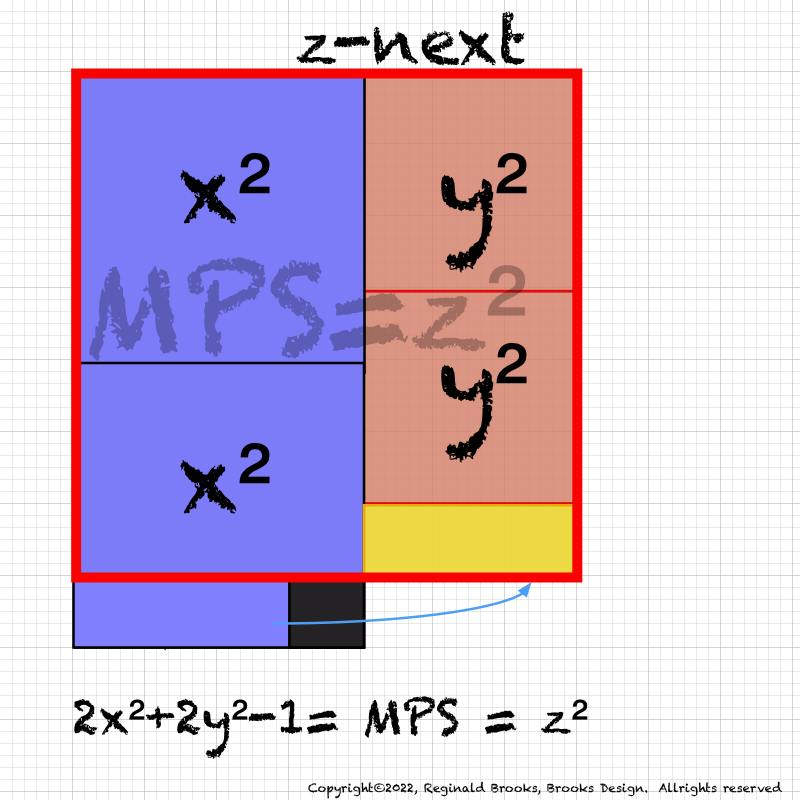
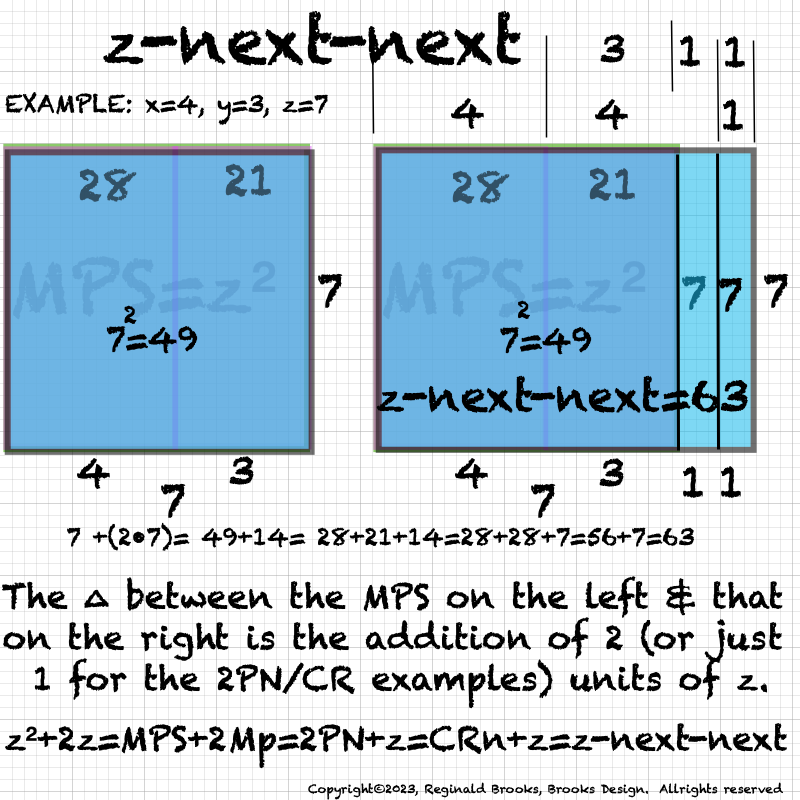
IMG_7076.PNG. What follows is highly informative visual simplification of the geometry of the MPS on the BIM series. The rectangle image (Light BLUE) on the right is a reference image of the geometry. It depicts doubling the PNS=x2 and subtracting 1, the resulting quantity (Area) equals the value of the next z=Mp. The mixed color rectangle image on the left is the one under examination. Here, 2z2 + 2y + z are equivalent to the reference on the right and thus also equal the next z = z-next. Study reaps great rewards!
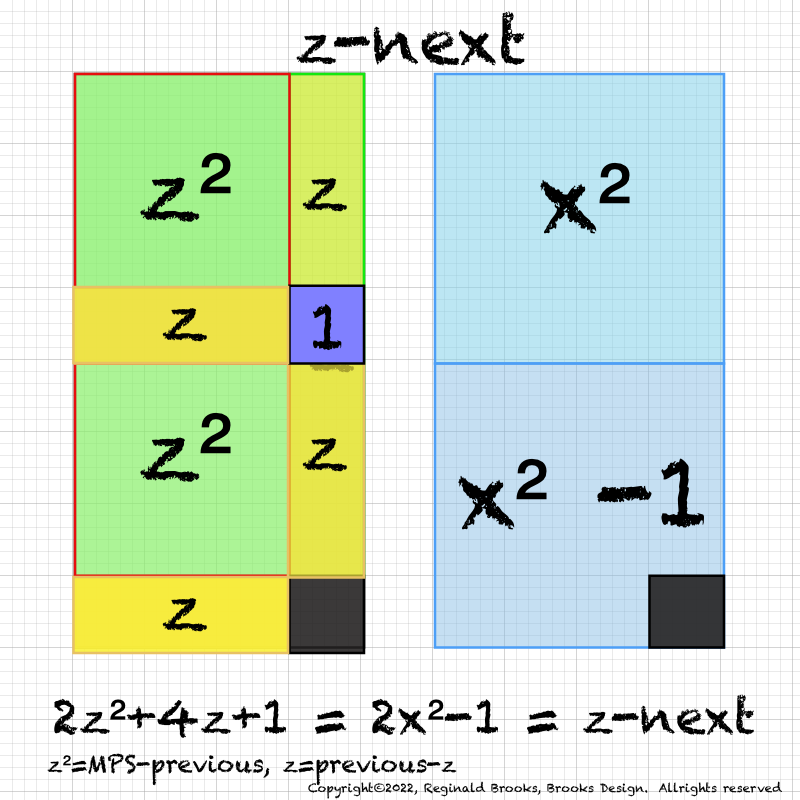
IMG_7078.PNG
IMG_7079.PNG
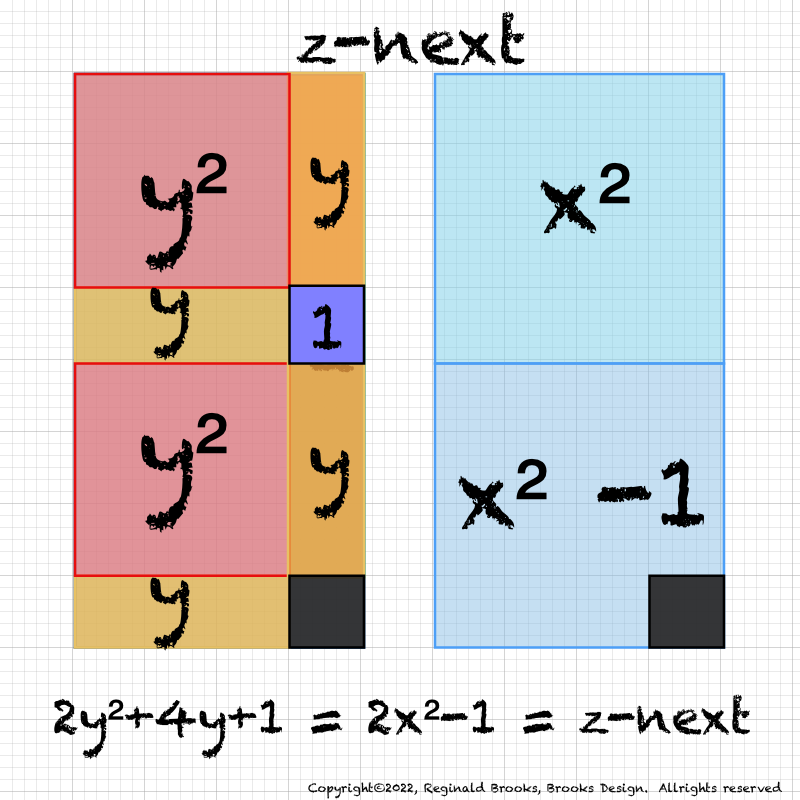
IMG_7081.PNG
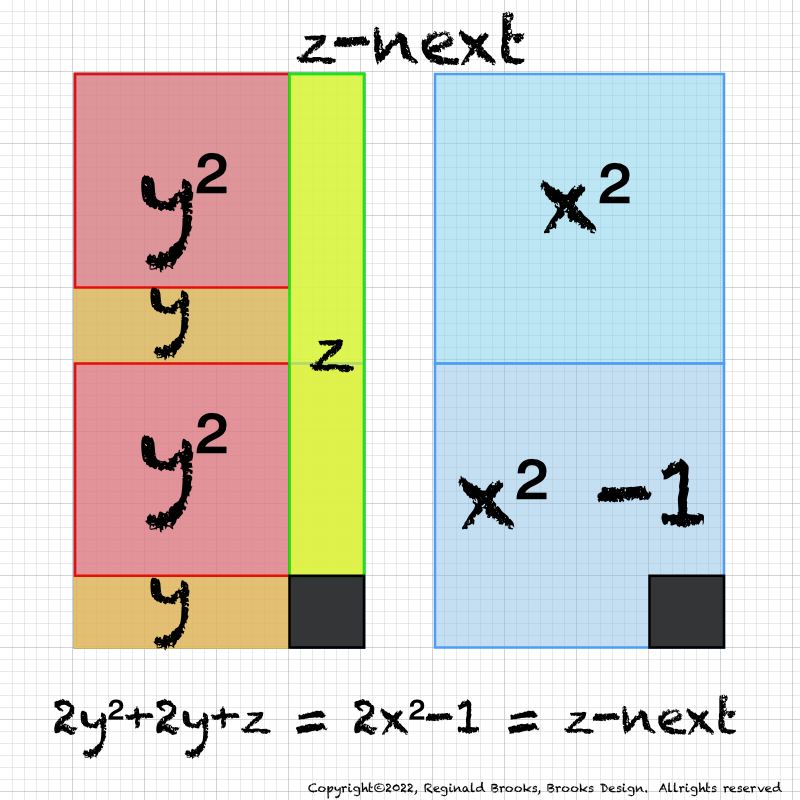
IMG_7082.PNG
IMG_7118.PNG
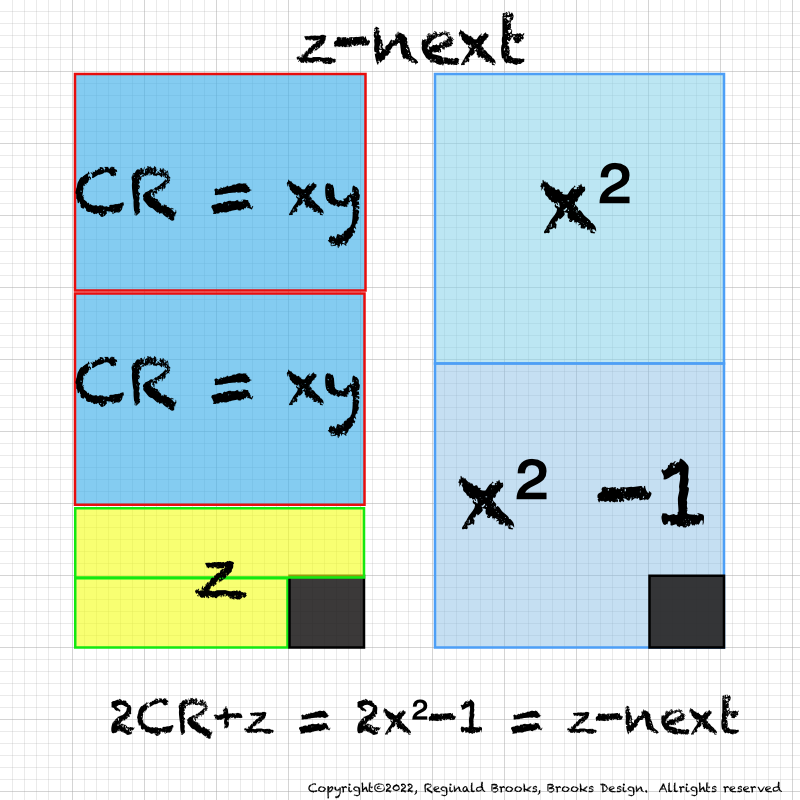
IMG_7085.PNG
IMG_7086.PNG
IMG_7084.PNG
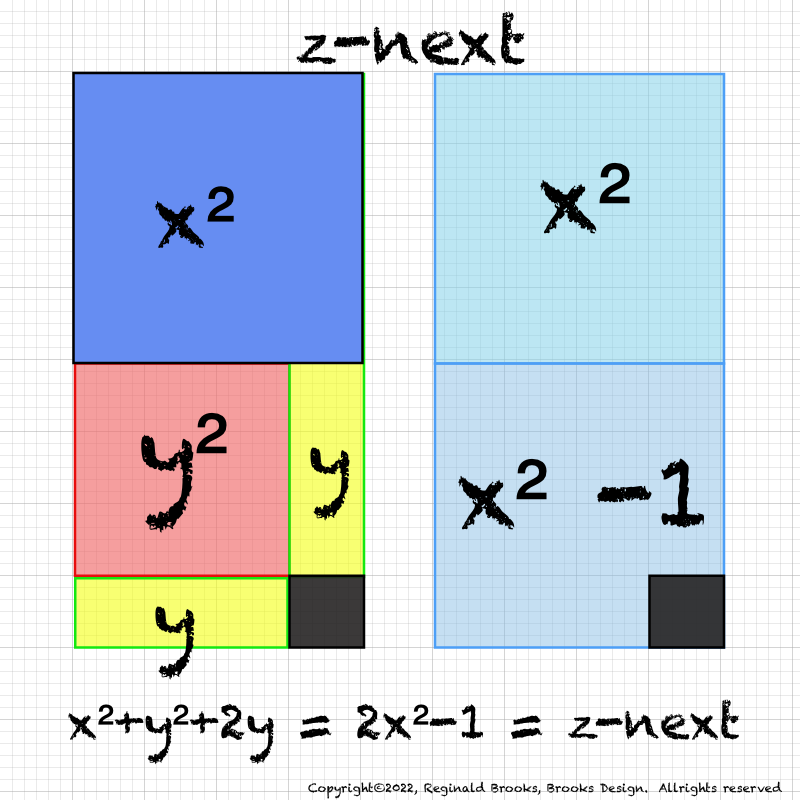
IMG_7117.PNG
IMG_7083.PNG
IMG_7119.PNG

Geometry_z-next_AREAS.pdf
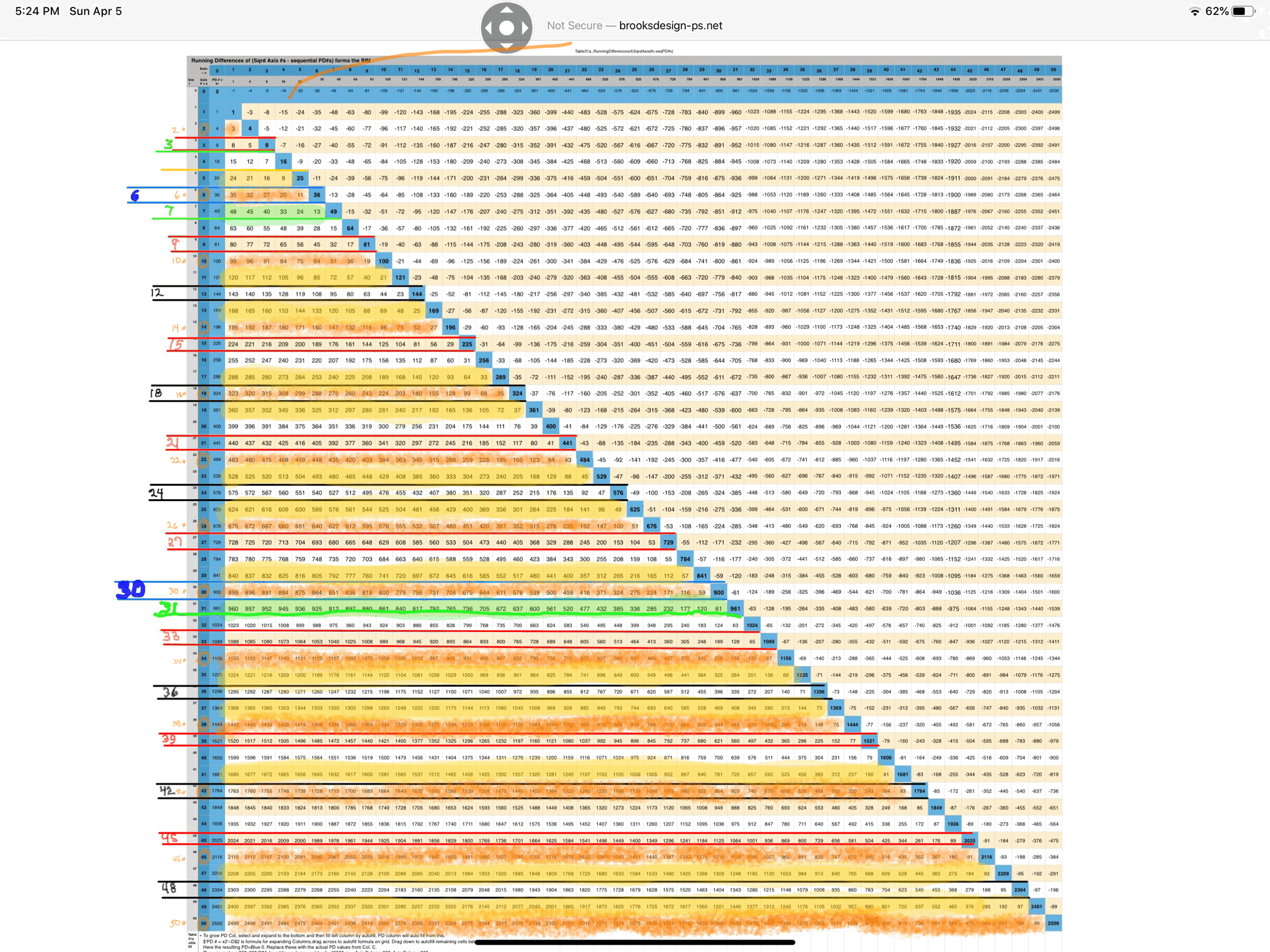
Tables often contain enormous amounts of data and their connections to each other. While "Tables" will be presented in a later section, Table 132a-e is worth a look now. Before resolving the geometries presented above, one connection after another of one piece of data tied to another kept coming up. It was only after placing it in table form did the more obvious solutions we see above come forth.
It is also that within the tables one sees the absolute requirement that ALL the "containers" be accounted for and included. The Number Pattern Sequences (NPS) of the MPS, Mp and PN parameters are dependent on this inclusion. And yes, this does mean including "p" values that are NOT Prime! That is the irony of the Primes to the Non-Primes, their NPS is not -- in any sense of the word -- obvious when treated as a separate group, but revealed within the larger set. One of the single most poignant revealations research on the Primes has brought out!
Speaking of "p" values: x=2p-1 which can be rewritten as x=2p/2. This translates to p=exponential that equals 2x as shown in the Tables 132 below. For example: let x=4, then 2x=8, and 2p solves for 8 when p=3. Another example, knowing now that 2x=2p, let's try it with x=64, then 2x=128=2p when p=7. Do remember that the "p" value also gives the number of fractal doubling levels for each respective Mp-PN-MPS set, e.i. if p=3, then there are 3 levels of R∑.
One can also solve for "p": As 2p=2x, take the logarithm of both sides, fill in the value of "x" and solve as p = ln(2x)/ln(2).
p = ln(2x)/ln(2)

Table132a_next_z-.pdf

Table132b_next_z.pdf

Table132c_next_z&x.pdf

Table132d_next_2PN=CRnext.pdf

Table132e_next_2PN=CRnext_2CR.pdf
In the meantime, here is another tidbit:
GeoAREAS_4-13.png
GeoAREAS_4-14.png
GeoAREAS_4-15.png
GeoAREAS_4-16.png
GeoAREAS_4-17.png
Geometry_z-next_AREAS-2.gif
What happens when you mix it up just a bit, leaving all other parameters in tack? What if y equals x+1, as y=x+1, instead of its real value of y=x-1?
In our example from above, x=4 and y previously equals 3, but now let y=x+1=4+1=5.
The yz=OC=5•7=35
Then PN + OC = 28+35=63
A smaller example, MPS=9, Mp=z=3, PN=xz=2•3=6 and the original OC=yz=1•3=3. Now change y from 1 to 3, then:
The yz=OC=3•3=9
Then PN + OC = 6+9=15
A larger example, MPS=225, Mp=z=15, PN=xz=8•15=120 and the original OC=yz=7•15=105. Now change y from 7 to 9, then:
The yz=OC=9•15=135
Then PN + OC = 120+135=255
A larger yet example, MPS=961, Mp=z=31, PN=xz=16•31=496 and the original OC=yz=15•31=465. Now change y from 15 to 17:
The yz=OC=17•31=527
Then PN + OC = 496+527=1023
What is happening here? Are we not just adding 2 units of "z" to the existing MPS? These skewed results nevertheless offer some interesting results.
The 15–63–255–1023 and the next one would 4095, are the y and/or y-container values!
A deep dive into the "Tables" section in the Appendix may help sort this one out. And what will become even more apparent in the Tables is that "z" and "y" share the same container space parameters (as do x and x2). This intriguing finding is a double-edged sword in the categorical sense. One difference to always keep in mind is that the actual Mp=z is a PRIME and never divisible by 3, while the "y" are always divisible by 3.
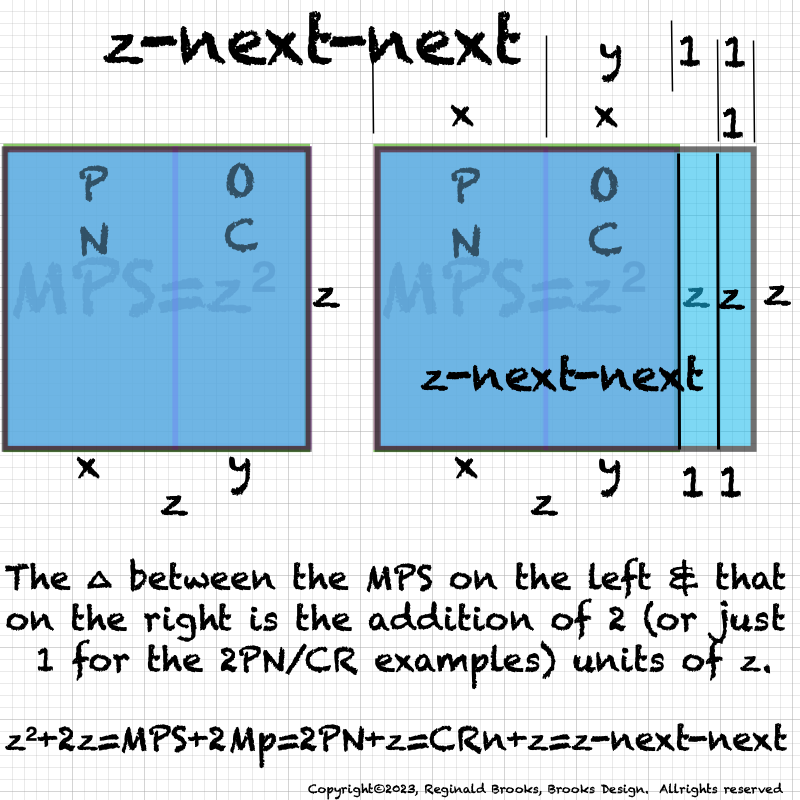
So if adding 2 units of "z" gives us new parameter information, what if we simple add 1 unit of "z" instead?
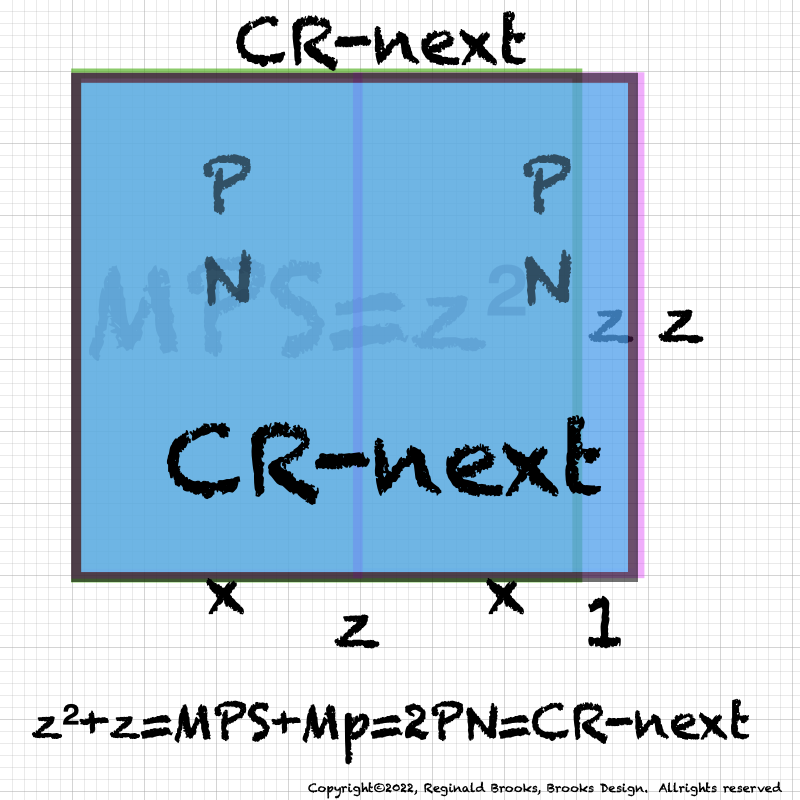
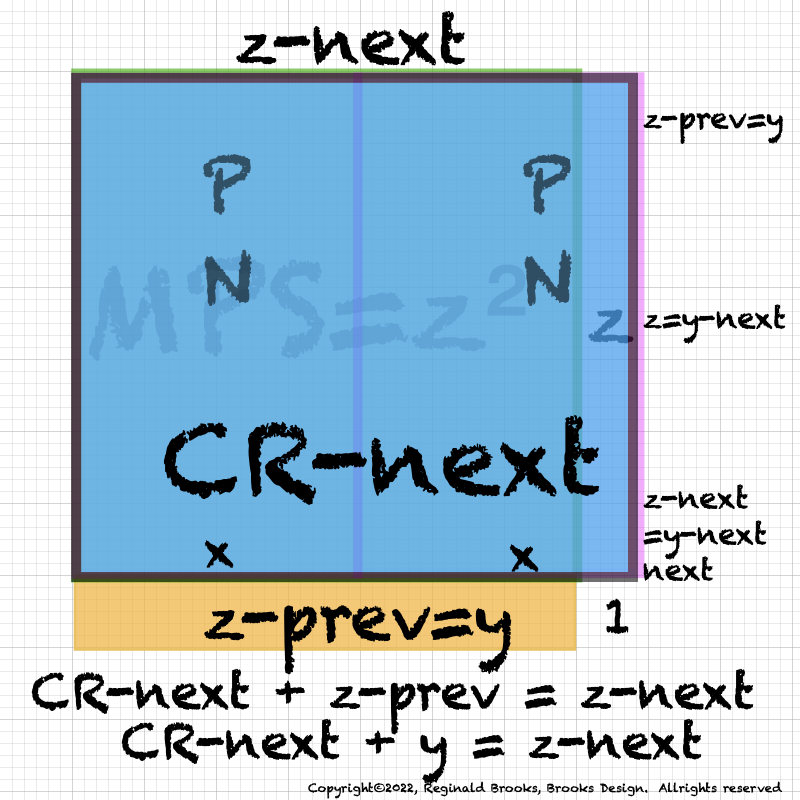
ANSWER: it gives the next CR! That's right, it gives CR-next (CRn) as shown in the middle and lower images in the graphic above.
NEXT: BOOK V: Periodic Table of Fractal-based Mersenne Prime - Perfect Numbers (PTOFBMPPN)
LINKS:
Mersenne Prime Squares (Part I) the Introductory white paper.
Mersenne Prime Squares (Part II) 3 Simple Intros.
Mersenne Prime Squares (Part III) the Advanced white paper.
The MPS Project The Mersenne Prime Squares Project.
LINKS:MathspeedST: TPISC Media Center
MathspeedST: eBook (free)
Apple Books
Artist Link in iTunes Apple Books Store:
Reginald Brooks
 KEYWORDS TAGS:
BMP, BIM-MersenneSquare-PerfectNumber, Mersenne Primes, Mersenne Prime Square, Perfect Number, Perfect Square, MPS, Mp, PTOP, Periodic Table Of PRIMES, PRIMES vs NO-PRIMES, algebraic geometry, BIM, TPISC, The Pythagorean - Inverse Square Connections, Pythagorean Triangles, DNA, Zika virus, pentagon, decagon, double pentagon, composite axial DNA double-helix, Pythagorean Triples, primitive Pythagorean Triples, non-primitive Pythagorean Triples, Pythagorean Theorem, Pythagorus Theorem, The Dickson Method, BBS-ISL Matrix, Expanded Dickson Method, r-sets, s-set, t-sets, Pair-sets, geometric proofs, MathspeedST, leapfrogging LightspeedST FASTER than the speed of light, Brooks (Base) Square- Inverse Square Law (ISL), BBS-ISL Matrix grid, The Architecture Of SpaceTime (TAOST), The Conspicuous Absence Of Primes (TCAOP), A Fresh Piece Of Pi(e), AFPOP, Numbers of Inevitability, LightspeedST, Teachers, Educators and Students (TES), number theory, ubiquitous information, FASTER than the speed of light, primes, prime numbers, fractals, mathematics, Universe, cosmos, patterns in number, DSEQEC, Double-Slit Experiment-Quantum Entanglement Conjecture, CaCost, Creation and Conservation of SpaceTime.
KEYWORDS TAGS:
BMP, BIM-MersenneSquare-PerfectNumber, Mersenne Primes, Mersenne Prime Square, Perfect Number, Perfect Square, MPS, Mp, PTOP, Periodic Table Of PRIMES, PRIMES vs NO-PRIMES, algebraic geometry, BIM, TPISC, The Pythagorean - Inverse Square Connections, Pythagorean Triangles, DNA, Zika virus, pentagon, decagon, double pentagon, composite axial DNA double-helix, Pythagorean Triples, primitive Pythagorean Triples, non-primitive Pythagorean Triples, Pythagorean Theorem, Pythagorus Theorem, The Dickson Method, BBS-ISL Matrix, Expanded Dickson Method, r-sets, s-set, t-sets, Pair-sets, geometric proofs, MathspeedST, leapfrogging LightspeedST FASTER than the speed of light, Brooks (Base) Square- Inverse Square Law (ISL), BBS-ISL Matrix grid, The Architecture Of SpaceTime (TAOST), The Conspicuous Absence Of Primes (TCAOP), A Fresh Piece Of Pi(e), AFPOP, Numbers of Inevitability, LightspeedST, Teachers, Educators and Students (TES), number theory, ubiquitous information, FASTER than the speed of light, primes, prime numbers, fractals, mathematics, Universe, cosmos, patterns in number, DSEQEC, Double-Slit Experiment-Quantum Entanglement Conjecture, CaCost, Creation and Conservation of SpaceTime.
| PIN: Pattern in Number...from primes to DNA. | PIN: Butterfly Primes...let the beauty seep in. | PIN: Butterfly Prime Directive...metamorphosis. | PIN: Butterfly Prime Determinant Number Array (DNA) ~conspicuous abstinence~. | GoDNA: the Geometry of DNA (axial view) revealed. | SCoDNA: the Structure and Chemistry of DNA (axial view). | The LUFE Matrix | The LUFE Matrix Supplement | The LUFE Matrix: Infinite Dimensions | The LUFE Matrix: E=mc2 | Dark Matter=Dark Energy | The History of the Universe in Scalar Graphics | The History of the Universe_update: The Big Void | Quantum Gravity ...by the book | The Conservation of SpaceTime | LUFE: The Layman's Unified Field Expose` | GoMAS: The Geometry of Music, Art and Structure ...linking science, art and esthetics. Part I | Brooks (Base) Square (BBS): The Architecture of Space-Time (TAOST) and The Conspicuous Absence of Primes (TCAOP) - a brief introduction to the series | more White Papers...
|
|
|
| net.art index | netart01: RealSurReal...aClone, 2001 | netart02: Hey!Ufunk'n with my DNA? | netart03: 9-11_remembered | netart04: Naughty Physics (a.k.a. The LUFE Matrix) | netart05: Your sFace or Mine? | netart06: Butterfly Primes | netart07: Music-Color-ISL | netart08: BBS-ISL matrix | netart09: BBS-interactive (I) | netart10: Sunspots and Solar Flares | netart11: Music-Color-ISL (II-III) | Art Theory 101: PIN, DNA, LUFE Matrix, GoMAS, BBS index | home
| Art Theory 101 / White Papers Index
|
Copyright 2021-23, Reginald Brooks, Brooks Design. All rights reserved.
|
|
iTunes, iTunes Store, Apple Books, iBooks, iBooks Store, iBooks Author, Mac OS are registered® trademarks of Apple Inc. and their use on this webpage does not reflect endorsement by Apple Inc.
|
TOP











 IMG_7271.png. Juxtaposing the BF Matrix next to the BIM shows how the former maps out on the BIM. Remember, every CR equals the doubling of the previous PN.
IMG_7271.png. Juxtaposing the BF Matrix next to the BIM shows how the former maps out on the BIM. Remember, every CR equals the doubling of the previous PN.