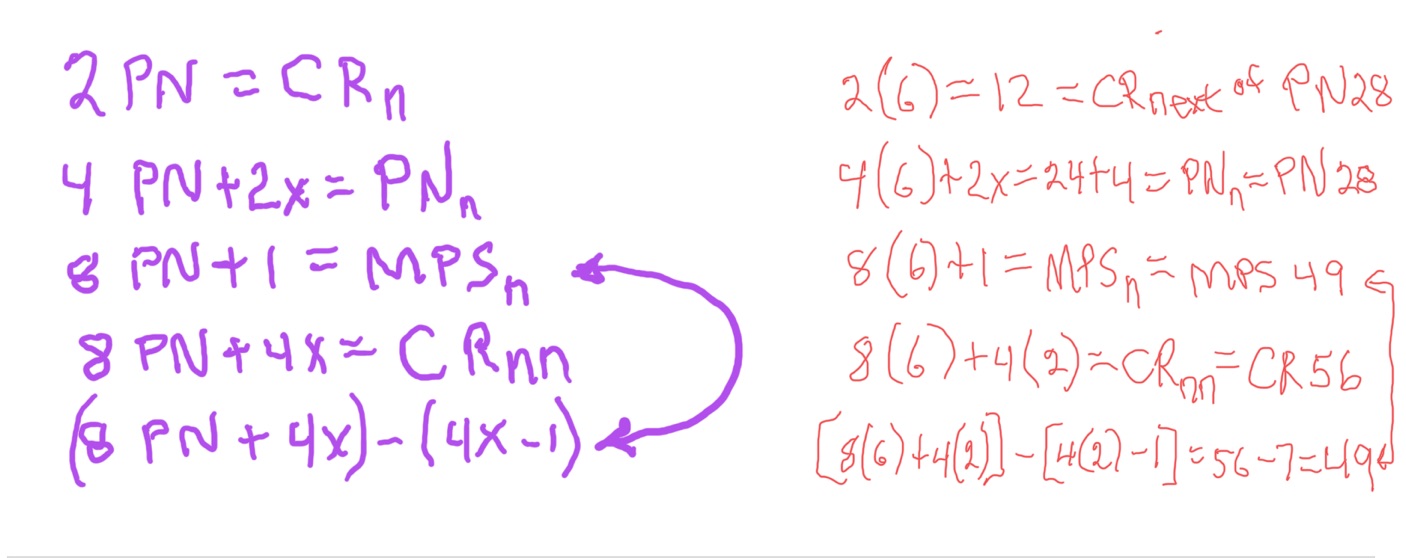Induction-Deduction
Definitions: https://www.dictionary.com/e/inductive-vs-deductive/
Oversimplified: Induction: specific ⸺>general Deduction: general⸺>specific
We use both!
Abstract
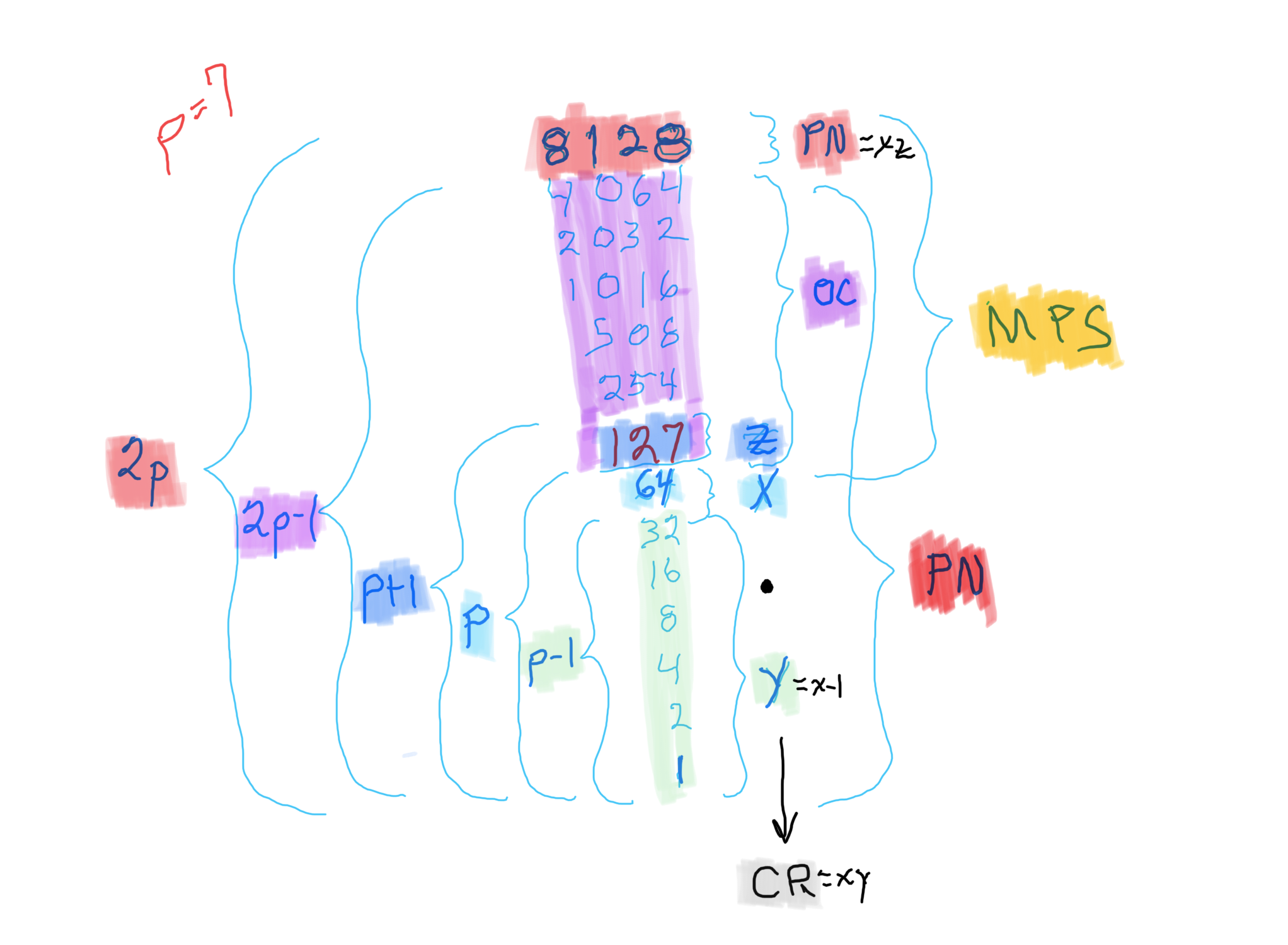
With the Euclid-Euler Theorem in mind (“PN = 2ᵖ⁻¹ • 2p -1“= xz), the combination of algebra and geometry (algebraic-geometry) has generated a deep profile of the Mersenne Prime (Mp=z) — Perfect Number (PN=xz, where x=(z+1/2), and y=x-1) pairing and has revealed both a Universal resonance with all EVEN numbers related to the Exponential Power of 2 (a.k.a. Butterfly Fractal 1, 2ⁿ ) via the inductive process, and, a striking, and very specific, exception to that general resonance in the form of a specific Number Pattern Sequence (NPS) within its constituent factors (divisors) under the lens of pure deduction.
Starting with the Butterfly Fractal 1 (Exponential Power of 2 and its Running Sums, ∑), one will generate — amongst the natural EVENs— Running Sums (∑) of ODDs that may be divided into three sets of “containers,” each with enormous differences in occurrence (density), starting with the rarest:
Set 1. ODDs that are Mersenne Primes (Primes that are formed from 2p -1 = z) coming from p=Mersenne Primes (Mp), e.i. z=3, 7, 31, 127... come from p=2,3, 5 and 7, respectively.
Set 2. ODDs that are neither Mp or Primes, coming from p=ODDs that may/may-not be PRIME, and never Mp, e.i. z=511, 2047, 2097151, 8388607... come from p=9, 11, 21, 23 respectively;
Set 3. ODDs that are neither of the above, coming from p=EVENs, e.i. z=15, 63, 255,... come from p=4, 6, and 8, respectively.
Consideration of *three sets has been necessary to distinguish one set of “containers”from another. Necessary, but fraught with false conclusions along the way. Set 3 ODDs are always ÷3, so may be dismissed early on, except for their role in seeing the overall NPS.
[*the term “containers” has been used to include all three Sets in general, with the qualifier “inActive” applied to those “containers” that do not contain TRUE Mp-PN pairings, i.e. Sets 2 and 3, above. The qualifiers TRUE Active “containers” is reserved specifically for Set 1 = Mp-PN pairings.]
By way of analogy and working backwards, one finds that the ODDs that are not Prime, and thus also not Mersenne Primes, are the predominate set of ODDs generated (Set 3), and are like a tone whose frequency evokes, but never reaches, the purity of a perfect pitch. We get much closer to that perfect pitch with the next set of ODDs — the *almost, but always Not Primes — in Set 2, but it is only with the rarest of ODDs — the Mersenne Primes — in Set 1 do we actually get the pure resonance of perfect pitch — pure tone without the sharps and flats of the other sets.
*some in Set 2 have p=PRIME values, but are NOT Mersenne Primes.
The profiling characterization of each of the three sets has generated a large body of work that — in itself — rewards careful study. NPSs abound! Most of this work has started with the base level of simple quantities — starting with the simplest, quantity 1 — and doubling them, while keeping tabs of the Running Sums (∑) along the way. Pure induction has shined a light on just how vast the spectrum of EVENs and ODDs generated from the simple doubling of quantities, is. It is the Ocean of Numbers of 2n within the larger Oceans of Numbers (∞).
However, it is when one specifically examines the NPS of the factors (divisors) of the Perfect Numbers (PN and their very similar, resonant “containers”) that the true differences in the profiles emerge.
The essence of those differences is this: In one set of ODDs — Set 1 — and only that set, the NPS of the EVEN Perfect Number divisors (i.e. the **factors + including the PN itself) follow a strict, minimalist, template-like pattern such that the # of divisors/p=2.
That’s right, only in Set 1 does p=# of divisors/2.
[**the definition of a Perfect Number (PN) is one whose factors — NOT counting the PN itself — sum up to equal the PN. Outside this definition, the word “divisors” refers to ALL the factors of a given number, including the # itself.]
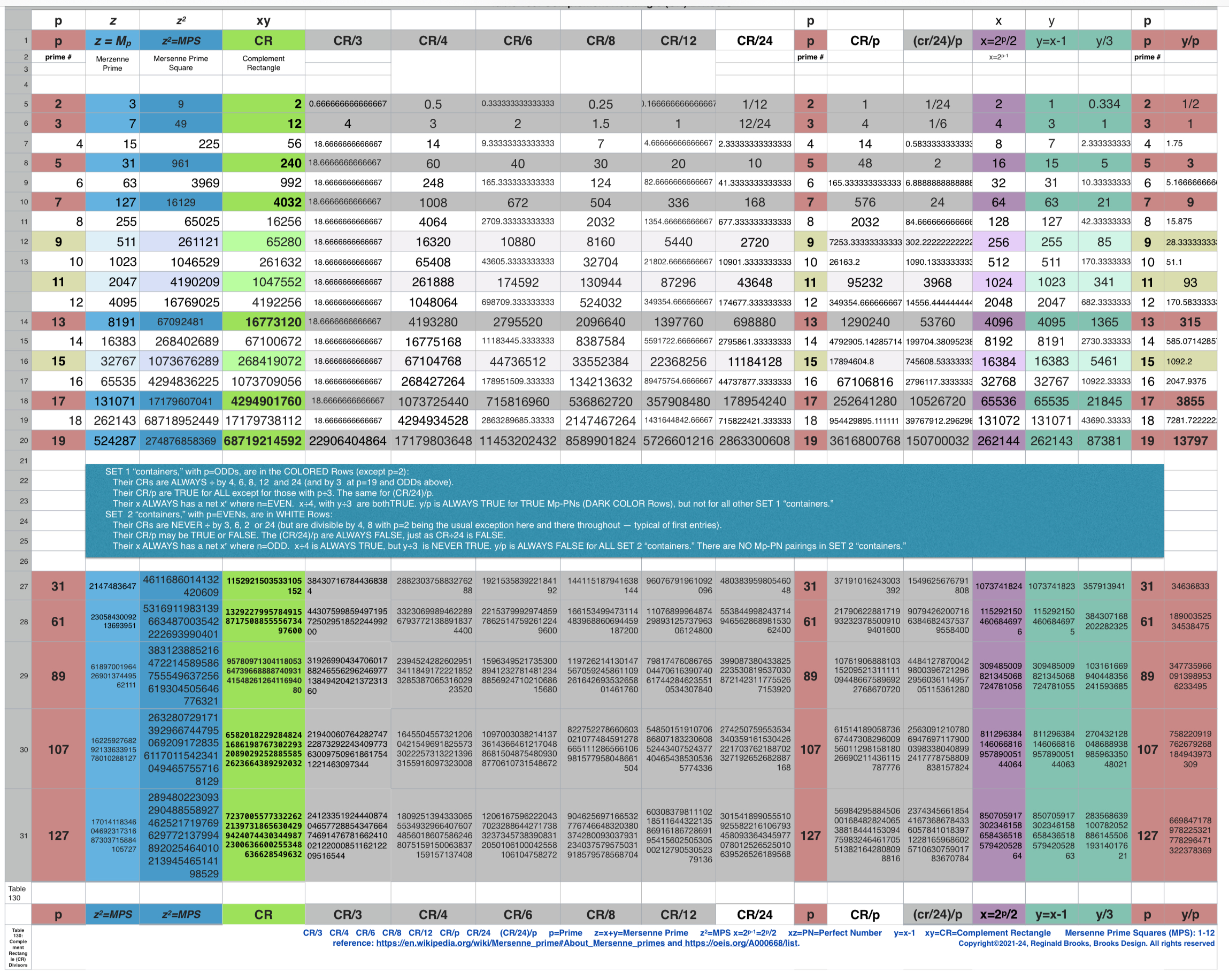
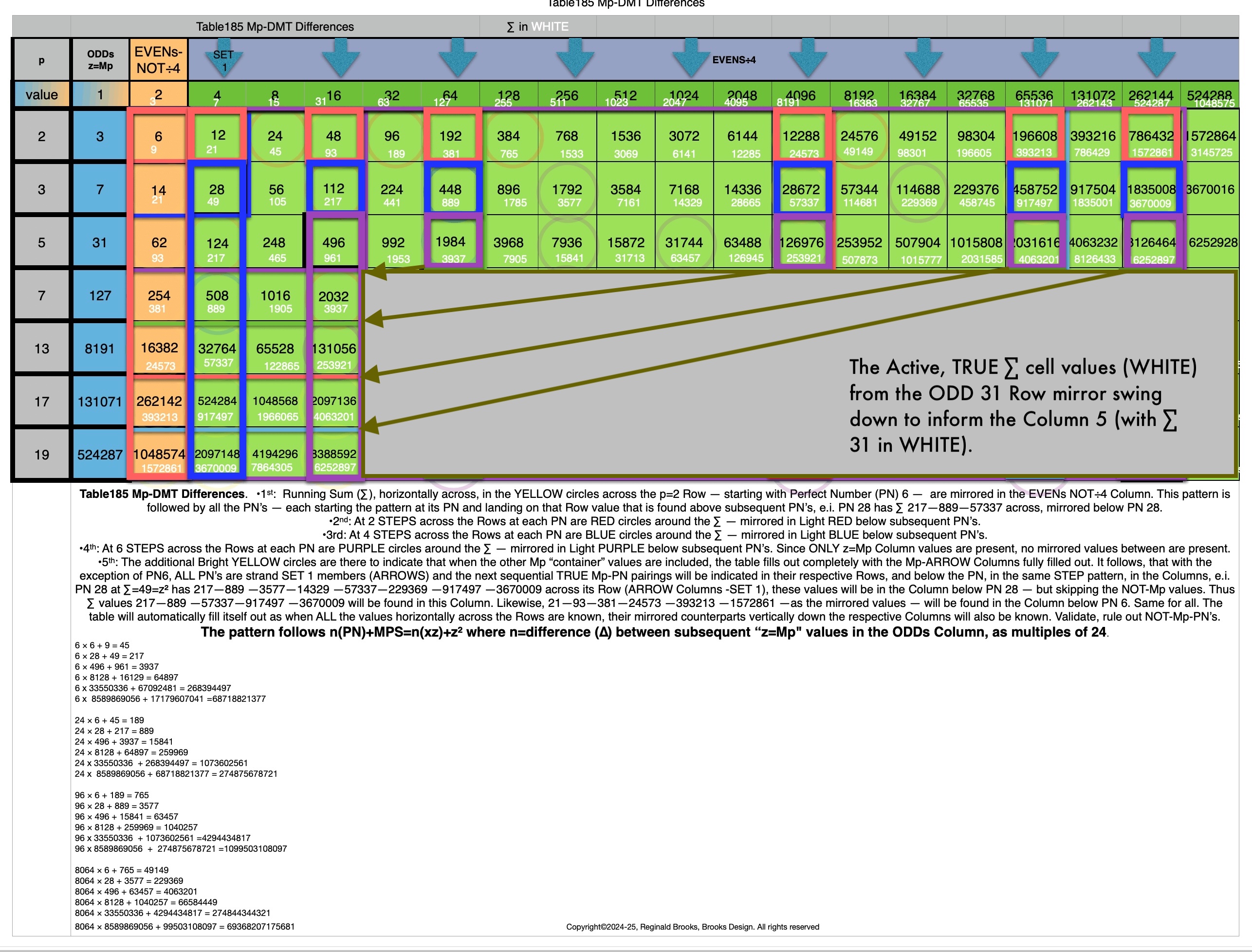
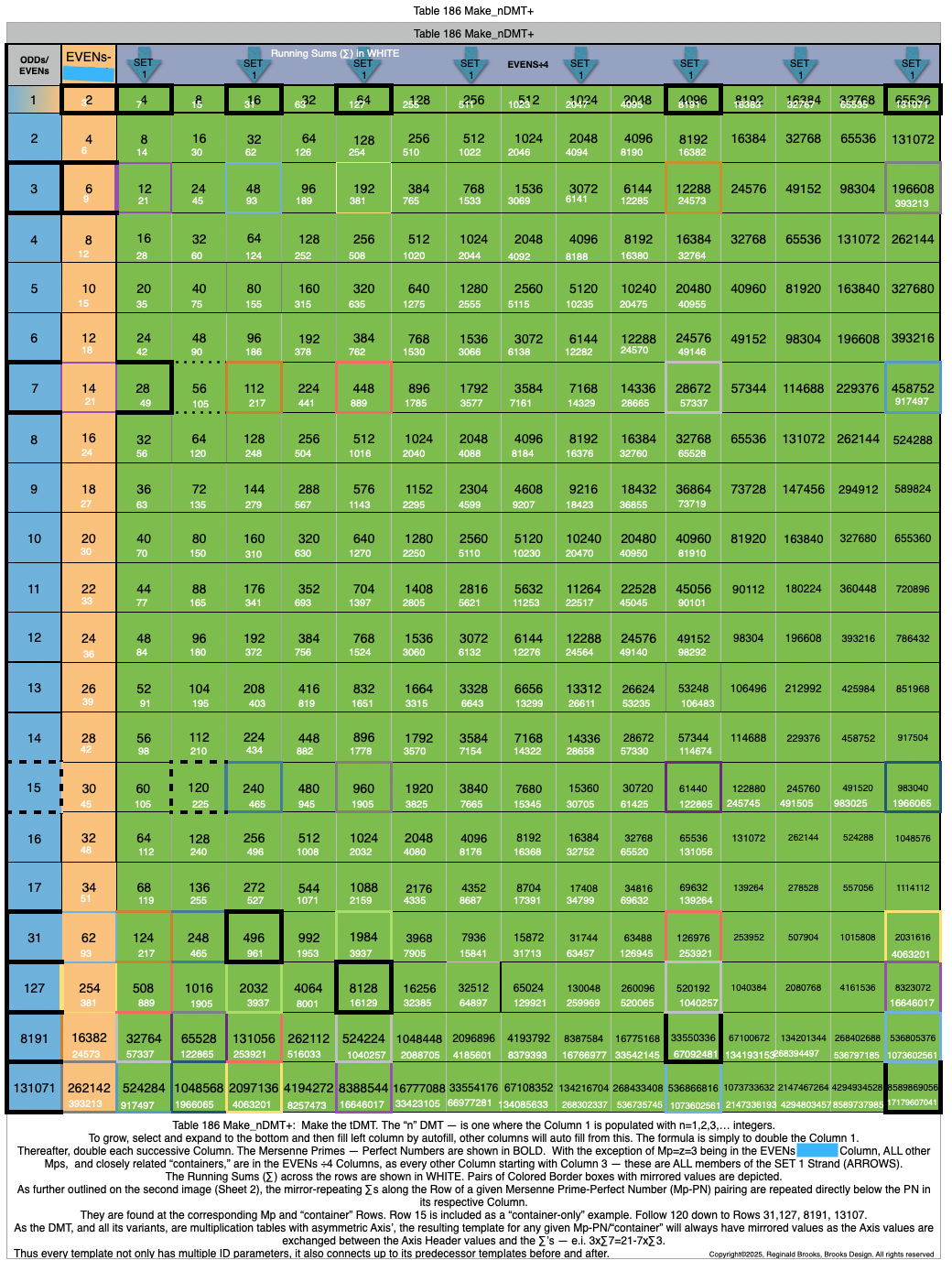
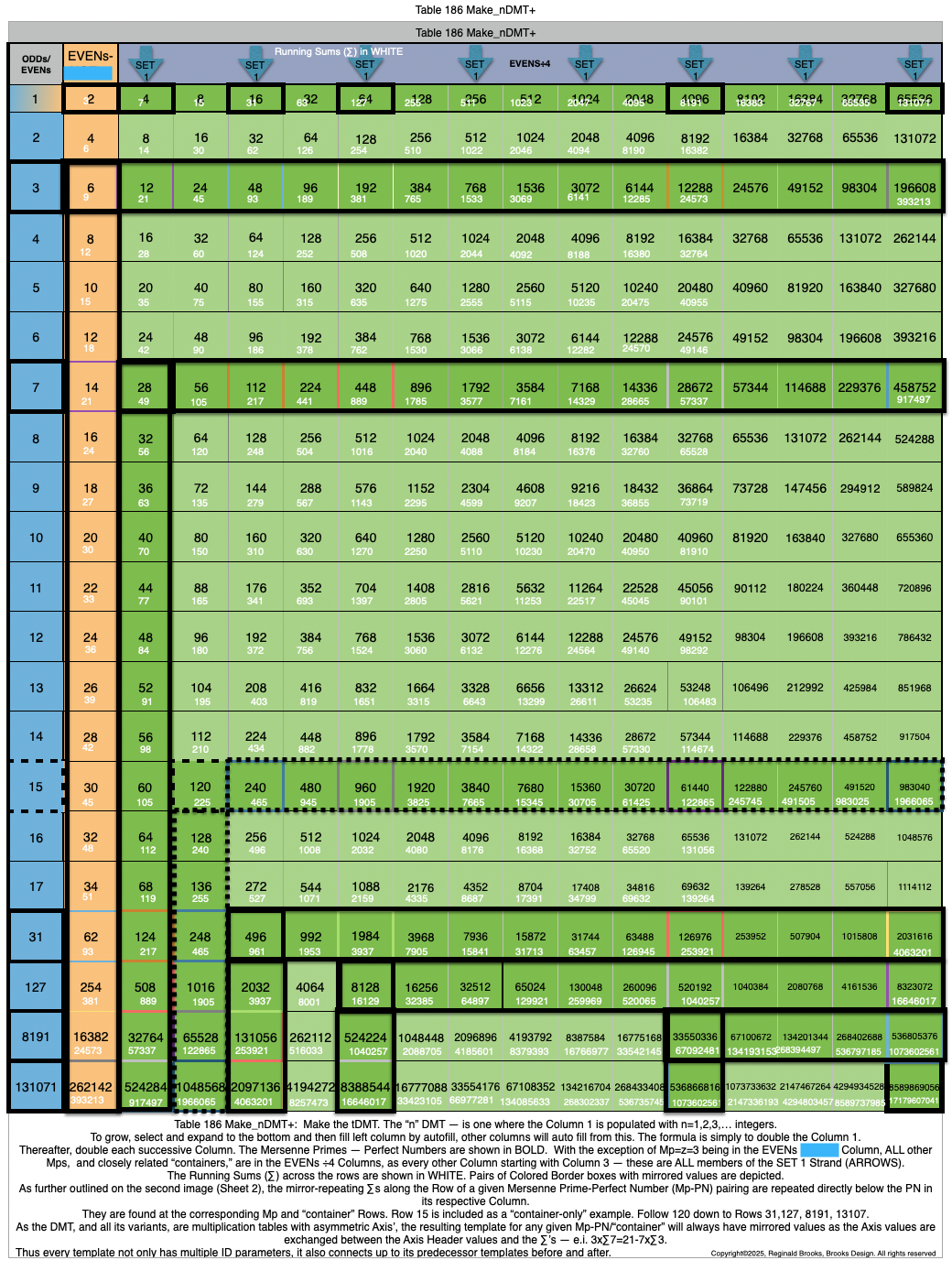
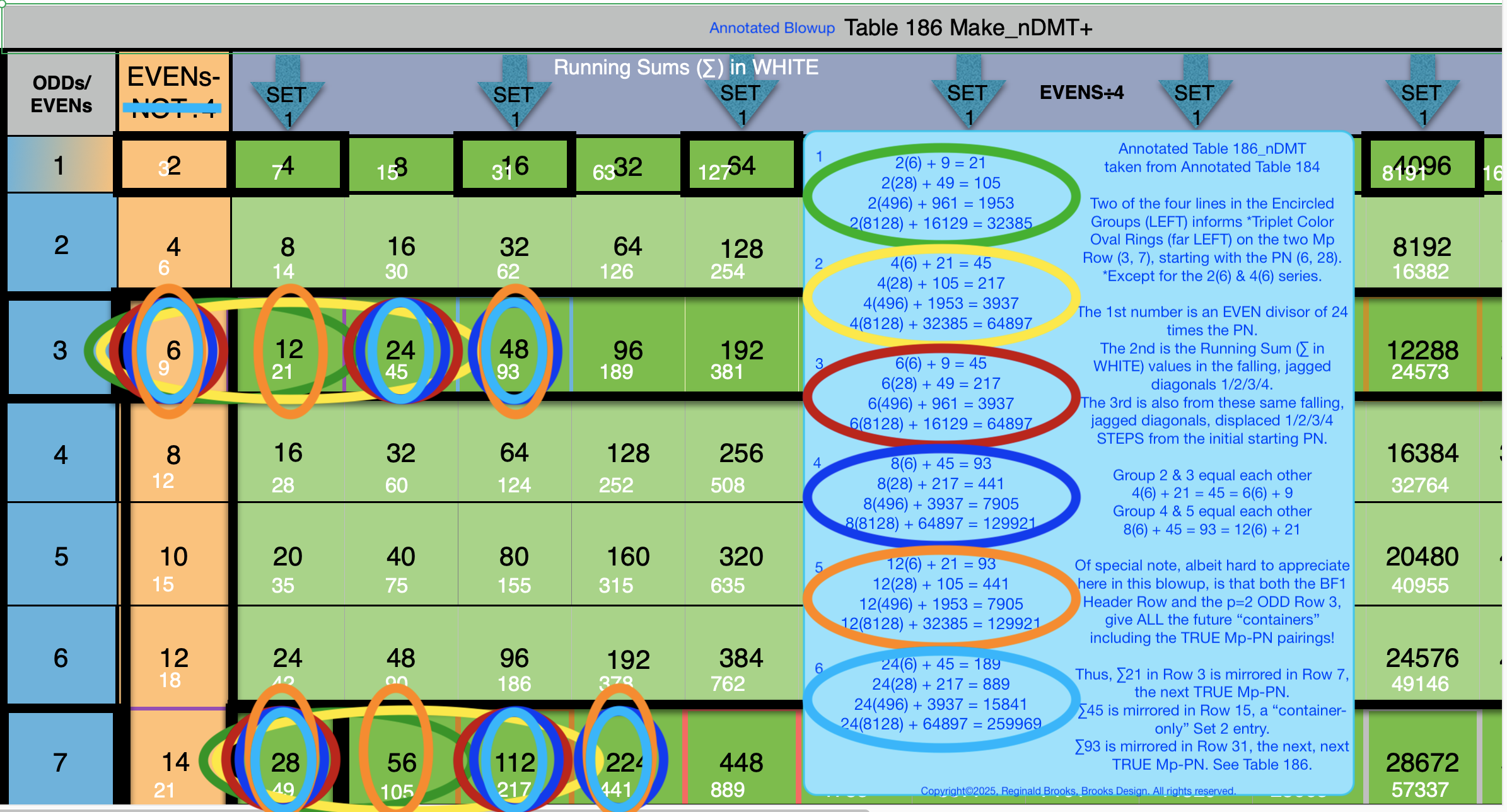
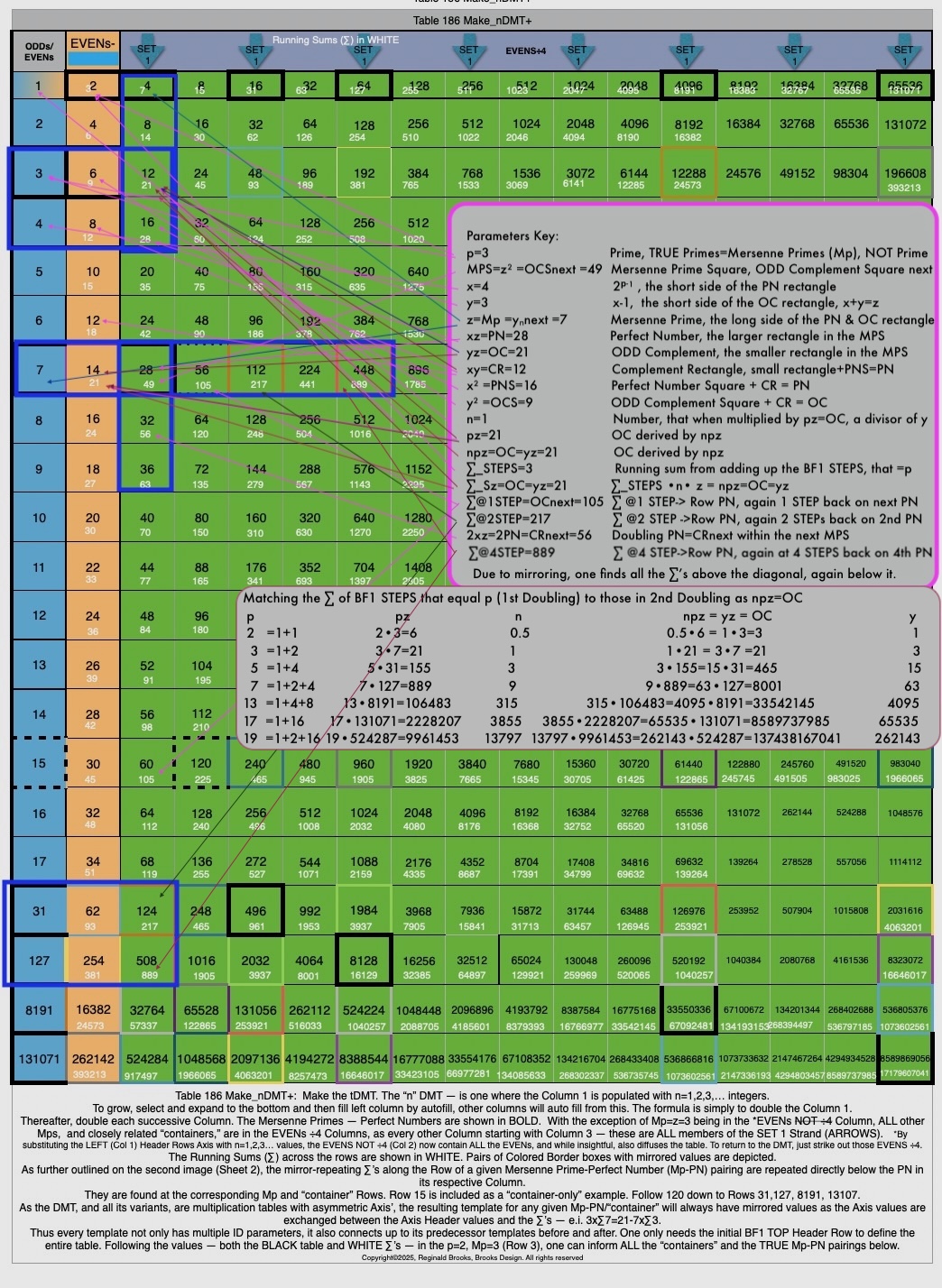
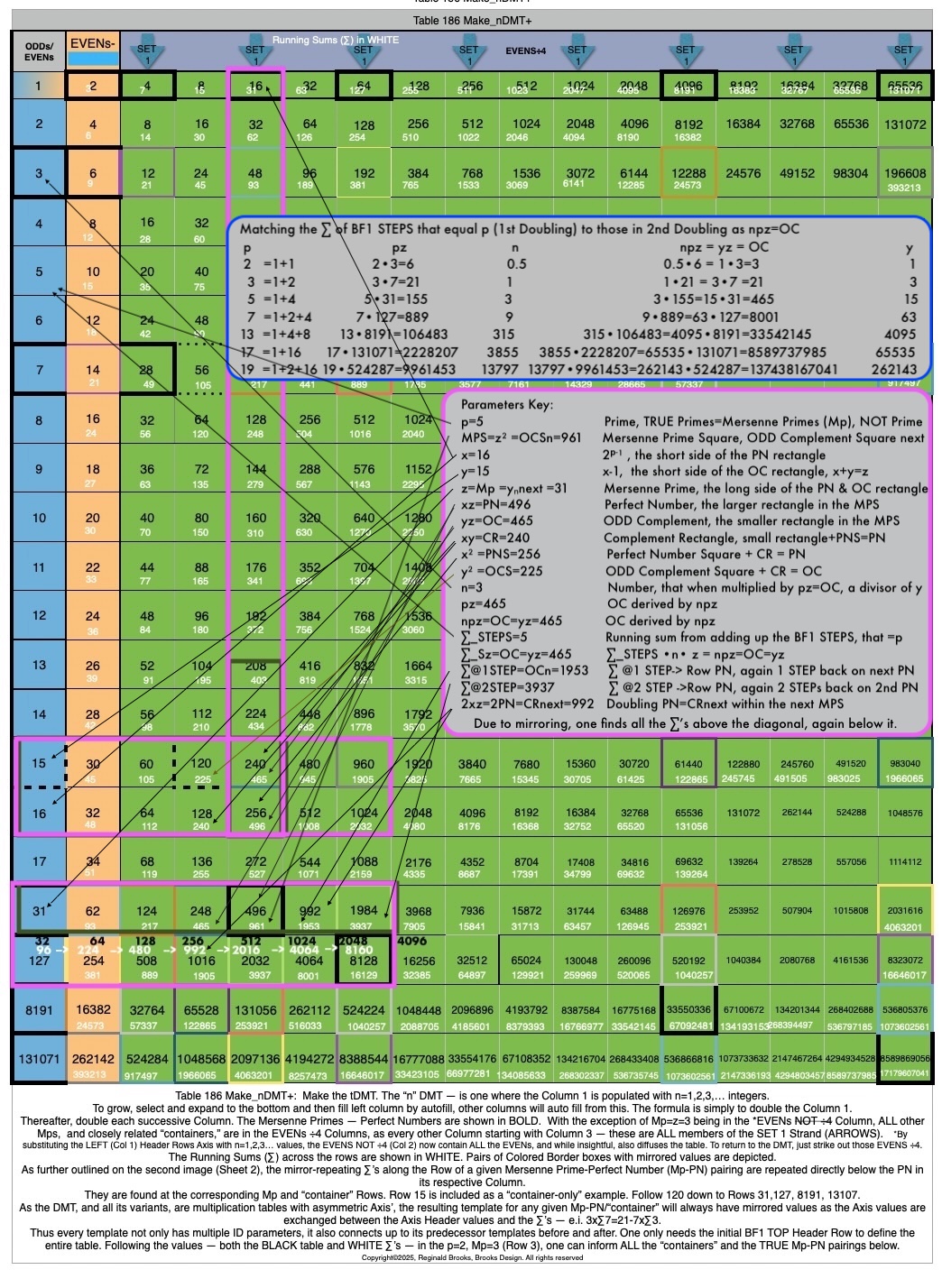
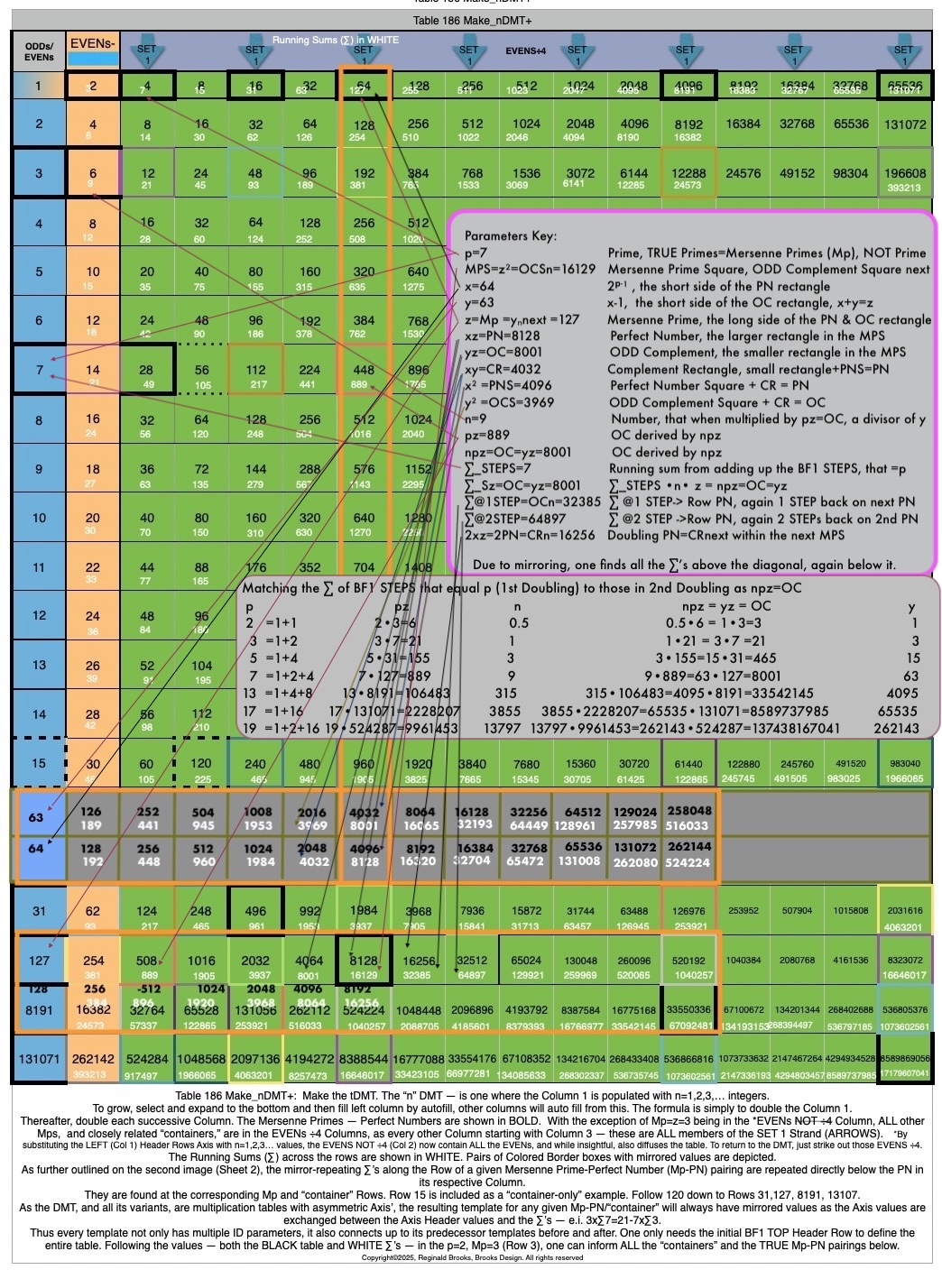
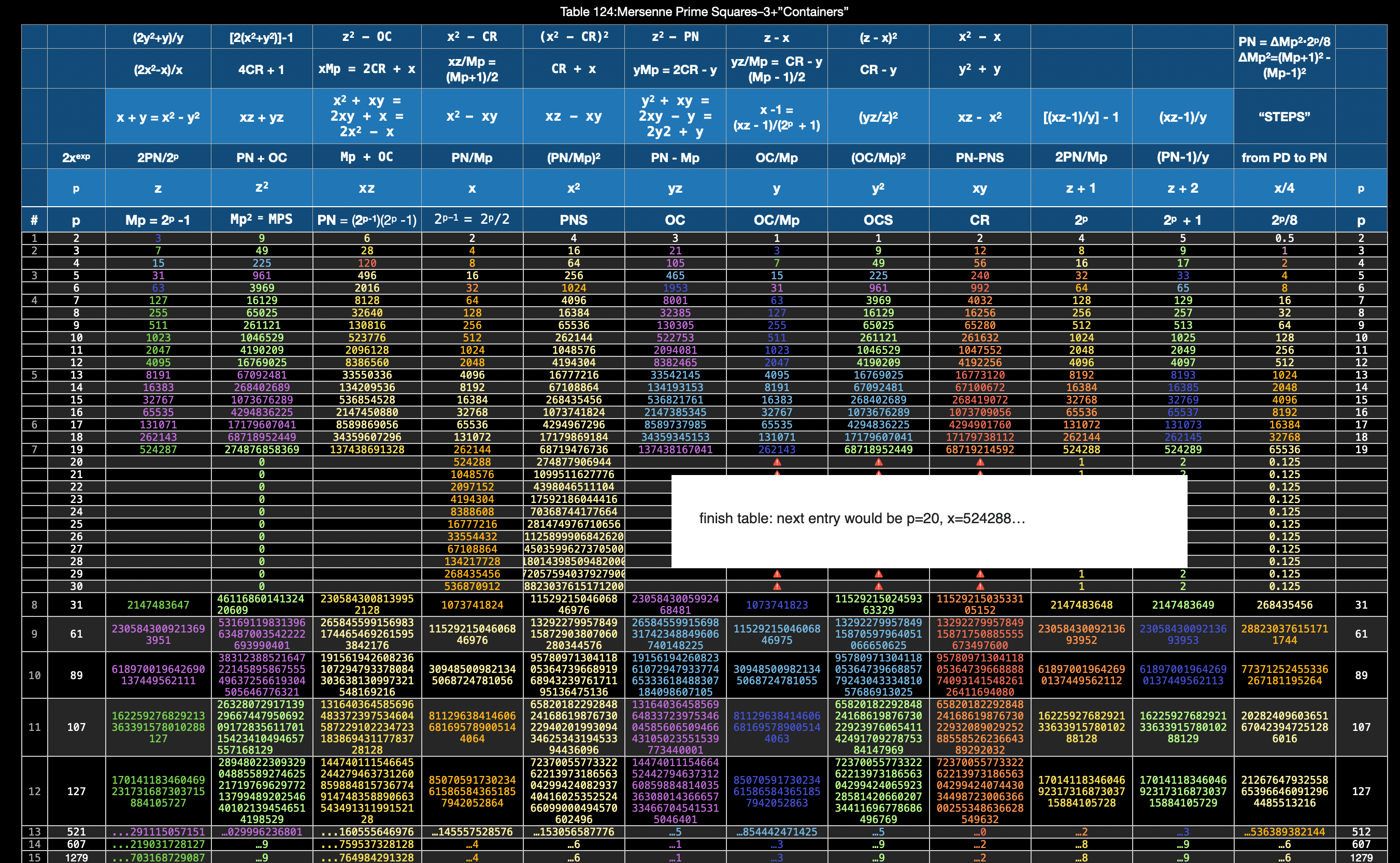
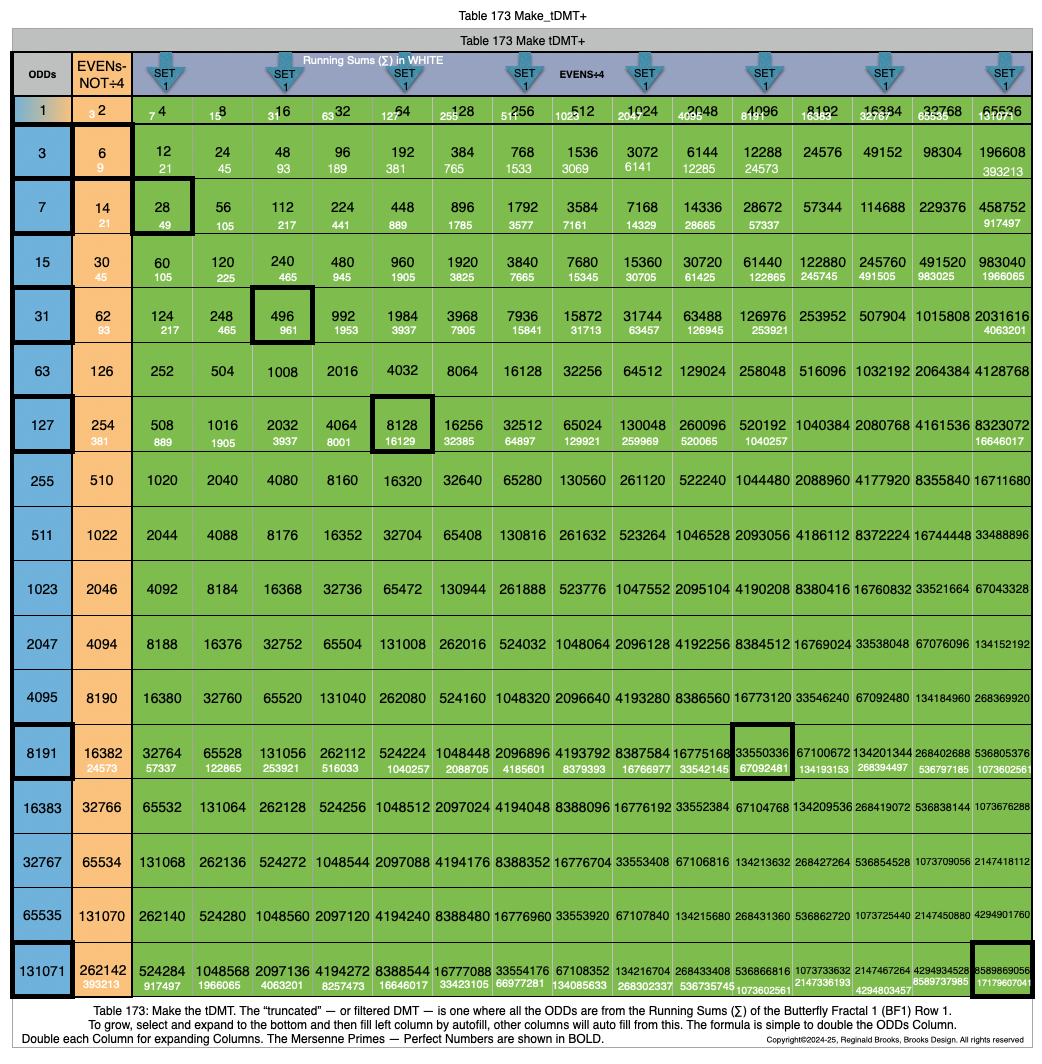
Additionally, Set 1=Mp-PN pairings differ from Sets 2 and 3 as seen in the following chart of Divisors and Factors of PN: Table 162: Sets & Divisors & Factors of PN.
(see Table 162)
Introduction
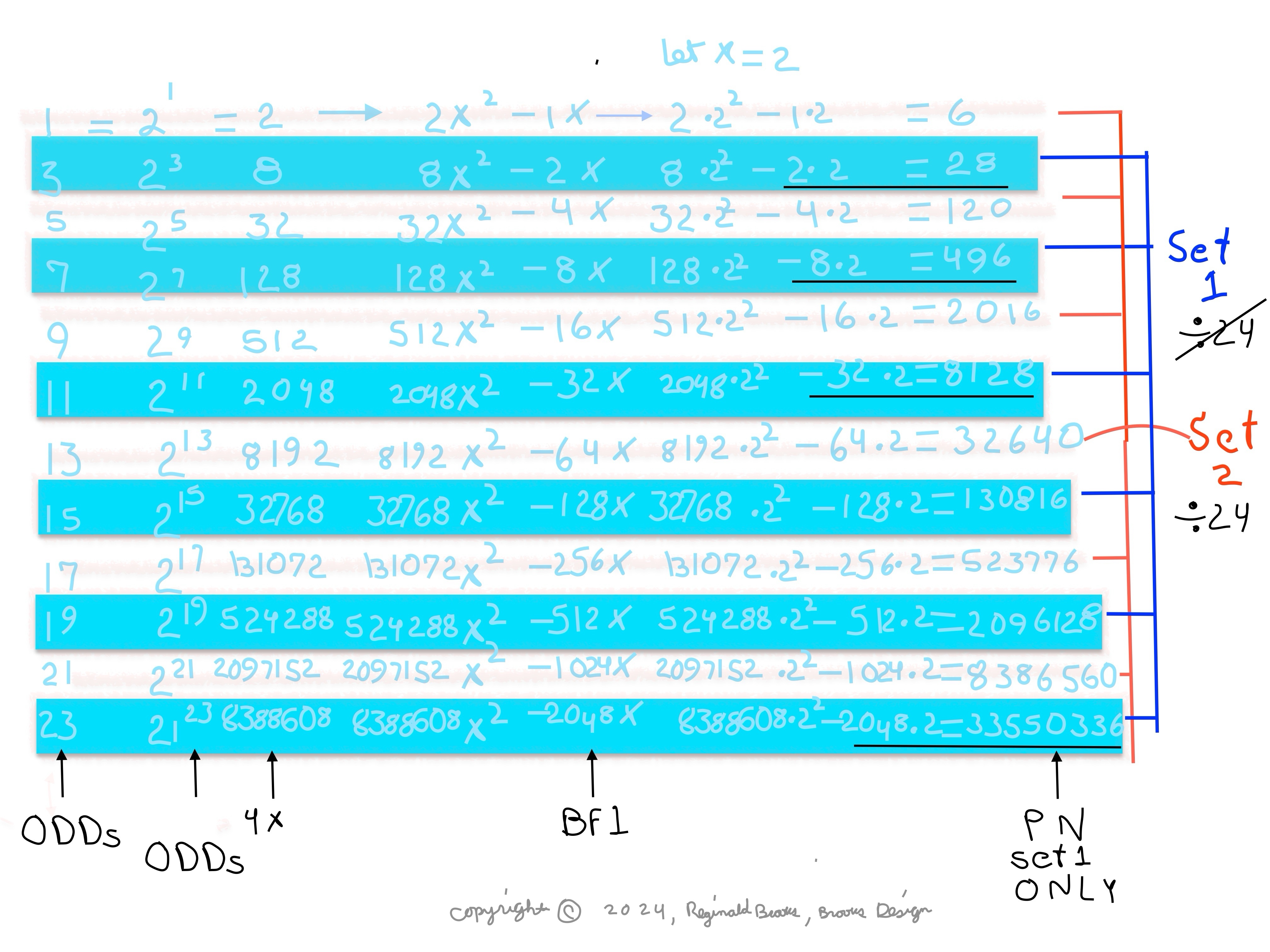
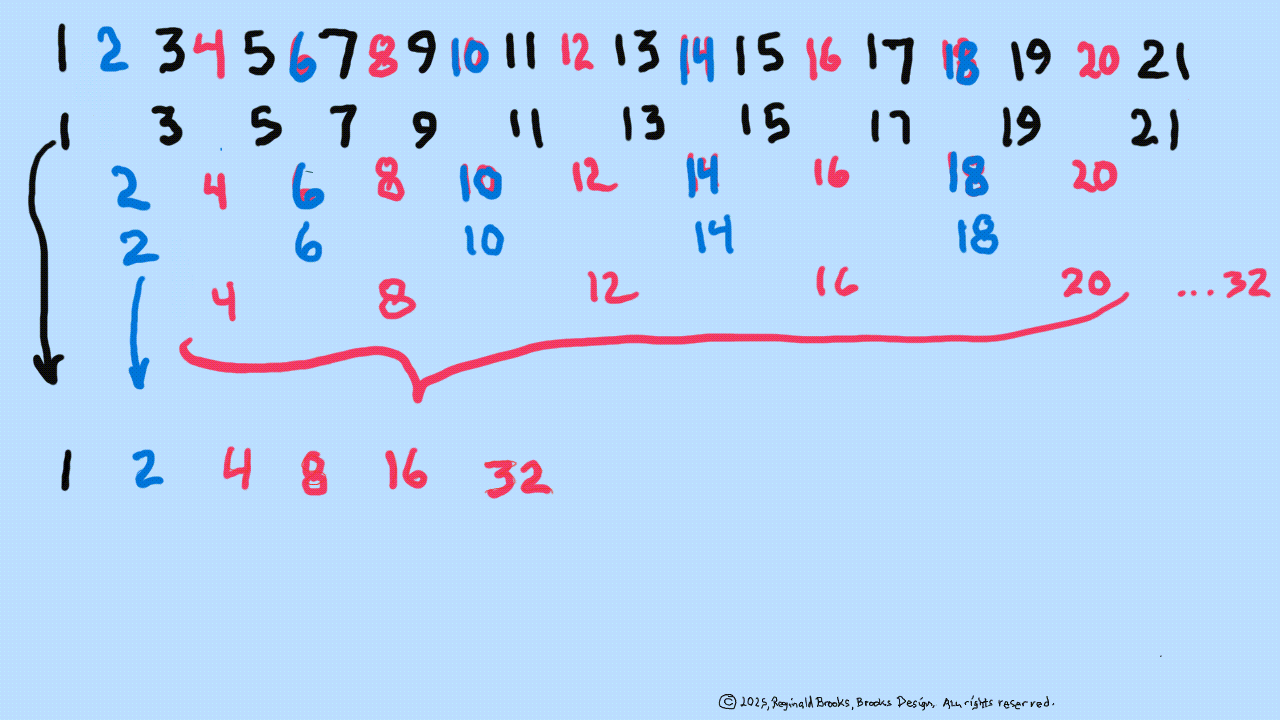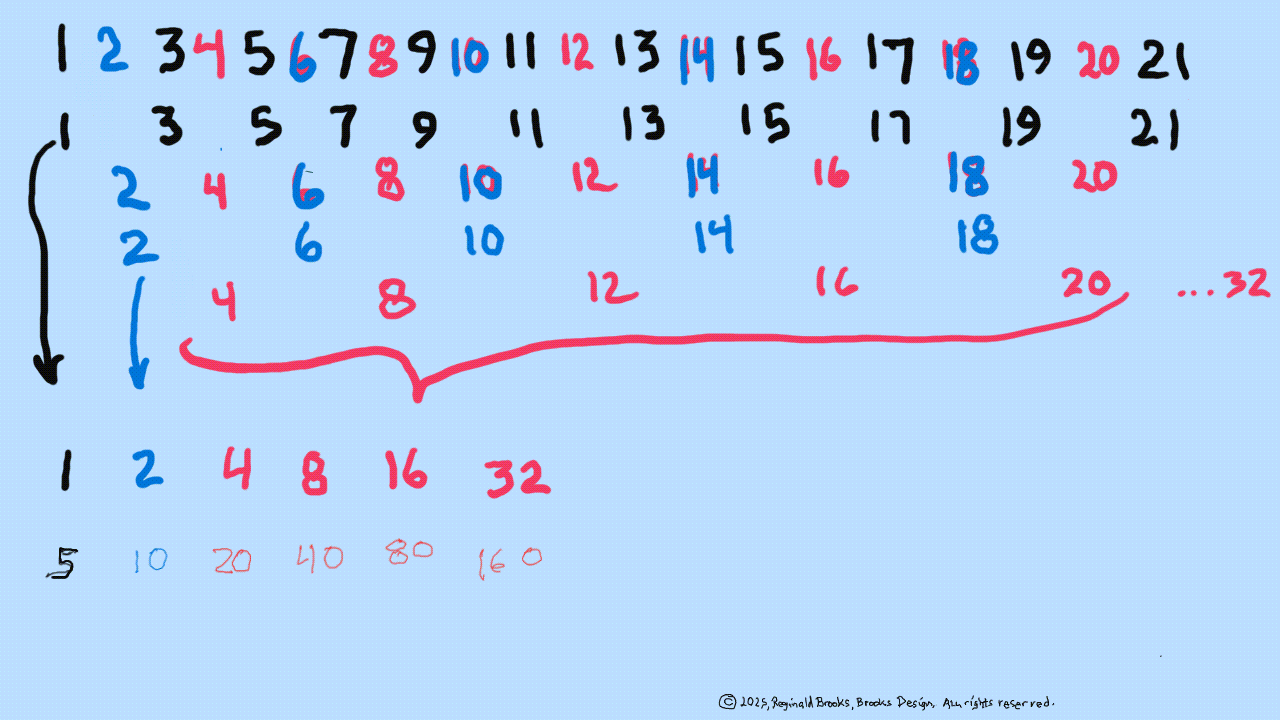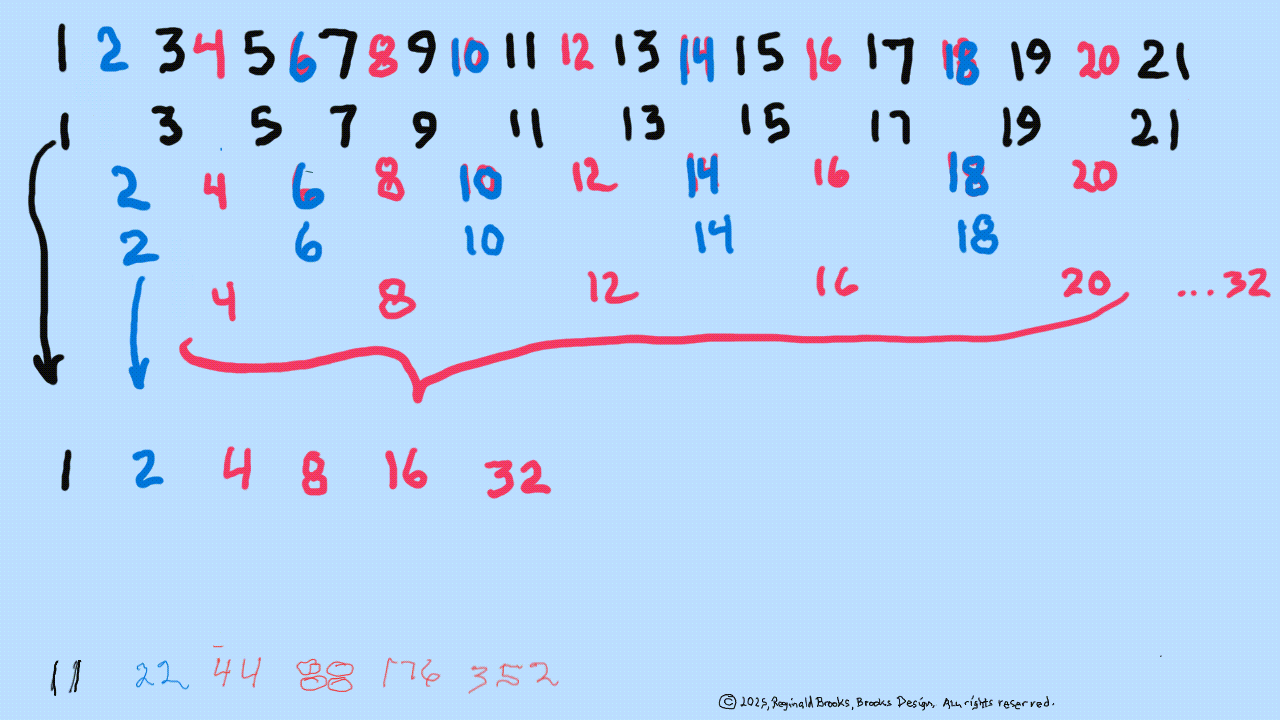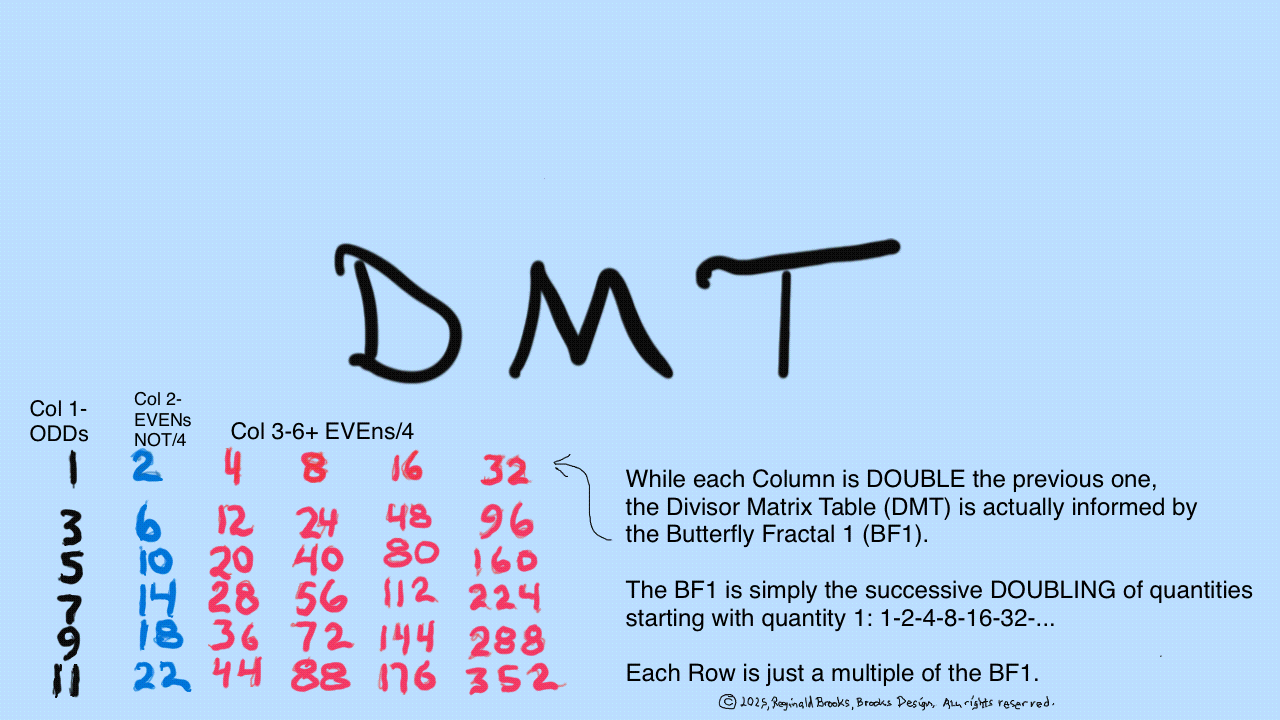
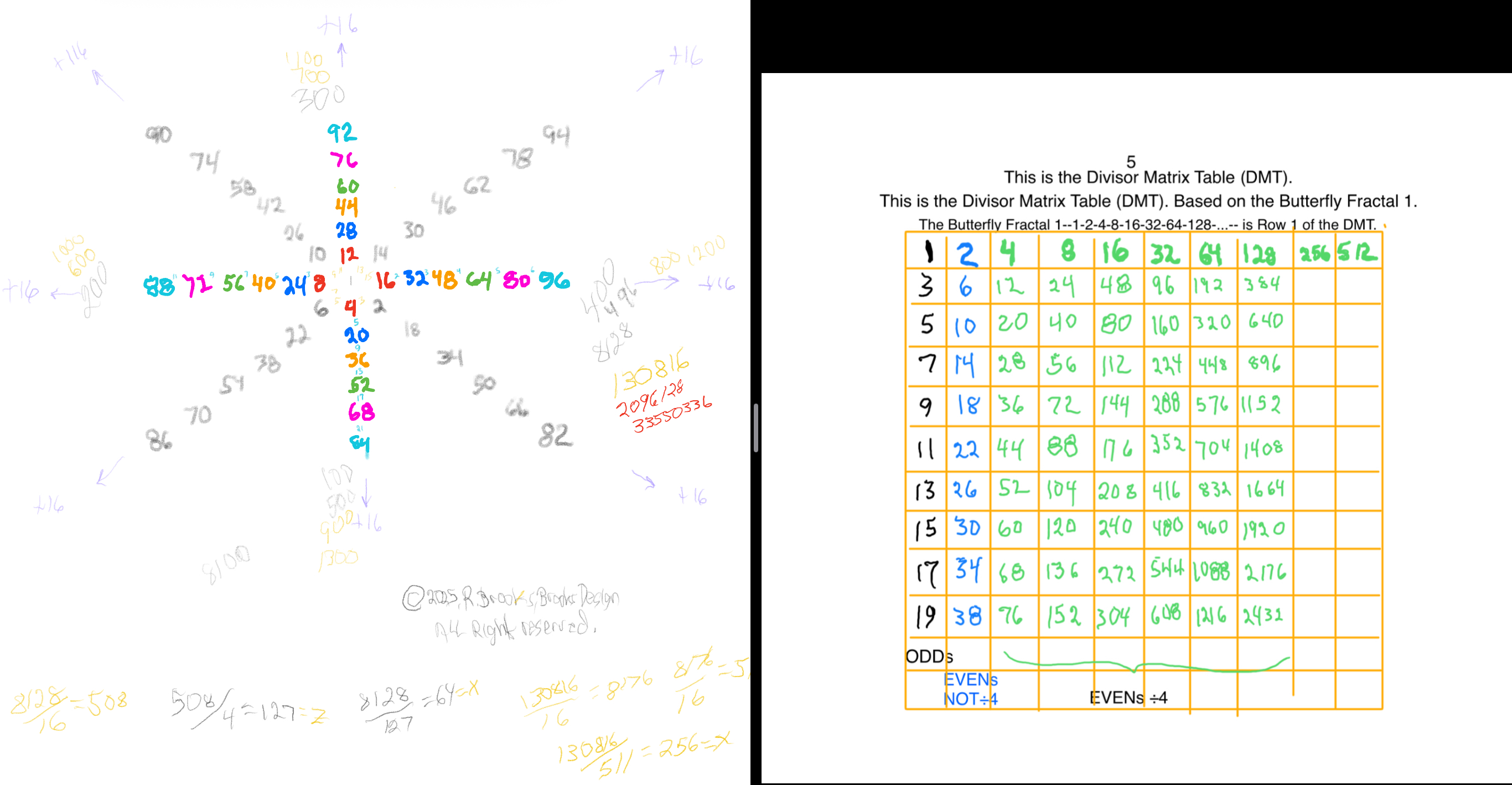
The Exponential Power of 2 (2ⁿ, where n=0,1,2,3,...), along with a Running Sums (∑) tally along the way, generates a seemingly very simple NPS that both represents
the simple doubling of quantity 1 to give 2, doubling 2 to give 4, doubling 4 to give 8,.... and gives amongst its “Oceans of Numbers” the rarest of the rare — Mersenne Prime - Perfect Number pairings.
<img src="/Users/RegWotten/Library/Application Support/typora-user-images/image-20240109115745222.png" alt="image-20240109115745222" style="zoom:67%;" /

Seemingly because that NPS is itself a fractal of itself, and thus expands out indefinitely. When laid out visually using only simple marks — like the number “1” — it starts to mimic the pattern of a butterfly, thus it has been named the Butterfly Fractal 1(BF1).
The 2ⁿ values starting with n=0 are: 1-2-4-8-16-32-64-128-256-512... It generates, through a combination of the simple geometry and the calculated Running Sums (∑) — a kind of geometric algebra or more commonly, algebraic geometry sequence: 1-2-3-4-7-8-15-16-31-32-63-64-127-128-255-256-511-512... One can see in this last sequence that the ∑s: the ODDs 3-7-15-31-63-127-255-511-... are embedded within the BF1 sequence above. Those ODDs are of particular significance as they form a series of “containers” that hold the contents of those doublings up to a given point in general. Within those “containers” are found — almost hiding in plain sight — certain very rare “containers” that hold the Mersenne Prime - Perfect Number pairings.
Hiding such that there are also “containers” that look, act and reveal parameters that the rare Mp-PN pairings hold, yet in total are not TRUE. These “look alike” “containers” predominant and seem to act like necessary place holders for the NPS of the Mp-PNs to be revealed.
So we have within the single larger group of “containers” following the BF1 template, several smaller resonant sets that closely resemble the parent set.
What are those differences? How do we separate them out?
Starting with the Butterfly Fractal 1 (Exponential Power of 2 and its Running Sums, ∑), one will generate — amongst the natural EVENs — Running Sums (∑) of ODDs that may be divided into three sets of “containers,” each with enormous differences in occurrence (density), starting with the rarest:
Set 1. ODDs that are Mersenne Primes (Primes that are formed from 2p -1 = z) coming from p=Mersenne Primes (Mp), e.i. z=3, 7, 31, 127... come from p=2, 3, 5 and 7, respectively.
Set 2. ODDs that are neither Mp or Primes, coming from p=ODDs that may/may-not be PRIME, and never Mp, e.i. z=511, 2047, 2097151, 8388607... come from p=9, 11, 21, 23 respectively;
Set 3. ODDs that are neither of the above, coming from p=EVENs, e.i. z=15, 63, 255,... come from p=4, 6, and 8, respectively.
Certainly, one may outright dismiss Sets 2 and 3 when parsing strictly for the TRUE Mp-PN pairings of Set 1, but that relinquishes the overall NPS in which embeds them all.
There are 3 major approaches to defining the TRUE Mp-PN pairings (Set 1) as they distinguish themselves from Sets 2 and 3 that are embedded within the 5 Section Headings:
Divisor-Factor Patterns (Part I, II and III)
Important SIDE NOTE-1!!!
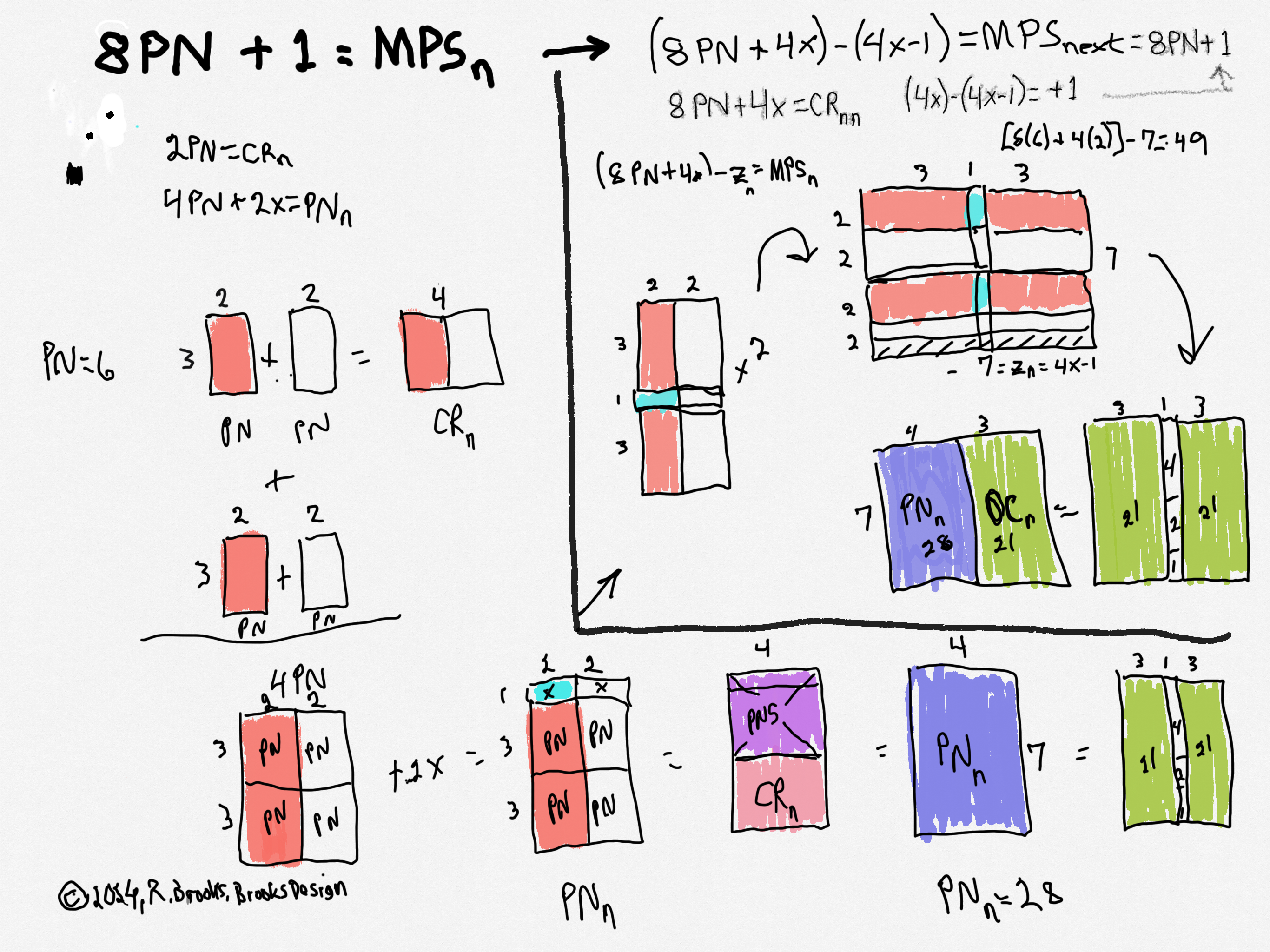
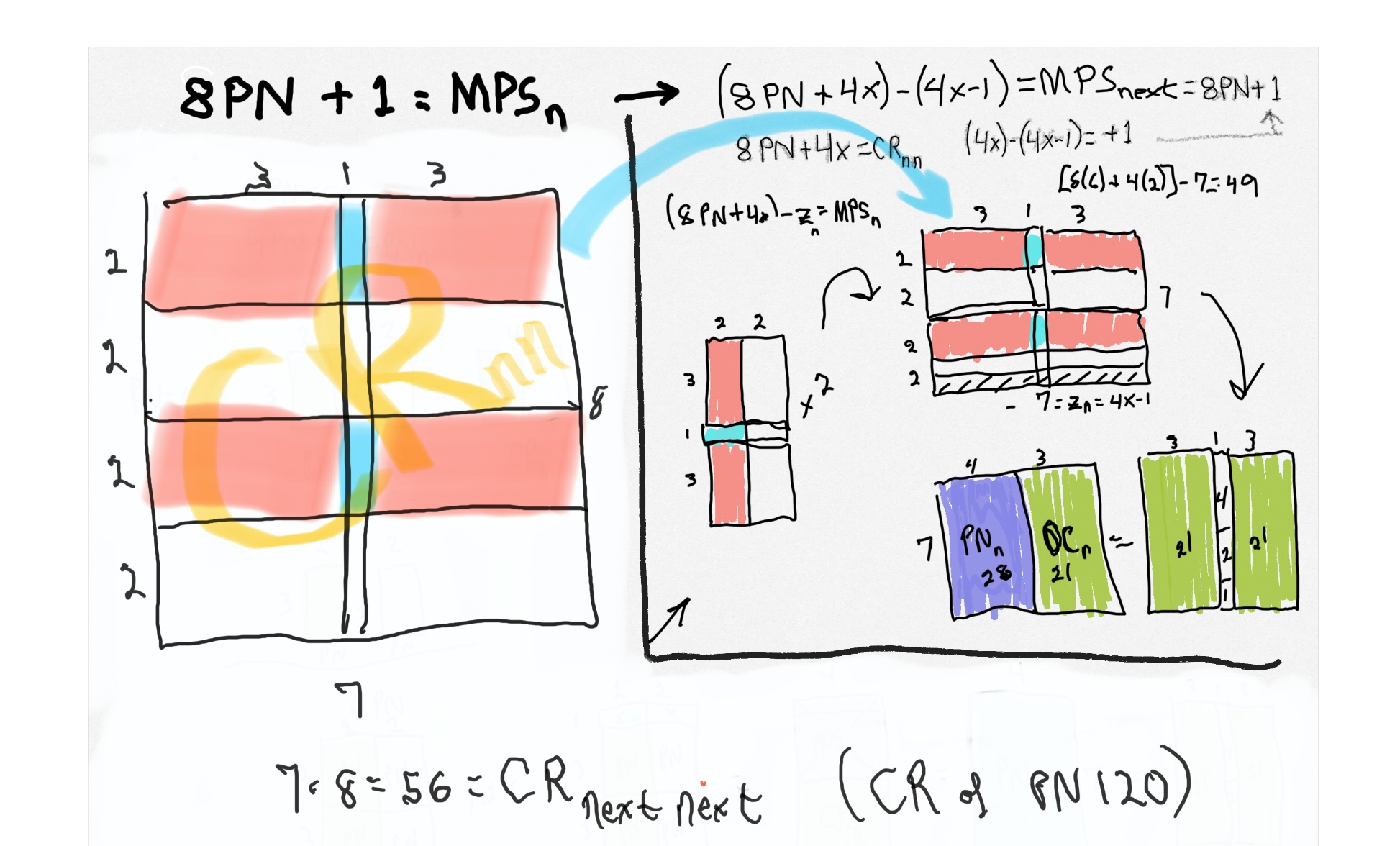
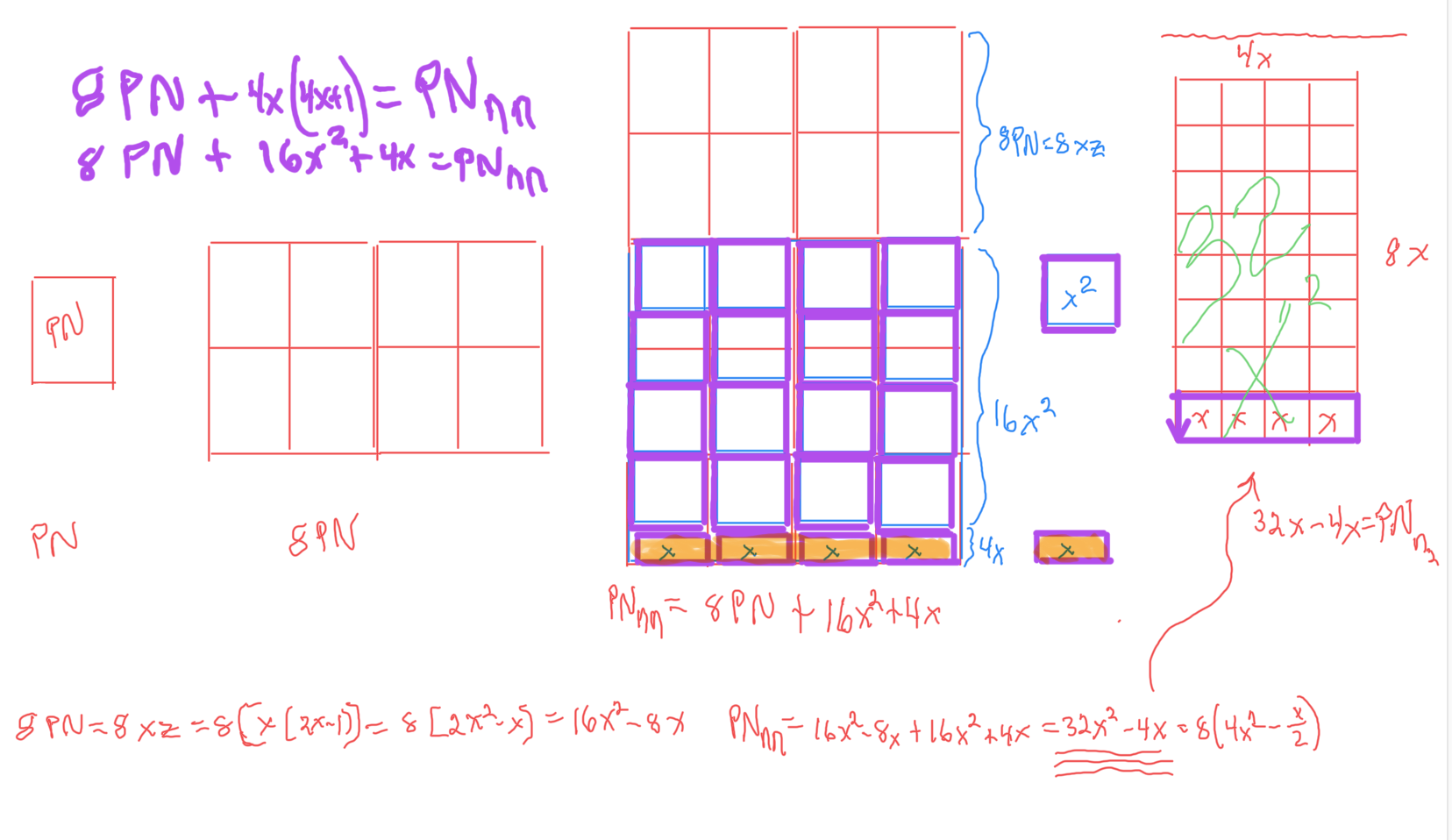
Identity by ÷24: (PN-PN)/24=n)
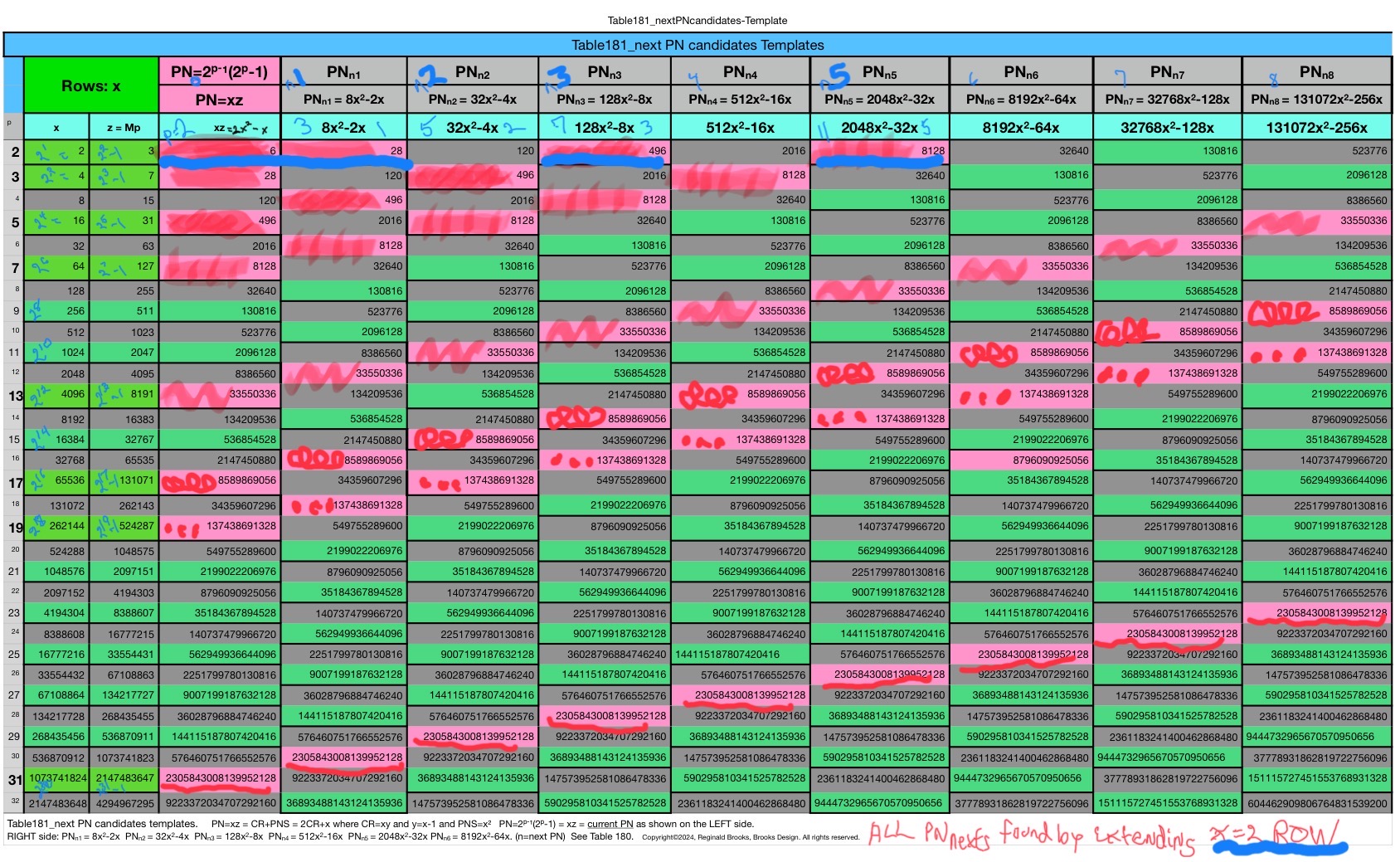
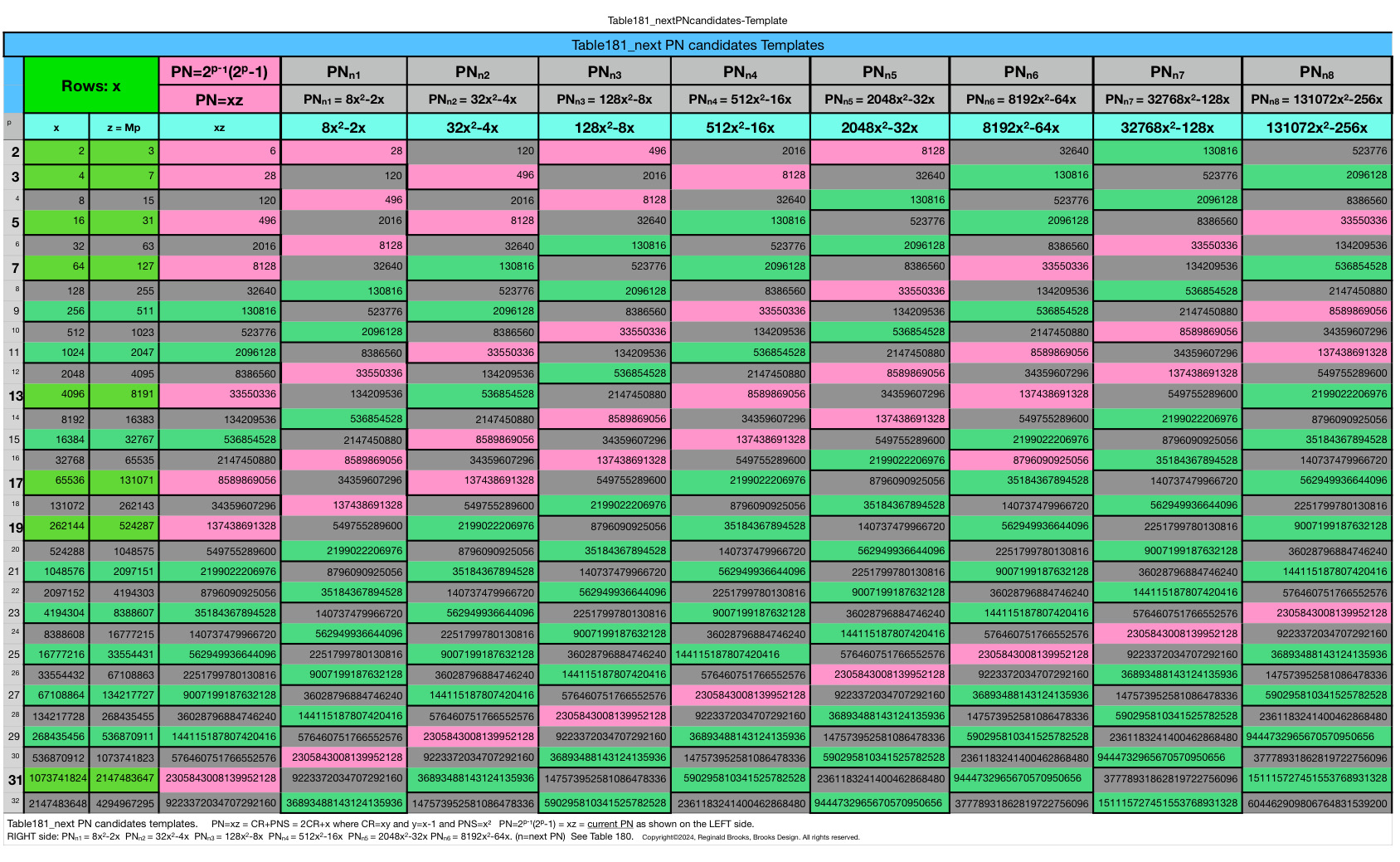
Next PN: 16PN+12x=PN next
Important SIDE NOTE-2!!!
And, from the Identity by ÷24 approach, one can see visually on the BIM that ALL TRUE PN (Set 1) lie exclusively on Axial Rows just BELOW the LOWER ACTIVE ROW that identifies ALL PRIME (and ALL Pythagorean Triples, separately) candidates, as presented in earlier works.
Remember, we are working with xz=PN, as defined by p that may be EVEN or ODD. ALL PNs and “x” are EVEN and ÷4. ALL “z” are ODD — but key here is that some are ÷3 (Set 3), some have some — but not all — PRIME, even Mersenne PRIME, parameters (Set 2), and some are fully, TRUE Mersenne PRIMES (Set 1).
seeing the NPS of the TRUE, ACTIVE Set 1 Mp-PNs within the vastly larger Ocean of Numbers has necessitated consistent labeling of ALL parameters of the Mp-PN throughout to avoid confusion — e.i. that results in a parameter like p=PRIME (and except for Prime 2, is always an ODD), to be used more generically as when p=EVEN like 4, 6, 8,... for those in Sets 2 and 3.
That’s because — as shown below — ALL p=ODDs (Sets 1 and 2) are on the Row (EVEN) below the LOWER ACTIVE ROW — AND — ALL p=EVENs (Set 3) are on the Row (EVEN) between the LOWER and UPPER ACTIVES ROWS.
This can be seen below as one ADDS or SUBTRACTS 1 from the PN # Row — effectively going up or down a Row on the BIM.
On the BIM Template: (BOLD=Row of ALL TRUE PNs located just below LOWER Active Row)
*Sets 1 and 2*:
ODD, Non-PRIME, Non-ACTIVE Row that is ÷3, i.e. Rows 3, 9,15, 21, 27, 33, 39, 45, …every 6th Row from Row 3
p=ODD: on THIS EVEN Row BELOW the* *LOWER ACTIVE ROW* ***(subtract 1 for proof)** =Sets 1 & 2***
LOWER, ODD ACTIVE ROW not÷3 — LOWER, ODD ACTIVE ROW not÷3
*Set 3:*
LOWER, ODD ACTIVE ROW not÷3 — LOWER, ODD ACTIVE ROW not÷3
p=EVEN: on THIS EVEN ROW between the UPPER & *LOWER ACTIVE ROWS =Set 3
UPPER, ODD ACTIVE ROW not÷3 — UPPER, ODD ACTIVE ROW not÷3
So we know that ALL TRUE PN Lie Axially on the EVEN Row just BELOW the LOWER ACTIVE ROW!!!!
TIPS:
ALL p=EVEN, PNs — Set 3 — are ÷3 and thus ALL +/- 1 Row are NOT÷3=inActive”containers” found between UPPER & LOWER ACTIVE ROWS. ei, 120/2=40, 120 inActive “container” found between UPPER & LOWER ACTIVE ROWS. One can dismiss Set 3 immediately when parsing.
ALL p=ODD, PNs are NOT ÷3, may be ACTIVE (Set 1) or inACTIVE (Set 2), and ALL are on THIS EVEN Row BELOW the LOWER ACTIVE ROW (subtract 1 for proof)
Any p=ODDs that are PRIME or NOT, e.i. 9,11,21,23... may still have PN like parameters that are like TRUE (Set 1) ACTIVES, but will be actual TRUE ACTIVES if, and only if, those p=ODDs=Mersenne Primes thus, e.i., p=11 is ODD=PRIME but is not≠Mp — so NOT a TRUE ACTIVE!!!!
All this re-enforces the Set 1, Set 2 and Set 3 categories or subset “containers” from the larger set of 2ⁿ related, doubling quantities of the BF1:
LARGEST: Set 3. ODDs that are neither 1 or 2 below, coming from p=EVENs, e.i. z=15, 63, 255,... come from p=4, 6, and 8, respectively.
MIDRANGE: Set 2. ODDs that are neither Mp or Primes, coming from p=ODDs that may/may-not be PRIME, and never Mp, e.i. z=511, 2047, 2097151, 8388607... come from p=9, 11, 21, 23 respectively
SMALLEST: Set 1. ODDs that are Mersenne Primes (Primes that are formed from 2p -1 = z) coming from p=Mersenne Primes (Mp), e.i. z=3, 7, 31, 127... come from p=2, 3, 5 and 7, respectively.
One can see that in parsing the sets that after dismissing Set 3, we find the challenge remaining is to separate Set 1 from the larger Set 2, as both occupy the same Row position on the BIM.
1. Divisor-Factor Patterns -Part I
It is when one specifically examines the NPS of the factors (divisors) of the Perfect Numbers (PN and their very similar, resonant “containers”) that the true differences in the Sets 1, 2 and 3 profiles emerge.
The essence of those differences are this: In one set of ODDs — Set 1 — and only that set, the NPS of the EVEN Perfect Number divisors (i.e. the factors including the PN itself) follow a strict, minimalist, template-like pattern such that the # of divisors/p=2. That’s right, only in Set 1 does p=# of divisors/2.
[**the definition of a Perfect Number (PN) is one whose factors — NOT counting the PN itself — sum up to equal the PN. Outside this definition, the word “divisors” refers to ALL the factors of a given number, including the # itself.]
Additionally, Set 1=Mp-PN pairings differs from Sets 2 and 3 as seen in the following chart of Divisors and Factors of PN: Table 162: Sets & Divisors & Factors of PN
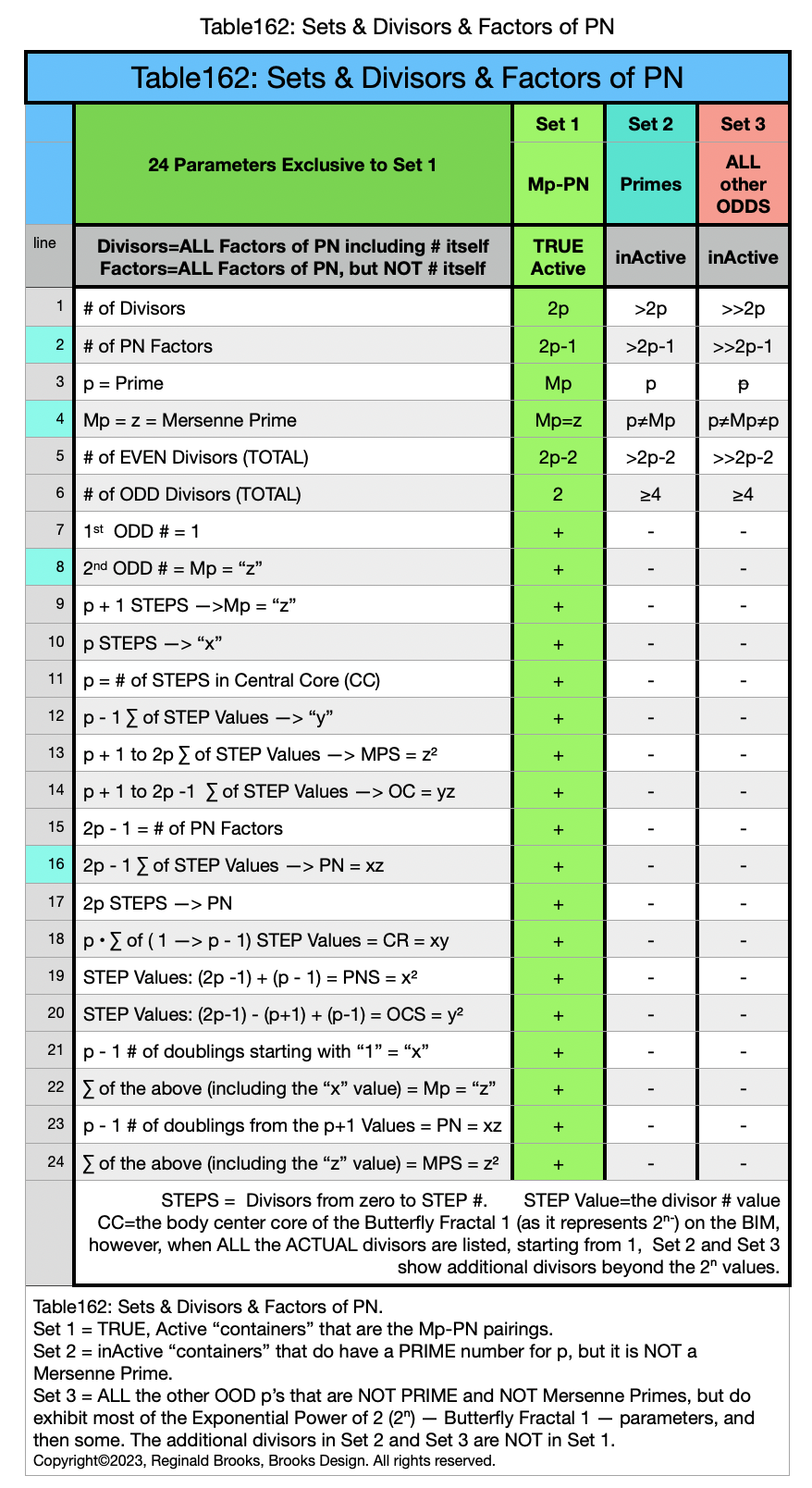
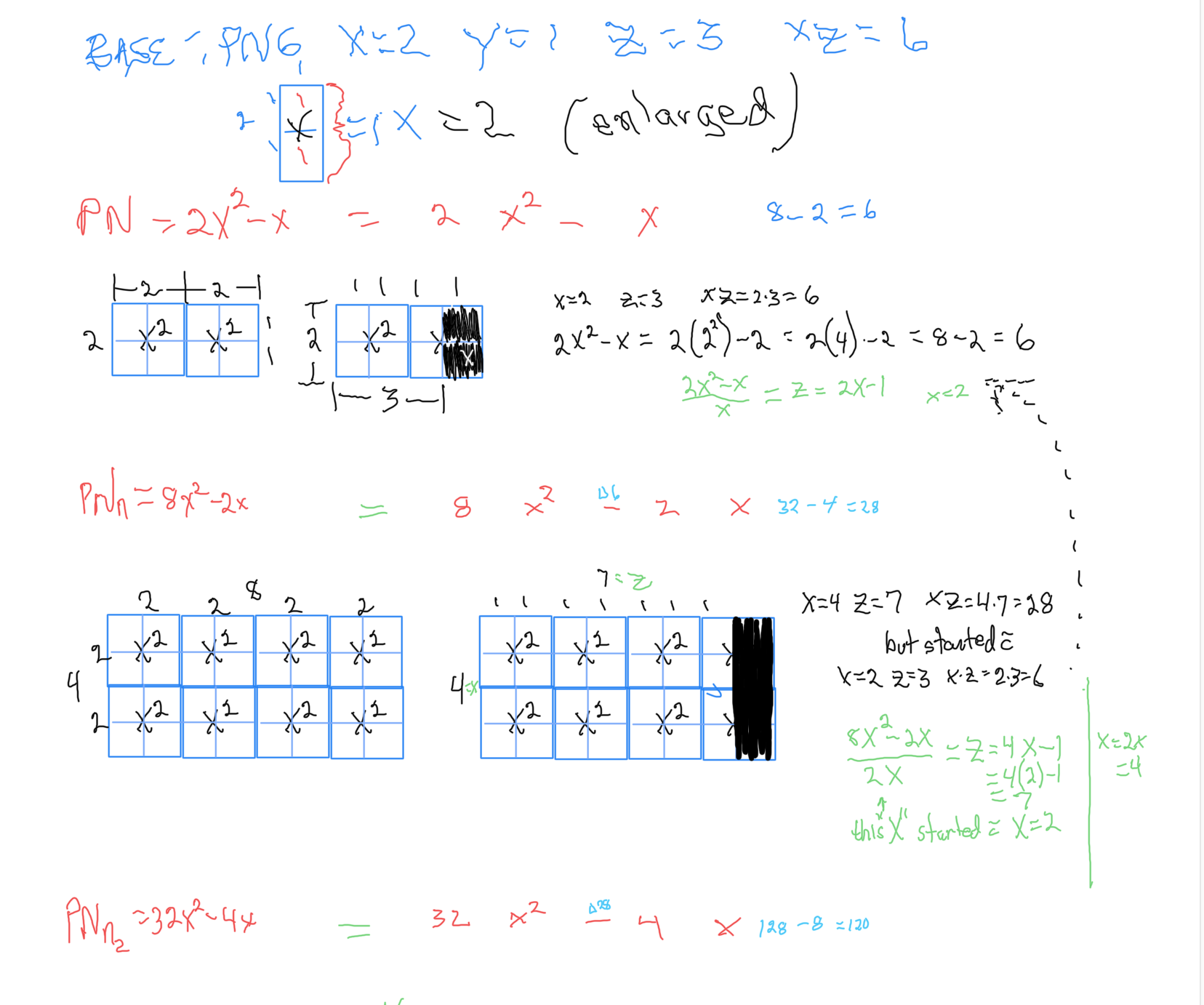
Note: As the PN=xz and z=Mp (Mersenne Prime), while x=(z+1)/2, All PN=EVEN as x=EVEN, z=ODD, and EVEN•ODD=EVEN.
Generic “containers” — as they contain all three Sets — are used in a general way and with the same terminology for number values that fill the same parameter slots. One must remain clear that only those in Set 1 are TRUE, Active “containers” holding Mp-PN pairings. All three Sets are required to see the underlying Butterfly Fractal 1 (2ⁿ) pattern. For example, p=Prime, but it is only a Mersenne Prime in Set 1, a simple, non-Mp in Set 2, and neither Mp, Prime or an ODD number in Set 3. p=n (where n=number 0,1,2,3...) when used in the context of “container” so as to bring out the underlying patterns that ALL three Sets enjoy.
Divisors are ALL the factors — including the # itself — for the PNs. Factors are ALL the factors — except for the # itself — for PNs.
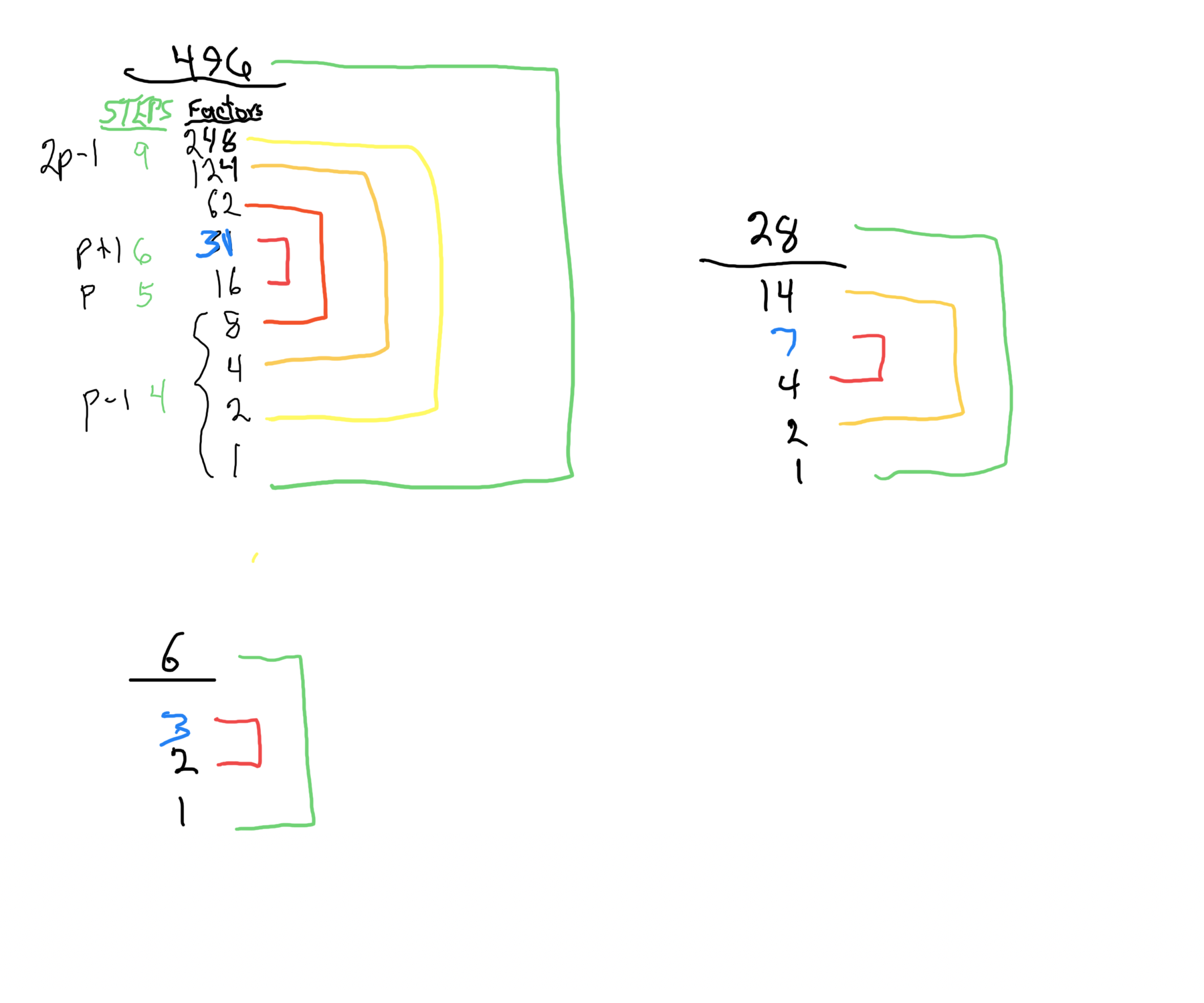
For PN: # of divisors - 1= # of factors.
p2
{1, 2, 3, 6} 4divisors -1= 3Factors
p3
{1, 2, 4, 7, 14, 28}. 6divisors -1=5Factors
p4 {1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120}. 15notP
16divisors -1=15Factors.
p5 {1, 2, 4, 8, 16, 31, 62, 124, 248, 496} 10divisors -1=9Factors.
p6 {1, 2, 3, 4, 6, 7, 8, 9, 12, 14, 16, 18, 21, 24, 28, 32, 36, 42, 48, 56, 63, 72, 84, 96, 112, 126, 144, 168, 224, 252, 288, 336, 504, 672, 1008, 2016} 36divisors -1=35Factors. ***63notP
p7 {1, 2, 4, 8, 16, 32, 64, 127, 254, 508, 1016, 2032, 4064, 8128} 14divisors -1=13Factors
p8 {1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40, 48, 51, 60, 64, 68, 80, 85, 96, 102, 120, 128, 136, 160, 170, 192, 204, 240, 255, 272, 320, 340, 384, 408, 480, 510, 544, 640, 680, 816, 960, 1020, 1088, 1360, 1632, 1920, 2040, 2176, 2720, 3264, 4080, 5440, 6528, 8160, 10880, 16320, 32640} 64divisors -1=63Factors. 255notP
p9 {1, 2, 4, 7, 8, 14, 16, 28, 32, 56, 64, 73, 112, 128, 146, 224, 256, 292, 448, 511, 584, 896, 1022, 1168, 1792, 2044, 2336, 4088, 4672, 8176, 9344, 16352, 18688, 32704, 65408, 130816} 36divisors -1=35Factors 511notP
p10 {1, 2, 3, 4, 6, 8, 11, 12, 16, 22, 24, 31, 32, 33, 44, 48, 62, 64, 66, 88, 93, 96, 124, 128, 132, 176, 186, 192, 248, 256, 264, 341, 352, 372, 384, 496, 512, 528, 682, 704, 744, 768, 992, 1023, 1056, 1364, 1408, 1488, 1536, 1984, 2046, 2112, 2728, 2816, 2976, 3968, 4092, 4224, 5456, 5632, 5952, 7936, 8184, 8448, 10912, 11904, 15872, 16368, 16896, 21824, 23808, 32736, 43648, 47616, 65472, 87296, 130944, 174592, 261888, 523776} 80divisors -1=79Factors 1023notP
p11 {1, 2, 4, 8, 16, 23, 32, 46, 64, 89, 92, 128, 178, 184, 256, 356, 368, 512, 712, 736, 1024, 1424, 1472, 2047, 2848, 2944, 4094, 5696, 5888, 8188, 11392, 11776, 16376, 22784, 23552, 32752, 45568, 65504, 91136, 131008, 262016, 524032, 1048064, 2096128} 44divisors -1=43Factors 2047notP
p12 {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 13, 14, 15, 16, 18, 20, 21, 24, 26, 28, 30, 32, 35, 36, 39, 40, 42, 45, 48, 52, 56, 60, 63, 64, 65, 70, 72, 78, 80, 84, 90, 91, 96, 104, 105, 112, 117, 120, 126, 128, 130, 140, 144, 156, 160, 168, 180, 182, 192, 195, 208, 210, 224, 234, 240, 252, 256, 260, 273, 280, 288, 312, 315, 320, 336, 360, 364, 384, 390, 416, 420, 448, 455, 468, 480, 504, 512, 520, 546, 560, 576, 585, 624, 630, 640, 672, 720, 728, 768, 780, 819, 832, 840, 896, 910, 936, 960, 1008, 1024, 1040, 1092, 1120, 1152, 1170, 1248, 1260, 1280, 1344, 1365, 1440, 1456, 1536, 1560, 1638, 1664, 1680, 1792, 1820, 1872, 1920, 2016, 2048, 2080, 2184, 2240, 2304, 2340, 2496, 2520, 2560, 2688, 2730, 2880, 2912, 3072, 3120, 3276, 3328, 3360, 3584, 3640, 3744, 3840, 4032, 4095, 4160, 4368, 4480, 4608, 4680, 4992, 5040, 5120, 5376, 5460, 5760, 5824, 6144, 6240, 6552, 6656, 6720, 7168, 7280, 7488, 7680, 8064, 8190, 8320, 8736, 8960, 9216, 9360, 9984, 10080, 10240, 10752, 10920, 11520, 11648, 12480, 13104, 13312, 13440, 14336, 14560, 14976, 15360, 16128, 16380, 16640, 17472, 17920, 18432, 18720, 19968, 20160, 21504, 21840, 23040, 23296, 24960, 26208, 26624, 26880, 29120, 29952, 30720, 32256, 32760, 33280, 34944, 35840, 37440, 39936, 40320, 43008, 43680, 46080, 46592, 49920, 52416, 53760, 58240, 59904, 64512, 65520, 66560, 69888, 71680, 74880, 79872, 80640, 87360, 92160, 93184, 99840, 104832, 107520, 116480, 119808, 129024, 131040, 133120, 139776, 149760, 161280, 174720, 186368, 199680, 209664, 215040, 232960, 239616, 262080, 279552, 299520, 322560, 349440, 399360, 419328, 465920, 524160, 559104, 599040, 645120, 698880, 838656, 931840, 1048320, 1198080, 1397760, 1677312, 2096640, 2795520, 4193280, 8386560} 288divisors -1=287Factors 4095notP
p13 {1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8191, 16382, 32764, 65528, 131056, 262112, 524224, 1048448, 2096896, 4193792, 8387584,16775168, 33550336} 26divisors -1=25Factors
p14 {1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 43, 48, 64, 86, 96, 127, 128, 129, 172, 192, 254, 256, 258, 344, 381, 384, 508, 512, 516, 688, 762, 768, 1016, 1024, 1032, 1376, 1524, 1536, 2032, 2048, 2064, 2752, 3048, 3072, 4064, 4096, 4128, 5461, 5504, 6096, 6144, 8128, 8192, 8256, 10922, 11008, 12192, 12288, 16256, 16383, 16512, 21844, 22016, 24384, 24576, 32512, 32766, 33024, 43688, 44032, 48768, 65024, 65532, 66048, 87376, 88064, 97536, 130048, 131064, 132096, 174752, 176128, 195072, 260096, 262128, 264192, 349504, 352256, 390144, 520192, 524256, 528384, 699008, 780288, 1040384, 1048512, 1056768, 1398016, 1560576, 2097024, 2796032, 3121152, 4194048, 5592064, 8388096, 11184128, 16776192, 22368256, 33552384, 44736512, 67104768, 134209536} 112divisors1 -1=111Factors 16383notP
p15 {1, 2, 4, 7, 8, 14, 16, 28, 31, 32, 56, 62, 64, 112, 124, 128, 151, 217, 224, 248, 256, 302, 434, 448, 496, 512, 604, 868, 896, 992, 1024, 1057, 1208, 1736, 1792, 1984, 2048, 2114, 2416, 3472, 3584, 3968, 4096, 4228, 4681, 4832, 6944, 7168, 7936, 8192, 8456, 9362, 9664, 13888, 14336, 15872, 16384, 16912, 18724, 19328, 27776, 28672, 31744, 32767, 33824, 37448, 38656, 55552, 57344, 63488, 65534, 67648, 74896, 77312, 111104, 114688, 126976, 131068, 135296, 149792, 154624, 222208, 253952, 262136, 270592, 299584, 309248, 444416, 507904, 524272, 541184, 599168, 618496, 888832, 1048544, 1082368, 1198336, 1236992, 1777664, 2097088, 2164736, 2396672, 2473984, 3555328, 4194176, 4329472, 4793344, 8388352, 8658944, 9586688, 16776704, 17317888, 19173376, 33553408, 38346752, 67106816, 76693504, 134213632, 268427264, 536854528} 120divisors -1=119Factors 32767notP
p16 {1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40, 48, 51, 60, 64, 68, 80, 85, 96, 102, 120, 128, 136, 160, 170, 192, 204, 240, 255, 256, 257, 272, 320, 340, 384, 408, 480, 510, 512, 514, 544, 640, 680, 768, 771, 816, 960, 1020, 1024, 1028, 1088, 1280, 1285, 1360, 1536, 1542, 1632, 1920, 2040, 2048, 2056, 2176, 2560, 2570, 2720, 3072, 3084, 3264, 3840, 3855, 4080, 4096, 4112, 4352, 4369, 5120, 5140, 5440, 6144, 6168, 6528, 7680, 7710, 8160, 8192, 8224, 8704, 8738, 10240, 10280, 10880, 12288, 12336, 13056, 13107, 15360, 15420, 16320, 16384, 16448, 17408, 17476, 20480, 20560, 21760, 21845, 24576, 24672, 26112, 26214, 30720, 30840, 32640, 32768, 32896, 34816, 34952, 40960, 41120, 43520, 43690, 49152, 49344, 52224, 52428, 61440, 61680, 65280, 65535, 65792, 69632, 69904, 81920, 82240, 87040, 87380, 98304, 98688, 104448, 104856, 122880, 123360, 130560, 131070, 131584, 139264, 139808, 163840, 164480, 174080, 174760, 197376, 208896, 209712, 245760, 246720, 261120, 262140, 263168, 278528, 279616, 328960, 348160, 349520, 394752, 417792, 419424,491520, 493440, 522240, 524280, 526336, 557056, 559232, 657920, 696320, 699040, 789504, 835584, 838848, 986880, 1044480, 1048560, 1052672, 1118464, 1315840, 1392640, 1398080, 1579008, 1671168, 1677696, 1973760, 2088960, 2097120, 2105344, 2236928, 2631680, 2785280, 2796160, 3158016, 3355392, 3947520, 4177920, 4194240, 4210688, 4473856, 5263360, 5592320, 6316032, 6710784, 7895040, 8355840, 8388480, 8421376, 8947712, 10526720, 11184640, 12632064, 13421568, 15790080, 16776960, 17895424, 21053440, 22369280, 25264128, 26843136, 31580160, 33553920, 35790848, 42106880, 44738560, 53686272, 63160320, 67107840, 71581696, 89477120, 107372544, 126320640, 134215680, 143163392, 178954240, 214745088, 268431360, 357908480, 429490176, 536862720, 715816960, 1073725440, 2147450880} 256divisors -1=255Factors 65535notP
p17
{1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, 16384, 32768, 65536, 131071, 262142, 524284, 1048568, 2097136, 4194272, 8388544, 16777088, 33554176, 67108352, 134216704, 268433408, 536866816, 1073733632, 2147467264, 4294934528, 8589869056} 34divisors -1=33Factors
p18 {1, 2, 3, 4, 6, 7, 8, 9, 12, 14, 16, 18, 19, 21, 24, 27, 28, 32, 36, 38, 42, 48, 54, 56, 57, 63, 64, 72, 73, 76, 84, 96, 108, 112, 114, 126, 128, 133, 144, 146, 152, 168, 171, 189, 192, 216, 219, 224, 228, 252, 256, 266, 288, 292, 304, 336, 342, 378, 384, 399, 432, 438, 448, 456, 504, 511, 512, 513, 532, 576, 584, 608, 657, 672, 684, 756, 768, 798, 864, 876, 896, 912, 1008, 1022, 1024, 1026, 1064, 1152, 1168, 1197, 1216, 1314, 1344, 1368, 1387, 1512, 1533, 1536, 1596, 1728, 1752, 1792, 1824, 1971, 2016, 2044, 2048, 2052, 2128, 2304, 2336, 2394, 2432, 2628, 2688, 2736, 2774, 3024, 3066, 3072, 3192, 3456, 3504, 3584, 3591, 3648, 3942, 4032, 4088, 4096, 4104, 4161, 4256, 4599, 4608, 4672, 4788, 4864, 5256, 5376, 5472, 5548, 6048, 6132, 6144, 6384, 6912, 7008, 7168, 7182, 7296, 7884, 8064, 8176, 8192, 8208, 8322, 8512, 9198, 9216, 9344, 9576, 9709, 9728, 10512, 10752, 10944, 11096, 12096, 12264, 12288, 12483, 12768, 13797, 13824, 14016, 14336, 14364, 14592, 15768, 16128, 16352, 16384, 16416, 16644, 17024, 18396, 18432, 18688, 19152, 19418, 19456, 21024, 21504, 21888, 22192, 24192, 24528, 24576, 24966, 25536, 27594, 27648, 28032, 28672, 28728, 29127, 29184, 31536, 32256, 32704, 32768, 32832, 33288, 34048, 36792, 36864, 37376, 37449, 38304, 38836, 38912, 42048, 43008, 43776, 44384, 48384, 49056, 49152, 49932, 51072, 55188, 55296, 56064, 57344, 57456, 58254, 58368, 63072, 64512, 65408, 65536, 65664, 66576, 68096, 73584, 73728, 74752, 74898, 76608, 77672, 77824, 84096, 86016, 87381, 87552, 88768, 96768, 98112, 98304, 99864, 102144, 110376, 110592, 112128, 114688, 114912, 116508, 116736, 126144, 129024, 130816, 131072, 131328, 133152, 136192, 147168, 147456, 149504, 149796, 153216, 155344, 155648, 168192, 172032, 174762, 175104,177536, 193536, 196224, 196608, 199728, 204288, 220752, 221184, 224256, 229376, 229824, 233016, 233472, 252288, 258048, 261632, 262143, 262656, 266304, 272384, 294336, 294912, 299008, 299592, 306432, 310688, 311296, 336384, 344064, 349524, 350208, 355072, 387072, 392448, 393216, 399456, 408576, 441504, 442368, 448512, 458752, 459648, 466032, 466944, 504576, 516096, 523264, 524286, 525312, 532608, 544768, 588672, 589824, 598016, 599184, 612864, 621376, 622592, 672768, 688128, 699048, 700416, 710144, 774144, 784896, 798912, 817152, 883008, 884736, 897024, 917504, 919296, 932064, 933888, 1009152, 1032192, 1046528, 1048572, 1050624, 1065216, 1089536, 1177344, 1179648, 1196032, 1198368, 1225728, 1242752, 1245184, 1345536, 1376256, 1398096, 1400832, 1420288, 1548288, 1569792, 1597824, 1634304, 1766016, 1769472, 1794048, 1838592, 1864128, 1867776, 2018304, 2064384, 2093056, 2097144, 2101248, 2130432, 2179072, 2354688, 2392064, 2396736, 2451456, 2485504, 2490368, 2691072, 2752512, 2796192, 2801664, 2840576, 3096576, 3139584, 3195648, 3268608, 3532032, 3538944, 3588096, 3677184, 3728256, 3735552, 4036608, 4128768, 4186112, 4194288, 4202496, 4260864, 4358144, 4709376, 4784128, 4793472, 4902912, 4971008, 5382144, 5592384, 5603328, 5681152, 6193152, 6279168, 6391296, 6537216, 7064064, 7176192, 7354368, 7456512, 7471104, 8073216, 8257536, 8372224, 8388576, 8404992, 8521728, 8716288, 9418752, 9568256, 9586944, 9805824, 9942016, 10764288, 11184768, 11206656, 11362304, 12386304, 12558336, 12782592, 13074432, 14128128, 14352384, 14708736, 14913024, 16146432, 16744448, 16777152, 16809984, 17043456, 17432576, 18837504, 19173888, 19611648, 19884032, 21528576, 22369536, 22413312, 22724608, 24772608, 25116672, 25565184, 26148864, 28256256, 28704768, 29417472, 29826048, 32292864, 33488896, 33554304, 33619968, 34086912, 37675008, 38347776, 39223296, 39768064, 43057152, 44739072, 45449216, 50233344, 51130368, 52297728, 56512512, 58834944, 59652096, 64585728, 66977792, 67108608, 67239936, 68173824, 75350016, 76695552, 78446592, 79536128, 86114304, 89478144, 90898432, 100466688, 102260736, 113025024, 117669888, 119304192, 129171456, 134217216, 136347648, 150700032, 153391104, 156893184, 159072256, 178956288, 181796864, 200933376, 204521472, 226050048, 235339776, 238608384, 258342912, 268434432, 272695296, 301400064, 306782208, 318144512, 357912576, 409042944, 452100096, 470679552, 477216768, 536868864, 545390592, 602800128, 613564416, 636289024, 715825152, 818085888, 904200192, 954433536, 1073737728, 1227128832, 1272578048, 1431650304, 1636171776, 1808400384, 1908867072, 2147475456, 2454257664, 2863300608, 3817734144, 4294950912, 4908515328, 5726601216, 8589901824, 11453202432, 17179803648, 34359607296} 576divisors -1=575Factors 262143notP
p19
{1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, 16384, 32768, 65536, 131072, 262144, 524287, 1048574, 2097148, 4194296, 8388592, 16777184, 33554368, 67108736, 134217472, 268434944, 536869888, 1073739776, 2147479552, 4294959104, 8589918208, 17179836416, 34359672832, 68719345664, 137438691328} 38divisors -1=37Factors
p20 {1, 2, 3, 4, 5, 6, 8, 10, 11, 12, 15, 16, 20, 22, 24, 25, 30, 31, 32, 33, 40, 41, 44, 48, 50, 55, 60, 62, 64, 66, 75, 80, 82, 88, 93, 96, 100, 110, 120, 123, 124, 128, 132, 150, 155, 160, 164, 165, 176, 186, 192, 200, 205, 220, 240, 246, 248, 256, 264, 275, 300, 310, 320, 328, 330, 341, 352, 372, 384, 400, 410, 440, 451, 465, 480, 492, 496, 512, 528, 550, 600, 615, 620, 640, 656, 660, 682, 704, 744, 768, 775, 800, 820, 825, 880, 902, 930, 960, 984, 992, 1023, 1024, 1025, 1056, 1100, 1200, 1230, 1240, 1271, 1280, 1312, 1320, 1353, 1364, 1408, 1488, 1536, 1550, 1600, 1640, 1650, 1705, 1760, 1804, 1860, 1920, 1968, 1984, 2046, 2048, 2050, 2112, 2200, 2255, 2325, 2400, 2460, 2480, 2542, 2560, 2624, 2640, 2706, 2728, 2816, 2976, 3072, 3075, 3100, 3200, 3280, 3300, 3410, 3520, 3608, 3720, 3813, 3840, 3936, 3968, 4092, 4096, 4100, 4224, 4400, 4510, 4650, 4800, 4920, 4960, 5084, 5115, 5120, 5248, 5280, 5412, 5456, 5632, 5952, 6144, 6150, 6200, 6355, 6400, 6560, 6600, 6765, 6820, 7040, 7216, 7440, 7626, 7680, 7872, 7936, 8184, 8192, 8200, 8448, 8525, 8800, 9020, 9300, 9600, 9840, 9920, 10168, 10230, 10240, 10496, 10560, 10824, 10912, 11264, 11275, 11904, 12288, 12300, 12400, 12710, 12800, 13120, 13200, 13530, 13640, 13981, 14080, 14432, 14880, 15252, 15360, 15744, 15872, 16368, 16384, 16400, 16896, 17050, 17600, 18040, 18600, 19065, 19200, 19680, 19840, 20336, 20460, 20480, 20992, 21120, 21648, 21824, 22528, 22550, 23808, 24576, 24600, 24800, 25420, 25575, 25600, 26240, 26400, 27060, 27280, 27962, 28160, 28864, 29760, 30504, 30720, 31488, 31744, 31775, 32736, 32768, 32800, 33792, 33825, 34100, 35200, 36080, 37200, 38130, 38400, 39360, 39680, 40672, 40920, 40960, 41943, 41984, 42240, 43296, 43648, 45056, 45100, 47616, 49152, 49200, 49600, 50840, 51150, 51200, 52480, 52800, 54120, 54560, 55924, 56320, 57728, 59520, 61008, 61440, 62976, 63488, 63550, 65472, 65536, 65600, 67584, 67650, 68200, 69905, 70400, 72160, 74400, 76260, 76800, 78720, 79360, 81344, 81840, 81920, 83886, 83968, 84480, 86592, 87296, 90112, 90200, 95232, 95325, 98304, 98400, 99200, 101680, 102300, 102400, 104960, 105600, 108240, 109120, 111848, 112640, 115456, 119040, 122016, 122880, 125952, 126976, 127100, 130944, 131072, 131200, 135168, 135300, 136400, 139810, 140800, 144320, 148800, 152520, 153600, 157440, 158720, 162688, 163680, 163840, 167772, 167936, 168960, 173184, 174592, 180224, 180400, 190464, 190650, 196608, 196800, 198400, 203360, 204600, 204800, 209715, 209920, 211200, 216480, 218240, 223696, 225280, 230912, 238080, 244032, 245760, 251904, 253952, 254200, 261888, 262144, 262400, 270336, 270600, 272800, 279620, 281600, 288640, 297600, 305040, 307200, 314880, 317440, 325376, 327360, 327680, 335544, 335872, 337920, 346368, 349184, 349525, 360448, 360800, 380928, 381300, 393216, 393600, 396800, 406720, 409200, 409600, 419430, 419840, 422400, 432960, 436480, 447392, 450560, 461824, 476160, 488064, 491520, 503808, 507904, 508400, 523776, 524288, 524800, 540672, 541200, 545600, 559240, 563200, 577280, 595200, 610080, 614400, 629760, 634880, 650752, 654720, 655360, 671088, 671744, 675840, 692736, 698368, 699050, 720896, 721600, 761856, 762600, 786432, 787200, 793600, 813440, 818400, 819200, 838860, 839680, 844800, 865920, 872960, 894784, 901120, 923648, 952320, 976128, 983040, 1007616, 1015808, 1016800, 1047552, 1048575, 1049600, 1081344, 1082400, 1091200, 1118480, 1126400, 1154560, 1190400, 1220160, 1228800, 1259520, 1269760, 1301504, 1309440, 1310720, 1342176, 1343488, 1351680, 1385472, 1396736, 1398100, 1441792, 1443200, 1523712, 1525200, 1572864, 1574400, 1587200, 1626880, 1636800, 1638400, 1677720, 1679360, 1689600, 1731840, 1745920, 1789568, 1802240, 1847296, 1904640, 1952256, 1966080, 2015232, 2031616, 2033600, 2095104, 2097150, 2099200, 2162688, 2164800, 2182400, 2236960, 2252800, 2309120, 2380800, 2440320, 2457600, 2519040, 2539520, 2603008, 2618880, 2621440, 2684352, 2686976, 2703360, 2770944, 2793472, 2796200, 2883584, 2886400, 3047424, 3050400, 3148800, 3174400, 3253760, 3273600, 3276800, 3355440, 3358720, 3379200, 3463680, 3491840, 3579136, 3604480, 3694592, 3809280, 3904512, 3932160, 4030464, 4063232, 4067200, 4190208, 4194300, 4198400, 4325376, 4329600, 4364800, 4473920, 4505600, 4618240, 4761600, 4880640, 4915200, 5038080, 5079040, 5206016, 5237760, 5368704, 5373952, 5406720, 5541888, 5586944, 5592400, 5767168, 5772800, 6094848, 6100800, 6297600, 6348800, 6507520, 6547200, 6553600, 6710880, 6717440, 6758400, 6927360, 6983680, 7158272, 7208960, 7389184, 7618560, 7809024, 7864320, 8060928, 8126464, 8134400, 8380416, 8388600, 8396800, 8650752, 8659200, 8729600, 8947840, 9011200, 9236480, 9523200, 9761280, 9830400, 10076160, 10158080, 10412032, 10475520, 10737408, 10747904, 10813440, 11083776, 11173888, 11184800, 11545600, 12189696, 12201600, 12595200, 12697600, 13015040, 13094400, 13107200, 13421760, 13434880, 13516800, 13854720, 13967360, 14316544, 14417920, 14778368, 15237120, 15618048, 16121856, 16252928, 16268800, 16760832, 16777200, 16793600, 17301504, 17318400, 17459200, 17895680, 18022400, 18472960, 19046400, 19522560, 19660800, 20152320, 20316160, 20824064, 20951040, 21474816, 21495808, 21626880, 22167552, 22347776, 22369600, 23091200, 24379392, 24403200, 25190400, 25395200, 26030080, 26188800, 26843520, 26869760, 27033600, 27709440, 27934720, 28633088, 28835840, 29556736, 30474240, 31236096, 32243712, 32537600, 33521664, 33554400, 33587200, 34636800, 34918400, 35791360, 36044800, 36945920, 38092800, 39045120, 39321600, 40304640, 40632320, 41648128, 41902080, 42949632, 43253760, 44335104, 44695552, 44739200, 46182400, 48758784, 48806400, 50380800, 50790400, 52060160, 52377600, 53687040, 53739520, 54067200, 55418880, 55869440, 57266176, 59113472, 60948480, 62472192, 64487424, 65075200, 67043328, 67108800, 67174400, 69273600, 69836800, 71582720, 72089600, 73891840, 76185600, 78090240, 80609280, 81264640, 83296256, 83804160, 85899264, 86507520, 88670208, 89391104, 89478400, 92364800, 97612800, 100761600, 101580800, 104120320, 104755200, 107374080, 107479040, 108134400, 110837760, 111738880, 114532352, 118226944, 121896960, 124944384, 130150400, 134086656, 134217600, 134348800, 138547200, 139673600, 143165440, 144179200, 147783680, 152371200, 156180480, 161218560, 166592512, 167608320, 171798528, 177340416, 178782208, 178956800, 184729600, 195225600, 201523200, 203161600, 208240640, 209510400, 214748160, 216268800, 221675520, 223477760, 229064704, 236453888, 243793920, 249888768, 260300800, 268173312, 268435200, 268697600, 277094400, 279347200, 286330880, 295567360, 304742400, 312360960, 322437120, 333185024, 335216640, 343597056, 354680832, 357913600, 369459200, 390451200, 403046400, 406323200, 416481280, 419020800, 429496320, 432537600, 443351040, 446955520, 458129408, 499777536, 520601600, 536346624, 536870400, 537395200, 554188800, 558694400, 572661760, 591134720, 609484800, 624721920, 666370048, 670433280, 687194112, 709361664, 715827200, 738918400, 780902400, 806092800, 832962560, 838041600, 858992640, 886702080, 893911040, 916258816, 999555072, 1041203200, 1073740800, 1108377600, 1117388800, 1145323520, 1182269440, 1218969600, 1249443840, 1340866560, 1374388224, 1431654400, 1477836800, 1561804800, 1612185600, 1665925120, 1676083200, 1717985280, 1773404160, 1832517632, 1999110144, 2082406400, 2147481600, 2216755200, 2234777600, 2290647040, 2498887680, 2681733120, 2748776448, 2863308800, 2955673600, 3123609600, 3331850240, 3352166400, 3435970560, 3546808320, 3665035264, 4164812800, 4294963200, 4433510400, 4469555200, 4581294080, 4997775360, 5497552896, 5726617600, 5911347200, 6247219200, 6704332800, 6871941120, 7330070528, 8329625600, 8589926400, 8867020800, 9162588160, 9995550720, 10995105792, 11453235200, 12494438400, 13408665600, 13743882240, 16659251200, 17179852800, 17734041600, 18325176320, 21990211584, 22906470400, 24988876800, 27487764480, 34359705600, 36650352640, 45812940800, 49977753600, 54975528960, 68719411200, 91625881600, 109951057920, 137438822400, 183251763200, 274877644800, 549755289600} 960 divisors -1=959Factors 1048575notP
p21 {1, 2, 4, 7, 8, 14, 16, 28, 32, 49, 56, 64, 98, 112, 127, 128, 196, 224, 254, 256, 337, 392, 448, 508, 512, 674, 784, 889, 896, 1016, 1024, 1348, 1568, 1778, 1792, 2032, 2048, 2359, 2696, 3136, 3556, 3584, 4064, 4096, 4718, 5392, 6223, 6272, 7112, 7168, 8128, 8192, 9436, 10784, 12446, 12544, 14224, 14336, 16256, 16384, 16513, 18872, 21568, 24892, 25088, 28448, 28672, 32512, 32768, 33026, 37744, 42799, 43136, 49784, 50176, 56896, 57344, 65024, 65536, 66052, 75488, 85598, 86272, 99568, 100352, 113792, 114688, 130048, 131072, 132104, 150976, 171196, 172544, 199136, 200704, 227584, 229376, 260096, 262144, 264208, 299593, 301952, 342392, 345088, 398272, 401408, 455168, 458752, 520192, 524288, 528416, 599186, 603904, 684784, 690176, 796544, 802816, 910336, 917504, 1040384, 1048576, 1056832, 1198372, 1207808, 1369568, 1380352, 1593088, 1605632, 1820672, 1835008, 2080768, 2097151, 2113664, 2396744, 2415616, 2739136, 2760704, 3186176, 3211264, 3641344, 3670016, 4161536, 4194302, 4227328, 4793488, 4831232, 5478272, 5521408, 6372352, 6422528, 7282688, 7340032, 8323072, 8388604, 8454656, 9586976, 9662464, 10956544, 11042816, 12744704, 12845056, 14565376, 16646144, 16777208, 16909312, 19173952, 19324928, 21913088, 22085632, 25489408, 25690112, 29130752, 33292288, 33554416, 33818624, 38347904, 38649856, 43826176, 44171264, 50978816, 51380224, 58261504, 66584576, 67108832, 67637248, 76695808, 77299712, 87652352, 88342528, 101957632, 116523008, 133169152, 134217664, 135274496, 153391616, 154599424, 175304704, 176685056, 203915264, 233046016, 268435328, 270548992, 306783232, 309198848, 350609408, 353370112, 407830528, 466092032, 536870656, 541097984, 613566464, 618397696, 701218816, 815661056, 932184064, 1073741312, 1082195968, 1227132928, 1236795392, 1402437632, 1631322112, 2147482624, 2164391936, 2454265856, 2473590784, 2804875264, 3262644224, 4294965248, 4328783872, 4908531712, 5609750528, 6525288448, 8589930496, 8657567744, 9817063424, 11219501056, 17179860992, 17315135488, 19634126848, 22439002112, 34359721984, 39268253696, 44878004224, 68719443968, 78536507392, 137438887936, 157073014784, 274877775872, 314146029568, 549755551744, 1099511103488, 2199022206976} 252 divisors -1=251Factors 2097151notP
p22 {1, 2, 3, 4, 6, 8, 12, 16, 23, 24, 32, 46, 48, 64, 69, 89, 92, 96, 128, 138, 178, 184, 192, 256, 267, 276, 356, 368, 384, 512, 534, 552, 683, 712, 736, 768, 1024, 1068, 1104, 1366, 1424, 1472, 1536, 2047, 2048, 2049, 2136, 2208, 2732, 2848, 2944, 3072, 4094, 4096, 4098, 4272, 4416, 5464, 5696, 5888, 6141, 6144, 8188, 8192, 8196, 8544, 8832, 10928, 11392, 11776, 12282, 12288, 15709, 16376, 16384, 16392, 17088, 17664, 21856, 22784, 23552, 24564, 24576, 31418, 32752, 32768, 32784, 34176, 35328, 43712, 45568, 47104, 47127, 49128, 49152, 60787, 62836, 65504, 65536, 65568, 68352, 70656, 87424, 91136, 94208, 94254, 98256, 98304, 121574, 125672, 131008, 131072, 131136, 136704, 141312, 174848, 182272, 182361, 188416, 188508, 196512, 196608, 243148, 251344, 262016, 262144, 262272, 273408, 282624, 349696, 364544, 364722, 376832, 377016, 393024, 393216, 486296, 502688, 524032, 524288, 524544, 546816, 565248, 699392, 729088, 729444, 753664, 754032, 786048, 786432, 972592, 1005376, 1048064, 1048576, 1049088, 1093632, 1130496, 1398101, 1398784, 1458176, 1458888, 1507328, 1508064, 1572096, 1572864, 1945184, 2010752, 2096128, 2097152, 2098176, 2187264, 2260992, 2796202, 2797568, 2916352, 2917776, 3014656, 3016128, 3144192, 3145728, 3890368, 4021504, 4192256, 4194303, 4196352, 4374528, 4521984, 5592404, 5595136, 5832704, 5835552, 6029312, 6032256, 6288384, 6291456, 7780736, 8043008, 8384512, 8388606, 8392704, 8749056, 9043968, 11184808, 11190272, 11665408, 11671104, 12058624, 12064512, 12576768, 15561472, 16086016, 16769024, 16777212, 16785408, 17498112, 18087936, 22369616, 22380544, 23330816, 23342208, 24117248, 24129024, 25153536, 31122944, 32172032, 33538048, 33554424, 33570816, 34996224, 36175872, 44739232, 44761088, 46661632, 46684416, 48234496, 48258048, 50307072, 62245888, 64344064, 67076096, 67108848, 67141632, 69992448, 72351744, 89478464, 89522176, 93323264, 93368832, 96516096, 100614144, 124491776, 128688128, 134152192, 134217696, 134283264, 139984896, 144703488, 178956928, 179044352, 186646528, 186737664, 193032192, 201228288, 248983552, 257376256, 268304384, 268435392, 268566528, 279969792, 357913856, 358088704, 373475328, 386064384, 402456576, 497967104, 514752512, 536608768, 536870784, 537133056, 559939584, 715827712, 716177408, 746950656, 772128768, 804913152, 995934208, 1029505024, 1073217536, 1073741568, 1074266112, 1431655424, 1432354816, 1493901312, 1544257536, 1609826304, 1991868416, 2059010048, 2146435072, 2147483136, 2148532224, 2863310848, 2987802624, 3088515072, 3219652608, 3983736832, 4118020096, 4292870144, 4294966272, 4297064448, 5726621696, 5975605248, 6177030144, 6439305216, 7967473664, 8236040192, 8589932544, 11453243392, 11951210496, 12354060288, 12878610432, 15934947328, 16472080384, 17179865088, 22906486784, 23902420992, 24708120576, 31869894656, 32944160768, 34359730176, 45812973568, 47804841984, 49416241152, 63739789312, 68719460352, 91625947136, 95609683968, 98832482304, 127479578624, 137438920704, 183251894272, 191219367936, 274877841408, 366503788544, 382438735872, 549755682816, 733007577088, 1099511365632, 1466015154176, 2199022731264, 2932030308352, 4398045462528, 8796090925056} 352 divisors -1=351Factors 4194303notP
p23 {1, 2, 4, 8, 16, 32, 47, 64, 94, 128, 188, 256, 376, 512, 752, 1024, 1504, 2048, 3008, 4096, 6016, 8192, 12032, 16384, 24064, 32768, 48128, 65536, 96256, 131072, 178481, 192512, 262144, 356962, 385024, 524288, 713924, 770048, 1048576, 1427848, 1540096, 2097152, 2855696, 3080192, 4194304, 5711392, 6160384, 8388607, 11422784, 12320768, 16777214, 22845568, 24641536, 33554428, 45691136, 49283072, 67108856, 91382272, 98566144, 134217712, 182764544, 197132288, 268435424, 365529088, 536870848, 731058176, 1073741696, 1462116352, 2147483392, 2924232704, 4294966784, 5848465408, 8589933568, 11696930816, 17179867136, 23393861632, 34359734272, 46787723264, 68719468544, 93575446528, 137438937088, 187150893056, 274877874176, 374301786112, 549755748352, 748603572224, 1099511496704, 2199022993408, 4398045986816, 8796091973632, 17592183947264, 35184367894528} 92 divisors -1-91Factors 8388607notP
p24 {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 13, 14, 15, 16, 17, 18, 20, 21, 24, 26, 28, 30, 32, 34, 35, 36, 39, 40, 42, 45, 48, 51, 52, 56, 60, 63, 64, 65, 68, 70, 72, 78, 80, 84, 85, 90, 91, 96, 102, 104, 105, 112, 117, 119, 120, 126, 128, 130, 136, 140, 144, 153, 156, 160, 168, 170, 180, 182, 192, 195, 204, 208, 210, 221, 224, 234, 238, 240, 241, 252, 255, 256, 260, 272, 273, 280, 288, 306, 312, 315, 320, 336, 340, 357, 360, 364, 384, 390, 408, 416, 420, 442, 448, 455, 468, 476, 480, 482, 504, 510, 512, 520, 544, 546, 560, 576, 585, 595, 612, 624, 630, 640, 663, 672, 680, 714, 720, 723, 728, 765, 768, 780, 816, 819, 832, 840, 884, 896, 910, 936, 952, 960, 964, 1008, 1020, 1024, 1040, 1071, 1088, 1092, 1105, 1120, 1152, 1170, 1190, 1205, 1224, 1248, 1260, 1280, 1326, 1344, 1360, 1365, 1428, 1440, 1446, 1456, 1530, 1536, 1547, 1560, 1632, 1638, 1664, 1680, 1687, 1768, 1785, 1792, 1820, 1872, 1904, 1920, 1928, 1989, 2016, 2040, 2048, 2080, 2142, 2169, 2176, 2184, 2210, 2240, 2304, 2340, 2380, 2410, 2448, 2496, 2520, 2560, 2652, 2688, 2720, 2730, 2856, 2880, 2892, 2912, 3060, 3072, 3094, 3120, 3133, 3264, 3276, 3315, 3328, 3360, 3374, 3536, 3570, 3584, 3615, 3640, 3744, 3808, 3840, 3856, 3978, 4032, 4080, 4095, 4096, 4097, 4160, 4284, 4338, 4352, 4368, 4420, 4480, 4608, 4641, 4680, 4760, 4820, 4896, 4992, 5040, 5061, 5120, 5304, 5355, 5376, 5440, 5460, 5712, 5760, 5784, 5824, 6120, 6144, 6188, 6240, 6266, 6528, 6552, 6630, 6656, 6720, 6748, 7072, 7140, 7168, 7230, 7280, 7488, 7616, 7680, 7712, 7735, 7956, 8064, 8160, 8190, 8192, 8194, 8320, 8435, 8568, 8676, 8704, 8736, 8840, 8960, 9216, 9282, 9360, 9399, 9520, 9640, 9792, 9945, 9984, 10080, ............. 140737479966720} 2304divisors -1-2303Factors
p25 {1, 2, 4, 8, 16, 31, 32, 62, 64, 124, 128, 248, 256, 496, 512, 601, 992, 1024, 1202, 1801, 1984, 2048, 2404, 3602, 3968, 4096, 4808, 7204, 7936, 8192, 9616, 14408, 15872, 16384, 18631, 19232, 28816, 31744, 32768, 37262, 38464, 55831, 57632, 63488, 65536, 74524, 76928, 111662, 115264, 126976, 131072, 149048, 153856, 223324, 230528, 253952, 262144, 298096, 307712, 446648, 461056, 507904, 524288, 596192, 615424, 893296, 922112, 1015808, 1048576, 1082401, 1192384, 1230848, 1786592, 1844224, 2031616, 2097152, 2164802, 2384768, 2461696, 3573184, 3688448, 4063232, 4194304, 4329604, 4769536, 4923392, 7146368, 7376896, 8126464, 8388608, 8659208, 9539072, 9846784, 14292736, .......562949936644096} 200divisors-1=199Factors
p26
{1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 64, 96, 128, 192, 256, 384, 512, 768, 1024, 1536, 2048, 2731, 3072, 4096, 5462, 6144, 8191, 8192, 8193, 10924, 12288, 16382, 16384, 16386, 21848, 24573, 24576, 32764, 32768, 32772, 43696, 49146, 49152, 65528, 65536, 65544, 87392, 98292, 98304, 131056, 131072, 131088, 174784, 196584, 196608, 262112, 262144, 262176, 349568, 393168, 393216, 524224, 524288, 524352, 699136, 786336, 786432, 1048448, 1048576, 1048704, 1398272, 1572672, 1572864, 2096896, 2097152, 2097408, 2796544, 3145344, 3145728, 4193792, 4194304, 4194816, 5593088, 6290688, 6291456, 8387584, 8388608, 8389632, 11186176, ...............2251799780130816} 208divisors -1=207Factors
p27 {1, 2, 4, 7, 8, 14, 16, 28, 32, 56, 64, 73, 112, 128, 146, 224, 256, 292, 448, 511, 512, 584, 896, 1022, 1024, 1168, 1792, 2044, 2048, 2336, 3584, 4088, 4096, 4672, 7168, 8176, 8192, 9344, 14336, 16352, 16384, 18688, 28672, 32704, 32768, 37376, 57344, 65408, 65536, 74752, 114688, 130816, 131072, 149504, 229376, 261632, 262144, 262657, 299008, 458752, 523264, 524288, 525314, 598016, 917504, 1046528, 1048576, 1050628, 1196032, 1835008, 1838599, 2093056, 2097152, 2101256, 2392064, 3670016, 3677198, 4186112, 4194304, 4202512, 4784128, 7340032, 7354396, 8372224, 8388608, 8405024, 9568256, 14680064, 14708792, 16744448, 16777216, 16810048, 19136512, 19173961, 29360128, 29417584, 33488896, 33554432, 33620096, 38273024, 38347922, 58720256, 58835168, 66977792, 67108864, 67240192, 76546048, 76695844, 117440512, ............. 9007199187632128} 216divisors -1=215Factors
p28 {1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 29, 30, 32, 40, 43, 48, 58, 60, 64, 80, 86, 87, 96, 113, 116, 120, 127, 128, 129, 145, 160, 172, 174, 192, 215, 226, 232, 240, 254, 256, 258, 290, 320, 339, 344, 348, 381, 384, 430, 435, 452, 464, 480, 508, 512, 516, 565, 580, 635, 640, 645, 678, 688, 696, 762, 768, 860, 870, 904, 928, 960, 1016, 1024, 1032, 1130, 1160, 1247, 1270, 1280, 1290, 1356, 1376, 1392, 1524, 1536, 1695, 1720, 1740, 1808, 1856, 1905, 1920, 2032, 2048, 2064, 2260, 2320, 2494, 2540, 2560, 2580, 2712, 2752, 2784, 3048, 3072, 3277, 3390, 3440, 3480, 3616, 3683, 3712, 3741, 3810, 3840, 4064, 4096, 4128, 4520, 4640, 4859, 4988, 5080, 5120, 5160, 5424, 5461, 5504, 5568, 6096, 6144, 6235, 6554, 6780, 6880, 6960, 7232, 7366, 7424, 7482, 7620, 7680, 8128, 8192, 8256, 9040, 9280, 9718, 9831, 9976, 10160, 10240, 10320, 10848, 10922, 11008, 11049, 11136, 12192, 12288, 12470, 13108, 13560, 13760, 13920, 14351, 14464, 14577, 14732, 14848, 14964, 15240, 15360, 16256, 16383, 16384, 16385, 16512, 18080, 18415, 18560, 18705, 19436, 19662, 19952, 20320, 20480, 20640, 21696, 21844, 22016, 22098, 22272, 24295, 24384, 24576, 24940, 26216, 27120, 27305, 27520, 27840, 28702, 28928, 29154, 29464, 29696, 29928, 30480, 30720, 32512, 32766, 32768, 32770, 33024, 36160, 36830, 37120, 37410, 38872, 39324, 39904, 40640, 40960, 41280, 43053, 43392, 43688, 44032, 44196, 44544, 48590, 48768, 49152, 49155, 49880, 52432, 54240, 54610, 55040, 55245, 55680, 57404, 57856, 58308, 58928, 59392, 59856, 60960, 61440, 65024, 65532, 65536, 65540, 66048, 71755, 72320, 72885, 73660, 74240, 74820, 77744, 78648, 79808, 81280, 81915, 81920, 82560, 86106, 86784, 87376, 88064, 88392, 89088, 97180, 97536, 98304, 98310, 99760, 104864, .................. 36028796884746240} 1792divisors -1=1791Factors
p29 {1, 2, 4, 8, 16, 32, 64, 128, 233, 256, 466, 512, 932, 1024, 1103, 1864, 2048, 2089, 2206, 3728, 4096, 4178, 4412, 7456, 8192, 8356, 8824, 14912, 16384, 16712, 17648, 29824, 32768, 33424, 35296, 59648, 65536, 66848, 70592, 119296, 131072, 133696, 141184, 238592, 256999, 262144, 267392, 282368, 477184, 486737, 513998, 524288, 534784, 564736, 954368, 973474, 1027996, 1048576, 1069568, 1129472, 1908736, 1946948, 2055992, 2097152, 2139136, 2258944, 2304167, 3817472, 3893896, 4111984, 4194304, 4278272, 4517888, 4608334, 7634944, 7787792, 8223968, 8388608, 8556544, 9035776, 9216668, 15269888, 15575584, 16447936, 16777216, 17113088, 18071552, 18433336, 30539776, 31151168, 32895872, 33554432, 34226176, 36143104, 36866672, 61079552, 62302336, 65791744, 67108864, 68452352, 72286208, 73733344, 122159104, 124604672, 131583488, 134217728, 136904704, 144572416, 147466688, 244318208, 249209344, 263166976, 268435456, 273809408, 289144832, 294933376, 488636416, 498418688, 526333952, 536870911, ............. 144115187807420416} 232divisors -1=231Factors
p30 {1, 2, 3, 4, 6, 7, 8, 9, 11, 12, 14, 16, 18, 21, 22, 24, 28, 31, 32, 33, 36, 42, 44, 48, 56, 62, 63, 64, 66, 72, 77, 84, 88, 93, 96, 99, 112, 124, 126, 128, 132, 144, 151, 154, 168, 176, 186, 192, 198, 217, 224, 231, 248, 252, 256, 264, 279, 288, 302, 308, 331, 336, 341, 352, 372, 384, 396, 434, 448, 453, 462, 496, 504, 512, 528, 558, 576, 604, 616, 651, 662, 672, 682, 693, 704, 744, 768, 792, 868, 896, 906, 924, 992, 993, 1008, 1023, 1024, 1056, 1057, 1116, 1152, 1208, 1232, 1302, 1324, 1344, 1359, 1364, 1386, 1408, 1488, 1536, 1584, 1661, 1736, 1792, 1812, 1848, 1953, 1984, 1986, 2016, 2046, 2048, 2112, 2114, 2232, 2304, 2317, 2387, 2416, 2464, 2604, 2648, 2688, 2718, 2728, 2772, 2816, 2976, 2979, 3069, 3072, 3168, 3171, 3322, 3472, 3584, 3624, 3641, 3696, 3906, 3968, 3972, 4032, 4092, 4096, 4224, 4228, 4464, 4608, 4634, 4681, 4774, 4832, 4928, 4983, 5208, 5296, 5376, 5436, 5456, 5544, 5632, 5952, 5958, 6138, 6144, 6336, 6342, 6644, 6944, 6951, 7161, 7168, 7248, 7282, 7392, 7812, 7936, 7944, 8064, 8184, 8192, 8448, 8456, 8928, 9216, 9268, 9362, 9513, 9548, 9664, 9856, 9966, 10261, 10416, 10592, 10752, 10872, 10912, 10923, 11088, 11264, 11627, 11904, 11916, 12276, 12288, 12672, 12684, 13288, 13888, 13902, 14043, 14322, 14336, 14496, 14564, 14784, 14949, 15624, 15872, 15888, 16128, 16368, 16384, 16896, 16912, 17856, 18432, 18536, 18724, 19026, 19096, 19328, 19712, 19932, 20522, 20832, 20853, 21184, 21483, 21504, 21744, 21824, 21846, 22176, 22528, 23254, 23808, 23832, 24552, 24576, 25344, 25368, 25487, 26576, 27776, 27804, 28086, 28644, 28672, 28992, 29128, 29568, 29898, 30783, 31248, 31744, 31776, 32256, 32736, 32767, 32768, 32769, 33792, 33824, 34881, 35712, 36864, 37072, 37448, 38052, 38192, 38656, 39424, 39864, 41044, 41664, 41706, 42129, 42368, 42966, 43008, 43488, 43648, 43692, 44352, 45056, 46508, 47616, 47664, 49104, 49152, 49981, 50688, 50736, 50974, 51491, 53152, 55552, 55608, 56172, 57288, 57344, 57984, 58256, 59136, 59796, 61566, 62496, 63488, 63552, 64512, 65472, 65534, 65536, 65538, 67584, 67648, 69762, 71424, 71827, 73728, 74144, 74896, 76104, 76384, 76461, 77312, 78848, 79728, 82088, 83328, 83412, 84258, 84736, 85932, 86016, 86976, 87296, 87384, 88704, 90112, 92349, 93016, 95232, 95328, 98208, 98301, 98304, 99962, 101376,..............576460751766552576} 2880divisors -1=2879Factors
p31
{1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, 16384, 32768, 65536, 131072, 262144, 524288, 1048576, 2097152, 4194304, 8388608, 16777216, 33554432, 67108864, 134217728, 268435456, 536870912, 1073741824, 2147483647, 4294967294, 8589934588, 17179869176, 34359738352, 68719476704, 137438953408, 274877906816, 549755813632, 1099511627264, 2199023254528, 4398046509056, 8796093018112, 17592186036224, 35184372072448, 70368744144896, 140737488289792, 281474976579584, 562949953159168, 1125899906318336, 2251799812636672, 4503599625273344, 9007199250546688, 18014398501093376, 36028797002186752, 72057594004373504, 144115188008747008, 288230376017494016, 576460752034988032, 1152921504069976064, 2305843008139952128} 62divisors -1=61Factors
p61
{1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, 16384, 32768, 65536, 131072, 262144, 524288, 1048576, 2097152, 4194304, 8388608, 16777216, 33554432, 67108864, 134217728, 268435456, 536870912, 1073741824, 2147483648, 4294967296, 8589934592, 17179869184, 34359738368, 68719476736, 137438953472, 274877906944, 549755813888, 1099511627776, 2199023255552, 4398046511104, 8796093022208, 17592186044416, 35184372088832, 70368744177664, 140737488355328, 281474976710656, 562949953421312, 1125899906842624, 2251799813685248, 4503599627370496, 9007199254740992, 18014398509481984, 36028797018963968, 72057594037927936, 144115188075855872, 288230376151711744, 576460752303423488, 1152921504606846976, 2305843009213693951, 4611686018427387902, 9223372036854775804, 18446744073709551608, 36893488147419103216, 73786976294838206432, 147573952589676412864, 295147905179352825728, 590295810358705651456, 1180591620717411302912, 2361183241434822605824, 4722366482869645211648, 9444732965739290423296, 18889465931478580846592, 37778931862957161693184, 75557863725914323386368, 151115727451828646772736, 302231454903657293545472, 604462909807314587090944, 1208925819614629174181888, 2417851639229258348363776, 4835703278458516696727552, 9671406556917033393455104, 19342813113834066786910208, 38685626227668133573820416, 77371252455336267147640832, 154742504910672534295281664, 309485009821345068590563328, 618970019642690137181126656, 1237940039285380274362253312, 2475880078570760548724506624, 4951760157141521097449013248, 9903520314283042194898026496, 19807040628566084389796052992, 39614081257132168779592105984, 79228162514264337559184211968, 158456325028528675118368423936, 316912650057057350236736847872, 633825300114114700473473695744, 1267650600228229400946947391488, 2535301200456458801893894782976, 5070602400912917603787789565952, 10141204801825835207575579131904, 20282409603651670415151158263808, 40564819207303340830302316527616, 81129638414606681660604633055232, 162259276829213363321209266110464, 324518553658426726642418532220928, 649037107316853453284837064441856, 1298074214633706906569674128883712, 2596148429267413813139348257767424, 5192296858534827626278696515534848, 10384593717069655252557393031069696, 20769187434139310505114786062139392, 41538374868278621010229572124278784, 83076749736557242020459144248557568, 166153499473114484040918288497115136, 332306998946228968081836576994230272, 664613997892457936163673153988460544, 1329227995784915872327346307976921088, 2658455991569831744654692615953842176} 122divisors -1=121Factors
p89
{1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, 16384, 32768, 65536, 131072, 262144, 524288, 1048576, 2097152, 4194304, 8388608, 16777216, 33554432, 67108864, 134217728, 268435456, 536870912, 1073741824, 2147483648, 4294967296, 8589934592, 17179869184, 34359738368, 68719476736, 137438953472, 274877906944, 549755813888, 1099511627776, 2199023255552, 4398046511104, 8796093022208, 17592186044416, 35184372088832, 70368744177664, 140737488355328, 281474976710656, 562949953421312, 1125899906842624, 2251799813685248, 4503599627370496, 9007199254740992, 18014398509481984, 36028797018963968, 72057594037927936, 144115188075855872, 288230376151711744, 576460752303423488, 1152921504606846976, 2305843009213693952, 4611686018427387904, 9223372036854775808, 18446744073709551616, 36893488147419103232, 73786976294838206464, 147573952589676412928, 295147905179352825856, 590295810358705651712, 1180591620717411303424, 2361183241434822606848, 4722366482869645213696, 9444732965739290427392, 18889465931478580854784, 37778931862957161709568, 75557863725914323419136, 151115727451828646838272, 302231454903657293676544, 604462909807314587353088, 1208925819614629174706176, 2417851639229258349412352, 4835703278458516698824704, 9671406556917033397649408, 19342813113834066795298816, 38685626227668133590597632, 77371252455336267181195264, 154742504910672534362390528, 309485009821345068724781056, 618970019642690137449562111, 1237940039285380274899124222, 2475880078570760549798248444, 4951760157141521099596496888, 9903520314283042199192993776, 19807040628566084398385987552, 39614081257132168796771975104, 79228162514264337593543950208, 158456325028528675187087900416, 316912650057057350374175800832, 633825300114114700748351601664, 1267650600228229401496703203328, 2535301200456458802993406406656, 5070602400912917605986812813312, 10141204801825835211973625626624, 20282409603651670423947251253248, 40564819207303340847894502506496, 81129638414606681695789005012992, 162259276829213363391578010025984, 324518553658426726783156020051968, 649037107316853453566312040103936, 1298074214633706907132624080207872, 2596148429267413814265248160415744, 5192296858534827628530496320831488, 10384593717069655257060992641662976, 20769187434139310514121985283325952, 41538374868278621028243970566651904, 83076749736557242056487941133303808, 166153499473114484112975882266607616, 332306998946228968225951764533215232, 664613997892457936451903529066430464, 1329227995784915872903807058132860928, 2658455991569831745807614116265721856, 5316911983139663491615228232531443712, 10633823966279326983230456465062887424, 21267647932558653966460912930125774848, 42535295865117307932921825860251549696, 85070591730234615865843651720503099392, 170141183460469231731687303441006198784, 340282366920938463463374606882012397568, 680564733841876926926749213764024795136, 1361129467683753853853498427528049590272, 2722258935367507707706996855056099180544, 5444517870735015415413993710112198361088, 10889035741470030830827987420224396722176, 21778071482940061661655974840448793444352, 43556142965880123323311949680897586888704, 87112285931760246646623899361795173777408, 174224571863520493293247798723590347554816, 348449143727040986586495597447180695109632, 696898287454081973172991194894361390219264, 1393796574908163946345982389788722780438528, 2787593149816327892691964779577445560877056, 5575186299632655785383929559154891121754112, 11150372599265311570767859118309782243508224, 22300745198530623141535718236619564487016448, 44601490397061246283071436473239128974032896, 89202980794122492566142872946478257948065792, 178405961588244985132285745892956515896131584, 356811923176489970264571491785913031792263168, 713623846352979940529142983571826063584526336, 1427247692705959881058285967143652127169052672, 2854495385411919762116571934287304254338105344, 5708990770823839524233143868574608508676210688, 11417981541647679048466287737149217017352421376, 22835963083295358096932575474298434034704842752, 45671926166590716193865150948596868069409685504, 91343852333181432387730301897193736138819371008, 182687704666362864775460603794387472277638742016, 365375409332725729550921207588774944555277484032, 730750818665451459101842415177549889110554968064, 1461501637330902918203684830355099778221109936128, 2923003274661805836407369660710199556442219872256, 5846006549323611672814739321420399112884439744512, 11692013098647223345629478642840798225768879489024, 23384026197294446691258957285681596451537758978048, 46768052394588893382517914571363192903075517956096, 93536104789177786765035829142726385806151035912192, 187072209578355573530071658285452771612302071824384, 374144419156711147060143316570905543224604143648768, 748288838313422294120286633141811086449208287297536, 1496577676626844588240573266283622172898416574595072, 2993155353253689176481146532567244345796833149190144, 5986310706507378352962293065134488691593666298380288, 11972621413014756705924586130268977383187332596760576, 23945242826029513411849172260537954766374665193521152, 47890485652059026823698344521075909532749330387042304, 95780971304118053647396689042151819065498660774084608, 191561942608236107294793378084303638130997321548169216} 178divisors -1=177Factors
p107
{1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, 16384, 32768, 65536, 131072, 262144, 524288, 1048576, 2097152, 4194304, 8388608, 16777216, 33554432, 67108864, 134217728, 268435456, 536870912, 1073741824, 2147483648, 4294967296, 8589934592, 17179869184, 34359738368, 68719476736, 137438953472, 274877906944, 549755813888, 1099511627776, 2199023255552, 4398046511104, 8796093022208, 17592186044416, 35184372088832, 70368744177664, 140737488355328, 281474976710656, 562949953421312, 1125899906842624, 2251799813685248, 4503599627370496, 9007199254740992, 18014398509481984, 36028797018963968, 72057594037927936, 144115188075855872, 288230376151711744, 576460752303423488, 1152921504606846976, 2305843009213693952, 4611686018427387904, 9223372036854775808, 18446744073709551616, 36893488147419103232, 73786976294838206464, 147573952589676412928, 295147905179352825856, 590295810358705651712, 1180591620717411303424, 2361183241434822606848, 4722366482869645213696, 9444732965739290427392, 18889465931478580854784, 37778931862957161709568, 75557863725914323419136, 151115727451828646838272, 302231454903657293676544, 604462909807314587353088, 1208925819614629174706176, 2417851639229258349412352, 4835703278458516698824704, 9671406556917033397649408, 19342813113834066795298816, 38685626227668133590597632, 77371252455336267181195264, 154742504910672534362390528, 309485009821345068724781056, 618970019642690137449562112, 1237940039285380274899124224, 2475880078570760549798248448, 4951760157141521099596496896, 9903520314283042199192993792, 19807040628566084398385987584, 39614081257132168796771975168, 79228162514264337593543950336, 158456325028528675187087900672, 316912650057057350374175801344, 633825300114114700748351602688, 1267650600228229401496703205376, 2535301200456458802993406410752, 5070602400912917605986812821504, 10141204801825835211973625643008, 20282409603651670423947251286016, 40564819207303340847894502572032, 81129638414606681695789005144064, 162259276829213363391578010288127, 324518553658426726783156020576254, 649037107316853453566312041152508, 1298074214633706907132624082305016, 2596148429267413814265248164610032, 5192296858534827628530496329220064, 10384593717069655257060992658440128, 20769187434139310514121985316880256, 41538374868278621028243970633760512, 83076749736557242056487941267521024, 166153499473114484112975882535042048, 332306998946228968225951765070084096, 664613997892457936451903530140168192, 1329227995784915872903807060280336384, 2658455991569831745807614120560672768, 5316911983139663491615228241121345536, 10633823966279326983230456482242691072, 21267647932558653966460912964485382144, 42535295865117307932921825928970764288, 85070591730234615865843651857941528576, 170141183460469231731687303715883057152, 340282366920938463463374607431766114304, 680564733841876926926749214863532228608, 1361129467683753853853498429727064457216, 2722258935367507707706996859454128914432, 5444517870735015415413993718908257828864, 10889035741470030830827987437816515657728, 21778071482940061661655974875633031315456, 43556142965880123323311949751266062630912, 87112285931760246646623899502532125261824, 174224571863520493293247799005064250523648, 348449143727040986586495598010128501047296, 696898287454081973172991196020257002094592, 1393796574908163946345982392040514004189184, 2787593149816327892691964784081028008378368, 5575186299632655785383929568162056016756736, 11150372599265311570767859136324112033513472, 22300745198530623141535718272648224067026944, 44601490397061246283071436545296448134053888, 89202980794122492566142873090592896268107776, 178405961588244985132285746181185792536215552, 356811923176489970264571492362371585072431104, 713623846352979940529142984724743170144862208, 1427247692705959881058285969449486340289724416, 2854495385411919762116571938898972680579448832, 5708990770823839524233143877797945361158897664, 11417981541647679048466287755595890722317795328, 22835963083295358096932575511191781444635590656, 45671926166590716193865151022383562889271181312, 91343852333181432387730302044767125778542362624, 182687704666362864775460604089534251557084725248, 365375409332725729550921208179068503114169450496, 730750818665451459101842416358137006228338900992, 1461501637330902918203684832716274012456677801984, 2923003274661805836407369665432548024913355603968, 5846006549323611672814739330865096049826711207936, 11692013098647223345629478661730192099653422415872, 23384026197294446691258957323460384199306844831744, 46768052394588893382517914646920768398613689663488, 93536104789177786765035829293841536797227379326976, 187072209578355573530071658587683073594454758653952, 374144419156711147060143317175366147188909517307904, 748288838313422294120286634350732294377819034615808, 1496577676626844588240573268701464588755638069231616, 2993155353253689176481146537402929177511276138463232, 5986310706507378352962293074805858355022552276926464, 11972621413014756705924586149611716710045104553852928, 23945242826029513411849172299223433420090209107705856, 47890485652059026823698344598446866840180418215411712, 95780971304118053647396689196893733680360836430823424, 191561942608236107294793378393787467360721672861646848, 383123885216472214589586756787574934721443345723293696, 766247770432944429179173513575149869442886691446587392, 1532495540865888858358347027150299738885773382893174784, 3064991081731777716716694054300599477771546765786349568, 6129982163463555433433388108601198955543093531572699136, 12259964326927110866866776217202397911086187063145398272, 24519928653854221733733552434404795822172374126290796544, 49039857307708443467467104868809591644344748252581593088, 98079714615416886934934209737619183288689496505163186176, 196159429230833773869868419475238366577378993010326372352, 392318858461667547739736838950476733154757986020652744704, 784637716923335095479473677900953466309515972041305489408, 1569275433846670190958947355801906932619031944082610978816, 3138550867693340381917894711603813865238063888165221957632, 6277101735386680763835789423207627730476127776330443915264, 12554203470773361527671578846415255460952255552660887830528, 25108406941546723055343157692830510921904511105321775661056, 50216813883093446110686315385661021843809022210643551322112, 100433627766186892221372630771322043687618044421287102644224, 200867255532373784442745261542644087375236088842574205288448, 401734511064747568885490523085288174750472177685148410576896, 803469022129495137770981046170576349500944355370296821153792, 1606938044258990275541962092341152699001888710740593642307584, 3213876088517980551083924184682305398003777421481187284615168, 6427752177035961102167848369364610796007554842962374569230336, 12855504354071922204335696738729221592015109685924749138460672, 25711008708143844408671393477458443184030219371849498276921344, 51422017416287688817342786954916886368060438743698996553842688, 102844034832575377634685573909833772736120877487397993107685376, 205688069665150755269371147819667545472241754974795986215370752, 411376139330301510538742295639335090944483509949591972430741504, 822752278660603021077484591278670181888967019899183944861483008, 1645504557321206042154969182557340363777934039798367889722966016 , 3291009114642412084309938365114680727555868079596735779445932032 , 6582018229284824168619876730229361455111736159193471558891864064, 131640364585696483372397534604587229102234723183869431177837 28128} 214divisors -1=213Factors
p127
{1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, 16384, 32768, 65536, 131072, 262144, 524288, 1048576, 2097152, 4194304, 8388608, 16777216, 33554432, 67108864, 134217728, 268435456, 536870912, 1073741824, 2147483648, 4294967296, 8589934592, 17179869184, 34359738368, 68719476736, 137438953472, 274877906944, 549755813888, 1099511627776, 2199023255552, 4398046511104, 8796093022208, 17592186044416, 35184372088832, 70368744177664, 140737488355328, 281474976710656, 562949953421312, 1125899906842624, 2251799813685248, 4503599627370496, 9007199254740992, 18014398509481984, 36028797018963968, 72057594037927936, 144115188075855872, 288230376151711744, 576460752303423488, 1152921504606846976, 2305843009213693952, 4611686018427387904, 9223372036854775808, 18446744073709551616, 36893488147419103232, 73786976294838206464, 147573952589676412928, 295147905179352825856, 590295810358705651712, 1180591620717411303424, 2361183241434822606848, 4722366482869645213696, 9444732965739290427392, 18889465931478580854784, 37778931862957161709568, 75557863725914323419136, 151115727451828646838272, 302231454903657293676544, 604462909807314587353088, 1208925819614629174706176, 2417851639229258349412352, 4835703278458516698824704, 9671406556917033397649408, 19342813113834066795298816, 38685626227668133590597632, 77371252455336267181195264, 154742504910672534362390528, 309485009821345068724781056, 618970019642690137449562112, 1237940039285380274899124224, 2475880078570760549798248448, 4951760157141521099596496896, 9903520314283042199192993792, 19807040628566084398385987584, 39614081257132168796771975168, 79228162514264337593543950336, 158456325028528675187087900672, 316912650057057350374175801344, 633825300114114700748351602688, 1267650600228229401496703205376, 2535301200456458802993406410752, 5070602400912917605986812821504, 10141204801825835211973625643008, 20282409603651670423947251286016, 40564819207303340847894502572032, 81129638414606681695789005144064, 162259276829213363391578010288128, 324518553658426726783156020576256, 649037107316853453566312041152512, 1298074214633706907132624082305024, 2596148429267413814265248164610048, 5192296858534827628530496329220096, 10384593717069655257060992658440192, 20769187434139310514121985316880384, 41538374868278621028243970633760768, 83076749736557242056487941267521536, 166153499473114484112975882535043072, 332306998946228968225951765070086144, 664613997892457936451903530140172288, 1329227995784915872903807060280344576, 2658455991569831745807614120560689152, 5316911983139663491615228241121378304, 10633823966279326983230456482242756608, 21267647932558653966460912964485513216, 42535295865117307932921825928971026432, 85070591730234615865843651857942052864, 170141183460469231731687303715884105727, 340282366920938463463374607431768211454, 680564733841876926926749214863536422908, 1361129467683753853853498429727072845816, 2722258935367507707706996859454145691632, 5444517870735015415413993718908291383264, 10889035741470030830827987437816582766528, 21778071482940061661655974875633165533056, 43556142965880123323311949751266331066112, 87112285931760246646623899502532662132224, 174224571863520493293247799005065324264448, 348449143727040986586495598010130648528896, 696898287454081973172991196020261297057792, 1393796574908163946345982392040522594115584, 2787593149816327892691964784081045188231168, 5575186299632655785383929568162090376462336, 11150372599265311570767859136324180752924672, 22300745198530623141535718272648361505849344, 44601490397061246283071436545296723011698688, 89202980794122492566142873090593446023397376, 178405961588244985132285746181186892046794752, 356811923176489970264571492362373784093589504, 713623846352979940529142984724747568187179008, 1427247692705959881058285969449495136374358016, 2854495385411919762116571938898990272748716032, 5708990770823839524233143877797980545497432064, 11417981541647679048466287755595961090994864128, 22835963083295358096932575511191922181989728256, 45671926166590716193865151022383844363979456512, 91343852333181432387730302044767688727958913024, 182687704666362864775460604089535377455917826048, 365375409332725729550921208179070754911835652096, 730750818665451459101842416358141509823671304192, 1461501637330902918203684832716283019647342608384, 2923003274661805836407369665432566039294685216768, 5846006549323611672814739330865132078589370433536, 11692013098647223345629478661730264157178740867072, 23384026197294446691258957323460528314357481734144, 46768052394588893382517914646921056628714963468288, 93536104789177786765035829293842113257429926936576, 187072209578355573530071658587684226514859853873152, 374144419156711147060143317175368453029719707746304, 748288838313422294120286634350736906059439415492608, 1496577676626844588240573268701473812118878830985216, 2993155353253689176481146537402947624237757661970432, 5986310706507378352962293074805895248475515323940864, 11972621413014756705924586149611790496951030647881728, 23945242826029513411849172299223580993902061295763456, 47890485652059026823698344598447161987804122591526912, 95780971304118053647396689196894323975608245183053824, 191561942608236107294793378393788647951216490366107648, 383123885216472214589586756787577295902432980732215296, 766247770432944429179173513575154591804865961464430592, 1532495540865888858358347027150309183609731922928861184, 3064991081731777716716694054300618367219463845857722368, 6129982163463555433433388108601236734438927691715444736, 12259964326927110866866776217202473468877855383430889472, 24519928653854221733733552434404946937755710766861778944, 49039857307708443467467104868809893875511421533723557888, 98079714615416886934934209737619787751022843067447115776, 196159429230833773869868419475239575502045686134894231552, 392318858461667547739736838950479151004091372269788463104, 784637716923335095479473677900958302008182744539576926208, 1569275433846670190958947355801916604016365489079153852416, 3138550867693340381917894711603833208032730978158307704832, 6277101735386680763835789423207666416065461956316615409664, 12554203470773361527671578846415332832130923912633230819328, 25108406941546723055343157692830665664261847825266461638656, 50216813883093446110686315385661331328523695650532923277312, 100433627766186892221372630771322662657047391301065846554624, 200867255532373784442745261542645325314094782602131693109248, 401734511064747568885490523085290650628189565204263386218496, 803469022129495137770981046170581301256379130408526772436992, 1606938044258990275541962092341162602512758260817053544873984, 3213876088517980551083924184682325205025516521634107089747968, 6427752177035961102167848369364650410051033043268214179495936, 12855504354071922204335696738729300820102066086536428358991872, 25711008708143844408671393477458601640204132173072856717983744, 51422017416287688817342786954917203280408264346145713435967488, 102844034832575377634685573909834406560816528692291426871934976, 205688069665150755269371147819668813121633057384582853743869952, 411376139330301510538742295639337626243266114769165707487739904, 822752278660603021077484591278675252486532229538331414975479808, 1645504557321206042154969182557350504973064459076662829950959616, 3291009114642412084309938365114701009946128918153325659901919232, 6582018229284824168619876730229402019892257836306651319803838464 , 131640364585696483372397534604588040397845156726133026396076769 28, 2632807291713929667447950692091760807956903134522660527921535385 6, 5265614583427859334895901384183521615913806269045321055843070771 2, 10531229166855718669791802768367043231827612538090642111686141542 4, 2106245833371143733958360553673408646365522507618128422337228308 48, 42124916667422874679167211073468172927310450152362568446744566169 6, 84249833334845749358334422146936345854620900304725136893489132 3392, 168499666669691498716668844293872691709241800609450273786978264 6784, 336999333339382997433337688587745383418483601218900547573956529 3568, 6739986666787659948666753771754907668369672024378010951479130587 136, 1347997333357531989733350754350981533673934404875602190295826117 4272, 2695994666715063979466701508701963067347868809751204380591652234 8544, 5391989333430127958933403017403926134695737619502408761183304469 7088, 107839786668602559178668060348078522693914752390048175223666089 394176, 2156795733372051183573361206961570453878295047800963504473321787 88352, 4313591466744102367146722413923140907756590095601927008946643575 76704, 86271829334882047342934448278462818155131801912038540178932871515 3408, 172543658669764094685868896556925636310263603824077080357865743 0306816, 345087317339528189371737793113851272620527207648154160715731486061 3632, 6901746346790563787434755862277025452410544152963083214314629721 227264, 1380349269358112757486951172455405090482108830592616642862925944 2454528, 2760698538716225514973902344910810180964217661185233285725851888 4909056, 5521397077432451029947804689821620361928435322370466571451703776 9818112, 110427941548649020598956093796432407238568706447409331429034075 539636224, 22085588309729804119791218759286481447713741289481866285806815107 9272448, 44171176619459608239582437518572962895427482578963732571613630215 8544896, 8834235323891921647916487503714592579085496515792746514322726043 17089792, 1766847064778384329583297500742918515817099303158549302864545208 634179584, 3533694129556768659166595001485837031634198606317098605729090417 268359168, 70673882591135373183331900029716740632683972126341972114581808345 36718336, 1413477651822707463666638000594334812653679442526839442291636166 9073436672, 282695530364541492733327600118866962530735888505367888458327233 38146873344, 5653910607290829854666552002377339250614717770107357769166544667 6293746688, 11307821214581659709333104004754678501229435540214715538333089335 2587493376, 2261564242916331941866620800950935700245887108042943107666617867 05174986752, 45231284858326638837332416019018714004917742160858862153332357341 0349973504, 339046256971665327767466483203803742800983548432171772430666471 46820699947008, 180925139433306555349329664076074856019670968643435448613329429 3641399894016, 3618502788666131106986593281521497120393419372868708972266588587 282799788032, 72370055773322622139731865630429942407868387457374179445331771745 65599576064, 144740111546645244279463731260859884815736774914748358890663 54349131199152128} 254divisors -1=253Factors
If we focus on the Set 2 ODDs we find the same simple BF1 Template pattern found in the TRUE Mp Set 1 ODDs, only it is buffered by additional factors.
Actually, the same is true for the Set 3 ODDs like 15, 63, 255..., only more so.
Here are some truncated examples from several of the Set 2 ODDs. Notice that the BF1 Template numbers (UNDERLINED) — shown below the actual factors line — are, indeed, embedded in the Divisor-Factor list. Sets 2 and 3 ALWAYS contain additional factor-divisors with Set 3>Set 2. Set 1 is distinguished by have NO additional factors other than the ones whose sum = PN.
p11 {1, 2, 4, 8, 16, 23, 32, 46, 64, 89, 92, 128, 178, 184, 256, 356, 368, 512, 712, 736, 1024, 1424, 1472, 2047,...
1-2–4–8–16⸻32⸻64⸻—-128⸻⸺-256⸻⸻512 ⸻⸻1024
p23 {1, 2, 4, 8, 16, 32, 47, 64, 94, 128, 188, 256, 376, 512, 752, 1024, 1504, 2048, 3008, 4096, 6016, 8192, 12032, 16384, 24064, 32768,
1-2–4–8–16—32⸺-64⸺-128⸻256⸻-512⸻1024⸻—2048 ⸻—4096⸻—8192⸻—-16384⸻⸺32768⸻
48128, 65536, 96256, 131072, 178481, 192512, 262144, 356962, 385024, 524288, 713924, 770048, 1048576, 1427848, 1540096,
⸻-65536⸻⸺131072⸻⸻⸻-262144 ⸻⸻⸻—-524288 ⸻⸻⸻—1048576⸻⸻⸻
2097152, 2855696, 3080192, 4194304, 5711392, 6160384, 8388607,...
2097152⸻⸻⸻⸺41943004
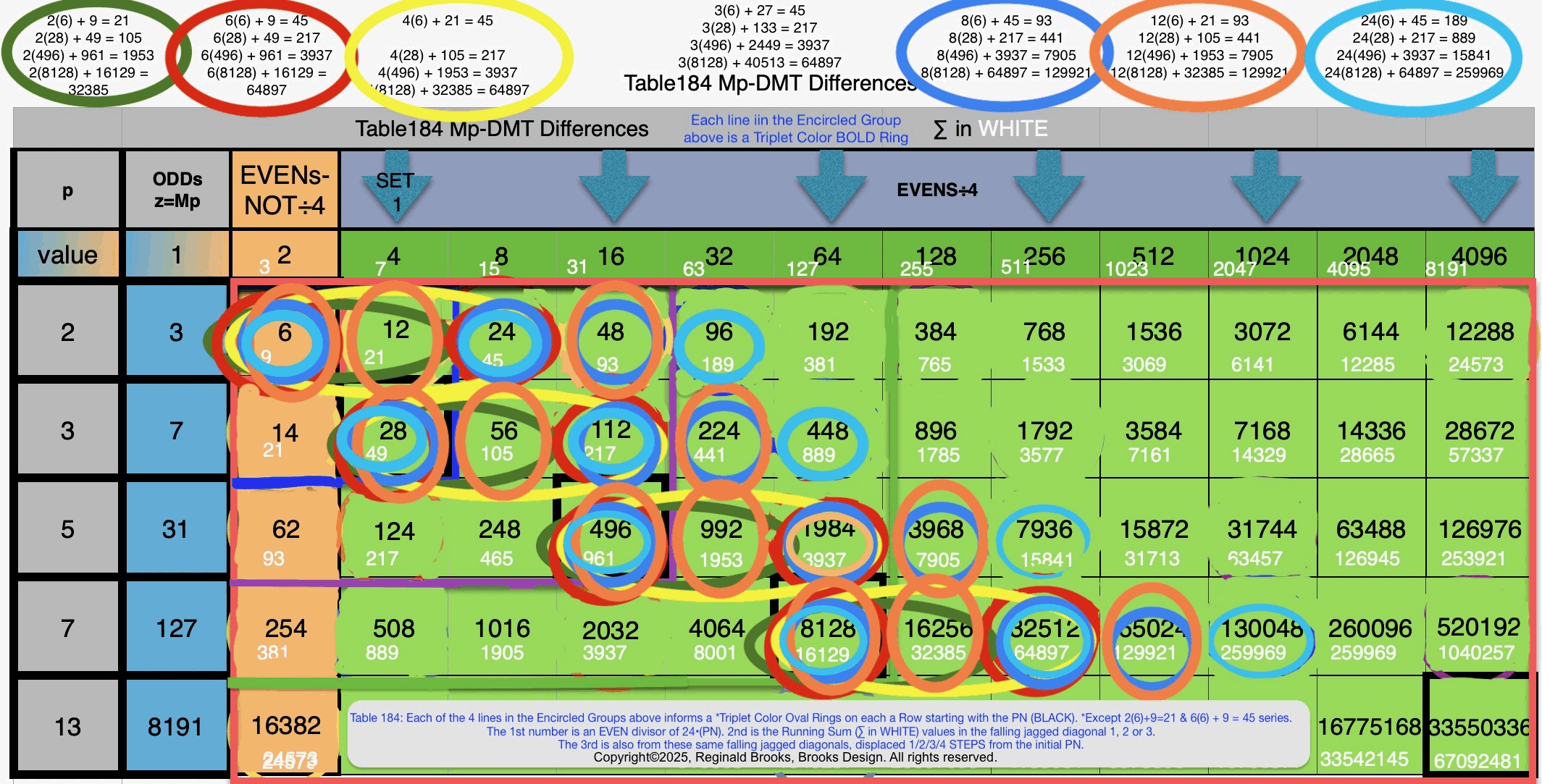
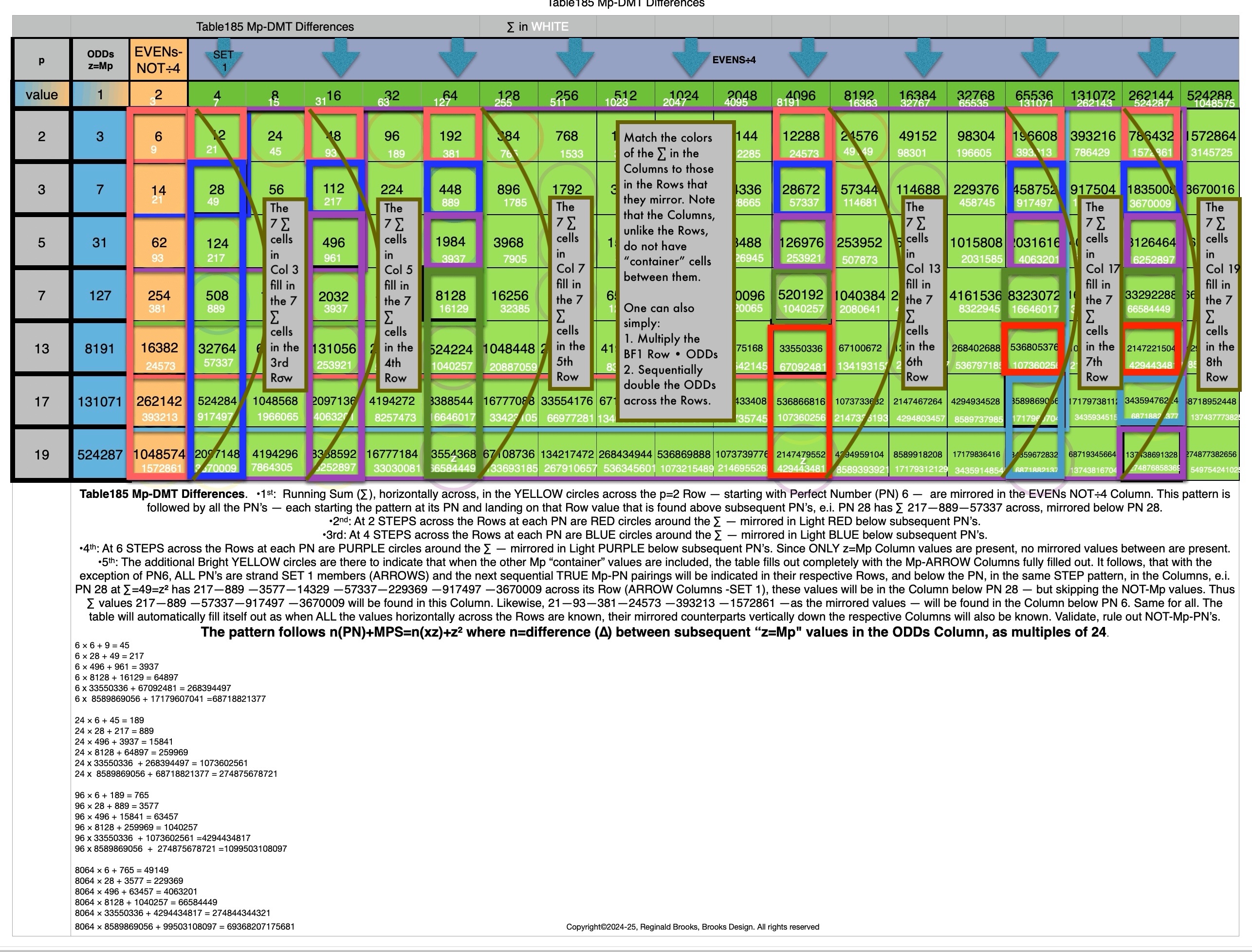
In earlier work in this series, we detailed how the TRUE Set 1 Mp-PN pairings played out in the formation of the Mersenne Prime Square (MPS=z² ). Set 2 and 3 entries — with their additional factor entries — ONLY follow this template pattern when ONLY the embedded BF1 factors are used.
Here is an example for the MPS=Mp² =z² =312 =961 with a PN=xz=496=16•31. The PN is composed of: 1•1
1•2
1•4
1•8
1•16
+
1•31
2•31
4•31
8•31
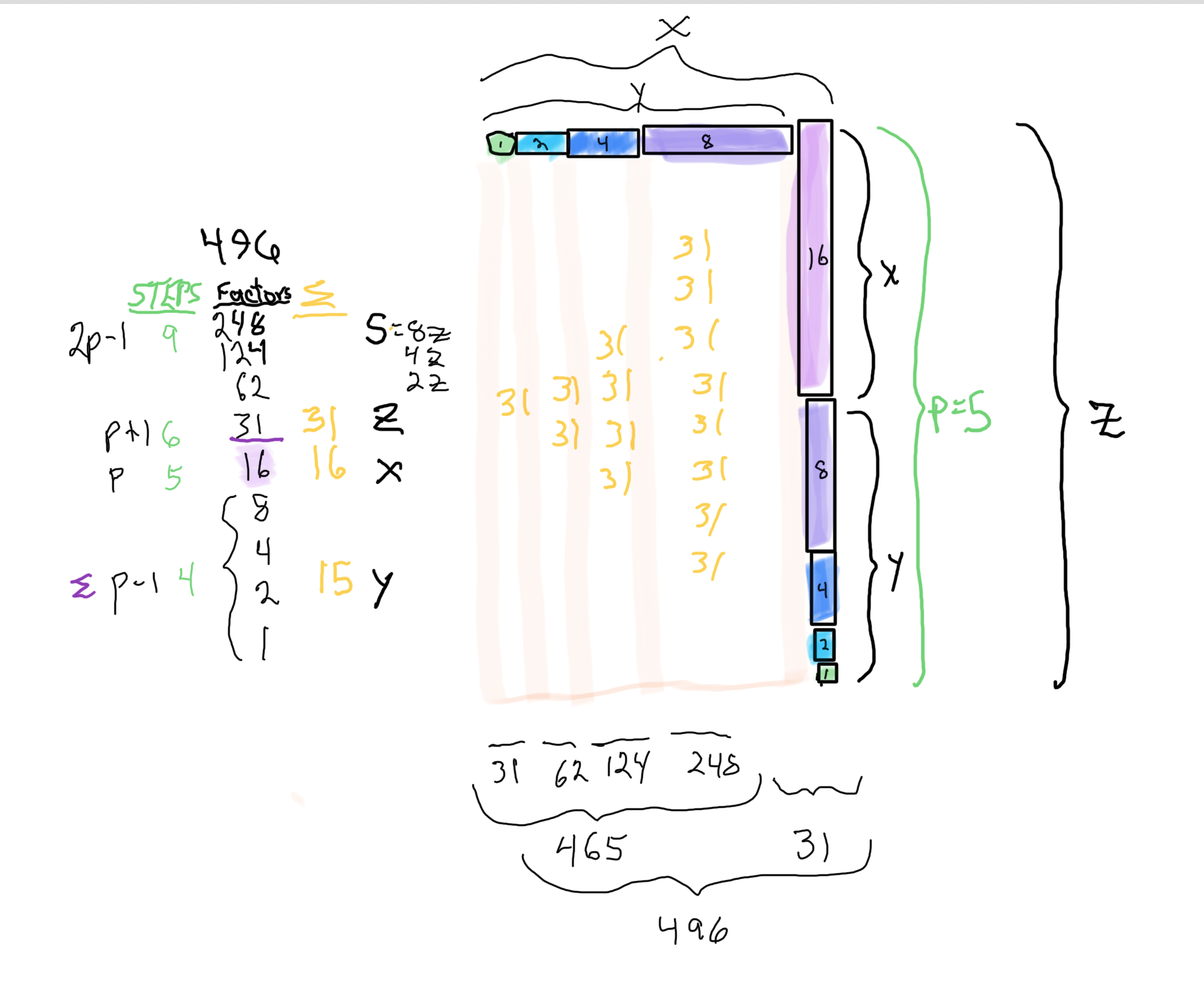
∑=496, where x=16, y=x-1=16-1=15=∑1+2+4+8 z=2x-1=32-1=31=∑1+2+4+8+16=x+y=16+15 p=5
Notice there are 5 entries (factors) in the Central Core (1-2-4-8-16)=p
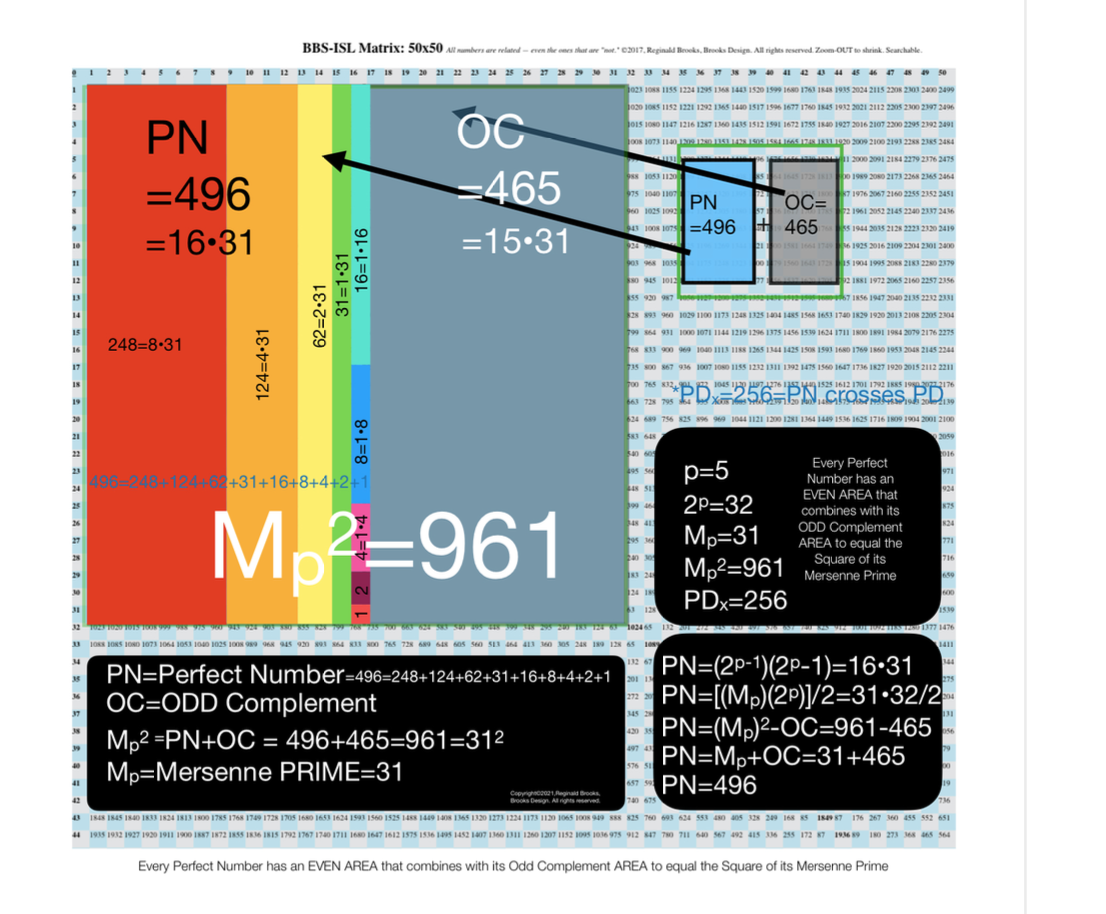
Below, we show how a sequential list of the Factors - Divisors informs the geometry of the Mp-PN pairing on the BIM. The order has been changed to highlight the symmetry inherent in both the geometry and the listing: With x=16 as the center and 8-4-2-1 on either side.
Especially do notice:
that there are NO additional factors outside of those required to sum up to equal the PN involved;
there are two fractal doublings occurring within the list;
one doubling starts with “1”— the 1st of ONLY 2 ODDs allowed — and ends with x=16 as p=5 STEPS
the second doubling starts with z=31 — the 2nd of ONLY 2 ODDs allowed — p+1=5+1=6 STEPS
there are two fractal doublings occurring within the geometry on the BIM;
one doubling starts with “1” on the Central Core (CC) ending with x=16 — forming the long side=z=x+y
this second doubling also starts with “1”, only here it forms the short side=x (as x=y+1) of the PN rectangle (xz) — and to correlate with the list — the AREAS of 1-2-4-8 times 31 gives us the 31-62-124-248 values (+ 1•31 for the CC value) that ∑ to equal the PN = 496.
ALL Set 1 Mp-PN pairings follow this pure template pattern.
ALL Set 2 & 3 entries can ONLY show this pattern if, and only if, their extra, additional factors are NOT included — as their extra additional factors include more than two ODDs, and, while demonstrated a similar fractal-double-doubling, it is NOT based on a central Mp as there is no such entity.

1. Divisor-Factor Patterns -Part II
P___divisors times
p2 --->4 x2
p3 --->6 x2
p4 --->16 4x4
p5 --->10 x2
p6 --->36 6x6
p7 --->14 x2
p8 --->64 8x8
p9 --->36 4x9
p10--->80 8x10
p11--->44 4x11
p12--->288 24x12
p13--->26 x2
p14--->112 8x14
p15--->120 8x15
p16--->256 16x16
p17--->34 x2
p18--->576 32x18
p19--->38 x2
p20--->960 48x20
p21--->252 12x21
p22--->352 16x22
p23--->92 4x23
p24--->2304 96x24
p25--->200 8x25
p26--->208 8x26
p27--->216 8x27
p28--->1792 64x28
p29--->232 8x29
p30--->2880 96x30
p31--->62 x2
p61--->122 x2
p89--->178 x2
p107--->214 x2
p127--->254 x2
The Divisors of TRUE MP-PN are ALWAYS 2•p; NEVER contain more than 2 ODDs (#one being a constant, 1); and NEVER (≥p=3) contain an ODD=3.
The Divisors of "containers" are ALWAYS >2•p -->2n4•p 4_6_8_12_16_24_48_96 so far in the ABOVE list; ALWAYS contain more than 2 ODDs (#one being a constant); and EVEN containers ALWAYS contain an ODD=3 divisor.
TRUE MP-PN ALWAYS generate the minimal # of divisors in their PN that =2p, that present themselves as two simple ublings:
The BF1 doubling starting with quantity 1,2,4,... (LOWER DOUBLING)
The Mp=z doubling starting with the ∑=z, 7,14,28 (UPPER DOUBLING)
And when laid out in the Matrix Table:
1. The BF1 is on one Axis (Horizontal) -- 1st Row
2. The MP=z is on the other Axis (Vertical) -- 1st Col.
3. The Matrix Table starts with the ODDS in the 1st Col
4. The Matrix Table fills out the rest (Col 2+) with the EVENs.
"Containers" ALWAYS generate more than >2p number of divisors, and while they do contain the same BF1 & Mp=z doublings as the TRUE, they also ALWAYS contain ADDITIONAL divisors/factors.
And when laid out in the Matrix Table:
1. The BF1 is on one Axis (Horizontal) -- 1st Row
2. The MP=z is on the other Axis (Vertical) -- 1st Col.
3. The Matrix Table starts with the ODDS in the 1st Col
4. The Matrix Table fills out the rest (Col 2+) with the EVENs.
That's right, the "container" Matrix Tables look similar to the TRUE tables in layout, only they ALWAYS contain more EVEN and ODD divisors/factors, thus their tables appear bloated relative to that of the TRUE, Active Mp-PN's.
1. In both, the length (STEPS) across Rows=p.
2. In both, the ∑ across the 1st Row = z.
3. In both, the ∑ across the LAST Row = z²=MPS.
4. As, in both, the ∑ across ANY Row=z•z-Axis.
Using the Matrix Tables gives quick visual referencing to both whether a given candidate is TRUE or NOT, and, it summarizes the key BF1 & Mp=z constituents in the 1st Row and 1st Column, respectively, regardless of whether or not they are TRUE.
Remember, ONLY TRUE Mp has BF1=p-STEPS and Mp=2p-STEPS number of divisors.
That said, one can also simply address the 1st Col. divisor values directly:
ALL TRUE Mp=z -- and *ONLY TRUE Mp=z -- will be present. *As "1" is ALWAYS included in any divisor/factor list it is always present.
ANY 1st Col. listing greater than 2 signals this to be a "container" even if it contains one or more Mp=z, as it will ALWAYS contain other ODDs that are NOT TRUE Mp=z.
Working with just those ODDs in the 1st Col. with both the TRUE and "container" only p-values gives one additional and quite vital distribution information when those ODDs are limited to Mp=z values.
Plotting such Mp=z values gives rise to several images and tables that summarize their distribution, often with highly suggestive NPS.
The most intriguing one may be the uncanny musical interval pattern reminiscent of the tunings based on the division of the monochord.
As pointed out repeatedly, the Mp-PN pairing relationship is defined by a pure, minimal "tonal" center for each of the 51 (discovered thus far). They accept NO additional "sharps" or "flats" in the way of additional divisors/ factors into their profile. See image from Table 166: p- distribution.
Here is another way to look at it: you start something with quantity 1 and you double it. Then you double it again. Perhaps again and again. But at any single point along the way of your doublings, you STOP and add up the quantities you made along the way, you will get a number -- an ODD number because you are always adding EVENs in the way of doublings to the original 1 -- that, if and only if it is a TRUE Mp=z number, then if you start a NEW second doubling of this ODD number, you will reach a new EVEN number that = the Running Sum (∑) of ALL the numbers (divisors) that came before and led up to it (not counting the last number itself). It is a Perfect Number! Divisors are used to describe ALL the number including the number itself, while factors describe ALL the numbers NOT including the number itself). And a PN=xz. On the Matrix Table, one adds ALL the numbers in both ROWs except for the very last number to get the PN.
Divisor-Factor Matrix Tables (DMT) have two forms:
TRUE Mp=z Template (Maximum 2 Rows. Only variable is to ADD Columns, where p=# of Columns, e.i. p5=5 Columns, but NEVER more than 2 Rows.
p5
{1,2,4,8,16,31,62,124,248,496}=10 divisors for p=5 or 2p. PN=xz=16*31=496 and PN=divisors -1 = factors, so 496 has 10-1=9 factors. ODDs Column doubles to—->EVEN Columns ⸻>double ⸻⸻>double⸻⸻>double—>...
| 1 | 2 | 4 | 8 | 16=x |
|---|---|---|---|---|
| 31=Mp=z | 62 | 124 | 248 | 496=PN=xz |
TOP Row: Butterfly Fractal 1 (BF1)
BOTTOM Row: ODD Fractal 1 (OF1)
Every “container” Template (Minimum 4 Rows + 4 Columns, where p=# of Columns, e.i. p6=6 Columns, but here it occupies 6 Rows.
p6 {1, 2, 3, 4, 6, 7, 8, 9, 12, 14, 16, 18, 21, 24, 28, 32, 36, 42, 48, 56, 63, 72, 84, 96, 112, 126, 144, 168, 224, 252, 288, 336, 504, 672, 1008, 2016} 36divisors -1=35Factors.
ODDs Column doubles to—->EVEN Columns ⸻>double ⸻>double⸻>double⸻>double—>...
| 1 | 2 | 4 | 8 | 16 | 32 |
|---|---|---|---|---|---|
| 3 | 6 | 12 | 24 | 48 | 96 |
| 7 | 14 | 28 | 56 | 112 | 224 |
| 9 | 18 | 36 | 72 | 144 | 288 |
| 21 | 42 | 84 | 168 | 336 | 672 |
| 63 | 126 | 252 | 504 | 1008 | 2016 |
TOP Row: Butterfly Fractal 1 (BF1)
BOTTOM Rows: ODD Fractal 1 (OF1)
Every TRUE Mp=z will look like #1 above, only growing to the right as the number of Columns increases as “p” increases, while ONLY having 2 Rows.
The Top Row is always the same BF1 sequence (doubling), while the Bottom Row is the OF1 sequence that also doubles, and , when multiplied by a Top cell, gives the result below it.
There is complete fractal symmetry both in how each Row doubles and in how the fractal-pairs that make up the divisors are distributed in the Divisor-Factor Matrix Tables (DMT).
Every “container” will look like #2 above, growing in both Rows and Columns, with the # of Columns also equal to “p”, but the # of Rows ALWAYS exceeding 2 Rows.
In the “container,” the Top Row BF1 is extracted from the much longer divisor list, with the Bottom Lower Rows of multiple OF1 ODDs, start each of those Rows of doublings.
xxxxxxxxxxA similar fractal doubling of each element on the left to its neighbor on the right — as in #1. — however there are ALWAYS more than 2 Rows. If it is an EVEN “p” it will ALWAYS have an ODD 3.
So why not just eliminate all the EVENs? The EVENs contain within their divisor listing/DFMT the “next” TRUE Mp=z, and often more than one, but not every future one will be in the next EVEN. (See Notes: p12)
Generic to both: The absolute beauty of the BF1 is that its fractal encompasses it all — 1 & 2. Subtract -1 from each doubling in the list below and you will obtain the Mp=z — or “container” equivalent. This is effectively the definition of a Mersenne Prime. You can get the same results when you take the Running Sum (∑) at any point along the way, e.i. 1+2+4+8+16=31. One can see the same in the DFMT above for p=5. Notice that there are 5=p values included in reaching p5=32 and 32-1=31. The Mp=z is always equal to the p+1 STEP values, with the p value itself being equal to the BF1 doublings, and 2p=PN=xz. In the list below, *BOLD designates the candidates for the TRUE Mp=z (once -1 is subtracted).
~~ *1
*1 x 2 = 2*
*2 × 2 = 4 p2*
*4 × 2 = 8 p3*
8 × 2 = 16
*16 × 2 = 32 p5*
32 × 2 = 64
*64 × 2 = 128 p7*
128 × 2 = 256
*256 × 2 = 512*
512 × 2 = 1024 10
*1024 × 2 = 2048*
2048 × 2 = 4096
*4096 × 2 = 8192 p13*
8192 × 2 = 16384
*16384 × 2 = 32768*
32768 × 2 = 65536
*65536 × 2 = 131072 p17*
131072 × 2 = 262144
*262144 × 2 = 524288 p19*
524288 × 2 = 1048576 20
*1048576 × 2 = 2097152*
2097152 × 2 = 4194304
*4194304 × 2 = 8388608*
8388608 × 2 = 16777216
*16777216 × 2 = 33554432*
33554432 × 2 = 67108864
*67108864 × 2 = 134217728*
134217728 × 2 = 268435456
*268435456 × 2 = 536870912*
536870912 × 2 = 1073741824 30
*1073741824 × 2 = 2147483648 p31*
2147483648 × 2 = 4294967296
*4294967296 × 2 = 8589934592*
8589934592 × 2 = 17179869184
*17179869184 × 2 = 34359738368*
34359738368 × 2 = 68719476736
*68719476736 × 2 = 137438953472*
137438953472 × 2 = 274877906944
*274877906944 × 2 = 549755813888*
549755813888 × 2 = 1099511627776 40
*1099511627776 × 2 = 2199023255552*
2199023255552 × 2 = 4398046511104
*4398046511104 × 2 = 8796093022208*
8796093022208 × 2 = 17592186044416
*17592186044416 × 2 = 35184372088832*
35184372088832 × 2 = 70368744177664
*70368744177664 × 2 = 140737488355328*
140737488355328 × 2 = 281474976710656
*281474976710656 × 2 = 562949953421312*
562949953421312 × 2 = 1125899906842624 50
*1125899906842624 × 2 = 2251799813685248*
2251799813685248 × 2 = 4503599627370496
*4503599627370496 × 2 = 9007199254740992*
9007199254740992 × 2 = 18014398509481984
*18014398509481984 × 2 = 36028797018963968*
36028797018963968 × 2 = 72057594037927936
*72057594037927936 × 2 = 144115188075855872*
144115188075855872 × 2 = 288230376151711744
*288230376151711744 × 2 = 576460752303423488*
576460752303423488 × 2 = 1152921504606846976 60
*1152921504606846976 × 2 = 2305843009213693952 p61*
2305843009213693952 × 2 = 4611686018427387904
*4611686018427387904 × 2 = 9223372036854775808*
9223372036854775808 × 2 = 18446744073709551616
*18446744073709551616 × 2 = 36893488147419103232*
36893488147419103232 × 2 = 73786976294838206464
*73786976294838206464 × 2 = 147573952589676412928*
147573952589676412928 × 2 = 295147905179352825856
*295147905179352825856 × 2 = 590295810358705651712*
590295810358705651712 × 2 = 1180591620717411303424 70
*1180591620717411303424 × 2 = 2361183241434822606848*
2361183241434822606848 × 2 = 4722366482869645213696
*4722366482869645213696 × 2 = 9444732965739290427392*
9444732965739290427392 × 2 = 18889465931478580854784
*18889465931478580854784 × 2 = 37778931862957161709568*
37778931862957161709568 × 2 = 75557863725914323419136
*75557863725914323419136 × 2 = 151115727451828646838272*
151115727451828646838272 × 2 = 302231454903657293676544
*302231454903657293676544 × 2 = 604462909807314587353088*
604462909807314587353088 × 2 = 1208925819614629174706176 80
*1208925819614629174706176 × 2 = 2417851639229258349412352*
2417851639229258349412352 × 2 = 4835703278458516698824704
*4835703278458516698824704 × 2 = 9671406556917033397649408*
9671406556917033397649408 × 2 = 1.934281311383406679529882e25
*1.934281311383406679529882e25 × 2 = 3.868562622766813359059763e25*
3.868562622766813359059763e25 × 2 = 7.737125245533626718119526e25
*7.737125245533626718119526e25 × 2 = 1.547425049106725343623905e26*
1.547425049106725343623905e26 × 2 = 3.094850098213450687247811e26
*3.094850098213450687247811e26 × 2 = 6.189700196426901374495621e26 p89*
6.189700196426901374495621e26 × 2 = 1.237940039285380274899124e27 90
*1.237940039285380274899124e27 × 2 = 2.475880078570760549798248e27*
2.475880078570760549798248e27 × 2 = 4.951760157141521099596497e27
*4.951760157141521099596497e27 × 2 = 9.903520314283042199192994e27*
9.903520314283042199192994e27 × 2 = 1.980704062856608439838599e28
*1.980704062856608439838599e28 × 2 = 3.961408125713216879677198e28*
3.961408125713216879677198e28 × 2 = 7.922816251426433759354395e28
*7.922816251426433759354395e28 × 2 = 1.584563250285286751870879e29*
1.584563250285286751870879e29 × 2 = 3.169126500570573503741758e29
*3.169126500570573503741758e29 × 2 = 6.338253001141147007483516e29*
6.338253001141147007483516e29 × 2 = 1.267650600228229401496703e30 100
*1.267650600228229401496703e30 × 2 = 2.535301200456458802993406e30*
2.535301200456458802993406e30 × 2 = 5.070602400912917605986813e30
*5.070602400912917605986813e30 × 2 = 1.014120480182583521197363e31*
1.014120480182583521197363e31 × 2 = 2.028240960365167042394725e31
*2.028240960365167042394725e31 × 2 = 4.05648192073033408478945e31*
4.05648192073033408478945e31 × 2 = 8.112963841460668169578901e31
*8.112963841460668169578901e31 × 2 = 1.62259276829213363391578e32 p107*
1.62259276829213363391578e32 × 2 = 3.24518553658426726783156e32
*3.24518553658426726783156e32 × 2 = 6.49037107316853453566312e32*
6.49037107316853453566312e32 × 2 = 1.298074214633706907132624e33 110
*1.298074214633706907132624e33 × 2 = 2.596148429267413814265248e33*
2.596148429267413814265248e33 × 2 = 5.192296858534827628530496e33
*5.192296858534827628530496e33 × 2 = 1.038459371706965525706099e34*
1.038459371706965525706099e34 × 2 = 2.076918743413931051412199e34
*2.076918743413931051412199e34 × 2 = 4.153837486827862102824397e34*
4.153837486827862102824397e34 × 2 = 8.307674973655724205648794e34
*8.307674973655724205648794e34 × 2 = 1.661534994731144841129759e35*
1.661534994731144841129759e35 × 2 = 3.323069989462289682259518e35
*3.323069989462289682259518e35 × 2 = 6.646139978924579364519035e35*
6.646139978924579364519035e35 × 2 = 1.329227995784915872903807e36 120
*1.329227995784915872903807e36 × 2 = 2.658455991569831745807614e36*
2.658455991569831745807614e36 × 2 = 5.316911983139663491615228e36
*5.316911983139663491615228e36 × 2 = 1.063382396627932698323046e37*
1.063382396627932698323046e37 × 2 = 2.126764793255865396646091e37
*2.126764793255865396646091e37 × 2 = 4.253529586511730793292183e37*
4.253529586511730793292183e37 × 2 = 8.507059173023461586584365e37
*8.507059173023461586584365e37 × 2 = 1.701411834604692317316873e38 p127*
~~
*If you double1.70014….e38 another 126 times=PN=1.447401117….e76 (and then* *double 1.44740111…e76 302doublings=6.864797660130609714981901e156 that =* *2^268 × 1.447401115466452442794637e76 = 6.864797660130609714981899e156=Mp=z of p521*
TRUE Mp=z Template (Maximum 2 Rows. Only variable is to ADD Columns, where p=# of Columns, e.i. p5=5 Columns, but NEVER more than 2 Rows.
1 2 4 8 16 31 62 124 248 496 ∑=32 ∑=64 ∑=128 ∑=256=x²=*(2p-1)+(p-1) ∑=512
p=Prime, however, “p” may also refer to STEPS, e.i. ∑=256=x²=(2p-1)+(p-1) as here 2p=2•5=10 STEPS (1-496), and subtracting -1, means go back 1 STEP to that value, as 248+8=256.
“container” Template (Minimum 4 Rows + 4 Columns, where p=# of Columns, e.i. p6=6 Columns, but here it occupies 6 Rows.
1 2 4 8 16 32 3 6 12 24 48 96 7 14 28 56 112 224 9 18 36 72 144 288 21 42 84 168 336 672 63 126 252 504 1008 2016 ∑=104 ∑=208 ∑=416 ∑=832 ∑=1664 ∑=3328
Above p2, ONLY every other Column is a viable candidate value for a future “next” TRUE Mp=z, and that actually is after two steps: Take the ∑ of the Column, and then subtract -1, e.i. the 3rd and 5th Columns are candidates. ∑128-1=127 and ∑512-1=511 are the two candidates, with 127=Mp=z of p7, while 511 is not prime and is ruled out.
The EVENs do not work this way. Their value as “container” candidates is that within their divisor listings, they will reveal a TRUE Mp=z as we can see individually above or collectively in the Notes: workcopyPNabbrev below.
1. Divisor-Factor Patterns -Part III
Here is a brief introduction:

The p value is on the 1st Column;
p underline=multiple of 12;
p underline + solid underline=multiple of 24;
Short dashed lines=first p that also have Mp=z (p2-3-5-7);
Long dashed lines=Mp=z candidates;
BOLD long dashed lines=TRUE Mp=z (they NEVER have “extra” ODDS);
3’s, starting with p2, found in ALL EVEN p, NEVER in ANY ODD p (translates to every other candidate: 2-4-6-...);
5’s, starting with p4 and every 4th candidate (4-8-12-...);
7’s starting with p3 and every 3rd candidate (3-6-9-...);
13’s, starting with p12 and every 12th candidate (12-24-36-...);
17’s, starting with p8 and every 8th candidate (8-16-24-...);
19’s, starting with p18 and every 18th candidate (18-36-54-...);
31’s, starting with p5 and every 5th candidate (5-10-15-...);
61’s, starting with p60 and every 60th candidate (60-120-180-...);
89’s, starting with p11 and every 11th candidate (11-22-33-...);
107’s, starting with p106 and every 106 candidate (106-212-318-...);
127’s, starting with p7 and every 7th candidate (7-14-21-...);
521’s, starting with p260 and every 260th candidate (260-520-780-...);
607’s, starting with p303 and every 303rd candidate (303-606-909-...)
1279’s, starting with 639 and every 639th candidate (639-1278-1917-...)
2203’s, starting with 734 and every 734th candidate (734-1468-2202-...)
2281’s, starting with 190 and every 190th candidate (190-380-570-760-1140-2280-...)
3217’s, starting with 804 and every 804th candidate (804-1608-2412-3216-...) and so on.
Starting with p2=3, can you predict the remaining “p’s” from the divisors of p-1 before you reach it as a prime?
Yes, ultimately ALL will have that next “p” value at least by the top divisor of p-1, e.i. 7, although it 1st appears at p3, @p6divisors it is present.


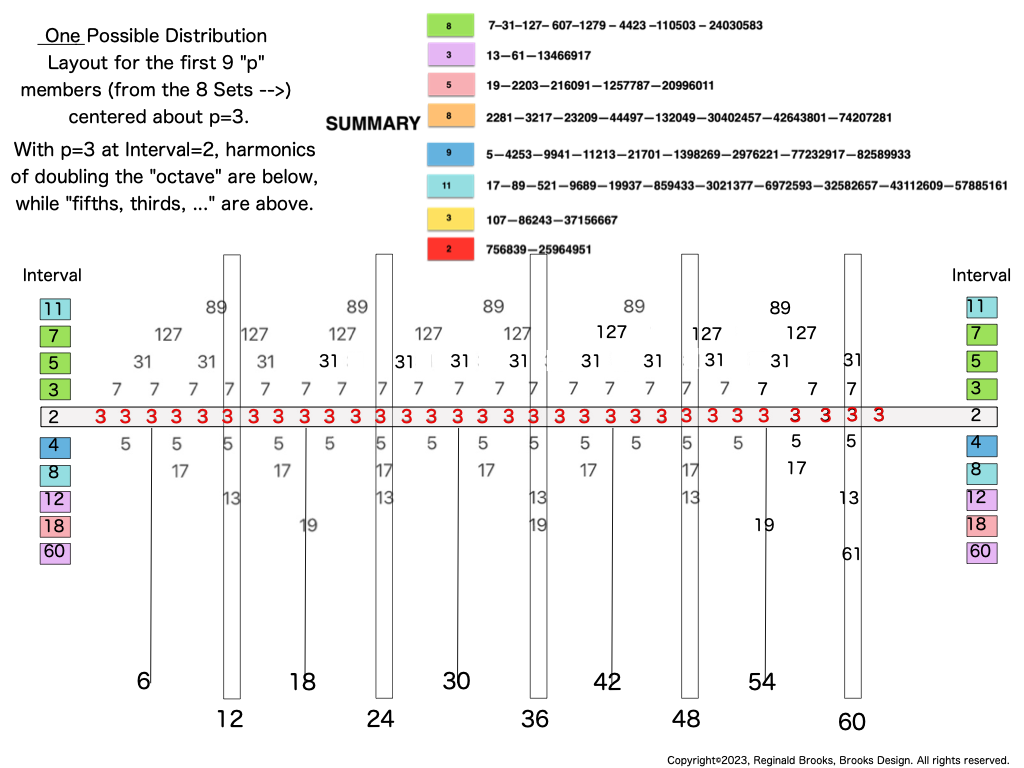


Now, back to the TRUE Mp-PNs:
Here are 3 examples of the DMT:
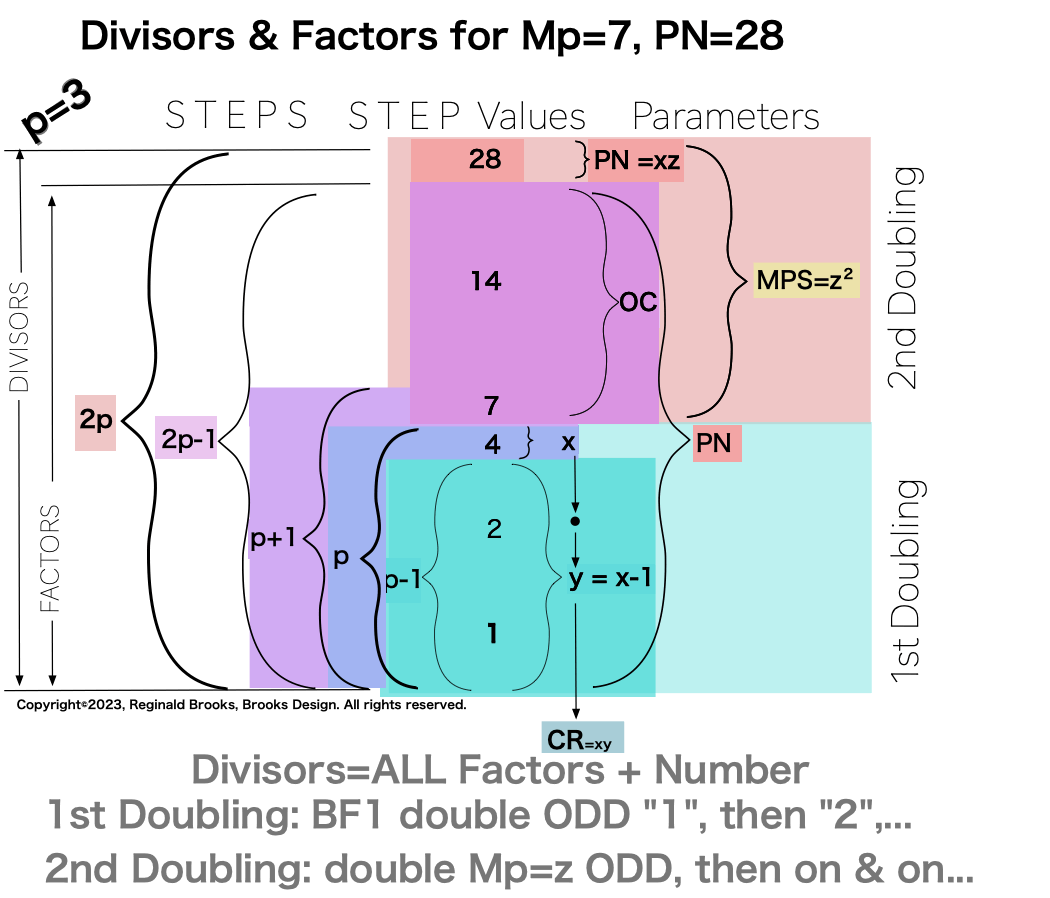

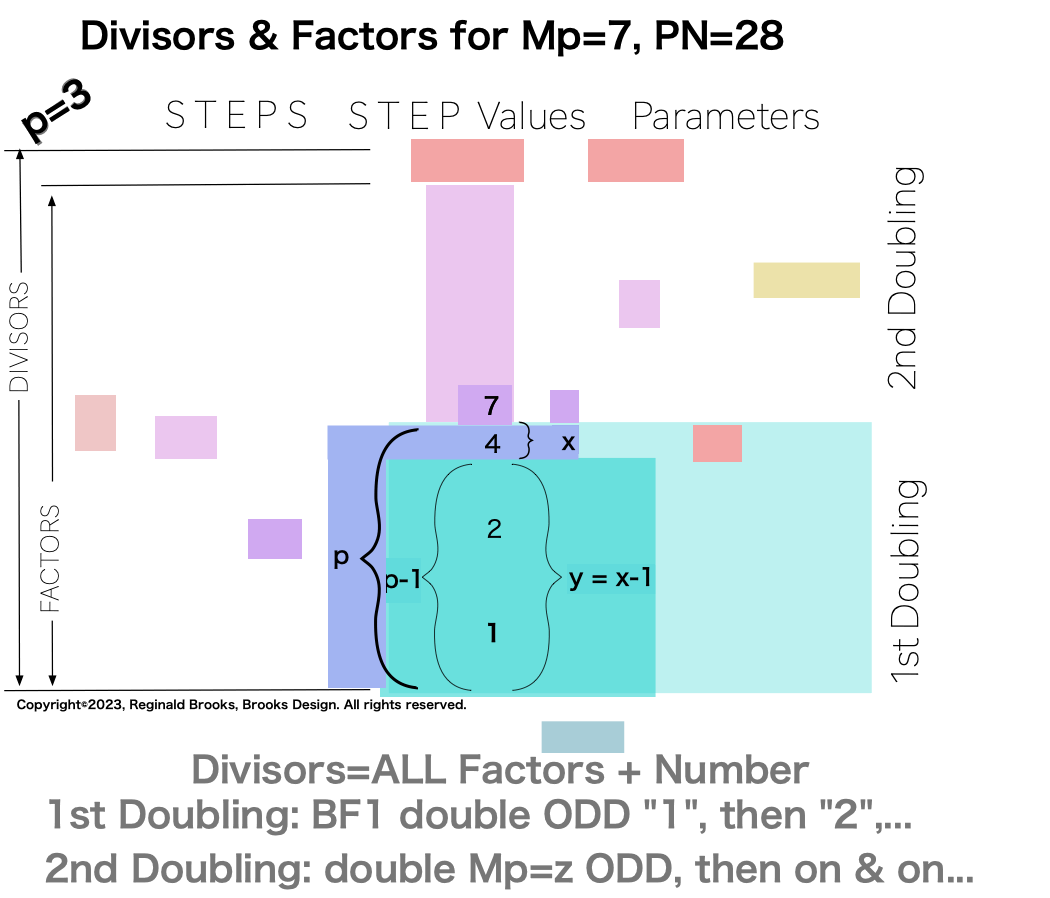
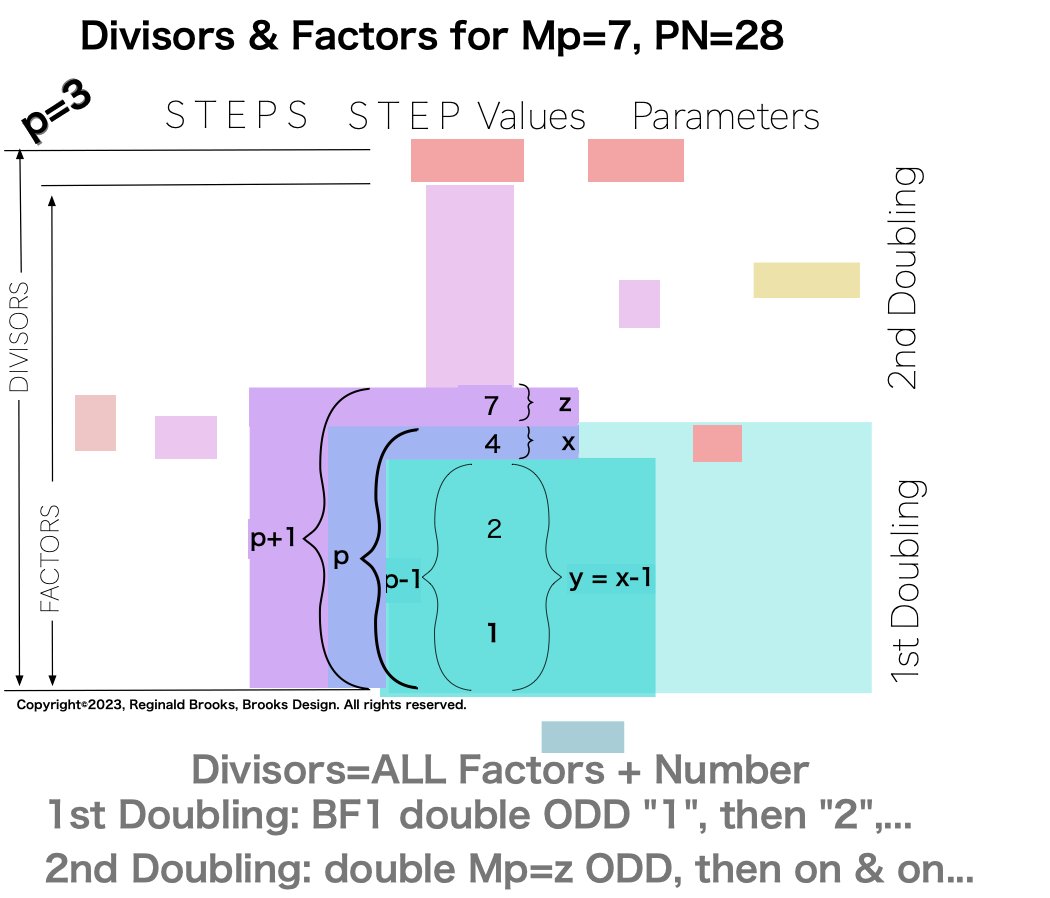
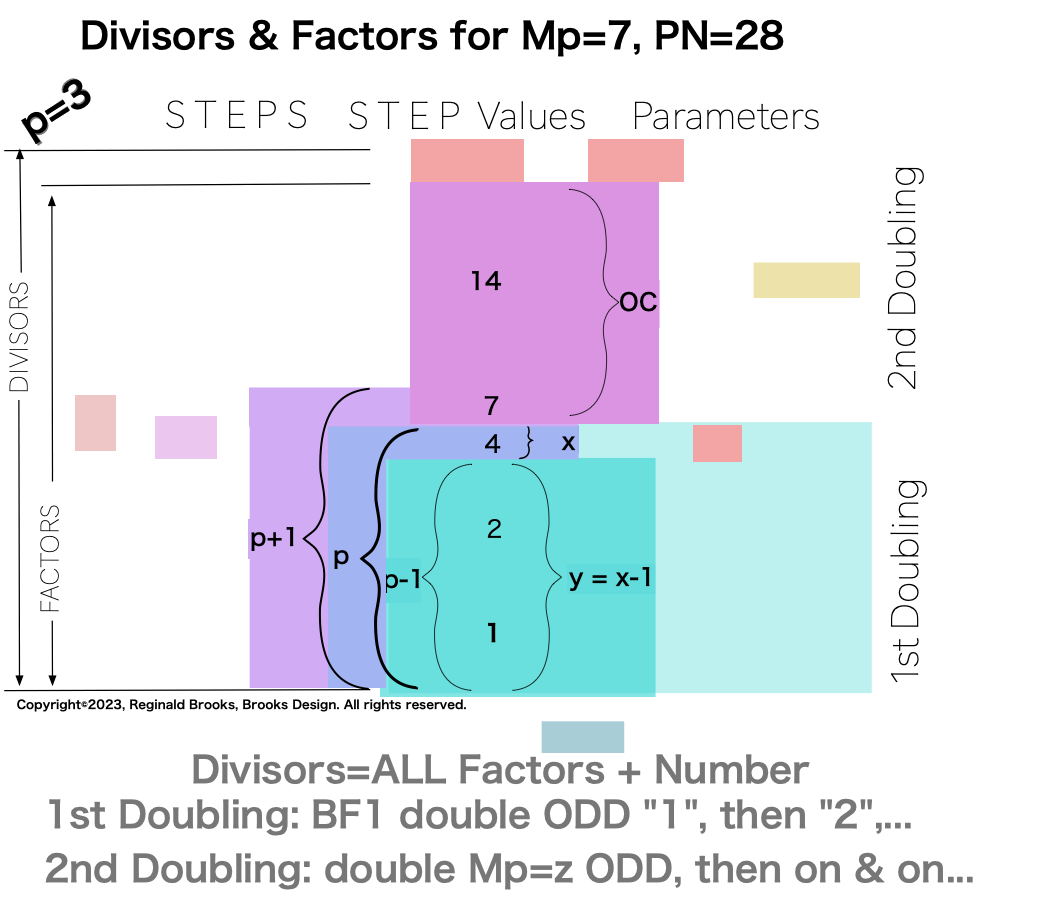
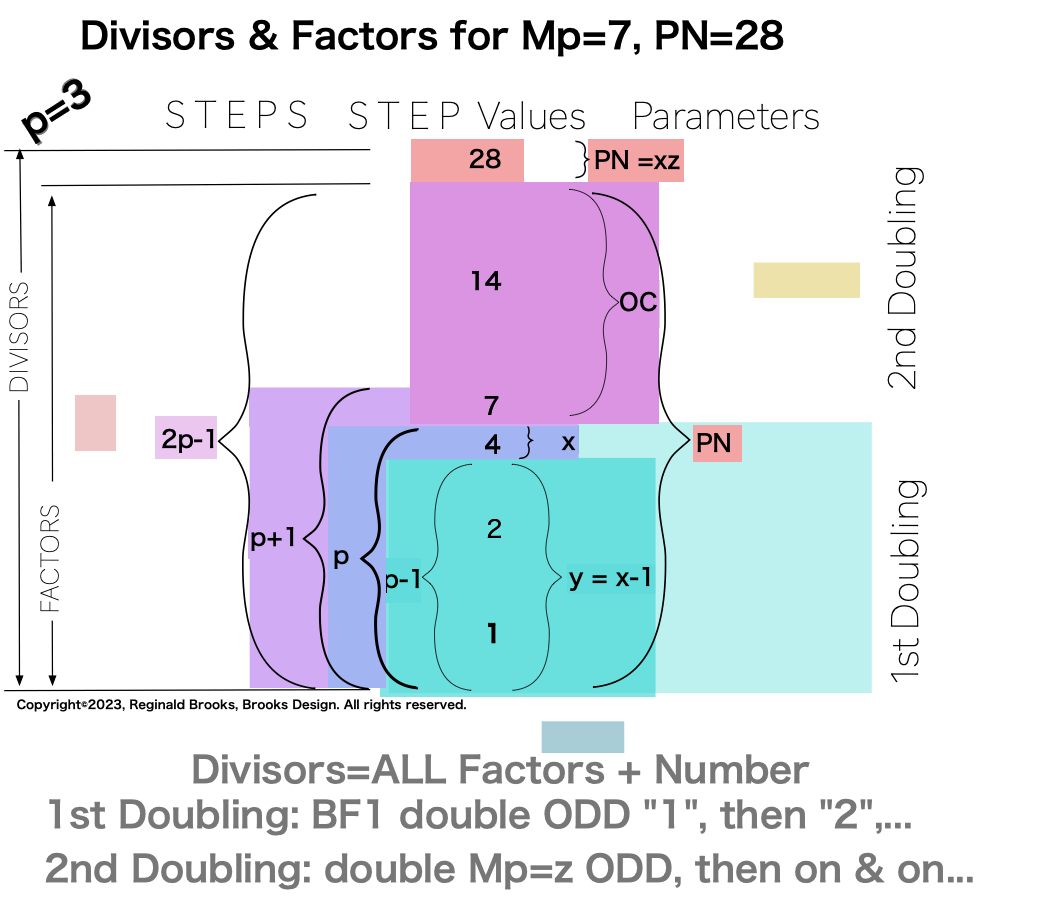
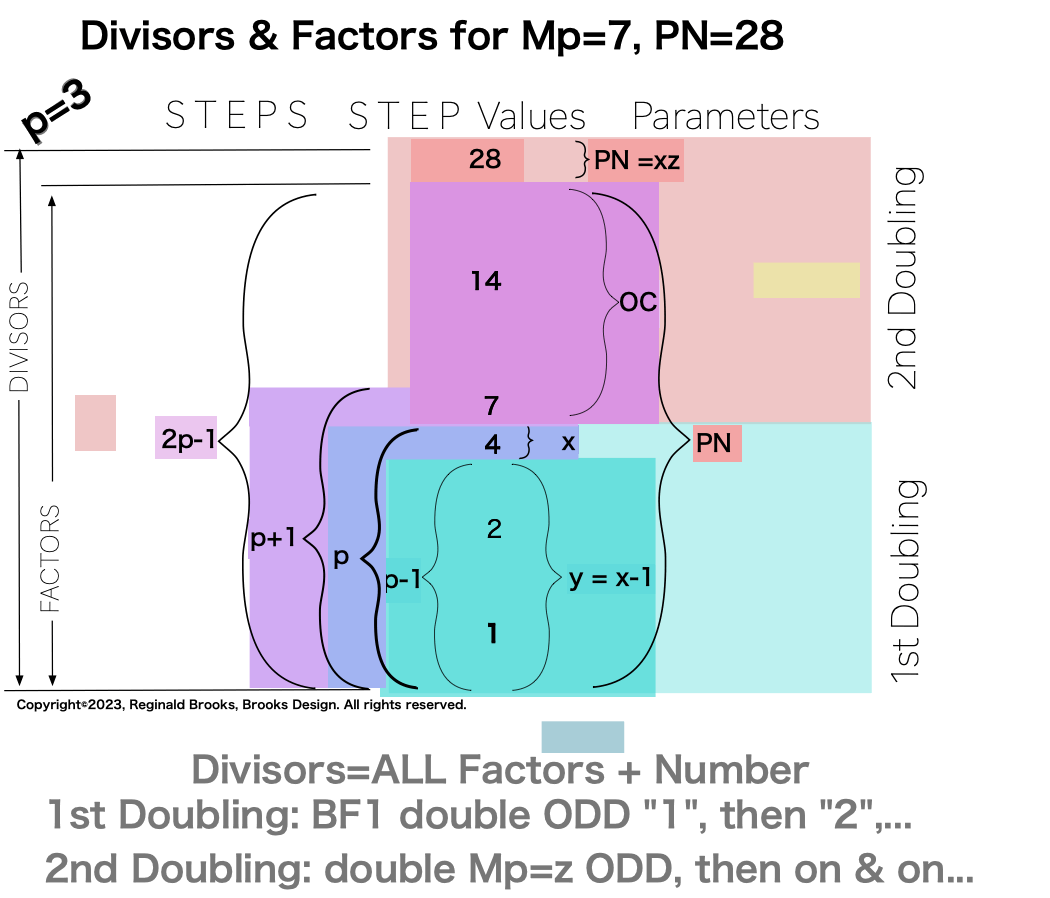
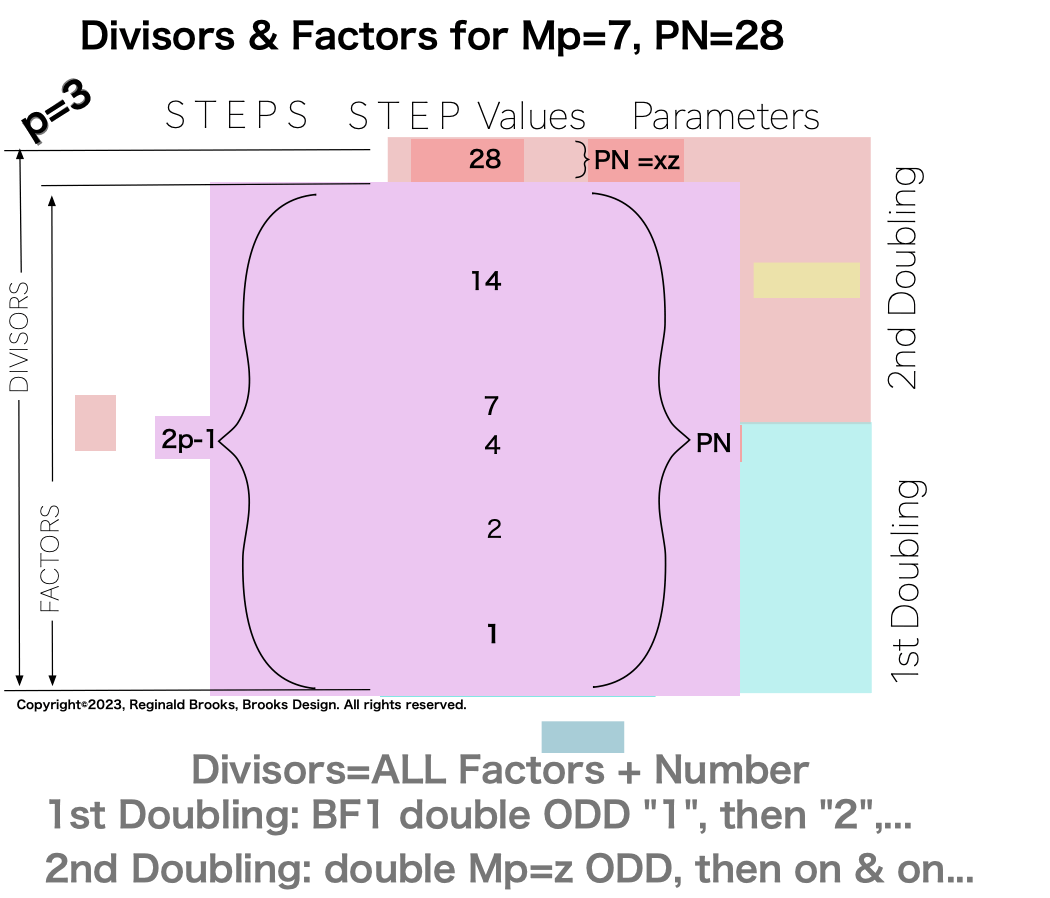
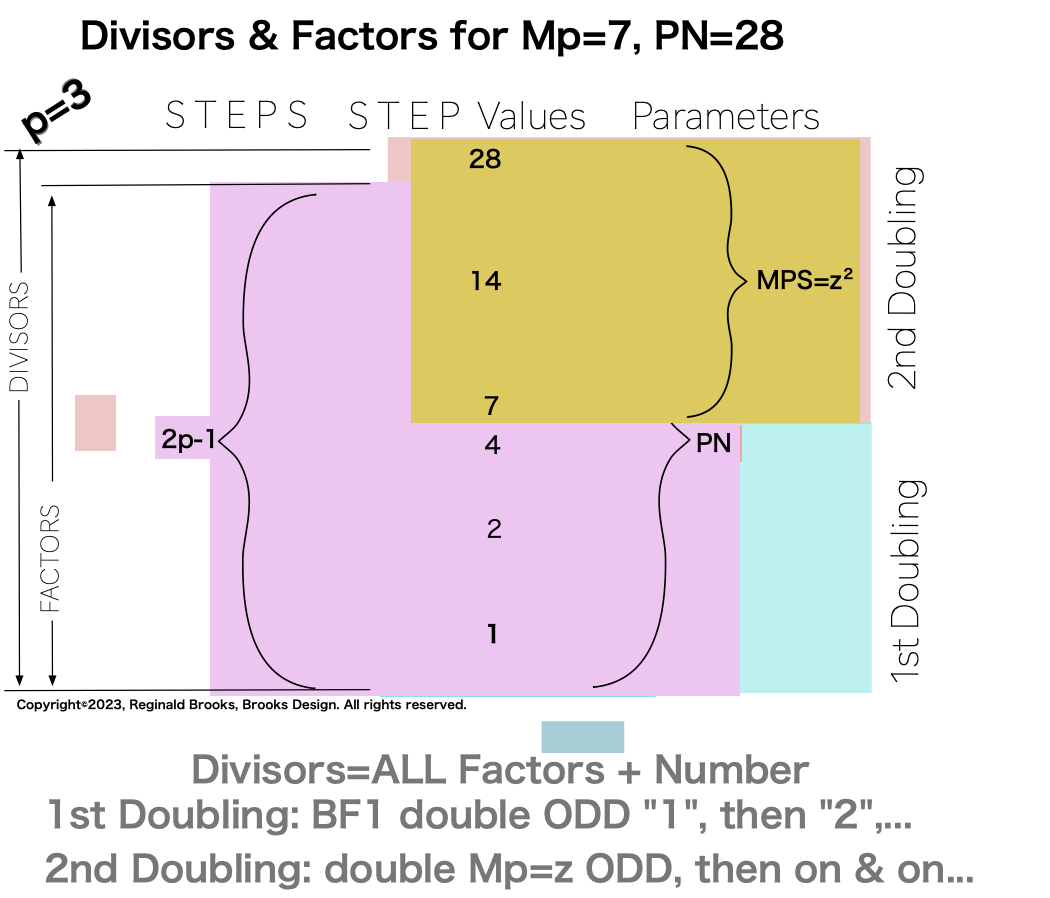
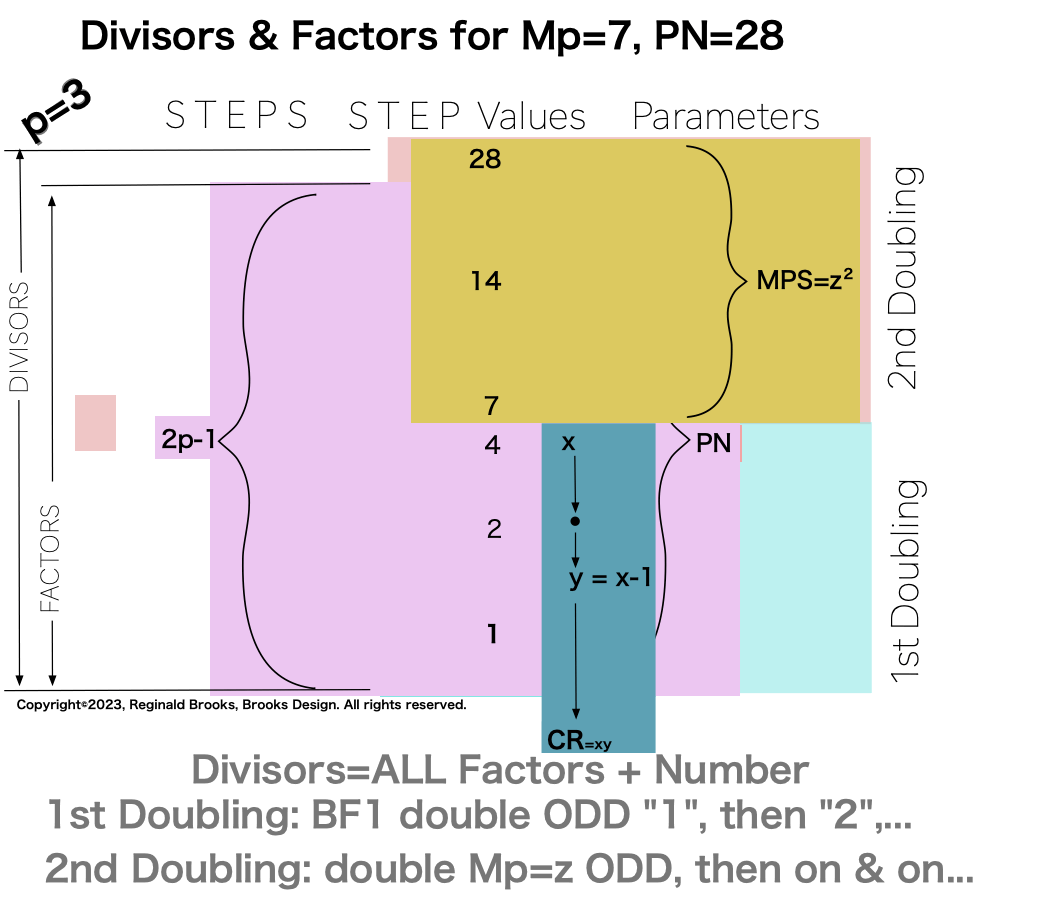
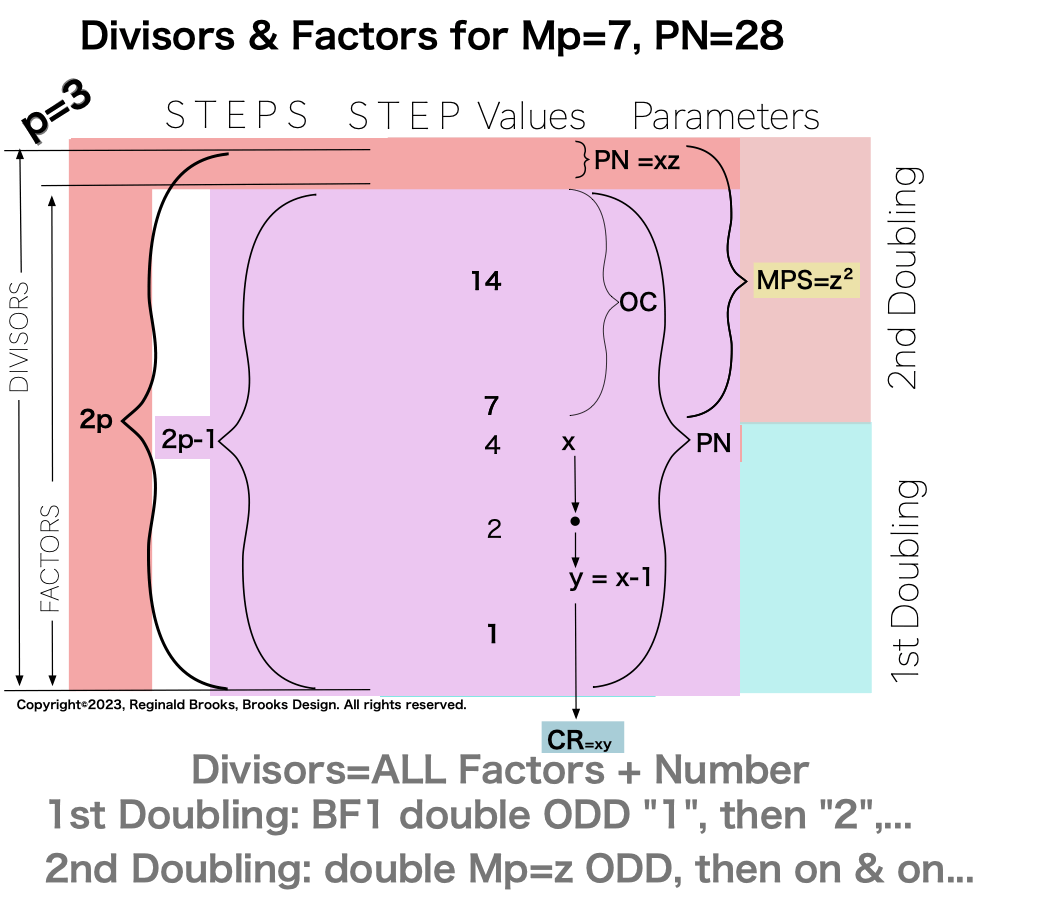



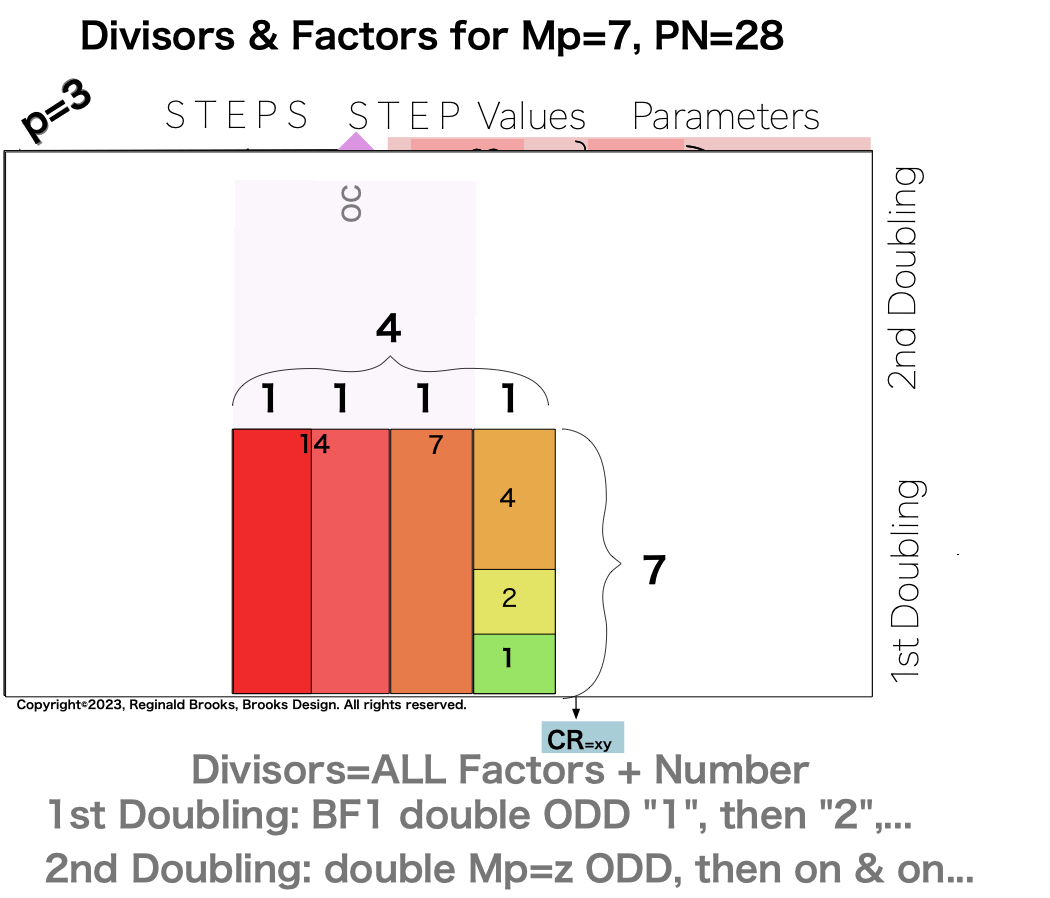
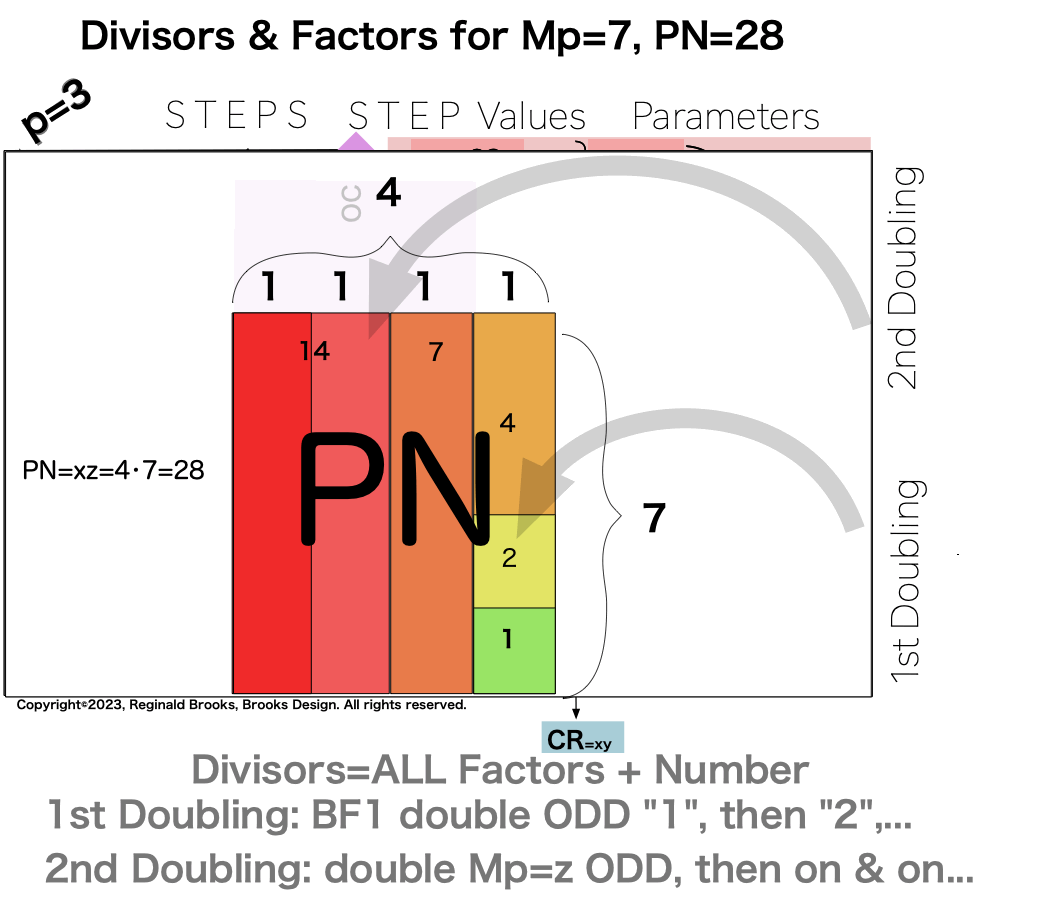
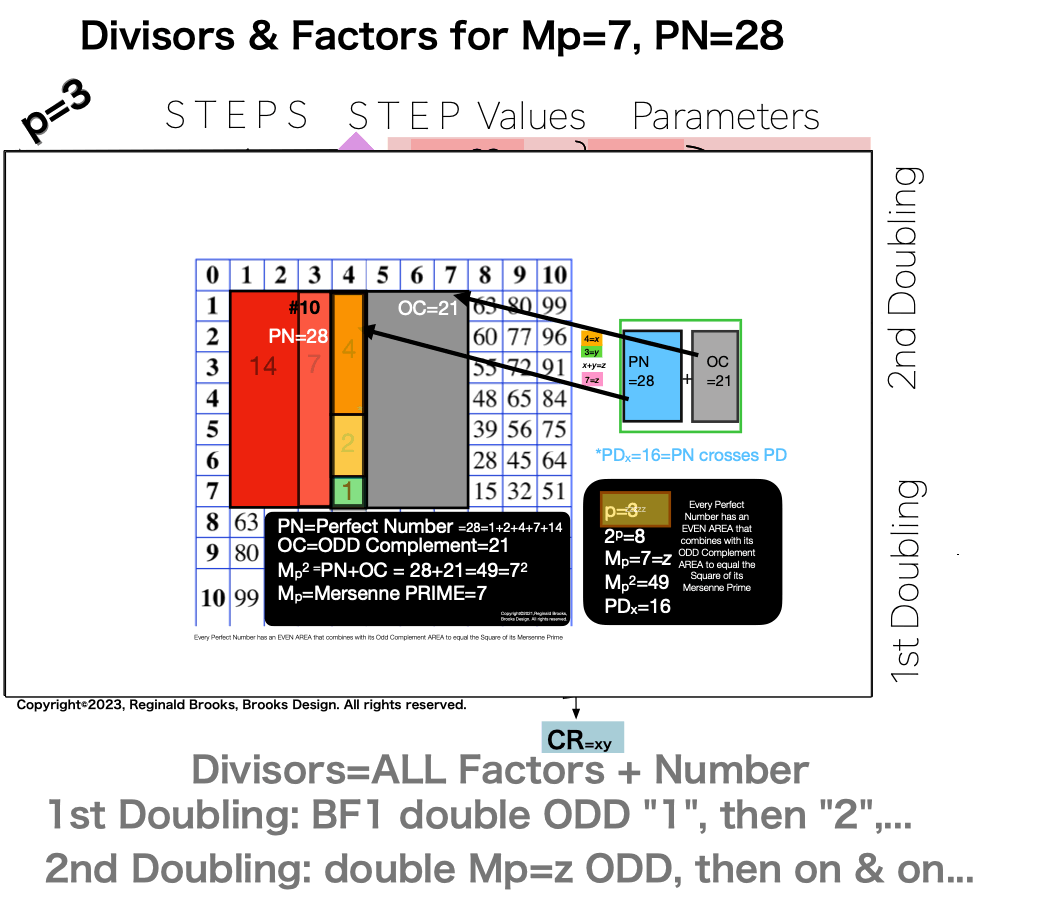

Animated Gif
Movie: right click and select "controls" to start movie
If one takes these two doublings - 1-2-4 and 7-14-28 into the #000000(DMT, featured below), one finds it to contain ALL the divisors of PN=28 -- where here we use the term "divisor" to include the number itself, and the the term "factor" to include the divisors without the said number itself. While All "containers" have this pattern of divisors within, they ALWAYS contain additional divisors beyond the bare minimum -- ONLY the TRUE Mp-PN pairings contain this minimal number of divisors to define itself. A crucial diffference! The DMT contains ALL the divisors of ALL the natural numbers, and as Mp-PN pairings subset within, ALL of these exquistily pure divisors of their PNs!
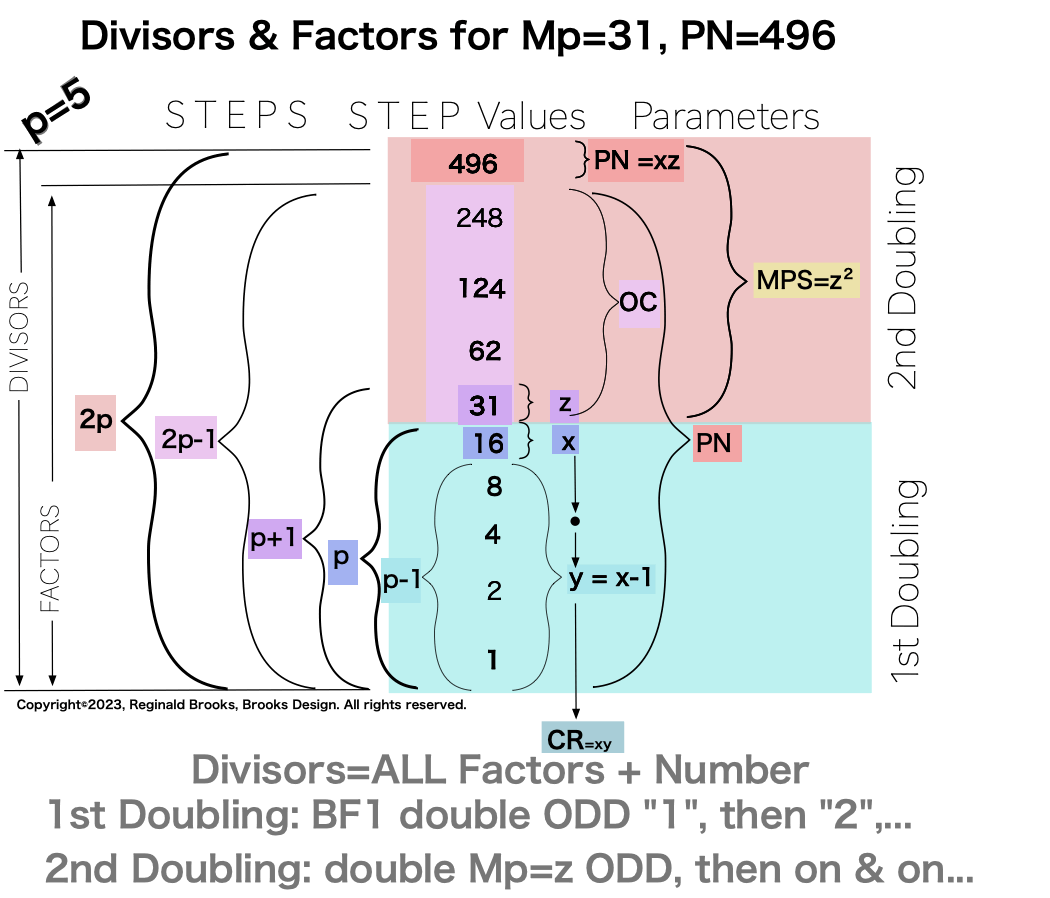

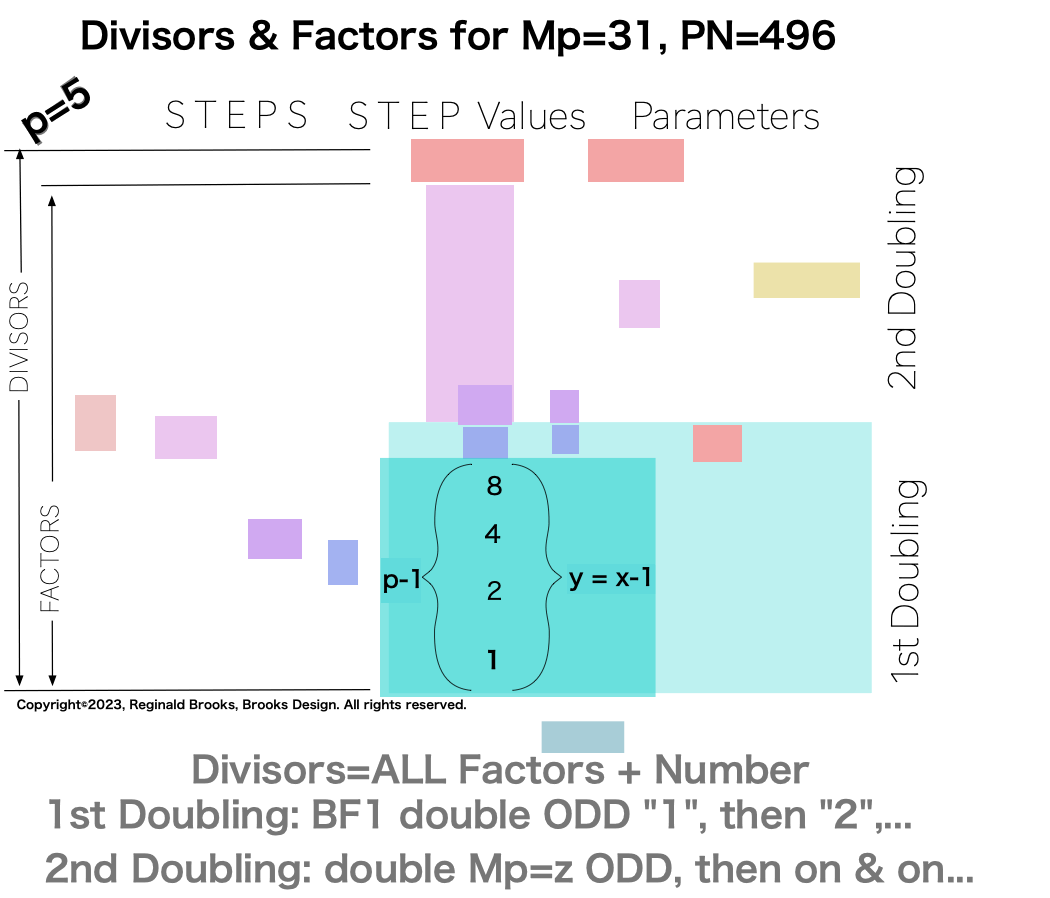
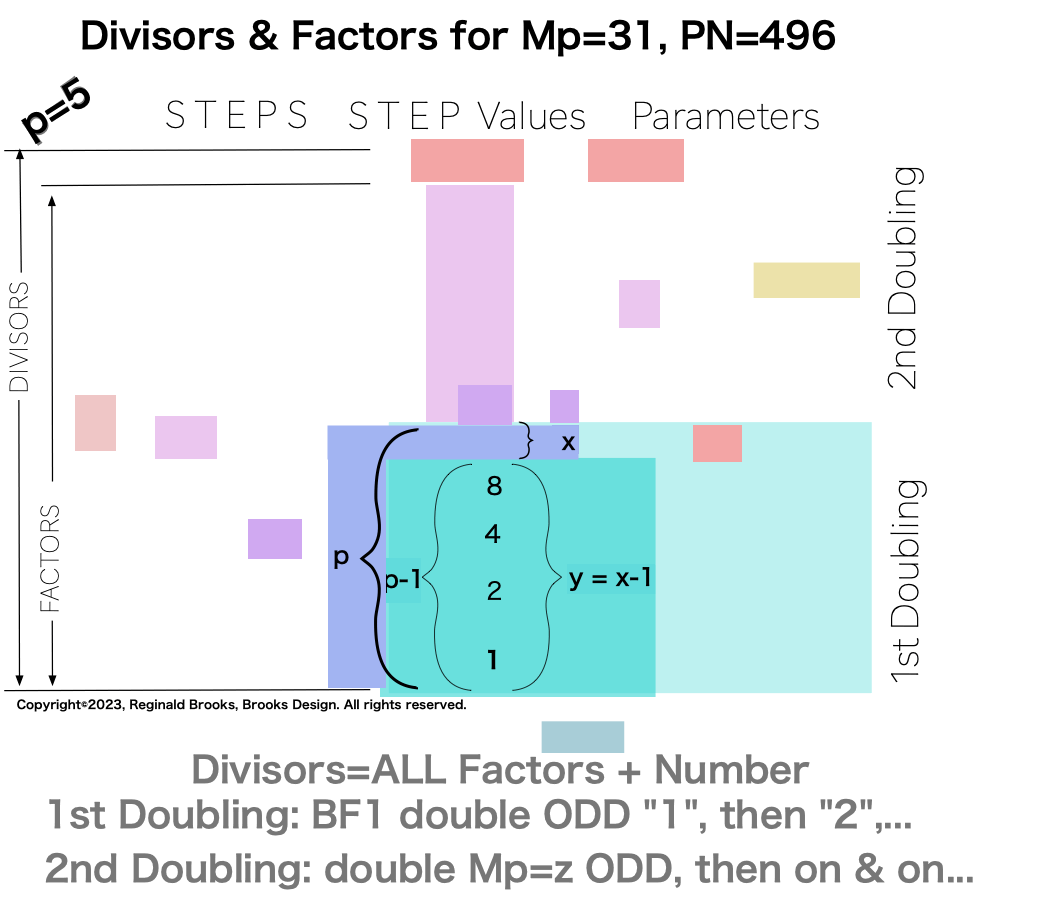
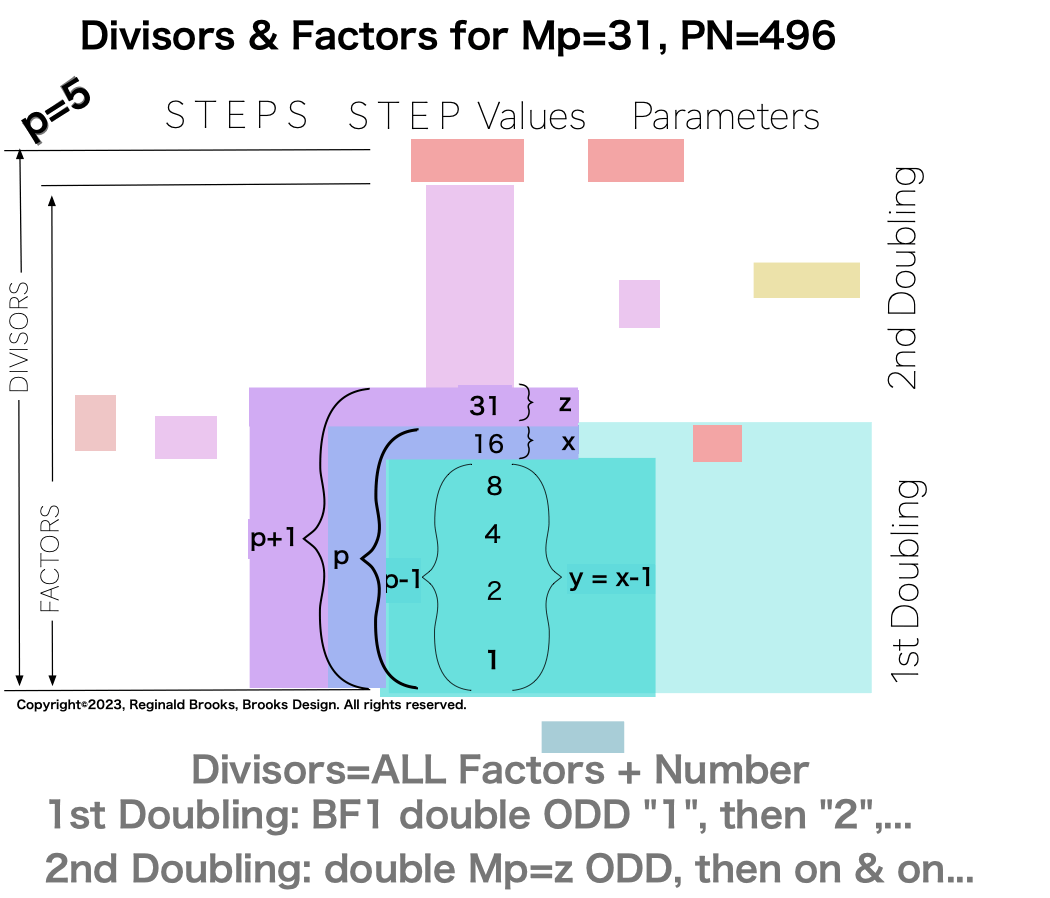
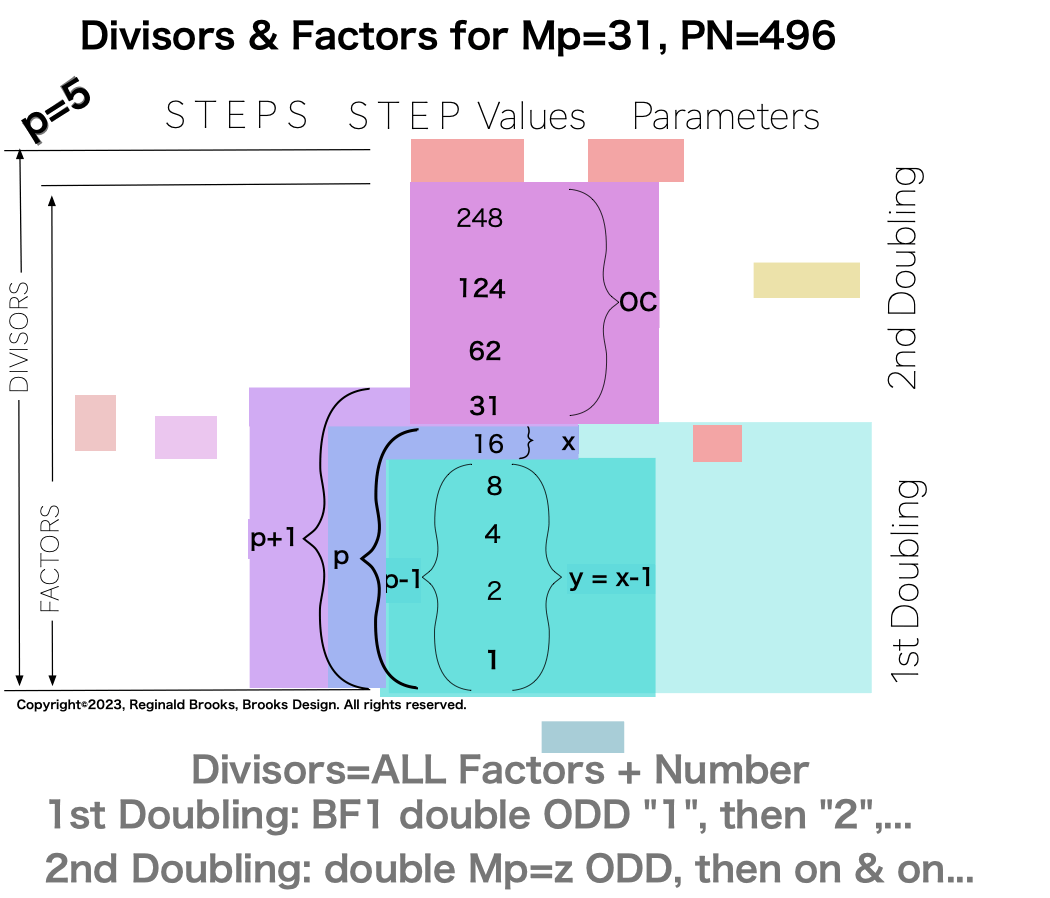

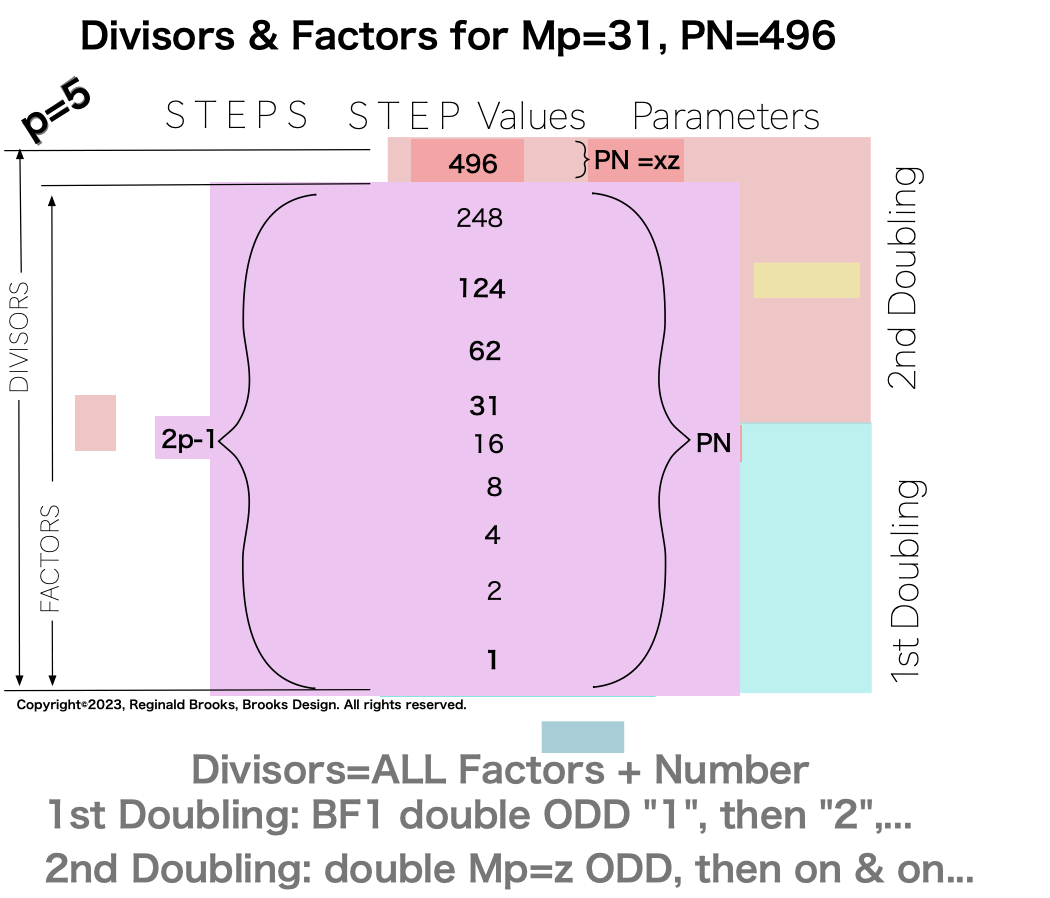
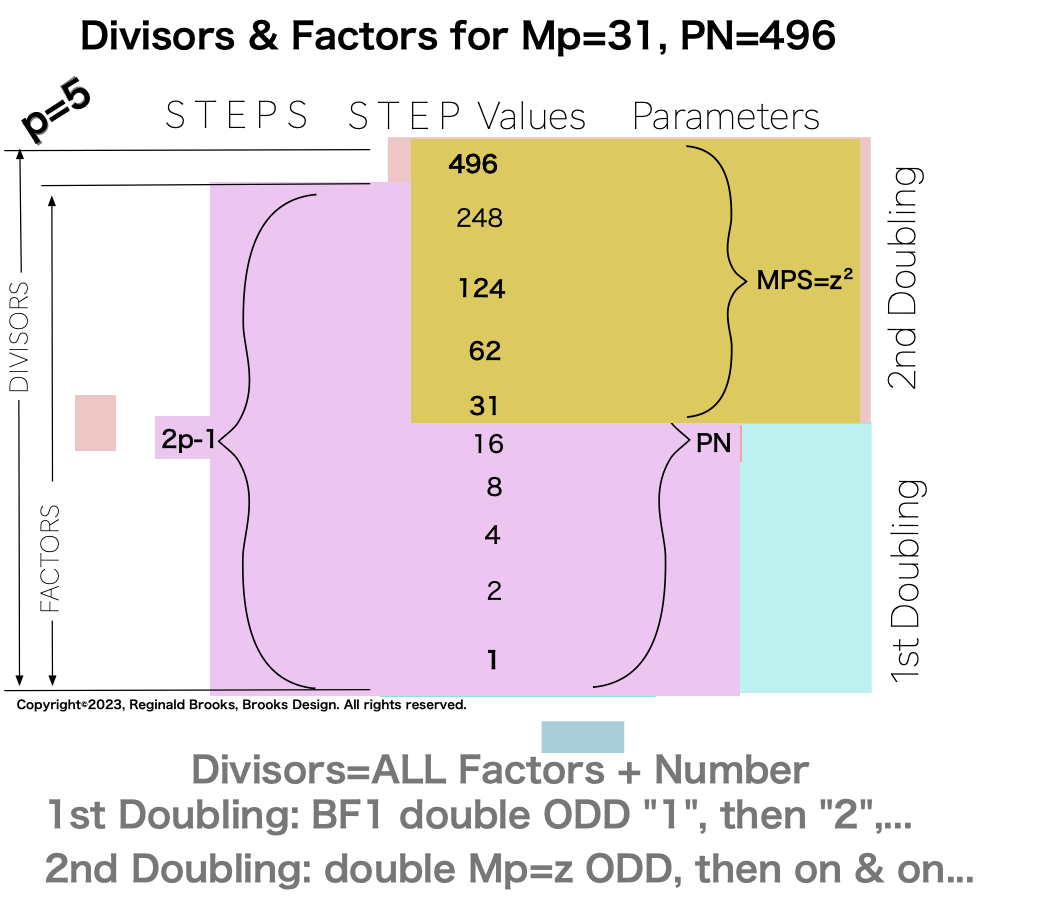
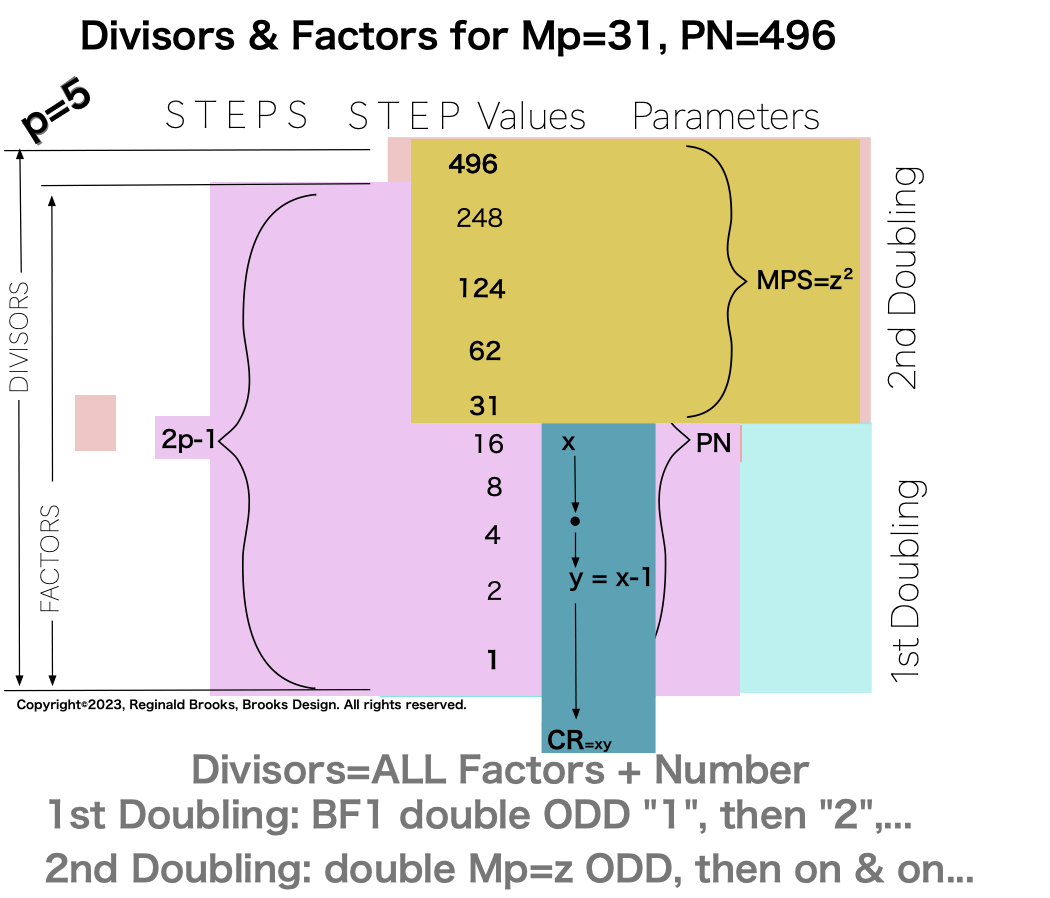
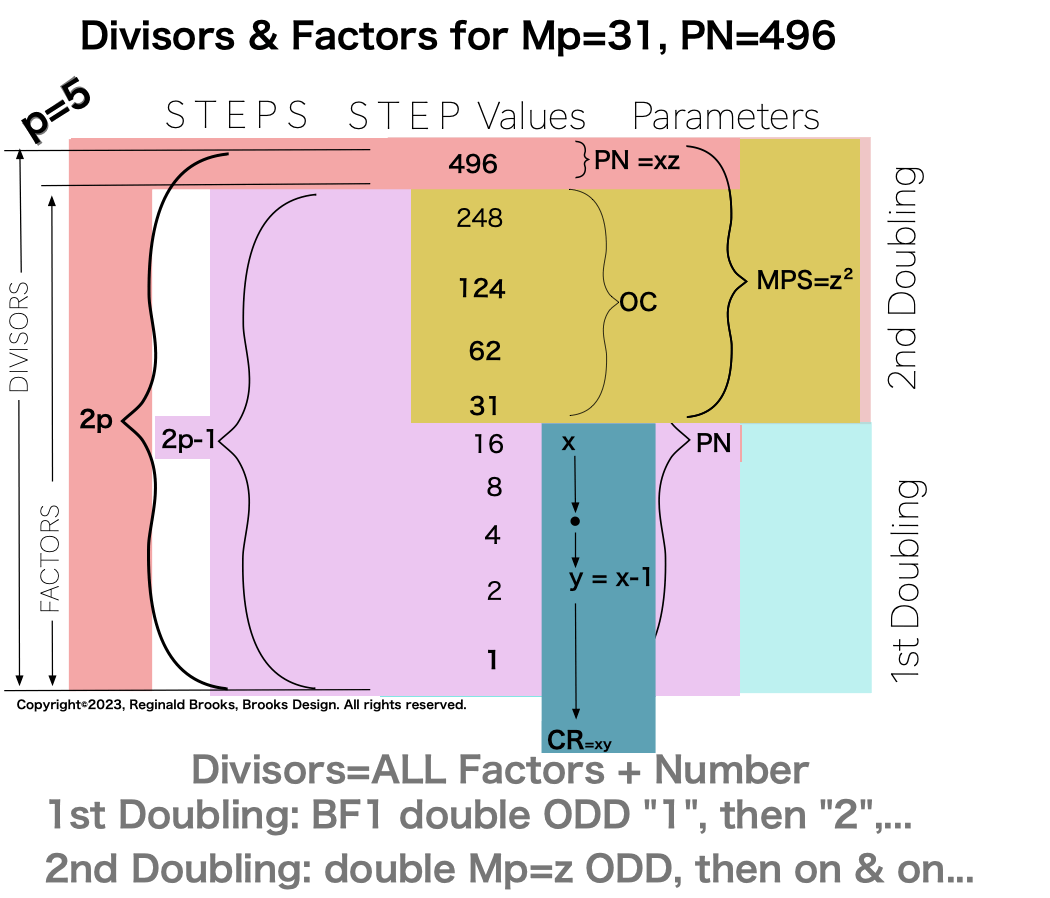
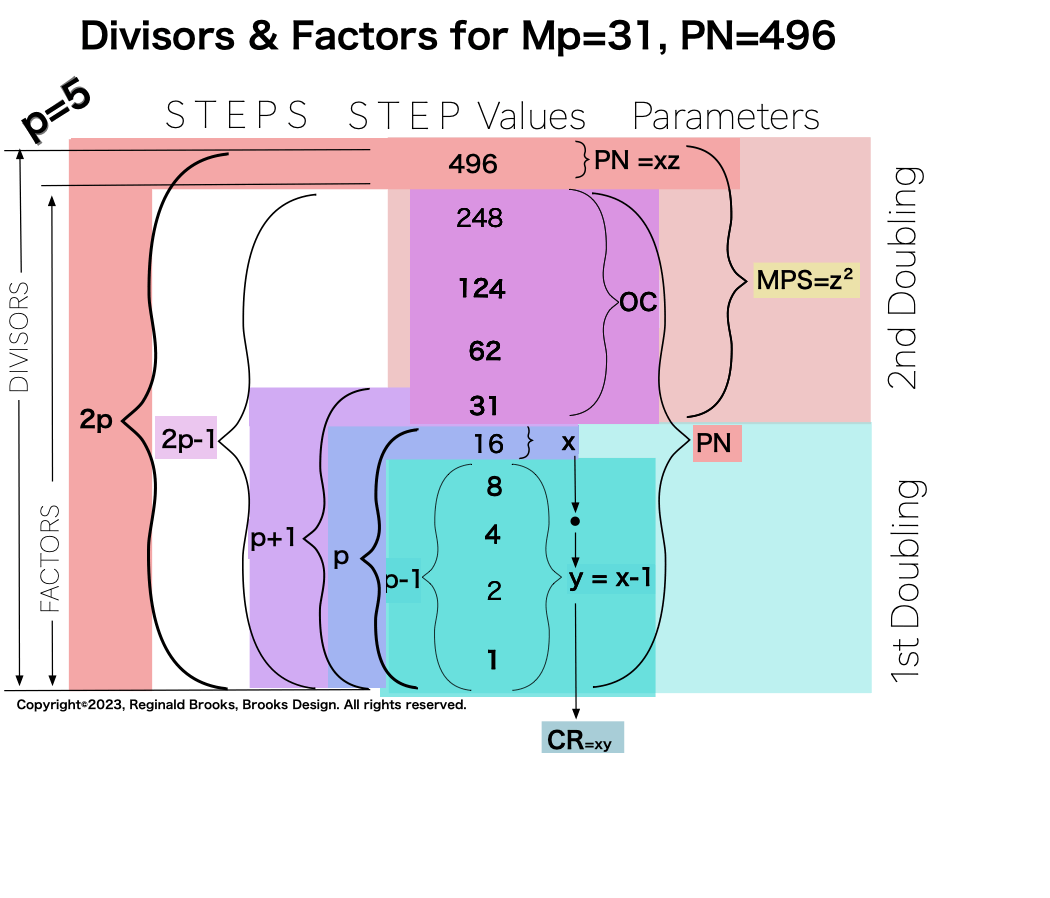

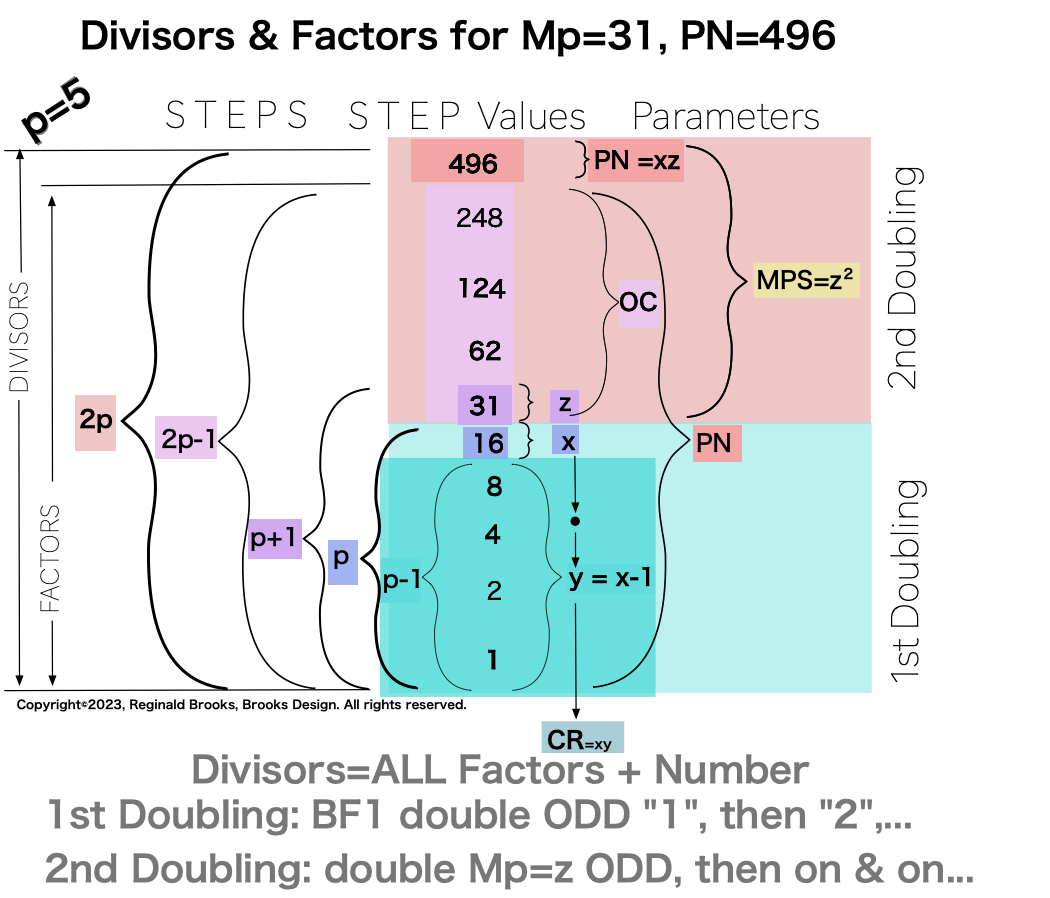
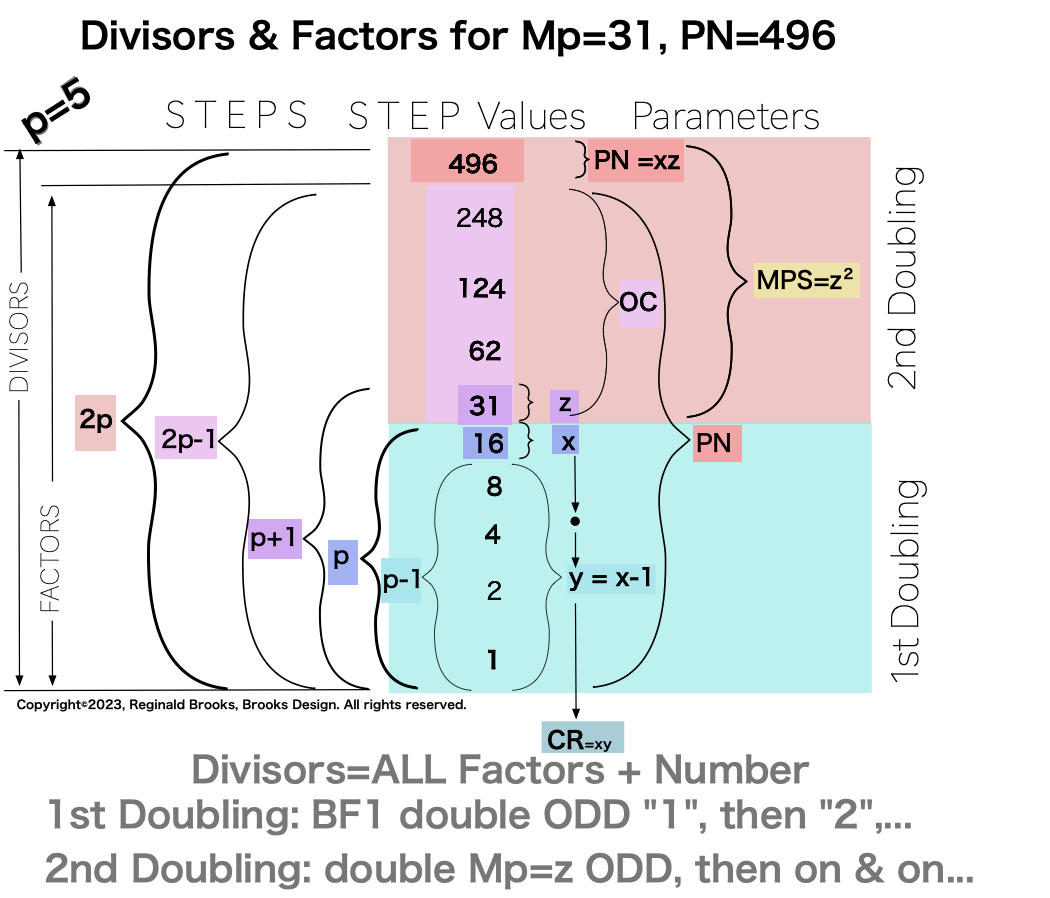

Animated Gif
Movie
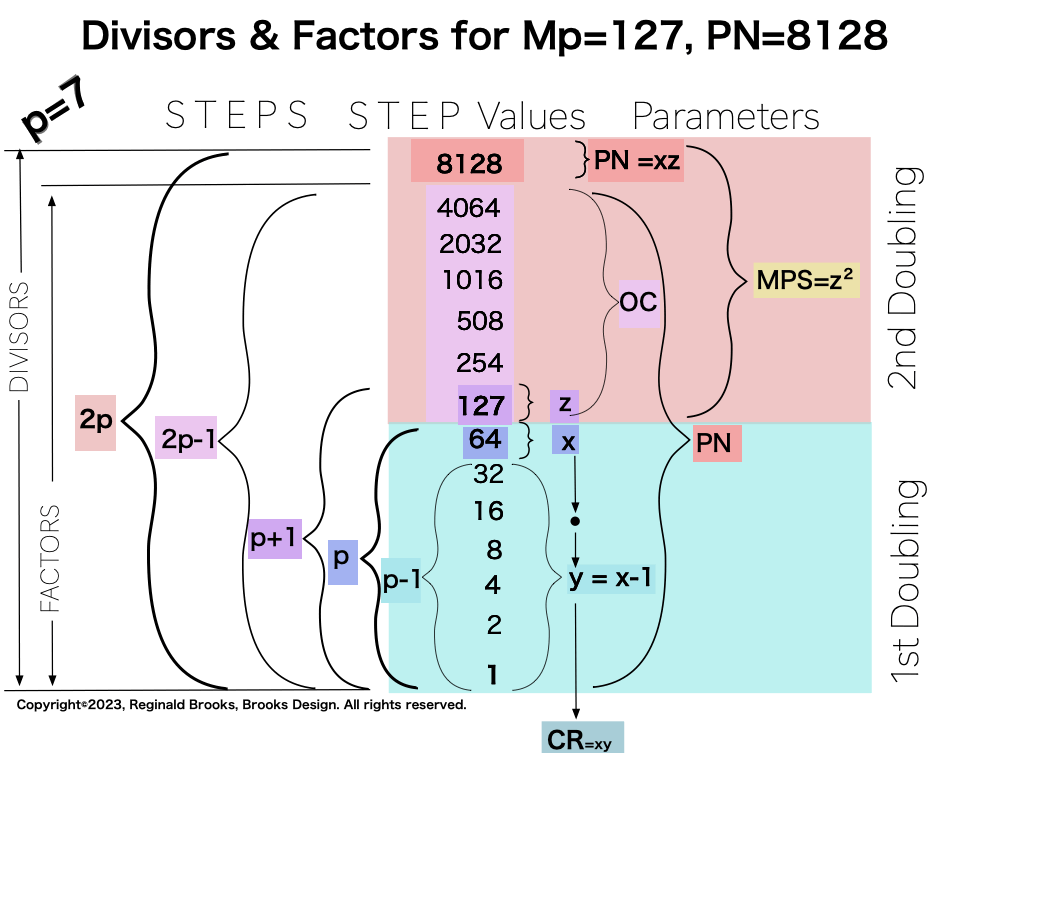

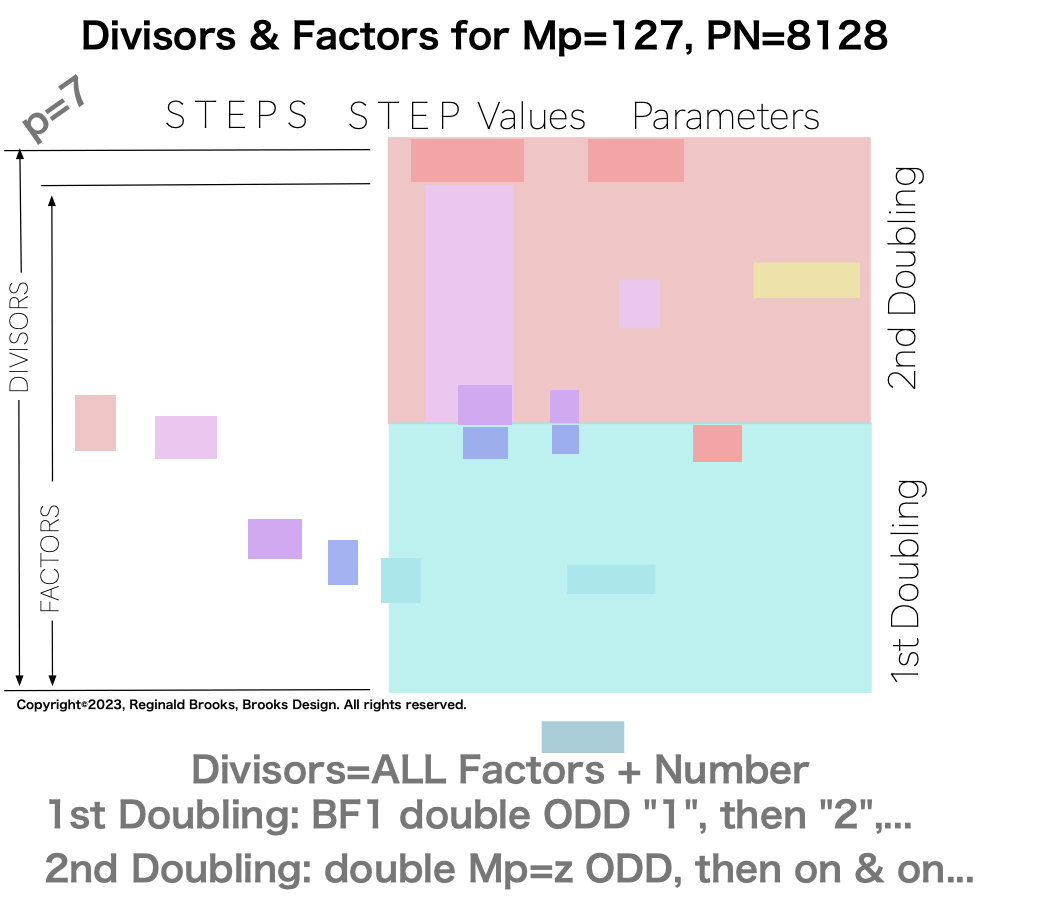
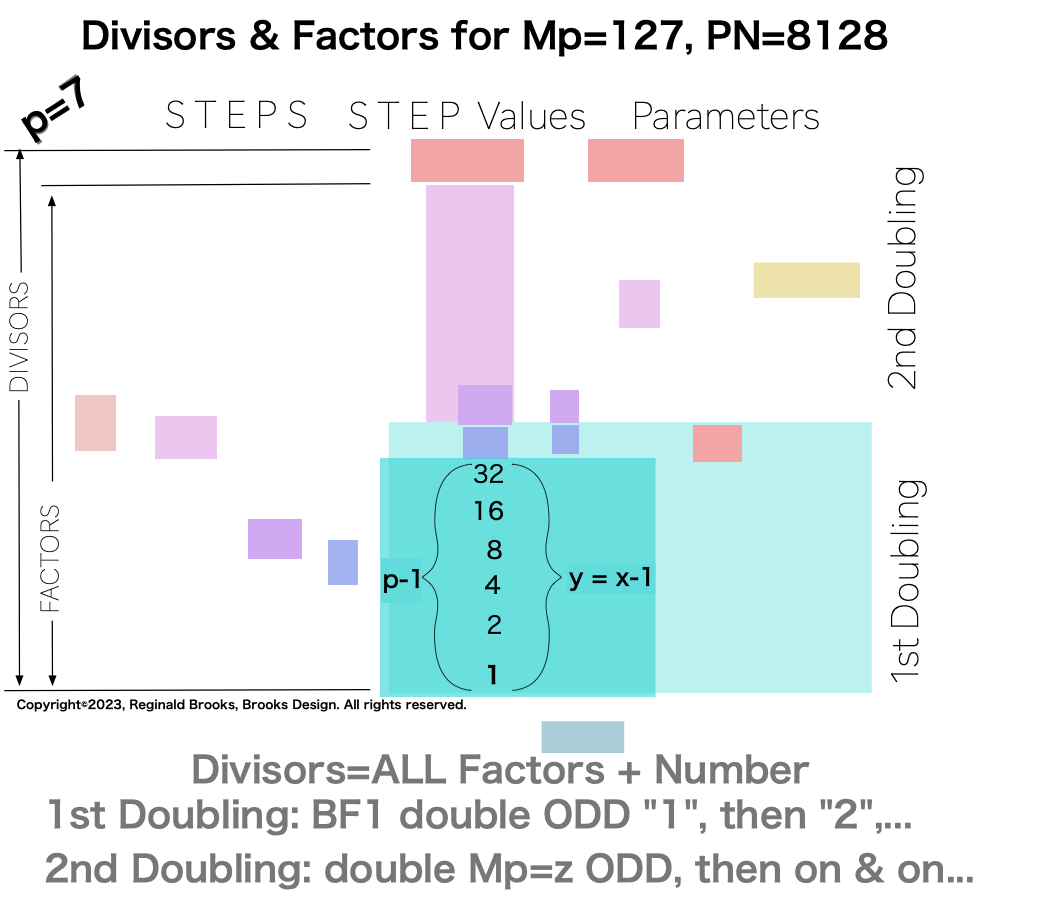
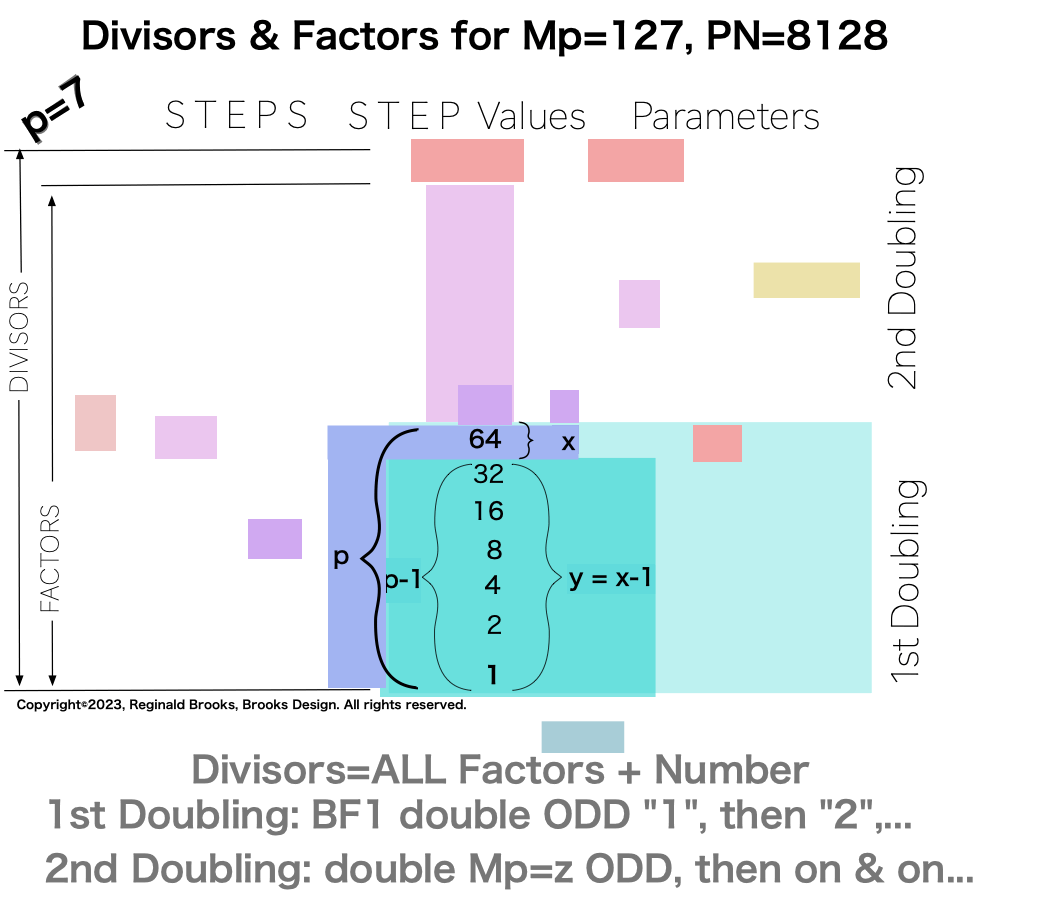
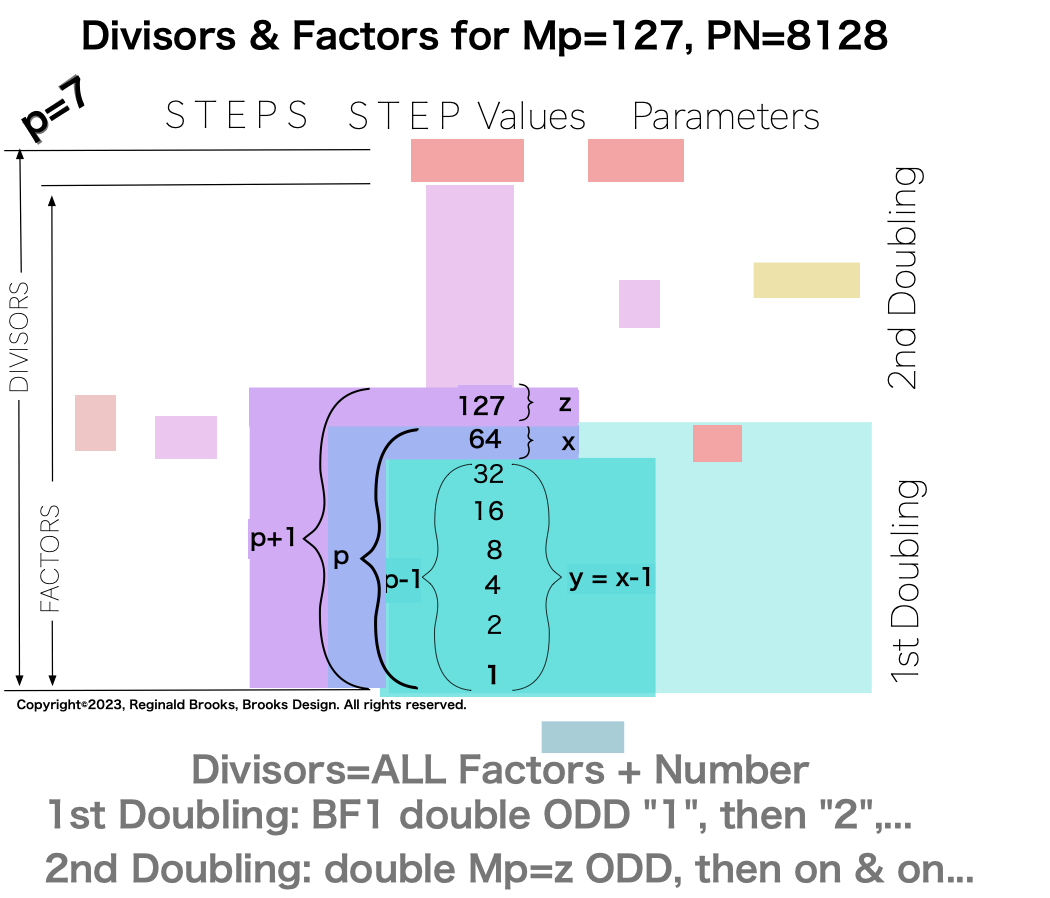
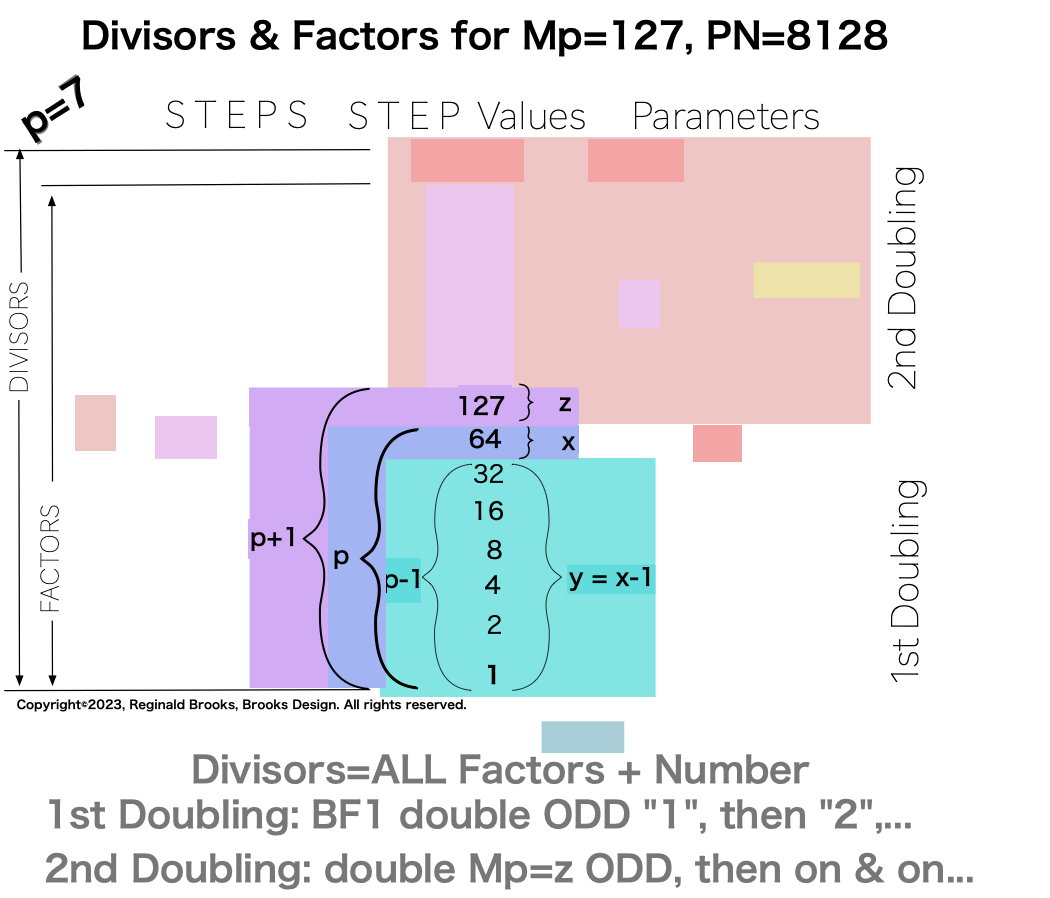
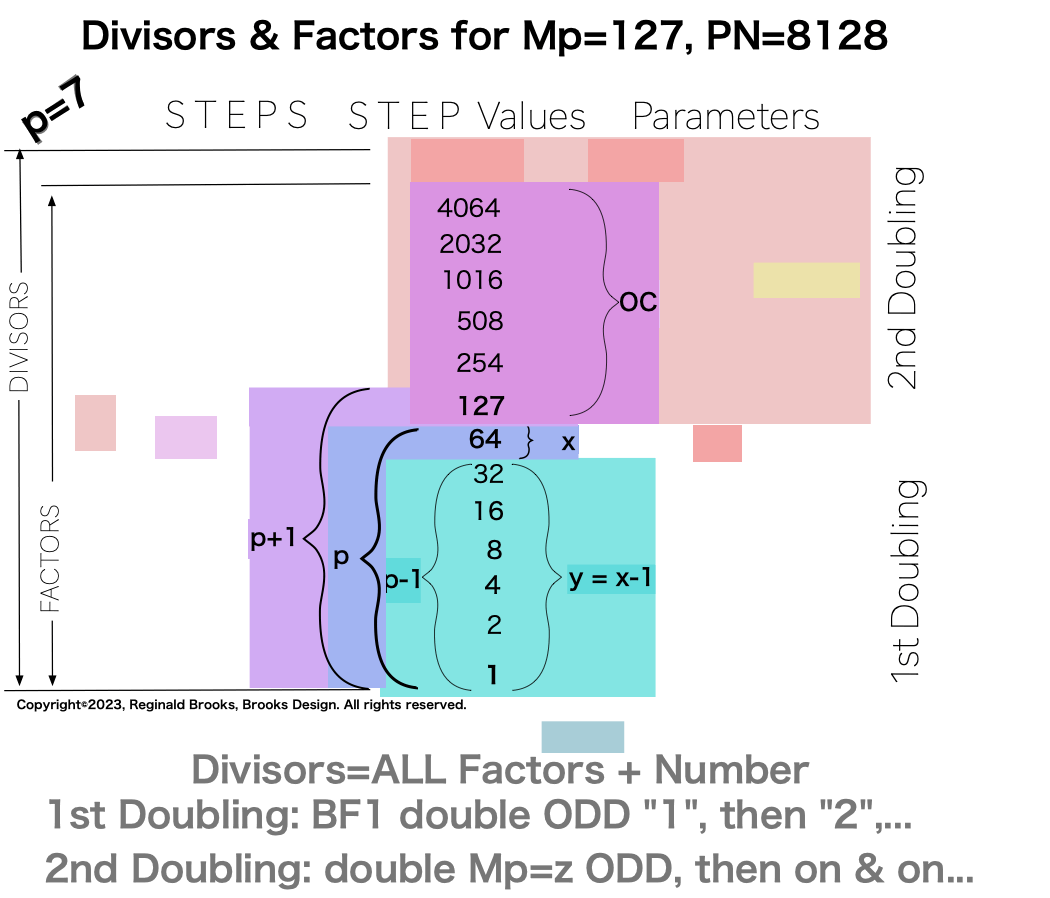
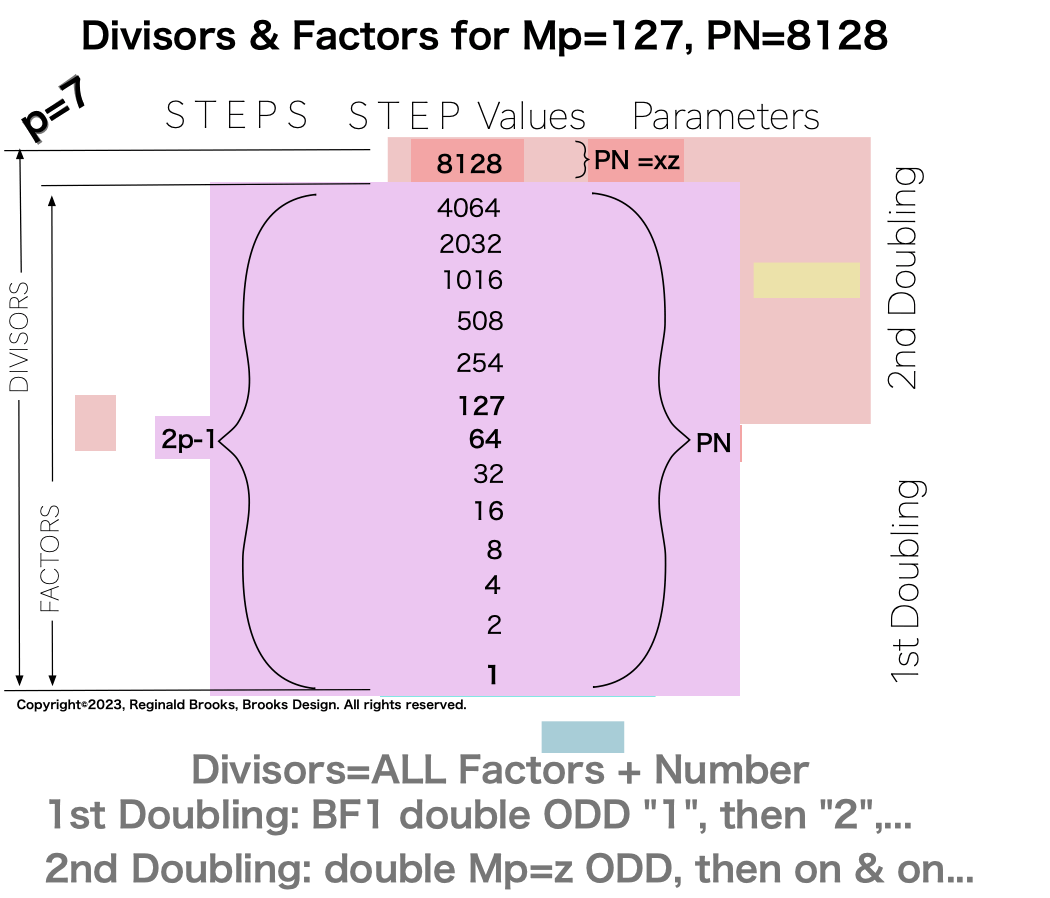
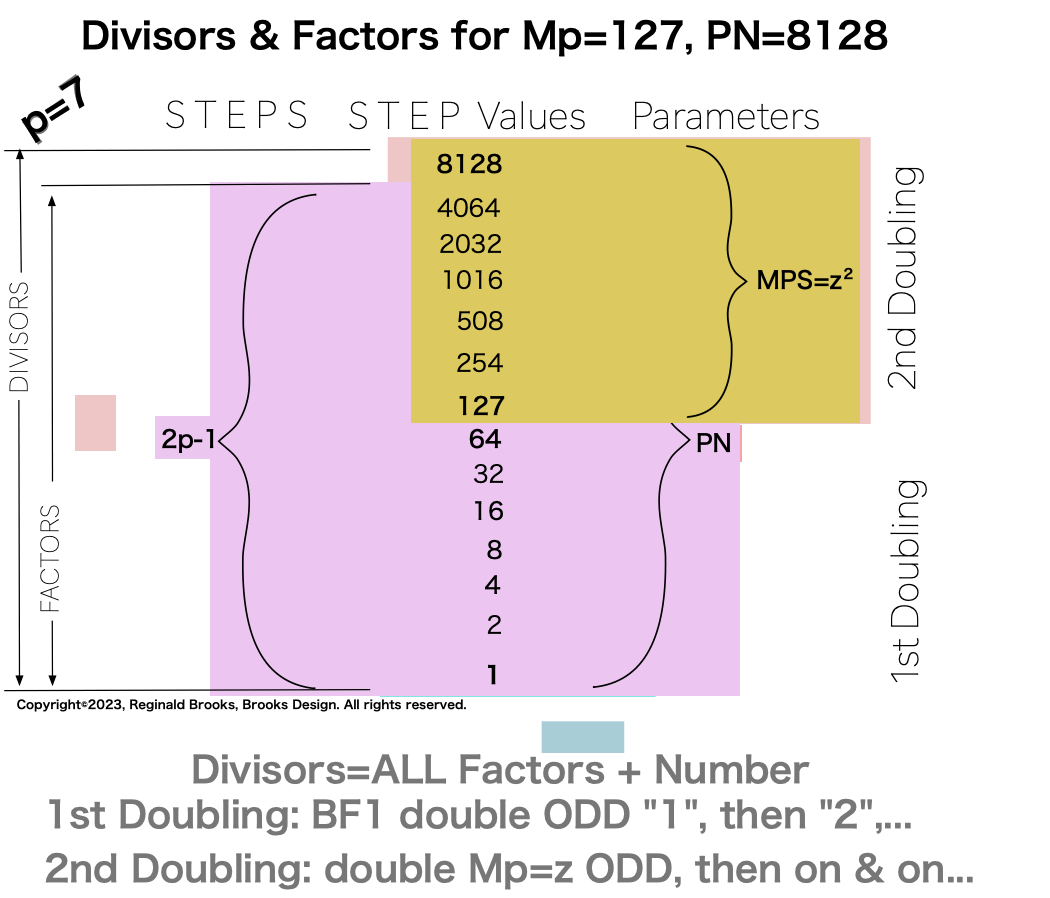
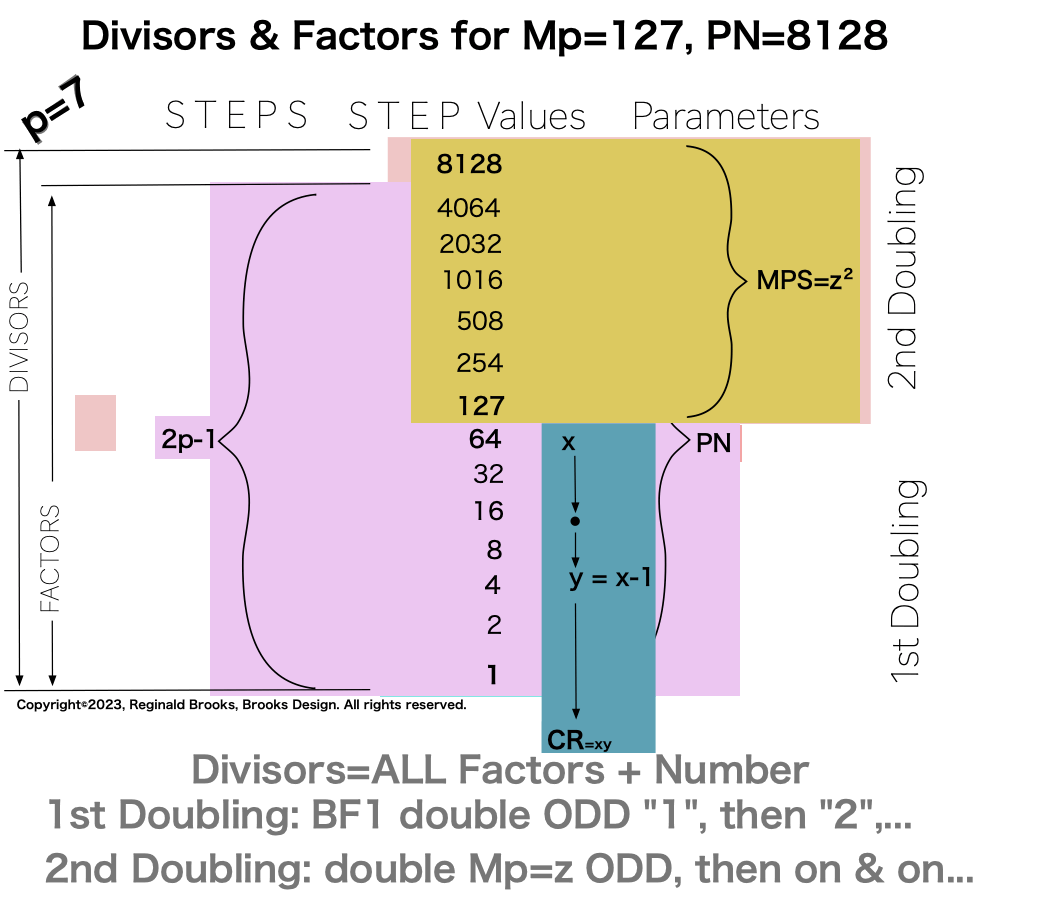
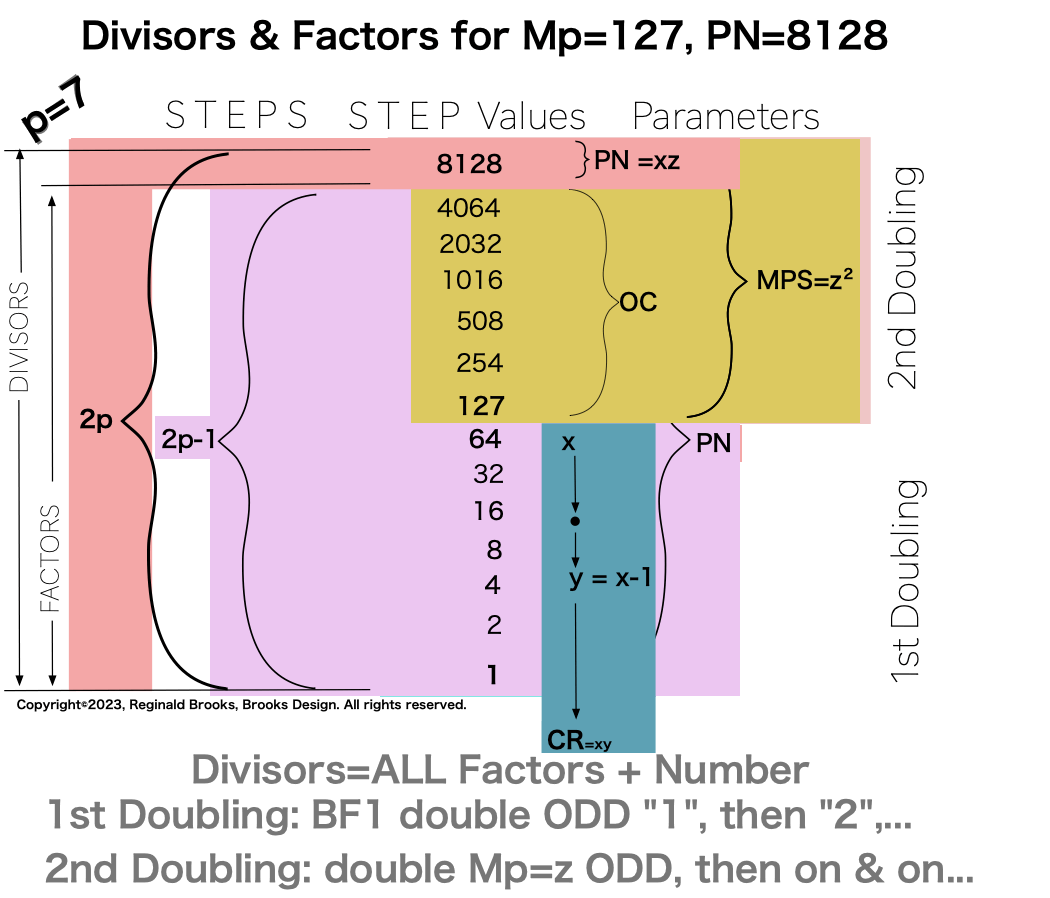
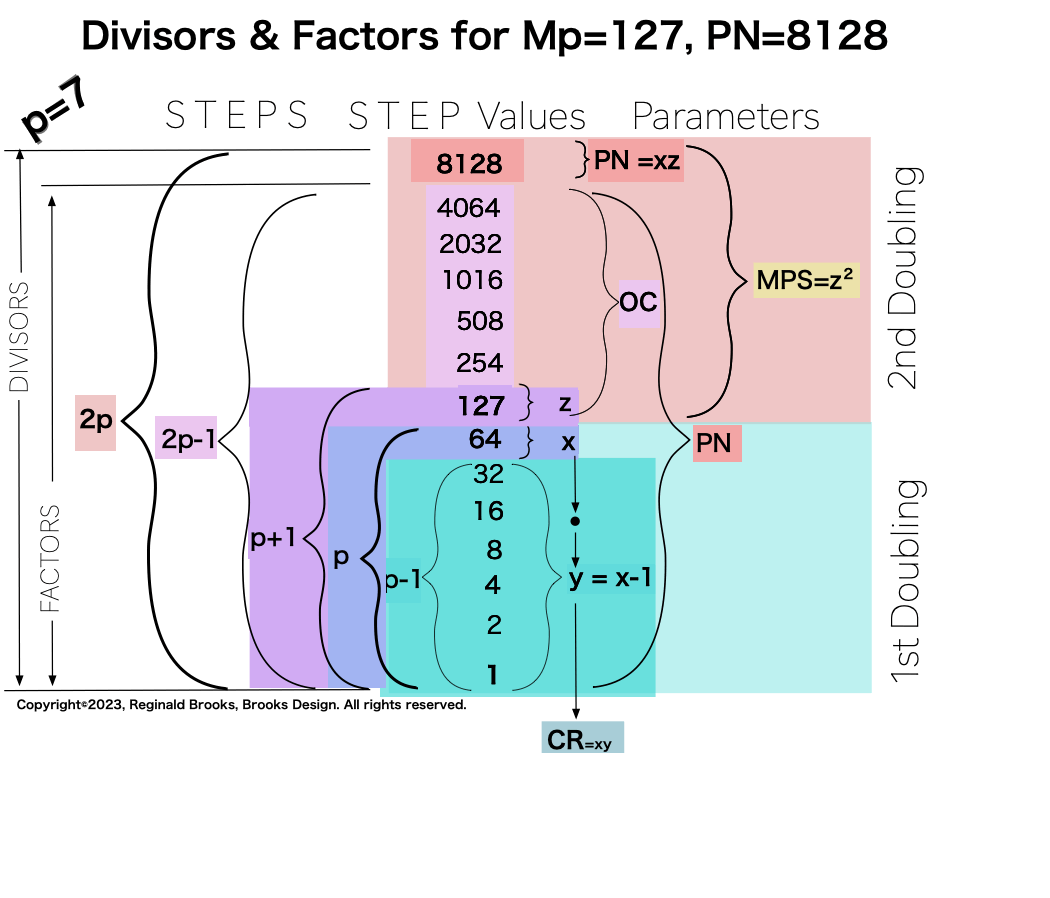
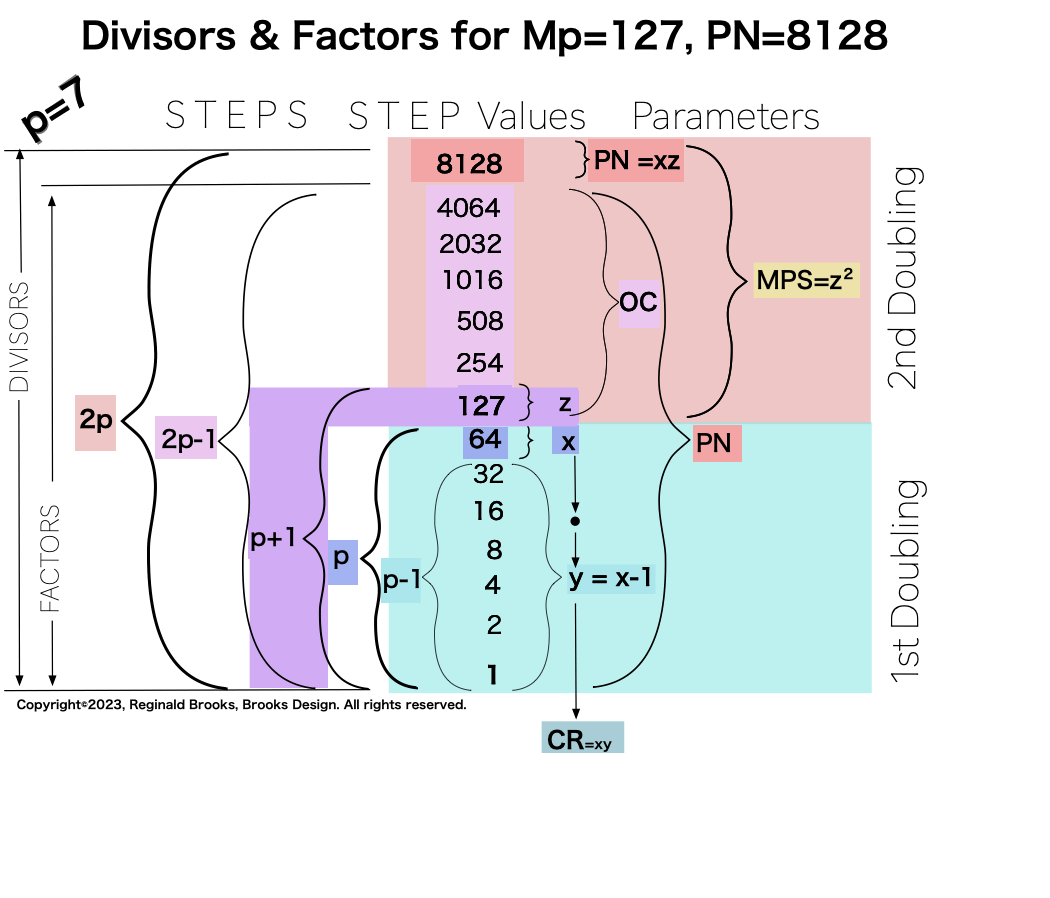
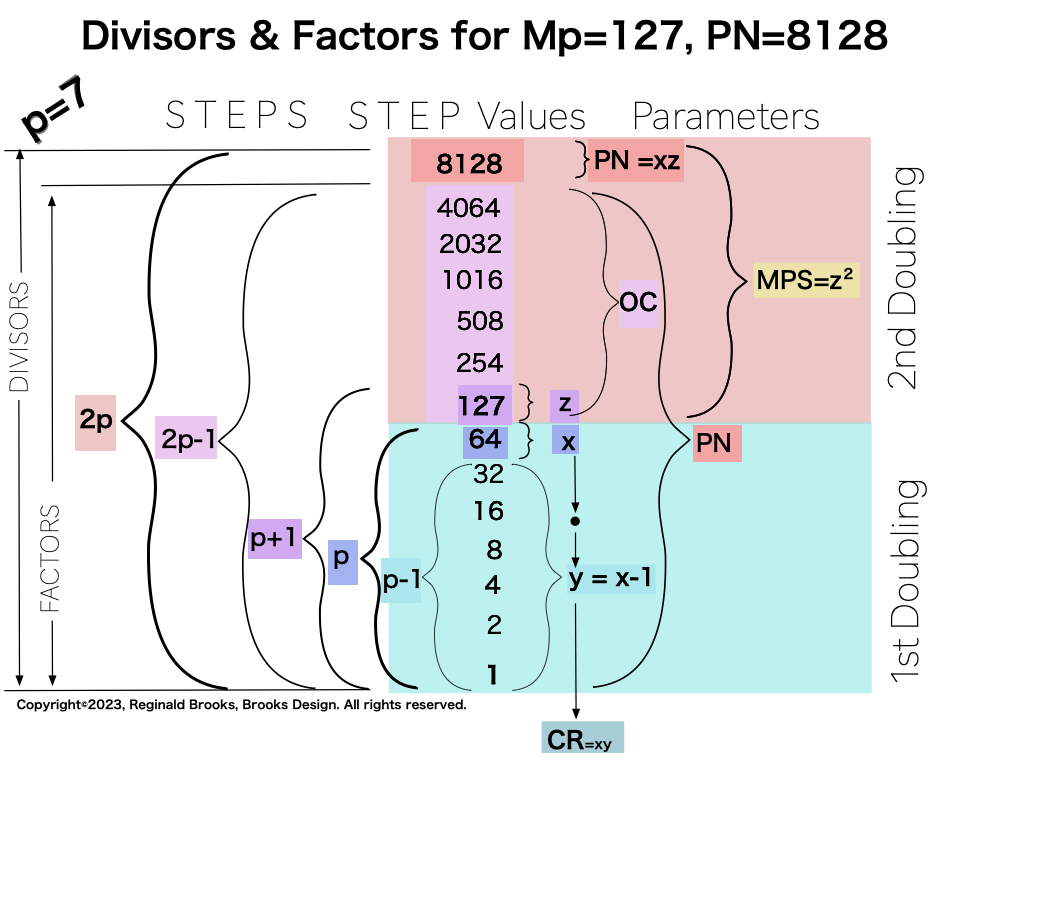
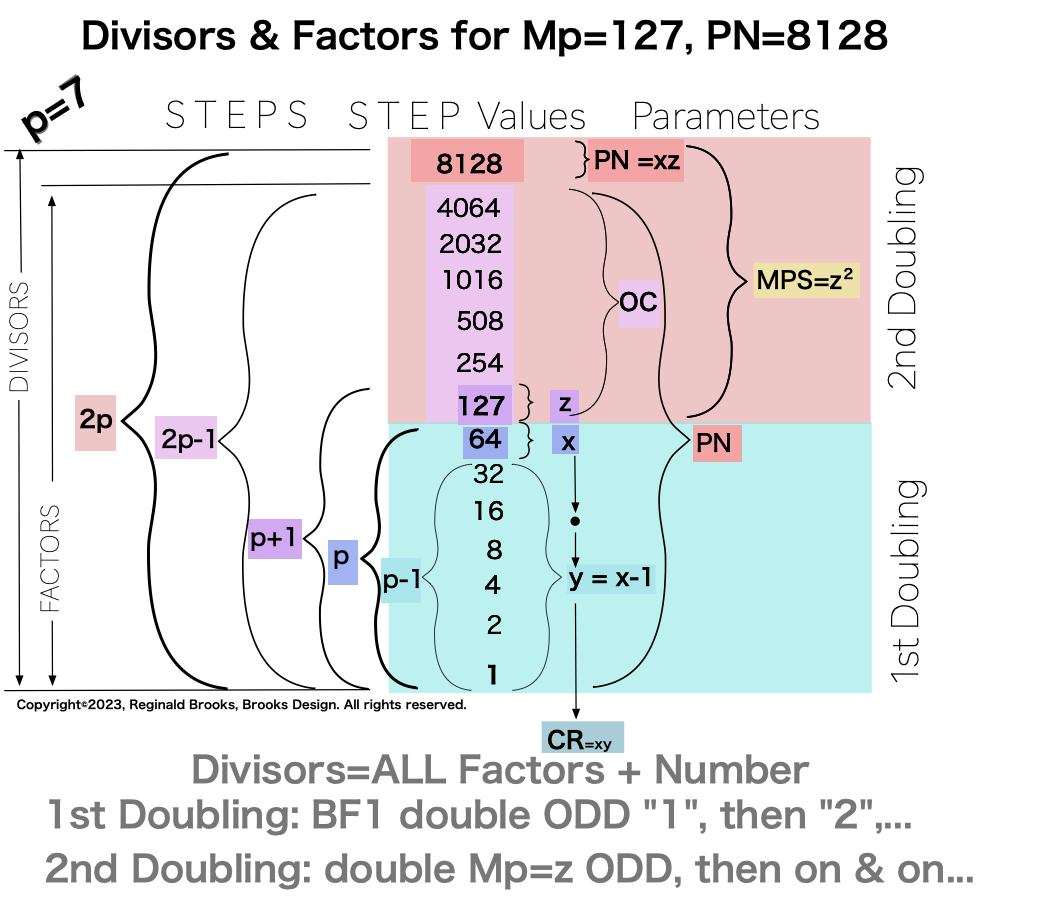
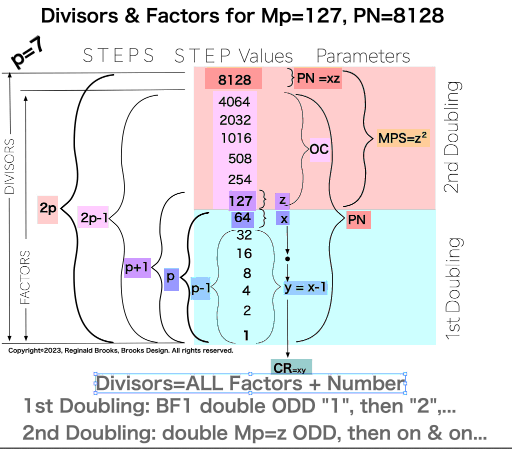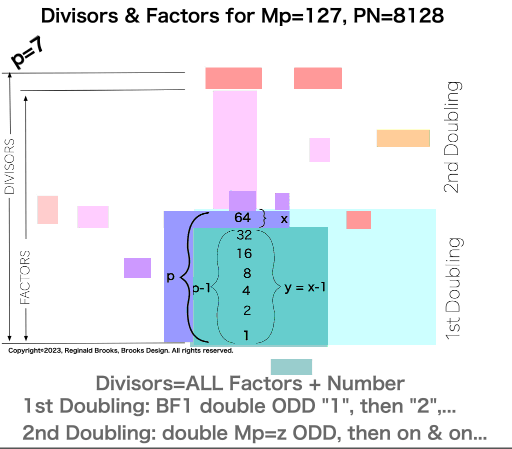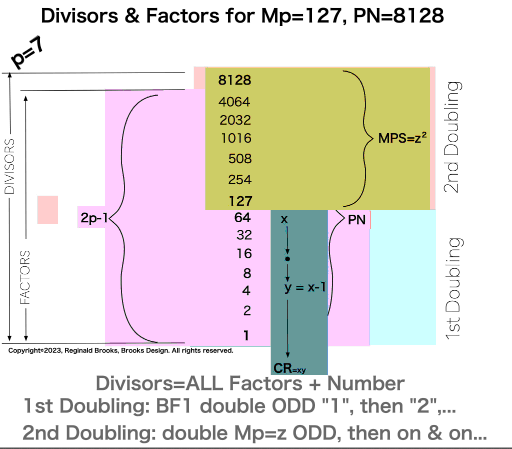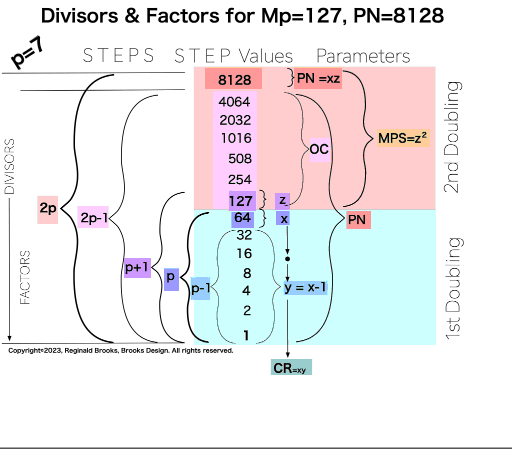
Animated Gif
Movie
2. Important Side Note-1: Generic DMT
SIDE NOTE
The examination of the divisors/factors of the PNs — based on the Exponential Power of 2 (BF1) driven Mersenne Primes — may beg the question: What is the pattern one sees for laying out the EVENs in general? Here we will take a brief look at the EVENs between 2 and 100 to see just what type of pattern is revealed. Of course, it encompasses the PN EVENs, but it also reveals a simple template pattern that works for ALL the EVENs. It also reveals a unique pattern for those EVENs that are divisors and multiples of 24 — an interesting finding that relates back to the earlier finding that ALL Squared Primes and ALL Squared Pythagorean Triple Hypotenuses (above a minimum) are separated by a multiple of 24!
What are the divisors of EVEN 60? The steps are the same for the *EVENs and EVENs-NOT.
Basically, one takes the EVEN number and divides it down sequentially by two until it reaches an ODD. The number of steps determines how many Columns there are in the Divisor Factor Matrix Table (DMT).
Now if that ODD is, other than “1”, a Prime, then the number of Rows is two — the BF1 Row starting with “1” and the second Row starting with said Prime.
However, if that ODD is a composite number, then each of the factor ODDs heads up its own Row or Rows between the BF1 (TOP) and the composite ODD (BOTTOM) Rows.
It is a simple template pattern that works for ALL the EVENs and EVENs-NOT.
Before showing the 2-100 EVENs, see the 5 examples of note below:
EVENs
EVENs-NOT
EVENs that are Exponential Powers of 2 (BF1)
EVENs (exception PN 6) that are PNs
EVEN 24 as it contains ALL its divisors/factors EVENs.
Here is an example for EVEN 60:
60/2=30 30/2=15 Bottom =3 cells wide
15 30 60
TOP=3 BF cells
1 2 4
15 is composite, so 15/3=5 and 15/3=5 become MIDDLE Rows
3 6 12
5 10 20
Sort and place Rows in order:
| 1 | 2 | 4 |
|---|---|---|
| 3 | 6 | 12 |
| 5 | 10 | 20 |
| 15 | 30 | 60 |
DMT: Divisor (Factor) Matrix Table of EVEN 60
Notice:
EVENs may have 2 or more BFM Columns of BF.
Some EVENs may have only 1 ODD (Row)—those that are Exponential Power of 2 (BF1).
Also notice the cross-products:
3x5=15
4x15=60
5x12=60
3x20=60
6x10=60
4x5=20
4x3=12
2x3=6
2x5=10
2x15=30.
The BOTTOM Column 1 value is found on 2xEVEN value, e.i. 17 on EVENs-NOT 34 is also found on EVEN 68.
ALL PN EVENs, by definition, have ONLY 2 Rows: the Upper (TOP) BF1 and the Lower (BOTTOM) ODD Factor (Mp), and, the number of Columns=p-value.
Works for BOTH EVENs (*ALL EVENs on BIM are ÷4, while EVENs-NOT=those EVENs NOT ÷4, e.i. 2-6-10… EVENs-NOT are revealed on the BIM when doubled or divided by two. They follow many of the same patterns on the BIM as the EVENs do, but are not directly involved with the Inverse Square Law (ISL)— the basis of the BIM — in that 1/r² always results in a value ÷4.)
Example for EVENs-NOT 70:
70/2=35 Bottom=2 cells wide
35 70
TOP=2 BF cells
1 2
35 is composite, so 35/5=7 and 35/7=5 becomes MIDDLE Rows
5 10
7 14
Sort and place Rows in order:
| 1 | 2 |
|---|---|
| 5 | 10 |
| 7 | 14 |
| 35 | 70 |
Notice:
ALL EVENs-NOT have ONLY 2 BFM Columns of BF 1 and 2.
ALL EVENs-NOT have AT LEAST 2 ODDs (Rows).
The cross-products are similar to the EVENs.
The BOTTOM Column 1 value follows the ODD number sequence.
There are*NO PN EVENs, by definition, within the EVENs-NOT.
*except PN 6
ALL EVENs -- EVENs and EVENs-NOT -- have Row 1 = BF1 (1-2-4...), and, except for #3 above -- EVENs that are Exponential Powers of 2 (BF1) -- have 2 or more Rows, with each Row starting with -- and only containing -- one ODD.
There are NO ODDs that fit this DMT pattern, unless they are doubled.
Examples for EVENs that are an Exponential Power of 2 (BF1):
EVEN 2 2¹=2
| 1 | 2 |
|---|---|
EVEN 4 2²=4
| 1 | 2 | 4 |
|---|---|---|
EVEN 8 2³=8
| 1 | 2 | 4 | 8 |
|---|---|---|---|
EVEN 16 2⁴=16
| 1 | 2 | 4 | 8 | 16 |
|---|---|---|---|---|
Always 1 Row!
Example for EVENs that are PN, here PN=28 and based on p=3, where p=3=number of Columns (True for ALL PNs):
| 1 | 2 | 4 |
|---|---|---|
| 7 | 14 | 28 |
Always 2 Rows!
Example for EVEN 24 as it contains ALL its divisors/factors:
| 1 | 2 | 4 | 8 |
|---|---|---|---|
| 3 | 6 | 12 | 24 |
EVEN 2
| 1 | 2 |
|---|---|
EVEN 4
| 1 | 2 | 4 |
|---|---|---|
EVEN 8
| 1 | 2 | 4 | 8 |
|---|---|---|---|
EVEN 6 contains ODD 3
| 1 | 2 |
|---|---|
| 3 | 6 |
EVEN 12 contains ODD 3
| 1 | 2 | 4 |
|---|---|---|
| 3 | 6 | 12 |
and, of course, 1 & 24. 24 and ALL subsequent doublings (96, 192, 384,...) always 2 Rows!
~~ ~~ ~~
Divisor_Factor_EVENs 2-100, 496 and 8128

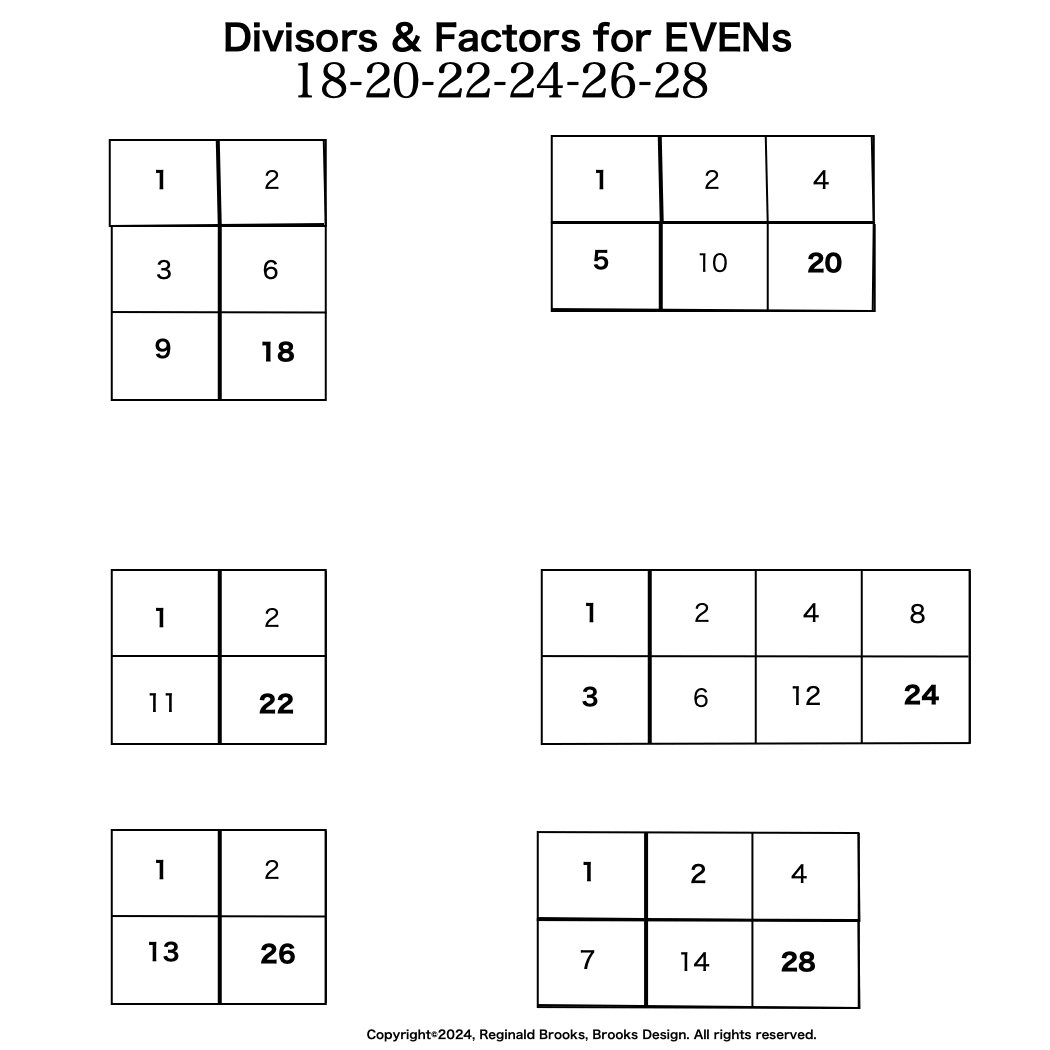
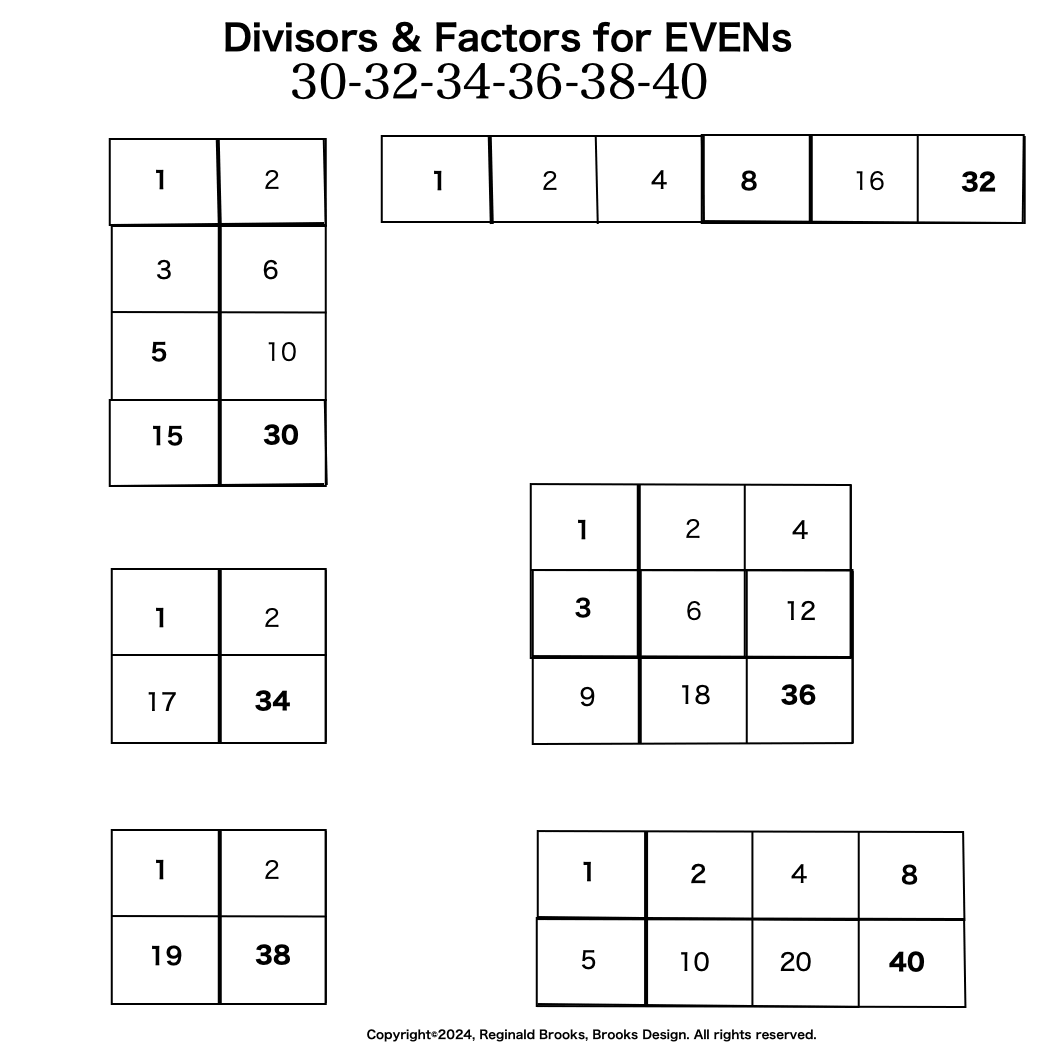

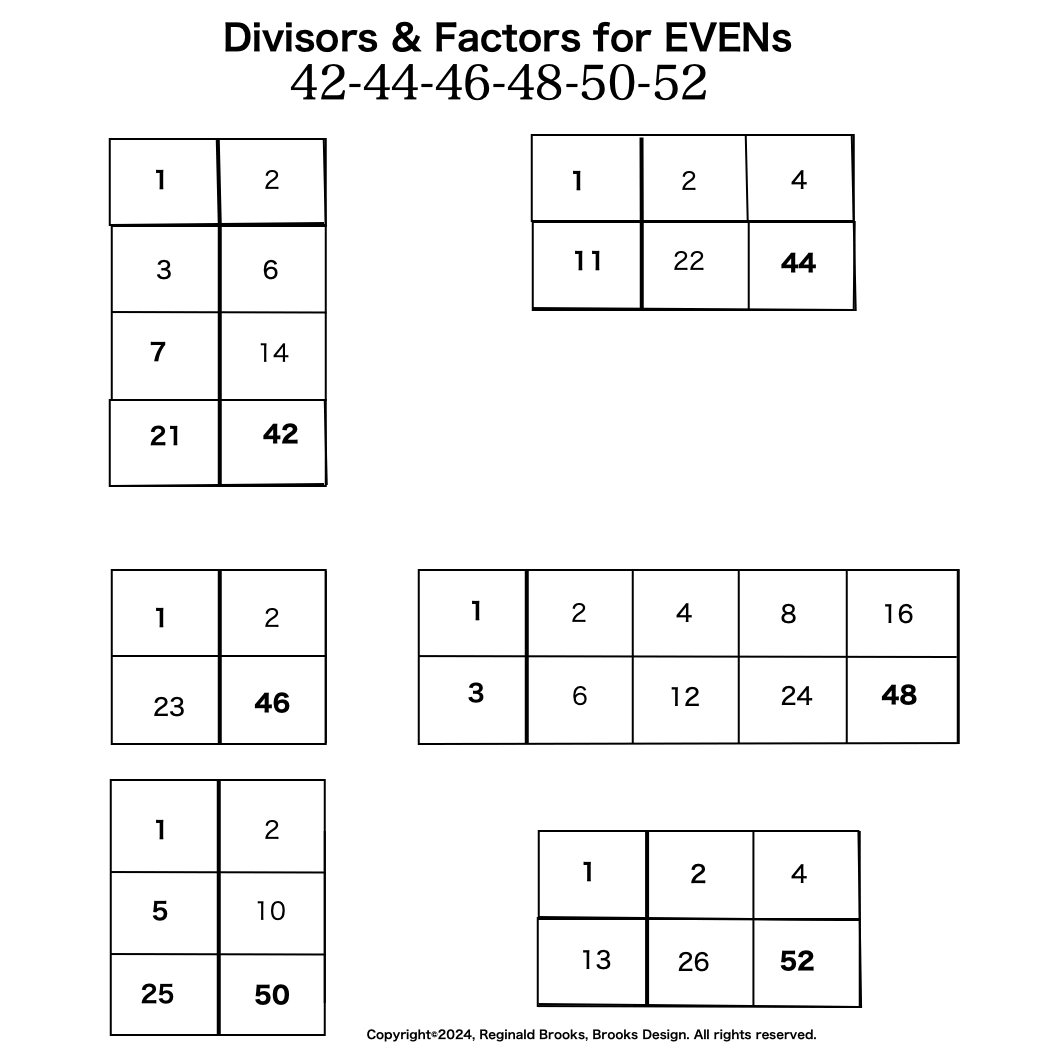
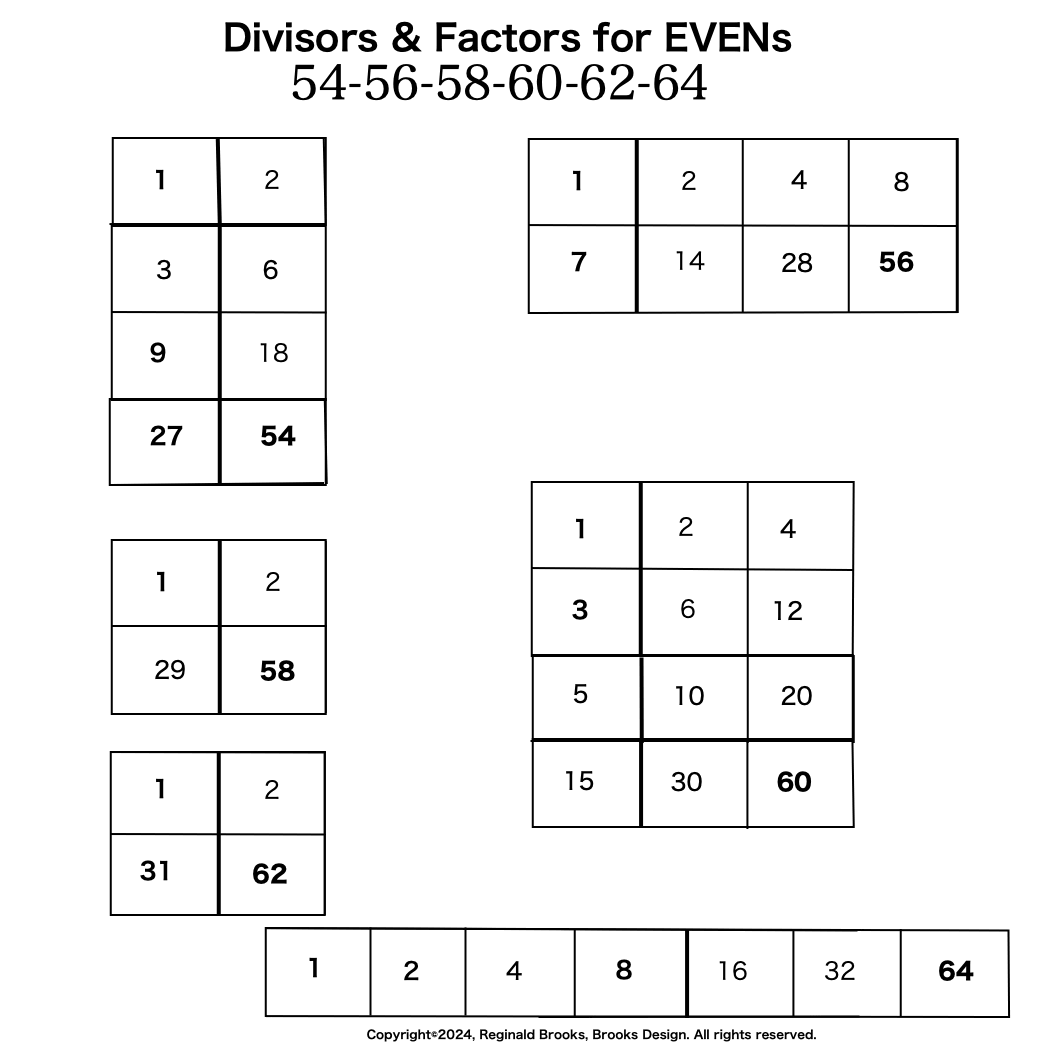
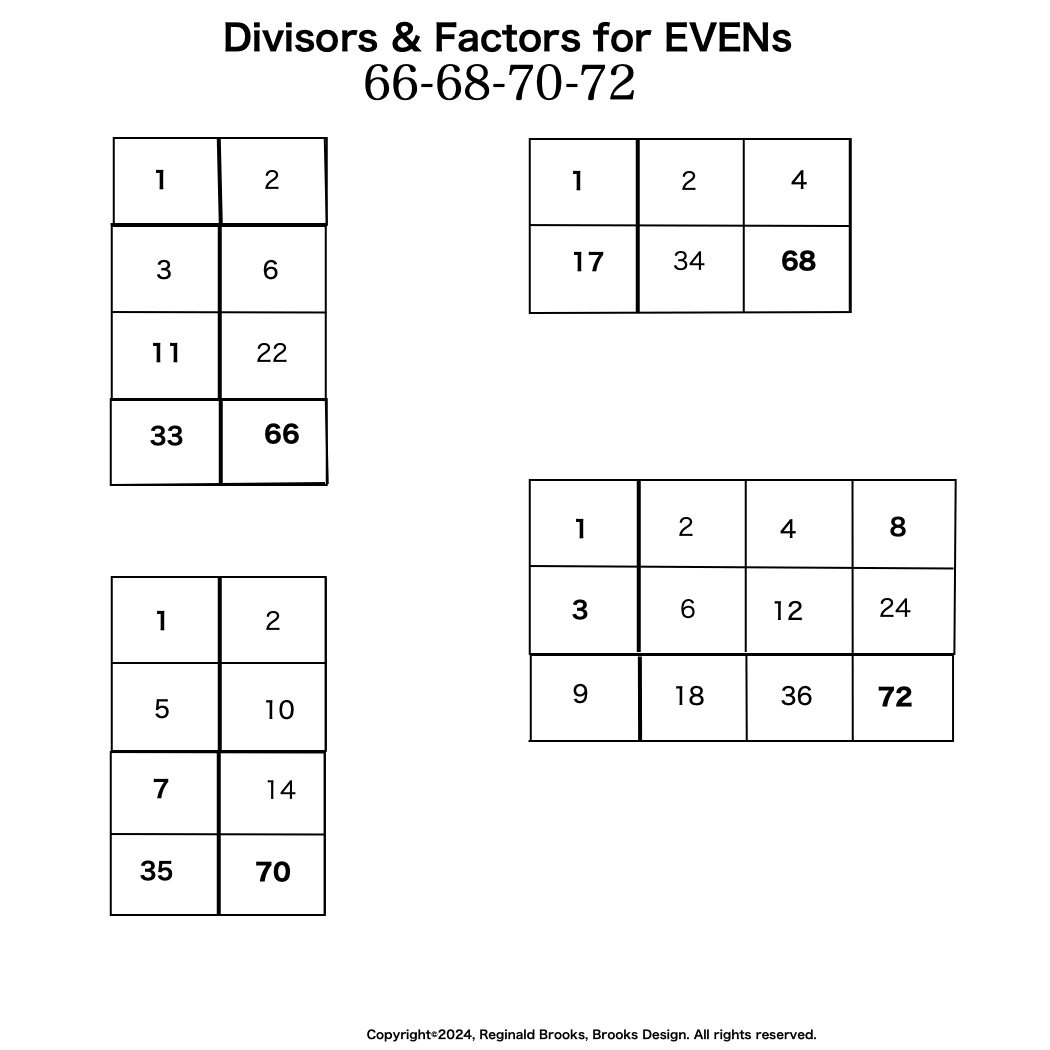
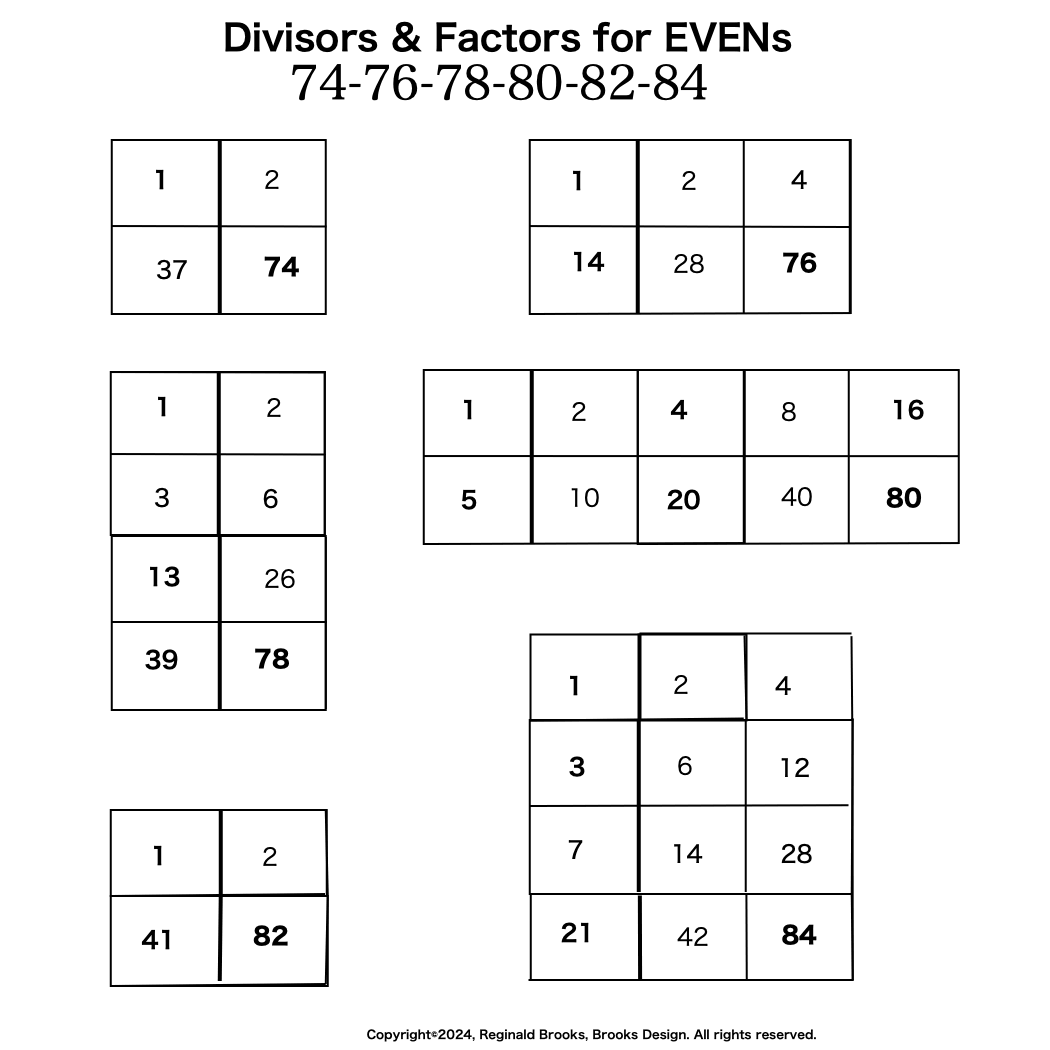
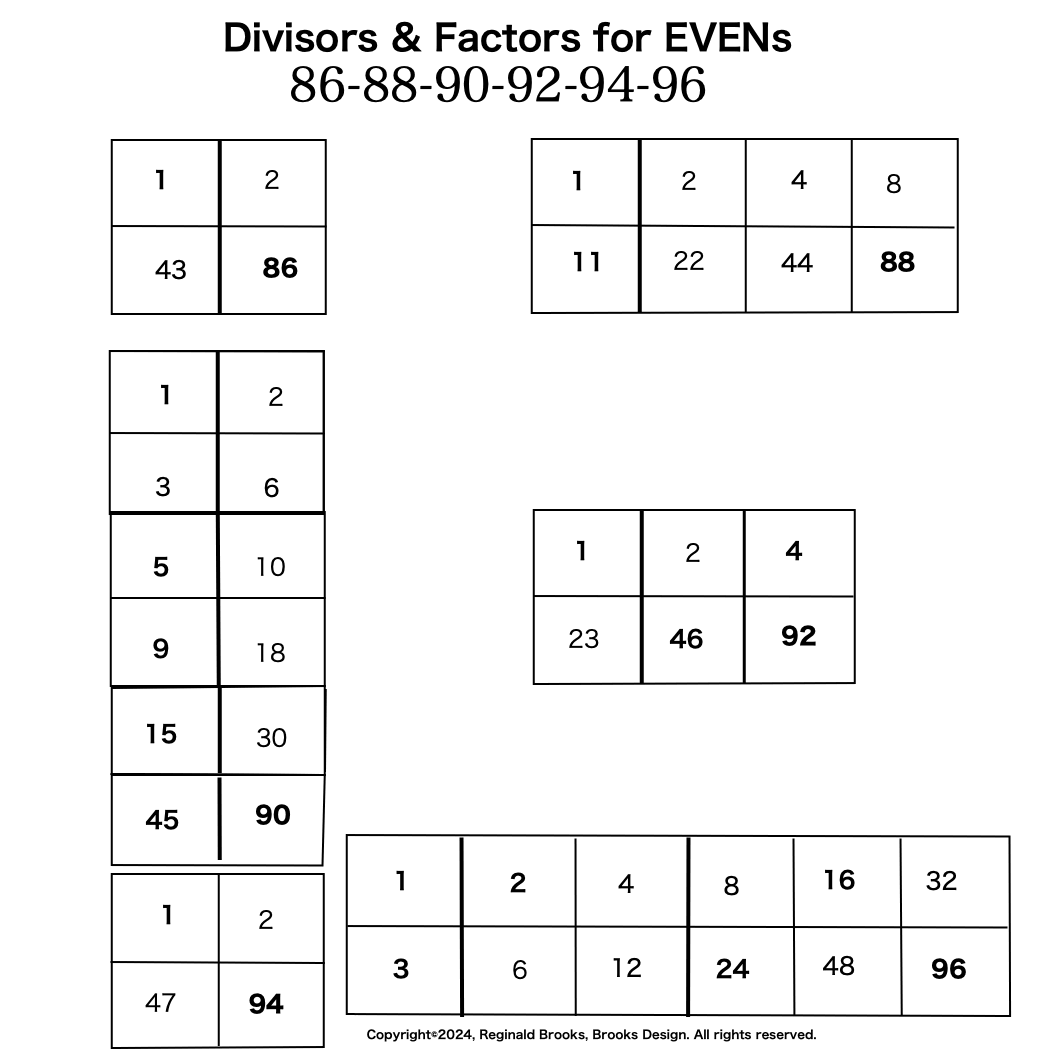
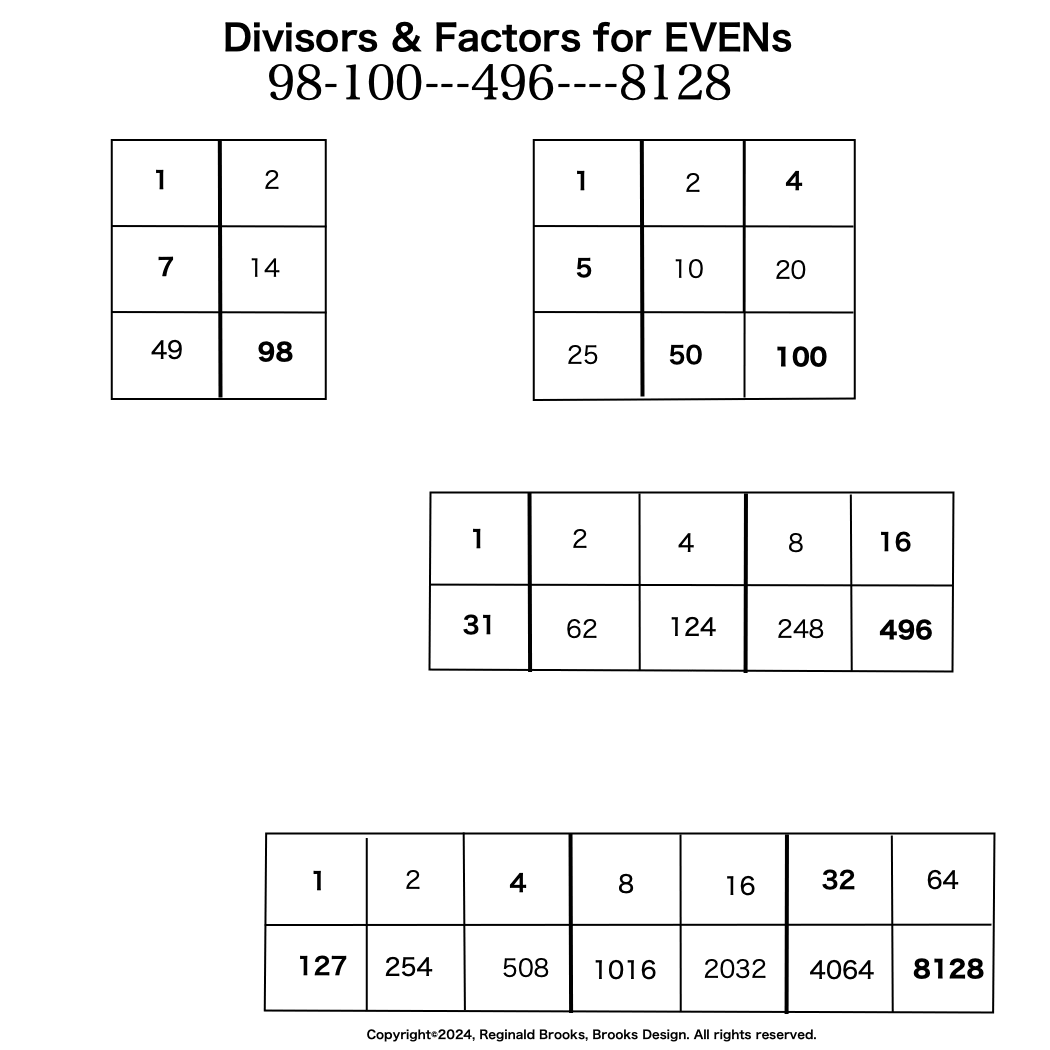
Table167_ODDs_EVENs_EVENs-NOT_Matrix.pdf
Table167_ODDs_EVENs_EVENs-NOT_Matrix.pdf
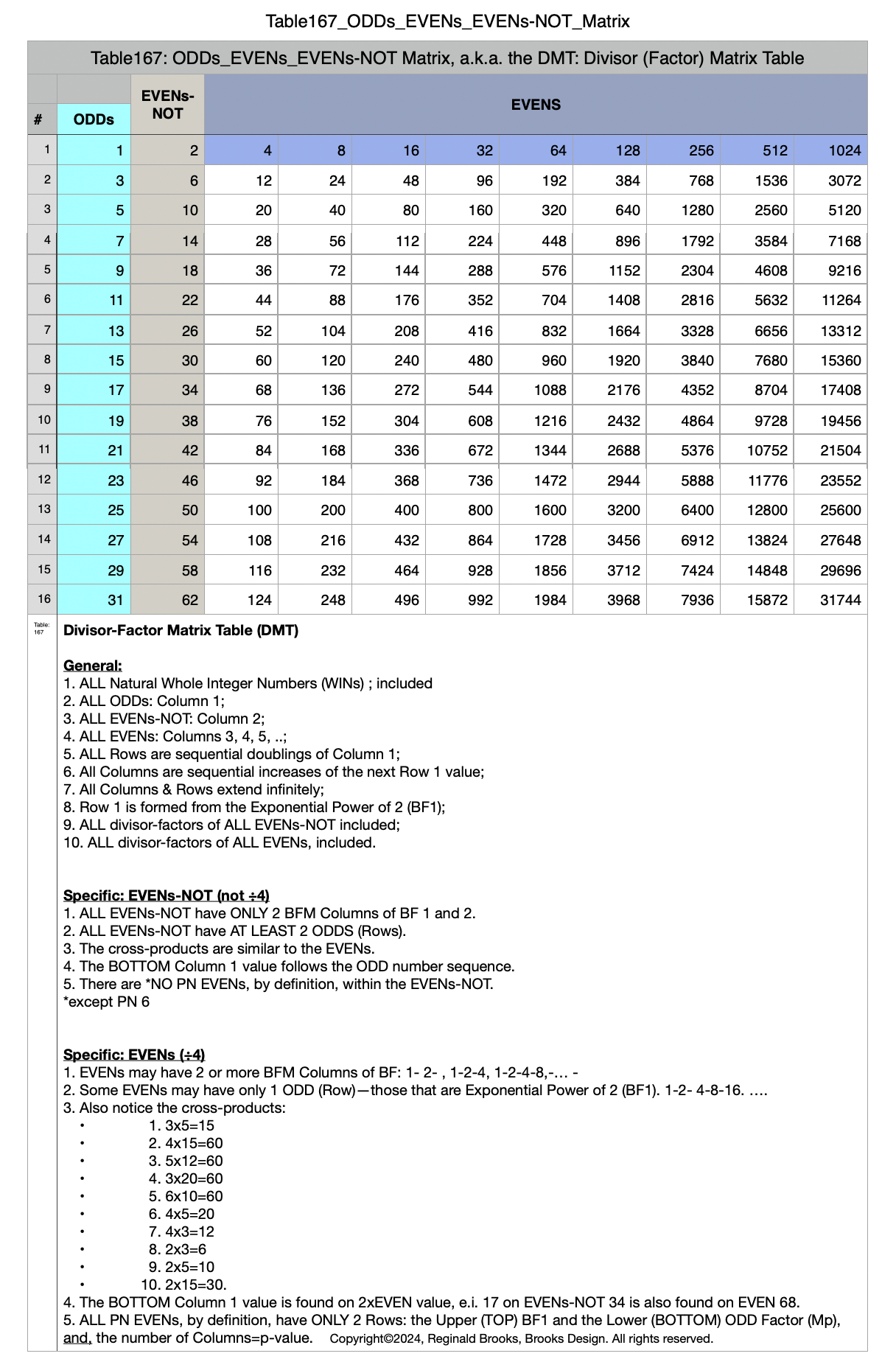
Table167_ODDs_EVENs_EVENs-NOT_Matrix.png
Divisor-Factor Matrix Table (DMT)
General:
ALL Natural Whole Integer Numbers (WINs) ; included
ALL ODDs: Column 1;
ALL EVENs-NOT: Column 2;
ALL EVENs: Columns 3, 4, 5, ..;
ALL Rows are sequential doublings of Column 1;
All Columns are sequential increases of the next Row 1 value;
All Columns & Rows extend infinitely;
Row 1 is formed from the Exponential Power of 2 (BF1);
ALL divisor-factors of ALL EVENs-NOT included;
ALL divisor-factors of ALL EVENs, included.
Specific: EVENs-NOT (not ÷4)
ALL EVENs-NOT have ONLY 2 BFM Columns of BF 1 and 2.
ALL EVENs-NOT have AT LEAST 2 ODDs (Rows).
The cross-products are similar to the EVENs.
The BOTTOM Column 1 value follows the ODD number sequence.
There are *NO PN EVENs, by definition, within the EVENs-NOT.
*except PN 6
Specific: EVENs (÷4)
EVENs may have 2 or more BFM Columns of BF: 1- 2- , 1-2-4, 1-2-4-8,-… -
Some EVENs may have only 1 ODD (Row)—those that are Exponential Power of 2 (BF1). 1-2- 4-8-16. ….
Also notice the cross-products:
3x5=15
4x15=60
5x12=60
3x20=60
6x10=60
4x5=20
4x3=12
2x3=6
2x5=10
2x15=30.
The BOTTOM Column 1 value is found on 2xEVEN value, e.i. 17 on EVENs-NOT 34 is also found on EVEN 68.
ALL PN EVENs, by definition, have ONLY 2 Rows: the Upper (TOP) BF1 and the Lower (BOTTOM) ODD Factor (Mp), and, the number of Columns=p-value.
Here is a 5 Col x 4 Row DMT:
| 1 | 2 | 4 | 8 | 16 |
|---|---|---|---|---|
| 3 | 6 | 12 | 24 | 48 |
| 5 | 10 | 20 | 40 | 80 |
| 7 | 14 | 28 | 56 | 112 |
To find the divisors-factors of any given EVEN:
Locate the EVEN, and check the *ODD that starts the Row;
Combine that EVEN Row with,
The BF1 Row above.
*if the ODD is a composite number, you then include each Row of the respective ODD factors, e.i. 35 = 5,7.
Example: EVEN 28
Locate 28, and 7 is the ODD that starts the Row;
It has 7-14-28 in its Row,
The BF1 Row above it is 1-2-4
Here is the solution: a 3 Col x 2 Row DFT:
| 1 | 2 | 4 |
|---|---|---|
| 7 | 14 | 28 |
Example: EVEN 36
Locate 36, and 9 is the ODD composite that starts the Row;
It has 9-18-36 in its Row, and 3-6-12 in the composite Row;
The BF1 Row above it is 1-2-4
Here is the solution: a 3 Col x 3 Row DMT:
| 1 | 2 | 4 |
|---|---|---|
| 3 | 6 | 12 |
| 9 | 18 | 36 |
Example: EVEN 496
Locate 496, and 31 is the ODD that starts the Row;
It has 31-62-124-496 in its Row;
The BF1 Row above it is 1-2-4-8-16
Here is the solution: a 5 Col x 2 Row DMT:
| 1 | 2 | 4 | 8 | 16 |
|---|---|---|---|---|
| 31 | 62 | 124 | 248 | 496 |
Here are some smaller and larger versions of the infinitely expandable DMT: x, z and PN=xz are in BOLD.
The DMT, it should be emphasized, contains ALL the natural WINs: All ODDs, ALL EVENs. As a fractally-defined matrix, the beauty and charm is that it simultaneously reveals ALL the Divisors and Factors of ALL the EVENs -- that, of course, includes those very rare and exquisitely formed Perfect Numbers!
PN 6, p=2, x=2, z=Mp=3 notice that there are only 2 Rows of divisors, each are p=2=# of Columns.
PN 28, p=3, x=4, z=Mp=7 notice that there are only 2 Rows of divisors, each are p=3=# of Columns.
PN 6, p=2, x=2, z=Mp=3 notice that there are only 2 Rows of divisors, each are p=2=# of Columns.
PN 28, p=3, x=4, z=Mp=7 notice that there are only 2 Rows of divisors, each are p=3=# of Columns.
PN 6, p=2, x=2, z=Mp=3 notice that there are only 2 Rows of divisors, each are p=2=# of Columns.
PN 28, p=3, x=4, z=Mp=7 notice that there are only 2 Rows of divisors, each are p=3=# of Columns.
PN 496, p=5, x=16, z=Mp=31 notice that there are only 2 Rows of divisors, each are p=5=# of Columns.
PN 8128, p=7, x=64, z=Mp=127 notice that there are only 2 Rows of divisors, each are p=7=# of Columns.
PN 33550336, p=13, x=4096, z=Mp=8191 notice that there are only 2 Rows of divisors, each are p=13=# of Columns.
PN 6, p=2, x=2, z=Mp=3 notice that there are only 2 Rows of divisors, each are p=2=# of Columns.
PN 28, p=3, x=4, z=Mp=7 notice that there are only 2 Rows of divisors, each are p=3=# of Columns.
PN 496, p=5, x=16, z=Mp=31 notice that there are only 2 Rows of divisors, each are p=5=# of Columns.
PN 8128, p=7, x=64, z=Mp=127 notice that there are only 2 Rows of divisors, each are p=7=# of Columns.
PN 33550336, p=13, x=4096, z=Mp=8191 notice that there are only 2 Rows of divisors, each are p=13=# of Columns.
Below are two simplified DMTs, one in standard format, the other in transposed format. Either is easily made in a spreadsheet (Numbers used here). The DMT is infinitely expandable and is quite trivial to do in the spreadsheet app!
In this transposed version of the standard DMT, Rows and Columns are switched, thus:
PN 6, p=2, x=2, z=Mp=3 notice that there are only 2 Columns of divisors, each are p=2=# of Rows.
PN 28, p=3, x=4, z=Mp=7 notice that there are only 2 Columns of divisors, each are p=3=# of Rows.
PN 496, p=5, x=16, z=Mp=31 notice that there are only 2 Columns of divisors, each are p=5=# of Rows.
If you understand this switch, then you are well on your way in the understanding of the standard DMT!
DMT on the BIM.

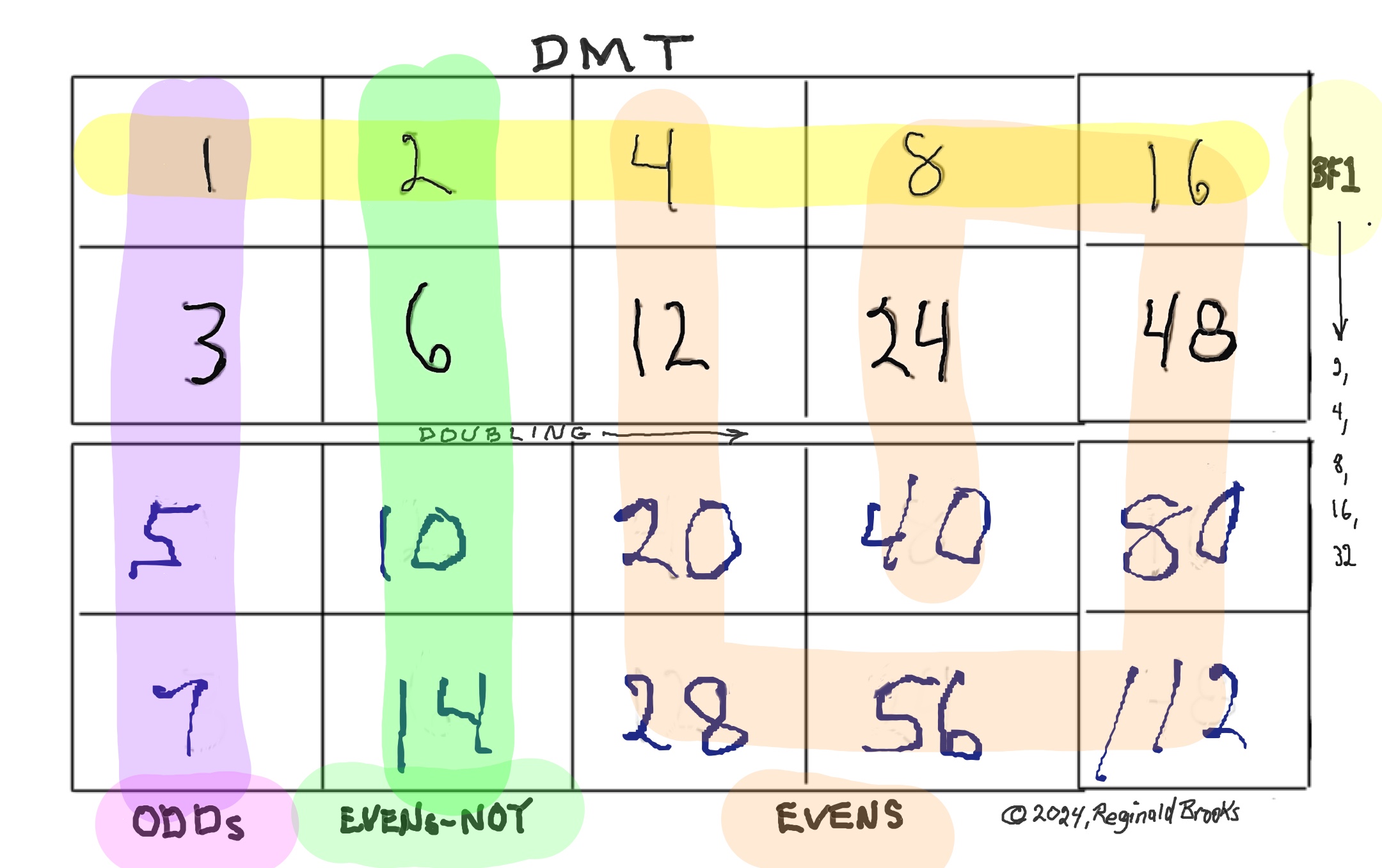
So what do we make of all these tables and matrixes?
The Multiplication Table has been around forever. It has ALL the numbers (WINs), Horizontal and Vertical Axis of 1,2,3,..., and a central or Primary Diagonal (PD) that divides the Inner Grid (IG) in equal, but opposite halves.
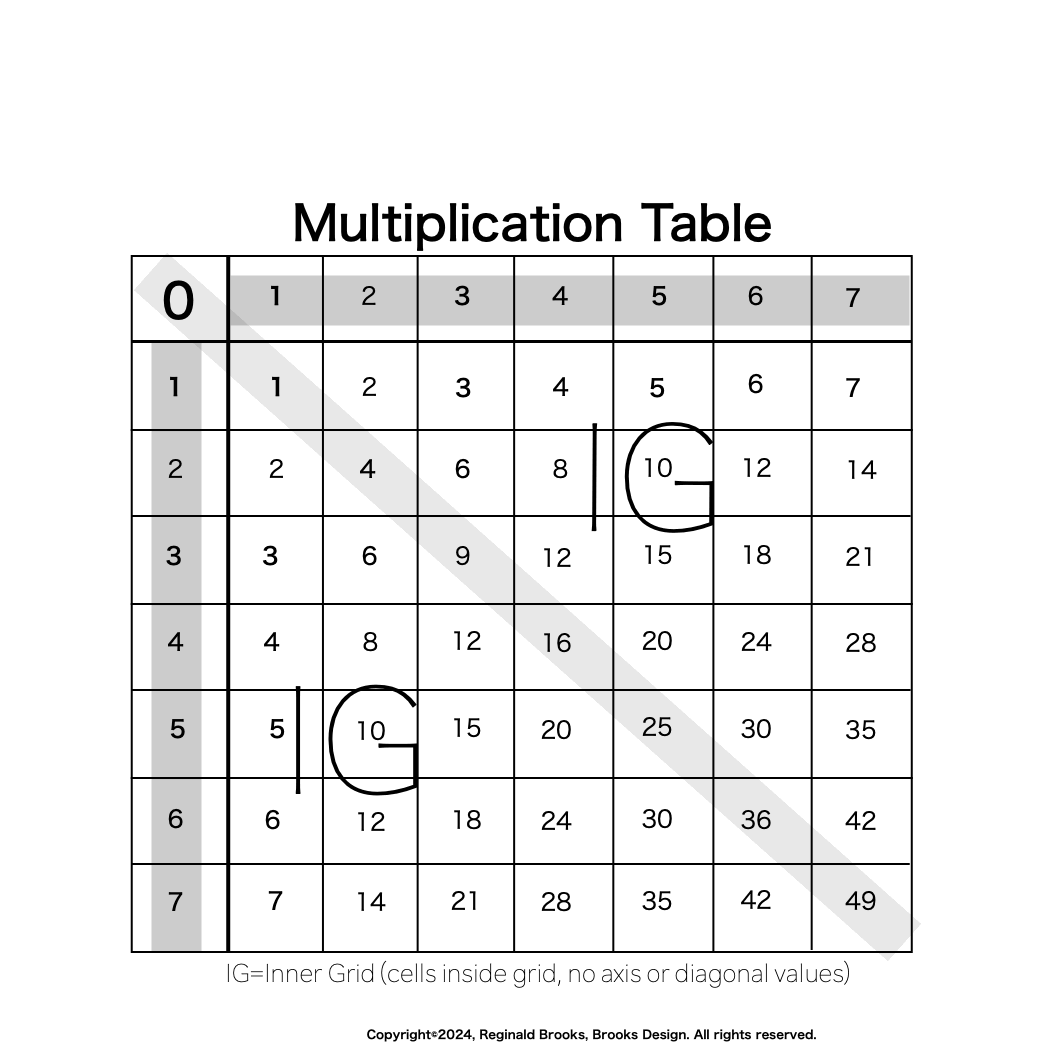
The BIM (BBS-ISL Matrix) was developed independently by the author in 2010 to bring out the Inverse Square Law (ISL). Over the next 10 years the focus was on the Primitive Pythagorean Triples and Primes, resulting in numerous white papers and some 10 ebooks.
On the BIM, the IG results from the difference between the Horizontal and Verticle values of the PD. There are at least 20 other ways to calculate these values, a fact that demonstrates just how universal this matrix is. The Active Rows on the BIM completely reveal and define all the Pythagorean Triples, all the Primes, Euler's Strong Form of the Goldbach Conjecture, and as we have seen earlier here, all the known Mersenne Primes - Perfect Number pairings. Do note, that unlike the Multiplication Table, the BIM -- other than the Axis numbers -- has NO EVENs that are NOT ÷4.
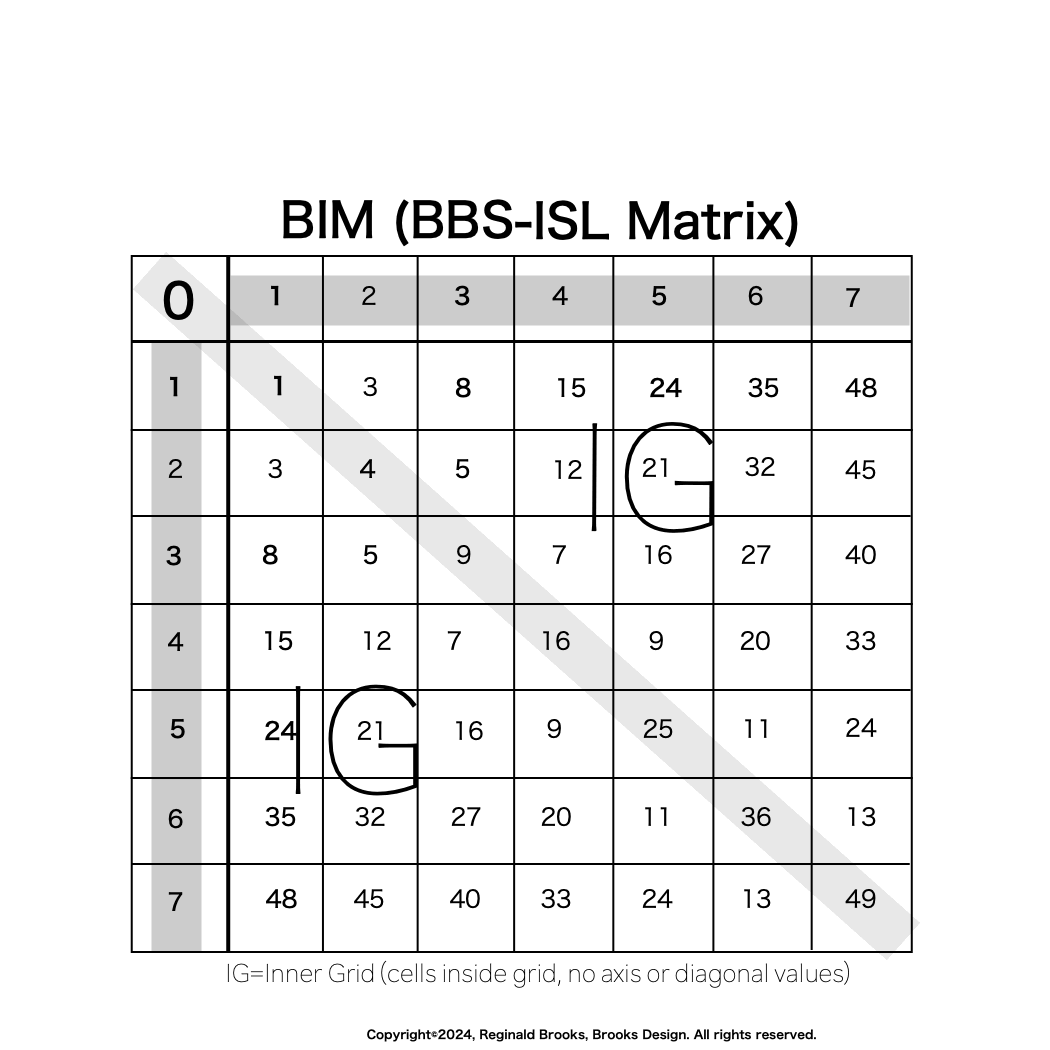
In the DMT, direct references to the Multiplicatiion Table and the BIM have been abandoned as the matrix table now reflects the distribution of the divisors (factors = divisors, but not the number itself):
The Left Column is formed of the ODDs;
The Second Column is formed of the EVENs NOT divisble by 4 = EVENs-NOT;
The remaining Columns to the Right are formed of the EVENs that are ÷4;
ALL Columns are formed from the sequential doubling of the previous cell value;
The 1st Row (TOP) is formed of the Butterfly Fractal 1 sequence -- doubling starting with quantity 1;
The Rows below increase sequentially by a difference (∆) of 2-4-8-16-32-64-...respectively;
ALL divisors of ALL EVENs and ALL EVENs-NOT are present as a combination of the BF1 Row + those Rows of said EVEN (+ those Rows of any composite ODD starting said Row);
It is a unique and distinguishing attribute that ALL EVENs that have a Mersenne Prime (ODD) starting their Row will have ONLY two Rows of divisors and the Rows will have the number of cells (divisors) = p.
ALL EVENs and EVENs-NOT can be found by following the diagonals in the BF1 Row back towards the ODDs.
To find ALL divisors of any EVEN, divide by 4 to see if it is an EVEN ÷4 or NOT, then divide said EVEN until an ODD is reached and now join those cells with the same number of BF1 cells. See images below.
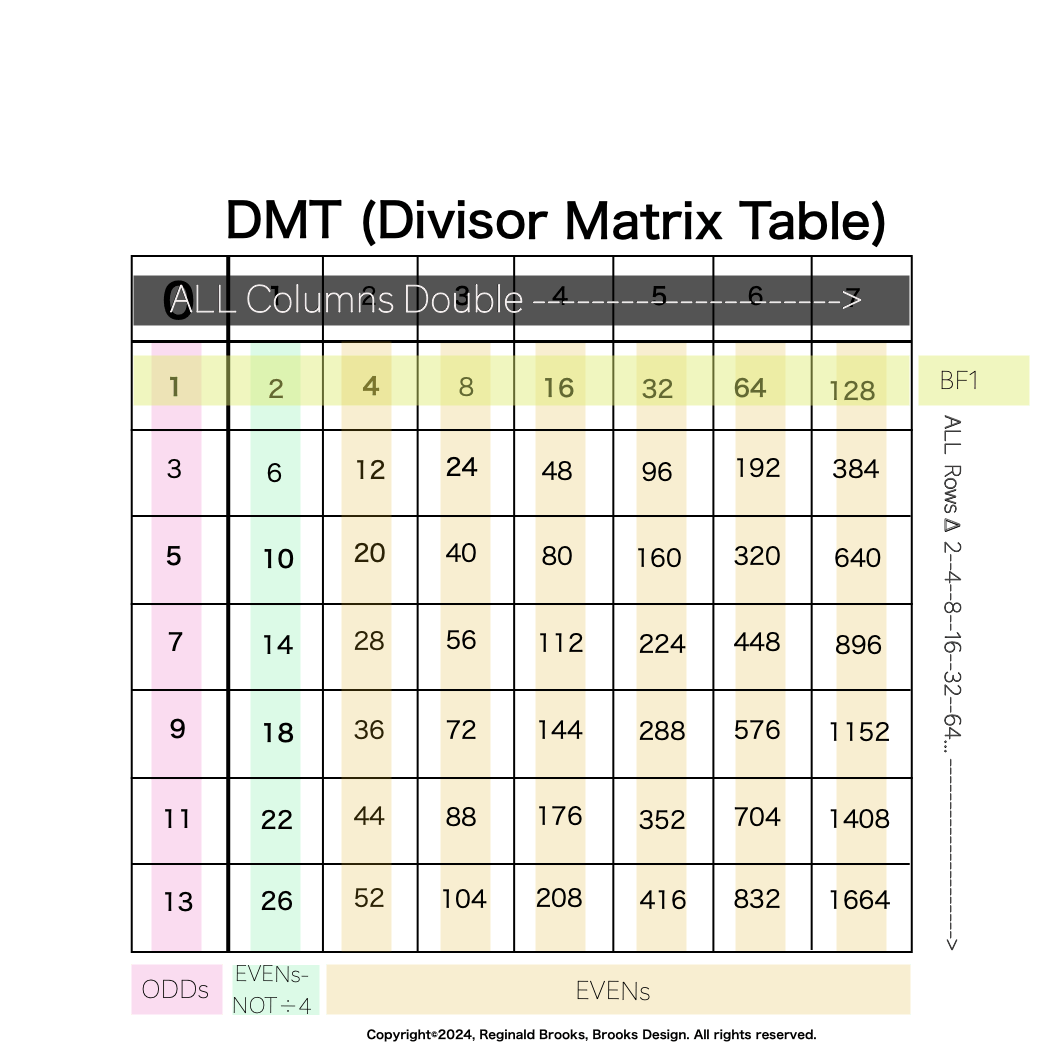
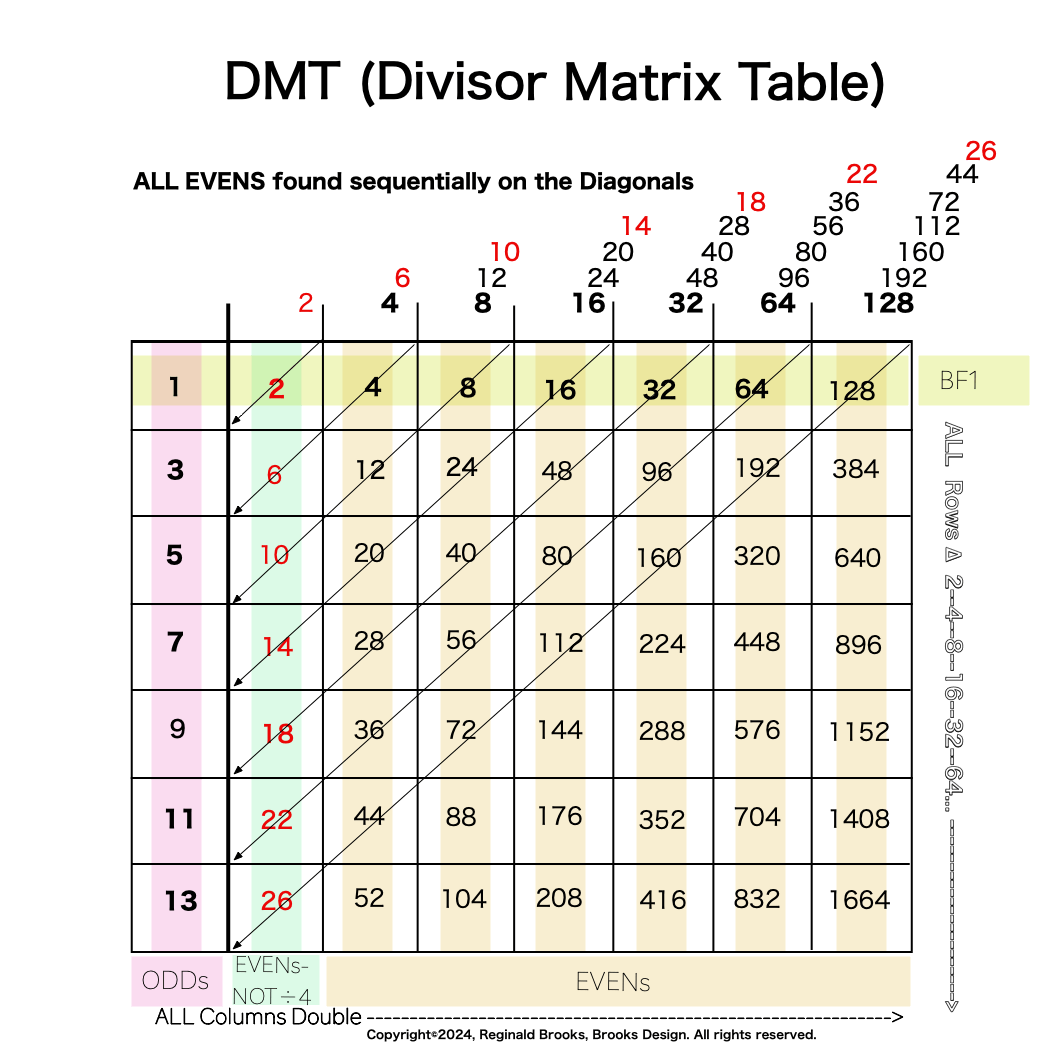
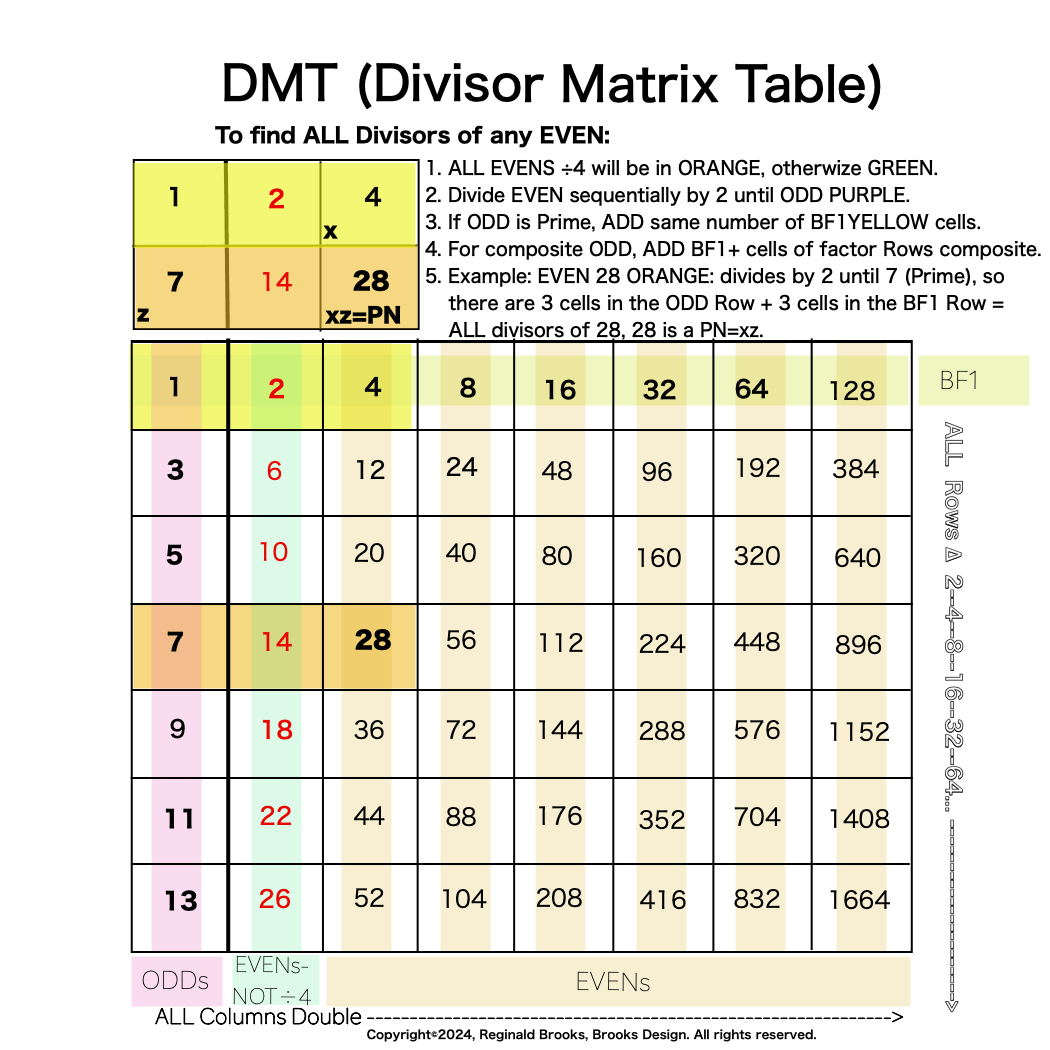
The DMT is another form of multiplication table in that ALL EVENs & EVENs-NOT are the product of the BF1 Row (YELLOW) x ODDs Column (PURPLE). The divisors that inform any of those EVENs are simply the cell values of the BF1 Row & each of the ODD Rows that begin with a Prime number. In the EVEN 28 example in the above image the ODD Row begins with the Prime 7, if instead we had chosen EVEN 36, it divides by 2 down to ODD 9 which is NOT Prime, but a composite of 3 x 3 Primes. Here we must ADD in the ODD Row 3 --3-6-12 -- to the BF1 Row of 1-2-4 and the ODD Row 9 of 9-18-36 to get ALL 9 of the divisors:
1--2--4
3--6-12
9-18-36
Notice the symmetries: 1-2-3-4-6-9-12-18-36 and 1-2-4--3---6---12--9-18-36 with 6 being the √36, but more importantly 4x9=36, 3x12=36, 2x18=36 and 1x36=36.
If we had chosen EVEN 72:
1--2--4--8
3--6-12-24
9-18-36-72
Notice that there is NO natural symmetry of the √72:
1-2-3-4-6-8-|-9-12-18-24-36-72 and 1-2-4-8--3-6----12-24--9-18-36-72.
The symmetries become more complex with larger EVENs with larger composite ODDs.
It is when the EVENs are limited to the product of x=2ᵖ⁻¹ and z=2ᵖ -1, i.e. x=BF1 and z=Mp=Mersenne Prime, that we get a TRUE, Active Perfect Number EVEN with exactly 2 Rows (BF1 + ODD Mp) of divisors whose cell lengths equal "p."
~~ ~~ ~~
It would be amiss to not look at just the EVENs-NOT DMT:
Basically, it is the same, only now the top Axis is the EVENs-NOT sequence -- 2-6-10-14--18--22--... There are NO ÷4 EVENs. This does result in there now being a bilateral symmetry of reflected values as the center diagonal is formed. The calculation of the EVENs-NOT divisors proceeds exactly as before:
To find ALL divisors of any EVEN, divide by 4 to see if it is an EVEN ÷4 or EVENs-NOT, then divide said EVENs-NOT until an ODD is reached and now join those cells with the same number of BF1 cells. As ALL EVENs-NOT only sequentially divide by 2 one time, there will only be a BF1 Row of 1-2 in all cases. ALL divisors of ALL EVENS and ALL EVENs-NOT are present as a combination of the BF1 Row + those Rows of said EVENs-NOT (+ those Rows of any composite ODD starting said Row). So basically, ALL divisors of any and all EVENs-NOT will be found in Columns 1 and 2 -- a series of 1 ODD + 1 EVENs-NOT, e.i. 30 divides by 2 down to 15, a composite of 3 and 5, so the divisors of 30 will be 1-2, 3-6, 5-10 and 15-30. See image below.
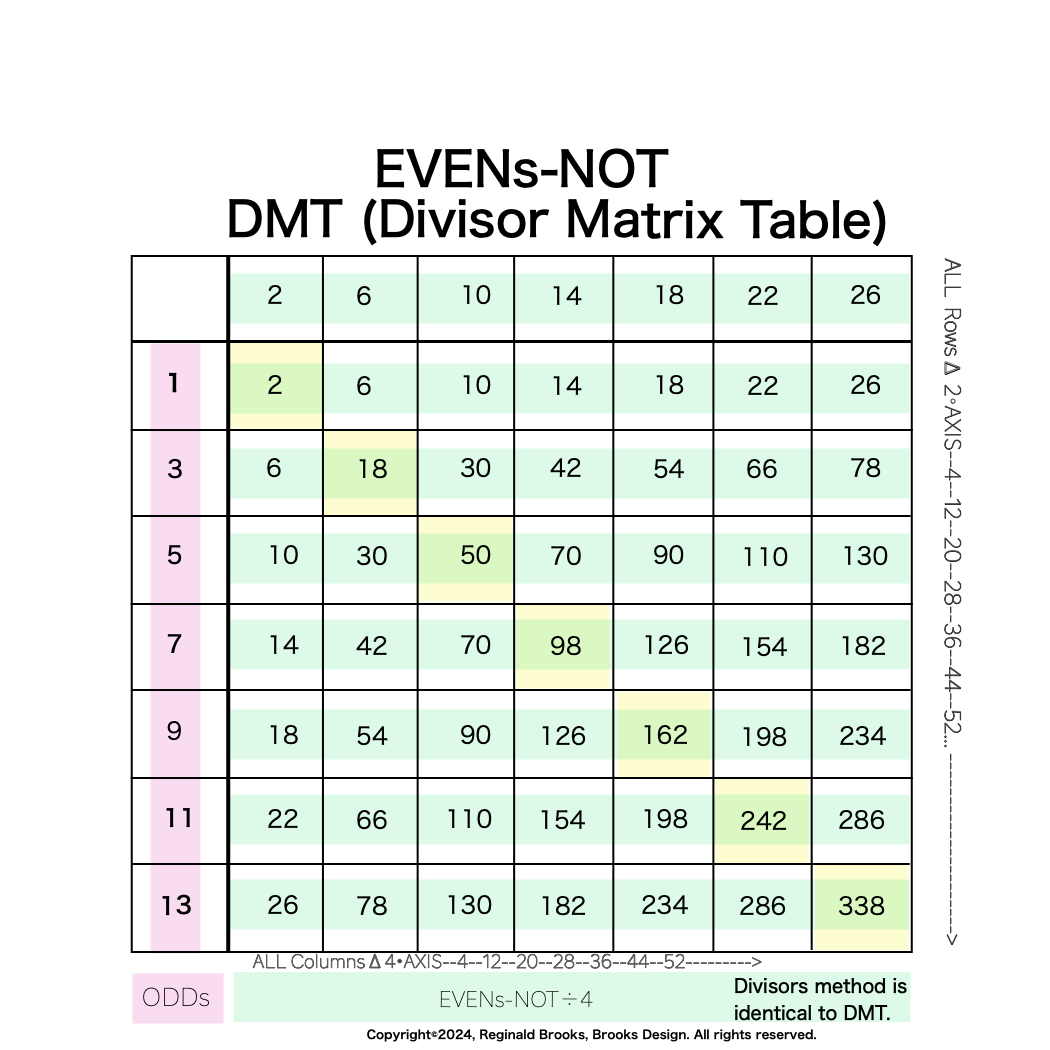
And, of course, the EVENs-NOT DMT begs the question: what about the ODDs and their divisors? Is there not an ODDs DMT?
The short answer is no. But there is a way that is already built into the 1st Column of ODDs in both DMTs:
Mark ALL Primes -- they are not composites and only have divisors 1 and themselves;
Divide ANY remaining composite ODDs by the Primes to get their divisors (all will be ODD, may or may not be Prime);
Notice that each of those designated divisor ODDs informs the other sibling ODDs, as well as the parent ODD, as the divisor value = STEPS to the next divisor of said parent ODD;
Example: ODD 15 is a composite and has divisors 1-3-5. One STEP from 1-->3 and one STEP from 3-->5 and 5 STEPS from 5 -->15 within the ODD Column;
Example: ODD 45 is a composite and has divisors 1-3-5-9-15-45, with 15 and 45 non-Prime ODDs. As ODD 15 and its divisors were spelled out above, we can see that 3 STEPS from 3 -->9, 3 STEPS from 9 -->15 and 15 STEPS from 9 -->45;
The ODDs divisors does not map out as pretty as the EVENs, yet we know ALL its divisors are present by definition;
Mapping the divisors by STEPS, though less eloquent, still provides a "spellcheck"-like function that may well warrant further investigation!
The DMTs warrant further investigation on a number of different levels, i.e. selecting different filters or sieves.
Final thoughts on this Side Note: The DMT is too important to leave out, yet really needing its own separate write up.
In some ways, the DMT is the simplest: one starts with the ODDs and simply doubles them across the Columns!
That's right, everything starts 1st with quantity 1, it doubles to 2 (forming the EVENs-NOT Column), doubling 2 to 4, to 8... (forming the rest of the EVENs).
The Running Sum (∑) of 1 + 2 = 3, the next ODD, doubles to the EVENs-NOT Column as 6, and 6 doubles to 12, 24, 48... as the EVENs Columns expand out.
The ∑ of 3 + 2 = 5, and so on. The fractal expression remains the same, only the starting numbers are larger.
The ODDs 1-3-5-7-9-11-13... -- a.k.a. the ODD number summation series -- becomes 1-4-9-16-25-36-49... or simply the square of 1-2-3-4-5-6-7... Do notice that the former is the PD of both the Multiplication Table and the BIM, and the latter informs their Axis. In fact, the BIM is completely formed around both!
Perhaps what we are seeing is that this DMT, presented here, is really the more fundamental relationship of the natural WINS! It has features of both the standard Multiplication Table and the BIM already built in.
Put another way:
In the beginning...
Long before we came up with the ubiquitous Multiplication Table -- in fact, long before anything -- there existed and has always existed certain relationships between the EVEN and ODD natural Whole Integer Numbers (WINs).
Any and all EVENs when sequentially divided down by 2 will end up with an ODD.
That means ODDs are more primitive -- fundamental -- than EVENs in that any and all EVENs can be formed by the sequential doubling of an ODD.
We also know -- or at least conjecture -- that every EVEN is formed of 2 Primes (Euler's Strong Form of the Goldbach Conjecture).
And since all Primes (except 2) are ODDs, once again the ODDs seem to be more atomic than the EVENs, and, the Primes the most atomic of all since all the ODDs can also be formed from the Primes.
But let's get back to just the inclusiveness of ALL the ODDs.
Place all the ODDs sequentially in a Column: 1-3-5-7-9-11-... Notice that they have a difference (∆) of 2. That ∆ is 2•1 or two times the first WIN in the first Column.
Next, double each ODD to form the second Column: 2-6-10-14-18-22-... Notice that they have a ∆ of 4. That ∆ is 2•2 or two times the first WIN in the second Column. Also note that NONE of these EVENs are divisible by 4. That makes them interesting!
Now we are going to form Columns three, four, five and so on (indefinitely) by doubling the previous Column each time.
Column three (3): 4-12-20-28-36-44-... Notice that they have a ∆ of 8 or 2•4 or two times the first WIN in the 3rd Column.
Column four (4): 8-24-40-56-72-88-... Notice that they have a ∆ of 16 or 2•8 or two time the first WIN in the 4th Column. And so on.
Notice that ALL the EVENs in Columns 3-4-5-... are divisible by 4. That makes them interesting, too, but one can easily see that that every other EVEN is divisible by 4, and all the EVENs between are not: 2-4-6-8-10-12-14-16-18-20-22-24-...
And what may seem obvious, our table has become another form of multiplication table: the top Row of doublings is one Axis and the first Column of ODDs another.
So what is the point!
The table so formed contains ALL the WINs.
It also contains ALL the divisors (factors) of ALL the EVENs in a simple Number Pattern Sequence (NPS).
The table is called the Divisor Matrix Table (DMT).
It is fundamental to ALL the other tables of WINs like the Multiplication Table and the BIM (BBS-ISL Matrix). The BIM table reflects the Inverse Square Law (ISL), Pythagorean Triples and the Primes -- especially the Mersenne Primes.
Note:
Both of the above tables have Axis 1-2-3-... with zero (0) where they meet, thus they both include ALL the WINS.
Both also have the squares of their Axis numbers in the diagonal that symmetrically divides the tables into two equal halves.
But that is where the similarities end and the differences begin between these two.
More amazing are the similarities and differences between the DMT and the BIM!
Similarities:
Both are built on the ODD number sequence 1-3-5-7-9-...
Differences:
The DMT has two different Axis -- one being 1-2-4-8-16-..., the other being 1-3-5-7-9-..., -- while the BIM has an Axis of (0)-1-2-3-4-5... on both sides;
The DMT, while being built on the ODD number sequence 1-3-5-7-9-... for the first Column, can also be said to be built on the first Row 1-2-4-8-16-... a.k.a. the Butterfly Fractal 1, that is itself the simple expression of the Exponential Power of 2 as 2⁰=1, 2¹=2, 2²=4, 2³=8, 2⁴=16 -- and each subsequent Row is but a sequential increase of the BF1 Row, while the BIM's IG is formed differently with each Row (or Column) value diminished by the ODD number sequence 1-3-5-7-9-...;
The DMT separates the ODDs from the EVENs NOT divisible by 4 (EVENs-NOT), and EVENs that are divisible by 4 (EVENs) from both, while the BIM alternates ODDs and EVENs, but contains no Primes or EVENs-NOT within the Inner Grid (IG);
The *DMT has no bilateral symmetry, while the BIM does;
*exception being for the more limited Only EVENs-NOT DMT
The DMT is a multiplication table within its IG, while the BIM is not (at least not directly);
The DMT specifically informs ALL the EVENs (EVENs and EVENs-NOT) divisors (factors), while the BIM informs ALL the Pythagorean Triples, and -- indirectly -- ALL the Mersenne Primes.
The combination of the DMT and BIM gives us the best overall profile of the Mersenne Prime Square and its 10 parameters: p, x, y, z, x², y², z², xy, xz, and yz.
Table167_ODDs_EVENs_EVENs-NOT_Matrix++24.pdf Here we see just why. Above PN 28, the difference between any and all PNs is divisible by n24. See Table 168 for reference.
3. Identity by ÷24: (PN-PN)/24=n and (Mp-Mp)/24=n
In earlier work, we found that on the BIM, ALL PRIMES and ALL Pythagorean Triples were found exclusively on the Active Rows, as a necessary, but insufficient condition, meaning that they both were only found here, but NOT ALL Active Rows had PRIMES, nor Pythagorean Triples, and some had both, while others had one but not the other. The Active Rows are those Axial Rows that are BOTH composed of ODDs and have the first value ÷24, e.i. Row 11 = 120-117-112-...121 and Row 13 = 168-165-160..169, and, 120/24=5 and 168/24=7. The Active Rows ALWAYS occur in pairs, with an EVEN Row between. One can easily find all such Active Rows by simply dividing the entire BIM/24 and picking out the highlighted Rows. The significance is that ANY Active Row (≥5) difference between it and ANY OTHER Active Row is ALWAYS ÷24. The difference between any two such PRIME2 is ÷24!
Active Rows are NEVER ÷3.
Now we find that TRUE, Active Set 1 and inActive Set 2 PNs are ALL on BIM EVEN ROWS just below the LOWER ACTIVE ROWS! And none are ÷3. And this contrasts starkly with the Set 3 PNs that are on the EVEN ROWS between the LOWER and UPPER ACTIVE ROWS, and furthermore, they are ALL ÷3.
We can calculate the ÷24 differences (Δ) between PNs as long as we do so from the same group of sets, i.e. PN Δ between Sets 1 & 1, 2 & 2, or 1 & 2, or separately 3 & 3, but not across as in 1 & 3 or 2 & 3. All this can easily be seen on the BIM as what this is showing is that the PNs from p=EVENs (Set 3) between the UPPER and LOWER ACTIVE ROWS do not mingle with the PNs from the p=ODDs (Sets 1 & 2) from the EVEN Row below the LOWER ACTIVE ROW.
496 - 28 = 468
468 / 24 = 19.5
2016 - 120 = 1896
1896 / 24 = 79
8128 - 496 = 7632
7632 / 24 = 318
32640 - 2016 = 30624
30624 / 24 = 1276
130816 - 8128 = 122688
122688 / 24 = 5112
523776 - 32640 = 491136
491136 / 24 = 20464
2096128 - 130816 = 1965312
1965312 / 24 = 81888
8386560 - 523776 = 7862784
7862784 / 24 = 327616
33550336 - 2096128 = 31454208
31454208 / 24 = 1310592
134209536 - 8386560 = 125822976
125822976 / 24 = 5242624
536854528 - 33550336 = 503304192
503304192 / 24 = 20971008
2147450880 - 134209536 = 2013241344
2013241344 / 24 = 83885056
8589869056 - 536854528 = 8053014528
8053014528 / 24 = 335542272
34359607296 - 2147450880 = 32212156416
32212156416 / 24 = 1342173184
137438691328 - 8589869056 = 128848822272
128848822272 / 24 = 5368700928 ~~~
~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~
Below are some useful tables. Often both pdf and png versions are shown.
Table159_PN_factors_divisors_Colors.pdf

Table160_ExpandingFractals+PNF.pdf
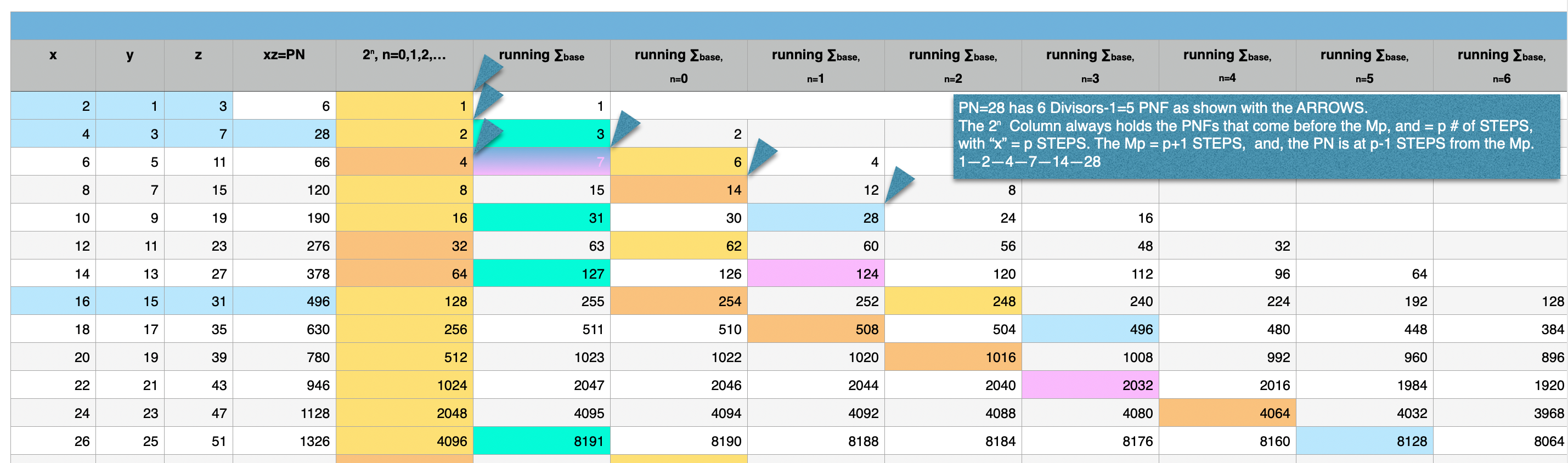
Table160_ExpandingFractals+PNF_detail.pdf
Table161_PNequals2n-x.pdf
Table 162: Sets & Divisors & Factors of PN.pdf

Table162sets+divisors.png
Table163_[(xz)-(xz)]divide24.pdf
![Table163_[(xz)-(xz)]divide24](../../../../../../../Images/MathspeedST/TPISC/TPISC_V_Images/Table163_[(xz)-(xz)]divide24.png)
Table163_[(xz)-(xz)]divide24.png
Table164_Mp_withinContainer_FactorsANNOT.pdf
Table165_Add24toPrimes.png
Table165_Add24toPrimes.pdf
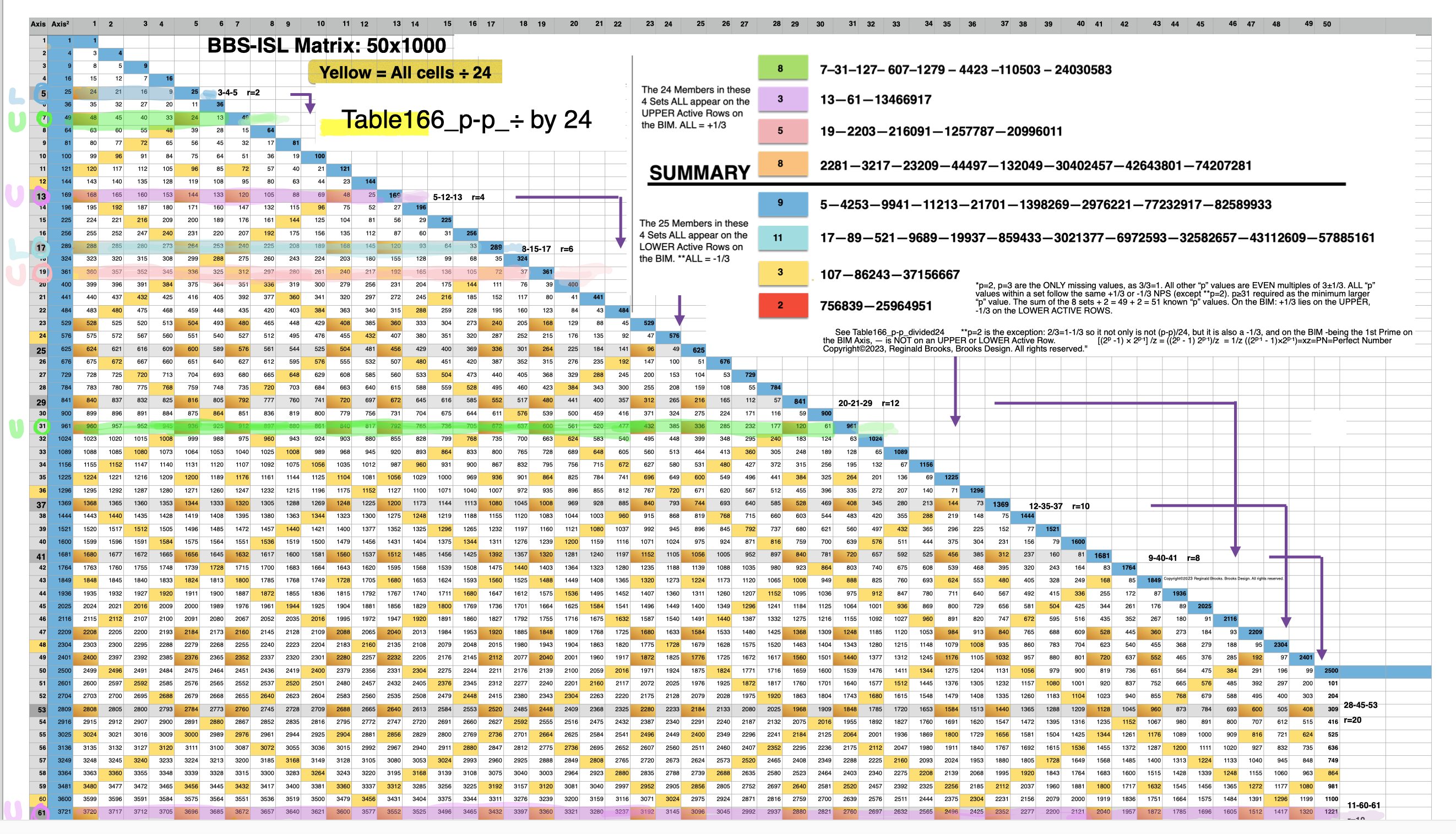
Table166_BIM_p-p_divide24closeup.png
Table166_BIM_p-p_divide24.pdf
Table166_p-p_divided24.pdf

Table166_p-p_divide24closeup.png
4. Next PN: 16PN+12x=PN next
A number of equations has been found that give the “next” x, y, z, xz,... parameter.
This one gives the “next” z=Mp (Set 1), as well as those in Set 2 and 3. TRUE, Actives in BOLD.
4z+3=z>next
1 x 4 + 3 = 7 p=2—>p=3
7 × 4 + 3 = 31 p=3—>p=5
31 × 4 + 3 = 127 p=5—>p=7
127 × 4 + 3 = 511
511 × 4 + 3 = 2047
2047 × 4 + 3 = 8191 p=11—> p=13
8191 × 4 + 3 = 32767
32767 × 4 + 3 = 131071 p**=15—> p=17**
131071 × 4 + 3 = 524287 p=17—> p=19
524287 × 4 + 3 = 2097151
2097151 × 4 + 3 = 8388607
8388607 × 4 + 3 = 33554431
33554431 × 4 + 3 = 134217727
134217727 × 4 + 3 = 536870911
536870911 × 4 + 3 = 2147483647 p=29—-> p=31
2147483647 × 4 + 3 = 8589934591
8589934591 × 4 + 3 = 34359738367
34359738367 × 4 + 3 = 137438953471
137438953471 × 4 + 3 = 549755813887
549755813887 × 4 + 3 = 2199023255551
2199023255551 × 4 + 3 = 8796093022207
8796093022207 × 4 + 3 = 35184372088831
35184372088831 × 4 + 3 = 140737488355327
140737488355327 × 4 + 3 = 562949953421311
562949953421311 × 4 + 3 = 2251799813685247
2251799813685247 × 4 + 3 = 9007199254740991
9007199254740991 × 4 + 3 = 36028797018963967
36028797018963967 × 4 + 3 = 144115188075855871
144115188075855871 × 4 + 3 = 576460752303423487
576460752303423487 × 4 + 3 = 2305843009213693951 p=59—> p=61
2305843009213693951 × 4 + 3 = 9223372036854775807
9223372036854775807 × 4 + 3 = 36893488147419103231
36893488147419103231 × 4 + 3 = 147573952589676412927
147573952589676412927 × 4 + 3 = 590295810358705651711
590295810358705651711 × 4 + 3 = 2361183241434822606847
2361183241434822606847 × 4 + 3 = 9444732965739290427391
9444732965739290427391 × 4 + 3 = 37778931862957161709567
37778931862957161709567 × 4 + 3 = 151115727451828646838271
151115727451828646838271 × 4 + 3 = 604462909807314587353087
604462909807314587353087 × 4 + 3 = 2417851639229258349412351
2417851639229258349412351 × 4 + 3 = 9671406556917033397649407
9671406556917033397649407 × 4 + 3 = 3.868562622766813359059763e25
3.868562622766813359059763e25 × 4 + 3 = 1.547425049106725343623905e26
1.547425049106725343623905e26 × 4 + 3 = 6.189700196426901374495621e26 p=87—-> p=89
x
Here is an example showing the “next” x. TRUE, Actives in BOLD.
4x=x>next
4•1=4 p=2—>p=3
4•4=16 p=3—>p=5
4•16=64 p=5—>p=7
4•64=256
4•256=1024
4•1024=4096 p=11—> p=13
4•4096=16384
4•16384=65536 p**=15—> p=17**
4•65536=262144 p=17—> p=19
4•262144=104856
4•104856=4194304
4•4194304=16777216
4•16777216=67108864
4•67108864=268435456
4•268435456=1073741824 p=29—-> p=31
xxxxxxxxxx
xxxxxxxxxx
Here are two examples showing the “next” PN. TRUE, Actives in BOLD. The first example shows Sets 1 and 2, but requires the “x” value of the “next” PN. The second part shows the same Sets 1 and 2, but uses the known “x” value of the current PN.
16xz+3x=PN>next
(4•6+2•2)=28 p=3
16•28+3•16=496 p=5
16•496+3•64=8128 p=7
16•8128+3•256=130816
16•130816+3•1024=2096128
16•2096128+3•4096=33550336 p=13
16•33550336+3•16384=536854528
16•536854528+3•65536=8589869056 p=17
16•8589869056+3•262144=137438691328 p=19
16•137438691328+3•1048576= 2199022206976
16•2199022206976 +3•4194304= 35184367894528
16•35184367894528 +3•16777216= 562949936644096
16•562949936644096 +3•67108864= 9.0071991876E15
16•9.0071991876E15 +3•268435456= 1.4411518781E17
16•1.4411518781E17 +3•1073741824= 2.3058430082E18 p=31
=
(4•6+2•2)=28 p=3
16•28+12•4=496 p=5
16•496+12•16=8128 p=7
16•8128+12•64=130816
16•130816+12•256=2096128
16•2096128+12•1024=33550336 p=13
16•33550336+12•4096=536854528
16•536854528+12•16384=8589869056 p=17
16•8589869056+12•65536=137438691328 p=19
16•137438691328+12•262144=2199022206976
16•2199022206976 +12•1048576= 35184367894528
16•35184367894528 +12•4194304= 562949936644096
16•562949936644096 +12•16777216= 9.0071991876E15
16•9.0071991876E15 +12•67108864 = 1.4411518781E17
16•1.4411518781E17 +12•268435456 = 2.3058430081E18 p=31
The latter (16xz+12x) uses x=current "x" associated with xz while the former (16xz+3x) uses x=new (next) associated with solution, x•4. The both use the same x sequence, only the starting point differs. Note that in the latter, shortcut method, "x" is often not BOLD.
This, again, shows the importance of the inActive Set 2 & 3 “containers” in the NPS.
4PN+2x=PNn gives the intermediary (p=EVENs, like p=4, PN=120) in Set 3, between those above.
5. Important Side Note-2: Algebraic Geometry
SIDE NOTE
Previously in earlier Sections, we covered a number of algebraic geometry solutions to finding the next z, z² and xy.
Here is a brief review:
Now, much later in this discovery process, a newer solution for "seeing" the Perfect Number (PN) arise from either the "p" or "x" given value is shown.
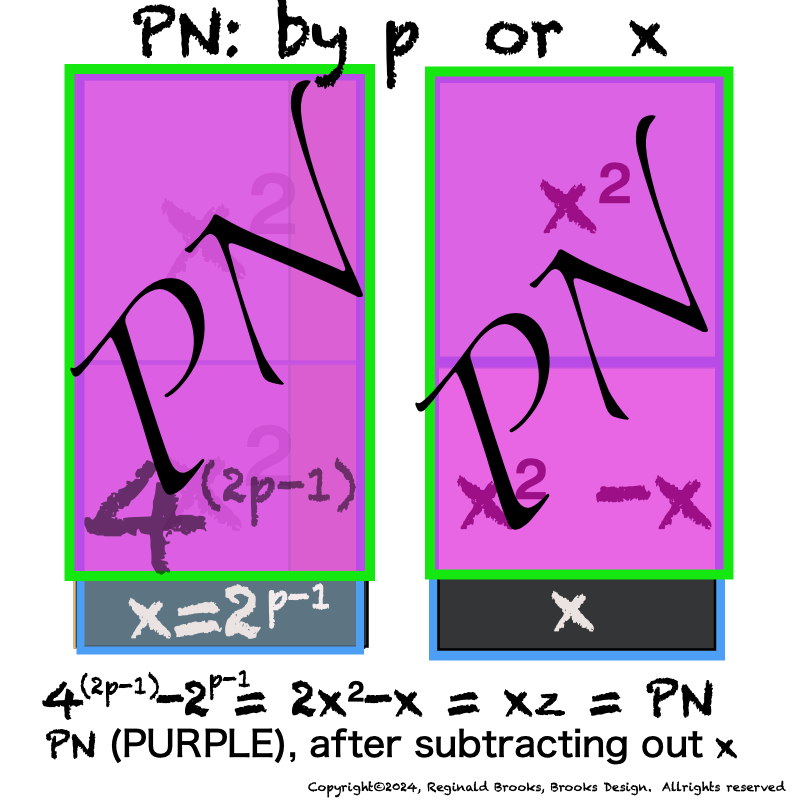
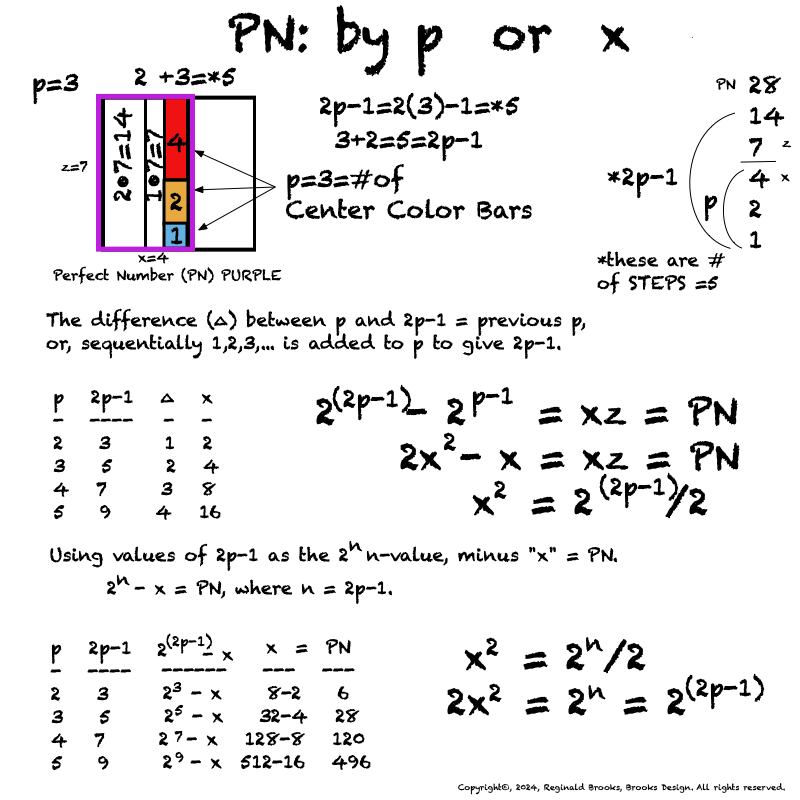
Knowing either "p" or "x"at the start, one can predictably find all the subsequent values -- and the remaining 10 parameters that profile any and all Mersenne Prime Squares (MPS) and their respective constituents.
A great deal is summarized here. Together with the DMT and BIM tables, one can profile ALL the Mersenne Prime - Perfect Number pairings.
~~ ~~ ~~ ~~ ~~
LOOKING BACK
When looking at the Mersenne Primes and their intimate connection with the Perfect Numbers, the tendency was to start with the Mp (z) and afterwards the PN. We might want to start the other way—with the PNs.
Imagine your on top of a waterbed — sheets, covers and bedspread — and you notice something move! What is that!
You notice — through all the coverings — that it has a shape. Maybe a square or a squarish-rectangle. You recall that a square is just a special case of rectangle — one whose sides are equal. And you know there are nearly square rectangles whose sides differ only slightly.
Peeling back the bedspread you find that it really is a square, but it has a line dividing it into two almost equal rectangles — both equally long, but one having its short side 1 unit larger than the other, e.i. one rectangle is 4x7 and the other 3x7, with respective areas of 28 and 21.
The bell rings as you realize 28 is a PN (1+2+14+4+7 =28 = the sum (∑) of 1+2+4+7+14, the factors of 28, not counting the #28 itself, and thus satisfying the definition of a PN).
The other ODD # area is a rectangle we call the ODD Complement (OC) because it's ODD and it complements the PN in that they ∑ up to form a square — 28+21 = 49. A square we call the Mersenne Prime Square (MPS) because it is formed from squaring the long, Mp=z side of the rectangle to give, in this example, 49 = 7².
Thinking back to the long EVEN # and shorter ODD# sides of the PN and OC rectangles, we realize we haven’t given them a name: how abut x = EVEN and y = ODD = x-1?
Now given that info, couldn’t one just start with the x and y, get z from adding them together, and get PN = xz, OC = yz and MPS = z²? How simple.
It seems if we start with either x or y — and it doesn’t matter which in that one is simply the other +/- 1 — and get to all the other larger parameters!
So really, the connections are so direct, that knowing any one of them, one can easily derive by simple algebra or geometry (or like I like to do, by both = algebraic geometry) any and all of the descriptive parameters.
But wait, the movement continues! As you draw back the covers — leaving only the sheet —you find the PN and OC have each been further divided into a square and rectangle. The square is just the square of the short side, e.i. x² = 4² = 16 and y² = 3² = 9. We call it the Perfect Number Square (PNS) and ODD Complement Square (OCS), respectively. The rectangle, common to both, and a complement to each, is fittingly called the Complement Rectangle (CR), and in our running example equals xy = 4•3 = 12 =CR.
Doing the math, we see it fits perfectly: PNS+CR = PN and OCS+CR = OC, and PN + OC = MPS.
Once again, we only need to know x, y or z to get it ALL! (z = 2x-1 and y = x-1).
But let’s go back to our initial pondering: what if we look at the x•z = PN differently?
We could start with our example — 4•7 = 28 — and think of it as four “7s”, i.e. four columns of 7 units each adds up to 28. This we have done extensively.
But what if we think of it as seven “4s”, instead. It really maths out to the same, but conceptually a bit different. How so?
4 4 4 4
4 4
4
Look familiar? It has the same pattern as the Butterfly Fractal 1 (BF1) that we discovered was the basis for the whole Exponential Power of 2 (2ⁿ) phenomena that informs the entire Mersenne Prime-Perfect Number enterprise!
4 4 4 4 = 16
4 4 = 8
4 = 4
∑ = 28 with a Running ∑ of 4, 12, 28
The same goes for the smaller OC side: seven “3s”:
3 3 3 3 = 12
3 3 = 6
3 = 3
∑ = 21 with a Running ∑ of 3, 9, 21
The basic fractal pattern of doubling — in these cases of a cluster — exactly mimics the BF1.
The full BF pattern, extensively covered in great detail, is given a quick look here:
∑ R∑
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 =16 31
1 1 1 1 1 1 1 1 = 8 15
xxxxxxxxxx1 1 1 1 = 4 7
1 1 = 2 3
1 = 1 1
The simple Sums of the rows (∑) = 2ⁿ = x and x² and the Running Sums (R∑) = y and z, containers both.
One sees that each PN an OC plugs into this same BF1, substituting the x or y cluster in place of the individual 1s.
Indeed, so can the MPS itself, e.i. 7²= 49 = seven “7s”:
7 7 7 7 =28
7 7 = 14
7 = 7
∑ =49 with a Running ∑ of 7, 21, 49.
What is becoming clear is that the notion of the fractal-concept-form is deeply involved in every aspect of the Mp-PN-MPS connection! Indeed, every Exponential Power of 2 "container" -- indeed, again, every EVENs or EVENs-NOT divisor -- is deeply reflected of this kind of quantity-based fractal expansion. Quantum entanglement is seeded in the innate relationships between quantities as expressed by natural Whole Integer Numbers (WINs)! But what about fractions? If you start you base low enough, all reducible fractions can be assigned WINs with their descendants being simply multiple-fractals of the base quantity.
So what’s under the sheets? Ah, my friend, that remains to be seen! But Oceans of Numbers will somehow inform it!
Epilog follows.
Epilog
Why study the Mersenne Primes?
The Mersenne Primes (Mp) are more than just an idle curiosity -- they are the rarest of the rare gems we know as Primes. Out of the entire infinity spectrum of whole integer numbers -- aka Natural Numbers -- only 51 have been discovered so far!
Even more important than their rarity is their pristine existence!
How so?
Every Mp is paired with a Perfect Number (PN) and here is where this Mp-PN pairing really shines.
How so?
When digging for precious stones, one first locates a promising vein to follow with hopes that it will lead to a big vein that culminates at the jackpot.
When tuning your instrument you loosen or tighten the strings to bring it into perfect pitch, everything else being a bit sharp or flat to it.
What do these two metaphors have to do with the Mp-PNs?
In the mining metaphor, the early smaller veins of discovery are like finding the underlying Number Pattern Sequence (NPS) that relates the Mp-PNs to a larger pattern set. Once the jackpot is found it becomes ever so clear that it is just a purer, more pristine version of the same NPS you found in the initial vein of minerals.
Musically, one may relate that initial NPS to the various frequencies that inform a tonal scale, with the actual Mp-PNs being those frequencies that acoustically, harmonically and mathematical generate the rare perfect pitch frequency of any given note.
An analogy would be like that of the Oceans of Numbers metaphor used earlier in this series. Of all the possible waves that could potentially wash up against shore, only a select positively interfere to make it so, and only a very select, and very rare number so perfectly interfere and resonate with an underlying pattern generator that they form a perfect standing wave/tsunami.
Elucidation please?
From all the whole numbers, one can pre-select those that are based on the simple doubling of the number before, starting with quantity 1. This is the Exponential Power of 2 and it visually forms a butterfly-like pattern fractal of 1's -- we call it the Butterfly Fractal 1.
When you take the Running Sum (∑) of any part of it along its expansion you will get an ODD number (because you start with 1).
All those ODD numbers can -- just like the initial 1 fractal in the BF1 -- double up repeatedly to form ODD & EVEN Fractal values (OF1, EF2,3,4,...).
Together -- BF1 & OF1, OF2, OF3, ...-- form that larger NPS we alluded to earlier that we now call the set of "containers" in that they "contain" the pattern generically. The Mp-PNs are a pristine subset of the "containers" set.
Now, let's put that together:
In the Mp-PN pairings, the PN divisors are strictly limited to the BF1 and one -- and only one -- OF1 pattern.
While the "containers" (other than the Mp-PNs), will have a BF1 doubling and two or more OF1, OF2, ... doublings.
That's right, the Mp-PN are a subset that is composed of strictly the minimal number of PN divisors to define itself, while the much larger "container" set is composed of vastly more divisors -- including more ODDS -- to define itself.
It is like Nature has kicked out all the superfluous ODDS and EVENS within the generic "containers" to define an extremely rare subset with a "perfect pitch" frequency without any spurious sharps and/or flats! We refer to them as the "TRUES"-- The TRUE Mp-PNs.
And that, is exactly what defines and makes so pristine the Mp-PN pairings!
Is there more to this story?
There is, of course, more to the story. There always is.
Those "containers" have the same NPS as the TRUE's and then some. And within the latter are definite clues as to the TRUES.
How do you mean?
When you examine the multitude of "containers" for the same parameters you find in the TRUES, you find many, but NEVER all, of those defining the TRUES. And, in fact, with the divisors of the "container" wanna-be-PNs (that are NOT actual PN), one will always find actual Mersenne Primes ahead of their appearance as actual TRUE Mp-PN pairings.
This occurs to such an extent that one is afforded a complete frequency distribution array of ALL of the future TRUE Mp values that reads like a wave-interference pattern!
It is the contention of this author that that is exactly what is happening. The wave-interference pattern that defines the Exponential Power of 2 as seen in the BF1 extends through and includes a harmonic overlay (itself but a repeat of the BF1 now as OF1-EF2-EF3...) that, when the math comes together to form the rare "perfect pitch" of interfering frequencies, generates the Mp-PN pairings.
In retrospect, this is not such a surprise when considering both Euler's Strong form of the Goldbach Conjecture -- where every EVEN is the sum of two Primes -- and, the author's earlier work showing that the PN is itself but a geometric area within a larger Mersenne Prime Square (formed as z² = MPS).
As a pure gem stone of the finest, rarest kind, the Mersenne Prime - Perfect Number pairing within the MPS is a true wonder of the Universe! Surely it is there to do more than just please the eye -- and mind -- of the viewer!
Consider, if you will, an even wider extrapolation: That elusive concept of consciousness that we humans like to attribute to organic forms with us at the top, may, indeed, be of something all-together different: it may be that the logic of numbers -- that wondrous, and often inexplicable connectiveness -- is itself "consciousness!" That that logic becomes a form of inevitable "self-awareness" is but a small step from the logic of the numbers that is built in from the start and reacts in profound ways when one set of numbers rubs up next to another! A connection "knows" when it is connected, with the greater the degree of logical connection the greater its inevitable connection asserts "awareness." Works for me!
Carrying this a step further, entanglement -- yes, quantum entanglement -- may very well be based on this same "self-aware" consciousness-connectivity logic of the whole numbers. As we have now seen, quantum entanglement defies the "information traveling faster than the speed of light" by definition in that, regardless the distance of separation, one entangled particle is always aware of the status of its equal, but opposite, counter-particle. It does so not by sending information to the other particle, but rather by being inherently connected (entangled) with the other particle. That inherent entangled connection may very well be the logic of the numbers for any set of local particles within the logic of numbers of the whole Universe. The Conservation Laws demand this to be so. The logic of the Universal connection of numbers includes this structural consideration: it is ubiquitous and does not need transportation from point A to B as all matter, energy and fields exits within the larger logic of the numbers.
~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~
A metaphor is
A metaphor is
Not like an analogy
A visual kiss
5 dots walk into a bar.
They seem to be together, but more like a spectrum than a group.
Dot 1 is pure science. Dot 5 pure art.
Actually, Dots 1-3 seem like science and 3-5 seem like art. What gives?
We start with observation, examination and categorization or definition. That’s Dots 1-3.
But with the latter we start to enter the seemingly more subjective world of interpretation, though we call it documentation. That’s Dot 3’s turf. And what a broad, expanding turf it is!
In fact, it is so broad and rich that it is fertile ground for even more interpretation — even embellishment.
Enter the land of the analogy. The land where everything is “like” something else. Your reflection in the mirror is like — very much like — you. You, only a reverse of you! Not just “only a reverse of you,” but a reverse image of you. It is an image of you — albeit reversed. But it is not “you!” It’s only “like” you. And, it is not even what everyone else knows as you — unless they too are looking at the reflection of you. You know — that little mole on the right side of your cheek — everything is reversed in the reflected image. Everyone else sees that mole correctly on the right side of your check! But not you1
So Dot 4, a.k.a. “analogy” is really a form of simile — literally “similar” to. Our mirror reflection is a bit tricky. It has it’s technical base in pure science, yet it is illusionary. Is it the same? Or is it simply similar? One could one even say it is false. An un-truth. Another could say it is a true and accurate accounting — reflection — of the real source, with the one proviso: it is *mirror symmetric, not left to right, but front to back. Bilateral symmetry draws a axial line down the center and reflects the sides equal but oppositely. But wait, you object, that would mean our cheek mole would be on both sides of the reflected face, or, on neither side. Right you are if you hold the mirror right up to your nose. No, in this plain old mirror reflection, the entire image of your face is reversed as each and every photon bouncing off your actual face is flipped 180° — not left to right — from its order, front to back. An image that “is a lie, that reveals a truth” as in Picasso’s definition of what art is. Yes, your reflection is a work of art, so go take — or is it “make” — a photo of it and do what’s best for you. You might want to take a selfie photo and compare it with the mirror-reflection photo to see which one(s) you like best! Of course lighting is everything so you will want to get it the same. It might be harder than you think.
Moving on to the last dot, Dot 5: Metaphor — the pure art of metaphor. Another form of analogy — but lose the “like” and replace it with the “is.” We are no longer caressing the “this is like” analogous art form anchored on a more direct linkage to a previous image. No, we are now taking the big jump — across the terra-firma linkage within one continent, if you will — across great bodies of water onto new lands, completing our mixed metaphoric journey of interpretive presentation. We can no longer get by on this or that is “like” — no — now it “is.” It is what it is. It will be up to our own individual, imaginative and highly subjective interpretation of what we see, hear, feel — experience — that informs us. Now one might ask, “Which is the true truth?” The truth that science expounds or the truth that experience reveals?
Could it be that all five dots are but oversimplified categorizations of a natural spectrum of acquisition? An acquisition of what is in front of you, how can you make sense of it, to what degree is it helpful versus harmful to your meaningful survival and what can you do about it?
Dot 1: Observation
Dot 2: Examination
Dot 3: Documentation
Dot 4: Analogy-Simile
Dot 5: Metaphor
Five dots that represent a spectrum line from logic to emotion intelligence. To erase — or simple ignore — one part of the line is “like” — no “is” — a reflection without a source.
~~~
Reference: https://writers.com/simile-vs-metaphor-vs-analogy-definitions-and-examples
*Here's a video with Richard Feynman explaining mirror reflection.
~~~
That said, just what is the connection to math? Specifically to numbers?
OMG, I am so astonished! So thrilled! So beyond belief that you asked! And so humbled. Is it possible for me to share my own overwhelming joy at studying simple Whole Integer Numbers (WIN) and the whole spectral line of richness that it reveals?
No.
Well, not to the level I would like you to experience.
Equations, formulas, geometric shapes, all that math language is not in and of itself sublimely beautiful. Well, actually, yes it is! That is, once you think through — even past — the math language. In my second year of Latin back in high school (which I barely passed), my teacher explained that one never really gets the language — the culture that it embodies — until you think through and past the words. At first the object horse translates to English word “horse” and then to the Latin “equus.” It’s only when horse = “equus” that one begins to experience it immersed within the culture. The same goes for math. Yes, some of the equations are absolutely beautiful in their profound encapsulation of something larger!
But more to the point: it has been my experience that the relationship of quantities — expressed as WINs — informs every aspect of every version of the Universe we are blinking our eyes at! Groups and connections, seamlessly linked by simple arithmetic, can ruthlessly account for every aspect of the spectrum line alluded to above. Yes, that includes everything form the metaphorical - emotional intelligence to the objective-driven observational realm! A=B, B=C, A=C may rule the roost at one end, but it does not, in and of itself, preclude A=B, B≠C, A=C at the other end. Why? If we use “A” and only “A” to define the rest of the alphabet, it may be true — but only in the sense of “A” — yet if we remain open to other means, we may find the truth of “C” both in terms of “A” and in terms of B_C_D_E_F_G_H_I_J_K_L_M_N_O_P_Q_R_S_T_U_V_W_X_Y_Z. And that’s just in the English alphabet!
Let’s go back for a moment to the self-reflection, you know, the mirror reflection of oneself. Now let’s look at it with two other lenses — or filters, if you will — entanglement and the general notion of a fractal.
A fractal is a self-similar, repeating, reiterative expression of self that generates a whole that mimics that expression-self.
Entanglement presents as two spacetime (ST) units that are equal, but opposite in some key measurable parameter like spin, e.i. a pair of two duplicate photons with opposite spin traveling away from each other. They are entangled when, despite any degree of separation, changing the spin value of either photon simultaneously changes that of the other member of the pair. Einstein famously called it “spooky action at a distance.” And he didn’t like it because it appears to violate the constant speed of light principle that lies at the heart of relativity.
~~~
https://astronomy.com/news/2022/10/what-is-quantum-entanglement
~~~
So if our self-reflection is like an entangled particle with everything equal — but some parameter opposite — to it’s co-joined mate, what happens if we change the source — you — in some way: you close your right eye. Does not the reflected self simultaneously close its left eye?
Is your self-reflection in any way a fractal-like expression? Well, it does generate itself by a self-similar, repeating, reiterative expression of its source — you — with the exception that there is a front-to-back rotational symmetry of each part that generates the whole, leaving the self-reflection as similar — very, very similar — to the source, but with mirror symmetry.
If we could maintain everything about the source—reflection while increasing the distance of separation, would that not change everything about what we think we really know about the Universe(s)? Imagine when you alternately open and close each eye here on earth and your self-reflection on the moon does so equally — but oppositely — and simultaneously in time! Now that’s what I call a good time!
Doesn’t it just beg the question: is quantum entanglement some form of mirror, front-to-back reflection, and, is it not driven by some form of fractal-expression? My bet is “you bet!” We typically only “see” one side of an alternating expression of the Universe, but you can bet your booty the other side simultaneously exists! This “opposite” but “self-similar” version — think: antimatter, dark matter and energy SpaceTime (ST) and all the Conservation Laws — must co-exist to account for both. If you want to “see” it, you have to dream! That’s what sleep is all about. It’s a reset so all the fractals can realign.
And of course you know all fractals are but an arithmetic-based accounting for simple quantities. Everything is numbers and numbers are just the addition of dots!
~~~
So 12 dots walk into a bar!
“OMG!” says our friend the bartender. “Now what?”
“Here’s something to spin your platter!” “do re mi fa sol la ti do” each dot chimes out in order.
To which the bartender questions: “Ah, what about the other 4 dots — 5 really as the last one was simply a doubling of the first?”
“Sharps and flats my friend. The 8 whole tones — 7 really as the eight is just a doubling of the first — that span the ‘octave’ actually sit within a span of 12-semitones or half-steps that inform said ‘octave’ in a rigorous manner, assuring harmony between the Major and Minor scales throughout the frequency spectrum.
“The fractal-basis of the Exponential Power of 2 — as presented as the Butterfly Fractal — is just a scale, a repeating, reiterative, self-similar diatonic scale. If one doubles it you raise to the next octave, if halved, you lower to the octave before. Within, it is all about ratios. Division of the monochord and ratios of the ensuing lengths gives us the 12 semitones of the octave. Tonic, Dominant and Subdominant 3-tone chords harmonically define the spectrum within, while the Circle of Fifths mathematically walks one around all 12 natural sequences.
“When you think about it, they are just the “containers” for some — even most — of our music in the West. Every great work was composed of sequencing these “containers” in a definitive, compositional way.
“And within those possibilities, each and every one of the 51 known — thus far — Mersenne Prime - Perfect Number pairings have been found!”
~~ ~~
“A Mersenne number is a number of the form
M_n=2^n-1,
where n is an integer.
In order for the Mersenne number M_n to be prime, n must be prime. (Reference: https://mathworld.wolfram.com/MersenneNumber.html )
“A Mersenne prime is a Mersenne number, i.e., a number of the form
M_n=2^n-1,
that is prime. In order for M_n to be prime, n must itself be prime. (Reference: https://mathworld.wolfram.com/MersennePrime.html, https://en.wikipedia.org/wiki/Mersenne_prime )
“In number theory, a perfect number is a positive integer that is equal to the sum of its positive divisors, excluding the number itself. For instance, 6 has divisors 1, 2 and 3 (excluding itself), and 1 + 2 + 3 = 6, so 6 is a perfect number. (Reference: https://en.wikipedia.org/wiki/Perfect_number ).”
~~ ~~
“To keep things simple and avoid confusion, we refer to the Mersenne number series — individuals within may or may not be PRIME — as “containers” and when NOT PRIME as active, NOT TRUE. When the individual “container” holds a PRIME — a.k.a. a Mersenne prime — it is referred to as active, TRUE.
“And perhaps the most amazing finding is that the simple matrix for visualizing the inverse square law — the BIM = BBS-ISL Matrix — should so definitively layout the Mersenne Prime - Perfect Number pairing within the geometry of the Mersenne Prime Squares (MPS)!”
To which the bartender said, “It’s time to go. Besides, everyone has already left!”
"And they didn't even get to the really new stuff: the Divisor Matrix Table (DMT) that lies beneath it all!"
~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~
The bartender's wet dream -- yeah, he's really gotten into this math thing. It seems time spent in math-space is serene, without conflict, without prejudice and even without politeness. The latter becomes true simply because of the former. Yes, there is contrast -- ODDs and EVENS, Primes and Non-Primes, Mersenne Primes and Non-Mersenne Primes, ...--- but contrast doesn't require prejudice and ensuing conflict. It just is and is part of the whole, and wholly accepted. Besides, as he has found all along: every number counts -- even those that don't! On to the dream!
He's in his bar, nice and clean and full of dots at each table.
He had asked dot 1 (quantity 1), to set up all the other other dots -- ODD and EVEN numbers -- such that at each table there clusters of dots, each representing the divisors-factors of a Perfect Number (PN), as part of its intimate matching to a Mersenne Prime (Mp).
That meant there were 51 tables representing the 51 currently known Mp-PN pairings and the Primes (p) that informed them were: 2-3-5-7-13-17-19-31-61-89-107-127-521-607-... such that when inserted into the Euclid-Euler Theorem (PN=2ᵖ⁻¹ (2ᵖ -1)) , they would yield Mp -- PN's of: (3, 6)--(7, 28)--(31, 496)--(127, 8128 )..., respectively.
He visits each table -- starting with p=2, to glow in the spectacular beauty each represents.
You see, he knows that these 51 -- and only these 51 (thus far) -- are truly unique within the entire spectrum of whole numbers, but especially within the rather more limited set of "containers" -- i.e. those that are born of the Exponential Power of 2 (a.k.a. The Butterfly Fractal 1) -- that also is the home to the very tiny set of Mp-PNs. Their uniqueness lies in the absolute minimalist number of divisors (factors) that define the PN within that Mp-PN pairing.
Not only are there no extra ODDs or EVENS, but the "p" value explicitly equals the number of BF1 doublings, and twice "p" again explicitly equals the total number of the PN divisors. He notes that the convention for counting the divisors to sum up to equal said PN does not include the PN itself, and as such, the divisors minus one equals the factors, e.i. PN 6 has 4 divisors -- 1-2-3-6, but in Perfect Number summing only the 1+2+3 factors are added to equal 6. Notice here that for this p=2 example, there are two sets of divisors -- 1-2 in the 1st BF1 Doubling, and two more divisors -- 3-6 in the 2nd *OF1 Doubling, or 2p=4 divisors total. This pattern fits ALL the Mp-PN pairings and NONE of the Non-Mp-PN "container" only's.
*ODD Fractal 1. The BF1 always starts with 1, the OF1 starts with sum (∑) of the BF1 that always equals the Mp.
Of course, what makes the bartender's dream so spectacular is how the PN divisors are laid out on each table. What symmetry. What fractal expression!
With a simple glance he can see that it goes like this: Every table will have two symmetrical stacks of dots -- where the dots represent the PN divisor values. The bottom of each stack will be an ODD, and since there are only 2 ODD divisors in any PN, one will be 1, and the other will be a Mp=∑ of the 1st stack.
Each stack will then grow up vertically by doubling the dot-value of the one below: thus the first stack is the BF1 -- 1-2-4... and the second stack is the OF1 -- 7-14-28 in this example of p=3. And, as you see, there are 3 divisors in stack 1 and 3 divisors in stack 2 and each stack follows the ODD+EVEN doubling+EVEN doubling...
The next table of p=5 has 1-2-4-8-16 in the BF1 of stack 1, and 31-62-124-248-496 in the OF1 of stack 2. And, as promised, the 31=1+2+4+8+16=∑of BF1=OF1. Each stack follows the ODD+EVEN doubling+EVEN doubling+EVEN doubling+EVEN doubling...
Each subsequent table of increasing p-values is laid out exactly the same. Once you know the template pattern for any one Mp-PN pairing, you know how every other one will look. Indeed, you can find, see and/or calculate any of the 10 common parameters that profile any Mp-PN pairing found in the Mersenne Prime Square (MPS)!
Now deep into his luscious dream, the bartender is getting really excited. The number 1 used to be considered "Prime" until just a few hundred years ago. If one were to reconsider 1 as "Prime," would not p=1 be the actual first Mp-PN pairing? Simple put: if p=1, then for each element in the Euclid-Euler Theorem -- (PN=2ᵖ⁻¹ (2ᵖ -1)) we have:
2ᵖ⁻¹ = 2⁰ = 1 and 2ᵖ -1 = 2 -1 = 1, thus 1•1 = 1 and there are p=1 BF1 values =1 -- the same for the OF1 value =1 -- making the sum of BF1 + OD1 doublings (and, of course, here there are no additional doublings, only the 1 + 1 = 2) equal to 2. The 10 parameters would be:
p=1
x=1
x² =1
y=0=x-1
y² =0
z=1=Mp=x+y
z² =1=MPS
xz=1=PN
yz=0•1=0=OC
xy=1•0=0=CR
and you basically end up with a square, as x=z and x² =1 as does z² =1. Since y=x-1=(z-1)/2=0, this makes "y" a zero value that makes the OC and CR equal zero as well. The MPS of p=1 means at the base level, the PN=PNS=MPS=Mp=x!
~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~
FINAL THOUGHTS (#24)
In the beginning -- the beginning --- there was quantity 1.
Nothing else, just quantity 1 (•).
When doubled -- like a fractal re-iterating itself -- it became quantity 2 (••). (Early on, both were considered Prime, only much later on, 1 was dropped.)
If the fractal iterations were considered along with the original 1, we end up with • and ••, and summed up (∑) they = 3 (•••), yet another Prime joins the growing list -- (1)-2-3. Notice that we have two accounting systems: the individual re-iterative doublings, and, their running ∑s.
Of course, there is nothing preventing 1 (•), or for that matter 2 (••), from being added to either 1, 2, or 3, with a different running ∑ generated:
• + • = •• (2)
• + ** = ••• (3)
•• + •• = •••• (4)
•• + ••• = ••••• (5), and so on. Nothing fancy, but profound in the simplicity of its implications.
Eventually all quantities -- as represented by either dots (•) or numbers (0, 1, 2, 3,...) -- can be formed. (NOTE: here we are talking about fractal re-iterations of an initial whole quantity as represented by a whole • or natural Whole Integer Number, WIN.)
With ALL these •'s and WINs, what generalizations might we make early on?
ALL WINs may be divided into ODDs or EVENs;
ALL *Primes -- except 2 -- are ODDs, so we have tow groups of ODDs -- Primes and NOT-Primes;
ALL NOT-Primes can be generated by the sum of two or more Primes;
ALL ODDs, when doubled, form the EVENs-NOT subgroup -- EVENs NOT ÷4;
ALL EVENs-NOT, when doubled, form the EVENs subgroup -- EVENs ÷ 4;
ALL EVENs, when doubled -- including all subsequent doublings of their sums, exclusively form additional EVENs;
ALL EVENs -- both EVENs ÷4 and EVENs-NOT ÷4 subgroups -- are divided equally in distribution, i.e. every EVENs ÷2 = EVENs-NOT.;
ALL EVENs from either subgroup can be generated by the sum of two Primes (Euler's Strong Form of the Goldbach Conjecture).
Placing ALL ODDs sequentially in Column One, when doubled, forms Column Two that = ALL EVENs-NOT, and subsequent and sequentially doublings of this column forms Columns Two-Three-Four-... that = ALL the EVENs, together generates the Divisor Matrix Table (DMT);
The DMT contains ALL the divisors of ALL WINs, but is especially declaritive in showing graphically -- within the table itself -- ALL the divisors of ALL the EVEN numbers -- EVENs and EVENs-NOT;
The DMT reveals that ALL EVENs-NOT have divisors found exclusively in Column One (ODDs) and Column Two (EVENs-NOT), and, with the exception of the first PN 6, no other PNs;
The DMT reveals that ALL PNs (except PN 6), are found exclusively in Columns Two-Three-Four... of the EVENs, and, exclusive to and thus identifying the PNs, the divisors found are ALWAYS limited to two ODDs -- 1 and an ODD found by the sequentially division of the PN -- and, as such, only have 2 Rows of divisors, along the number of Columns that = p-value!
*The central importance of prime numbers to number theory and mathematics in general stems from the fundamental theorem of arithmetic.[44] This theorem states that every integer larger than 1 can be written as a product of one or more primes. Ref: https://en.wikipedia.org/wiki/Prime_number

~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~
FINAL THOUGHTS (#24 and more!)
As noted, there is so much more to the DMT than first meets the eye!
ALL *10 profiling parameters of any "container," and of any special expression of the "container" profile as with the Active TRUE Mp-PN pairings, can be found within a rectangular boundary on the DMT.
- Form a rectangle from the PN expression back to the origin;
- Calculate the Running Sums across the Rows within;
- Assign these values next to the respective table values;
- Mark the 10 parameter values;
- There will be 12+ marked values as some repeat;
- 6 values will always be found in the last Column + an 2 more in the last Row;
- The pattern is the same for all such rectangles;
- The p-value = the number of Columns;
*exception, x2 is found exclusively on the TOP, BF1 Row, unless one includes the Running Sums down the Columns where all x2 are found multiple times -- as a fractal re-iteration of the BF1 Row.
- z2=MPS,
- xz=PN,
- yz=OC,
- x2=PNS, *exception,
- xy=CR,
- y2=OCS,
- z=Mp=2p-1,
- x=(z+1)/2=y+1=2p-1,
- y=x-1=(z-1)/2,
- p=Prime (or EVEN for generic "containers"), and, # of Columns.
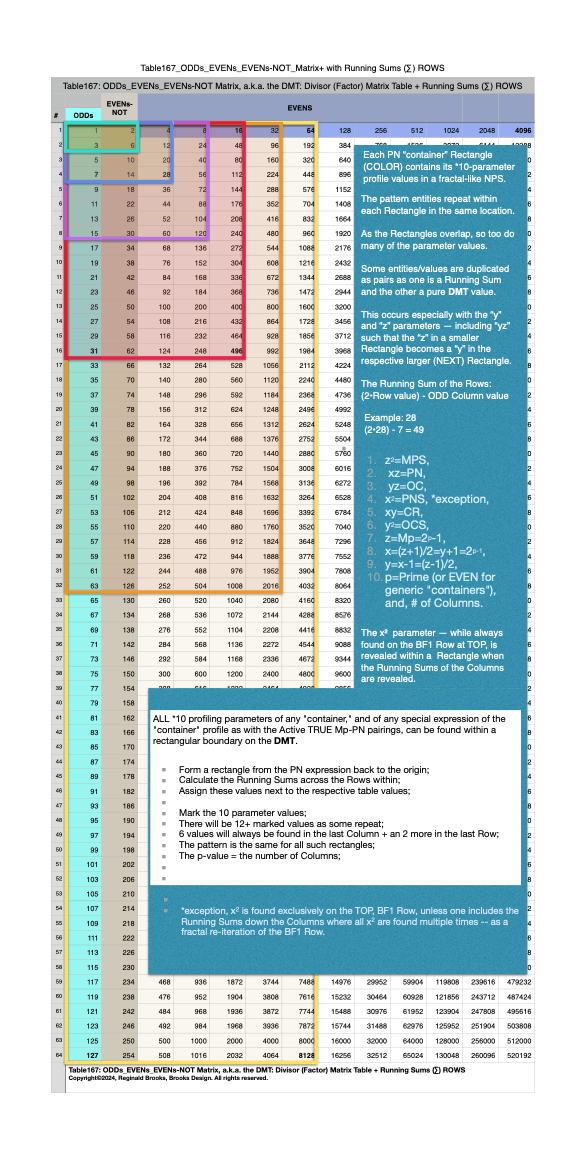
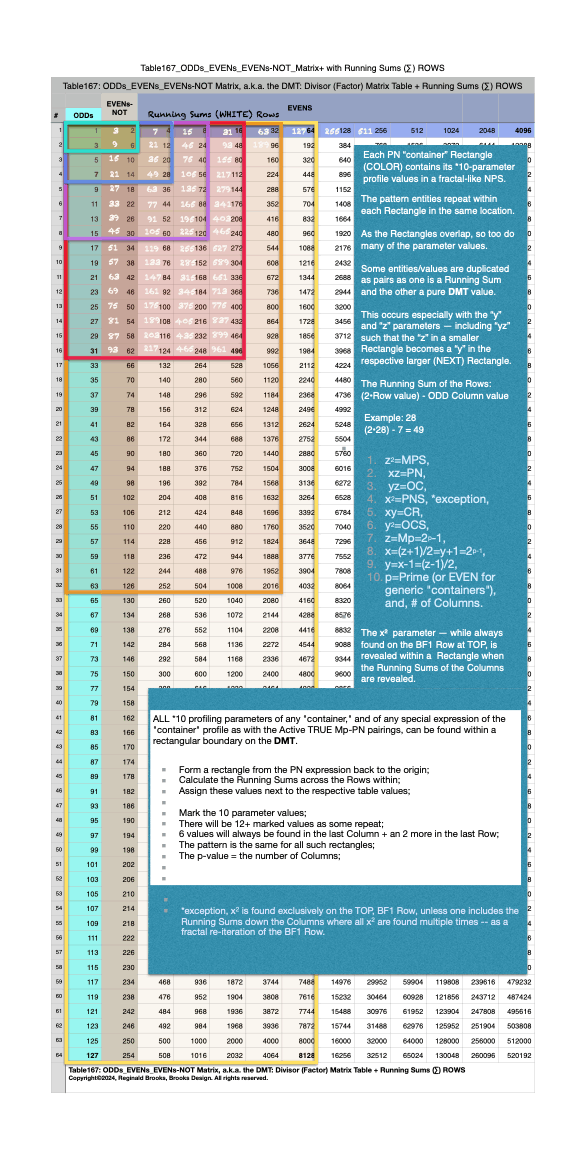
SUMMARY
EVEN numbers, while looking alike, actually come in two forms:
-those that when divided by two ALWAYS give an ODD;
-those that when divided by two ALWAYS give an EVEN.
There additional differences:
-the 1st group that divides to an ODD, is NEVER ÷ by 4;
-the 2nd group that divides to an EVEN, is ALWAYS ÷ 4.
Also (rephrasing the aboves):
-the 1st group, when doubled, ALWAYS gives the 2nd group;
-the 2nd group, when doubled, ALWAYS gives more 2nd group.
That is to say:
-the 1st group of EVENs-NOT÷4 are "primative" parent EVENS;
-the 2nd group of EVENs÷4 are "fractal, re-iterative" child EVENS.
That leads to:
-ALL EVENs are derived from (doublings) the EVENs-NOT;
-ALL EVENs-NOT are derived from (doubling) the ODDs.
And that, to this:
-The ODDs, which also come in two forms, are fundamental to ALL EVEN numbers;
-The ODDs are either Prime or Not-Prime.
The Divisor Matrix Table (DMT) is formed from the above simple principles:
Column 1: ALL ODDs in sequential order;
Column 2: ALL EVENs-NOT (formed by doubling ODDs in Column 1);
Column 3: ALL 1st generation EVENs (formed by the doubling of EVENs-NOT in Col. 2);
Column 4: ALL 2nd generation EVENs (formed by the doubling of EVENs in Col. 3);
Columns 5, 6, 7, ... ALL 3rd, 4th, 5th, ... generation EVENs (formed by doubling previous columns);
Row 1: the Exponential Power of 2, (2ⁿ) -- a.k.a. the Butterfly Fractal 1 -- forms naturally from the columns;
Rows 2,3,4, ... form in a similar, natural manner from the columns, and are products of the ODDs 3, 5, 7, ...;
ALL Divisors of ALL numbers are found within the DMT, with an overt visualization of the EVEN divisors;
The visualizations of the very rare and quite unique Mp-PN pairings are but one of its outstanding virtues!
The redundant, re-iterative and self-similar fractal Number Pattern Sequences of either Axis inform it all!
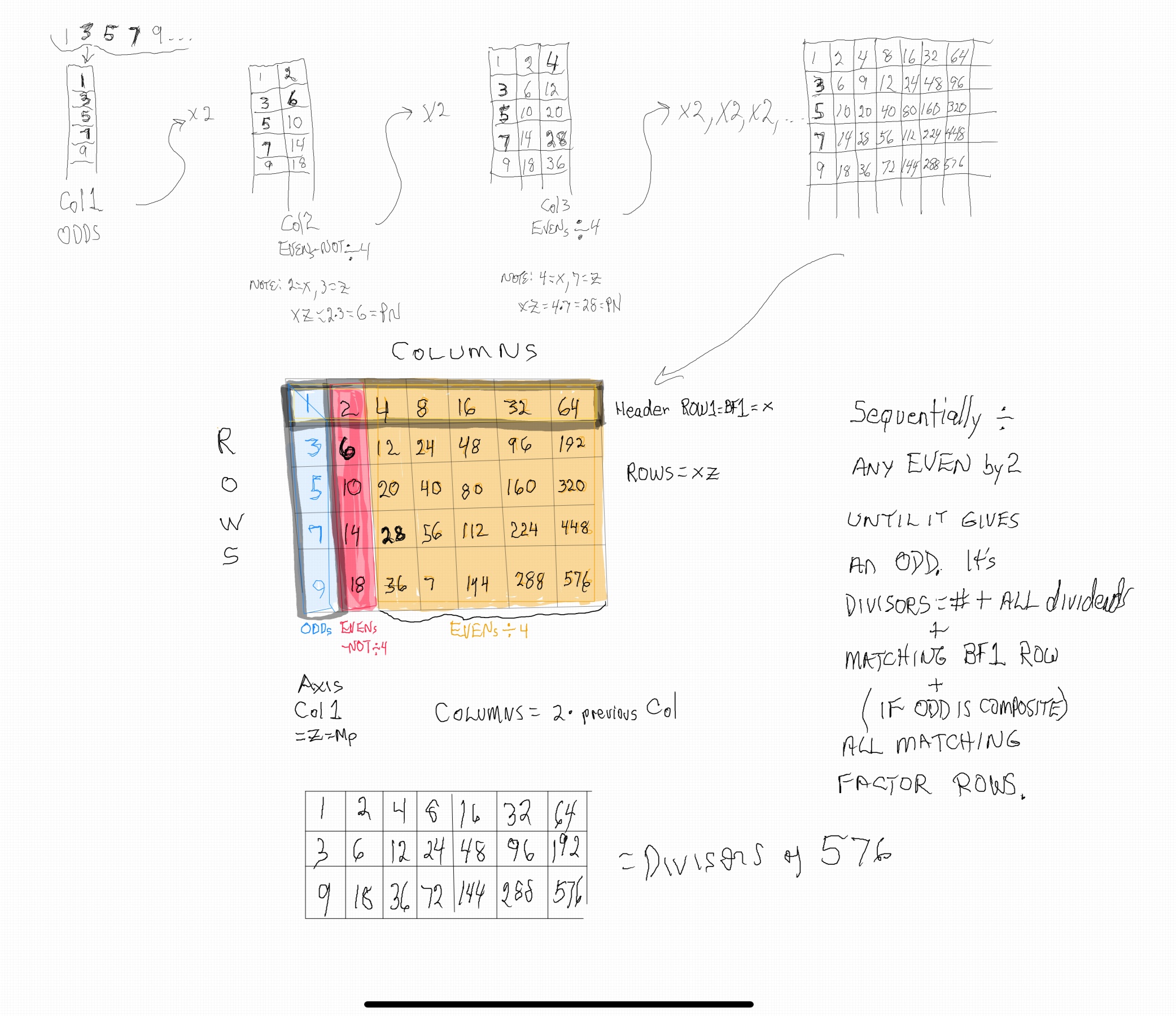
DMT summary
DMT -0: animated gif














-(xz)divide24.pdf)







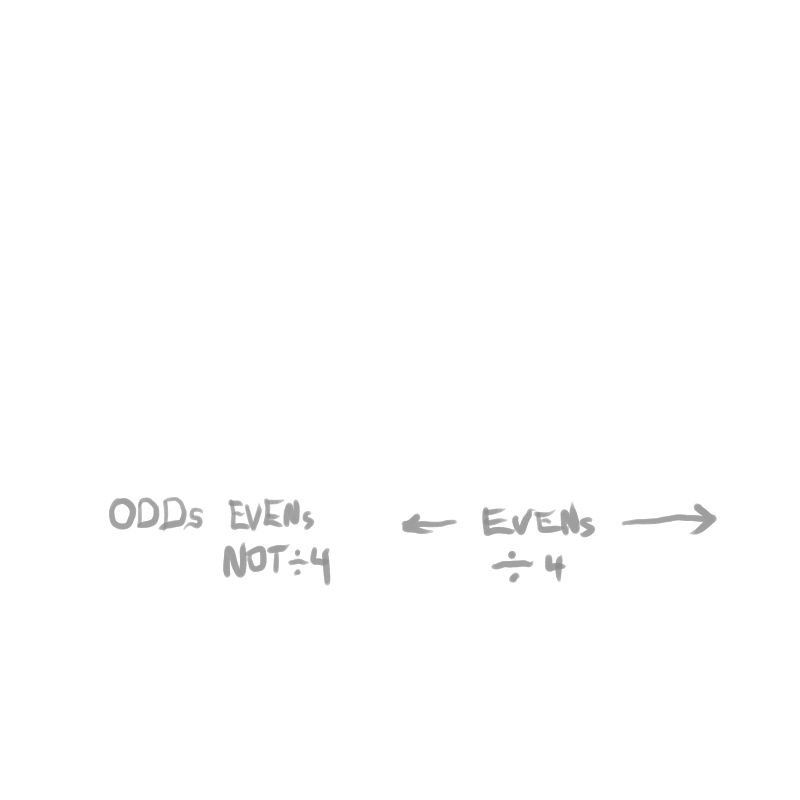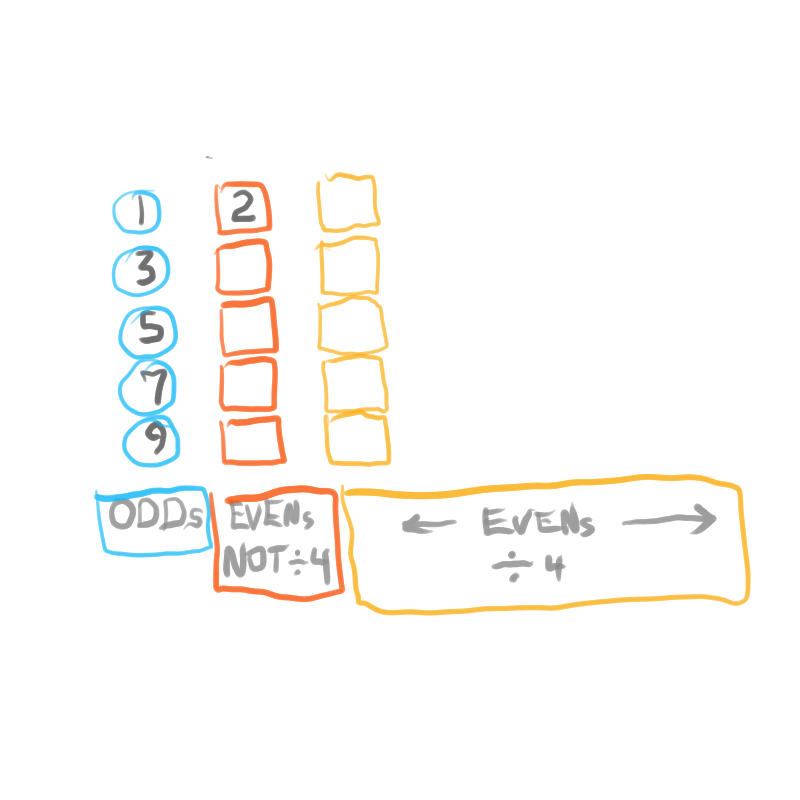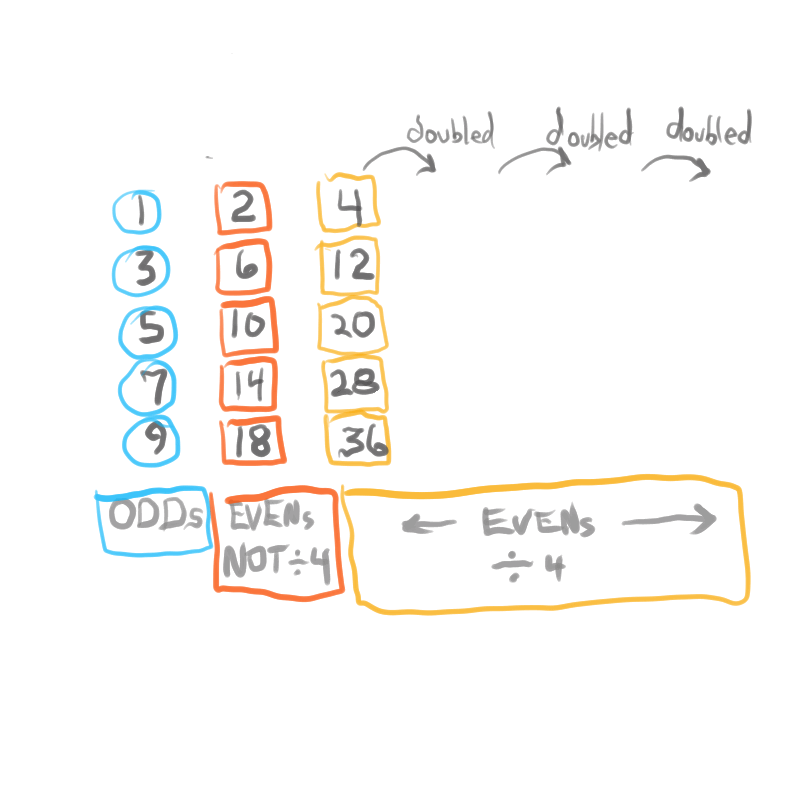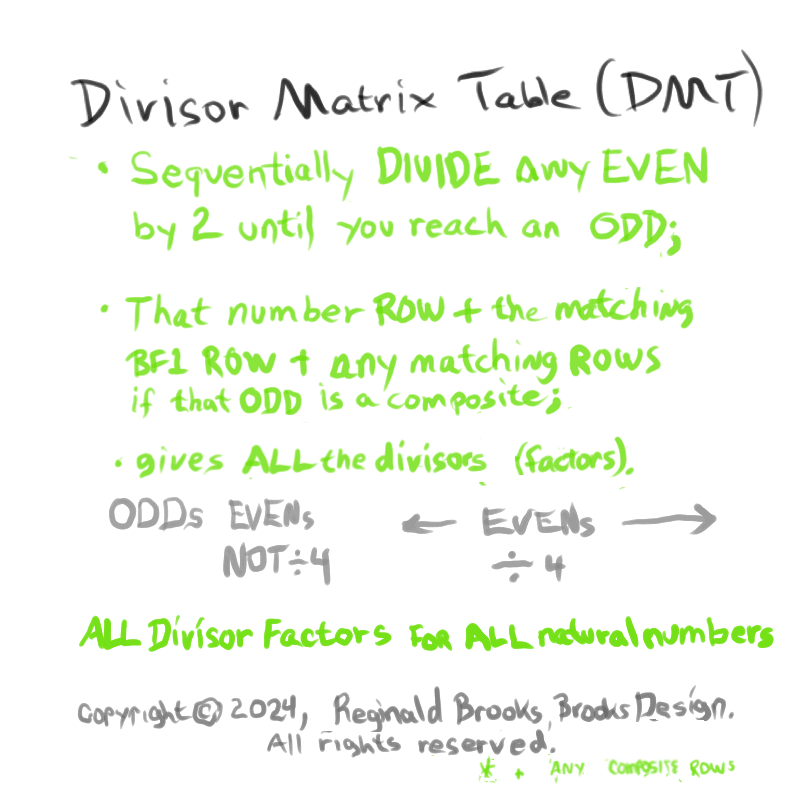
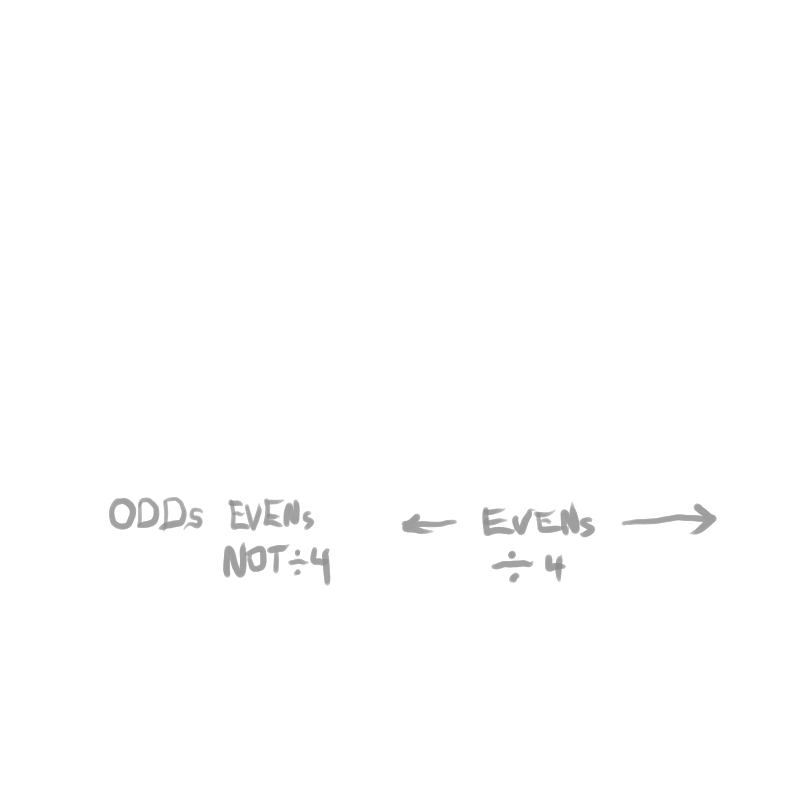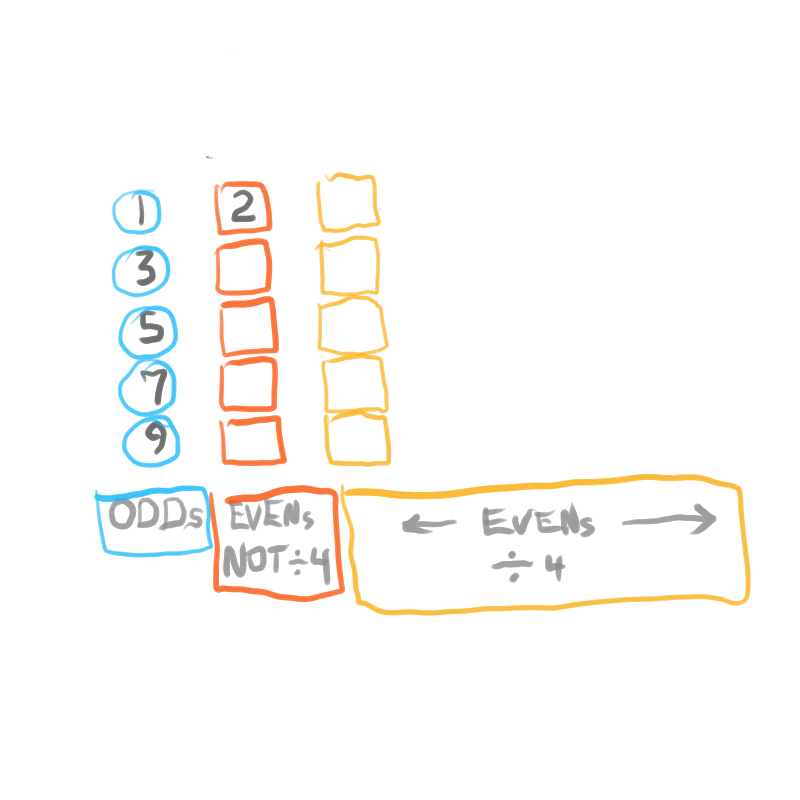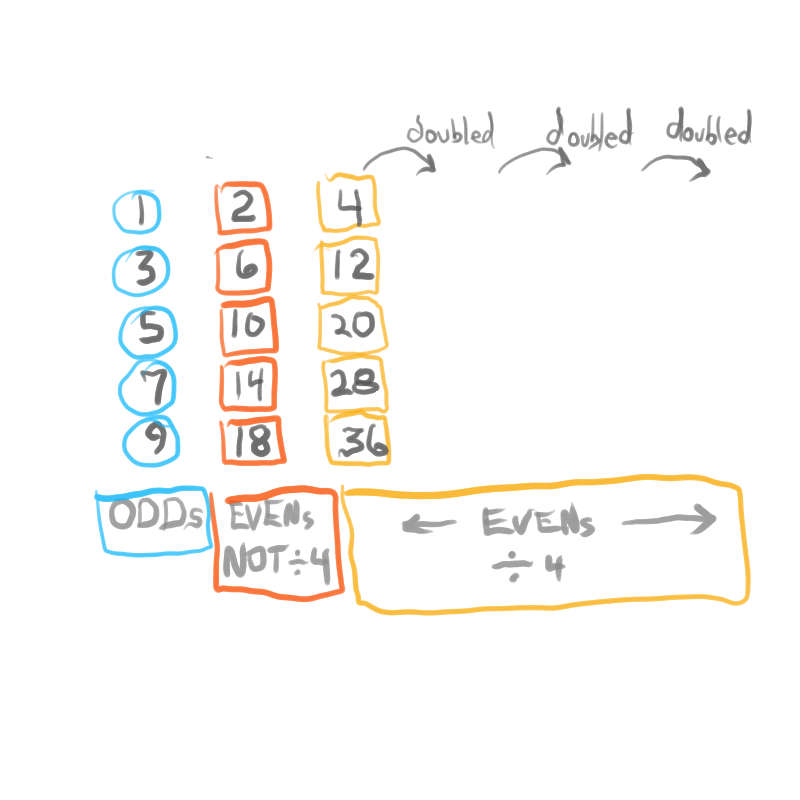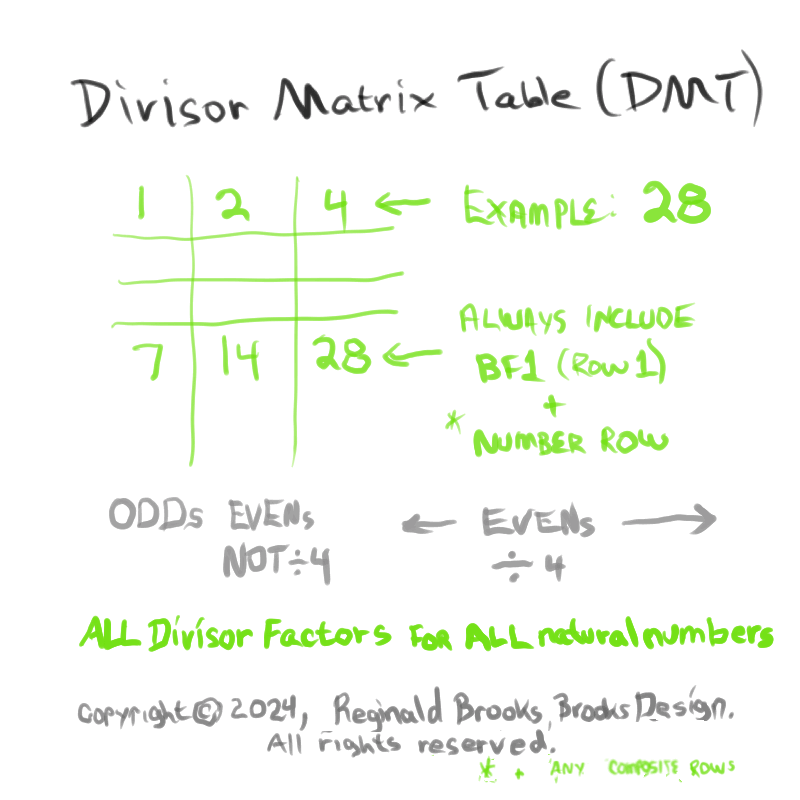
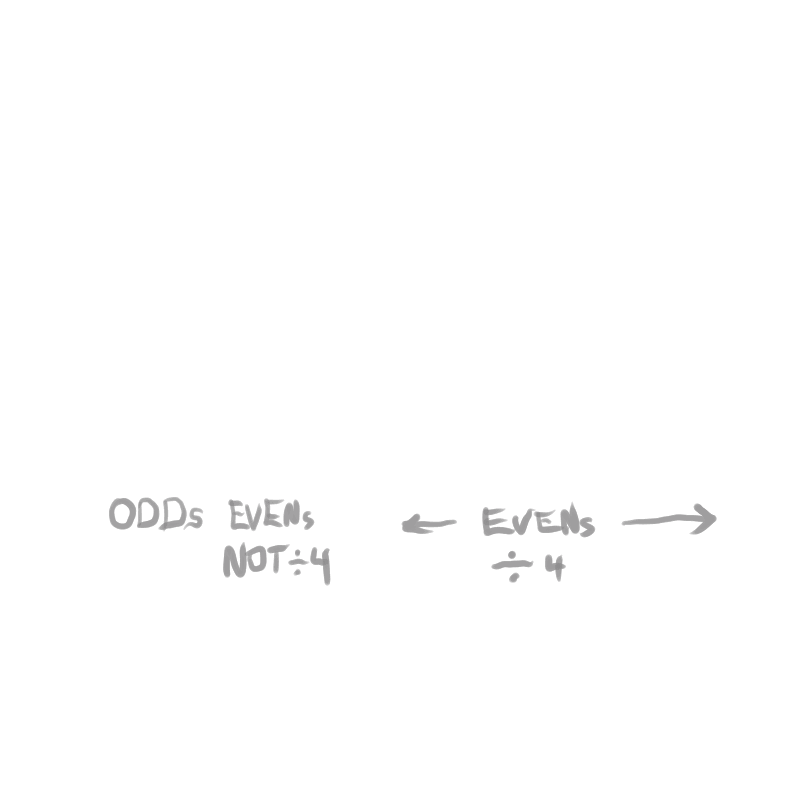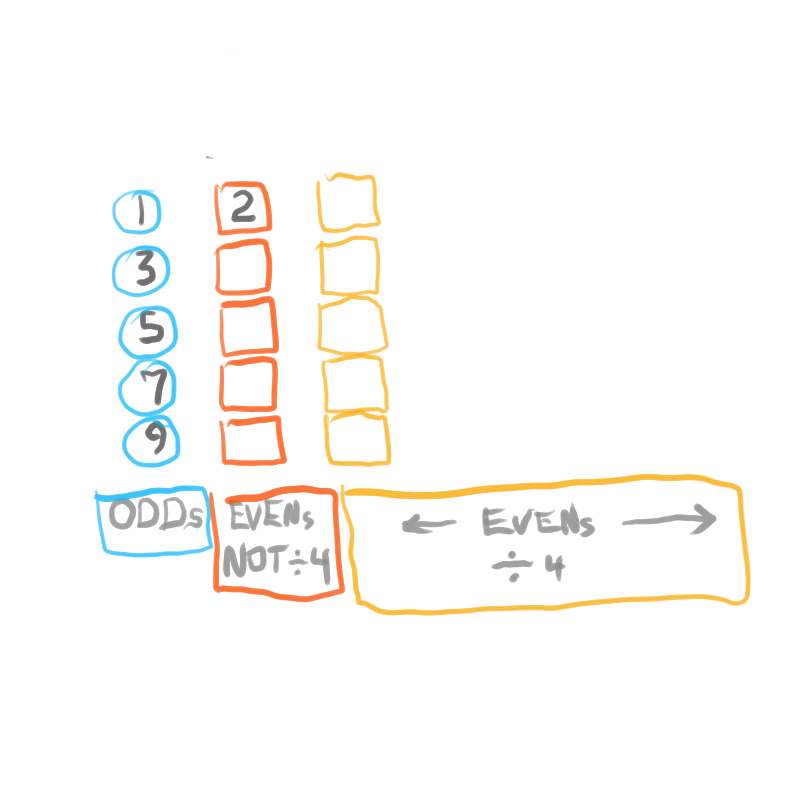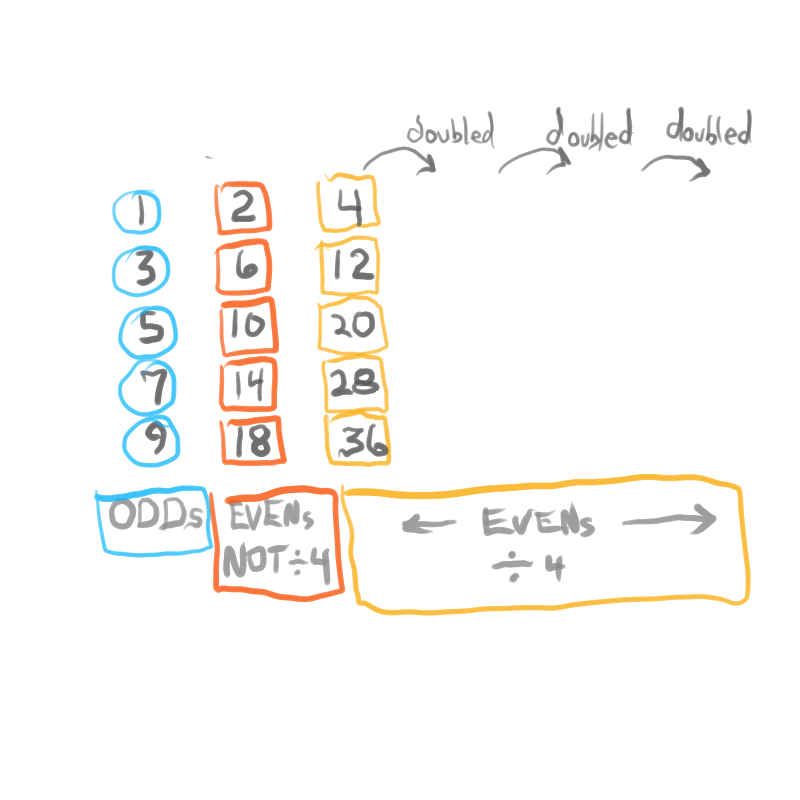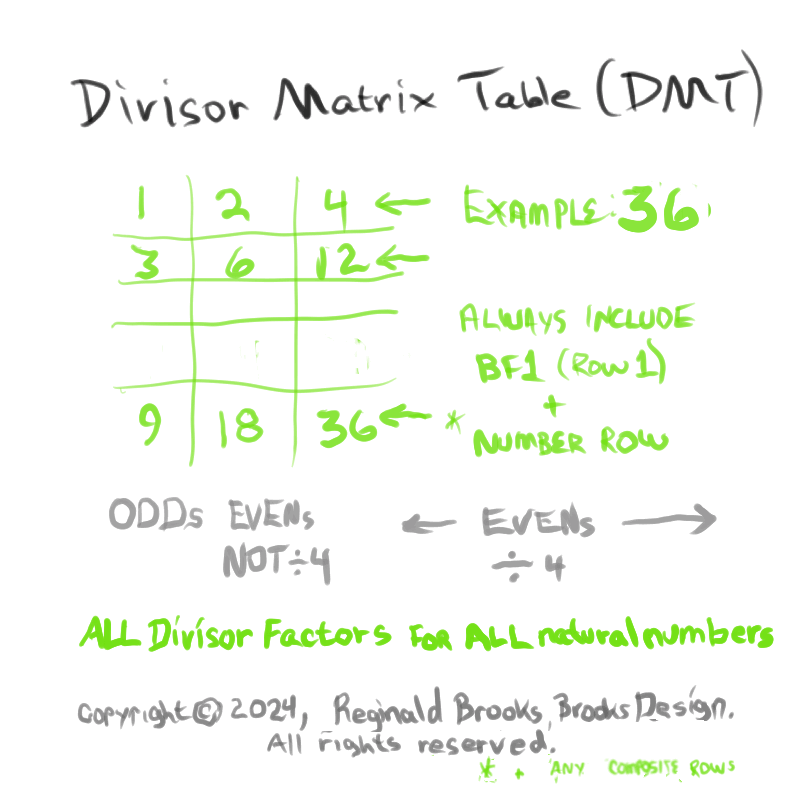
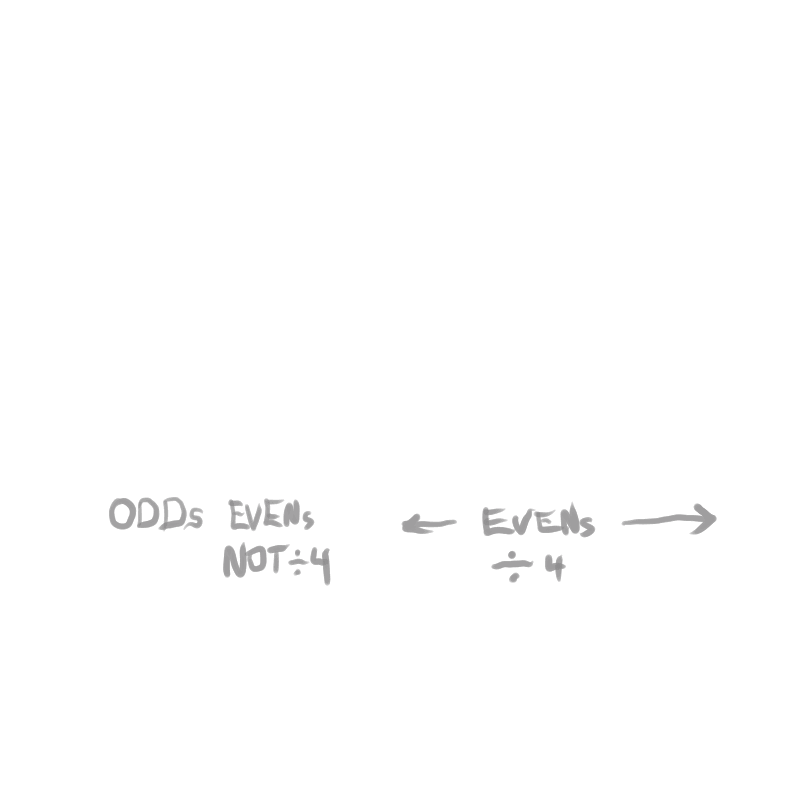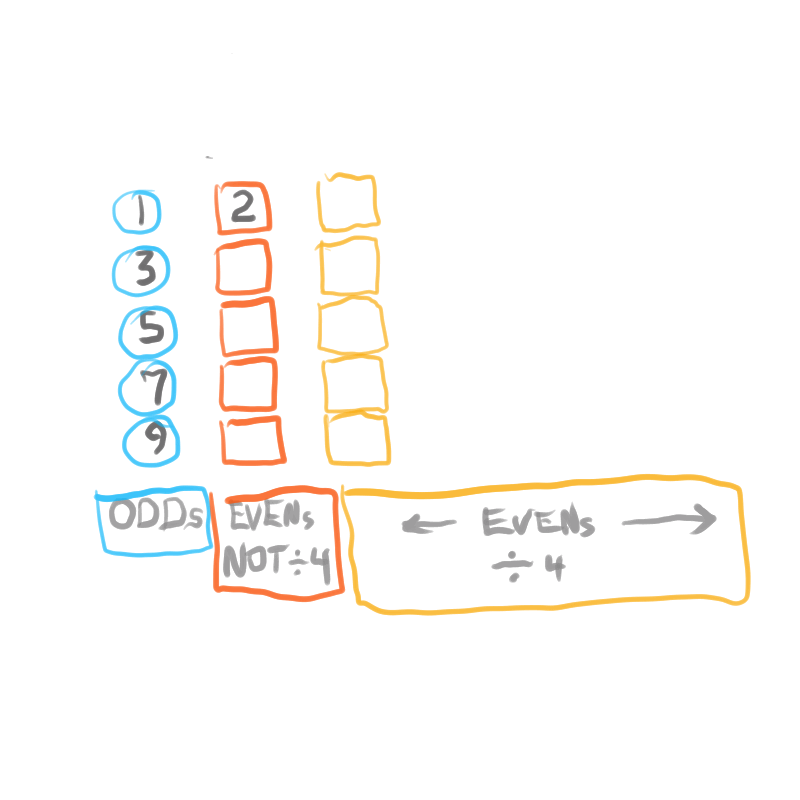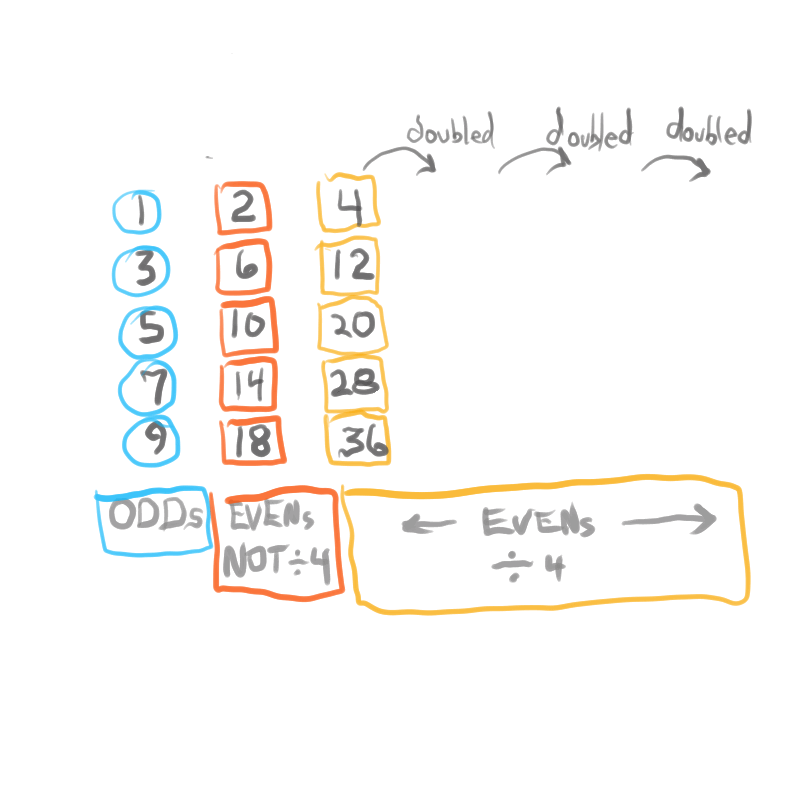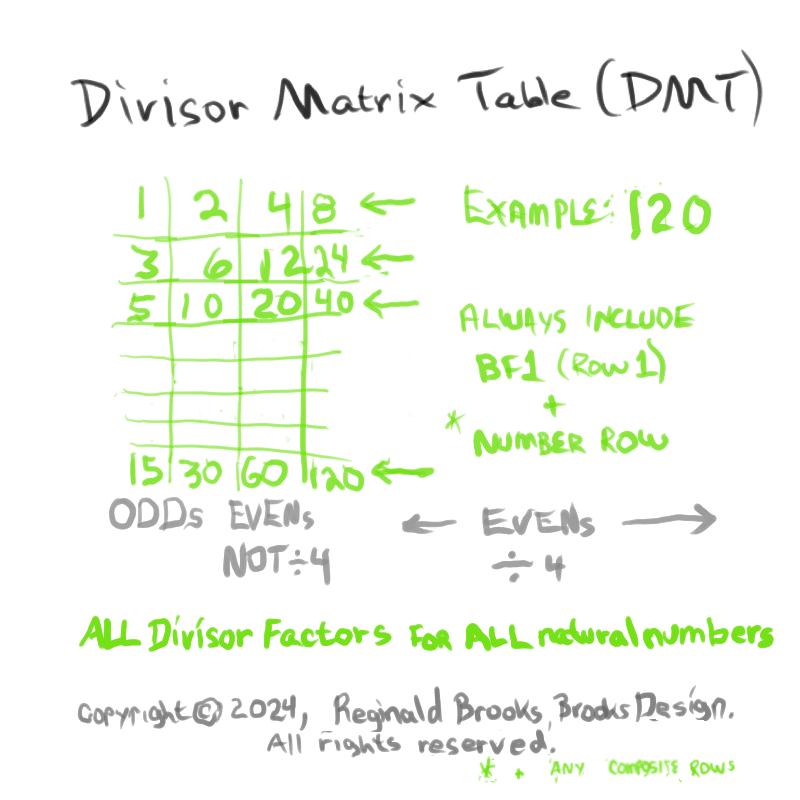
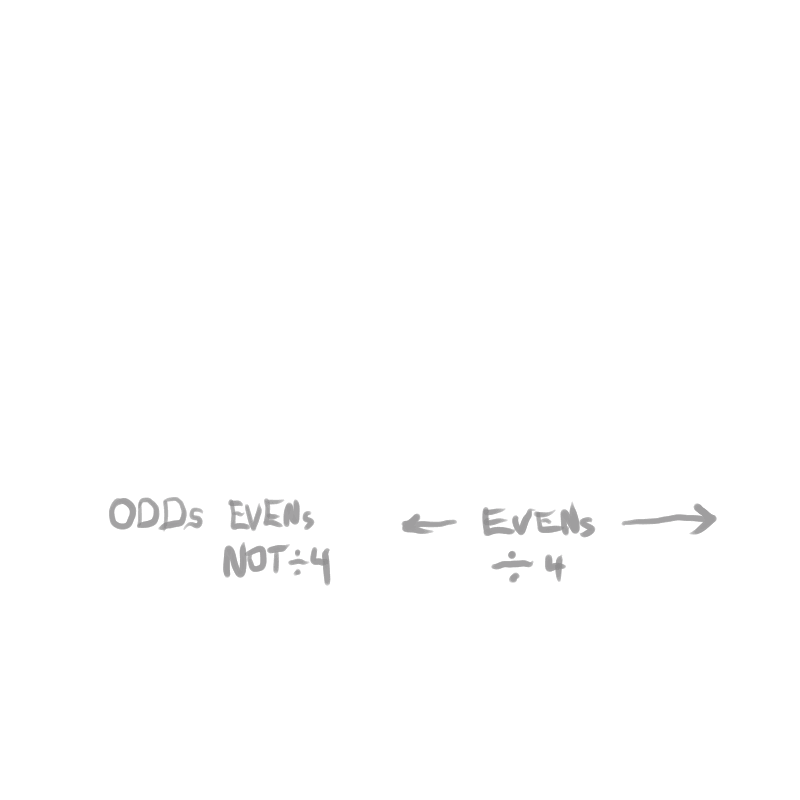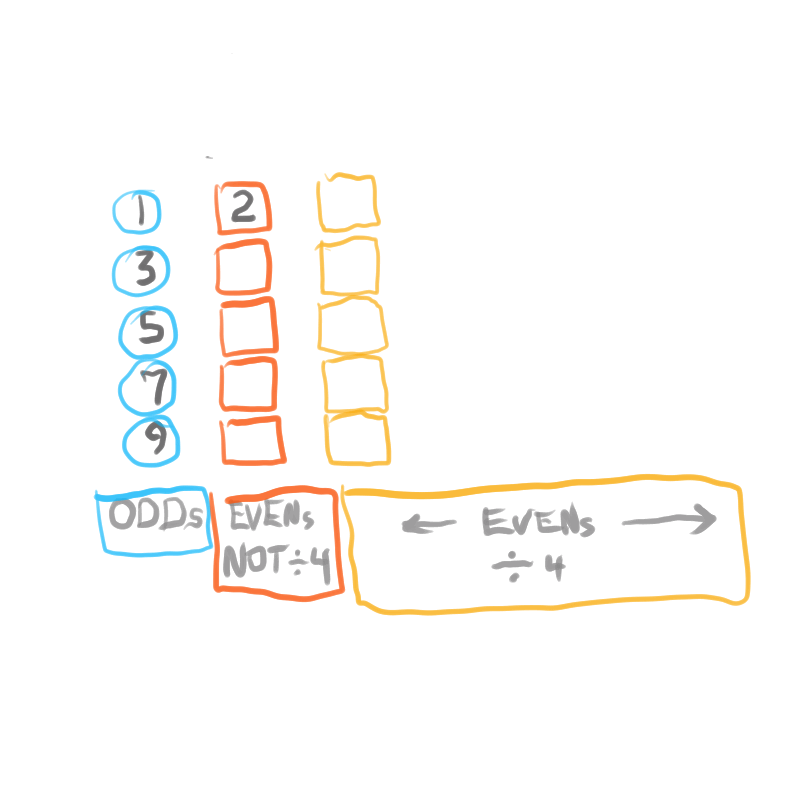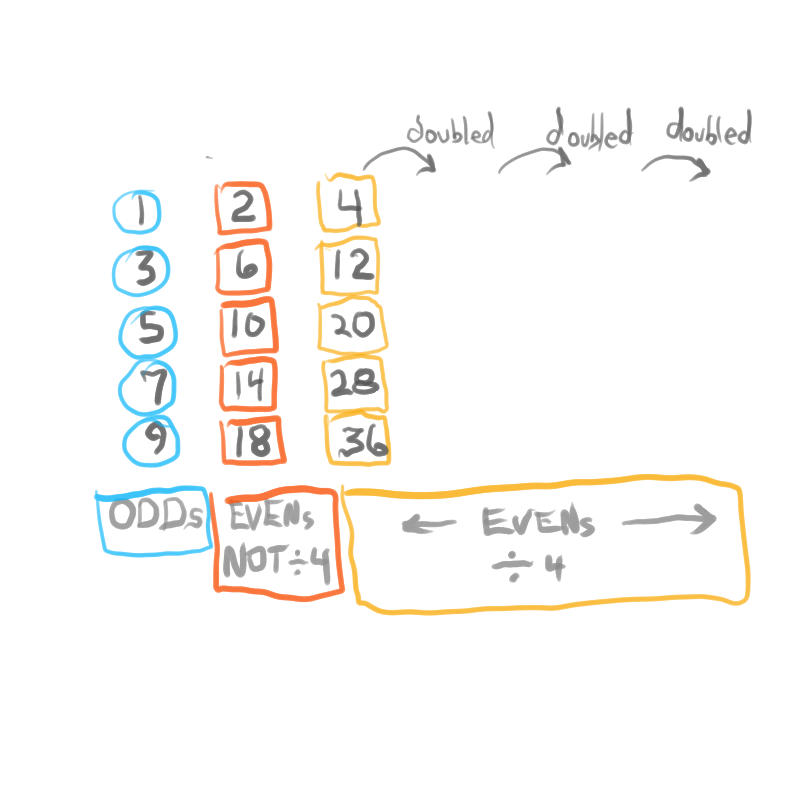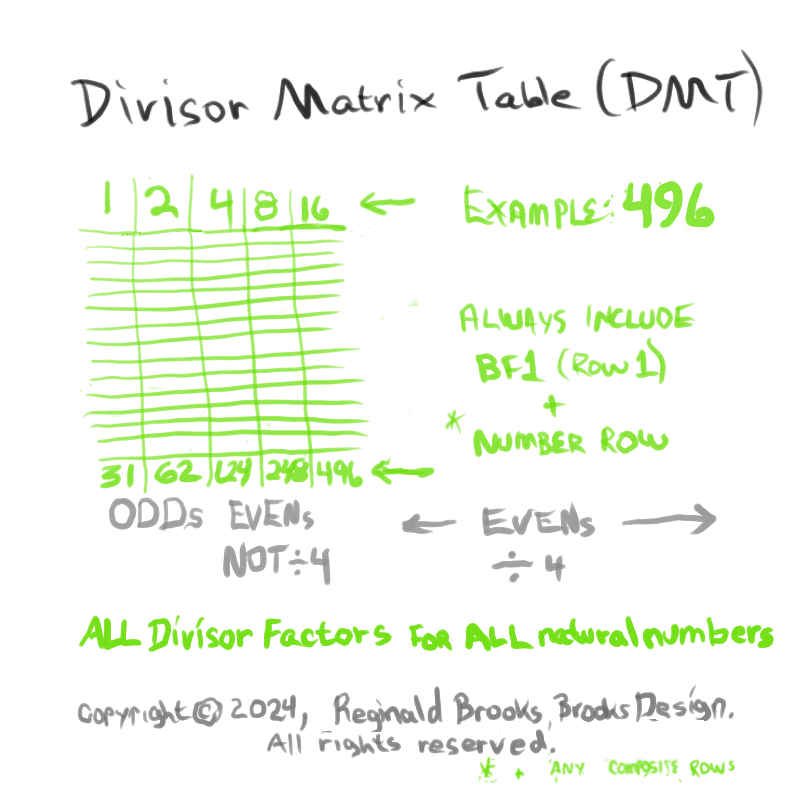
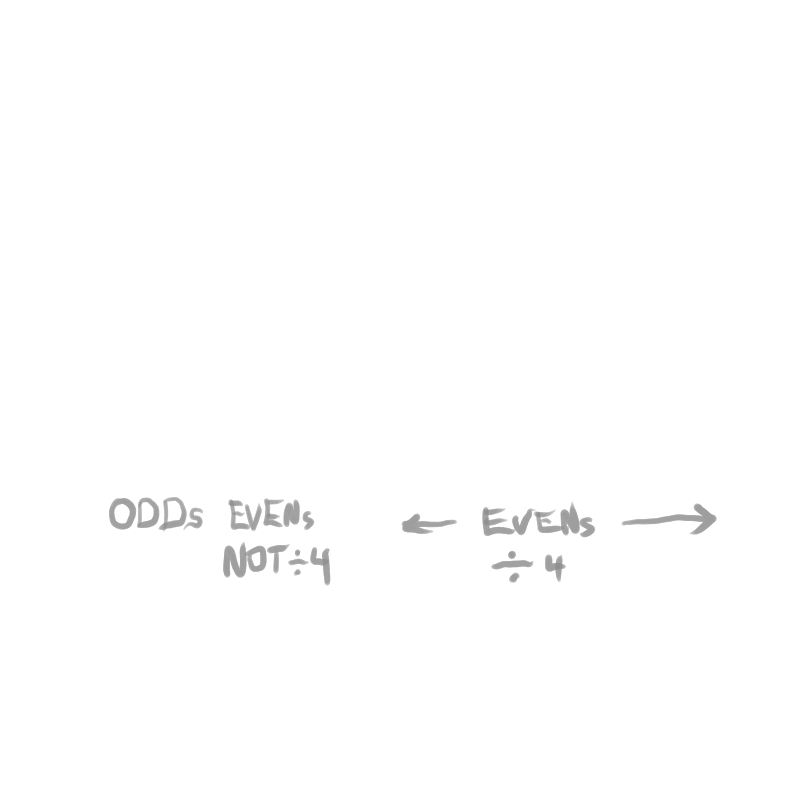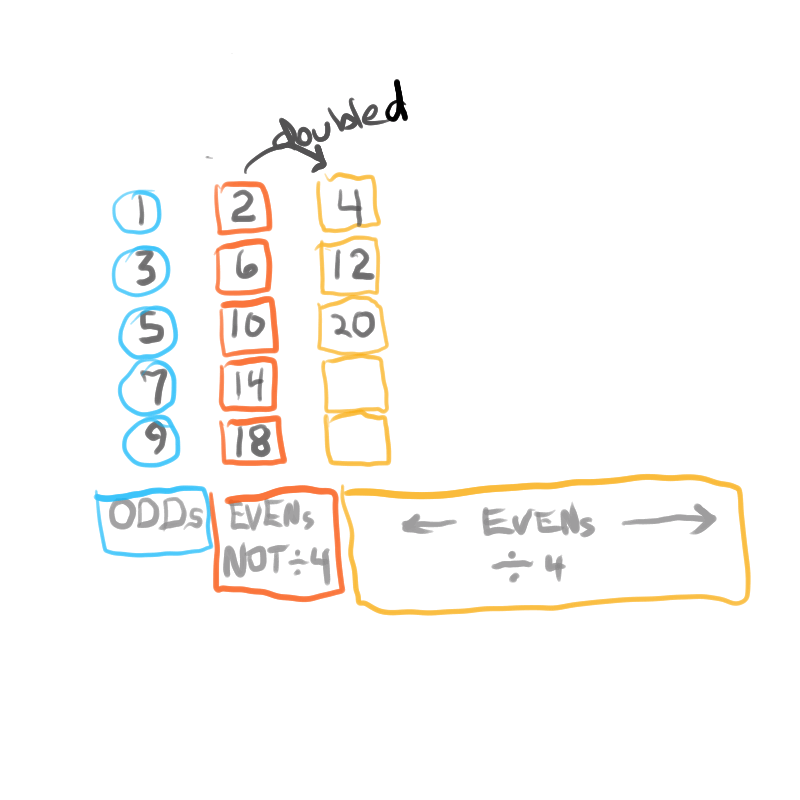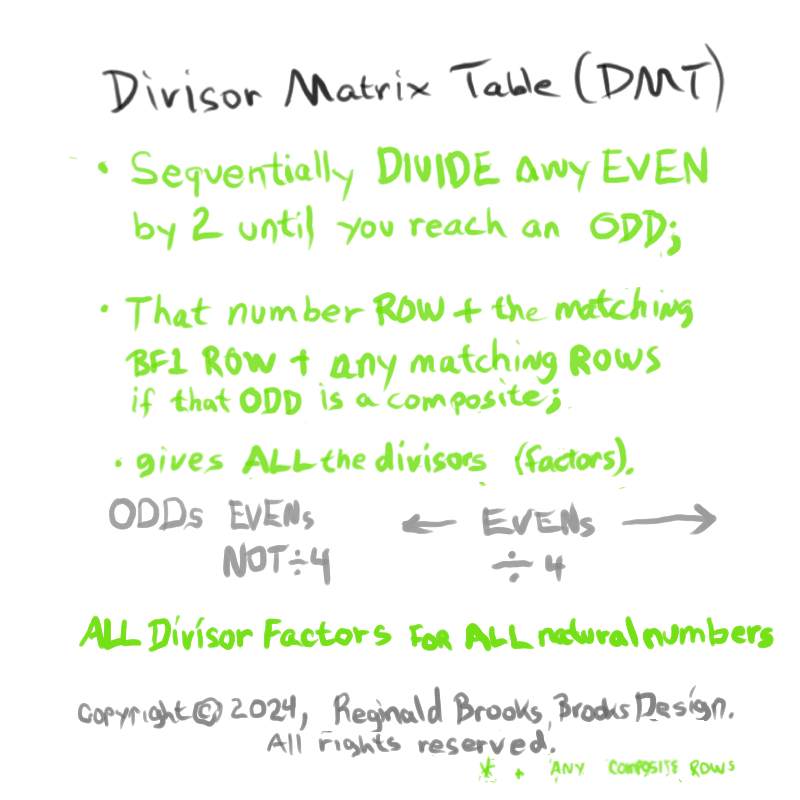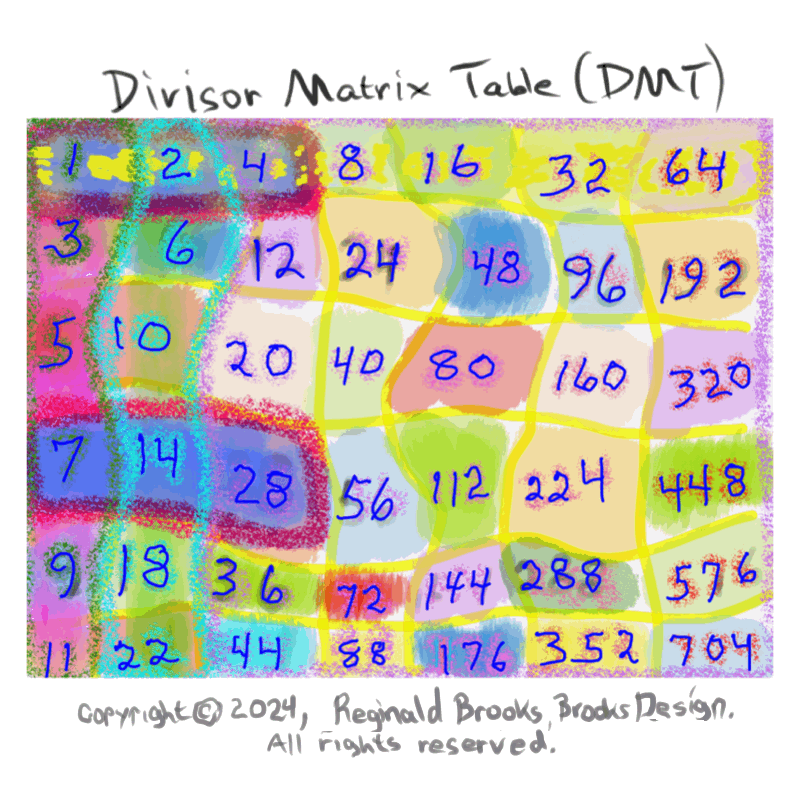




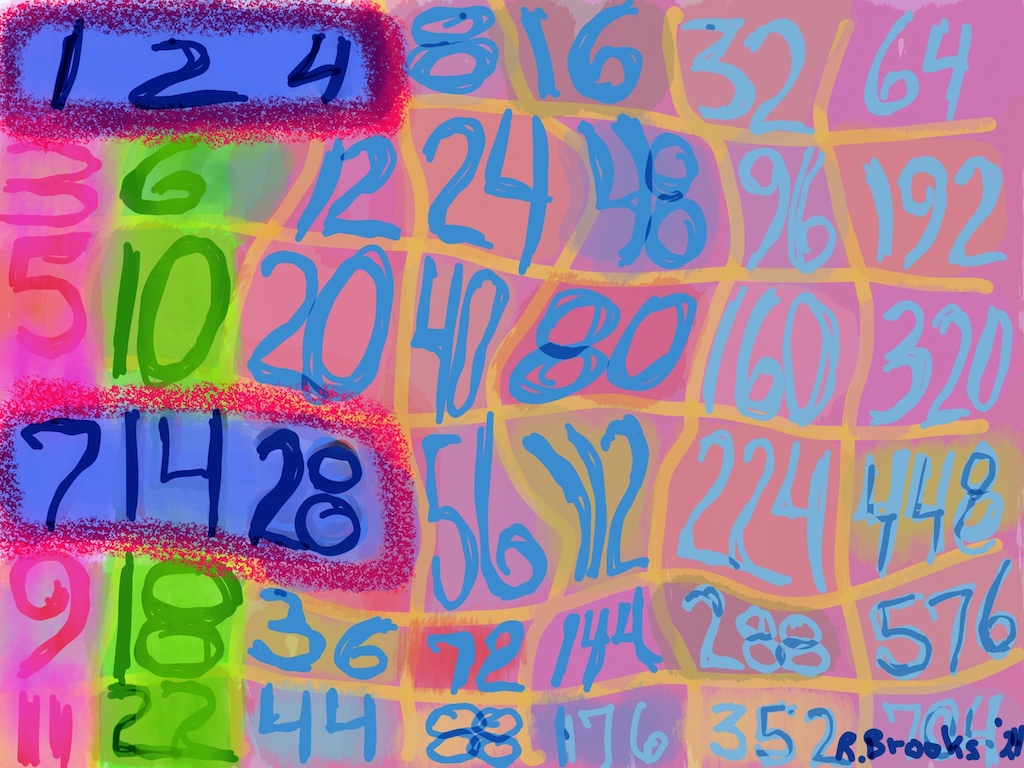
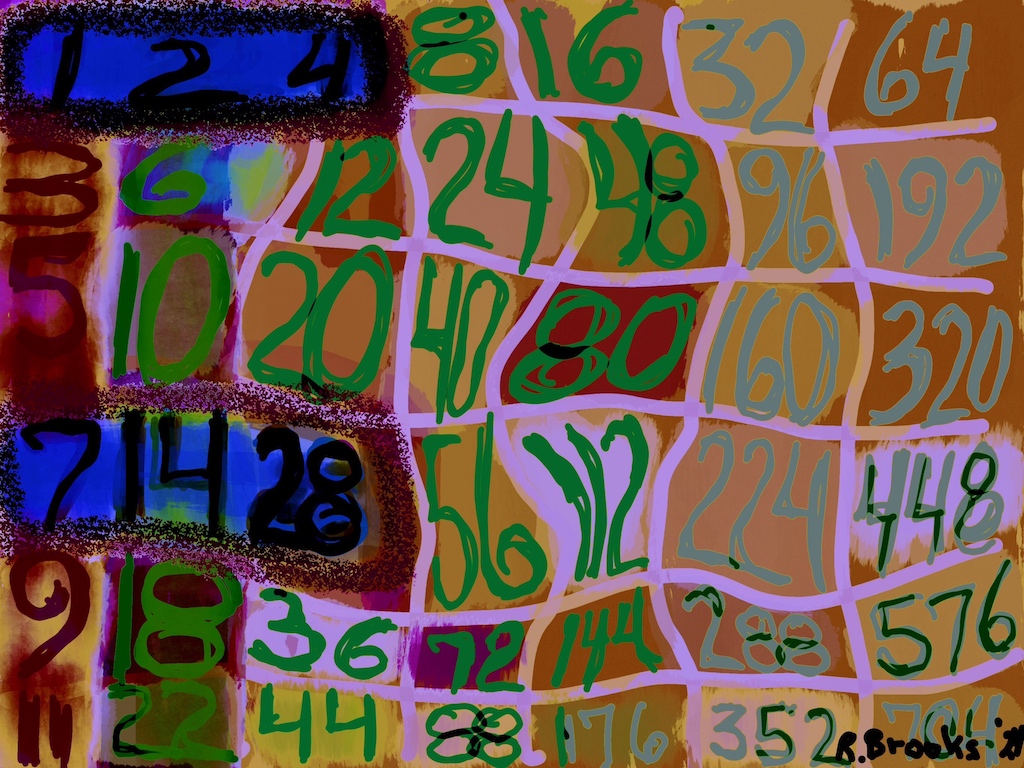




















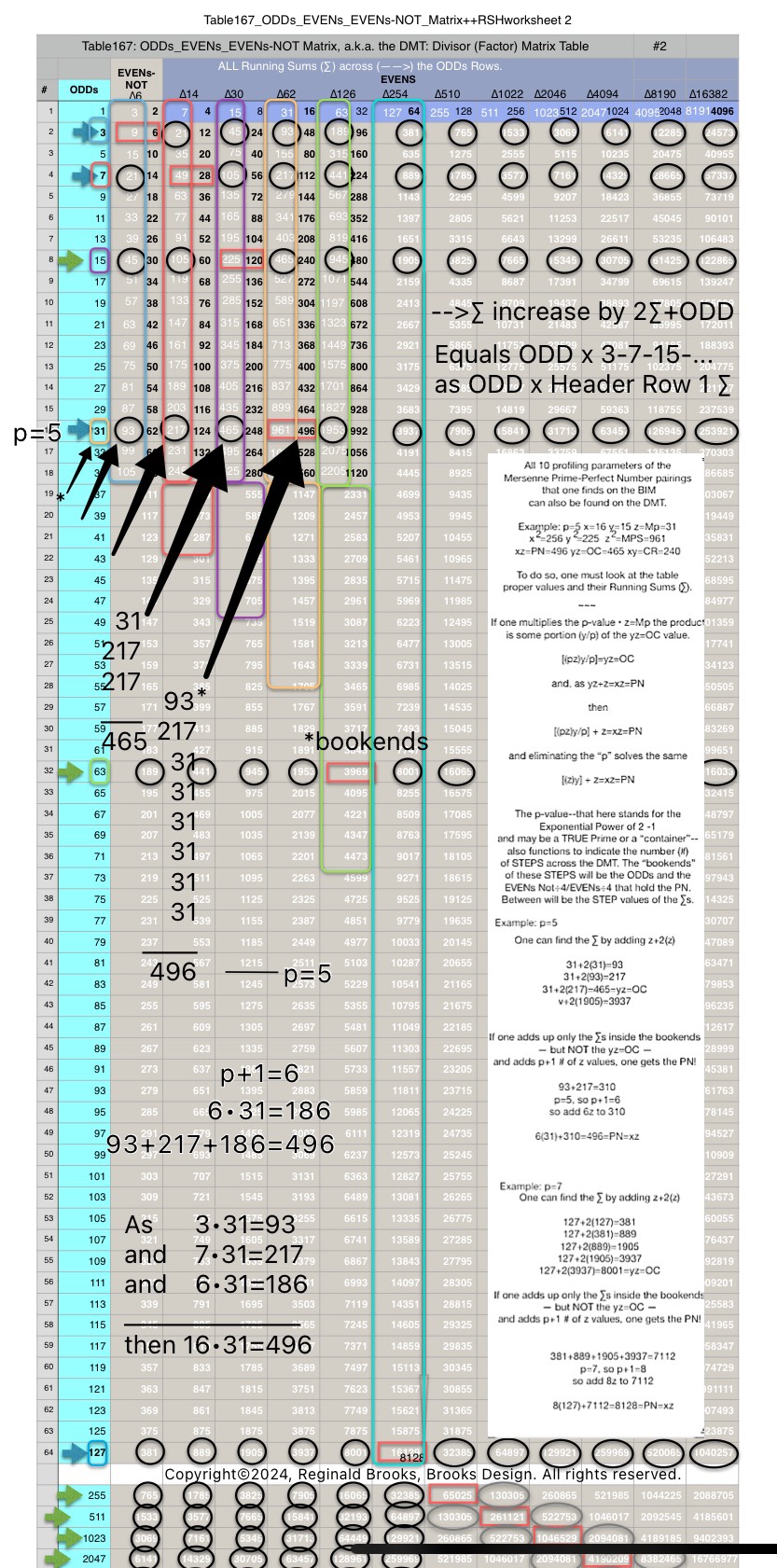
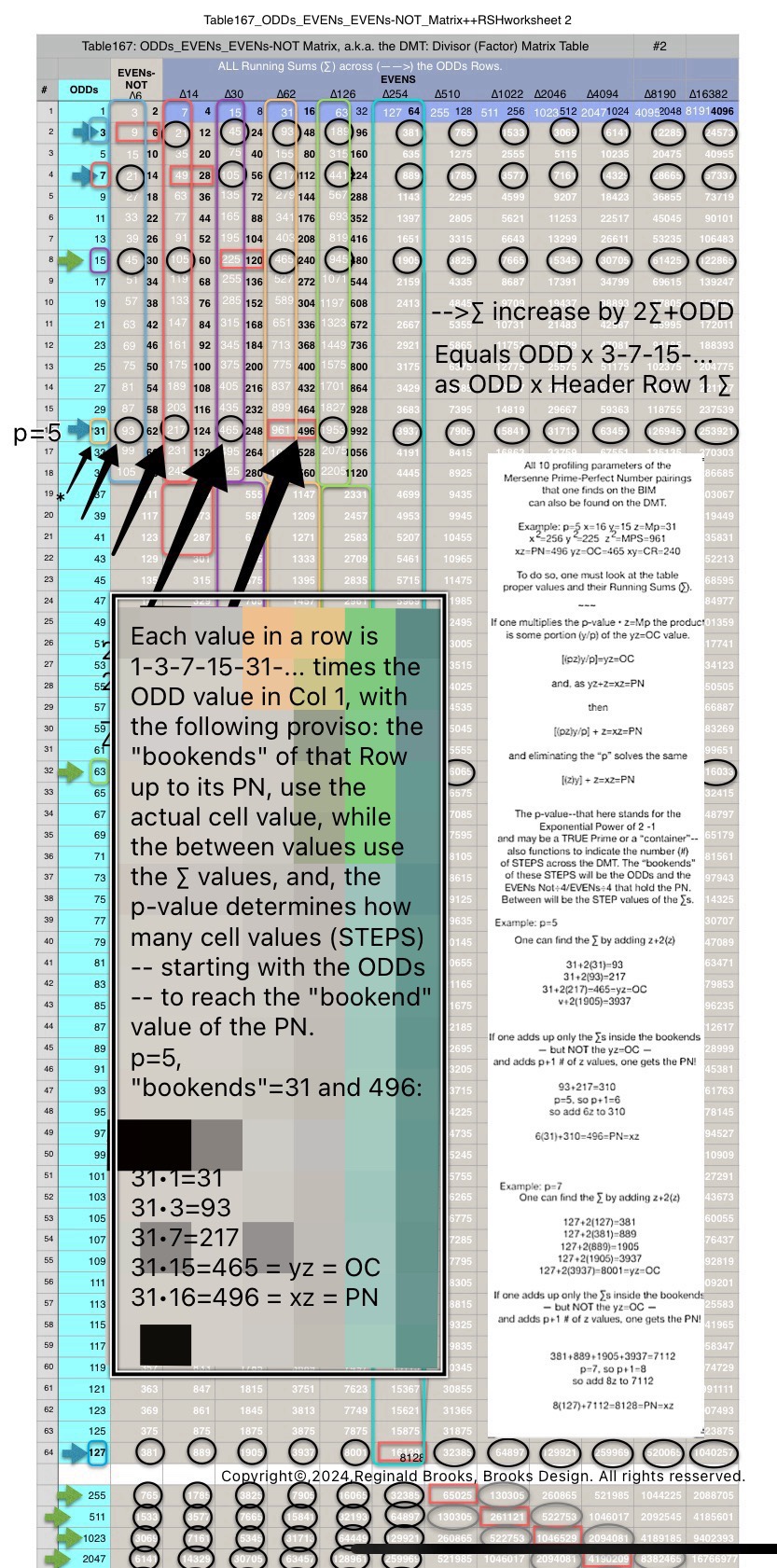

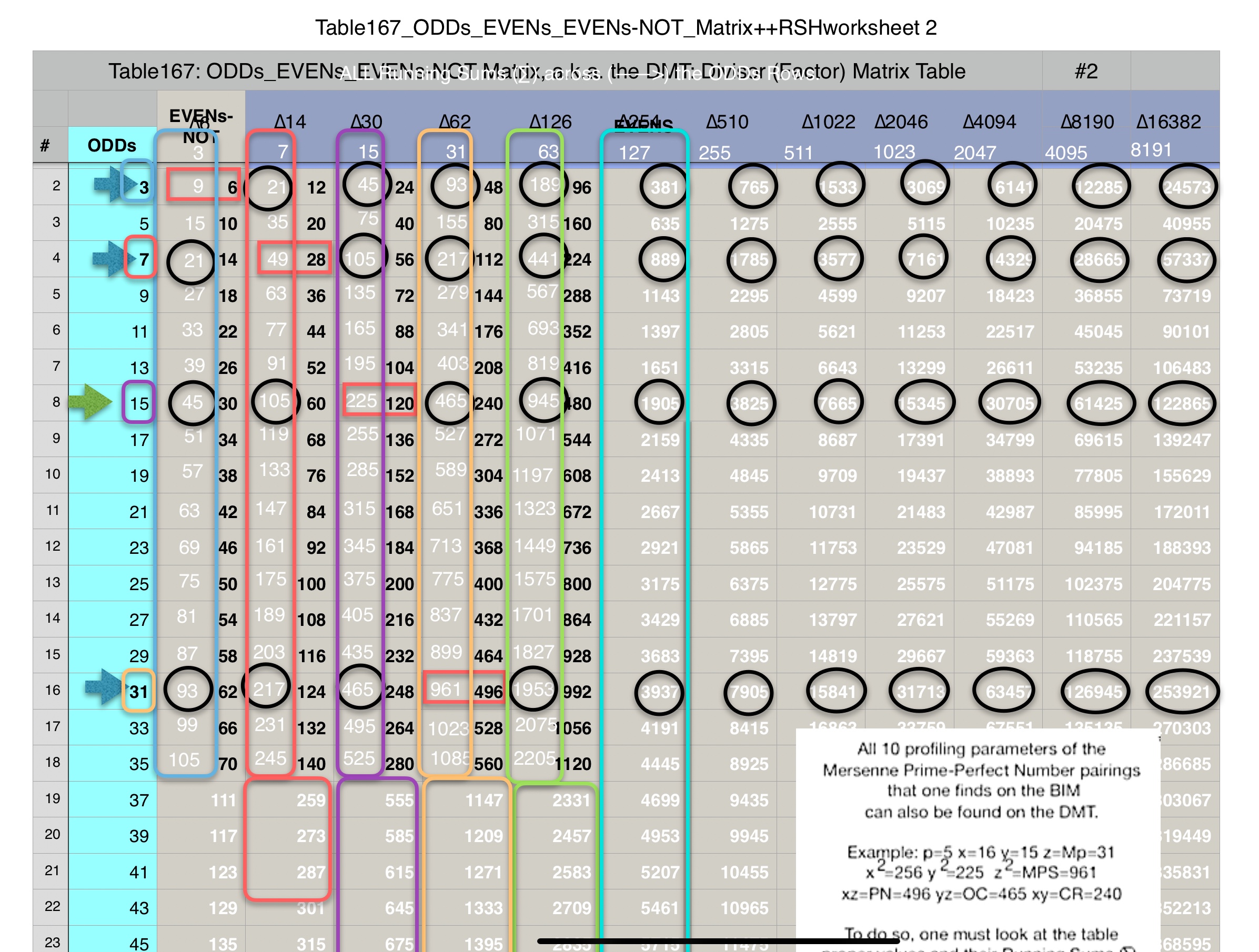

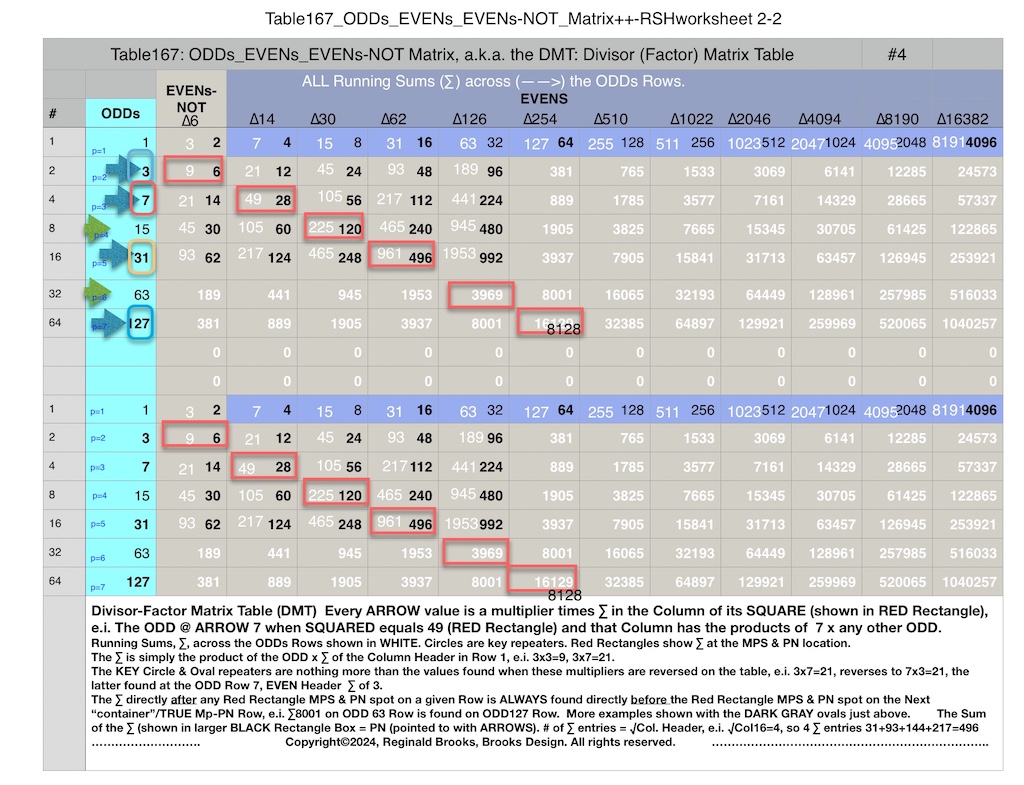
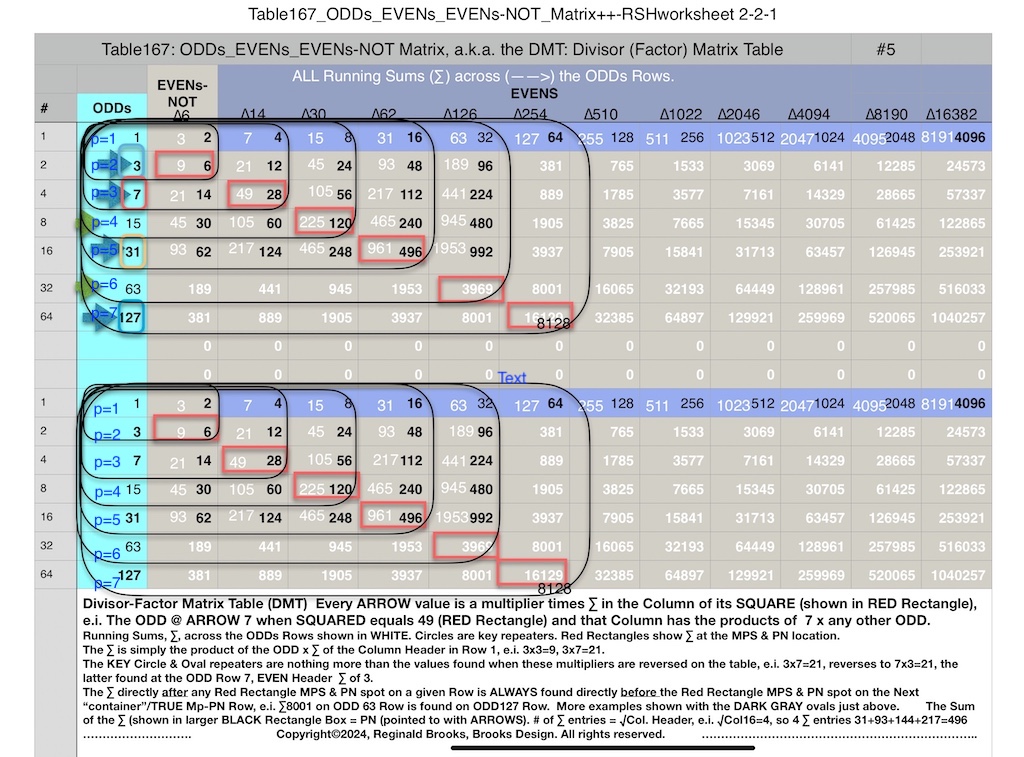
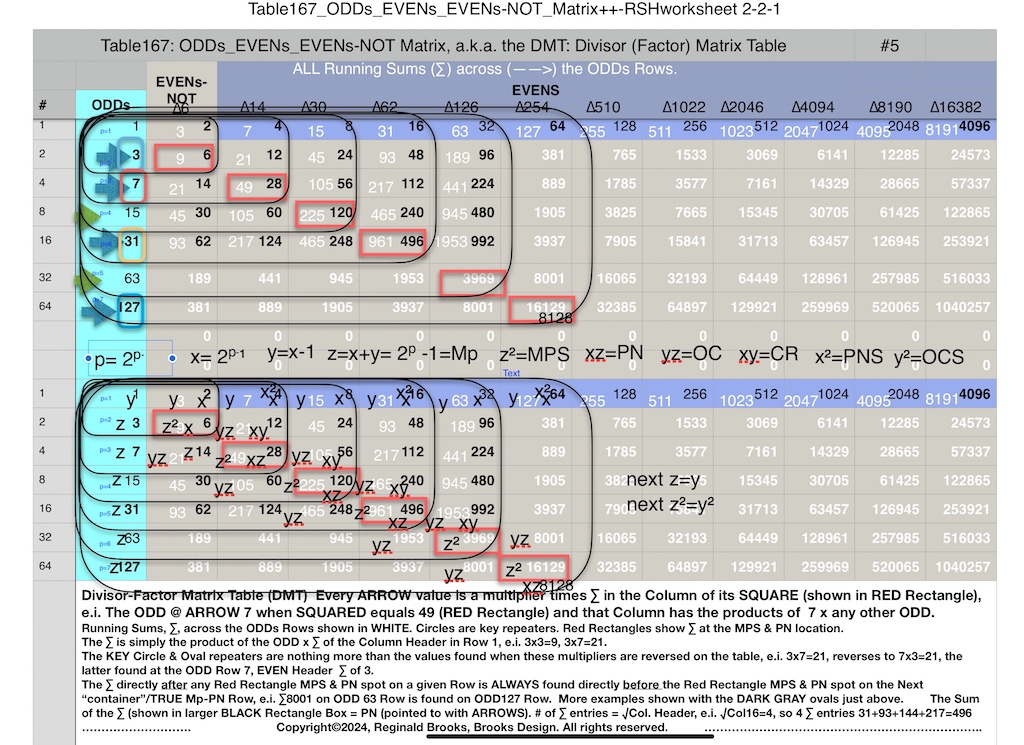
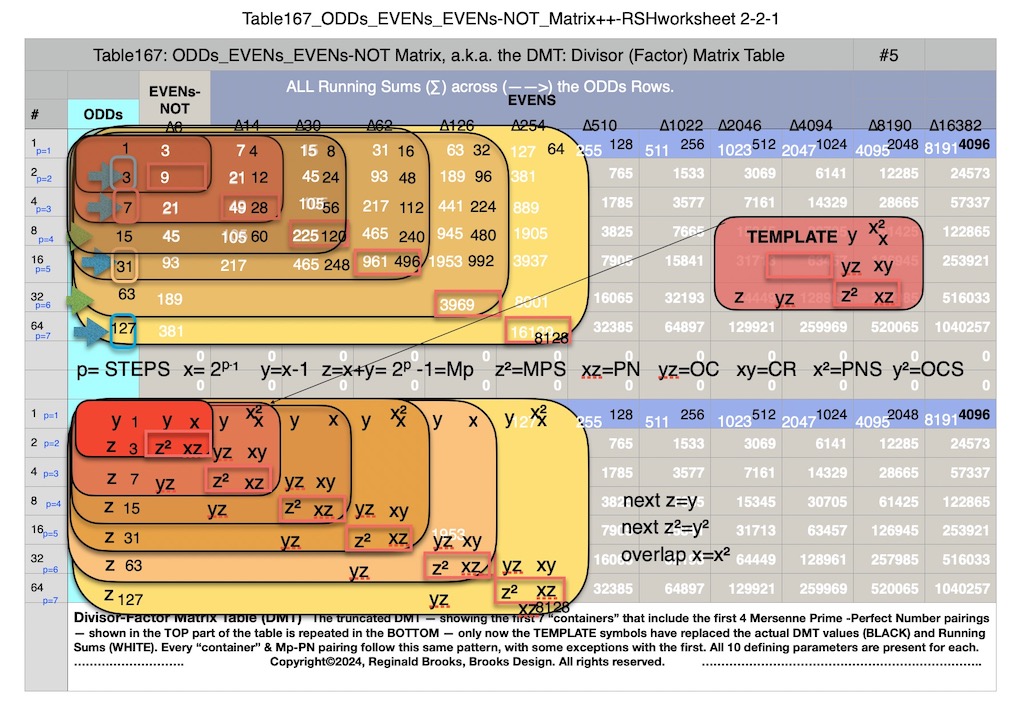
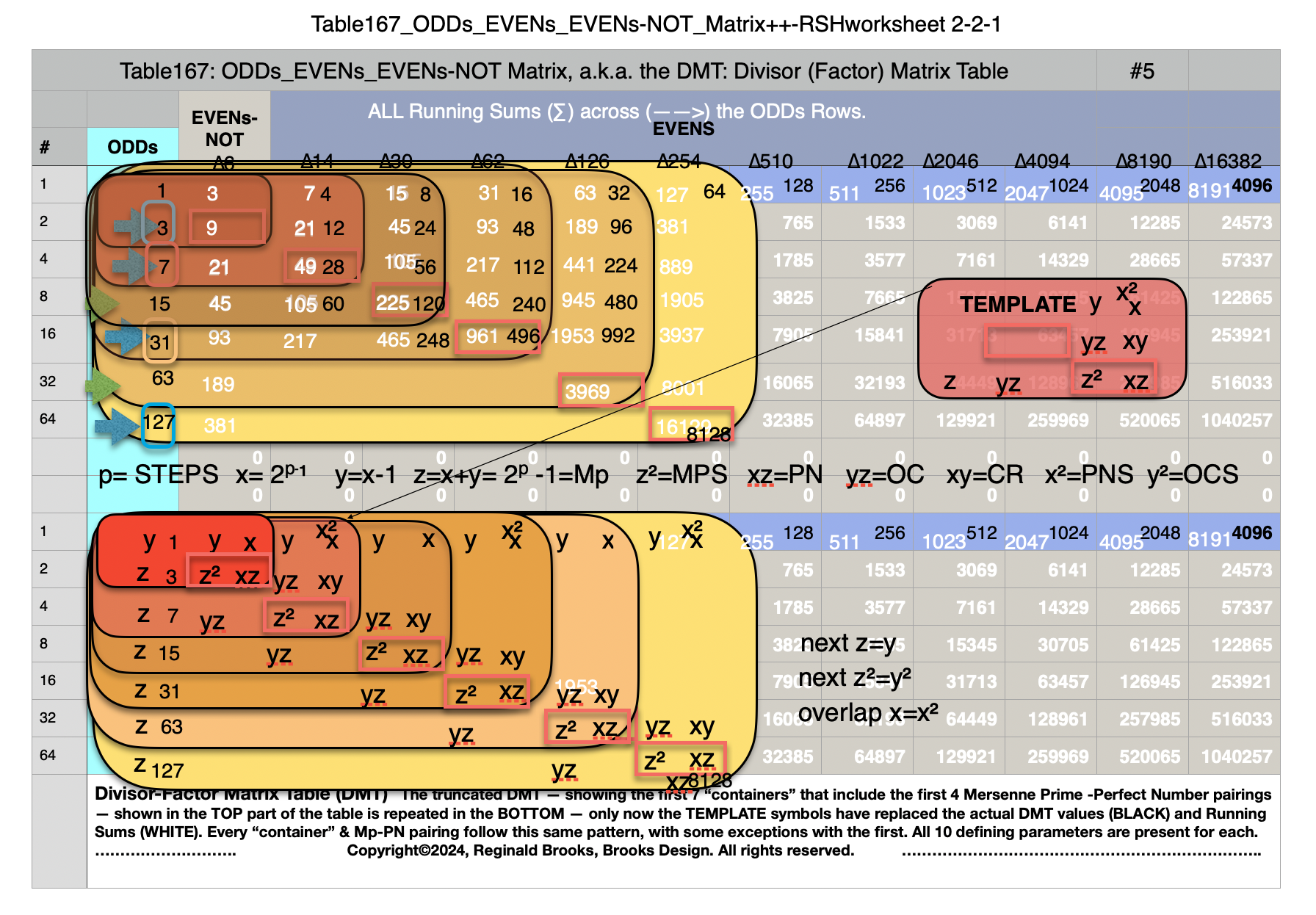
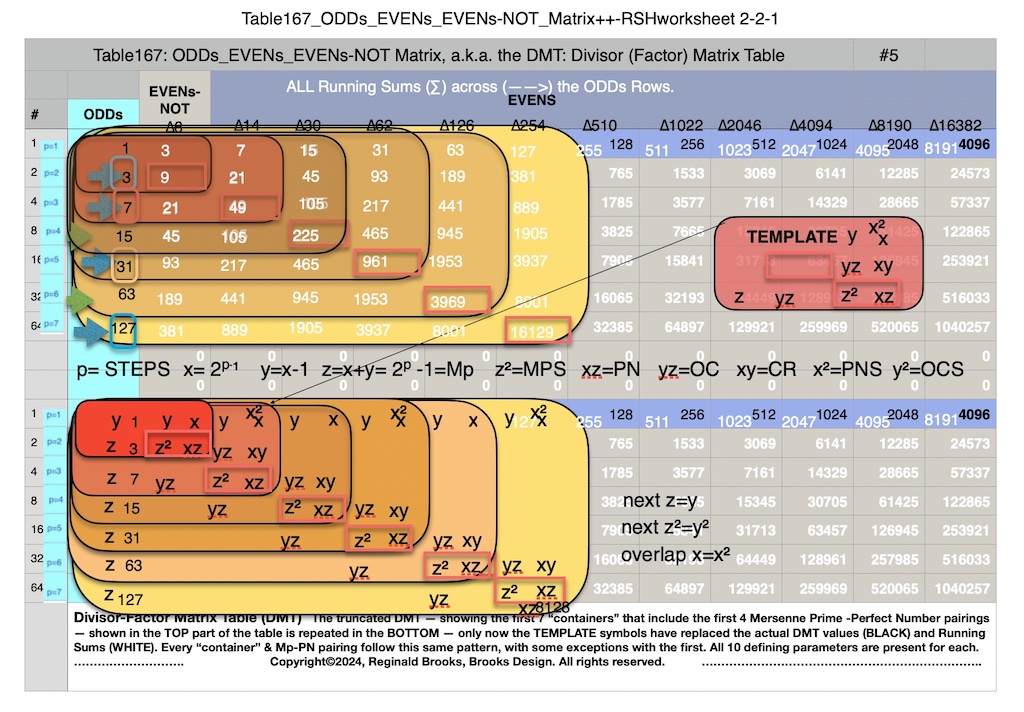
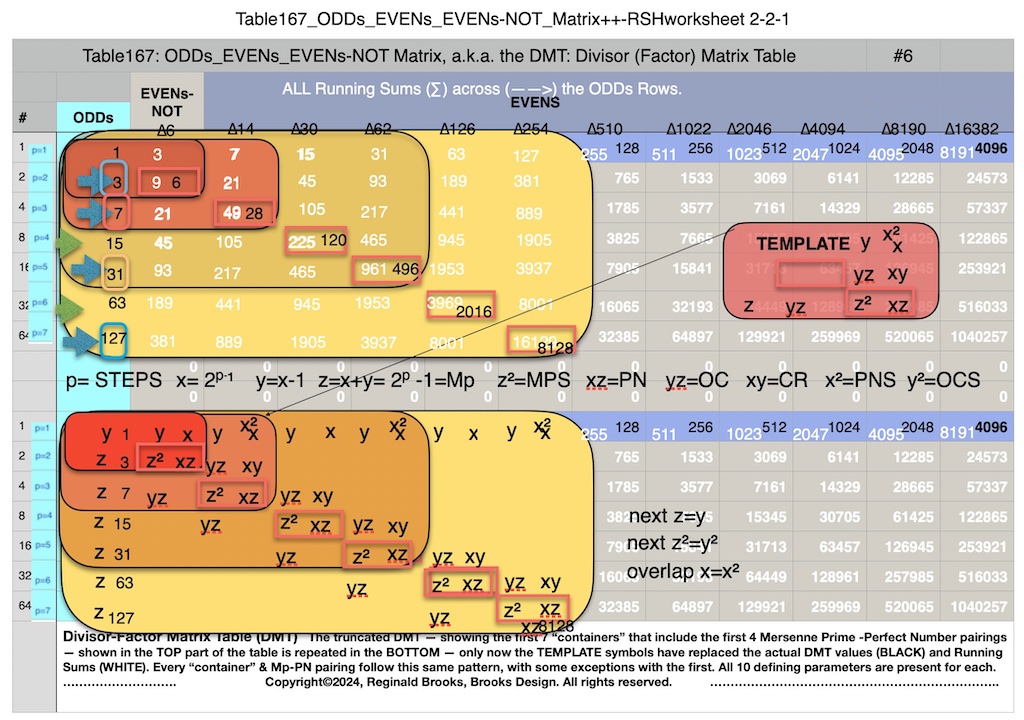









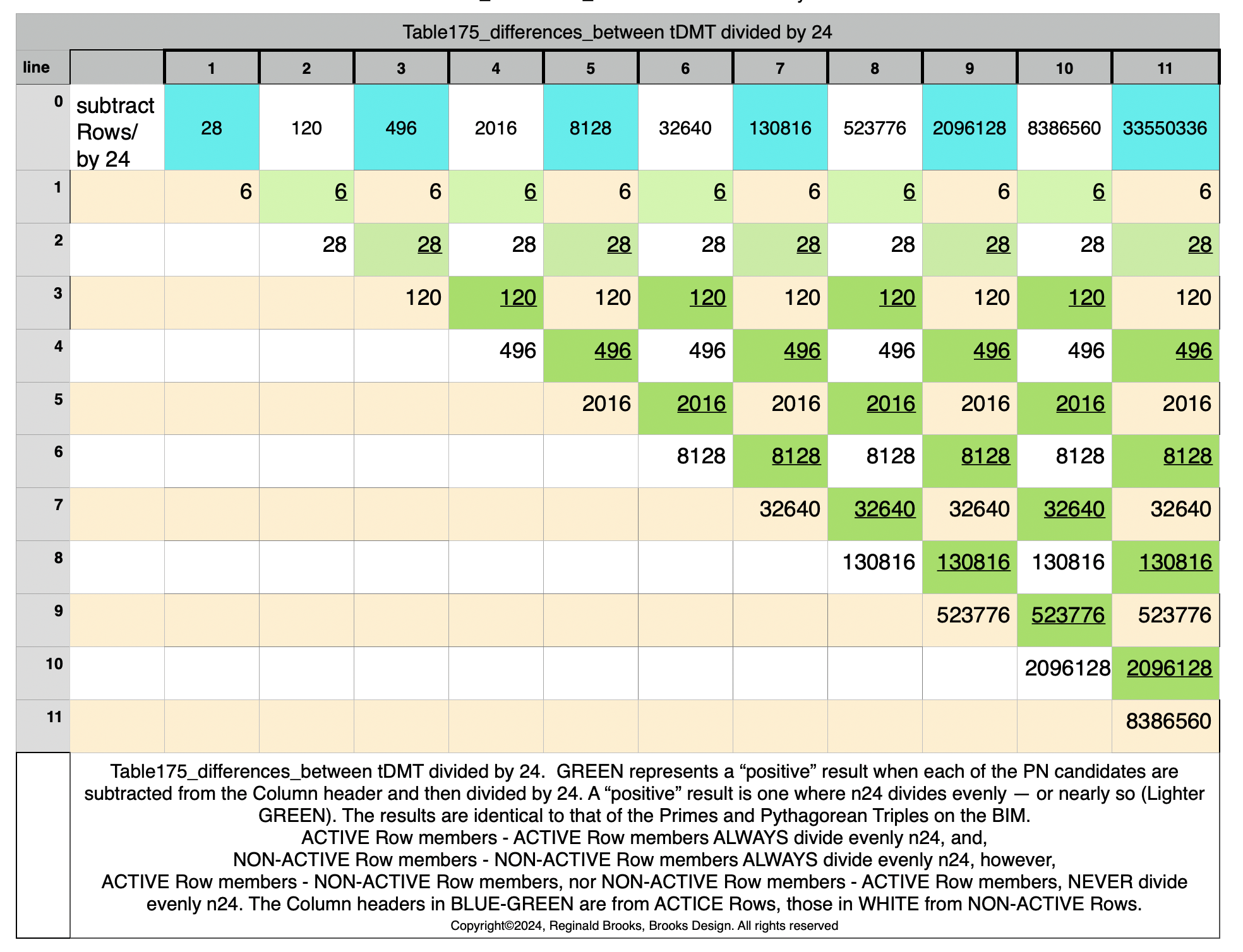
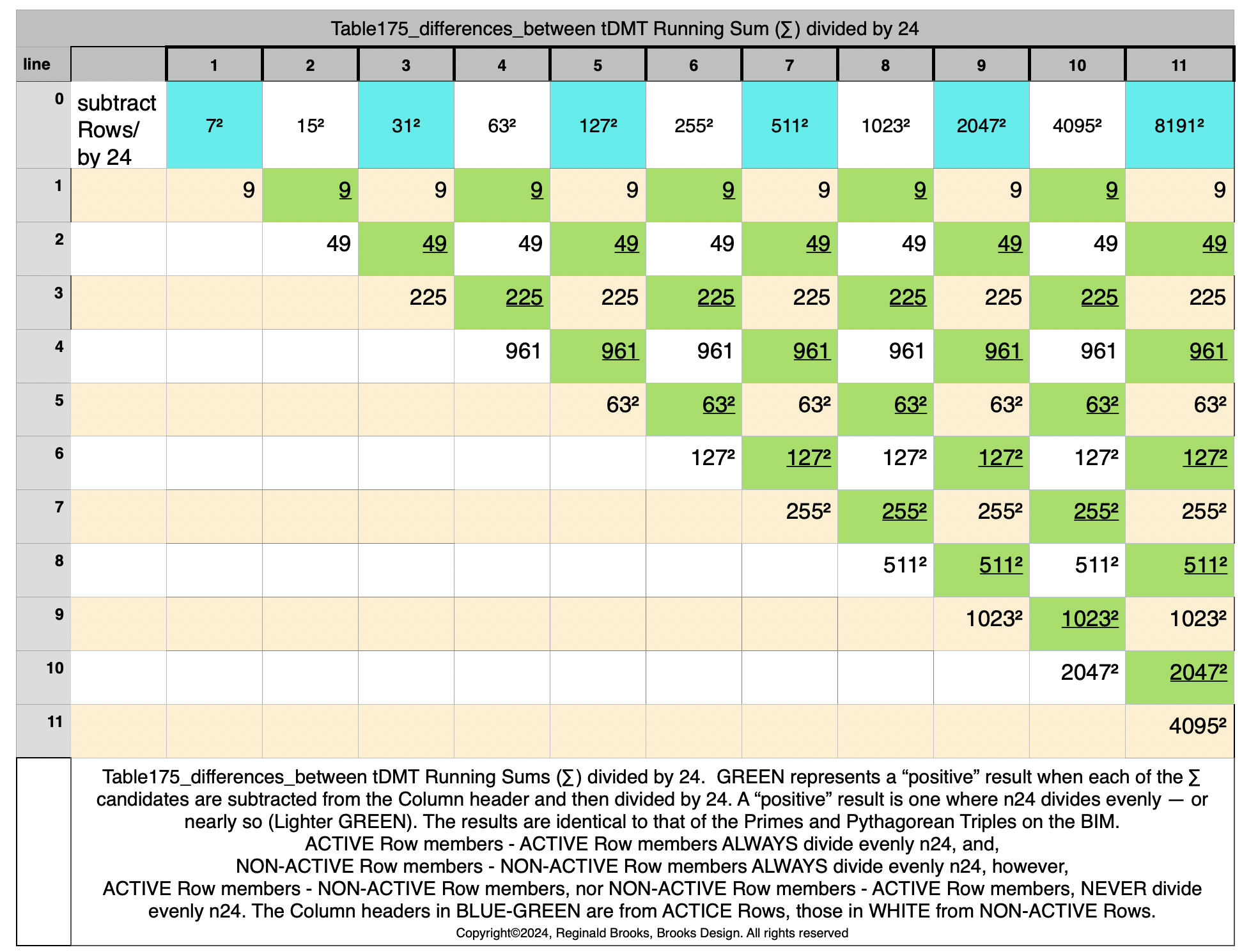











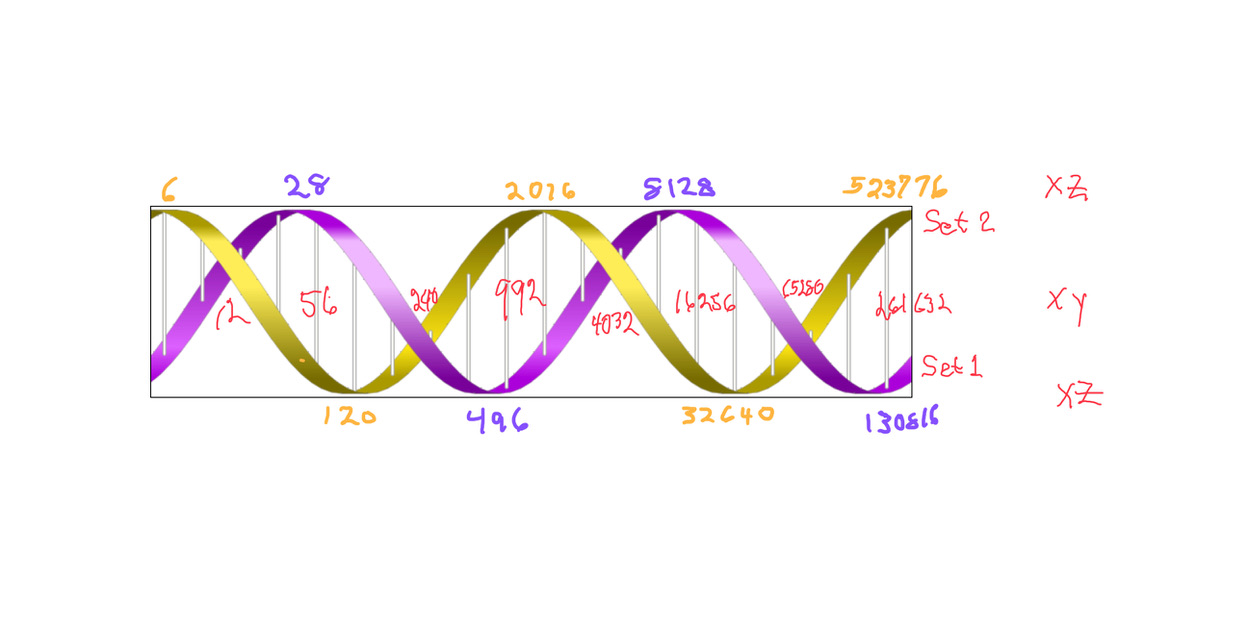
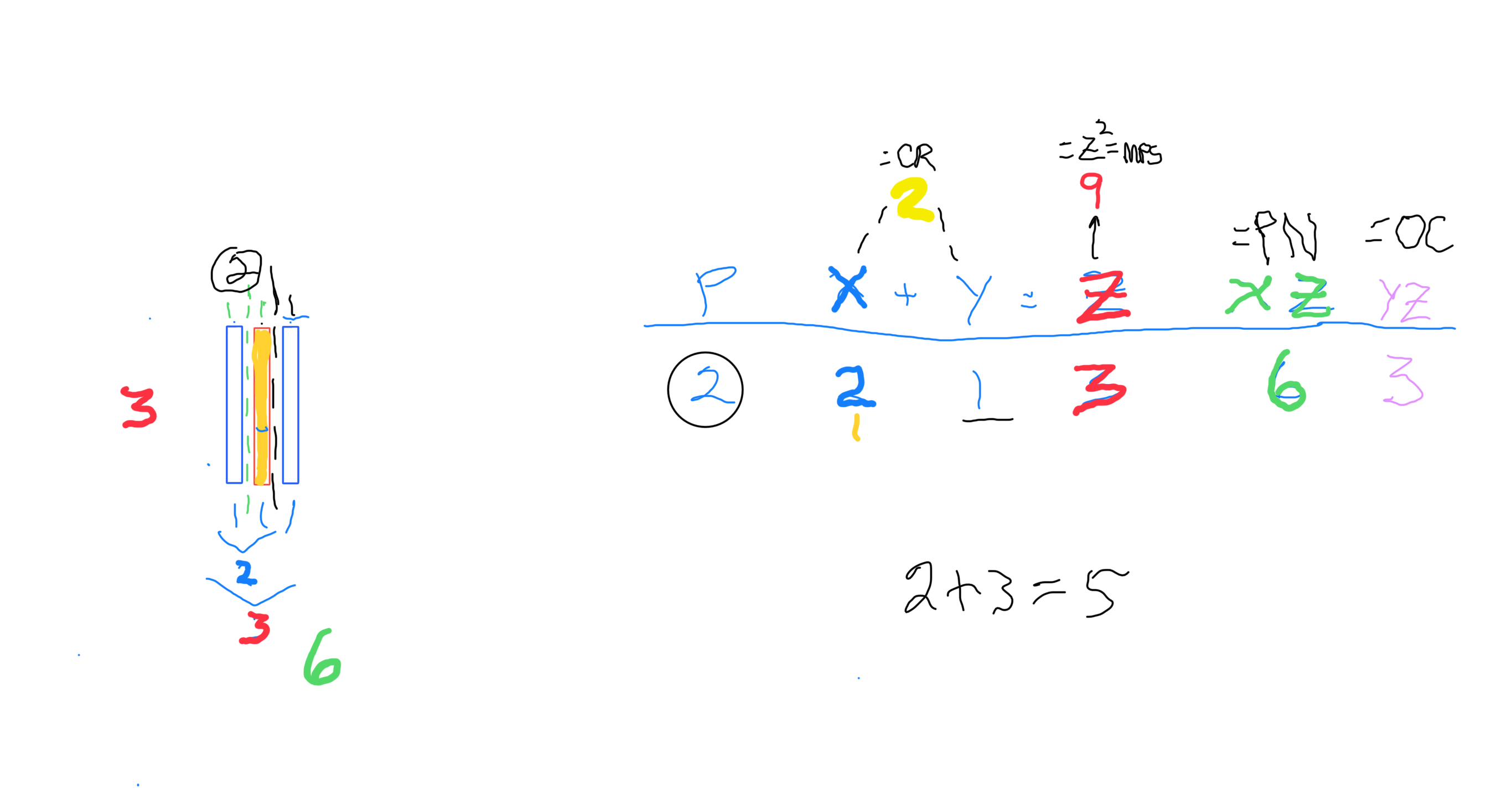
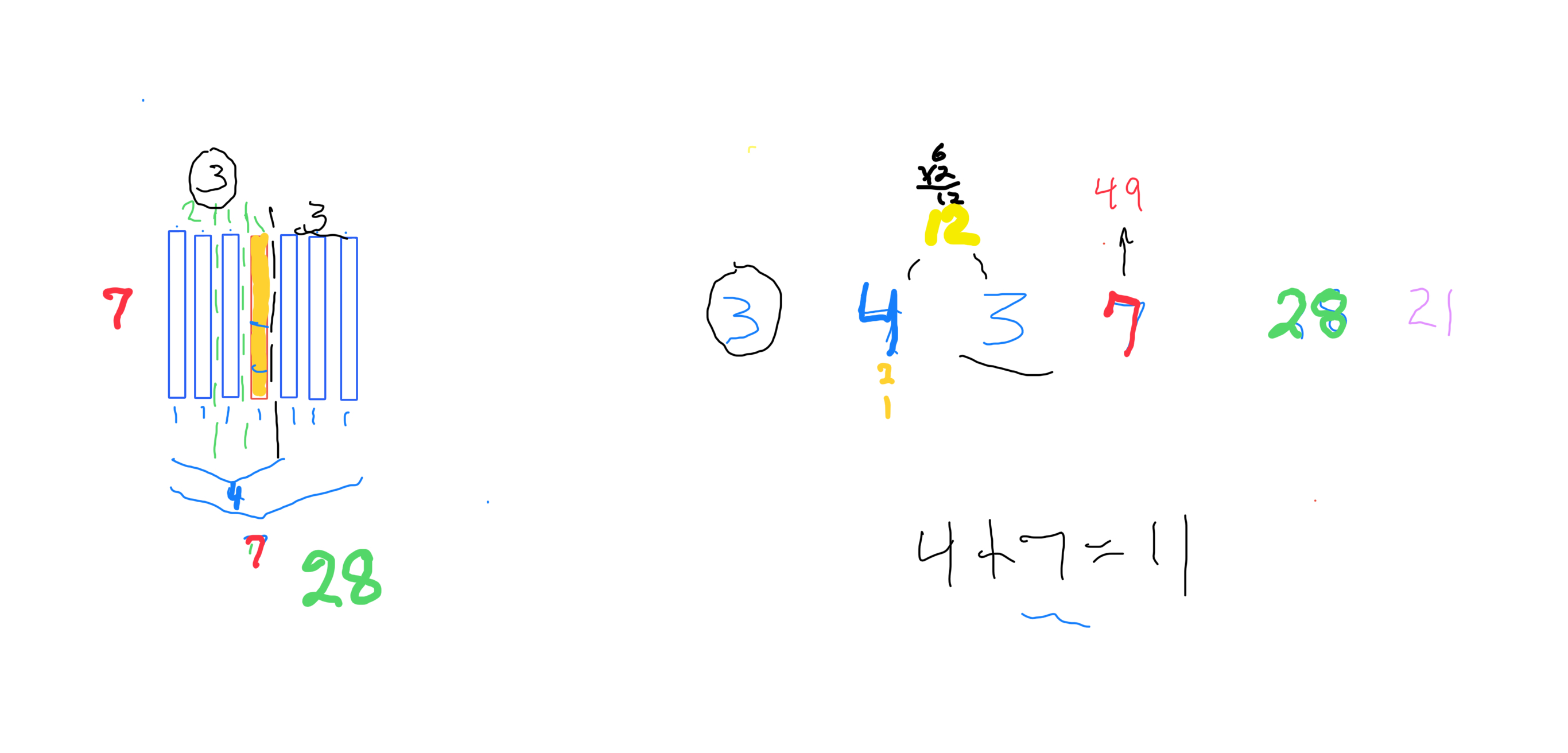
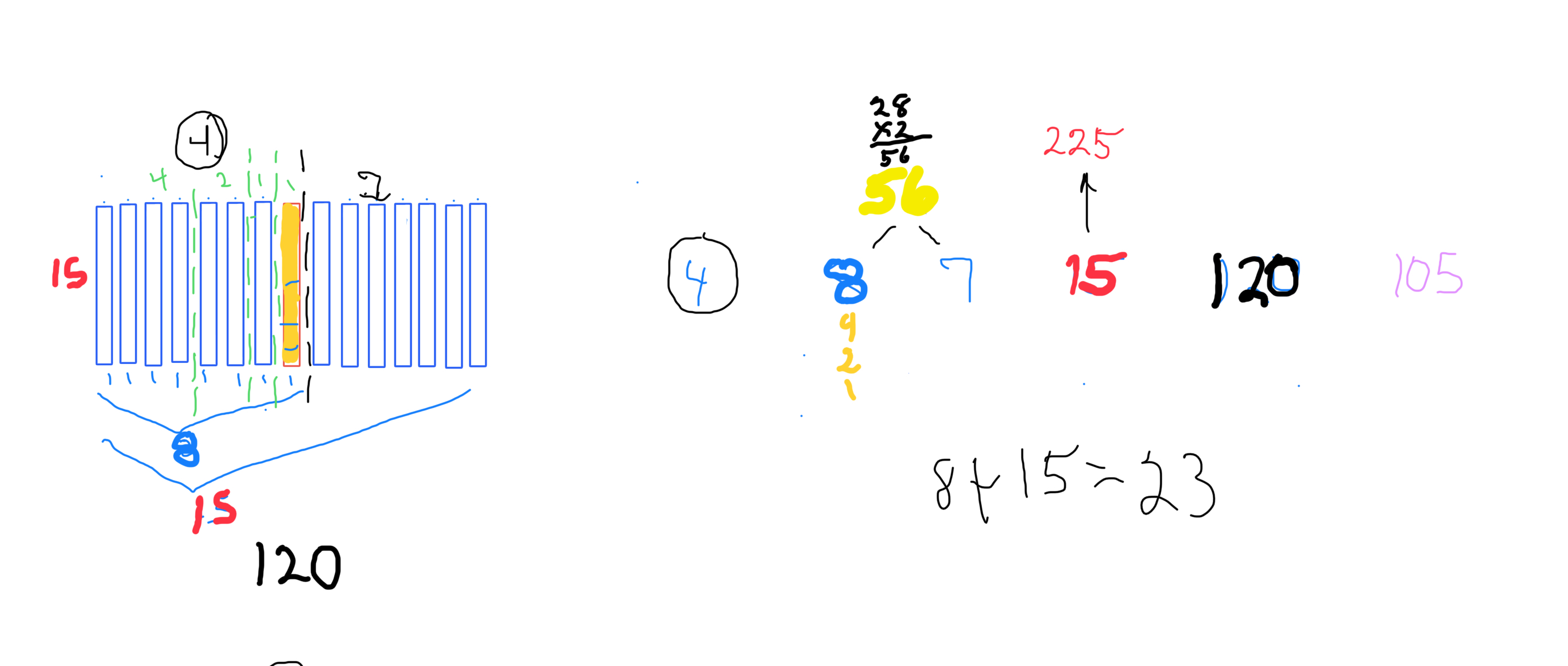
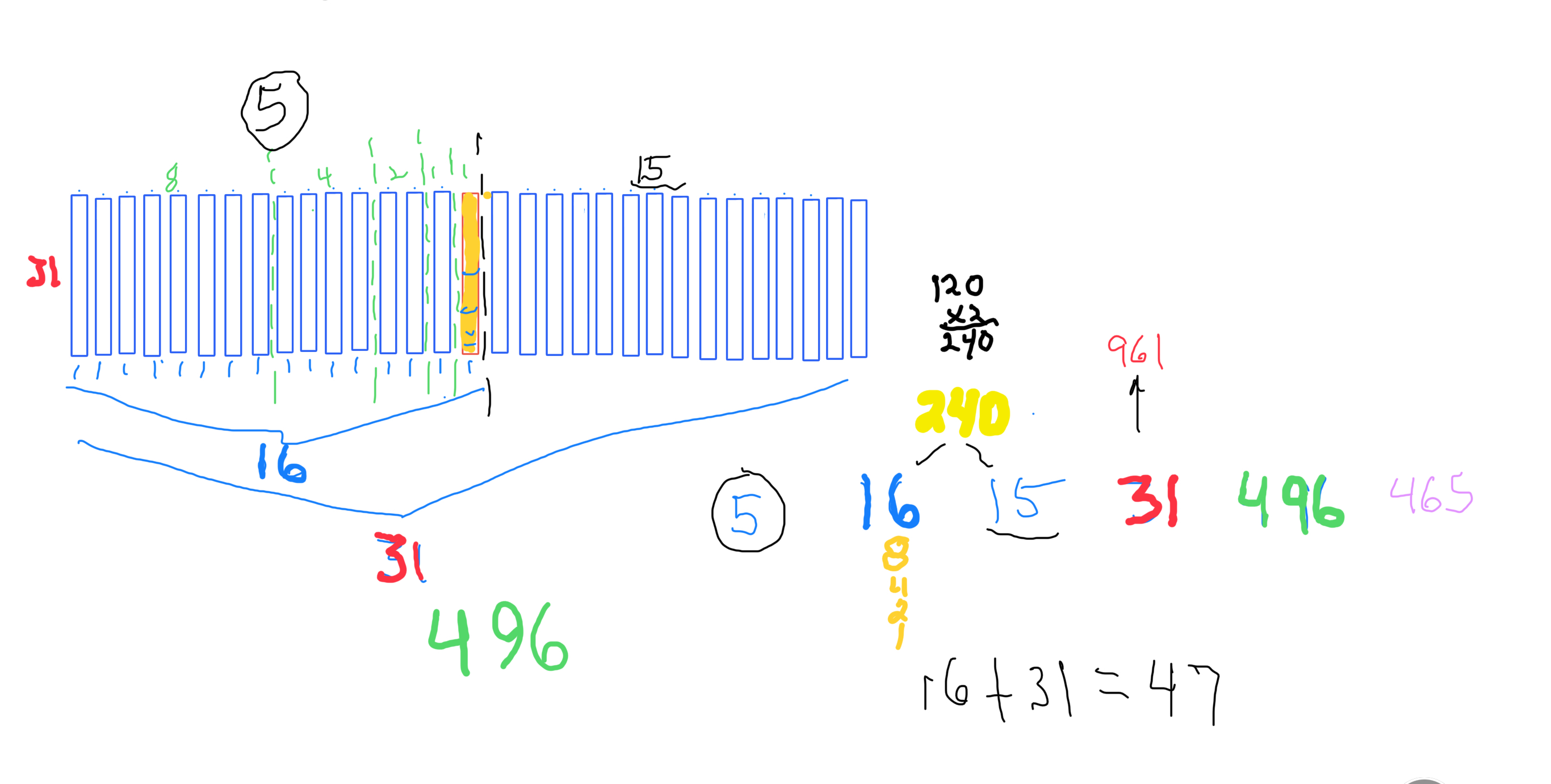
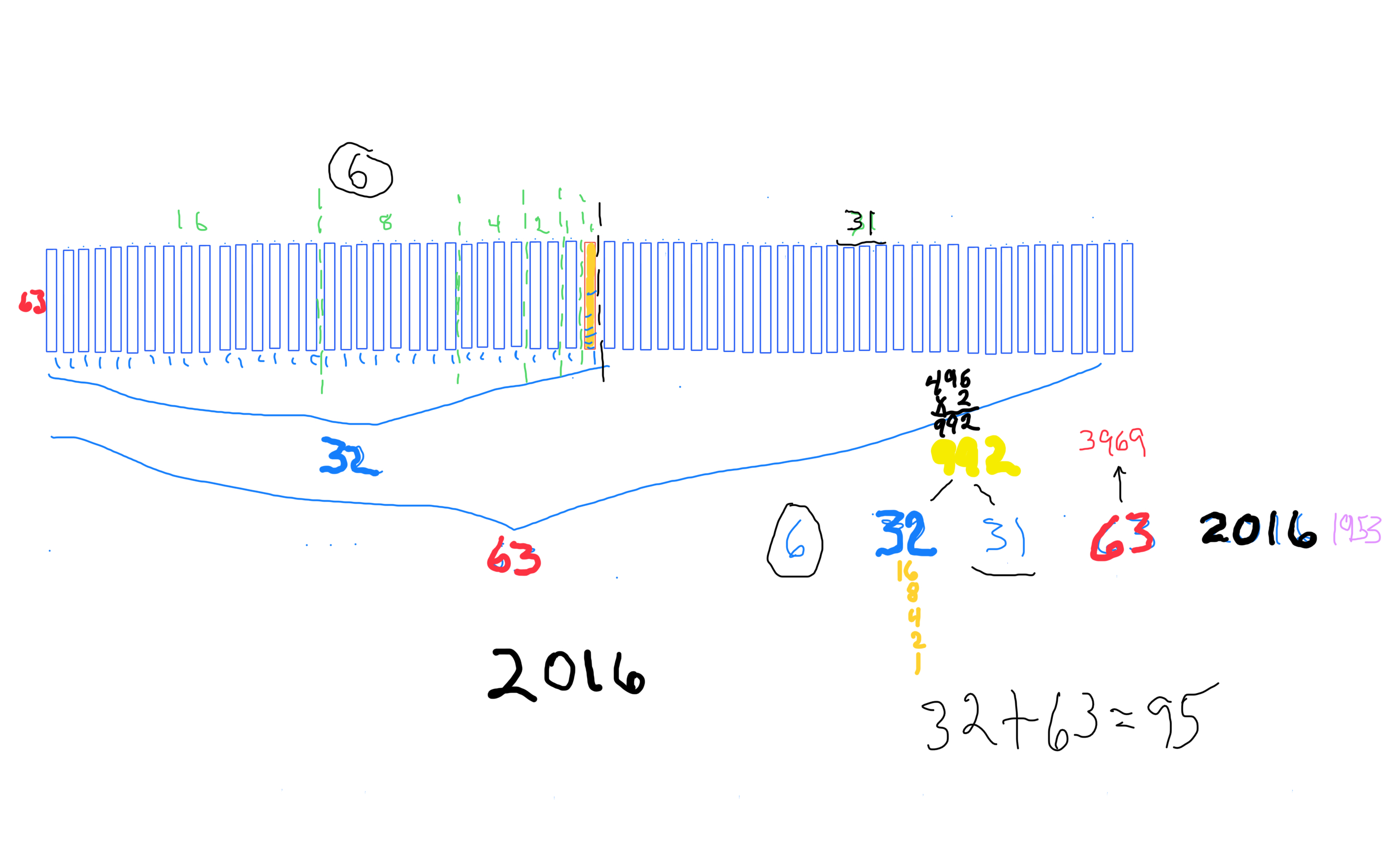
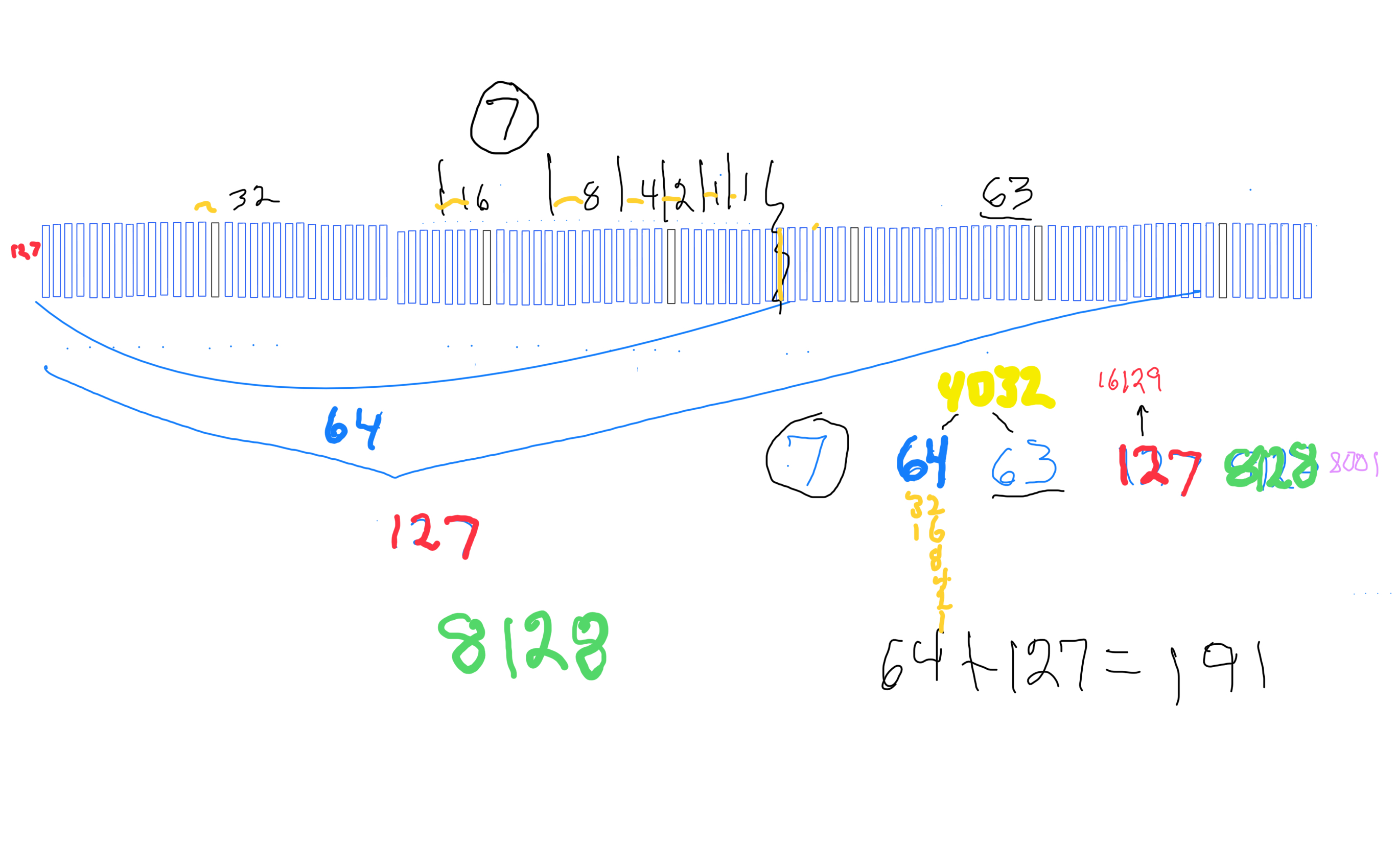
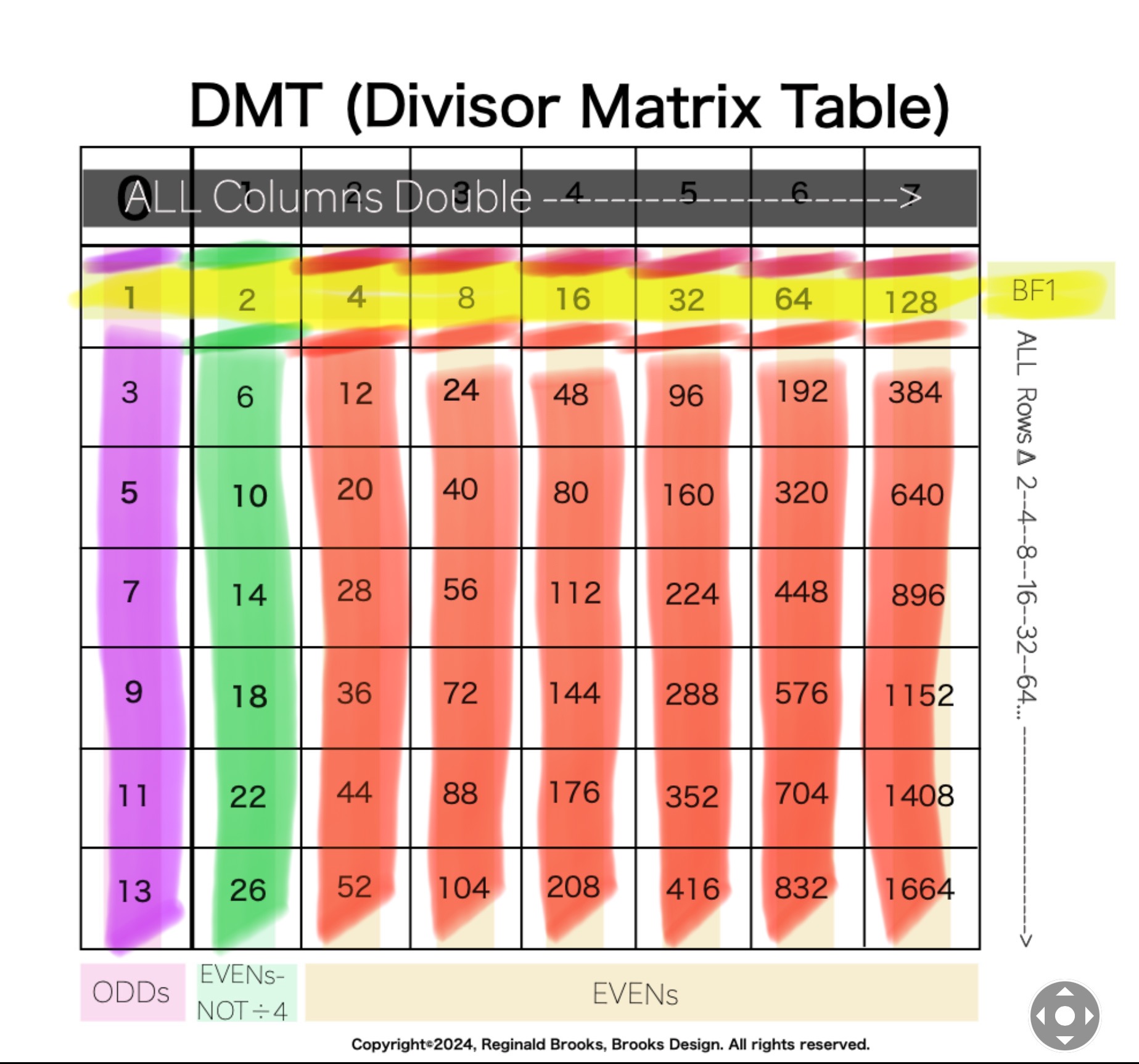

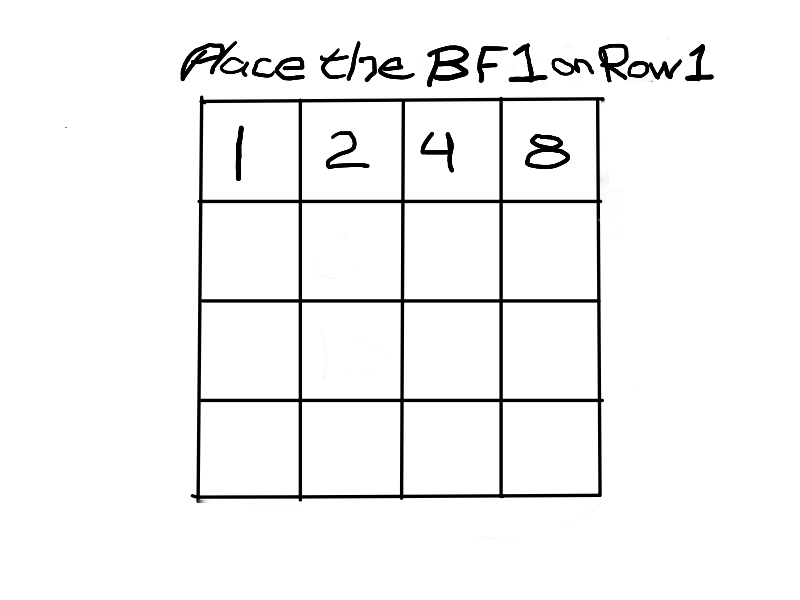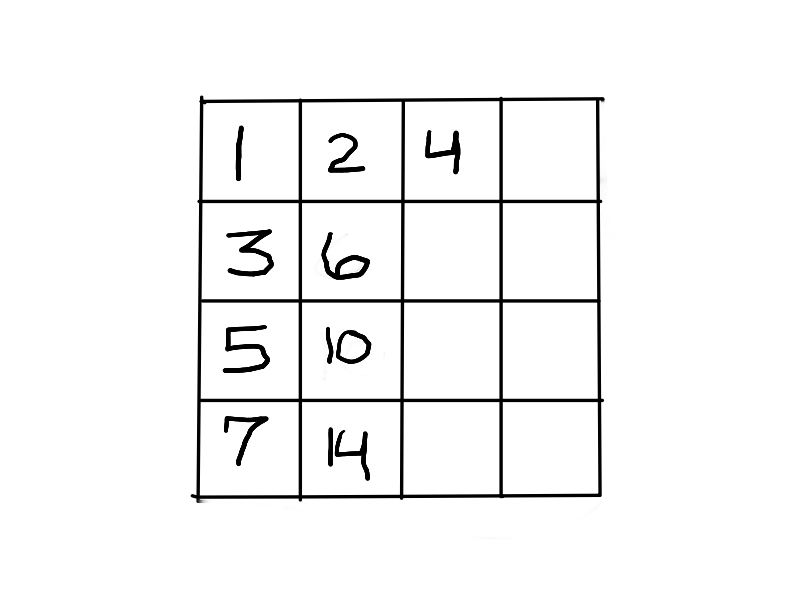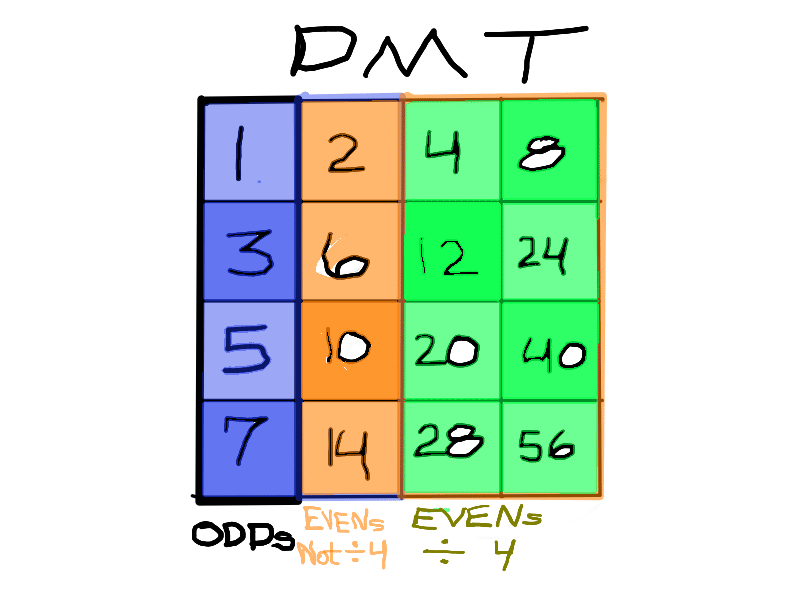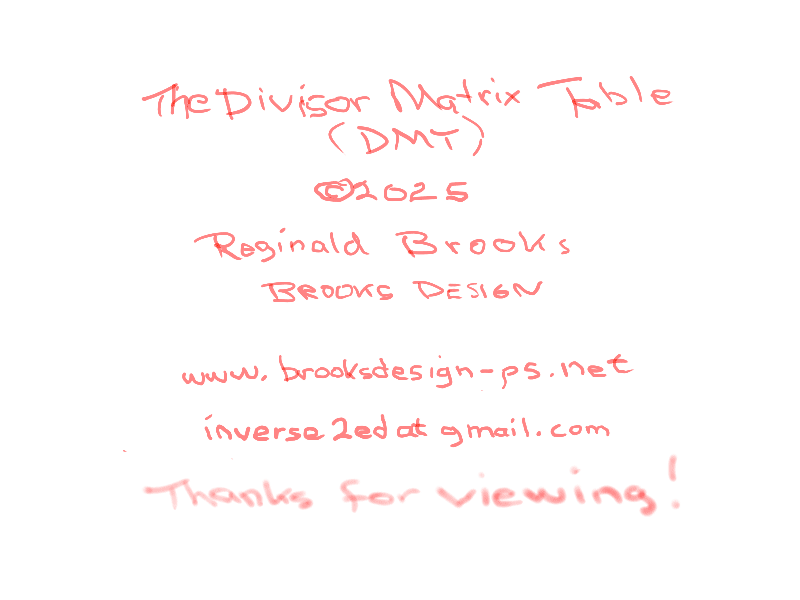
+.gif)