TPISC_III_BIMtree, copyright 2017, Reginald Brooks. All rights reserved.

TPISC III: Clarity—Simplified — ToPPT

~(Tree of Primitive Pythagorean Triples) ~

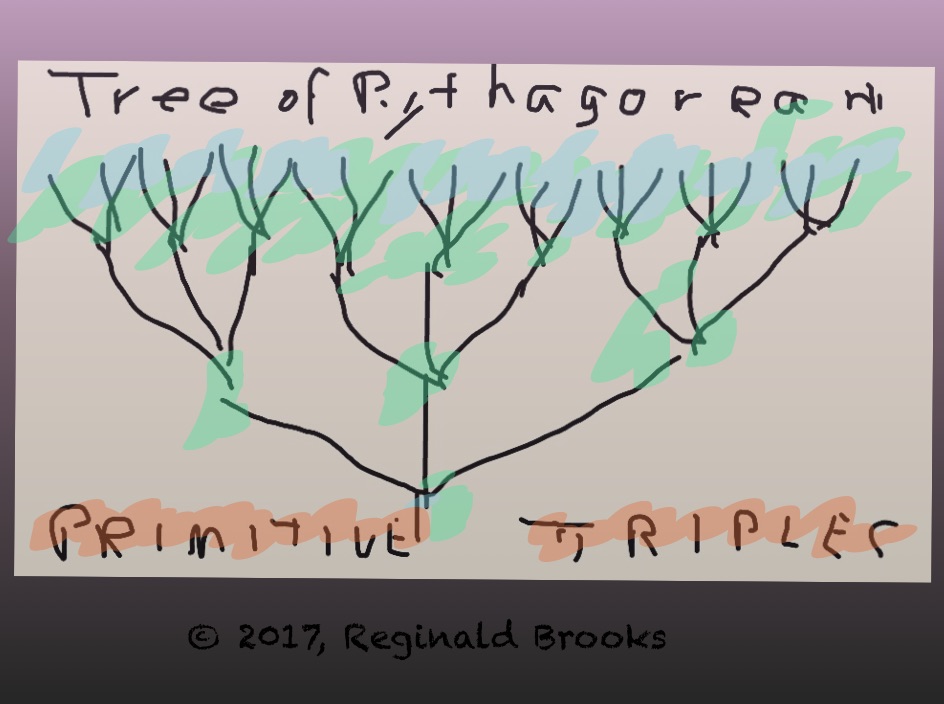Fig.0 "Tree of Primitive Pythagorean Triples, ToPPT"

~(Tree of Primitive Pythagorean Triples) ~ForwardA Pictoral Overview!I. IntroThe MathspeedST Supplements:II. BBS-ISL Matrix = BIMA. Introduction to BIMB. Number Pattern Sequences (NPS)C. MathspeedSTIII. TPISC: the Pythagorean—Inverse Square ConnectionA. TPISC I: BasicsB. TPISC II: AdvancedC. TPISC III: Clarity—Simplified—ToPPTThe BIM is the geometry defining SpaceTime!IV. ToPPT: LayoutA. Structure: Outward = BRANCHES (TIERS)B. Structure: Across = CLUSTERSC. Definitions and ReferencesV. ToPPT: LinkageA. Outward: Branches — TIERSB. Across: CLUSTERSTable 2u."BIM tree": Every CLUSTER consists of an UPPER, MIDDLE, and LOWER PPT. The f-value of the MIDDLE PPT of a given CLUSTER is IDENTICAL to the previous MIDDLE PPT in the CLUSTER before. The UPPER & LOWER f-value is calculated as : f=p + ∆p/2. Every CLUSTER follows this NPS. Follow the UPPER & LOWER. See Tables 2e,g,j,k & l for examples of √(8A+ƒ2)=ƒ~u/l-next~.C. Specials: Pythagorean, Middle & Plato BranchesTable5b." BBS-ISL_Matrix-FPS": Factor Pairs Sets and Row & Column values (lower half: 35x35)VI. SummaryVII. ConclusionVIII. ReferencesIX. AppendixA. Appendix A: Fully Extended Dickson Method Equations for TPISC III, IV and V.ADDITIONSCOMMON EQUATIONS REFERENCING IMAGES FOCUSING ON AREAS:CORRECTIONS:B. Appendix B: Step-by-Step Tutorial on making the 5th Tertiary Branch of the ToPPT.X. LINKSHighlight Interactive BBS-ISL Matrix at:BBS-ISL & TPISC Resources at:BBS-ISL & TPISC Media Center at:Interactive Matrix pages at:more...

Forward

1 banana, 2 banana, 3 banana, 4 … and there’s so much more!

A simple curiosity on how even simpler Whole Integer Numbers (WINs), when squared, form a law that rules the Universe — indeed, SpaceTime (ST) itself — has been a source of awe and wonder for quite some time. This is the Inverse Square Law (ISL).

The “inverse” means it’s per area. When the WINs are squared, you get the area.

The forms and forces of Nature obey the ISL. The initial concentration of an impulse or influence of energy dissipates in a known manner as it expands out from its source. A wonderful and ubiquitous law in forming the ST that builds the Universe. And it doesn’t even need to travel to get there…it is known!

Now, on top of this beautiful law and all the magnificent forms and expressions it can offer, comes yet another sublimely beautiful law — or theorem — that also relates areas to significant form — the Pythagorean Theorem: the long, hypotenuse side squared = the sum of the two squared shorter sides of a 90°-right triangle.

When these triangles are made solely of WINs, we have Pythagorean Triples (PTs).

The PTs are a major subset of the ISL and as such are both infinite in number and ubiquitous in distribution along with the ISL. Their structural beauty lies in the fractal-nodes of slight asymmetry they give to the expanding expression of the ISL. They give new forms!

Not only can these PT fractals be located throughout the ISL Matrix, together they form a linked structure relating all the parts to the whole, in the form the Tree of Primitive Pythagorean Triples (ToPPT).

This clarity and simplification of form has become the focus of this (my) work. The non-isosceles right triangles, rectangles and ovals of the ToPPT join with the isosceles right triangles, squares and circles of the ISL to generate our ST Universe — giving expression to the Universal mathematical constructs.

3 potato, 4 potato, 5 potato squared …

~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~

Things you might want to know:

The image (Fig.0) of the Tree of Primitive Pythagorean Triples (ToPPT) on the top cover is, of course, WRONG!

It's what we want to see — a tree organized into smaller and smaller growth shoots. Just like a real tree!

The actual ToPPT is just the opposite!

Each Tertiary/Tier Branch is composed of larger and larger growth shoots — Pythagorean Triples (PTs).

The "trunk" is actually the smallest PT in the whole ToPPT!

Fig.1. ToPPT 1.1

So what! Why is this important?

As SpaceTime (ST) unfolds — repeatedly as pulse-propagating ST units — it does so from its infinitely small (Singularity) beginnings outward to its infinitely large fulfillment. It does so as the Inverse Square Law (ISL) informs its every space and time disposition — jointly as ST.

The ISL is based on the AREAS of pure Squares and Circles as depicted in the BBS-ISL Matrix (BIM for short), utilizing simple Whole Interger Numbers (WIN) …1,2,3,...

Thus one (1) and two (2) WINs gives us perfect Circles and Squares.

What of three (3)?

Well, three (3) WINs gives us a Triangle and when they form a non-isosceles 90°-right triangle, we have a PT! As TPISC I and II have shown, every possible PT is found on the BIM — each being ½ of a Rectangle (non-square)!

Not only are they ALL present, but — as shown in TPISC III — they are ALL connected and ultimately derived from the first and smallest PT — the 3-4-5 PT — as revealed in the ToPPT.

(NOTE: Primitive PTs, PPT, are unique. Each has multiple enlargements of itself as non-Primitive PTs, nPPT.)

Again, so what! Why is this important?

The PTs are a BIM subset of fractals that introduce a bit of asymmetry into the otherwise perfect symmetry of the Squares and Circles. They introduce a type of bilateral symmetry in the form of non-isosceles 90°-right triangles — that when mirrored form non-square Rectangles. They do so at what at first glance appears to be in a random, albeit ubiquitous, manner. It will be the subject and goal of this work to show just exactly how un-random, completely inter-related each PT is throughout the infinitely expandable BIM!

The BIMtree gets larger and larger with growth!

The internal logic of the BIM and BIMtree is a blueprint embedded in ALL ST and its expansion.

As shown in LightspeedST and MathspeedST, it is part and parcel of ST itself and thus, whether or not its information — its geometry — travels at or faster than the speed of light, is irrelevant!

Irrelevant as it is already ubiquitously known — it does not travel! Once the seed of ST begins, the geometry of its expansion is automatically, simultaneously and ubiquitously known!

In fact, light itself — being born of ST itself — has a built-in and constant speed limit c, the velocity of light = the formation velocity of ST!

So how does the BIM and BIMtree help us define the Universe?

The details will be presented in TPISC IV and V, but for now, let's suggest the following conjecture will be paramount:

The Double-Slit Experiment & Quantum Entanglement Conjecture (DSEQEC): Two sides of the same coin.

Aside from the more modern dilemma of Dark Matter and Dark Energy, there are two major — and largely unanswered — questions that have historically persisted to this day at the heart of the Standard Model and its description by Quantum Mechanics: the Double-Slit Experiment and Quantum Entanglement.

The DSEQEC states that the two are really just two sides of the same coin. Both being explained by the BIM and BIMtree.

The geometry of ST formation generates descriptive parameters referred to as quantum numbers or their quantum number state — unique identifiers for each and every subatomic particle. These wave-particle ST units exhibit unusual and non-intuitive behaviors that reveal a connection to each other below the physical reality we observe. The Conjecture is that that underlying connection is the BIM and BIMtree geometry that informs the creation and disposition of ALL ST — including their quantum number state identifiers.

A bit more of this teaser is presented in the Conclusion, but really is the subject of TPISC IV and V.

A Pictoral Overview!

BIMtree-ToPPT-Areas Figure-Intro (AREAS)

See the slideshow at 12 Easy Pieces (AREAS)

I. Intro

Art & Science — but two sides of the same coin —are the very currency of the of our existence. The former gives us experience, the latter, numbers. Yes, numbers — simply, whole integer numbers — that fundamentally represent quantities over a time interval. They are the both the ultimate abstraction and the most “figurative” and literal description of that that we know.

Substance:

Part I

Below that layer of physical objects, lies an even more fundamental number-based reality. Is this the fractal? Yes, but what lies below?

Instead of deducing from larger generalities down to the specific, what if we could somehow get a grasp of the core, fundamental linkage between simple numbers and their relationships (connections) to each other — self-similar, re-iterative number-pattern sequences (linkages) that expand outward to infinity. Would this not be the definition of a true and pure fractal right down to its core?

Let’s back up for just a second. Space-Time (ST), given its most visualized form by Einstein, is a non-static, geometry-based medium — not a background or substrate upon which the Universe is embedded, but rather all objects — matter & energy ( particles and fields) — are a manifestation of that ST medium. ST that is informed by and responds to the energy density in which it is found. ST visualization is deeply rooted in the mathematics — the geometry of numbers — that informs it. As first described by Newton, that gravitational force follows the Inverse Square Law, as does Electromagnetism. In fact, a Universal Law of Nature is that all energy, all light, sound, … follows the ISL.

Wow! Such a Universal Law! Surely, it must be at the base-core of any ST formation as well.

Any description of the Universe incorporating the matter and energy of ST absolutely must have the ISL incorporated within.

If one where to lay out the very, very simple number relationships of the most basic and fundamental description of the ISL in a simple grid form, what does one come up with? The BBS-ISL Matrix, BIM for short, describes, in a simple, infinitely expanding grid, the linkages of the numbers that makeup the mathematical description (equation, ISL=1/r²) of the ISL.

It is the core, fundamental, re-iterating fractal generator of the ST Universe. And it is all based on simple, whole number linkages!

Part II

BIM is based on simple, pure squares and circles. It is the larger symmetry.

Enter non-square rectangles and their equivalent ovals. Enter the Pythagorean Triples (PT); non-isosceles, right-triangles composed —of course — of strictly whole number integers. .

Turns out that every possible PT — and there are an infinite number of them — is located on a specific Row (and Column if you look at the other symmetrical side) on the BIM. Every one!

It also turns out that each PT Row has within it the a², b² and c² squared sides of the Pythagorean Theorem, as well as the Area (x4) and a whole host of other detailed number information describing that particular a-b-c PT uniquely situated on its Row!

Visually, more than just numbers occupying the grid cells on the BIM, the ACTUAL PT triangle is present — on rotation — on that ROW. The PROOF is easily seen as well. I say PTs plural, because each PT when mirror flipped gives 2 PTs, and because they are both symmetrically duplicated in the other half of the symmetric BIM, the total equals 4 PTs visualized for each PT described. This is what “TPISC I (Basics)” shows, while “TPISC II (Advanced)” demonstrates the PROOF when the PTs are slid up to the top.

Fig.2 "TPISC I" acrylic on canvas 48”x56"" 2016

Fig.3 "TPISC II" acrylic on canvas 48”x56” 2017

Part III

The Tree of Primitive Pythagorean Triples dates, in part, to Pythagoras, and later, Plato, though reference to Pythagorean Triples is found in Babylonian Times, and throughout ancient cultures.

As simply defined in Wikipedia:

"In mathematics, a tree of primitive Pythagorean triples is a data tree in which each node branches to three subsequent nodes with the infinite set of all nodes giving all (and only) primitive Pythagorean triples without duplication.

A Pythagorean triple is a set of three positive integers a, b, and c having the property that they can be respectively the two legs and the hypotenuse of a right triangle, thus satisfying the equation a² + b² = c²; the triple is said to be primitive if and only if a, b, and c share no common divisor. The set of all primitive Pythagorean triples has the structure of a rooted tree, specifically a ternary tree, in a natural way". Wikipedia: Tree of primitive Pythagorean triples

Within BIM, not only is every possible Pythagorean Triple (PT)— and it proof—found, but the ENTIRE ToPPT is wonderfully, logically and inevitably present from the Trunk to the infinite number of Tertiary Branches and the Branch Clusters that are splayed out across the expanding grid. The BIMtree, as it will be referred to, is a fractal data tree with very specific linkages both up and down the Branches, as well as across the 3-branch Clusters that form from each and every Tertiary Branch. The ENTIRE ToPPT is present on BIM as an inter-connected tree whose crown ONLY reaches further and further out to the infinite skies of Space-Time (ST) itself.

We demonstrate five (5) Tertiary Branches—i.e. 243 individual branches of PPTs—but the Number Pattern Sequences (NPSs) that define the fractal tree allow the tree to be enumerated to infinity. A clearer picture of the ToPPT has evolved with the BIMtree.

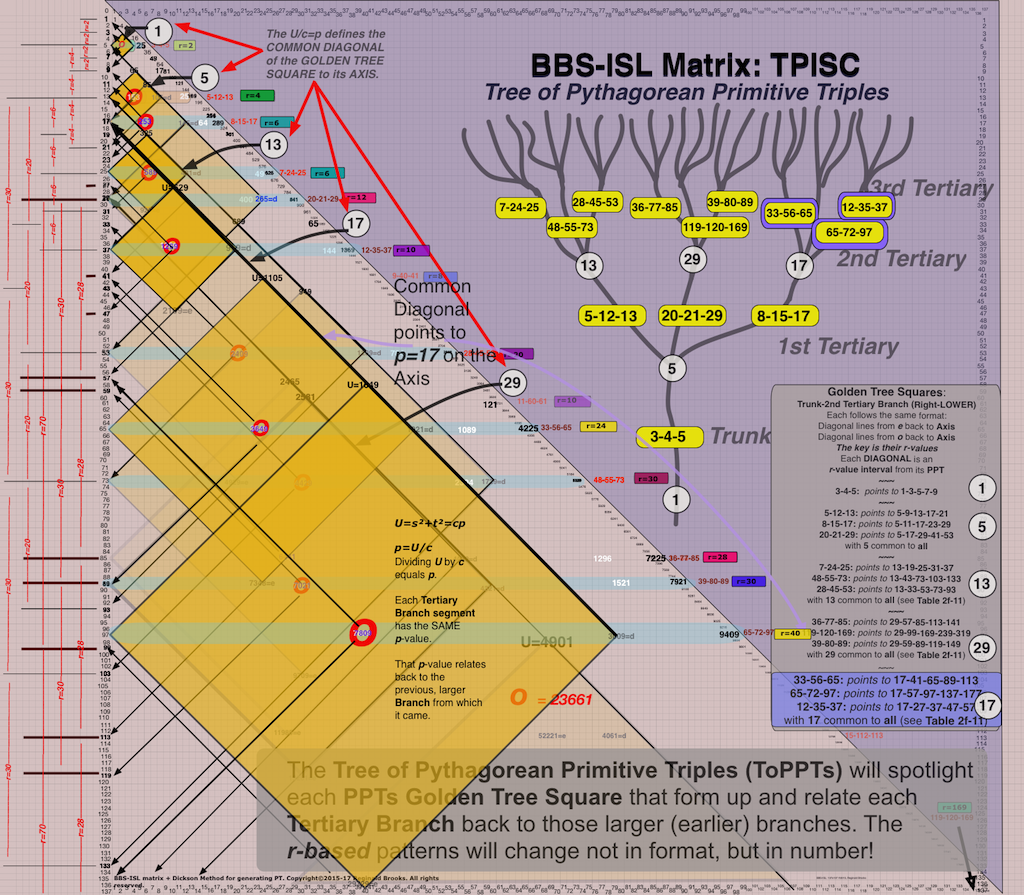Fig.4 "BIMtree_ToPPT" (preview of the 3rd Tertiary Branch Cluster. Clusters always have a common diagonal line pointing to their common p-value!)

Significance:

Where does this all go?

The BIM describes the ISL-defined ST structure of the Universe. But are pure squares and circles enough?

Enter the PTs. The non-isosceles, right-triangle PTs form non-square rectangles and ovals that inherently bring a different type-class of symmetry to the grid. Now, sprinkled ubiquitously across the infinitely expanding BIM, we have infinitely expanding (and linked), non-square rectangles and ovals of the PTs (Two PTs = 1 non-square rectangle).

The nodes form points of articulation throughout the ST forming framework of the BIM. In doing so, this change in geometry allows for specific — and always relatable — linkage back to the pure square-circle based symmetry of the BIM — giving a NEW fractal generator!

Thus, through entirely simple means, Nature takes the pure forms of squares and circles, combined with the slightly asymmetrical (i.e. bilateral symmetry) of the PTs, to form the infinitely rich structural ST that informs the Universe at large — that Dahlia blooming in your garden! Or should we say, that magnificent tree growing in ST!

As discovery gives to presentation, it is my goal to present this “linkage” in a form that both challenges and delights the curious viewer. A pictorial journey.

Before you start, the short video below will give you a very informative and helpful overview of just how the Pythagorean Triples are found, described and manipulated on the BIM.

BIM_FEDM(2017)_INTRO from Reginald Brooks on Vimeo.

The video gives a visual sequence to key PARAMETERS that anchor the "specific individual" PT to the BIM, as well as the "Universal" PARAMETERS that ALL PTs follow throughout the BIM.

Rather than trying to get all the exact details right now, this is presented here to provide you with an context overview to which you will build up your understanding as you proceed. Scan the video a few times for the general view — it really helps!

~~ ~~ ~~

You may find it helpful to keep these 10 points in mind while examining, exploring and discovering the BIM:

BBS-ISL Matrix (BIM) :

The BIM is fundamentally Inverse-Square-Law-related AREAS on a Matrix of Whole Integer Numbers (WINs).
Every WIN on the Inner Grid (IG) is simply the ∆PD-PD (or its square root derivative: Ax₁ Ax₂).
All PTs are simply AREAS on the BIM.
Every PT is simply two IG#s on a Row — mirroring PD#s.
The ToPPT grows as PT Composite AREAS form new PT AREAS.
All Exponentials are simply AREAS following diagonals on the BIM.
Every X² is an Exponential AREA on the PD.
All X^>2 Exponentials are IG# AREAS on a diagonal — some mirroring, some not, the PD#s.
Both PTs and Exponentials have Number Pattern Sequences (NPS) that map on the BIM.
The Axis (Ax), acting as Factor Pair Sets (FP or FS), complement the PD#s in defining the AREAS on the BIM.

BIM is the geometry defining SpaceTime!

The MathspeedST Supplements:

TPISC I: Basics

TPISC II: Advanced

TPISC III: Clarity & Simplification (ToPPT)

TPISC IV: Details

TPISC V: Exponentials

The BBS-ISL Matrix is a deceptively simple matrix grid built on the Inverse Square Law (ISL). The whole number integers — 1,2,3,… — that form the basis of both the PT and the BBS-ISL reveal many deeper inter-connections. These often non-intuitive inter-connections belie the more simple connections lying on the surface. Nature builds her amazing richness of complexities and inter-connections by the simplest of means. You don’t get much simpler than the quantities — as represented by the whole number integers — 1,2,3,….

The Dickson Method *(DM) — a simple algebraic method for generating ALL Pythagorean Triples (PTs) by** **Algebraic *CALCULATIONS — has become the Expanded Dickson Method (EDM) so as to be easily visualized on the BBS-ISL Matrix (TPISC I: Basics and TPISC II: Advanced).

The Dickson Method (DM) takes the even numbers — r=2,4,6,… — squares them as r², divides this by two as in r²/2, and from this result determines the sets of Factor-Pairs (F-Ps) that exist to form this result. These F-Ps are labeled “s” and “t.” Recombining r+s, r+b, and r+s+t gives the a-b-c, respectively, side leg values of ALL possible PTs! The DM uses the “x,y,z” symbol system to reconstruct the a² + b² = c² Pythagorean Theorem. The *EDM brings out several more inter-connections that become readily visible on the BBS-ISL Matrix.

~~~

New in TPISC III, IV and V, will be the Fully Expanded Dickson Method (FEDM). Expanding the connections on the BIM reveals the basis for the ToPPT and more!

My biggest tip:

If you are like me, it is often best to look over the Summary & Conclusion Sections first thing!

This gives you a larger context into which you may more profitably insert the content.

See the video montage on Vimeo.

II. BBS-ISL Matrix = BIM

BBS-ISL Matrix Arrow of Time Overview video on Vimeo.

BBS-ISL Matrix ArrowOfTime from Reginald Brooks on Vimeo.

A. Introduction to BIM

The simplicity of the BIM hides the richness within!

Basically, if you take the whole integer numbers, 1,2,3,.. as the Axis on a grid and establish the square values on the diagonal so formed, you have the basic of the BIM.

The Inner Grid (IG), is simply the number values of the cells inside. They are ALL derived from and reflect that Prime Diagonal (PD) that symmetrically divides the square into two equal and opposite triangles.

There are dozens of ways to fill in the IG numbers: perhaps the simplest is the difference (∆) between the PD numbers intersecting vertically from above and horizontally from the side, e.i., 5=9-4.

Another simple and useful method is to multiply the Axis number x 2 = value, and now sequentially add that value to each subsequent sum, ∑, as you proceed diagonally down the grid (parallel to the PD), e.i., Axis 1x2=2 value, add 2 to the running sum, ∑, starting with the first cell in the 1st diagonal parallel to the PD. (HINT: since the BIM is symmetrical, just follow the pattern on the Lower-Left side to keep it simple.) This gives 3,5,7,9,11,13,...

Now try it on the 2nd Parallel Diagonal. Axis number 2x2=4 value. Add 4 to the running ∑ starting with the first cell in the 2nd Parallel Diagonal. 8,12,16,20,...

And so on. That's it. It is truly simple. You can now apply either of these simple methods to make any size BIM from 0 to infinity (if you have the time...and space!)

The proofs are just as easy to see. See MathspeedST below.

more...

even more...

Fig.5 "BIM 5x5"

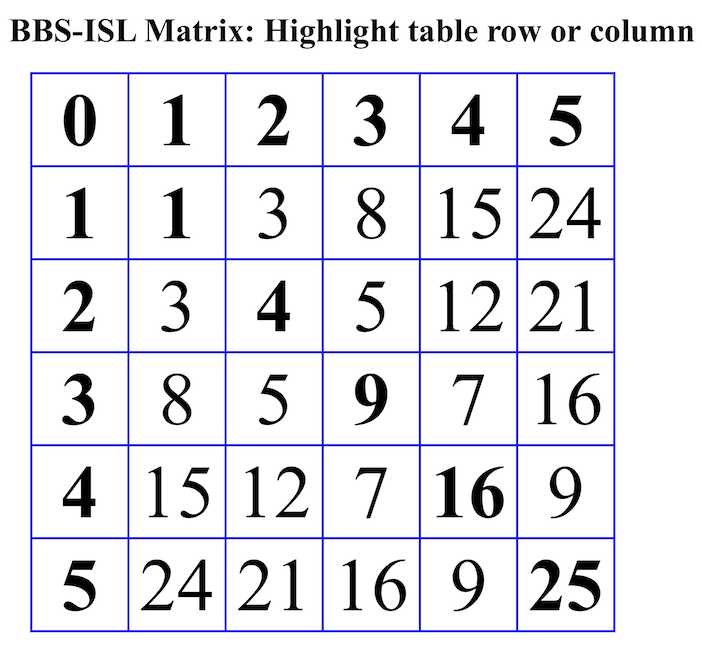Fig.6 "BIM 5x5"

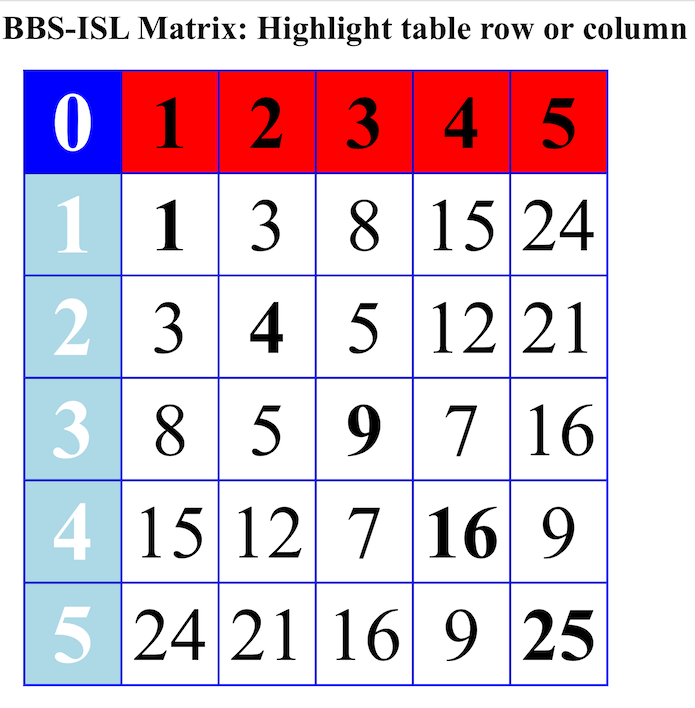Fig.7 "BIM 5x5"

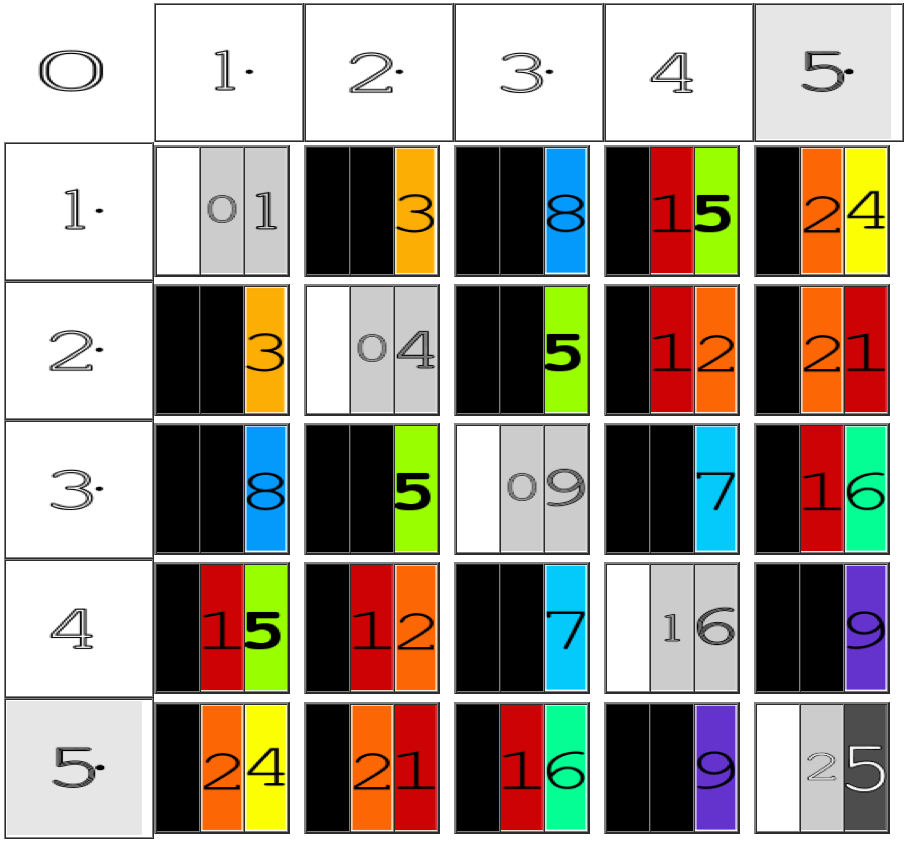Fig.8 "BIM 5x5"

Fig.9 "BIM 10x10"

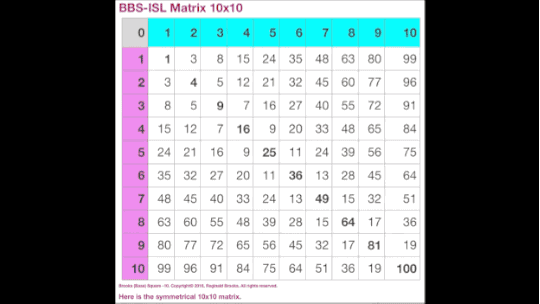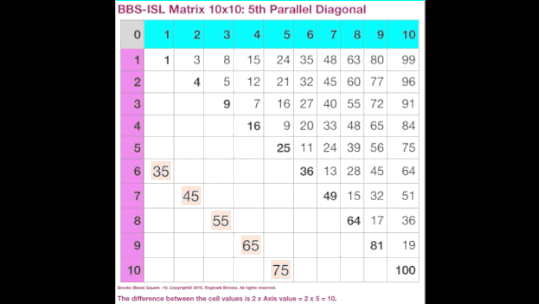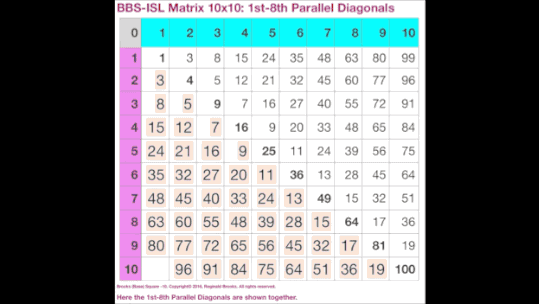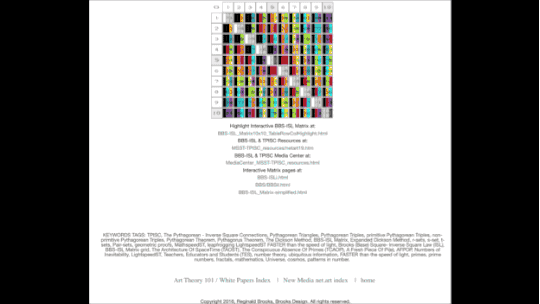Fig.10 "BIM 10x10"

Fig.11 "BIM 15x15"

Fig.12 "BIM 25x25"

Fig.13 "BIM 35x35"

Fig.14 "BIM 50x50"

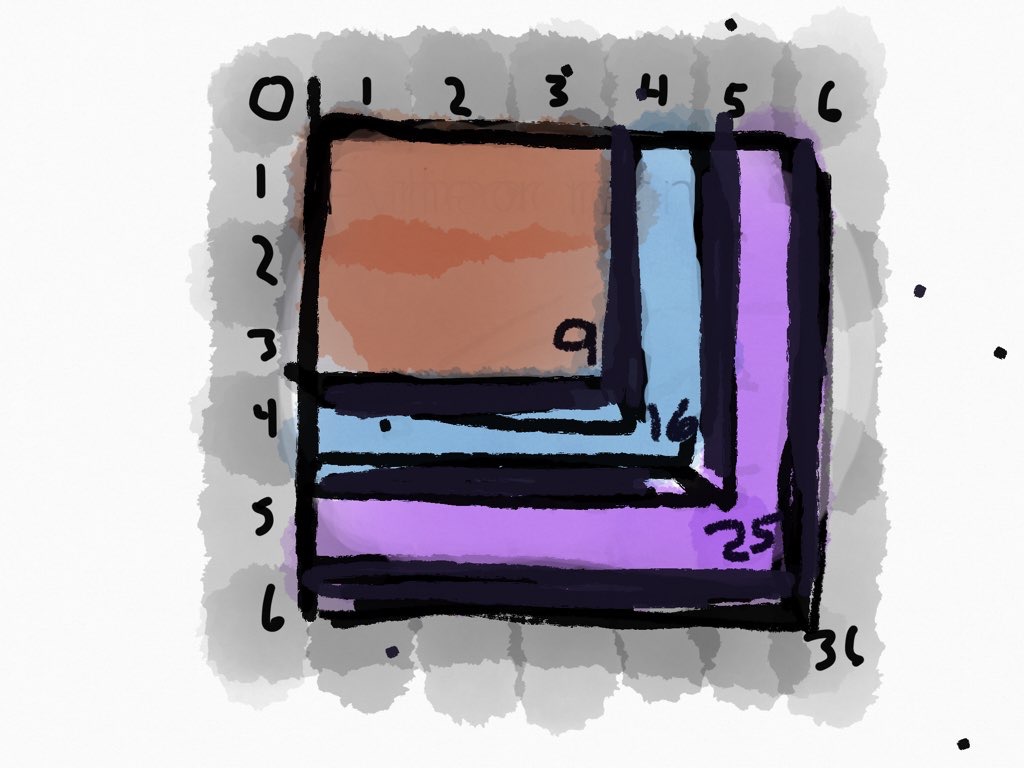Fig.15 "BIM 5x5 proof"

B. Number Pattern Sequences (NPS)

Throughout BIM, a constant recurring theme is that of Number Pattern Sequences (NPS). In fact, the very innate fractal generating purpose of the ISL is to relate space and time to each other and this is the primary function of the NPS! The BIM is criss-crossed every which way in every imaginable way with each and every such path related and inter-connected to the grid as a whole through the NPS. The simplicity of the grid itself and any single NPS belies the truly amazing richness of the quantified landscape of ST that unfolds!

Perhaps, here would be a good spot to introduce a few such NPSs. It was discovered back in 2010 when the BIM was formed that the entire grid is laced with multiples of the 3-4-5 Primitive Pythagorean Triple (PPT). At the time, the significance of this pattern was not yet fully appreciated. Years and several iBooks later on The Pythagorean-Inverse Square Connection (TPISC) this pattern became the spark for further investigations into the very intimate relationship between the Pythagorean Theorem and the ISL!

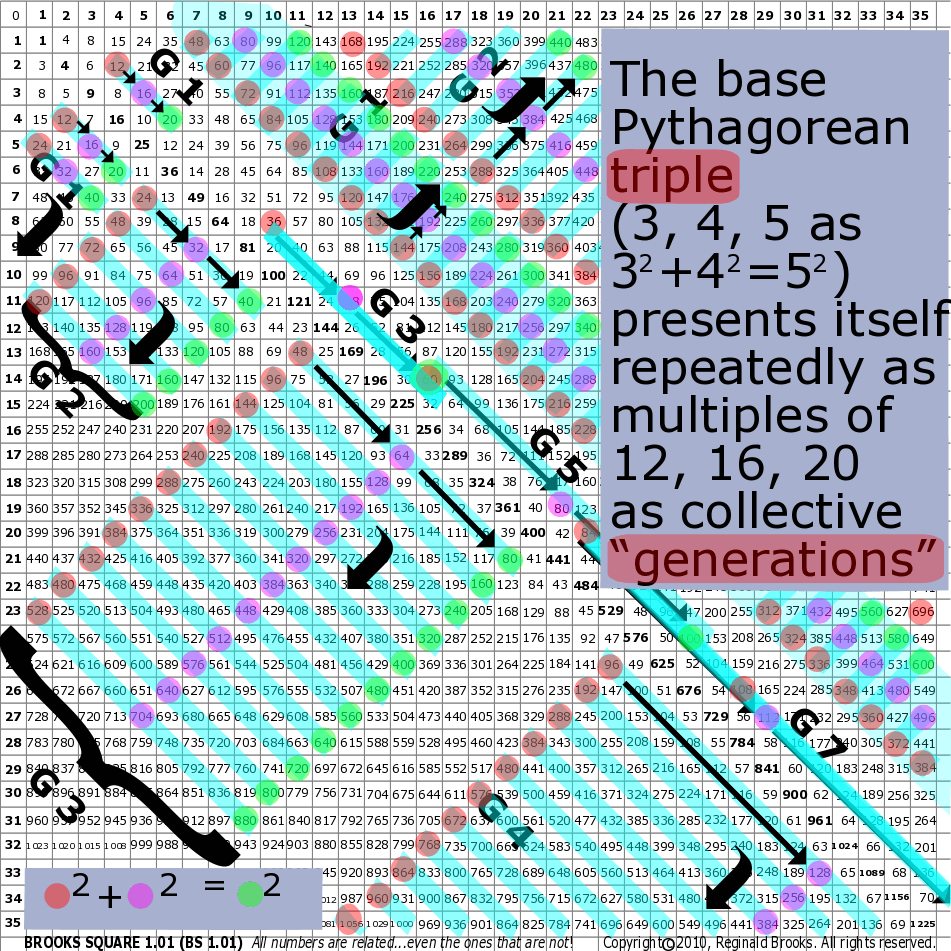Fig.16 "BIM multiples of the 3-4-5 PPT ratio".

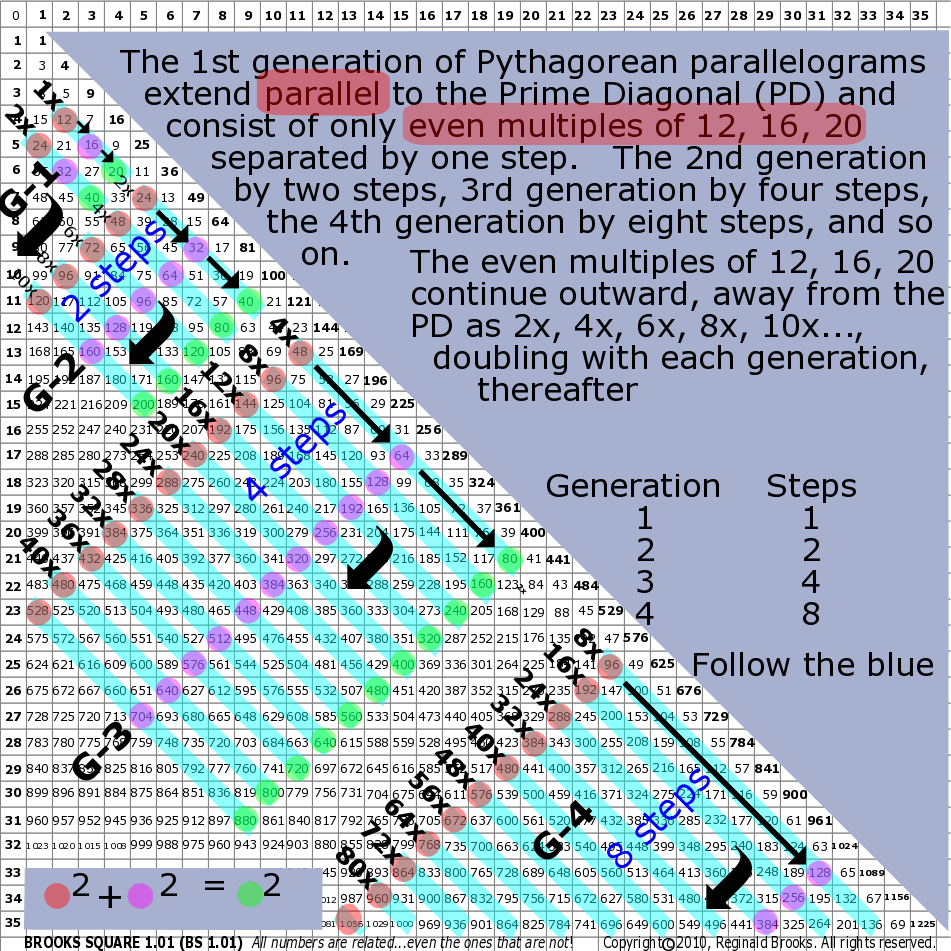Fig.17 "BIM multiples of the 3-4-5 PPT ratio"

Fig.18 "BIM multiples of the 3-4-5 PPT ratio"

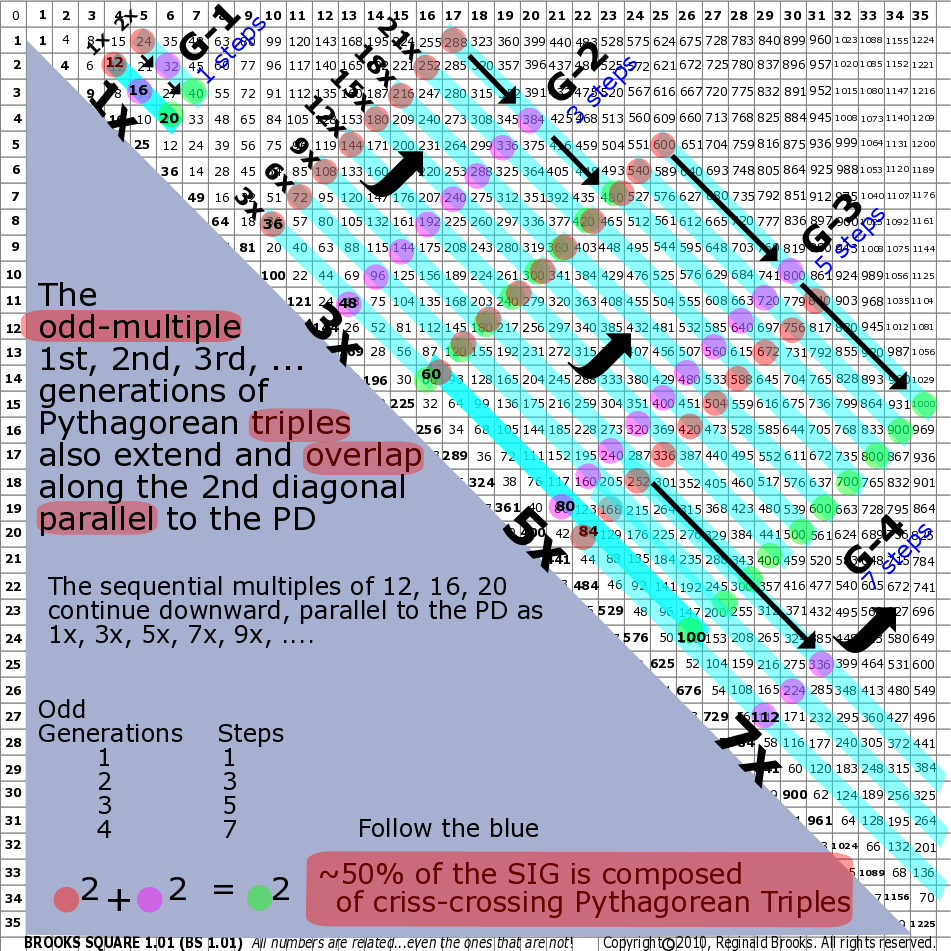Fig.19 "BIM multiples of the 3-4-5 PPT ratio"

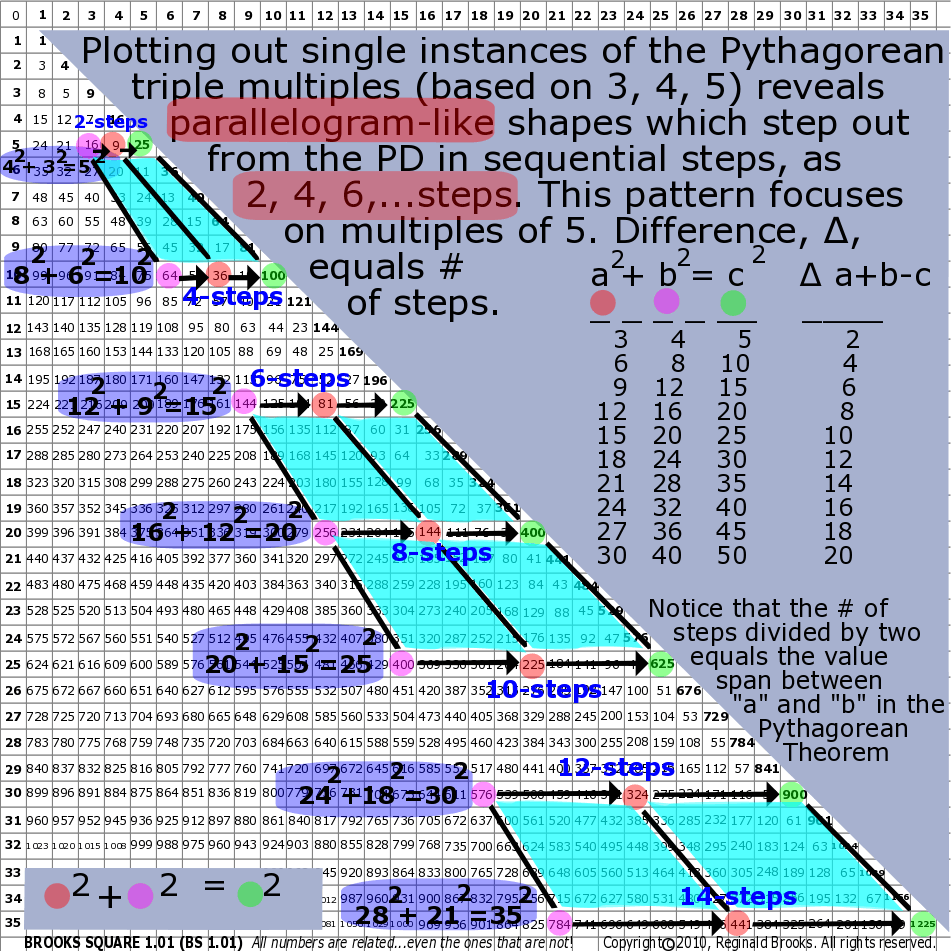Fig.20 "BIM multiples of the 3-4-5 PPT ratio"

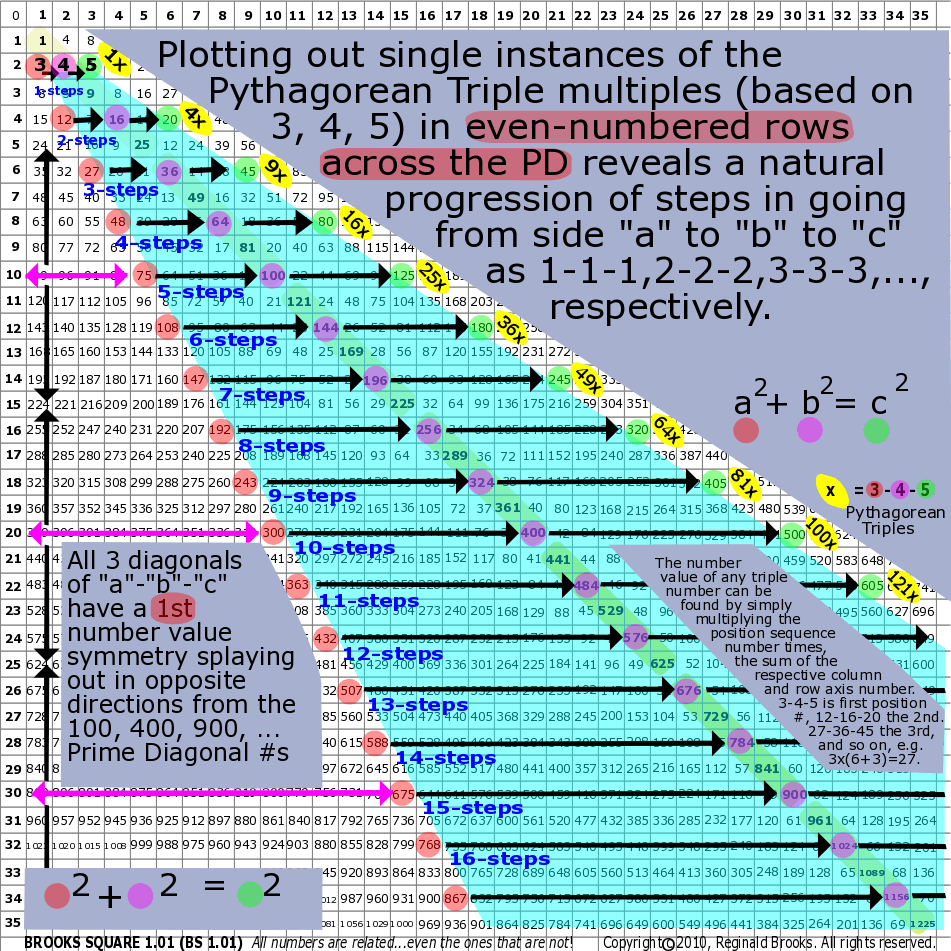Fig.21 "BIM multiples of the 3-4-5 PPT ratio"

C. MathspeedST

Introducing MathspeedST, an ebook. MathspeedST is the complement to LightspeedST (published in June, 2013).
While LightspeedST addressed the ultimate question: “Why is the speed of light constant?” MathspeedST addresses the fundamental, underlying question: “How can information be ubiquitous, effectively traveling FASTER than the speed of light?”
LightspeedST describes how the formation of spacetime (ST) is intimately tied to the speed of light—all within the Observable Universe.
In the Observable Universe, nothing can travel faster than the speed of light—and this includes any information contained within a tangible form.
In order to satisfy a higher rule, The Conservation of Energy—you know, energy (along with its progeny: momentum, charge, spin, etc.) can neither be net created nor destroyed—clearly a mechanism must be in place to account for the distribution of said energy. Not only that, but such mechanism must do the accounting before—not after—the fact. Enter MathspeedST.
"MathspeedST: Leapfrogging Lightspeed FASTER than The Speed of Light” provides the fundamental mathematical basis—lying hidden below—for the accounting and distribution of all spacetime and its subsequent expression as energy, matter and fields in the Observable Universe above.
This freely available interactive ebook brings together under one publication the Brooks (Base) Square-Inverse Square Law, or BBS-ISL Matrix (BIM for short), under the title MathspeedST. It includes hundreds of images, a number of videos and lots of test-yourself, interactive widgets in presenting the derivation, layout, rules, patterns and ISL-derived mathematical basis of the matrix. Ages 8-10 and up.
A new paradigm in the visualization of basic mathematics is presented!
MathspeedST is a freely available iBook that describes and illustrates the BIM. MathspeedST

III. TPISC: the Pythagorean—Inverse Square Connection

A. TPISC I: Basics

http://www.brooksdesign-ps.net/Reginald_Brooks/Code/Html/MSST/TPISC/TPISC.html

Be prepared to find two very simple geometries ubiquitously joined together!

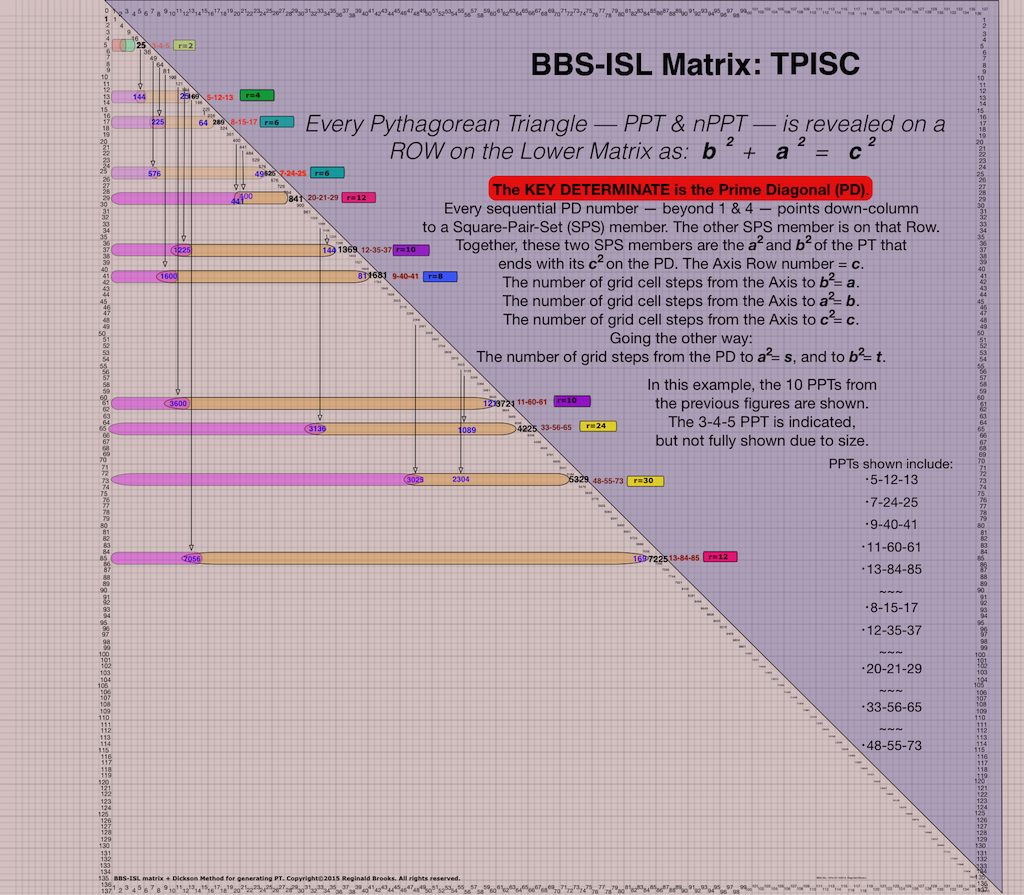
Fig.22 "BIM_PPT"

~~~

Abstract

There is a simple whole number (integer) matrix grid table that every possible whole number Pythagorean Triangle — a.k.a. Pythagorean Triple — can be found and proved. The Brooks Base Square - Inverse Square Law (BBS-ISL) Matrix is an infinitely expandable grid that reveals ALL Pythagorean Triples — both Primitive Triples (PPT) and their non-Primitive multiples (nPTT). An extremely simple geometric AREA proof of the Pythagorean Theorem — c²=a²+b² — is built into the BBS-ISL Matrix.

Not only does the Inverse Square Law describe, define and quantify our most important energies (and their expressions as force) — gravity, light, sound, electromagnetism… — the BBS-ISL Matrix grid is composed of Pythagorean Triples crisscrossing over much of the entire grid. An intimate inter-connection way beyond a simple, casual association has been revealed. The Dickson Method confirms, validates and provides insight into the generation of ALL Pythagorean Triples.

The Pythagorean Theorem and the Inverse Square Law share the same code. In this respect, the c² of c²=a²+b² equals the r² of 1/r² (ISL) by means of the Prime Diagonal. Embedded within the BBS-ISL Matrix — that is essentially based on the squares of whole numbers — are the Pythagorean Triples — whole number right-angle triangles of uneven legs whose AREA Squares equal in sum that of their longer hypotenuse side. Numbers of inevitability.

~~~

Introduction:

The Pythagorean - Inverse Square Law Connection or “How the Pythagorean Theorem is intimately embedded within the The Architecture Of SpaceTime (TAOST)" as described by the BBS-ISL Matrix is first and foremost the topic of this book. It is a MathspeedST Supplement.

As one of the most influential mathematical descriptions of all time, there is no shortage of writings, descriptions and/or proofs of this most profound theorem.

The reason that this work is being presented is precisely because the very nature of that geometric relationship of the Pythagorean Triangle (PT) — whereby the AREA of the square of the long side (hypotenuse) is equal to the sum of the Squares of the two shorter SIDES (legs) — is so intimately related to the Inverse Square Law (ISL), as depicted in the BBS-ISL Matrix (Brooks Base Square - Inverse Square Law Matrix), that a cause and effect relationship between the two is unavoidable.

That the BBS-ISL Matrix also provides perhaps the simplest, most intuitively obvious proof to the Theorem directly on the grid only supports the argument. Every possible PT, and its proof, is visually and mathematical present. The Dickson Method confirms this.

Confidence that this is definitive means that not only can we locate and define any and all PTs on the BBS-ISL Matrix (theoretically, that is, as both expand to infinity), but that the BBS-ISL Matrix itself can be reverse-engineered from those very same PTs! Now that is what you might call true inter-dependence, inter-connection and ultimately driving the same underlying physical law(s) of Nature.

The Pythagorean - Inverse Square Law Connection will often be referenced as TPISC.

~~~

Overview:

Pythagorean Theorem

The history, derivation, use and the hundreds of proofs of the Pythagorean Theorem would fill a library all onto itself. Classic proofs from Pythagoras, Euclid, da Vinci, Newton, Bhaskara, Einstein, Garfield, and the list goes on, are well documented — many with beautiful and clever animations. These proofs generally rely on rearrangement, similarity, or division of the triangle to reveal the equality of the AREA formed. Algebraic and other forms of abstract mathematics can also do the trick.

The Pythagorean Triangle (PT) is right-angle triangle composed of whole number (integer) SIDES. It is commonly referred to as a Pythagorean Triple (PT). The two shorter SIDES or legs, a and b, are of differing lengths, as is the longer or hypotenuse side. Note that other right-angle triangles with fractional SIDES follow the Pythagorean Theorem — but are not Pythagorean Triangles.

The PTs can be divided into two groups: Primitives and non-Primitives. The Primitive PT (PPT) is one that is irreducible. The non-Primitive (nPPT) is simply a multiple of a Primitive, e.i. a 6-8-10 nPPT is simply a double of the 3-4-5 PPT.

As the matrix grows, these PPT’s provide specific nodal articulation points providing structural framework for fractal-like, non-symmetric growth and form realization beyond that of the limitations of a stricter symmetrical approach — all the while maintaining inter-connections to the BBS-ISL Matrix grid.

Every grid cell number within the BBS-ISL Matrix is determined by the Prime Diagonal numbers and every possible PT is embedded within the BBS-ISL Matrix, and as every PT is also determined by the Prime Diagonal numbers, every PT —PPT & nPPT —is an expression — a particular, articulated expression — of the ISL. There is a structural framework embedded within the infinitely expansive ISL — a scaffold — that provides key points of asymmetrical articulation — fractal-nodes — that guide SpaceTime expansion from the simple to the complex.

The pyramidal relationship between every PT — PPT & nPPT — the DM/EDM r-set values, and, the BBS-ISL Matrix, reveals the intimate connection between The Pythagorean Theorem and the Inverse Square Law (TPISC).

The PTs, just like the circle and square, define the ISL!

The pervasive distribution of all the possible PTs (PPT and nPPT) is amazing — going to infinity.

So in the end, what are we to make of all this? Why the BBS-ISL Matrix — which begs the question:

Why the Inverse Square Law (ISL) — and why the Pythagorean Triples?
- And so what if they are both made up of whole integer numbers?
- And so what if they both expand to infinity?
- And so what if the the PTs seem to be all inter-connected?
- And so what if the PTs seem to be infinitely embedded within the BBS-ISL Matrix?
- And so what if there is a pattern to how they are embedded?
- And so what if they both share a common pattern of 90° right-angle isosceles triangle relationships?
- And so what if the ISL informs all of SpaceTime?
- And so what if the ISL thus informs all expressions of energy as matter & waves — particles & fields?
- And so what if all such interactions — including those of growth — is predicated on the unfolding of the ISL-dependent SpaceTime?
And so what if those simple PTs — pattern- peppered throughout the BBS-ISL Matrix — are laying down networking nodes of optimal 90° right-angle connections amongst the more widely distributed ISL background structure?
Are not the PTs there to organize it all?

Let’s say I have convinced you all PTs can be seen and appreciated — by both the VISUALIZATION and CALCULATION Methods — throughout the BBS-ISL Matrix. What do you mean, you might say, about this so-called function — i.e., purpose — as an organizing principle, or even “force,” within the larger ISL organizing background structure informing all ST?

Here’s one approach. Look at the beginning of all ST — each and every formation of ST — and you are the ISL! You lay out this simple, yet incredibly profound, law that all ST shall be organized such that any influence energy/force/momentum/light/sound/etc. — shall universally dissipate inversely, i.e., as you double the distance from the source of the influence, its impact — as density, concentration, distribution, etc. — shall be reduced by 1/r², or in this case, 1/2²=1/4. This influence may be from a point source, fanning out in all 360° directions or be funneled/filtered (not focused) to a narrower path — the distribution results are the same — 1/r².

Mathematically, you can represent yourself as a simple matrix grid — whole integer numbers on each Axis, their Squares forming a symmetrically dividing Prime Diagonal (PD) down the center. Every number in every cell is unique to that cell and strictly follows a pattern — vertically, horizontally and diagonally from the Axis and PD. Furthermore, every interior or Inner Grid cell value is, in the end, determined by the PD numbers. And last, but not least, because your matrix grid is composed of the geometries of the Square — and thus the 90° right-angle isosceles triangles that make up all Squares — there is no end to the networking inter-connections between the grid cells on the matrix we call the BBS-ISL Matrix.

So, for all forming and expanding ST you have these ISL-networked Squares providing the essential primordial background structure for all energy expression. But is that enough? Is more than this simple geometric footprint needed?

Enter the PTs. Whole integer, 90° right-angle NON-isosceles triangles. That’s right. With their strictly defined a²+ b²=c² Pythagorean proportion constraints embedded within each and every PT, and, with each and every PT uniquely distributed within the ubiquity of the BBS-ISL Matrix, you now have a second — “engineered” — organizer of all ST as embedded within the ISL. The PTs provide those critical, resonant, interference-generated nodes of perfect mathematical consonance at those points throughout the infinitely expanding BBS-ISL Matrix.

These PT nodal points, if you will, provide structural focus points for the scaffolding of the unfolding ST. Their complete dependence on the PD, their built-in Pythagorean proportions and their 90° right-angle NON-isosceles arrangement assure complete harmony with the larger ISL, yet provide for precisely the resonant articulation points upon which “structure” can be built.

No wonder the more we look, the deeper we look, the more we see that we are all one!

~~~

Distribution:

The distribution of the PTs is perhaps the most interesting aspect of their existence. Once we understand how they are embedded all over the BBS-ISL Matrix, the real question becomes how do these SIDES and AREAS of the Squares formed become distributed over the grid. Since ALL possible PT and their proofs exist on the matrix — though not on every Row, Column or Diagonal — what are the patterns of SIDES and AREAS telling us about:

The actual formation of the PTs — both PPT and nPPT?

The nature of the BBS-ISL Matrix itself?

~~~

Summary: The BBS-ISL Matrix reveals ALL PTs.

It is ultimately the nature of how dimensions — line, area, volume —numerically interact with scaling that defines the geometry of the Universe. The addition of time dimensions, as well as additional space dimensions, via rotation, movement, scaling, included in the mix adds to the mysterious richness and complexity that issues forth. It belies us to examine the central, fundamental role that line, area, and volume play in all realizations of spacetime (ST).

The journey has been long, yet revealing. The formidable numerical relationships embedded within the BBS-ISL Matrix through TPISC, The Pythagorean — Inverse Square Connection, only re-affirms the fundamental nature of the Inverse Square Law in defining the very Nature within which we exist!

1. The BBS-ISL Matrix displays ALL PTs and their proofs. (And it can be shown that All PTs ultimately relate back to the 1st PPT: 3-4-5.)
1. The Dickson Method generates ALL PTs.
1. The Dickson Method decodes the BBS-ISL Matrix into classes by default:
- a. "Have" (Rows/Columns that "have") b. "Have Nots" (Rows/Columns that "have not."
1. The Dickson Method only reveals the "Haves."
1. The "Haves" are Rows/Columns of the BBS-ISL Matrix that have pair-sets of PD Square numbers — these are the PTs.
1. The "Have Nots" are Rows/Columns that do NOT have PD Square numbers.
1. The "r=EVEN number" in the Dickson Method effectively factors all Square numbers for Factor-Pairs (i.e. pair-sets) and this shows on the BBS-ISL Matrix as "Haves" Rows/Columns.
1. The "r²=2st=4PD" in the Dickson Method is the pathway to finding the Factor-Pairs/pair-sets for any even number=r.
1. The resulting "s,t" values equal the the Factor-Pairs in the Dickson Method, AND, the pair-sets within the Rows/Columns of the BBS-ISL Matrix.
1. All PTs occupy a "Haves" Row/Column on the BBS-ISL Matrix, with their distance in grid cell-STEPS from the PD being the "s,t" values of the Dickson Method marking the actual location (and thus cell value) of the two short Leg AREAS (a²+b²), whose sum = the hypotenuse AREA (c²).

~~~

Conclusion

More than adequately covered in the literature, writings, songs and art of all cultures, it has been an attempt here to present an entirely new manner of looking at the Pythagorean Triples, their proofs, distribution and ultimately their inter-connections. As it turns out, the inter-connections with the BBS-ISL Matrix are what has become the main theme. As the Inverse Square Law (ISL) upon which the BBS-ISL Matrix is formed is, in many respects, one of, if not the main, “laws” or relationship informing principles in all of science — most especially physics and mathematics. That the PT should be so intimately born, described and proved within that matrix is not without great introspection. If the ISL is fundamentally about how influence is distributed — spread out and diluted — over SpaceTime (ST), then the Pythagorean Theorem is a natural, built-in measure of that.

Detailed in the latter part of the Distribution section is a detailed look at the Dickson Method for generating ALL PTs. The a-b-c and a²-b²-c² values of PT are deconstructed down to Factor-Pair sets — sets of two factors (s,t) that when multiplied together equal r²/2, where r=an EVEN number. The additions of the r, s, an t values for each Factor-Pair set, in combinations, will give the PT values.

Further deconstruction and overlapping with the BBS-ISL Matrix has shown that the Dickson Method acts like a Rosetta Stone in that the very same Factor-Pair sets are equivalent to the STEPS separating the AREA Squares of the PT on the grid.

Both the Dickson algebraic CALCULATION Method and the BBS-ISL geometric matrix VISUALIZATION Method reveal exactly the same PT. The Factor-Pairs = STEPS pair sets.

The BBS-ISL Matrix method has the added advantage in that it presents ALL PTs in an AREA Proofs visual manner as well as in listing the AREAS of each PT on the Rows (or Columns). Additionally, All PT SIDES (above a minimum size) are presented Diagonally over the entire matrix.

The inter-connections between these two methods are so tight that little daylight has any chance of separating the two.

~~~

TPISC I: Basics

TPISC I: The Pythagorean - Inverse Square Connection: Basics revealed the presence, proofs and and overall idea of the distribution of the Pythagorean Triples (PTs) upon the BBS-ISL Matrix.

Most of the information presented is on the initial discovery and the profoundly simple geometric proofs of all PTs straight on the matrix.

The distribution was shown as occurring on, and only on, each and every Row/Column that contained AREA Squares. Scan the Rows and if they contained Pair-Sets of these AREA Squares — subsequently referred to as Square-Pair-Sets (SPS) — you would always find a PT there.

TPISC II: Advanced

TPISC II: The Pythagorean - Inverse Square Connection: Advanced profoundly enlarges upon Dickson Method — giving the Extended Dickson Method — which has opened the doors to the real connection between the ISL and the PTs.

Patterns of Fractal-like Relationships, is a descriptive phrase loaded with the implications that the PTs, while ubiquitously embedded throughout the infinite BBS-ISL Matrix, grow within it in a profoundly fractal-like pattern.

Parsing these into r-set and s-set groups becomes key in determining the pattern distribution of ALL PTs and when applied to the BBS-ISL Matrix, a complete patterned VISUALIZATION of all PTs and their connections and inter-connections can be found, giving us TPISC!

TPISC III: Clarity — Simplified: ToPPT (Tree of Primitive Pythagorean Triples) ———this work!

TPISC I: Basics a freely available iBook.

more...

B. TPISC II: Advanced

TPISC II: The Pythagorean - Inverse Square Connection: Advanced

A MathspeedST Supplement

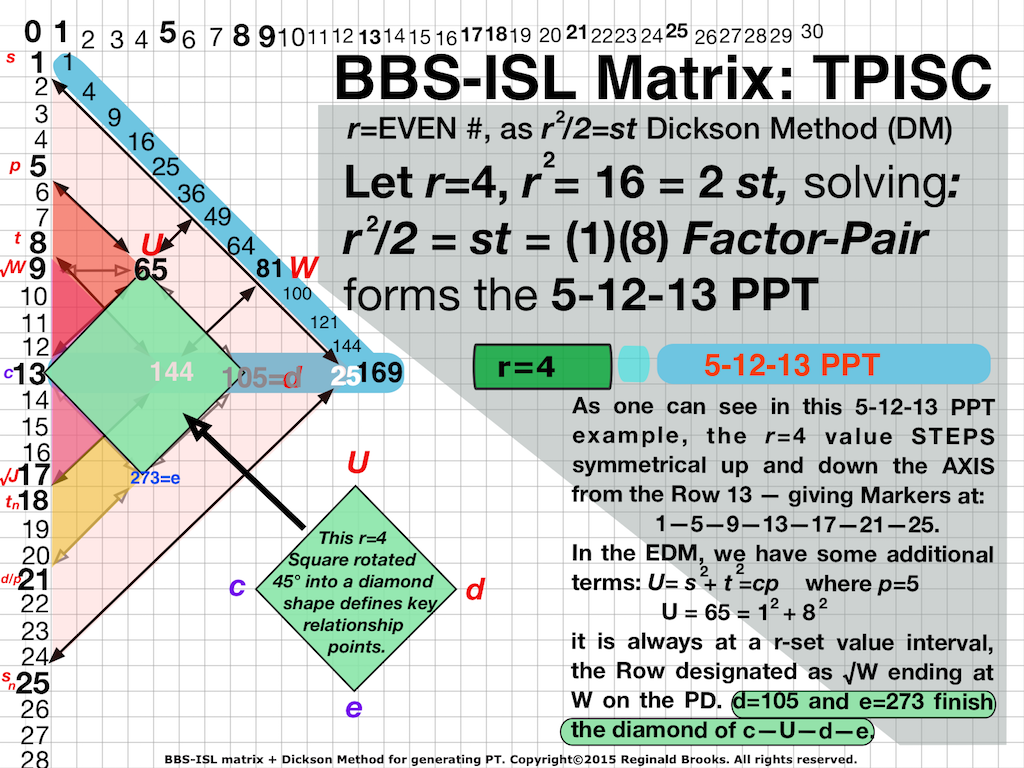
Fig.23 "BIM_TPISC" overview

The Pythagorean - Inverse Square Law Connection or “How the Pythagorean Theorem is intimately embedded within the The Architecture Of SpaceTime (TAOST) as described by the BBS-ISL Matrix” is first and foremost the topic of this book. It is a MathspeedST Supplement.

As one of the most influential mathematical descriptions of all time, there is no shortage of writings, descriptions and/or proofs of this most profound theorem.

The reason that this work is being presented is precisely because the very nature of that geometric relationship of the Pythagorean Triangle (PT) — whereby the area of the square of the long side (hypotenuse) is equal to the sum of the squares of the two shorter sides (legs) — is so intimately related to the Inverse Square Law (ISL), as depicted in the BBS-ISL Matrix (Brooks Base Square - Inverse Square Law Matrix or BIM for short), that a cause and effect relationship between the two is unavoidable.

The Pythagorean - Inverse Square Law Connection will often be referenced as TPISC.

TPISC I: Basics

TPISC I: The Pythagorean - Inverse Square Connection: Basics revealed the presence, proofs and and overall idea of the distribution of the Pythagorean Triples (PTs) upon the BBS-ISL Matrix.

Most of the information presented was on the initial discovery and the profoundly simple geometric proofs of all PTs straight on the matrix.

TPISC II: Advanced

TPISC II: The Pythagorean - Inverse Square Connection: Advanced profoundly enlarges upon Dickson Method — giving the Extended Dickson Method — which has opened the doors to the real connection between the ISL and the PTs.

Parsing these into r-set and s-set groups becomes key in determining the pattern distribution of ALL PTs and when applied to the BBS-ISL Matrix, a complete patterned *VISUALIZATION of all PTs and their connections and inter-connections can be found, giving us TPISC!

r-sets: The foundation of the DM is that you start with r= EVEN number such that r² = 2st. This produces a series, or group, of r-sets. These r-sets contain the Factor-Pairs, that when multiplied together, give r²/2. The also give the STEPS.

r²/2: equals st. s and t are the Factor-Pair solutions to r²/2 and these s,t values define every PT.

s-sets: The Factor-Pairs s,t are derived from the r-sets . The s-sets are simply a group of all those PTs with the same s-value. Adding r + s = a, and, r + s + t = c. The s-value is the number of STEPS from the Prime Diagonal to the a² SPS on the matrix.

t-sets: The Factor-Pairs s, t can also form groups of all those PTs with same t-value. r + t = b, and, r +s +t = c and the t-value is the number of STEPS from the Prime Diagonal to the b² SPS on the matrix.

Re-stated: The Dickson Method (DM) — a simple algebraic method for generating ALL Pythagorean Triples (PTs) by CALCULATIONS — has become the Expanded Dickson Method (EDM) so as to be easily visualized on the BBS-ISL Matrix.

The Dickson Method (DM) takes the even numbers — r=2,4,6,… — squares them as r², divides this by two as in r²/2, and from this result determines the sets of Factor-Pairs (F-Ps) that exist to form this result. These F-Ps are labeled “s” and “t.” Recombining r+s, r+b, and r+s+t gives the a-b-c, respectively, side leg values of ALL possible PTs! The DM uses the “x,y,z” symbol system to reconstruct the a² + b² = c² Pythagorean Theorem. The EDM brings out several more inter-connections that become readily visible on the BBS-ISL Matrix.

No different from the BBS-ISL Matrix itself, TPISC just keeps giving and giving. Wrapping up within Conclusion _Part I, a whole new set of Number Patterned Sequences issued forth providing some new, and quite astounding, revelations into the whole Pythagorean Triples landscape. So climb aboard! The going will be a little rough at first, but once had, the clarity — the ultimately, sublimely beautiful landscape panorama — will present itself with actual simplification. Yes, greater simplicity through deeper insight. Here we go!

We see that the initial DM — and now the EDM — simply pick out right-isosceles triangle relationships — all of which emanate from the PD — the PD itself being the Squares of the Axis numbers.

The DM/EDM selects out r=EVEN # r-sets, i.e., r=2,4,6,….

All the r-sets are universal —identical — in their framework template, varying only in scale, as in r=2,4,6,….

Each r-set itself acts like a container rail/track that holds two or more (beyond r=2 which only has 1) PTs.

Each contained PT follows that r-set template — only their location on that rail-track varies — up and down.

As the r-sets grow in size, so do the # of PTs contained in — and placed up and down on — that rail-track. However, the # of PPTs within each r-set is limited — and patterned.

So once again, we come back to the fact that since every grid cell # within the BBS-ISL Matrix is determined by the PD #s and every possible PT is embedded within the BBS-ISL Matrix, every PT is determined by the Prime Diagonal #s and thus, every PT —PPT & nPPT —is an expression — a particular, articulated expression — of the ISL. There is a structural framework embedded within the infinitely expansive ISL — a scaffold — that provides key points of asymmetrical articulation — fractal-nodes — that guide SpaceTime expansion from the simple to the complex.

The pyramidal relationship between every PT — PPT & nPPT — the DM/EDM r-set values, and, the BBS-ISL Matrix, reveals the intimate connection between the Pythagorean Theorem and the Inverse Square Law (TPISC).

The PTs, just like the circle and square, define the ISL!

So in the end, what are we to make of all this?

Why the BBS-ISL Matrix — which begs the question: Why the Inverse Square Law (ISL) — and why the

Pythagorean Triples?

And so what if they are both made up of whole integer #s?
And so what if they both expand to infinity?
And so what if the the PTs seem to be all inter-connected?
And so what if the PTs seem to be infinitely embedded within the BBS-ISL Matrix?
And so what if there is a pattern to how they are embedded?
And so what if they both share a common pattern of 90° right-angle isosceles triangle relationships?
And so what if the ISL informs all of SpaceTime?
And so what if the ISL thus informs all expressions of energy as matter & waves — particles & fields?
And so what if all such interactions — including those of growth — are predicated on the unfolding of the ISL-dependent SpaceTime?
And so what if those simple PTs — pattern- peppered throughout the BBS-ISL Matrix — are laying down networking nodes of optimal 90° right-angle connections amongst the more widely distributed ISL background structure?
Are not the PTs there to organize it all?

TPISC, The Pythagorean — Inverse Square Connection, is about shining some light on how Nature ubiquitously builds combining simple, elemental forms into sentient constructs able to reflect the light all the way back home!

TPISC II: Advanced iBook

more...

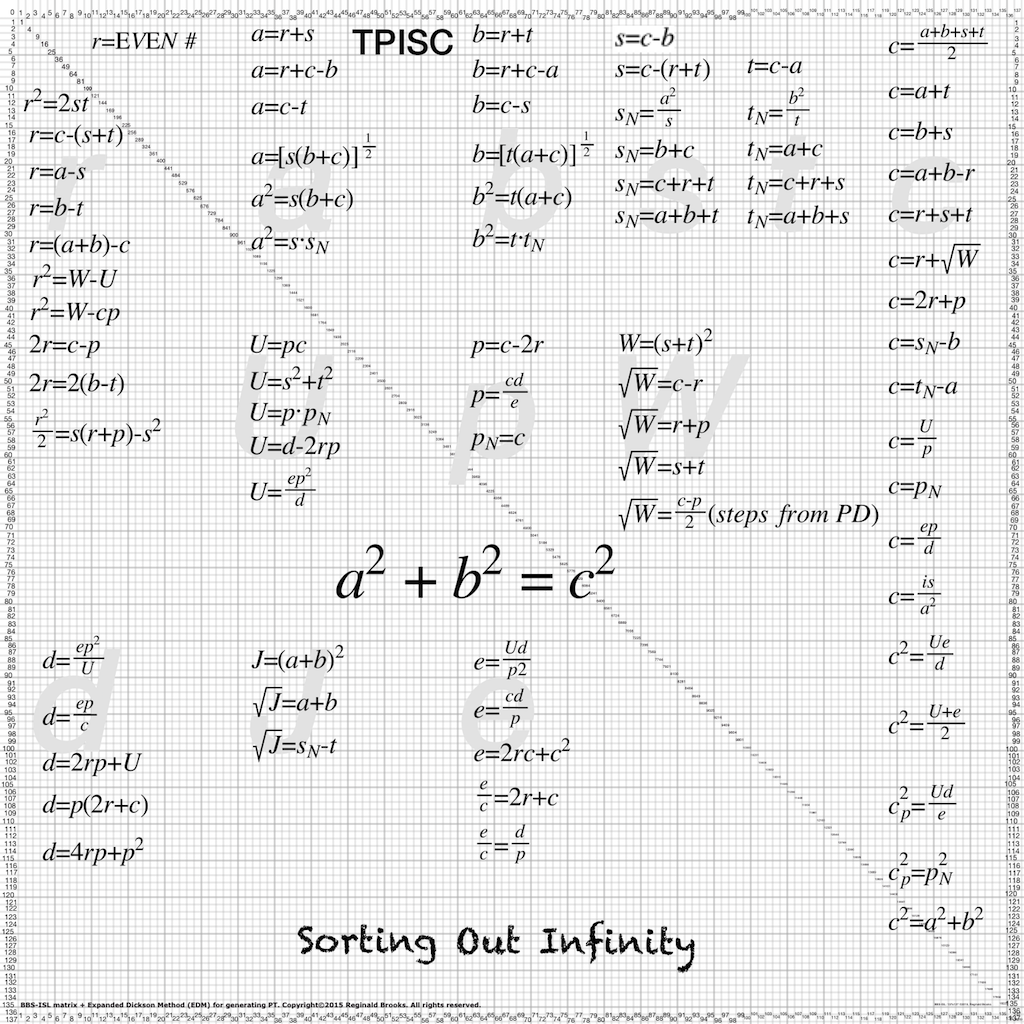Fig.24 "BIM_TPISC: EDM" equations

Fig.25 "BIM_TPISC" overview detail 1

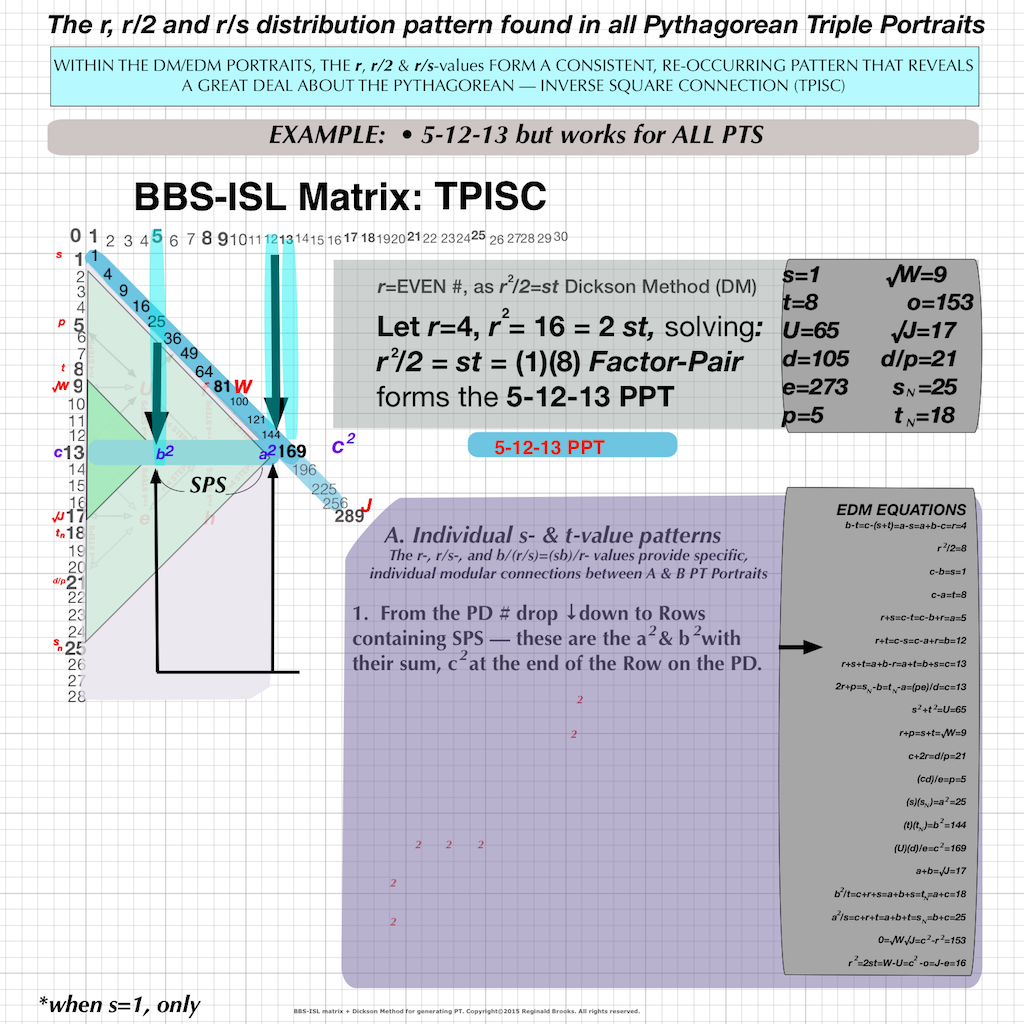Fig.26 "BIM_TPISC" overview detail 2

Fig.27 "BIM_TPISC" overview detail 3

Fig.28 "BIM_TPISC" overview detail 4

Fig.29 "BIM_TPISC" overview detail 5

Fig.30 "BIM_TPISC" overview detail 6

Fig.31 "BIM_TPISC" overview detail 7

Fig32 "BIM_TPISC" overview detail 8

Fig.33 "BIM_TPISC" overview detail 9

Fig.34 "BIM_TPISC" overview detail 10

Fig.35 "BIM_TPISC" overview detail 11

Fig.36 "BIM_TPISC" overview detail 12

Fig.37 "BIM_TPISC" overview detail 13

C. TPISC III: Clarity—Simplified—ToPPT

A recent paper “Cliques of Neurons Bound into Cavities Provide a Missing Link between Structure and Function” by M.W.Reimann, et al (Front. Comput. Neurosci., 12 June 2017 | https://doi.org/10.3389/fncom.2017.00048), stated that the highly entangled neuronal distribution pattern of the brain, proven to not be random, was instead a direct reflection of shape patterns within the mathematical space of 4,5,6,7 and more dimensions. With up to 11 dimensions found, it begs the question: surely, the multi-dimensional neuronal structure of the brain must exist within the multi-dimensional Universe that created it?

So what lies below? What informs the multi-dimensional Universe itself?

Algebraic Geometry (Topology) — combining algebra, geometry and number theory (and additionally fed by a host of other mathematical disciplines — describes the shaping phenomena resulting from the interplay on Number Pattern Sequences (NPS) generated from connecting the dots in different arrays. These arrays — and the consequent voids/“cavities”/negative spaces — together give birth to multi-dimensions. As summarized in the June 19, 2017 Phys.org newsletter “Blue Brain team discovers a multi- dimensional universe in brain networks,” and I quote:

“When the researchers presented the virtual brain tissue with a stimulus, cliques of progressively higher dimensions assembled momentarily to enclose high-dimensional holes, that the researchers refer to as cavities. "The appearance of high-dimensional cavities when the brain is processing information means that the neurons in the network react to stimuli in an extremely organized manner," says Levi. "It is as if the brain reacts to a stimulus by building then razing a tower of multi-dimensional blocks, starting with rods (1D), then planks (2D), then cubes (3D), and then more complex geometries with 4D, 5D, etc. The progression of activity through the brain resembles a multi-dimensional sandcastle that materializes out of the sand and then disintegrates."

It is the repetition — the re-iteration — of the NPS creating the pattern within the pattern that the whole notion of a fractal generator is born. When the fractal dots are connected, a dimension(s) is/are created.

So what is the basis of a fractal generator? What basics (Number Theory, Arithmetic Geometry) could give rise to NPS (Algebra), that would shape (Geometry, Topology), those elemental, whole number integers. into a fractal generator (Algebraic Geometry) that informs the very SpaceTime (ST) of the multi-dimensional Universe that we wake up to every morning?

~ ~ ~

In reviewing a substantial new body of NPS resulting from the even more extended Extended Dickson Method (EDM) — The Fully Extended Dickson Method (FEDM) — I ran across the Tree of Primitive Pythagorean Triples (as described in the References section). What was intriguing is that the ToPPT reveals ALL possible PPTs and that they are ALL only represented once. This is what the literature says and I have found no reason to question those proofs.

What was found, however, was that the two versions of the ToPPT profiled were both limited to showing only three (3) generations — Tertiary Branches — and insufficient pattern description to fully flush out ALL the subsequent generations. Not to take anything away from their beautiful work, in truth, they simply were not armed with the BIMtree layout that is front and center today. The BIMtree will show the true, consistent and all-encompassing NPS that informs the entire ToPPT from the Trunk to an infinite number of Tertiary Branches in a logical and visual demonstration of the true power and predictability of the intimate Pythagorean — Inverse Square Connection (TPISC).

So hang on because this ride is bumpy with so much simple — but look-alike — information of numbers in charts and tables that one may not readily see the ultimate and profound simplicity of forest for the trees — in this case, the trees for the branches, the clusters for the branches, the individual PPTs for the clusters.

Bottom line: Every PPT growing outward from the Trunk (3-4-5), does so in a strict NPS that relates vertically to every PPT before and after, as well a relating horizontally to every PPT in the Clusters that form across the Branches.

When laid out on the BIMtree, every Cluster is strictly related by having the SAME diagonal (parallel to the PD). This diagonal forms one side of the Golden Diamond Square on the BIM. It can be shown going from “d” on the PPT Row, diagonally through “U” above, ending at the Axis (vertical) with the “p-value.” VERY IMPORTANT GEOMETRY HERE! This provides a very strong and clear visual as the 3 PPTs that make up a Cluster, will pictorially (Arithmetic Geometry) line up such that they all have this Common Diagonal Border (p-value).

This brings a beautiful order to the ToPPT as it expands outward to infinity. (And NO, it does NOT have its branches turn back down forming an infinitely diminishing, self-contained structural presentation as has been reported. Quite the opposite, the ToPPT wonderfully grows outward to infinity as each subsequent Tertiary Branch and its 3-PPTs Clusters become larger and larger!)

The purpose of this work is to layout the ToPPT within the context of the BIM — thus the BIMtree. To both satisfy the needs of critical proof (which it hardily passes), the journey of parsing the numbers into charts and tables, and, to SIMPLIFY the results, without overly diminishing the necessary details that actually prove the points, will be the goal. This is both necessary and, I believe, valuable for future developments.

~~~

Significance (worth repeating):

Where does this all go?

The BIM describes the ISL-defined ST structure of the Universe. But are pure squares and circles enough?

Enter the PTs. The non-isosceles, right-triangle PTs form non-square rectangles and ovals that inherently bring a different type-class of symmetry to the grid.

Now, sprinkled ubiquitously across the infinitely expanding BIM, we have infinitely expanding (and linked), non-square rectangles and ovals of the PTs (Two PTs = 1 non-square rectangle).

Or should we say, that magnificent tree growing in ST!

As discovery gives to presentation, it is my goal to present this “linkage” in a form that both challenges and delights the curious viewer. A pictorial journey.

Before you start, the short video below will give you a very informative and helpful overview of just how the Pythagorean Triples are found, described and manipulated on the BIM.

BIM_FEDM(2017)_INTRO from Reginald Brooks on Vimeo.

The video gives a visual sequence to key PARAMETERS that anchor the "specific individual" PT to the BIM, as well as the "Universal" PARAMETERS that ALL PTs follow throughout the BIM.

Rather than trying to get all the exact details right now, this is presented here to provide you with a context overview to which you will build up your understanding as you proceed. Scan the video a few times for the general view — it really helps!

~~ ~~ ~~

You may find it helpful to keep these 10 points in mind while examining, exploring and discovering the BIM:

BBS-ISL Matrix (BIM) :

The BIM is fundamentally Inverse-Square-Law-related AREAS on a Matrix of Whole Integer Numbers (WINs).
Every WIN on the Inner Grid (IG) is simply the ∆PD-PD (or its square root derivative: Ax₁ Ax₂).
All PTs are simply AREAS on the BIM.
Every PT is simply two IG#s on a Row — mirroring PD#s.
The ToPPT grows as PT Composite AREAS form new PT AREAS.
All Exponentials are simply AREAS following diagonals on the BIM.
Every X² is an Exponential AREA on the PD.
All X^>2 Exponentials are IG# AREAS on a diagonal — some mirroring, some not, the PD#s.
Both PTs and Exponentials have Number Pattern Sequences (NPS) that map on the BIM.
The Axis (Ax), acting as Factor Pair Sets (FP or FS), complement the PD#s in defining the AREAS on the BIM.

~~~

Significance (worth repeating):

Where does this all go?

The BIM describes the ISL-defined ST structure of the Universe. But are pure squares and circles enough?

Enter the PTs. The non-isosceles, right-triangle PTs form non-square rectangles and ovals that inherently bring a different type-class of symmetry to the grid.

Now, sprinkled ubiquitously across the infinitely expanding BIM, we have infinitely expanding (and linked), non-square rectangles and ovals of the PTs (Two PTs = 1 non-square rectangle).

Or should we say, that magnificent tree growing in ST!

As discovery gives to presentation, it is my goal to present this “linkage” in a form that both challenges and delights the curious viewer. A pictorial journey.

Before you start, the short video below will give you a very informative and helpful overview of just how the Pythagorean Triples are found, described and manipulated on the BIM.

BIM_FEDM(2017)_INTRO from Reginald Brooks on Vimeo.

The video gives a visual sequence to key PARAMETERS that anchor the "specific individual" PT to the BIM, as well as the "Universal" PARAMETERS that ALL PTs follow throughout the BIM.

~~ ~~ ~~

You may find it helpful to keep these 10 points in mind while examining, exploring and discovering the BIM:

BBS-ISL Matrix (BIM) :

The BIM is fundamentally Inverse-Square-Law-related AREAS on a Matrix of Whole Integer Numbers (WINs).
Every WIN on the Inner Grid (IG) is simply the ∆PD-PD (or its square root derivative: Ax₁ Ax₂).
All PTs are simply AREAS on the BIM.
Every PT is simply two IG#s on a Row — mirroring PD#s.
The ToPPT grows as PT Composite AREAS form new PT AREAS.
All Exponentials are simply AREAS following diagonals on the BIM.
Every X² is an Exponential AREA on the PD.
All X^>2 Exponentials are IG# AREAS on a diagonal — some mirroring, some not, the PD#s.
Both PTs and Exponentials have Number Pattern Sequences (NPS) that map on the BIM.
The Axis (Ax), acting as Factor Pair Sets (FP or FS), complement the PD#s in defining the AREAS on the BIM.

The BIM* is the geometry defining SpaceTime!*

IV. ToPPT: Layout

A. Structure: Outward = BRANCHES (TIERS)

From the Trunk — which forms the 1^st Tertiary Branch — each subsequent Branch forms a Cluster of 3 Branches, and, that Tier formed is referred to as the 1^st, 2^nd, 3^rd, 4^th, 5^th,… Tertiary Branch/Tier.

B. Structure: Across = CLUSTERS

Each Tertiary Branch/Tier consists of 3-Branch Clusters. These increase as 3^X, where x=Tertiary/Tier #.

Thus:

3¹=3 = 1 Cluster of 3 PPTs = 3 PPTs
3²=9 = 3 Clusters of 3 PPTS = 9 PPTs
3³=27 = 9 Clusters of 3 PPTs = 27 PPTs
3⁴=81= 27 Clusters of 3 PPTs = 81 PPTs
3⁵=243 = 81 Clusters of 3 PPTs = 243 PPTs
...

C. Definitions and References

PT: Pythagorean Triple-non-isosceles, right triangle composed of whole integer numbers satisfying a²+b²=c² (Pythagorean Theorem)
ToPPT: Tree of Primitive Pythagorean Triples
PPT: Primitive Pythagorean Triple (non-reducible parent)
nPPT: non-Primitive Pythagorean Triple (reducible child)
BIM: BBS-ISL Matrix=Brooks Base Square-Inverse Square Law Matrix
BIMtree: BIM + ToPPT
Tertiary Branch: A Tier of growth(linkage) in which the node from the Branch (or Trunk) before forms 3 NEW Branches — forming a Cluster
Cluster: the 3-PPTS that form 3 related Branches, all from the SAME Branch node before. The PPTs within a Cluster ALWAYS have the SAME p-value — and subsequently, enjoy the SAME Common Diagonal Border on the BIMtree.
Dickson Method (DM): All PPTs — PPT & nPPT — can be found as r²=2st, such that r+s=a, r+t=b, and r+s+t=c.
Extended Dickson Method (EDM): Within the BIM, the values of the DM become STEPS between grid cells. The Arithmetic Geometry that results has led to defining the parameters at which the geometric vertices cross.
Fully Extended Dickson Method (FEDM): As additional geometries unfolded, it became necessary to fully extend the parameters to cover the additional relationships, resulting in additional parameter names.
r-value: by definition in the DM, r=EVEN whole integer number satisfying r²=2st. The r-value is pivotal in defining the PT on the BIM, and therefore, in defining the ToPPT on the BIMtree.
s-value: solving r²=2st for the s & t factor values forming r²/2 gives s, another pivotal parameter.
t-value: solving r²=2st for the s & t factor values forming r²/2 gives t, another pivotal parameter.
p-value: From the EDM, the p-value defines the Common Diagonal Border of the Clusters, as U/c=p=c-2r.
U-value: From the EDM, the U-value =p x c. A line from the d-value, through U points to the p-value on the Axis.
d-value: From the EDM, the d-value =2r STEPS from the Axis. A line from the d-value, through U points to the p-value on the Axis.
o-value: From the EDM. the o-value is the CENTER POINT of the Golden Square-Diamond defining any PT. It is centrally located 1 r-STEP from the vertices, located on the PT Row.
e-value: From the FEDM, the e-value =1r STEP from the Axis. A line from the e-value, parallel to the Common Diagonal Border of the Golden Square-Diamond, points to the c-value on the Axis.
f-value: From the EDM, f=t-s=b-a. The f-value is also pivotal in defining the ToPPT linkages.
f²-value: From the FEDM, f²=(t-s)²=(b-a)². The f²-value is also pivotal in defining the PT proofs.

Table 1a. All PPTs r=2 to r=100.

Fig.38 "BIMtreeTemplate-1"

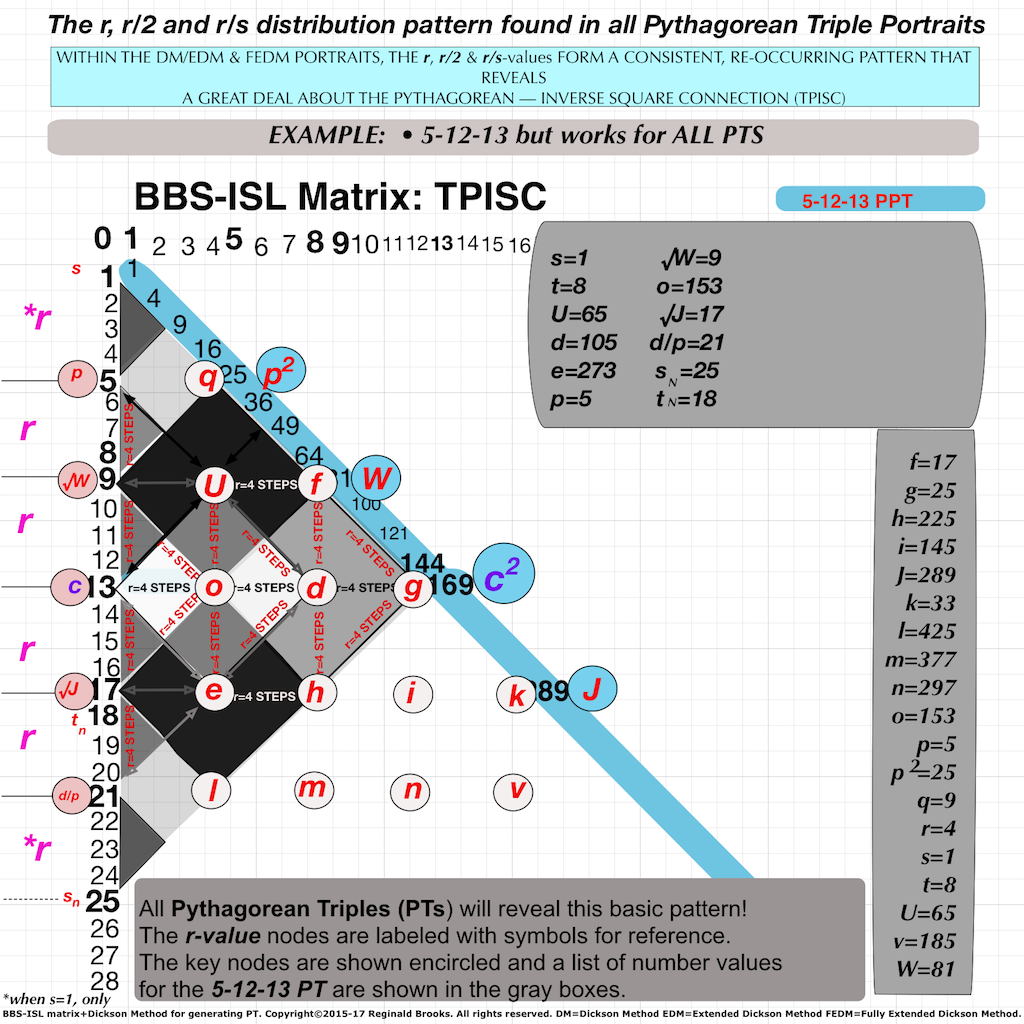Fig.39 "BIMtreeTemplate-2"

Fig.40 "BIMtreeTemplate-3"

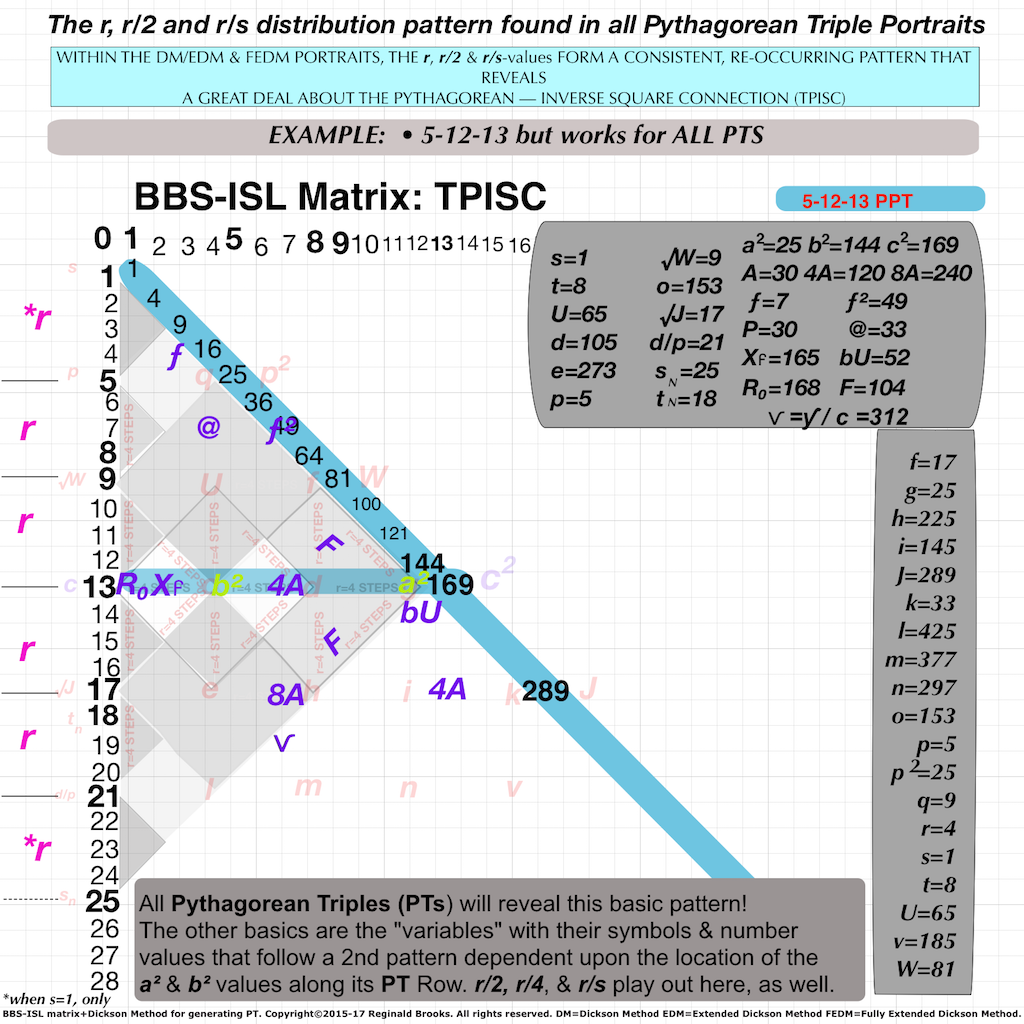Fig.41 "BIMtreeTemplate-4"

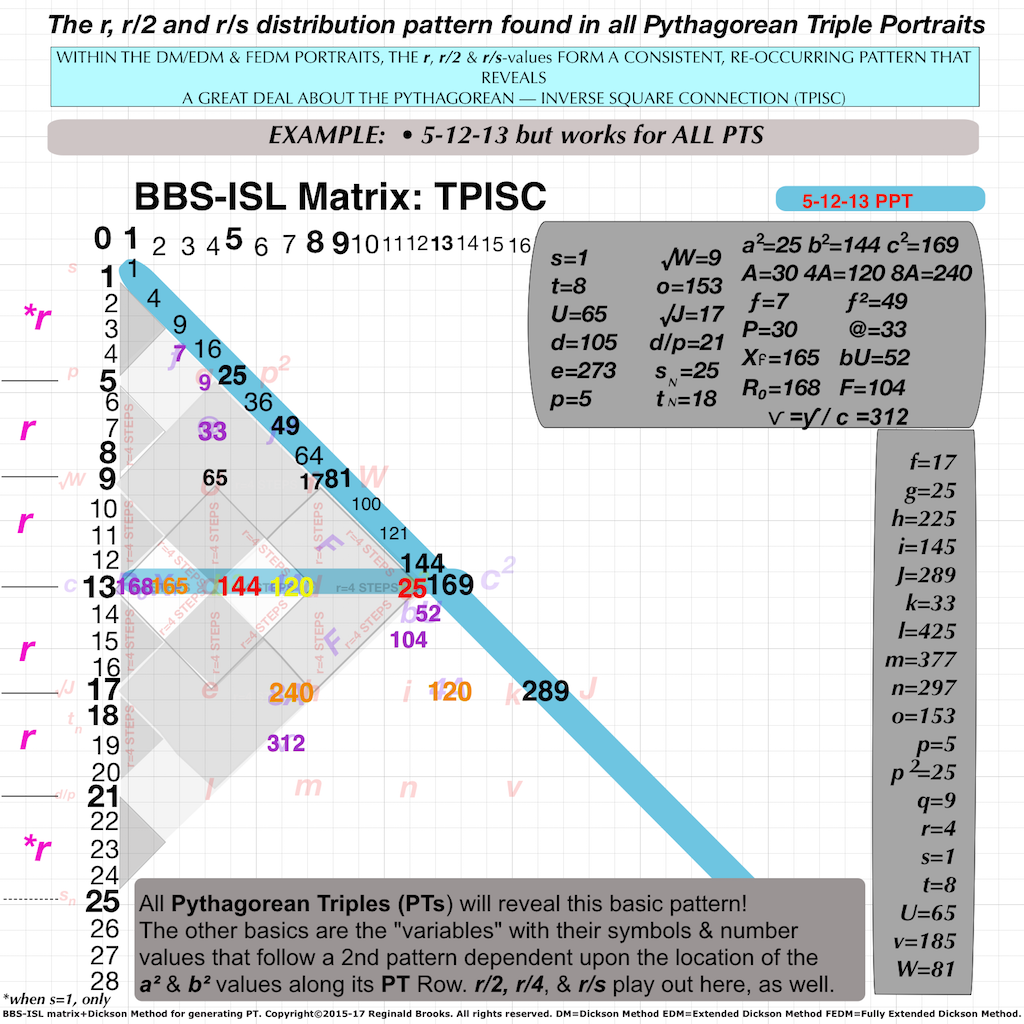Fig42 "BIMtreeTemplate-5"

Fig.43 "BIMtreeTemplate-6"

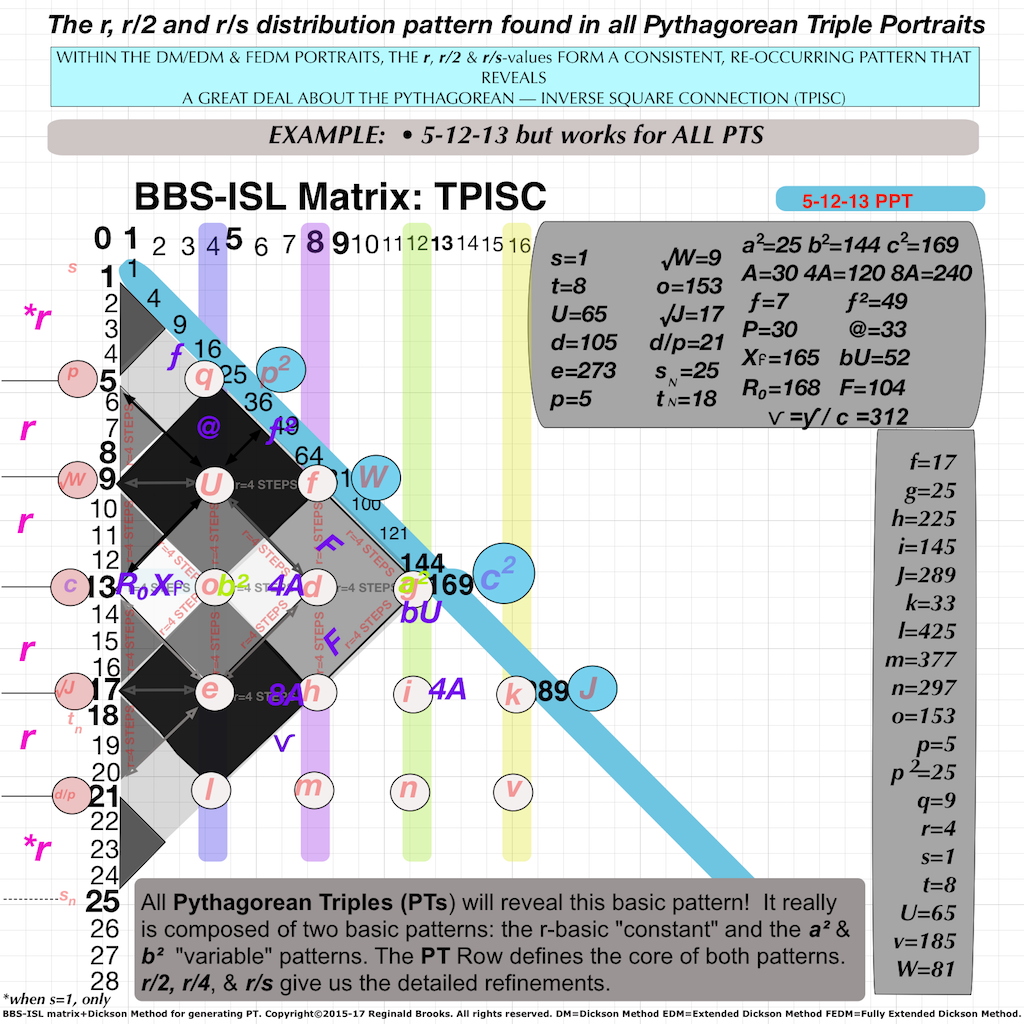Fig.44 "BIMtreeTemplate-7"

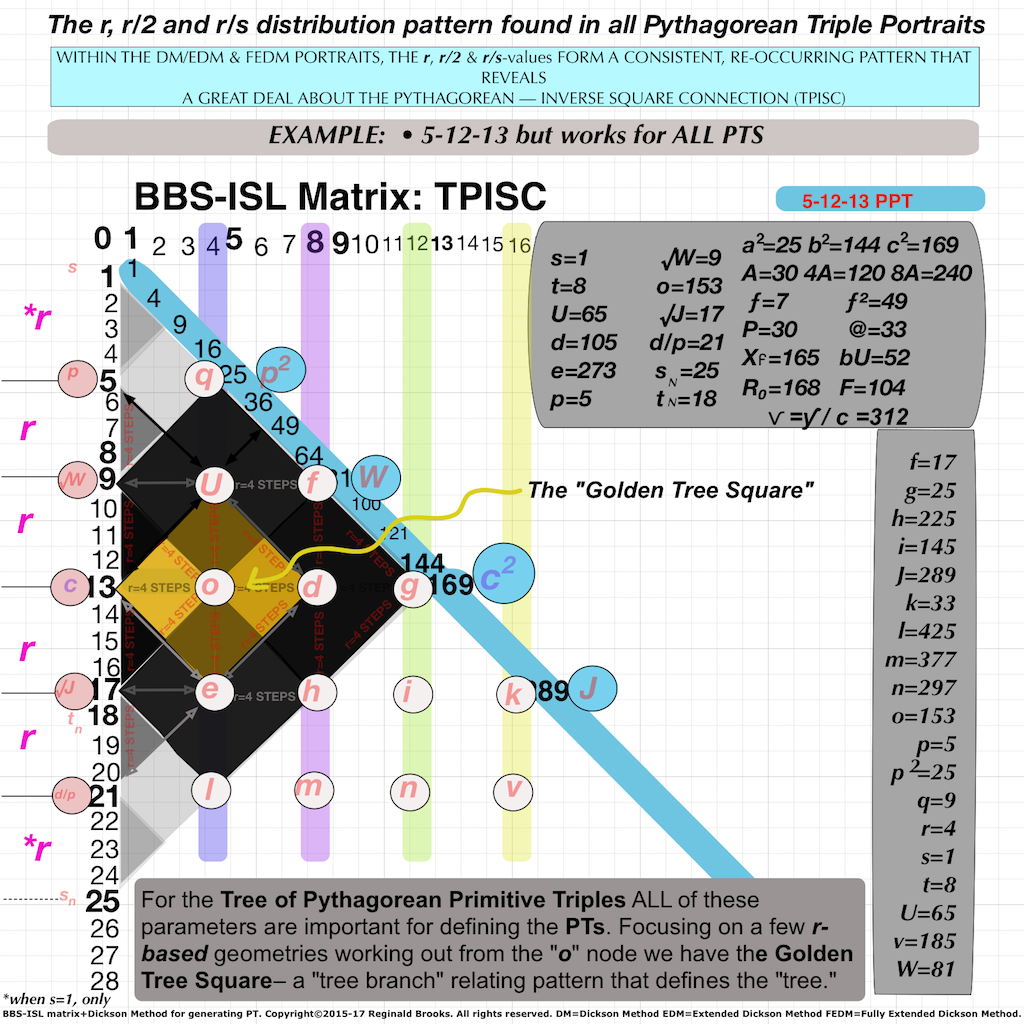Fig.45 "BIMtreeTemplate-8"

Fig.46 "BIMtreeTemplate-9"

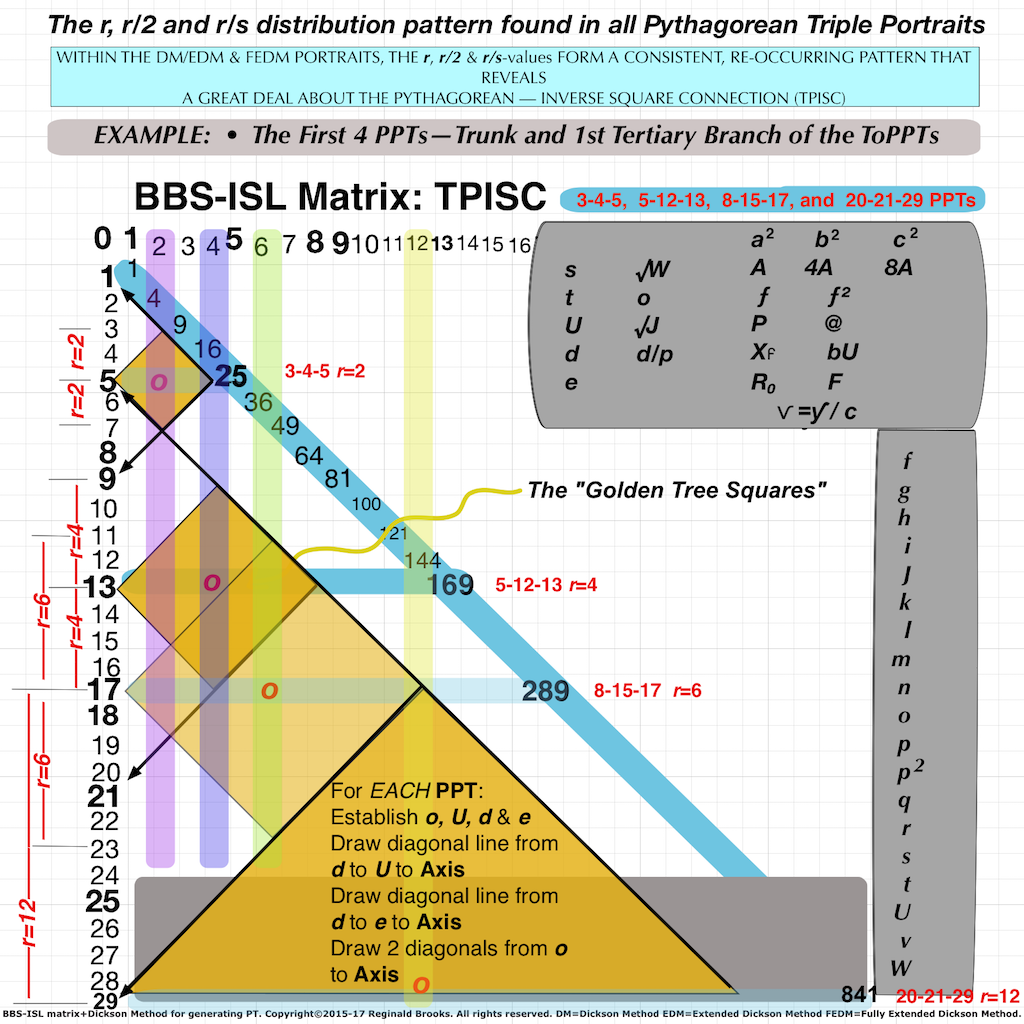Fig.47 "BIMtreeTemplate-10": a pivotal image as it shows the 1^st Cluster having the SAME p-value.

Fig.48 "BIMtree-1"

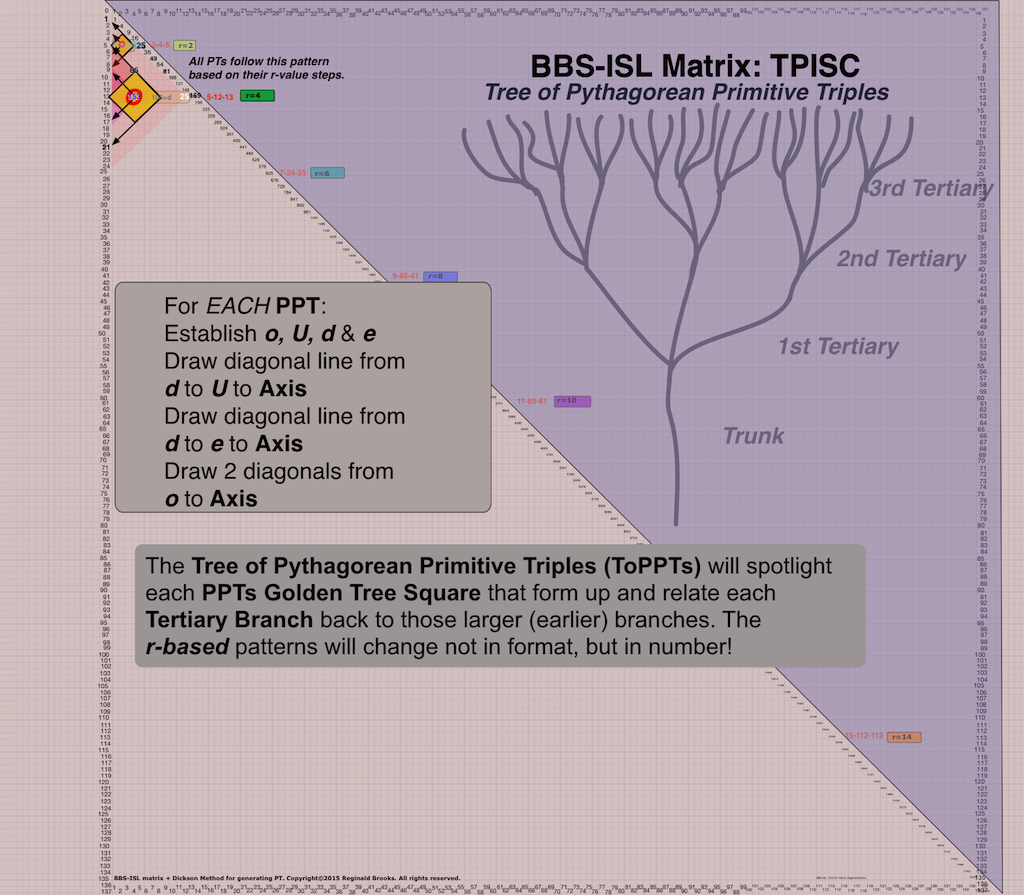Fig.49 "BIMtree-2"

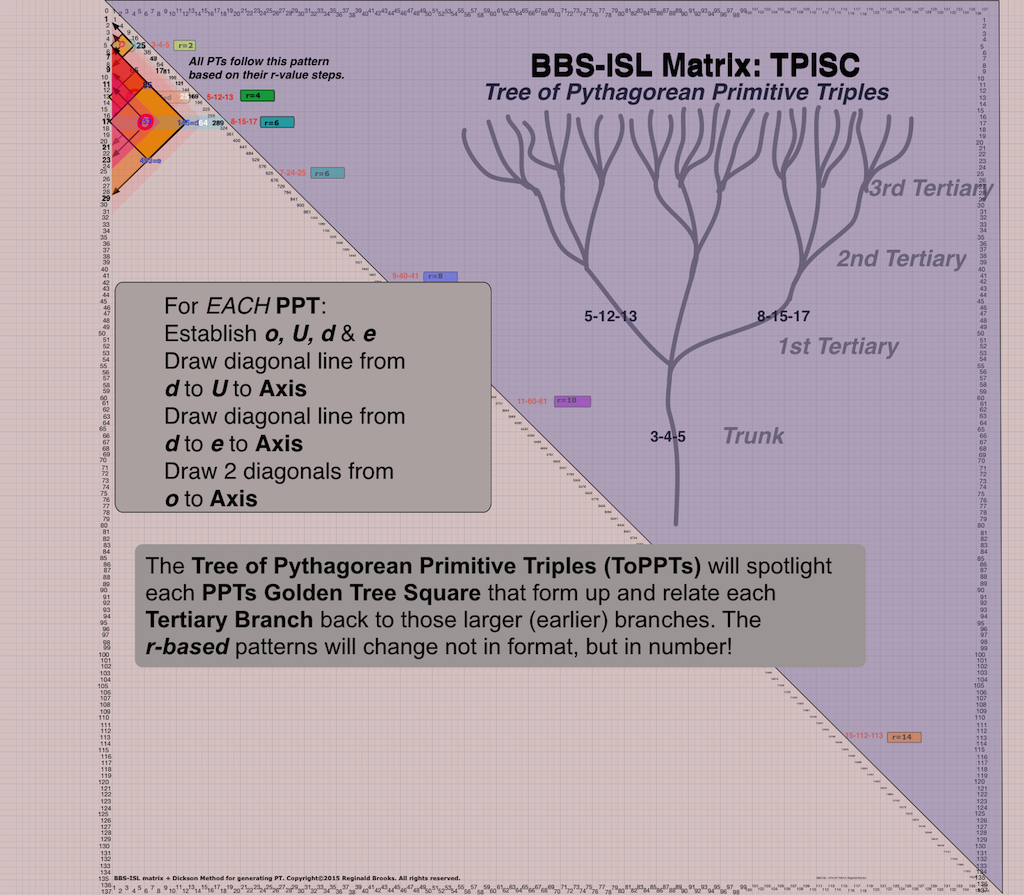Fig.50 "BIMtree-3"

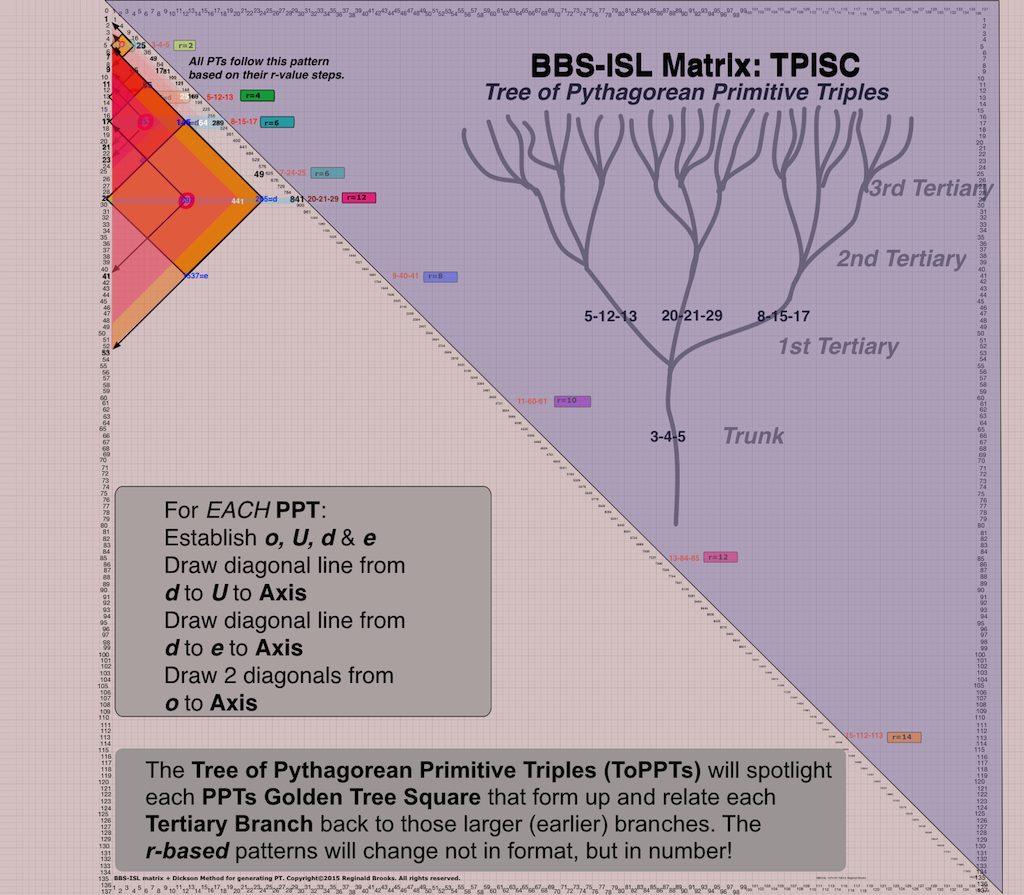Fig.51 "BIMtree-4"

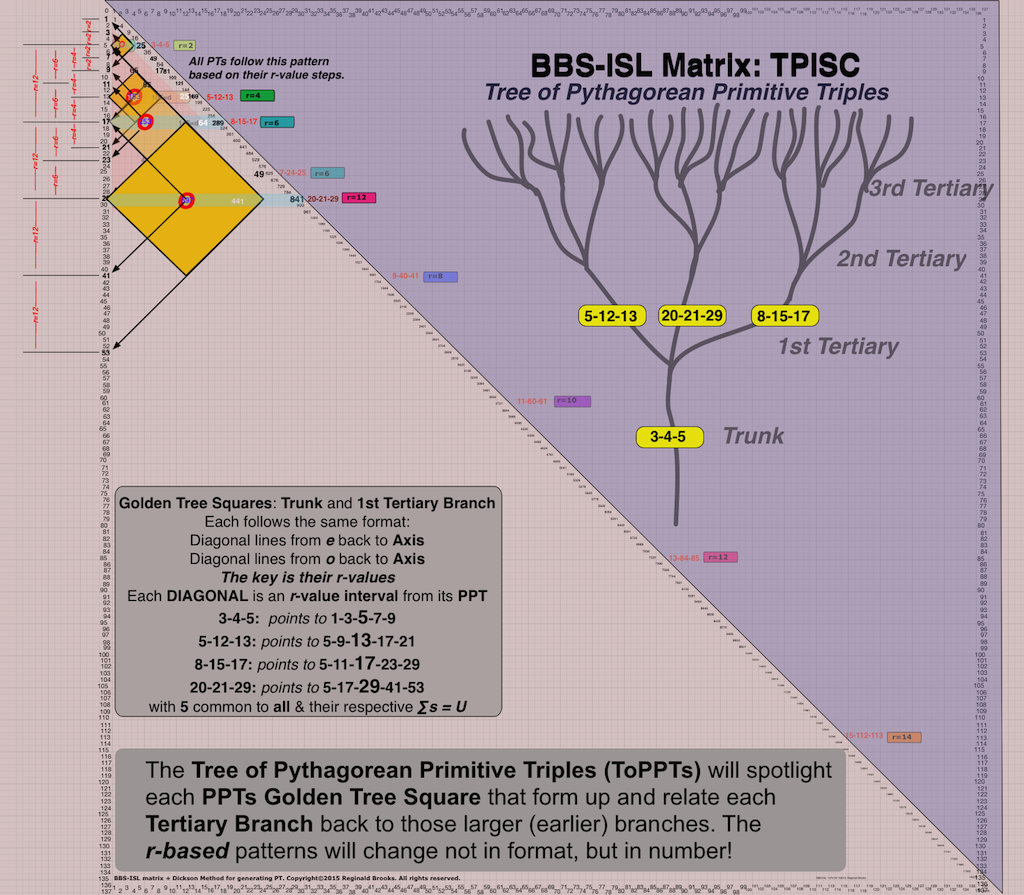Fig.52 "BIMtree-5"

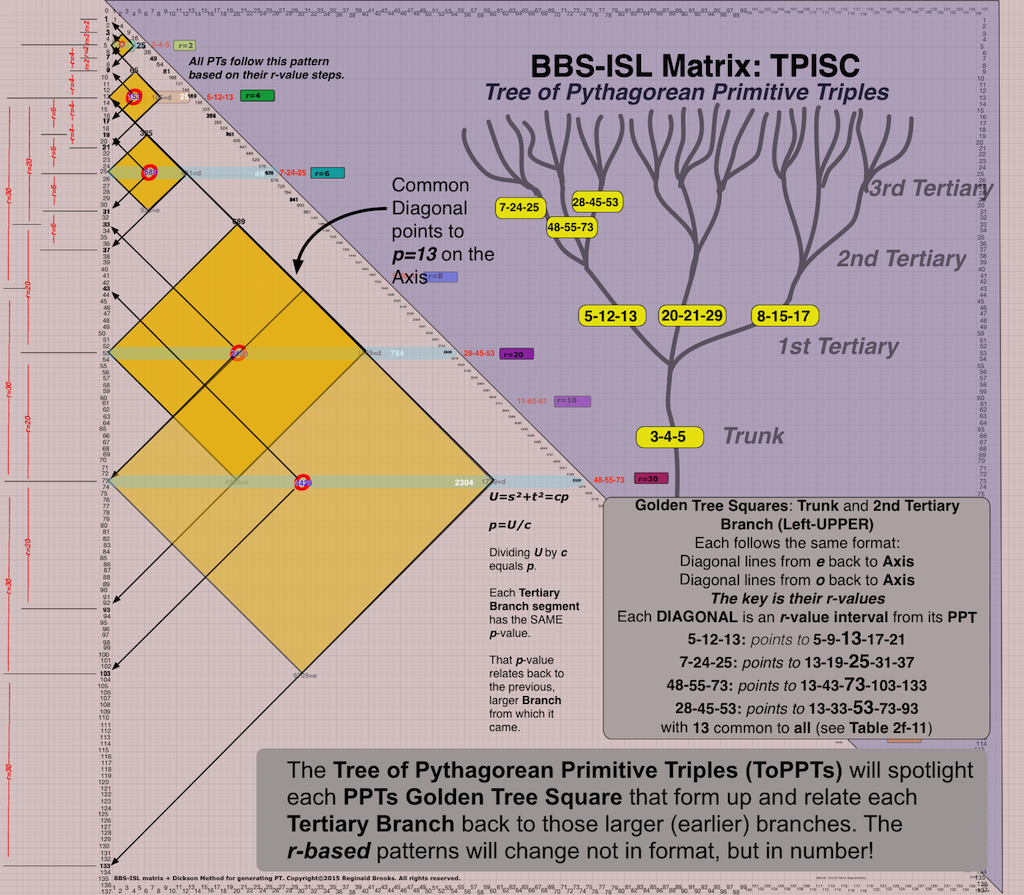Fig.53 "BIMtree-6"

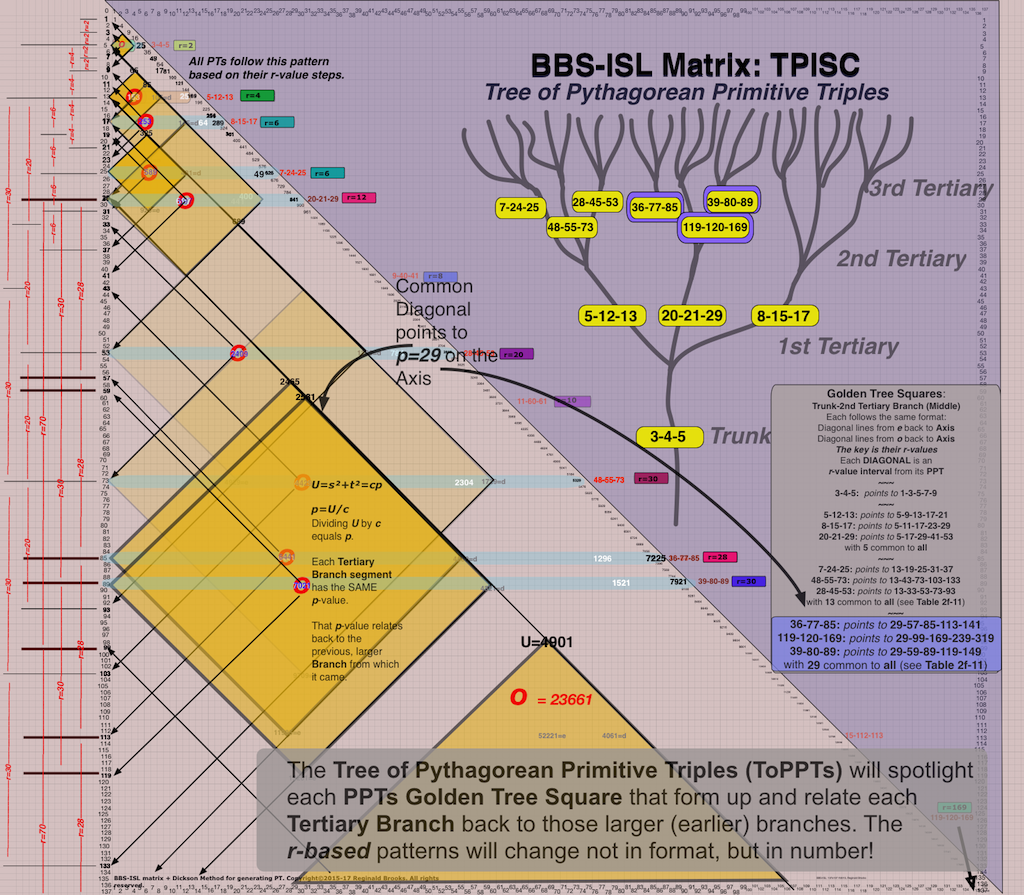Fig.54 "BIMtree-7"

Fig.55 "BIMtree-8"

BIMtree_p-patternUpperPythag Fig.56 "BIMtree-Upper (outer) Pythagoras Branch": Each is part of a different, separate Cluster.

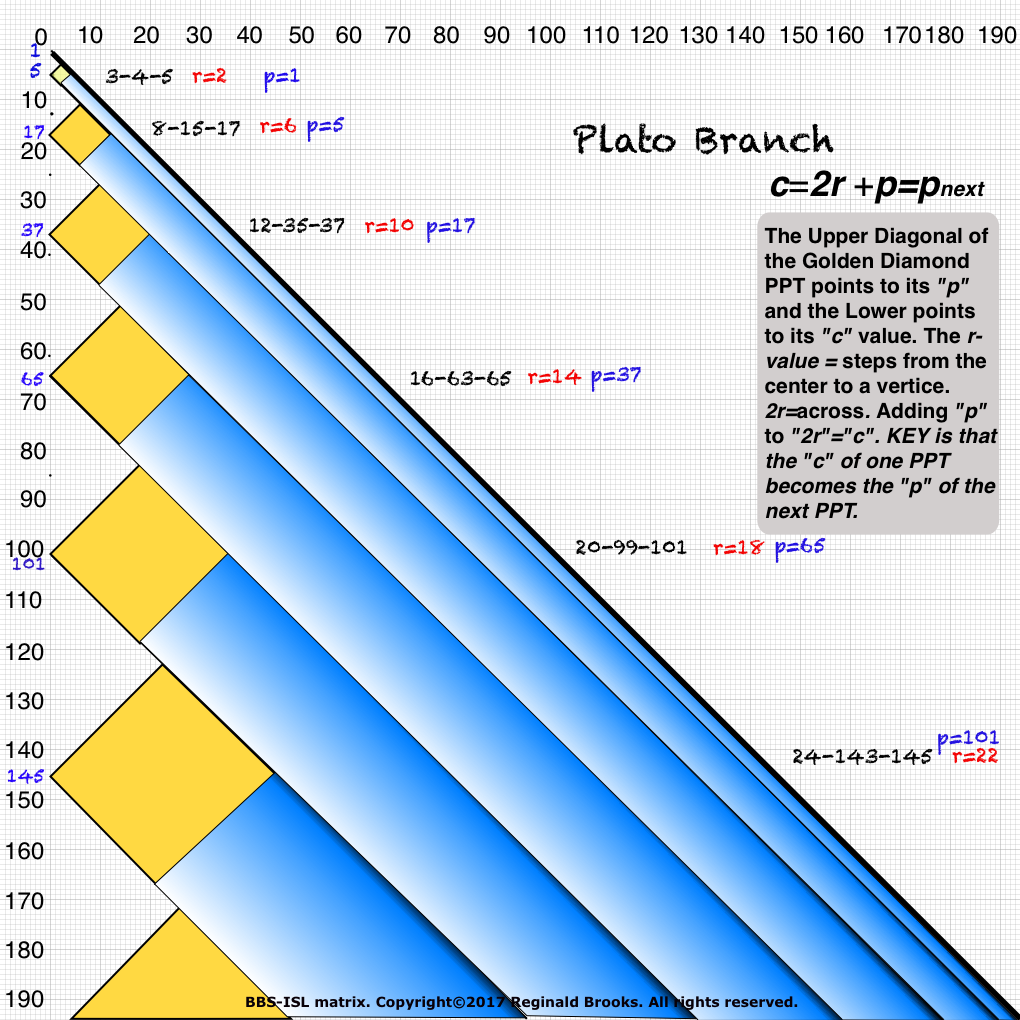Fig.57 "BIMtree-Lower (outer) Plato Branch": Each is part of a different, separate Cluster.

Fig.58 "BIMtree-Middle (inner) Pythagoras Branch": Each is part of a different, separate Cluster.

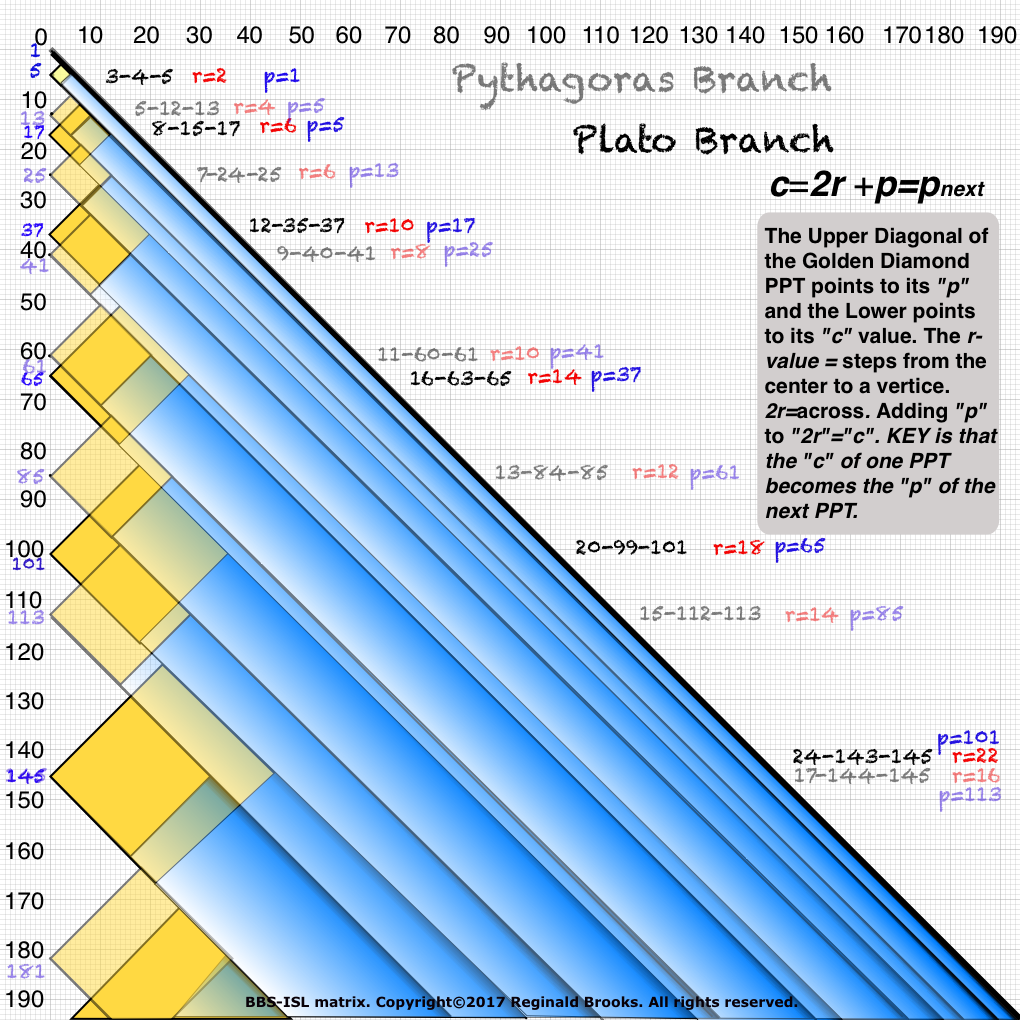Fig.59 "BIMtree-Upper (outer) Pythagoras Branch + Lower (inner) Plato Branches combined"

Fig.60 "BIMtree-Upper (outer) Pythagoras Branch + Middle (inner) Branch combined"

Fig.61 "BIMtree-Middle (inner) Branch + Lower (outer) Plato Branch combined"

Fig.62 "BIMtree-Upper (outer) Pythagoras+ Middle (inner) + Lower (outer) Plato Branches combined"

Fig.63 "BIMtree-Upper Pythagoras, Middle, Lower Plato + other Branches combined"

Fig.64 "BIMtree-Upper Pythagoras, Middle, Lower Plato + other Branches combined 2"

V. ToPPT: Linkage

A. Outward: Branches — TIERS

Go here for large table images.

Table 2a. "BIM tree": Trunk + 3 Tertiary Branches/Tiers. Each Branch makes a NEW 3-PPT Cluster Branch.

Table 2b. "BIM tree": Trunk + 3 Tertiary Branches/Tiers: making Upper & Lower Branches of a Cluster.

Table 2c."BIM tree": Trunk + 3 Tertiary Branches/Tiers: making the Middle Branch of a Cluster.

Table 2d. "BIM tree": Trunk + 3 Tertiary Branches/Tiers: making the 3 Branches of a Cluster.

Table 2e. "BIM tree": Trunk + 3 Tertiary Branches/Tiers: making the 3 Branches of a Cluster following f.

Table 2f-1. "BIM tree": Trunk + 3 Tertiary Branches/Tiers: making the 3 Branches of a Cluster step by step.

Table 2f-2. "BIM tree": Trunk + 3 Tertiary Branches/Tiers: making the 3 Branches of a Cluster step by step.

Table 2f-3. "BIM tree": Trunk + 3 Tertiary Branches/Tiers: making the 3 Branches of a Cluster step by step.

Table 2f-4. "BIM tree": Trunk + 3 Tertiary Branches/Tiers: making the 3 Branches of a Cluster step by step.

Table 2f-5. "BIM tree": Trunk + 3 Tertiary Branches/Tiers: making the 3 Branches of a Cluster step by step.

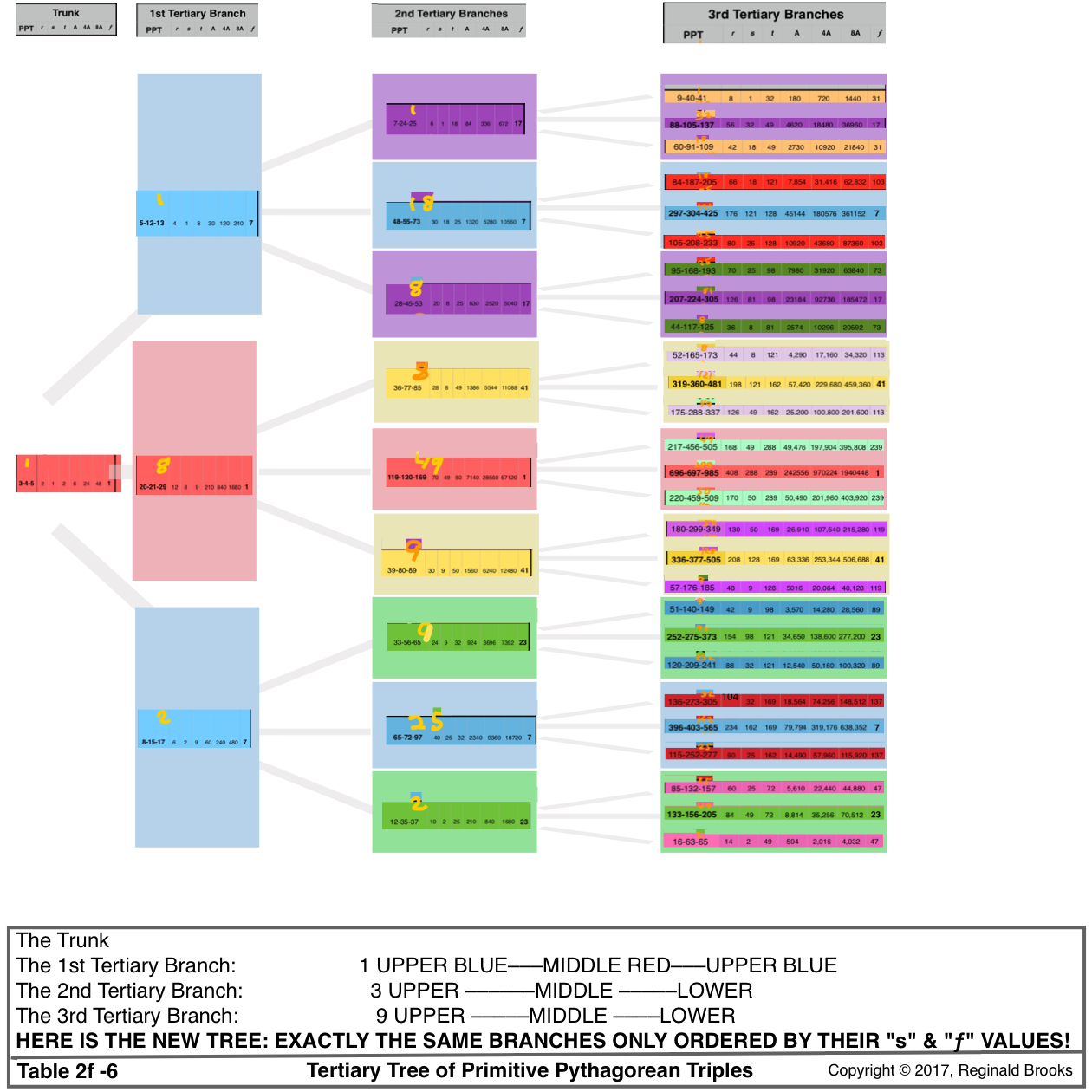Table 2f-6. "BIM tree": Trunk + 3 Tertiary Branches/Tiers: making the 3 Branches of a Cluster step by step.

Table 2f-7. "BIM tree": Trunk + 3 Tertiary Branches/Tiers: making the 3 Branches of a Cluster step by step.

Table 2f-8. "BIM tree": Trunk + 3 Tertiary Branches/Tiers: making the 3 Branches of a Cluster step by step.

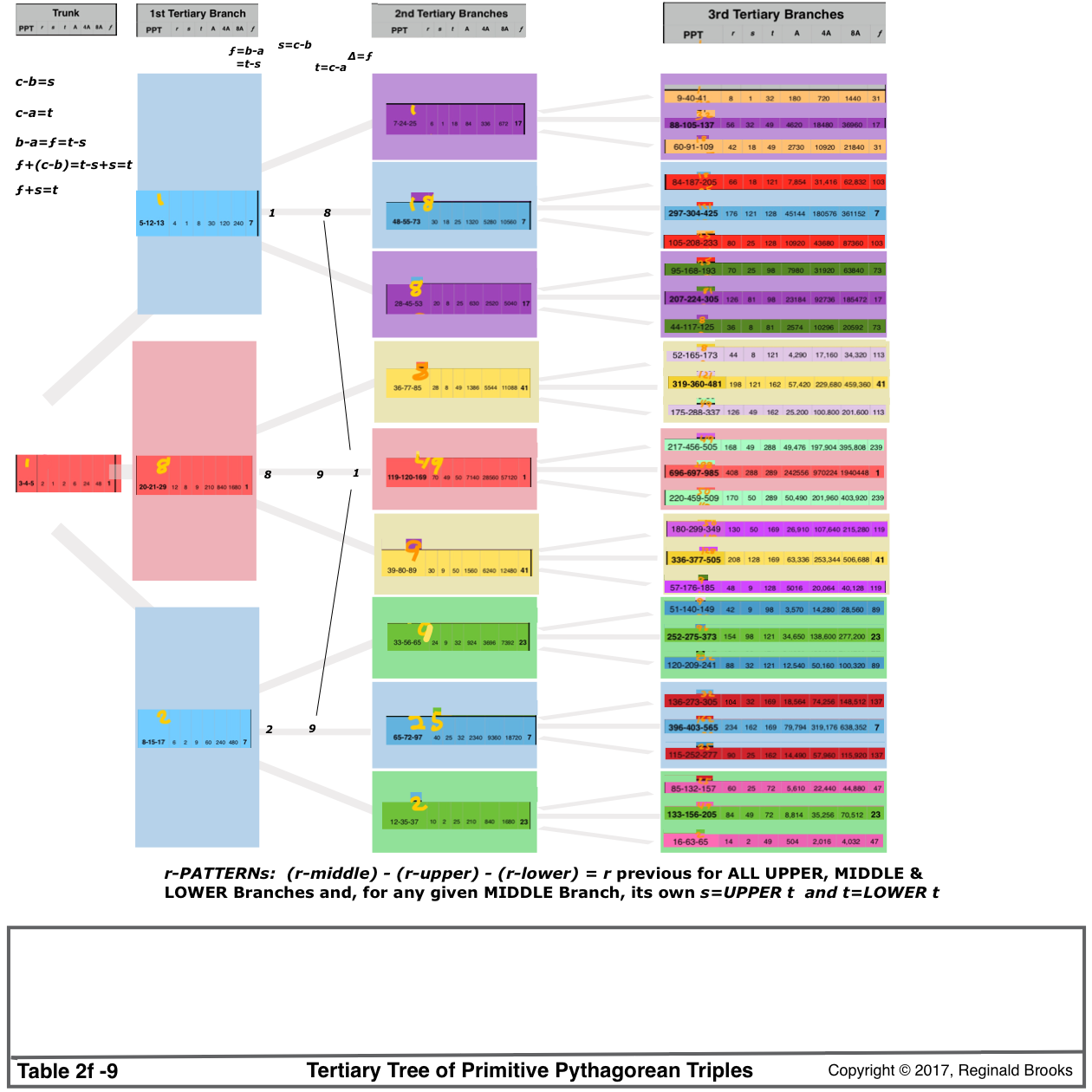Table 2f-9. "BIM tree": Trunk + 3 Tertiary Branches/Tiers: making the 3 Branches of a Cluster step by step.

Table 2f-10. "BIM tree": Trunk + 3 Tertiary Branches/Tiers: making the 3 Branches of a Cluster step by step.

Table 2f-11. "BIM tree": Trunk + 3 Tertiary Branches/Tiers: making the 3 Branches of a Cluster step by step.

Table 2g. "BIM tree": Trunk + 3 Tertiary Branches/Tiers: making the 3 Branches of a Cluster following.

Table 2h."BIM tree": Trunk + 3 Tertiary Branches/Tiers: making the 3 Branches of a Cluster following p.

Table 2i. "BIM tree": Trunk + 4 Tertiary Branches/Tiers.

Table 2j. "BIM tree": Trunk + 3 Tertiary Branches/Tiers: making the 3 Branches of a Cluster.

Table 2k. "BIM tree": Trunk + 3 Tertiary Branches/Tiers: making the 3 Branches of a Cluster.

Table 2l. "BIM tree": Trunk + 3 Tertiary Branches/Tiers: making the 3 Branches of a Cluster.

Table 2m-1. "BIM tree": Steps making the 5^th Tertiary Branch/Tier, Cluster by Cluster using r ,s ,t ,f & p.

Follow the 9 step-by-steps as the 5th Tertiary Branch — all 243 PPTs — are filled in leading to Table 2n below. See Appendix at the bottom.

Table 2n. "BIM tree": Steps making the 5th Tertiary Branch/Tier, Cluster by Cluster using r ,s ,t ,f & p.

Table 2o. "BIM tree": Differences (∆) in p-values within Clusters gives previous p-values in Branches before. The sum,∑ of the differences, ∆, in the p-values UPPER & LOWER, minus the ∆p MIDDLE, divided by 4, equals the previous p-value in the CLUSTER before. See Tables 2e,g,j,k & l for examples of √(8A+ƒ²)=ƒ_~u/l-next~.

Table 2p."BIM tree": Differences (∆) in p-values within Clusters gives previous p-values in Branches before. The sum,∑ of the differences, ∆, in the p-values UPPER & LOWER, minus the ∆p MIDDLE,, equals the previous-previous p-value in TWO CLUSTERs before.See Tables 2e,g,j,k & l for examples of √(8A+ƒ²)=ƒ_~u/l-next~.

Table 2q. "BIM tree": Differences (∆) in 5-Column values within Clusters give c=p-values in Branches before.

Table 2r. "BIM tree": Differences (∆) in 5-Column values within Clusters give c=p-values in Branches before.

Table 2s."BIM tree": Differences (∆) in 5-Column values within Clusters give c=p-values in Branches before.

B. Across: CLUSTERS

Table 2t."BIM tree": Every CLUSTER consists of an UPPER, MIDDLE, and LOWER PPT. The f-value of the MIDDLE PPT of a given CLUSTER is IDENTICAL to the previous MIDDLE PPT in the CLUSTER before. The UPPER & LOWER f-value is calculated as : f=p + ∆p/2. Every CLUSTER follows this NPS. Follow the MIDDLE. See Tables 2e,g,j,k & l for examples of √(8A+ƒ²)=ƒ_~u/l-next~.

Table 2u."BIM tree": Every CLUSTER consists of an UPPER, MIDDLE, and LOWER PPT. The f-value of the MIDDLE PPT of a given CLUSTER is IDENTICAL to the previous MIDDLE PPT in the CLUSTER before. The UPPER & LOWER f-value is calculated as : f=p + ∆p/2. Every CLUSTER follows this NPS. Follow the UPPER & LOWER. See Tables 2e,g,j,k & l for examples of √(8A+ƒ²)=ƒ_~u/l-next~.

Fig.65 "BIMtree"-Each 3-PPT CLUSTER has an UPPER, MIDDLE, and LOWER PPT. Each shares a Common p-value Diagonal Border. Each CLUSTER also has NPS across as well as from the CLUSTER before, from which it came. The ƒ-value — ƒ= t - s = b - a — is IDENTICAL for the MIDDLE PPT of any given CLUSTER growth, while the UPPER and LOWER PPTs are calculated from the MIDDLE as : ƒ = p + ∆p/2. Here the Golden Yellow Diamonds are the CLUSTER of the 1st Tertiary Branch/Tier.

Fig.66 "BIMtree"-Each 3-PPT CLUSTER has an UPPER, MIDDLE, and LOWER PPT. Each shares a Common p-value Diagonal Border. Each CLUSTER also has NPS across as well as from the CLUSTER before, from which it came. The ƒ-value — ƒ= *t - s* = *b - a* — is IDENTICAL for the MIDDLE PPT of any given CLUSTER growth, while the UPPER and LOWER PPTs are calculated from the MIDDLE as : ƒ = p + ∆p/2. Here the Pink Diamonds are the CLUSTER of the 2nd Tertiary Branch/Tier.

Fig.67 "BIMtre"-Each 3-PPT CLUSTER has an UPPER, MIDDLE, and LOWER PPT. Each shares a Common p-value Diagonal Border. Each CLUSTER also has NPS across as well as from the CLUSTER before, from which it came. The ƒ-value — ƒ= *t - s* = *b - a* — is IDENTICAL for the MIDDLE PPT of any given CLUSTER growth, while the UPPER and LOWER PPTs are calculated from the MIDDLE as : ƒ = p + ∆p/2. Here the Golden Yellow Diamonds are combined with the Pink Diamonds of the CLUSTERS of the 1st and 2nd Tertiary Branch/Tiers.

See Tables 2e,g,j,k & l for examples of √(8A+ƒ²)=ƒ_~u/l-next~.

Important in that in the Advanced Proof of the Pythagorean Theorem as applied to the PTs, the exact same geometry and its listings on BIM also provide the connecting link to the NEXT ƒ-values of the NEXT Tier CLUSTERS.

The 4A value — 4 x the AREA — is listed on the PT Row (or Column) directly down from its ƒ²-value on the Prime Diagonal. No small coincidence! c²= 4A + ƒ².

One can also find the 8A on the BIM: drop down r-value number of grid cell STEPS from the 4A location on the Row.

Thus for every PT, the ƒ², 4A and 8A values lie on a line perpendicular to the PT Row. The significance is that knowing these values, along with the r-, s-, t-, p- and the Perimeter, P- values, one can calculate any PTT in any CLUSTER on any Branch/Tier of the entire ToPPT.

The examples of the Advanced Proof shown below — demonstrating the proof on an easy to see 9-12-15 nPPT — are universal and apply to ALL PPTs.

Fig 68. The 9-12-15 nPPT on BIM: showing Simple & Advanced Proofs with application to the ToPPT.

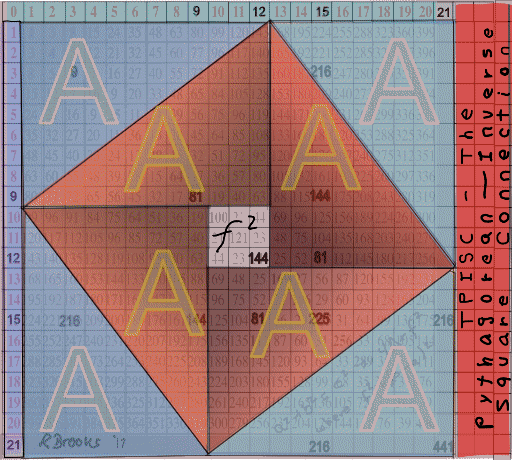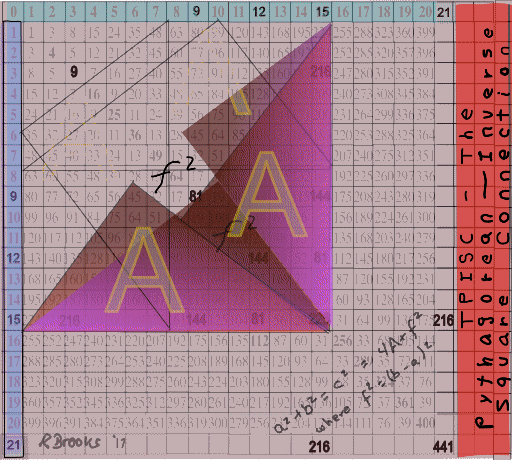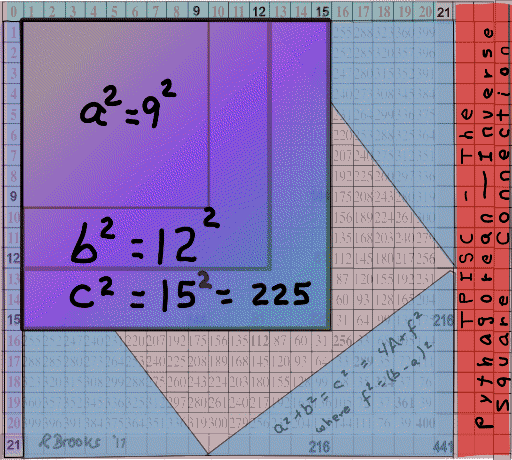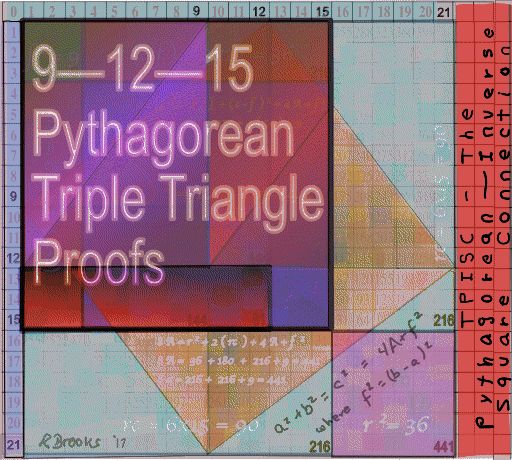Fig 69. The 9-12-15 nPPT on BIM: showing Simple & Advanced Proofs with application to the ToPPT.

A short video is also available on Vimeo.

https://vimeo.com/212972290

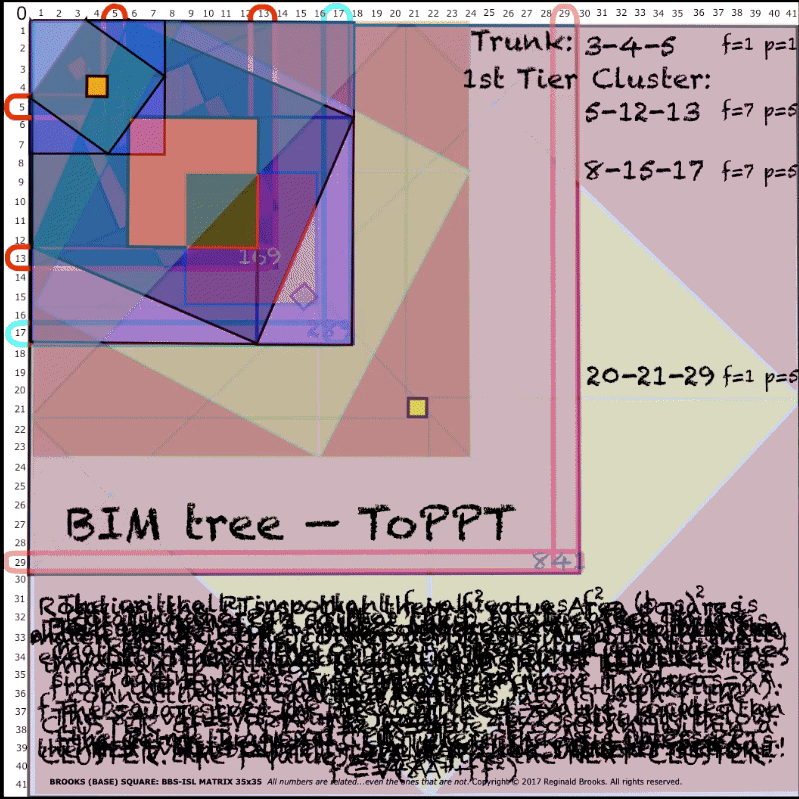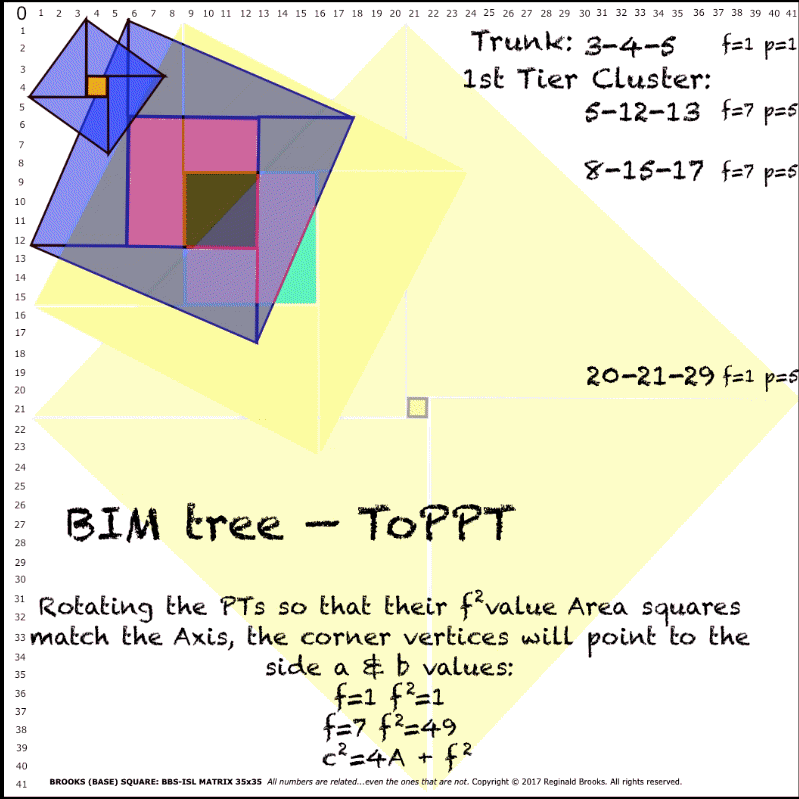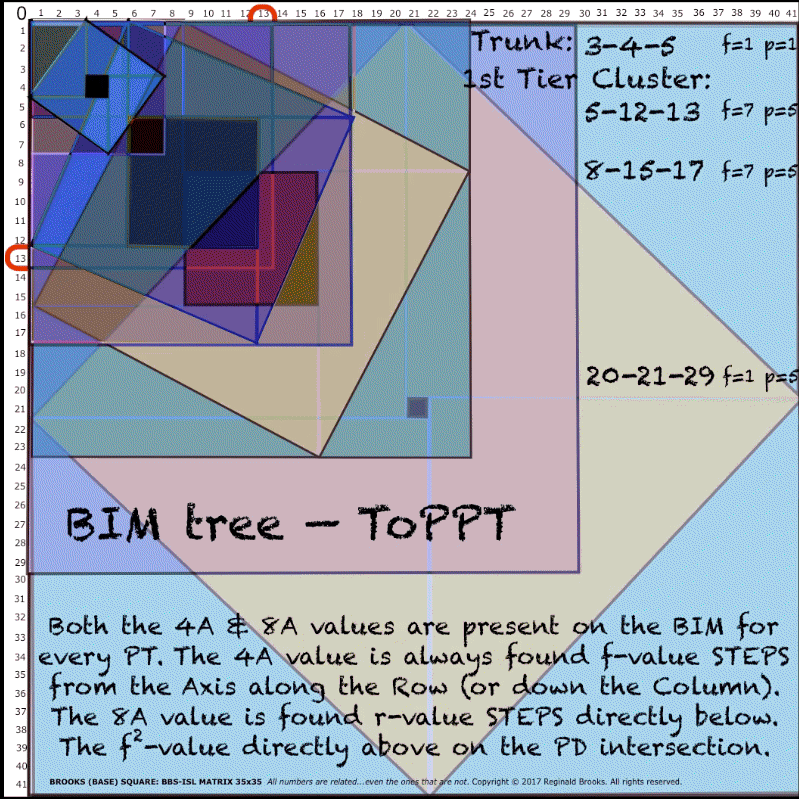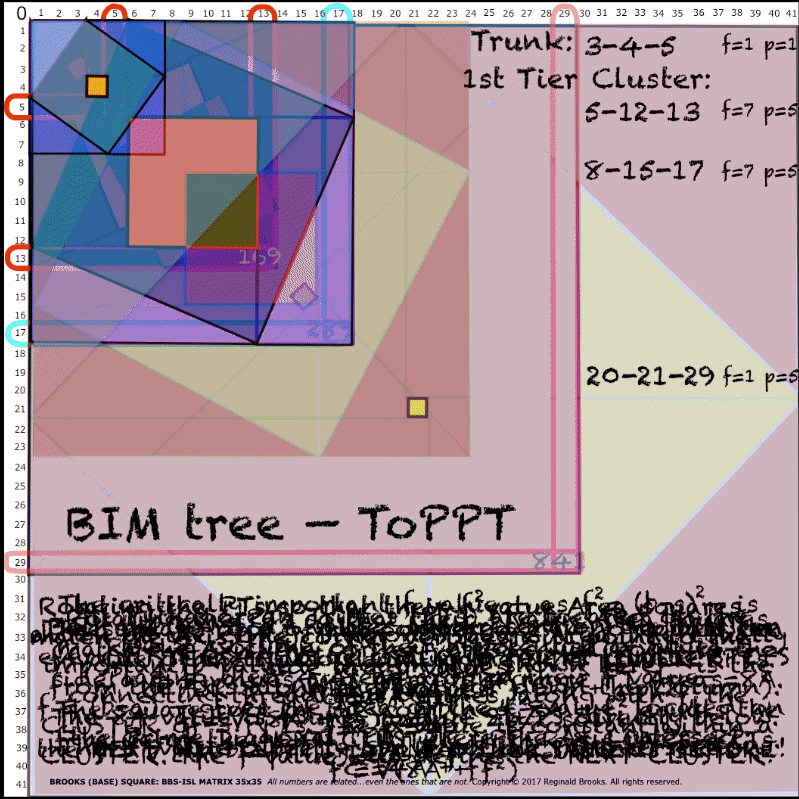Fig 70. The 3-4-5 Trunk PPT + 5-12-13, 8-15-17, and 20-21-29 CLUSTER of PPTs from the 1st Tertiary Branch/Tier on BIM: showing Simple & Advanced Proofs with specific application to the ToPPT.

Fig 71. The 3-4-5 Trunk PPT + 5-12-13, 7-24-25, and 9-40-41 Pythagoras Branch PPTs demonstrate a universal growth-linkage pattern found in all Branches of the ToPPT. Like Russian Nesting Dolls, the (8A+ƒ² ) complete AREA of an earlier, related PPT, becomes the ƒ² AREA of the NEXT UPPER & LOWER PPT! This nesting repeats through ALL the PPTs related by their CLUSTERs in each subsequent Tertiary Branch/Tier.

The examples shown herein: the combined (8A+ƒ² ) complete AREA of the Trunk 3-4-5 PT becomes the NEXT ƒ2 AREA of the NEXT UPPER & LOWER PPT, in this case the UPPER 5-12-13 PT of the Pythagoras Branch. In doing so, the c=5 value of the 3-4-5 becomes the p=5 value of the 5-12-13 PT.

Now, the combined (8A+ƒ² ) complete AREA of the 1st Tier 5-12-13 PT becomes the NEXT ƒ² AREA of the NEXT UPPER & LOWER PPT, in this case the UPPER 7-24-25 PT of the Pythagoras Branch 2nd Tier. In doing so, the c=13 value of the 5-12-13 becomes the p=13 value of the 7-24-25 PT.

Next, the combined (8A+ƒ² ) complete AREA of the 2nd Tier 7-24-25 PT becomes the NEXT ƒ² AREA of the NEXT UPPER & LOWER PPT, in this case the UPPER 9-40-41 PT of the Pythagoras Branch 3rd Tier. In doing so, the c=25 value of the 7-24-25 becomes the p=25 value of the 9-40-41 PT .

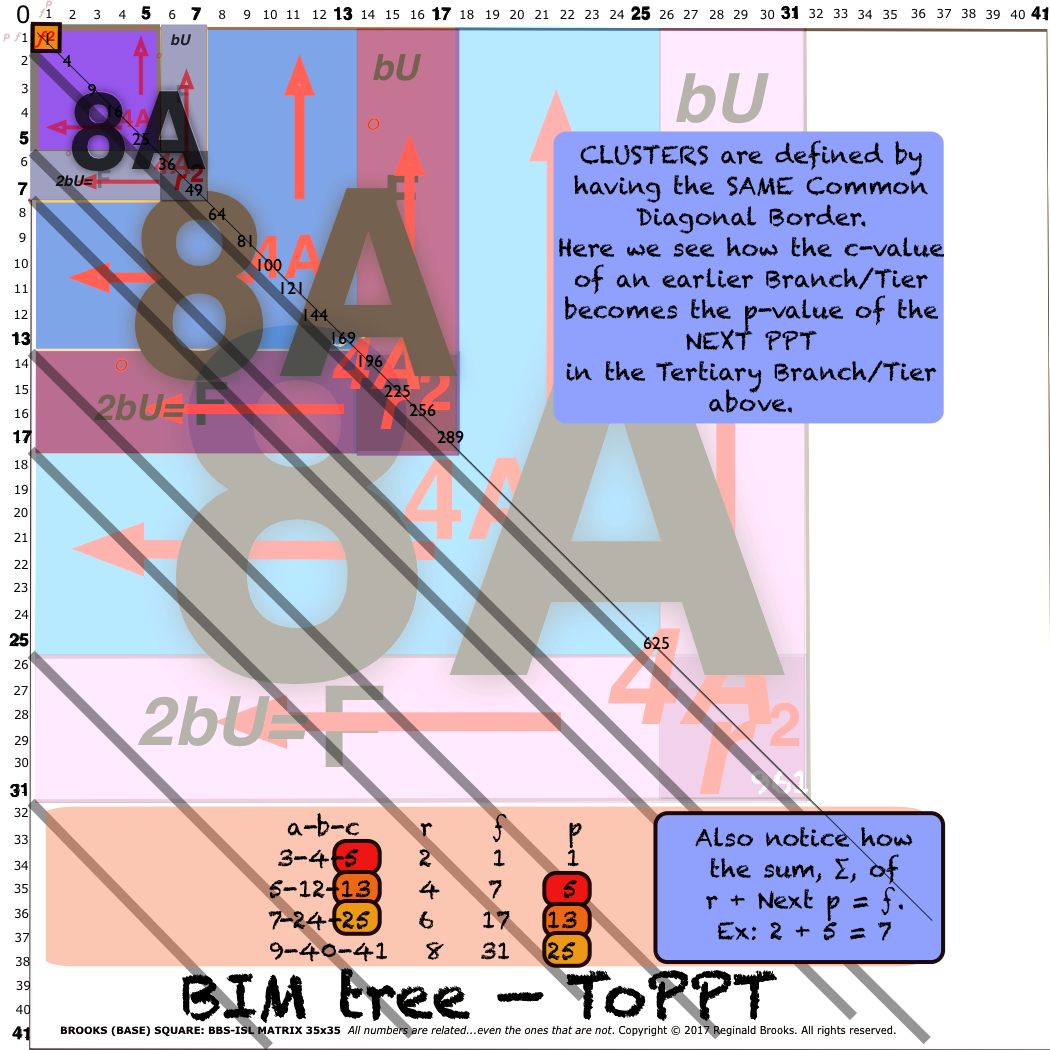Fig 72. The 3-4-5 Trunk PPT + 5-12-13, 7-24-25, and 9-40-41 Pythagoras Branch PPTs demonstrate a universal growth-linkage pattern found in all Branches of the ToPPT. Like Russian Nesting Dolls, the (8A+ƒ² ) complete AREA of an earlier, related PPT, becomes the ƒ² AREA of the NEXT UPPER & LOWER PPT! This nesting repeats through ALL the PPTs related by their CLUSTERs in each subsequent Tertiary Branch/Tier.

The examples shown herein: the combined (8A+ƒ² ) complete AREA of the Trunk 3-4-5 PT becomes the NEXT ƒ² AREA of the NEXT UPPER & LOWER PPT, in this case the UPPER 5-12-13 PT of the Pythagoras Branch. In doing so, the c=5 value of the 3-4-5 becomes the p=5 value of the 5-12-13 PT.

In addition, notice how the sum (∑), of the r-value + p_NEXT - value = ƒ-value of that NEXT PT!

The following two videos present much of the same information, now in the video format:

The SHORT video version of BIMtree-ToPPT gives an overview of the more detailed view below.

BIM—ToPPT (short) from Reginald Brooks on Vimeo.

The video version of BIMtree-ToPPT allows one to stop any image for further viewing.

BIMtree-ToPPT from Reginald Brooks on Vimeo.

C. Specials: Pythagorean, Middle & Plato Branches

Calculating the two outer branches — the Pythagorean and Plato, UPPER and LOWER Branches, respectively — along with the constant ƒ-value of the MIDDLE Branch, is the surest way to start building the ToPPT.

Table 3a. "BIM tree": The Pythagoras Branch (UUUUU), the outermost branch on the UPPER side.

Table 3b."BIM tree": The Plato Branch (LLLLL), the outermost branch on the LOWER side.

Table 3c. "BIM tree": The Middle Branch (MMMMM), the inner-center branch on the Middle Branch.

Table 4a. List of ALL Primitive Pythagorean Triples up to c=2100 in 4 parts a-d.

Table 4b. List of ALL Primitive Pythagorean Triples up to c=2100 in 4 parts a-d.

Table 4c. List of ALL Primitive Pythagorean Triples up to c=2100 in 4 parts a-d. Table 4d. List of ALL Primitive Pythagorean Triples up to c=2100 in 4 parts a-d.

Table5a. "BBS-ISL_Matrix-FPS": Factor Pairs Sets and Row & Column values (lower half: 25x25)

Table5b." BBS-ISL_Matrix-FPS": Factor Pairs Sets and Row & Column values (lower half: 35x35)

VI. Summary

It has been firmly established that light diminishes with distance — as does energy.

Once we accept that ALL energy is made up of and is a manifestation of spacetime (ST), we can make a major connection!

ST itself must expand to create and fill-out the Universe. It must constantly refresh itself to account for the energy flux. We call this “pulse-propagating ST.”

Each quantum unit of ST pulse-propagates into — and out of — existence at its wavelength and frequency, generating the speed of light influence that expansively propagates outward from its source (singularity).

The Universal Law that describes the overall density distribution of this pulse-propagating ST influence is the Inverse Square Law (ISL), and, the matrix grid that visualizes it, the BBS-ISL Matrix (BIM for short).

The BIM is all based on AREAS — areas of perfect Squares — described in simple Whole Integer Numbers (WIN).

The Axes are simply WINs 1,2,3,… and the Prime Diagonal (PD) is their Square AREAS 1²,2²,3²,… as 1,4,9,…

The AREA Squares on the PD naturally have 4—90°-right-angles. 90°-right-angles are key in defining ST!

All the Inner Grid (IG) cells are simply the 90°-right-angle difference (∆) between two PD#s.

Now, a really interesting thing occurs: the pure AREA Squares of the PD appear mirrored onto the IG, but NOT just anywhere. They are mirrored onto the IG in groups of two (Paired Sets) on select Rows (and Columns) ONLY.

These mirrored-AREA Squares become the the AREA Squares — i.e. Squared AREAS — of the shorter a & b sides of a Pythagorean Triple (PT) triangle as a² & b². Their sums (∑) equal the long side — c² (hypotenuse) — on the PD where the Row and Column intersect.

~~ ~~ ~~

Well, let’s not stop here!

The AREA of that PT × 4 — 4A — is found on that SAME Row (or Column), and, the ∑ of 4 AREAS +ƒ² = c², where ƒ² is the ∆ between side b & a, squared, as (b-a)².

8A is also present on the BIM, below the 4A.

Combining 8A + ƒ² = the NEW “Next” ƒ² of the “Next” PT growth along a Branch on the Tree of Primitive Pythagorean Triples (ToPPT).

Clusters — the UPPER, MIDDLE and LOWER PT triplets extending each Branch — are connected to each other and provide linkage to the BIM in that they ALWAYS have the SAME p-value Diagonal of the Golden Squares that they form! This is clearly shown on the BIM via the Fully Extended Dickson Method (FEDM).

The multitude of 90° right-angle-related parameters — all based on their respective r-value (STEPS) interval — fully defines a given PT profile, its built-in proof and its linkage connecting it to other PTs.

This combination of algebra and geometry — algebraic geometry — is referred to as the FEDM and forms the core of TPISC IV: Details.

In TPISC V: Exponentials, we find that ALL X² values are found as AREAS on the PD, while ALL Exponentials greater than X², are found internally on the IG as AREAS sequentially distributed on Diagonals parallel to the PD.

Exponentials also follow a simply Number Pattern Sequence (NPS) of AREAS & STEPS both along X³, X⁴, X⁵,… and across 2³, 3³, 4³,… their sequential arrays.

Their NPSs are based on their Row & Column values that are simply their Factor Pair Sets (FPS or FS), set at 90°right-angles to each other.

ALL AREAS of Exponentials are related back to their source.

And while ALL Exponential AREAS that are perfect Square AREAS are also related to PTs, NOT ALL Exponential AREAS are Square AREAS — some being non-square Rectangle AREAS. This topic is covered in TPISC V: Exponentials.

Re-arrangement of the Branches of the Tree of Primitive Pythagorean Triples allows their natural placement on the BIM forming the BIMtree.

Number Pattern Sequences completely define the natural "growth" of the Tertiary Branches into Tiers containing Clusters.

Each Cluster consists of three (3) related PPT Branches.

Each PPT within its Cluster has the SAME IDENTICAL p-value and thus enjoys a COMMON DIAGONAL BORDER of the Golden Square Diamond that graphically depicts it presence on the BIM.

Within a Tertiary Branch Tier Cluster, across Clusters, and between Clusters on Tertiary Branches previous and next to the one under consideration, a NPS based on differences in the p-values (and c-values) connects each and every PPT to every other PPT throughout the ToPPT, right down to the 3-4-5 PPT of the Trunk.

The NPS allows the ToPPT to be extended indefinitely to infinity.

And to re-emphasize: The ToPPT grows inverse to that of the often portrayed natural tree. Its 3-4-5 PPT Trunk is the smallest PT, with each Tertiary Branch forming Tiers with increasingly LARGER PTs!

Little doubt remains that The Pythagorean - Inverse Square Connection (TPISC) is intimate, formidable, and structurally informative in such a deep and profound way that — as repeated before — they are nearly interchangeable. Knowing one allows the building of the other! As the ISL informs the very fundamentals of ST formation —zowie— so does the ToPPT, or more specifically, the Pythagorean Triples!

VII. Conclusion

Thomas Young established the wave nature of light in the Young Double-Slit Experiment.
Max Planck established the quantum nature of light energy mathematically (E=hⱱ).
Albert Einstein established that ALL energy is quantized (E=hⱱ), energy and matter are inter-convertible ((E=mc²), and that the speed of light is always constant (c=ƴⱱ) — and later, the curvature of ST as the driving dynamic informing gravitation (General Relativity).
Niels Bohr established the quantization of the atomic orbitals within the atom (Bohr Model of the Atom). Along with Heisenberg, the leading voices in the Copenhagen Interpretation of Quantum Mechanics.
Louis de Broglie established the all objects express the wave-particle duality as defined by its momentum being its energy per wavelength (p=h/ƴ).
Werner Heisenberg established the Uncertainty Principle that reveals the limitation of precisely and simultaneously defining both an objects position and its momentum (∆x∆p≥h/2𝛑).
Arnold Schrödinger established the time-dependent Schrödinger (Quantum) Wave Equation.
Max Born established the statistical basis of the same Quantum Wave function.
Wolfgang Pauli established the Pauli Exclusion Principle that disallows any quantum particle to occupy the same quantum state (parameters) within the same ST.
Paul Dirac established the Dirac Equation, a relativistic generalization of the Schrödinger equation
wave equation for fermionic spin ½ particles, bringing together the two pillars of special relativity (3 dimensions of space+1 dimension of time, and the constancy of the speed of light, c=ƴⱱ) and quantum mechanics (h/2𝛑=E/v) leading to Quantum Field Theory and the Standard Model.
Quantum Entanglement , initially raised in opposition in 1935 in the Einstein, Podolsky, Rosen paper (EPD Paradox) and papers by Schrödinger, was brought to the forefront of debate in 1964 with John Stewart Bell's Inequality Theorem ruled out the "local hidden variables" of the opposition. Since then the quantum entanglement — i.e., particles bound in entanglement cannot be factored out into separate states that would explain their entanglement, the particles act together as a whole, not the sum or product of their parts — has been successfully tested and appears to be profoundly consistent with the Quantum Field theory. It is in direct opposition to Einstein's nothing — no information — can travel faster than the speed of light. And yet, here we have proofs stacking up show that, for example, two entangled particles with equal but opposite spin will simultaneously settle into one of the other spin directions opposite its entangled partner instantly once its partner's spin is determined — faster than the speed of light. Einstein's "local hidden variables" may not be completely ruled out if, indeed, one reveals a different sort of underlying geometric order that sidesteps being ruled out by the Inequality Theorem — a geometric order that precedes the very formation of ST itself (BIM-BIMtree).

Double-Slit Experiment:

In essence, even a single photon or electron passing through a double-slit will display interference, collapsing upon any interacting measurement upon the initiating wave particle.

Fig.73. Double-Slit Experiment

Quantum Entanglement:

In essence, any two (and possibly more) wave-particle ST units born of and thus assigned the same, equal but opposite quantum number state, i.e. spin angular momentum, will maintain and function as a single wave-particle system having a single quantum number state regardless of distance or time separation, in the absence of external negating influences. Transference is possible.

If c, the speed of light, is fundamentally buit into the formation of ST itself — moving ƴ distance with each pulse-propagating ⱱ frequency — as described in LightspeedST — and as combined with MathspeedST, i.e. through the BIM informing that same ST pulse-propagating unit — all potential ST information, as to density and disposition of space per time, is inherently known!

The BIM itself is defined as a Universal Relationship. Its numerical value of the quantity of parts (the value in each grid cell), in relation to its whole (the square values of the PD — that, by the way, directly inform the parts) is instantly and ubiquitously known for every value throughout BIM as extended to infinity.

There is no propagation of information faster than c because all its information is simultaneously known. We thus have a basis for Quantum Entanglement: two or more particles born of the same quantum number state wholy remain connected regardless of distance of separation precisely because they are informed by the SAME BIM-derived ST pulse. No information is exchanged — no violation of faster-than-light signals because both (all) particles have the SAME BIM information map informing their quantum state parameters at any and all ST unit pulses (ⱱ).

The Quantum Entanglement example most referenced is that of spin, a vector momentum parameter.

Two entangled particles (e.i., two photons or an electron-positron pair) are simultaneoulsy born, each existing with both possible equal but opposite spin states.

Upon any distance (or time) separation, determining the spin quantum state of one particle — collapsing its wave potential of both into that of one polemic — immediately determines the other as equal but opposite.

Equal and opposite what?

The spin quantum state is a vector whose magnitude and expression is dependent on orientation (direction).

So, for whatever context that vector exists within, a polemic is established, i.e., +/-, ↑/↓, yes/no, that inherently establishes a positive and negative state (Dirac Equation) — e.i., matter/anti-matter, +charge/-charge, spin+/spin-.

The Quantum Entanglement State (QES) is just such a context — a container, if you will — holding the full potential of either/or vector states within its potential wave form.

Measurement (Heisenberg Uncertainty Principle) —that is interacting with such potential state — necessarily collapses the potential wave-state into a definitive, particulate-like state — call it +/-, ↑/↓, yes/no, or Even/Odd.

In effect, one has induced the vector state. In doing so, the other entangled member has its vector state induced to that equal, but opposite polemic value to its partner.

Now, let the QES=BIM. Let collapsing the wave-potential (the entire BIM) = √BIM. Since BIM is built on squaring the 1,2,3… Axis numbers to give the PD — and all the Inner Grid cell values as its children — taking the √BIM is akin to collapsing BIM back to the equal and symmetrical opposite Axial numbers along the horizontal and vertical Axises.

Alternatively, the BIM may indeed project into the imaginary number space, i, giving the equal but opposite value a more hidden meaning.

Yet another alternative — and within the context of the current mathematical space the BIM occupies — one may induce the ubiquitous and infinity expanding Pythagorean Triples to provide the necessary polemical expression of a vector from the multi-potential of its wave-form. In this case — and exactly in tune with the BIM layout — there is a 90°-right angle relationship between the sides. In the BIM it is within a square, within the PTs it is within a rectangle (formed from the two orientations of the triangle). Both have a symmetry involved. The BIM has an absolute, bilateral mirror-reflection symmetry. The latter an algebraic symmetry in that various whole integer combinations of a² + b² =c².

In fact, there are, as we mentioned in the Intro, 4 geometric manifestations of each algebraically described PT. Two for each side of the bilaterally symmetric BIM, and two orientations (180° flips along the row/column). Perhaps the polemic we are looking for is simply the wave-collapse selection of one of the 4 possible orientations of the PT, with its opposite simply its mirror reflection on the other side of the BIM.

Fig 74. The Quantum Entanglement Conjecture. Every PT has 4 potential presentations: each has a mirror symmetry, and because BIM has itself reflective, mirror bilateral symmetry, there are two more.

The Quantum Entanglement Conjecture:
Every PT has 4 potential presentations: each has a mirror symmetry, and because BIM is internally itself reflective, mirror bilateral symmetry, there are two more.
For simplicity, the TPISC painting image (Fig.74.) has been overlaid with three sets of PTs — each having 4 potential presentations. Exactly the same is true for the strictly Primitive PTs within the ToPPT.
As ST formation is informed most certainly by the ISL (BIM), the PTs, and most especially the Primitive PTs within the ToPPT, are viable candidates for laying down a bit of slightly asymmetrical bilateral symmetry framework embedded within the perfect rotational and bilateral symmetry the perfect squares and circles generated by the BIM.
While the BIM itself is composed of alternating ODD and EVEN whole integer numbers, the PTs, especially the PPTs, pick these ODD and EVEN numbers out as part of their natural structure. Every PPT has one short side made of an ODD number and the other is always the opposite — an EVEN number.
If one pictures the 4 potential presentations of the PT as existing as the wave-potential state of a forming particle, the naturally built-in polemics of these ubiquitous triangles comes into play: selecting to "measure" any one parameter as say, the spin ½ momentum vector, could collapse the wave function such that the other, opposite side of the polemic — which is always known as part of the Entangled Quantum State — could only express that opposite value.
It could be something as simple as solving the Pythagorean Theorem. If you measure (solve) for one short side — an let's say it is an EVEN whole integer number — you instantaneously know the other side is ODD. You also can know its value if you know the hypotenuse.
If you measure (solve) for one short side — an let's say it is an ODD whole integer number — you instantaneously know the other side is EVEN. You also can know its value if you know the hypotenuse.
The geometry of ST formation generates descriptive parameters referred to as quantum numbers or their quantum number state — unique identifiers for each and every subatomic particle. These wave-particle ST units exhibit unusual and non-intuitive behaviors that reveal a connection to each other below the physical reality we observe. The Conjecture is that that underlying connection is the BIM and BIMtree geometry that informs the creation and disposition of ALL ST — including their quantum number state identifiers.
Back to the Double-Slit Experiment Conjecture:
In the simplest terms, the ST formation of the wave-particle pulse-propagates into and out of existence according to its energy.
Each pulse expands form its own singularity outward via the BIM.
The ST-BIM expands outward in all directions as a sphere, despite its forward motion as a vector. Thus it travels through both slits and interferes with itself on the other side.
It is the BIM geometry information that is traveling through both slits, i.e. it doesn’t actually travel, rather it is known.
If you block one of the slits or otherwise collapse the geometry wave by measuring or interacting with it, no interference occurs.
How does it work?
There are several possibilities.
It may be as simple as positive interference patterns may appear when the same Square/Circle WIN values of the BIM resonate and negative when they do not — giving the classical light-dark-light-dark pattern.
Or, it may be the same resonance interference positive/negative superpositions for the PTs. As ST expands, a positive interference pattern would result when two (or more) 3-4-5 PPTs harmoniously arrive at the same ST location on the screen. The same for the 5-12-13, 8-15-17, etc. In either case, if you block one slit or collapse the expanding BIM geometry before entering the slit, interference will also collapse.
A third, and perhaps more relevant possibility includes the interaction with the slit material itself. Remember, ALL ST pulse-propagates into and out of existence. All matter and all energy, including the material that the slits are made of, pulse. When only a single slit is open, the BIM geometry of the incoming wave-particle interacting with the slit ST does NOT generate an interference pattern.
However, when two slits are open, the BIM-ST geometry of the slit material favorably interacts with the BIM-ST geometry of the wave-particle to generate interference!
One cannot ignore the contribution of the slit BIM-ST geometry in forming the net pattern. Having more than a single wave-particle ST unit passing through the slit(s) is simply magnifying the fundamental interaction between the slit material and wave-particle BIM-ST geometries!
As Heisenberg so profoundly pointed out, all contributions to any observation-measurement scenario must be accounted for.
Together, the Double-Slit Experiment and Quantum Entanglement Conjecture (DSEQEC) are but two sides of the same coin. Details to follow in TPISC IV and V.
The absolut key notion in the DSEQEC is that the geometry of the BIM and BIMtree both simultaneously and automatically precede and inform the subsequent ST unit expression, and, that this geometry is ubiquitous — expanding to infinity!

Aside from the Conjecture, we have firmly established the true and complete description of the ToPPT as embedded ubiquitously throughout the infinite BIM. Every PPT forming every Cluster within every Branch forming every Tertiary Branch Tier can be defined and related back to the Trunk — the fundamental 3-4-5.

The essence of this linkage is that:

every 3-PPT CLUSTER is bound and defined by having the SAME COMMON BORDER DIAGONAL (ending up on the Axis as the p-value);
the (8A+ƒ² ) complete AREA of an earlier, related PPT on the same Branching , becomes the ƒ² AREA of the NEXT UPPER (& LOWER) PPT along that Branch;
the MIDDLE PPTs ALWAYS maintain the SAME ƒ-value throughout the Branching, thus no nesting of ƒ² AREAs;
the c-value of lower Branching PPT becomes the p-value of the NEXT PPT along that Branching sequence;
the sum (∑), of the r-value + p_NEXT - value = ƒ-value of that NEXT PPT.

Knowing just a few of the PPT, r, s, t, f, p and A (4A, 8A) values allows one to calculate ANY & ALL PPTS within any CLUSTER on ANY Branch/Tier throughout the ENTIRE ToPPT!

MathspeedST: The Ubiquitous Information of Numbers, or,How Fractals Exceed the Speed Limit of Light

The General Ubiquity Rule: The General Ubiquity Rule (GUR) in effect, asserts that if you have a fixed numerical pattern that is ubiquitously present across all space and time (spacetime, ST), that information is present across the same, passing any need to actually travel or transports said information at or above the speed of light.

Fig. 75. The General Ubiquity Rule (GUR): Bottom UP

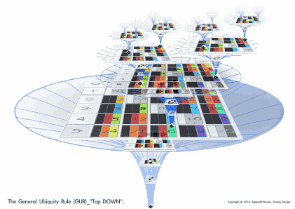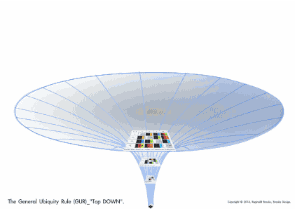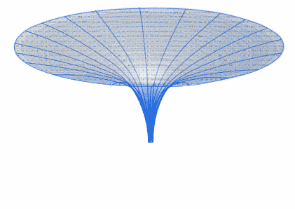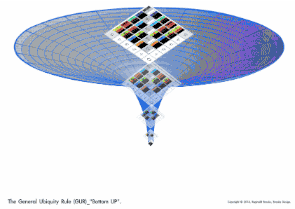Fig. 76. The General Ubiquity Rule (GUR): Top DOWN

Fig.77. Double-Slit Experiment

Closing thoughts

The Conservation Laws, and specifically the Conservation of Energy — the Conservation of Lightspeed — the Conservation of SpaceTime — has been at the center of the discovery of the BIM. The ISL is at the heart of ST formation and its expression as matter and fields. At the “end of the day” it must be conserved!

And while discovering how intimately and profoundly the Pythagorean Triples — especially in the form of the ToPPTs — are so incredibly Number Pattern Sequence inter-related to each other and their placement on the BIM — as also referred to as the BIMtree — is a giant step forward, it is its structural implications that give it meaning. The PTs give structural nodes and forms to the generalized BIM structure in the unfolding of ST.

As ST forms, i.e. expresses itself as, matter and waves, it must address the underlying imperative that in total, its Conservation Laws must be upheld.

If the ST parameters that give identity to wave-particle forms of matter and/or to wave-particle forms of an energy field — parameters such as energy, momentum, charge, baryon number, and lepton number — are a manifestation of their underlying quantum number state, then these too must be intimately involved in the Conservation Laws.

When a wave-particle ST unit seems to either separate into two parts that later recombine as they interfere with each other (Double-Slit Experiment), and/or, when they are part of a system of two (or more) ST units entangled (Quantum Entanglement) via sharing the same quantum number state, they BOTH MUST DO SO IN A WAY THAT SATISFIES THE CONSERVATION LAWS!

The total angular spin momentum of any system must be such that it does NOT violate the Conservation Laws. Naturally, if the entangled ST units have spin measured UP on one axis of one of the entangled pairs, it MUST measure DOWN on the same axis of measurement on the other entangled unit. This is the Conservation Law in action.

If the ST that informs the wave-particle and its parameters ALWAYS obeys the Conservation Laws, then the geometry that informs that ST formation must in and of itself ALWAYS obey the same laws.

The BIM and BIMtree, being the geometry of the BIM and BIMtree expression,both simultaneously and automatically precede and inform any and all subsequent ST unit expression, and, that this geometry is ubiquitous — expanding to infinity!

~~ ~~ ~~

From the introduction to The Pythagorean—Inverse Square Connection (TPISC I: Basics) to its proof and distribution (TPISC II: Advanced) on the BBS-ISL Matrix (BIM), we have now come full circle to TPISC III: Clarity & Simplification: Tree of Primitive Pythagorean Triples (ToPPT).
Here we “see” the pattern: the arrangement of PPTs into triplet branches (Cluster of Tertiary Branches/Tiers) as organized into the ToPPT — with each and every PPT related within a Cluster, Cluster to Cluster, Cluster to Branch and Branch to Branch, back to the initiating 3-4-5 PPT Trunk.
The devilish details proving the linkage nevertheless — in the end — serve the clarity and simplification!
That a SpaceTime (ST)-forming Matrix patterned on simple Squares (& Circles) — a.k.a. the ISL — should pair-up their Squares to become and reveal in their sum, a larger Square — i.e. a²+b²=c² — forming fractal iterations of Pythagorean Triples (PTs), themselves patterned throughout the BIM, is a sublime beauty to be realized with a small effort.
The fractal within a fractal!
Such profound harmony of form naturally begs the question: to what effect?
Several conjectures come to mind:
Would not the fractal-nodes of the PTs lead to structural articulation points along the expanding ST that would allow the geometry of the Squares to be enhanced by the embedded geometry of the non-Square Rectangles holding these PTs?
Would not these same fractal-nodes of the PTs be internal, integral and identifying structural parameters (Quantum State Numbers) of any wave-particle ST unit formed?
Would not the immensely inter-connecting linkage of the PTs, between the PTs and between the PTs and the BIM itself, provide the very basis of the wave-particle duality and entanglement phenomenon we see in the Double-Slit Experiment and the Quantum Entanglement (DSEQEConjecture) that lies at the core of our understanding the Quantum Universe?
Form follows function — function follows Form!

~~ ~~ ~~

Fig.78. TPISC_I (acrylic painting)

Fig.79. TPISC_II (acrylic painting)

Fig. 80. TPISC_I-II_Simplified (acrylic painting)

Fig. 81. TPISC_III_Clarity-1 (acrylic painting)

Fig. 82. TPISC_III_Clarity-2 (acrylic painting)

Fig. 83. TPISC_III_Clarity-3 (acrylic painting)

Fig. 84. TPISC_III_Clarity-4 (acrylic painting)

Fig. 85. TPISC_III_Clarity-5 (digital painting)

Fig. 86. TPISC_III_Clarity-5 (digital painting)

Fig. 87. TPISC_III_Clarity-5 (digital painting)

Fig. 88. TPISC_III_Clarity-5 (digital painting)

Currently, there are some 40+ variations on the ToPPT Logo:

click here for audio enhanced video on Vimeo.

VIII. References

References Internal: see LINKS below the Appendix.

References External: general @ Wikipedia

References External: relevant

R. C. Alperin, The Modular Tree of Pythagoras, Amer. Math. Monthly 112 (2005), 807–816. http://www.math.sjsu.edu/~alperin/pt.pdf
F. J. M. Barning, Over Pythagorese en bijna-Pythagorese driehoeken en een generatieproces met behulp van unimodulaire matrices, Math. Centrum, Amsterdam, Dept. Pure Math. ZW-011 (1963), 37 pages.
B. Berggren, Pytagoreiska trianglar, Tidskrift fo ̈r Element ̈ar Matematik, Fysik och Kemi 17 (1934), 129–139.
Frank R. Bernhart, and H. Lee Price, "Pythagoras' garden, revisited", Australian Senior Mathematics Journal 01/2012; 26(1):29-40.http://files.eric.ed.gov/fulltext/EJ992372.pdf
A. R.Kanga, "The family tree of Pythagorean triples," Bulletin of the Institute of Mathematics and its Applications 26, January/February 1990, 15–17. https://www.revolvy.com/topic/Tree%20of%20primitive%20Pythagorean%20triples&uid=1575
KEITH CONRAD, “PYTHAGOREAN DESCENT”, http://www.math.uconn.edu/~kconrad/blurbs/linmultialg/descentPythag.pdf
H. L. Price, The Pythagorean Tree: A New Species, http://arxiv.org/abs/0809.4324. Oct 2011.
H. L. Price, “Diagrams: Two Trees of Pythagorean Triples”, https://www.researchgate.net/publication/305655204, 2016
Kevin Ryde, “Trees of Primitive Pythagorean Triples”, https://download.tuxfamily.org/user42/triples/triples.pdf, 2013
Luis Teia, “Anatomy of the Pythagoras' Tree”, Australian Senior Mathematics Journal vol. 30 no. 2, 2016 https://www.researchgate.net/publication/313389694Anatomy_of_the_Pythagoras%27Tree

Here is an exciting new reference that came in after this work was published. It shows Pythagorean Triples on the ancient Babylonian Tablet (Plimpton 322) :

Mansfield. D.F., Wildberger, N.J. Plimpton 322 is Babylonian exact sexagesimal trigonometry, Hist. Math. (2017), http://dx.doi.org/10.1016/j.hm.2017.08.001

IX. Appendix

A. Appendix A: Fully Extended Dickson Method Equations for TPISC III, IV and V.

ADDITIONS

Additions

~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~

Additions

COMMON EQUATIONS REFERENCING IMAGES FOCUSING ON AREAS:

Additions

CORRECTIONS:

Correction

B. Appendix B: Step-by-Step Tutorial on making the 5th Tertiary Branch of the ToPPT.

Follow the 9 step-by-steps as the 5th Tertiary Branch — all 243 PPTs — are filled in. Closeups of the 5th Tertiary Branch/Tier Clusters are shown at the bottom of this series.

Table 2m-1. "BIM tree": Steps making the 5^th Tertiary Branch/Tier, Cluster by Cluster using r ,s ,t ,f & p.

Table 2m-2. "BIM tree": Steps making the 5th Tertiary Branch/Tier, Cluster by Cluster using **r ,s ,t ,f & p.

Table 2m-3. "BIM tree": Steps making the 5th Tertiary Branch/Tier, Cluster by Cluster using **r ,s ,t ,f & p.

Table 2m-4. "BIM tree": Steps making the 5th Tertiary Branch/Tier, Cluster by Cluster using **r ,s ,t ,f & p.

Table 2m-5. "BIM tree": Steps making the 5th Tertiary Branch/Tier, Cluster by Cluster using **r ,s ,t ,f & p.

Table 2m-6. "BIM tree": Steps making the 5th Tertiary Branch/Tier, Cluster by Cluster using **r ,s ,t ,f & p.

Table 2m-7. "BIM tree": Steps making the 5th Tertiary Branch/Tier, Cluster by Cluster using **r ,s ,t ,f & p.

Table 2m-8. "BIM tree": Steps making the 5th Tertiary Branch/Tier, Cluster by Cluster using r ,s ,t ,f & p.

Table 2m-9. "BIM tree": Steps making the 5th Tertiary Branch/Tier, Cluster by Cluster using **r ,s ,t ,f & p.

Closeups of the 5th Tertiary Branch/Tier Clusters are shown below.

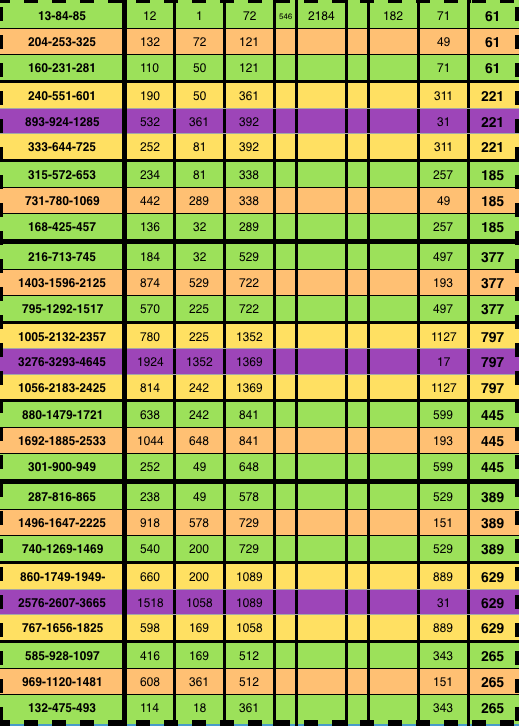Table 2t-1. "BIM tree": 9 3-branch Clusters of the 5th UUUUU-LLLUU Branches.

Columns: PPT—r-—s-—t-—skip 4 columns—ƒ-—p-values

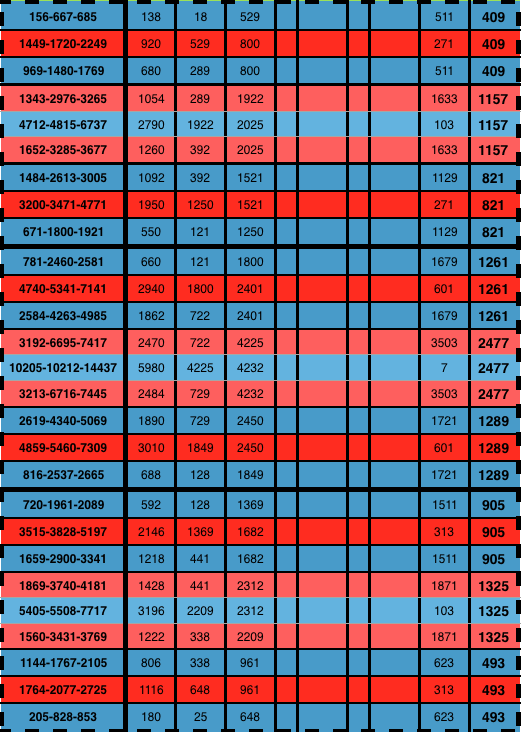Table 2t-2. "BIM tree": 9 3-branch Clusters of the 5th UUUMU-LLLMU Branches.

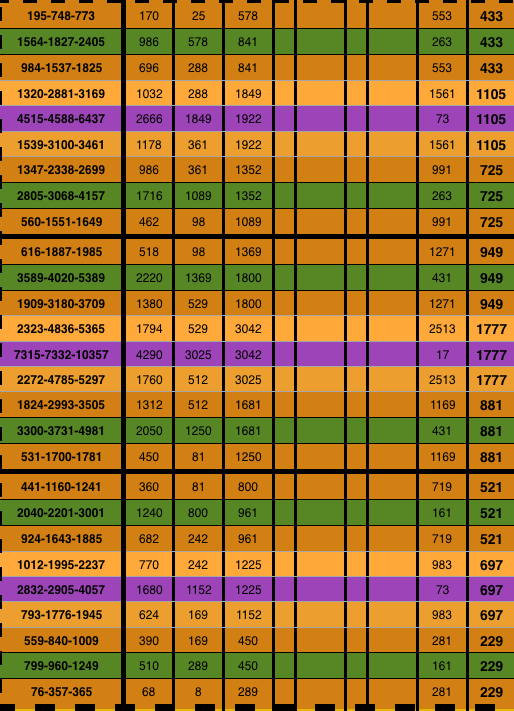Table 2t-3. "BIM tree": 9 3-branch Clusters of the 5th UUUUU-LLLUU Branches.

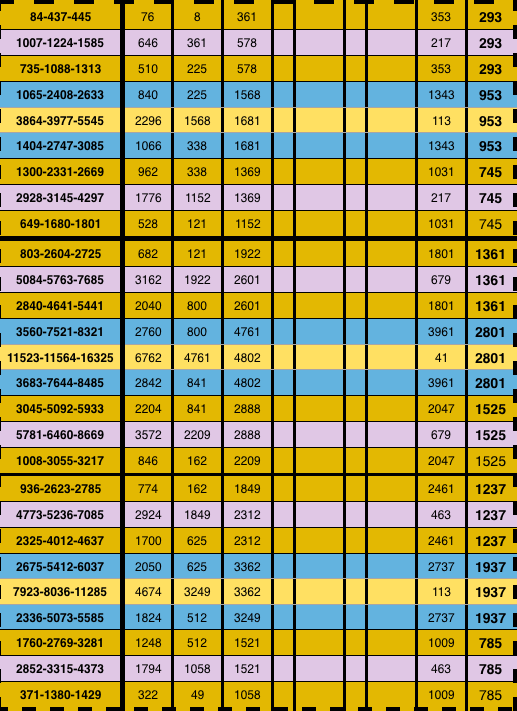Table 2t-4. "BIM tree": 9 3-branch Clusters of the 5th UUUUM-LLLUM Branches.

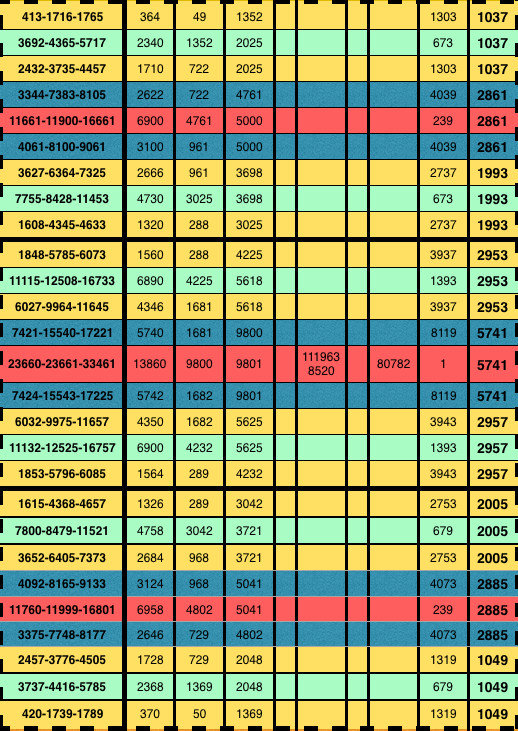Table 2t-5. "BIM tree": 9 3-branch Clusters of the 5th UUUMM-LUULM Branches.

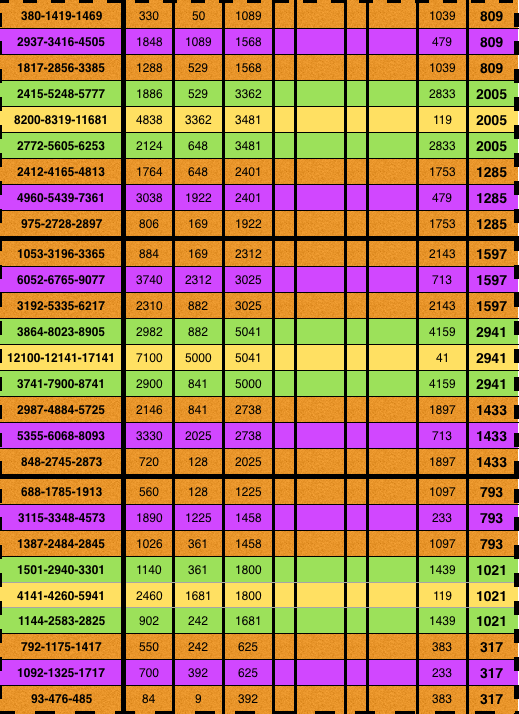Table 2t-6. "BIM tree": 9 3-branch Clusters of the 5th UMULM-LLLLM Branches.

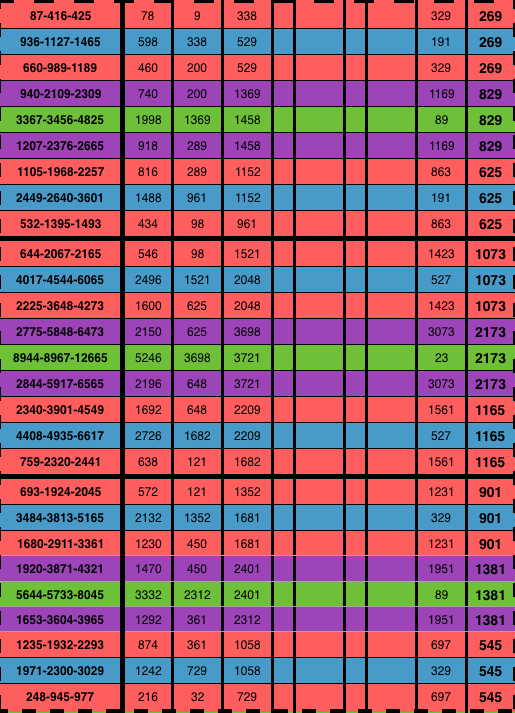Table 2t-7. "BIM tree": 9 3-branch Clusters of the 5th UUUUL-LLLUL Branches.

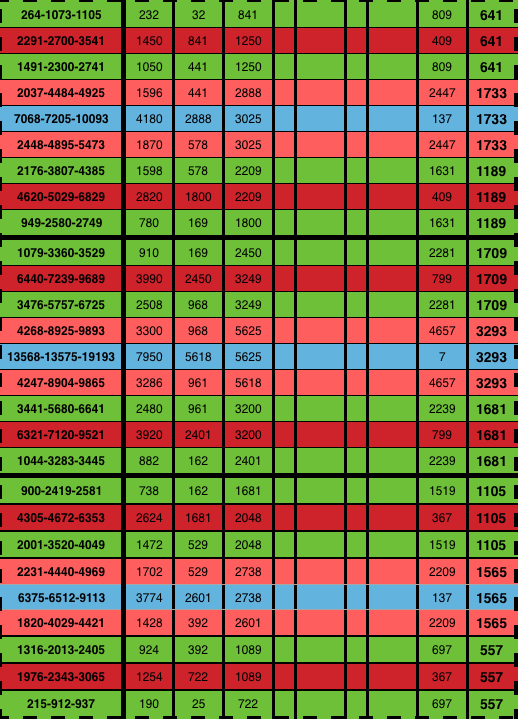Table 2t-8. "BIM tree": 9 3-branch Clusters of the 5th UUUML-LLLML Branches.

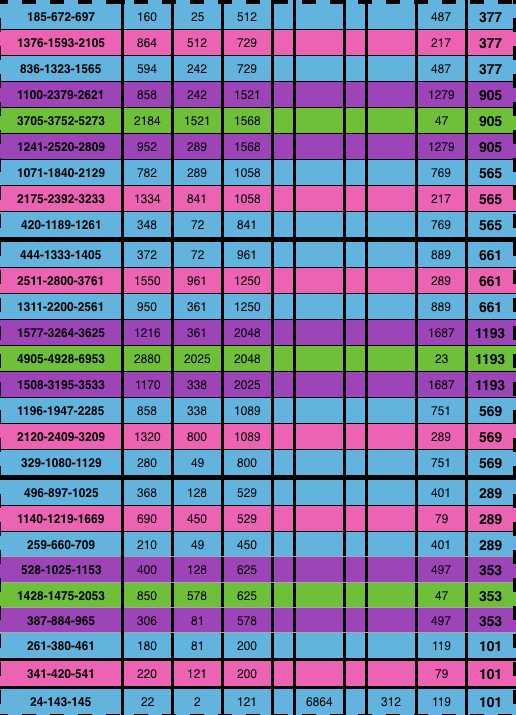Table 2t-9."BIM tree": 9 3-branch Clusters of the 5thUUULL-LLLLL Branches.

X. LINKS

more...

Find Row-Col Axis number of Any IG number:

BBS_FindRow-Col_Any_IG_number.pdf

BBS_FindRow-Col_Any_IG_number.html

Find Row-Col Axis number of Any IG number:

BBS_ToFindRow-ColAnyIGnumber.pdf

BBS_ToFindRow-ColAnyIGnumber.html

BBS_ToFindRow-ColAnyIGnumber-MARP.pdf

BBS-ISL_IGGR_TPISC_fundamental_rules:

BBS-ISL_IGGR_TPISC_rules.html

BBS-ISL_IGGR_TPISC_rules.pdf

BBS-ISL_IGGR_TPISC_rulesMARP.pdf

BBS-ISL_Matrix_Overview Slideshow:

BBS-ISL_Matrix_Overview_MARP.pdf

Simple Visual Guide to making a BBS-ISL Matrix:

BBS-ISL10x10+.html

Simple Highlight Table Row/Col:

highlightTableRowCol_BBBS-ISL.html

highlightTableRowCol_BBBS-ISL10x.html

highlightTableRowCol_BBBS-ISL20x.html

~~ ~~ ~~ ~~ ~~

The ideas presented here are primarily based on my own work building on and off the “Standard Model” and its many, many creators and architects. A complete list of works are found here.

Highlights include:

L.U.F.E. (Layman’s Unified Field Exposé) (1985), was the culmination of some 10 years of review and study of the “Standard Model” leading to a work that fundamentally captures the discrete-geometry-fractal basis of the cosmos as tied to the Conservation Laws.

The LUFE Matrix (1985), a mathematical-visual-physics-based working matrix was born from the original L.U.F.E. and thereafter greatly expanded on in The LUFE Matrix Supplement (1991, 2003).

A number of individual white papers followed:

Dark-Dark-Light: Dark Matter=Dark Energy (the inverse of) (2003); The History of the Universe in Scaler Graphics (2004); Quantum Gravity (2008); Conservation of SpaceTime (2008).

These ideas were all brought together in LightspeedST (2013) an interactive, iBook, published in the iTunes iBooks Store. The white papers are freely available.

Works on pure mathematics include:

PIN: Pattern in Number...from primes to DNA (2001); The Butterfly Primes series (2005, 2006, 2006); GoDNA: the Geometry of DNA (2001); GoMAS: The Geometry of Music, Art and Structure...linking science, art and esthetics (1987, 1996, 1998, 2009) with parts II and III (2012);

Brooks (Base) Square (BS): The Architecture of Space-Time (TOAST) and The Conspicuous Absence of Primes (TCAOP) - the complete work (Rules 1–177) (2009, 2010, 2011, 2012);

Brooks (Base) Square interactive (BBSi) Matrix: Part I: Basics (2011, 2013);

The Architecture of SpaceTime (TAOST) as defined by the Brooks (Base) Square Matrix and the Inverse Square Law (ISL) (2011);

Numbers Of Inevitability (2012); and, AFPOP: A Fresh Piece of Pi(e)...and the √2, too...Fractal-Fractal-Fractal (2012).

The BBS-ISL Matrix papers, videos, slideshows, etc. all culminated in MathspeedST (2013) an interactive iBook, published in the iTunes iBooks Store. Free. Most of the white papers are freely available.

TPISC I: Basics: The Pythagorean - Inverse Square Connection – a MathspeedST Supplement (2015) an interactive iBook, published in the iTunes iBooks Store. Free. Most of the white papers are freely available.

TPISC II: Advanced: The Pythagorean - Inverse Square Connection – a MathspeedST Supplement (2015) an interactive iBook, published in the iTunes iBooks Store. Most of the white papers are freely available.

TPISC III: Clarity & Simplification: Tree of Primitive Pythagorean Triples (ToPPT)– a MathspeedST Supplement* (2017) an interactive iBook, published in the iTunes iBooks Store. Most of the white papers are freely available. You are HERE! Note: The PDF version does not enlarge the very large tables. Go here for large table images.

Reginald Brooks: interactive, multi-touch iBooks (view in iTunes)
1.
- LightspeedST: Leapfrogging @ The Speed of Light
- View in iTunes
2.
- MathspeedST: Leapfrogging LightspeedST FASTER Than The Speed of Light
- View in iTunes
- TPISC I — Basics: The Pythagorean — Inverse Square Connection: Basics
- (~A MathspeedST Supplement~)
- View in iTunes
4.
- TPISC II: The Pythagorean - Inverse Square Connection: Advanced
- (~A MathspeedST Supplement~)
- View in iTunes
- TPISC III: Clarity & Simplification: Tree of Primitive Pythagorean Triples (ToPPT)
- (~A MathspeedST Supplement~)
- View in iTunes

https://itunes.apple.com/us/author/reginald-brooks/id657634078?mt=11

PIN: Pattern in Number...from primes to DNA. \| PIN: Butterfly Primes...let the beauty seep in. \| PIN: Butterfly Prime Directive...metamorphosis. \| PIN: Butterfly Prime Determinant Number Array (DNA) ~conspicuous abstinence~. \| GoDNA: the Geometry of DNA (axial view) revealed. \| SCoDNA: the Structure and Chemistry of DNA (axial view). \| The LUFE Matrix \| The LUFE Matrix Supplement \| The LUFE Matrix: Infinite Dimensions \| The LUFE Matrix: E=mc² \| Dark Matter=Dark Energy \| The History of the Universe in Scalar Graphics \| The History of the Universe_update: The Big Void \| Quantum Gravity ...by the book \| The Conservation of SpaceTime \| LUFE: The Layman's Unified Field Expose` \| GoMAS: The Geometry of Music, Art and Structure ...linking science, art and esthetics. Part I \| Brooks (Base) Square (BBS): The Architecture of Space-Time (TAOST) and The Conspicuous Absence of Primes (TCAOP) - a brief introduction to the series

net.art index \| netart01: RealSurReal...aClone, 2001 \| netart02: Hey!Ufunk'n with my DNA? \| netart03: 9-11_remembered \| netart04: Naughty Physics (a.k.a. The LUFE Matrix) \| netart05: Your sFace or Mine? \| netart06: Butterfly Primes \| netart07: Music-Color-ISL \| netart08: BBS-ISL matrix \| netart09: BBS-interactive (I) \| netart10: Sunspots and Solar Flares \| netart11: Music-Color-ISL (II-III) \| Art Theory 101: PIN, DNA, LUFE Matrix, GoMAS, BBS index \| test\|home

Copyright 2017, Reginald Brooks, Brooks Design. All rights reserved. .

iTunes, iTunes Store, iBooks, iBooks Store, iBooks Author, Mac OS are registered® trademarks of Apple Inc. and their use on this webpage does not reflect endorsement by Apple Inc.

~(Tree of Primitive Pythagorean Triples) ~

Forward

A Pictoral Overview!

I. Intro

The MathspeedST Supplements:

II. BBS-ISL Matrix = BIM

A. Introduction to BIM

B. Number Pattern Sequences (NPS)

C. MathspeedST

III. TPISC: the Pythagorean—Inverse Square Connection

A. TPISC I: Basics

B. TPISC II: Advanced

C. TPISC III: Clarity—Simplified—ToPPT

The BIM is the geometry defining SpaceTime!

IV. ToPPT: Layout

A. Structure: Outward = BRANCHES (TIERS)

B. Structure: Across = CLUSTERS

C. Definitions and References

V. ToPPT: Linkage

A. Outward: Branches — TIERS

B. Across: CLUSTERS

C. Specials: Pythagorean, Middle & Plato Branches

Table5b." BBS-ISL_Matrix-FPS": Factor Pairs Sets and Row & Column values (lower half: 35x35)

VI. Summary

VII. Conclusion

VIII. References

IX. Appendix

A. Appendix A: Fully Extended Dickson Method Equations for TPISC III, IV and V.

ADDITIONS

COMMON EQUATIONS REFERENCING IMAGES FOCUSING ON AREAS:

CORRECTIONS:

B. Appendix B: Step-by-Step Tutorial on making the 5th Tertiary Branch of the ToPPT.

X. LINKS

Highlight Interactive BBS-ISL Matrix at:

BBS-ISL & TPISC Resources at:

BBS-ISL & TPISC Media Center at:

Interactive Matrix pages at:

more...

Reginald Brooks: interactive, multi-touch iBooks (view in iTunes)

The BIM* is the geometry defining SpaceTime!*