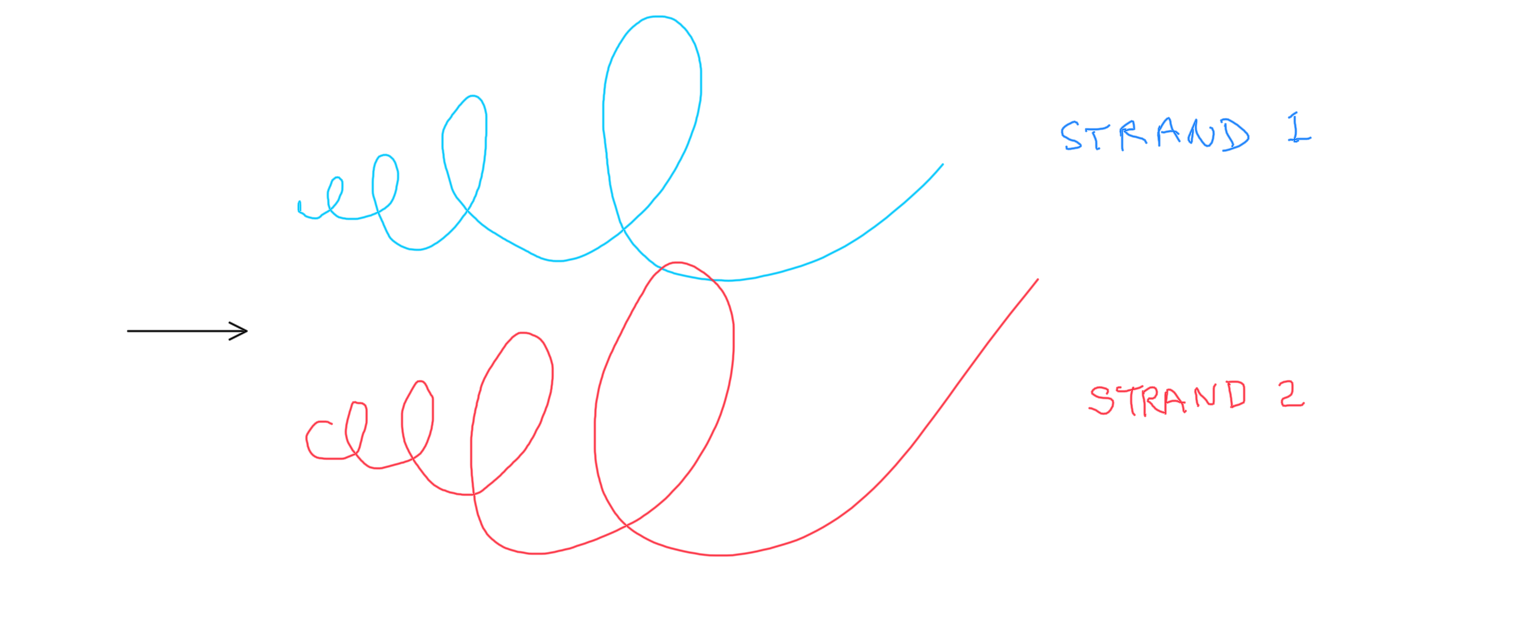Oceans of Numbers 3
Our favorite barkeep's ^ dream went something like this:
Before the spiraling double-helical structure of the DNA molecule came to being -- you know, two sugar-phosphate strands wrapping around each other in a cylindrical form that are connected by the complementary pairing of their inner amino acid bases -- there most likely had to have been some form of pre-cursor shape and attractor in play.
Well, let's skip all the intermediary forms and go way back to the number forms, keeping in mind that they are just symbols for the real conceptual form -- quantity. Quantity of space and quantity of time. Distance traveled over ticks of the clock. Quantity of SpaceTime (ST). Yes, when you go from quantity 1 to quantity 2 you have motion: ST begins. And yes, all manifestations of energy and fields are simply expressions of synchronous, re-iterative, fractal-based pulse-propagations of individual, granular, quantum ST units. We see, become aware, develop consciousness as sentient beings at the peaks and sleep in the valleys.
Drawing on our previous "Oceans of Numbers," where certain ST quantities derived from the Exponential Power of 2 -- a.k.a. the Butterfly Fractal 1 -- gives us the simplest expression of doubling quantity 1 -->2, 2-->4, 4-->8,... we have now found that the numbers generated fall into two nearly-identical SETS or STRANS that appear to spiral around each other -- connected by a specific number -- one that is simply double its predecessor, albeit its role upon connecting to the other strand is different -- in a form that initially resembled that of the DNA double-helix. We refer to the individual group of defining parameters for any and all doublings as "containers" -- as they both express the BF1 and are candidates for being TRUE Mersenne Prime-Perfect Number pairings. The overlapping similarities have shown that any pattern of the Mp-PN pairings is only apparent within the context of considering ALL the "containers" expressions.
The initial DNA-like diagrammatic of the two STRANDS (Sets) show the PN "container" candidates connected by the doubling of the smaller PN of one to the CR (Complement Rectangle=xy) of the other larger, e.i. 28 x 2 = 56 and 56 is the CR of 120.
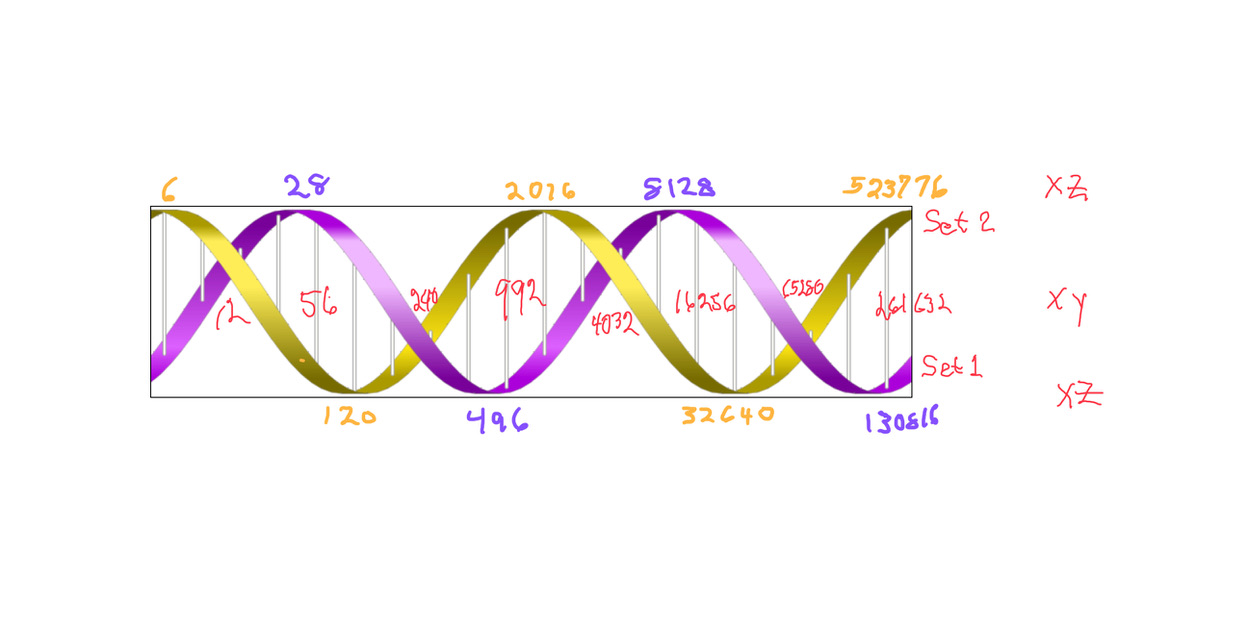
However, a crucial difference is apparent from the start. As one progresses along, all the numbers are expanding! We don't have a double-stranded cylindrical form -- no, we have a double-stranded conical form -- a cone! And a cone implies a small -- usually singular -- starting point that expands outward. Sound familiar? Yes, it is the shape of a quantum, granular number-fractal -- BF1 -- starting from quantity 1 and doubling itself as it pulse-propagates outward, before collapsing and repeating.
The STRAND 1 and 2 -- shown pulled apart -- coil together around each other, centered on their origin, quantity 1.
So what does this have to do with your Bank Account? Not much, but this analogy might help.
- At your bank, you might have two Accounts: 1 and 2.
• These accounts are nearly, but not exactly, identical.
• Each account has its own running balance.
• At this bank, you can get a total running balance of all your assets at any time.
• Account 1: The balance is never evenly divisible by 24 after deposit, but the balance difference from one deposit to another is ÷24.
• Account 2: The balance is always evenly divisible by 24, and the balance difference from one deposit to another is also ÷24.
• Caveat: The running balance after deposit across individual Accounts 1 & 2 is never evenly divisible by 24!
Differences between Account 1 & 2:
• Account 1: • The balance is NEVER evenly divisible by 24 after deposit. • The balance difference from one deposit to another is ÷24. • Account 2: • The balance is ALWAYS evenly divisible by 24. • The balance difference from one deposit to another is also ÷24. • Caveat: • The running balance after deposit across individual Accounts 1 & 2 is NEVER evenly divisible by 24!
The BF1 STRANDS 1 & 2 are just like that! And, well, yes -- there are a few other differences:
STRAND 1: -- and ONLY STRAND 1 -- holds the TRUE and extremely rare Mersenne Prime-Perfect Number pairings.
STRAND 2: -- while appearing similar to 1 -- never holds ANY of the rare Mersenne Prime-Perfect Number pairings.
It should be pointed out that STRAND 1 also holds other "containers" that are NOT TRUE Mp-PN pairings.
So what does this have to do with the rest of "Oceans of Numbers?"
The 51 known Mp-PN pairings found exclusively in STRAND 1 are not only nearly identical to all the other "containers" -- and as such are stealthily hidden amongst an infinity of look a-likes -- but reveal themselves in only their purest, most minimalist manner: they have the least, minimalist number of divisors within ALL the "containers!" They are pure gemstones! Their resonance is pure!
The discovery of the Divisor Matrix Table (DMT) has put the entire "Oceans of Numbers" into context. The DMT holds ALL the natural whole numbers, and, all of their divisors. It is built from the natural doubling of quantity 1 in the form of the BF1. Yes, simple re-iterations of the fractal BF1 generates the entire, all-encompassing table of numbers and their divisors -- including the rare Mp-PN pairings. The implications for entanglement -- quantum entanglement -- entropy, order, and the passage of time are real. The only disorder one sees is that that is not yet resolved.
A fractal is a fractal is a fractal
A fractal is, first and foremost, a numerical expression. You might even say, it is an entangled numerical expression. Of course, that would be a bit redundant as all numerical expression expresses some degree of entanglement. And, as entanglement implies some form of order -- versus the disorder of chaos -- one immediately sees that the terms and concepts that they embrace are "entangled!"
Let's focus on the basis of the fractal itself: numbers. And, as a fractal is a self-similar, re-iterative "mirroring" of its native generative form within any and all subsequently scaled larger (and smaller) forms, it behoves us to see just what is the simplest fractal form.
The simplest fractal form is the quantity one -- represented by the number 1.Double that by mirroring 1 and you get 2. Double that by mirroring and you get 4, and so on.
But wait, the act of "mirroring" is more virtual than real. Is there another way?
Yes. Double the 1 by forming two versions of the 1, so that now you have 2 numerical expressions: 1 and 2. The 2, of course, contains two 1s, so that your total Running Sum (∑) is 3.
Next, we double the 2 by forming two versions of the 2 -- which, as we stated above, is really two 1s -- so in effect we are getting 4, or a net of four 1s and a ∑ of 1+2+4=7. And so on.
Now, we can see that a larger, entangled form of 1s has been generated. It has a history, or tail, that is 1+2=3, and then 1+2+4=7, and so on. We have structural form made up of the completely entangled doubled numbers 1, 2, and 4 and their ∑s of 3 and 7. A fractal numerical expression formed from the initial generative fractal quantity 1! As we continue expanding the doublings and the subsequent ∑s a 2D pattern resembling that of the butterfly emerges, thus giving name to the Butterfly Fractal 1 (BF1) that describes this fundamental fractal form.
The difference between the doubling by mirroring and doubling by fractal addition is crucial. The former is more like cell division (mitosis) where 1 gets to 2 by dividing itself into two equal parts for a net of 2. The latter is more like making a deposit of double the size of the previous balance, to get a net Running Sum (∑) of 3. Each doubling and the resulting 2D BF1 is fractal addition — the addition of separate deposits that are double in size of the previous deposit. This gives structural history and ongoing ∑s to the fractal number expression.
How does the BF1 inform the Mersenne Prime Square (MPS)?
The short answer: it is everything!
The long answer: it is everything and then some!
The BF1 -- some part of -- is both the exclusive central vertical core (Column) of the MPS -- with the ODD Complement (OC=yz) flanked on either side, and, informs the MPS header Row as to how many Columns will be present in those OC flanks. And, as Perfect Number (PN=xz) is simply the BF1 + OC. -- as x=y+1 and x+y=z -- we have the MPS defined. The MPS=z² =PN+OC =OC+BF1+OC.
Once you know either the BF1 directly, or, the value of either x or y, ALL other defining parameters of the MPS fall into place. Please remember, these profiles inform ALL the "containers" -- both Set 1 that contain the subset of TRUE Mp-PNs, and, Set 2 that do not. It is quite helpful into envision the profiles as following a template that scales up as the numbers growl. A few examples of the early MPS "containers" follows.
Template: LEFT SIDE: MPS (skewed for clarity); RIGHT SIDE: Table listing key parameters.
Example:
MPS=z² =PN+OC =OC+BF1+OC equals MPS=9=z²=3² =PN(=xz=23=6)+OC (=yz=13=3) =OC+BF1+OC=3+3+3.
In addition, the Complement Rectangle (CR=xy), that bridges SETS 1 & 2 together, shown.
To be complete (but not shown) are x² and y², where (x²+CR) + (y²+CR)=MPS.
"p" is for Prime, used for ALL "containers" even when it is NOT Prime in many cases.
"p" also reveals how many STEPS along the BF1 are in place, e.i. here p=2=2 STEPS of BF1 -- 1 & 2.
"p" -- while ALWAYS ODD (>p=2) for ALL TRUE Mp-PNs is directly related to x and z in both the Euclid-Euler Theorem (PN=2ᵖ⁻¹ • 2ᵖ -1), and, in the MPS as x=2ᵖ/2 in ALL "containers."
Again, once one knows p, x or y, one can quickly determine ALL 10 defining parameters of any "container" filtering out those in Set 2 immediately and selectively those in Set 1 to end with only TRUE Mp-PNs.
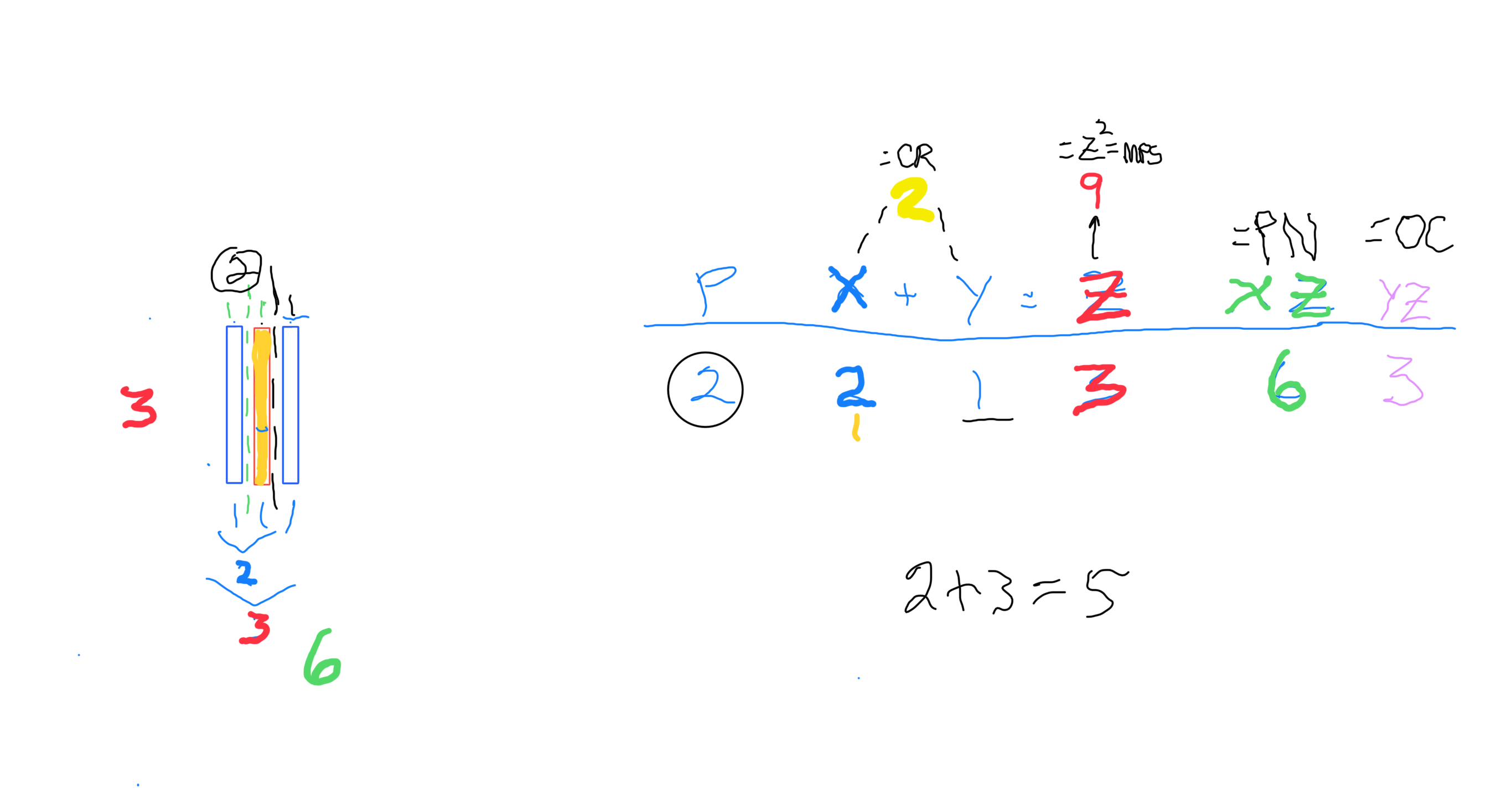
This is the first "container" on the list and is the example described above. It is the only p=EVEN that is a TRUE Mp-PN. "container"-- and the ONLY Set 2 example of a TRUE Mp-Pn.
Notice that the central BH1 fractal (YELLOW) is made up of the first two BF1 numbers, 1 & 2. Their ∑=3.
The other BH1 fractals to either side (WHITE) are identical -- composed of BF1 1 & 2. If we add up all three BF1 fractals we get a sum of 6 = 1+2+1+2.
The circled p=2, is both the p value and the number of fractal entries (which translates into the number of Columns) -- starting with and based on the central BH1 fractal (YELLOW) -- that will be present.
"x"=2 is the number of fractal components -- from the BH1 sequence 1-2-4-8-16-... -- that is present in the central BH1 fractal. “x”=y+1=(z+1)/2= 2^p/2.
“y”=1=x-1=(z-1)/2. “y’s” are directly related to previous, current and next “z’s.”
"z"=3 is the total number of BH1 fractal units across, and, the numerical value of that sum as seen along the outer axis (Don't forget, this is a square -- a MPS -- that is skewed for illustrational purposes).
The PN=6 is, of course, xz=2•3=6. The OC=yz=1•3=3, and the PN + OC =MPS. The CR=xy=1•2=2. The double of this PN=6 (2•6=12) becomes the CR of the next MPS. The MPS =49=z².
This template is followed throughout by ALL the "containers" that follow.
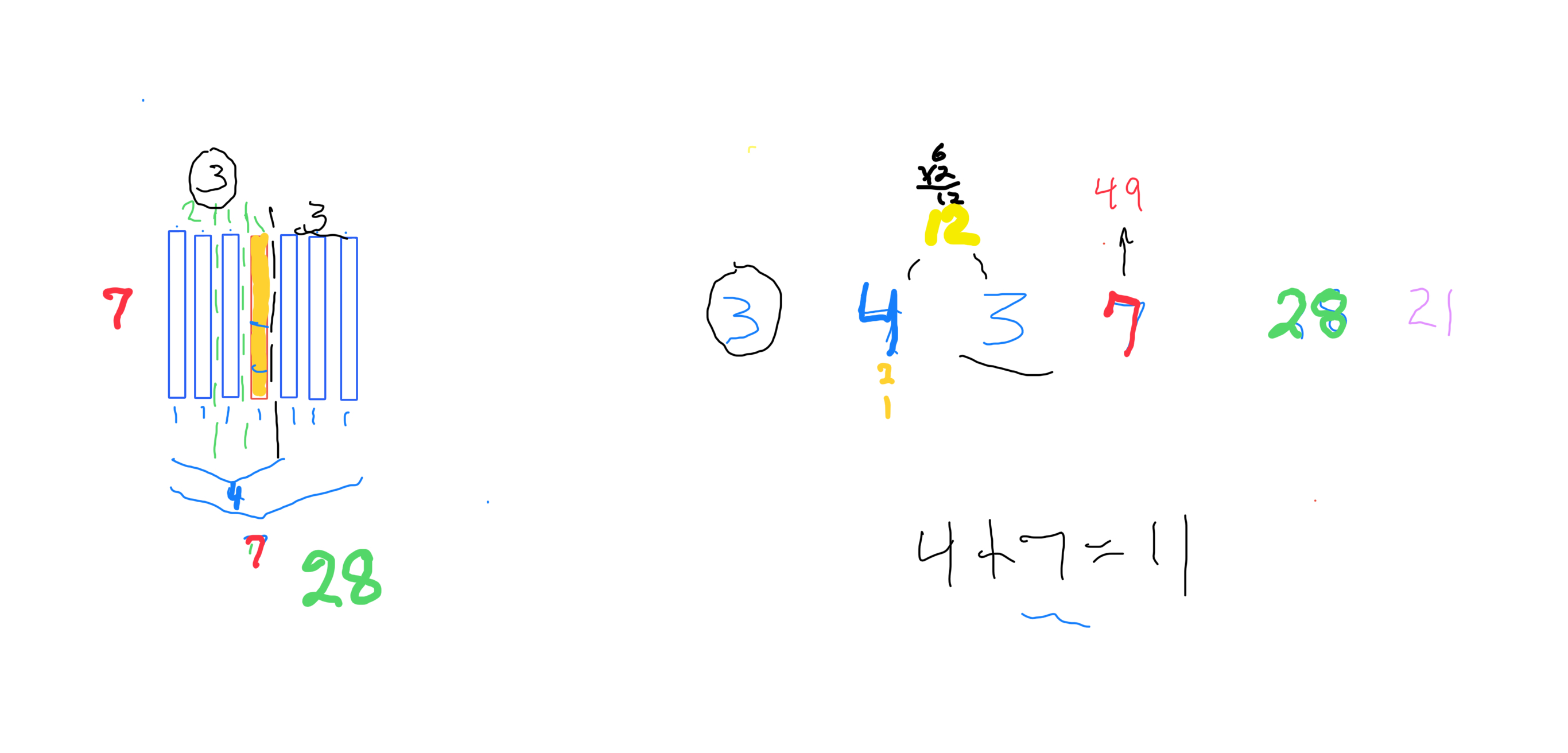
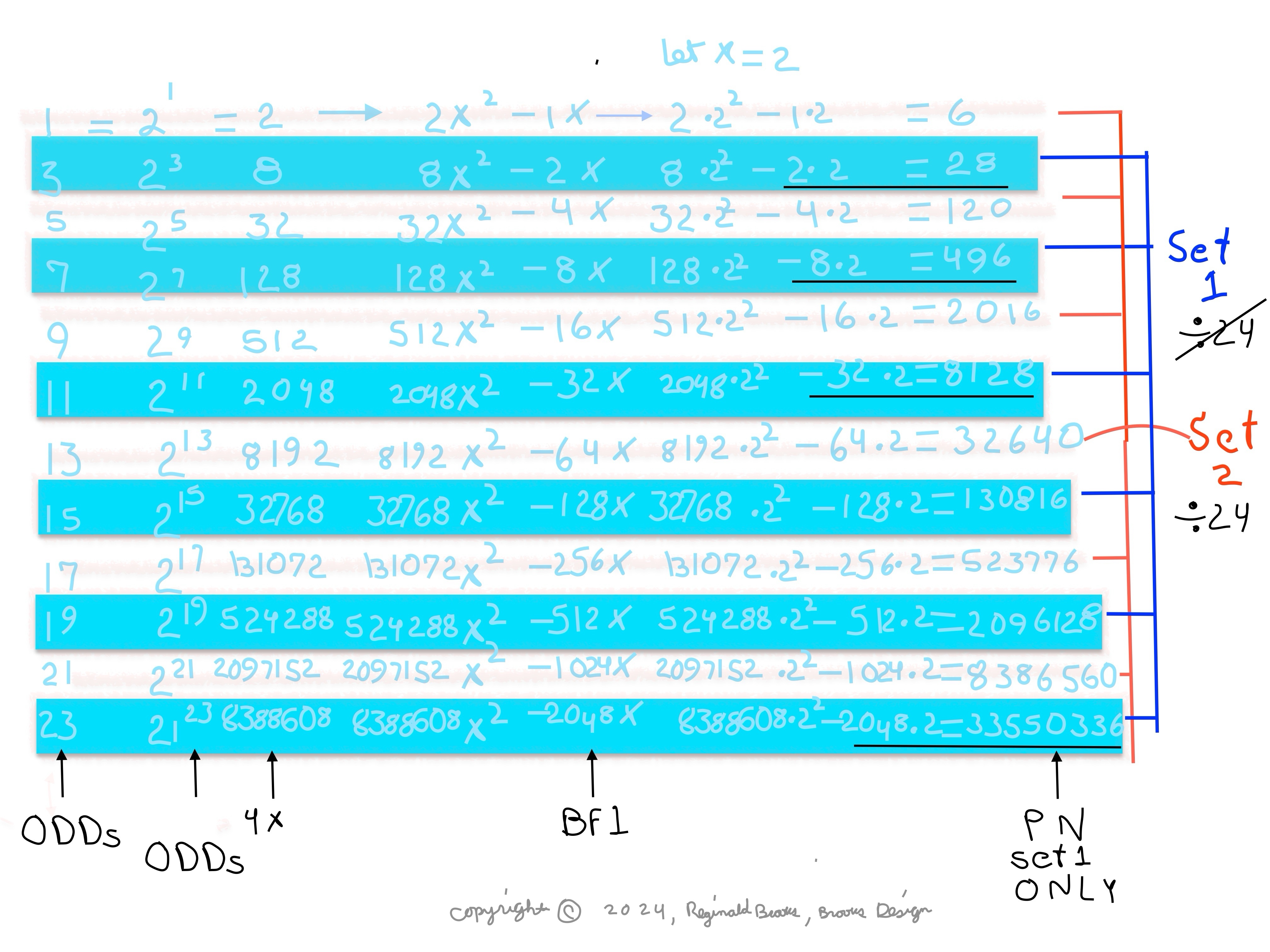
MPS 49=7² p=3=3 STEPS x=4 y=3 z=7 PN=xz=28 OC=yz=21 CR=xy=12 x²=16 y²=9 container"--Set 1 -- TRUE Mp-Pn.
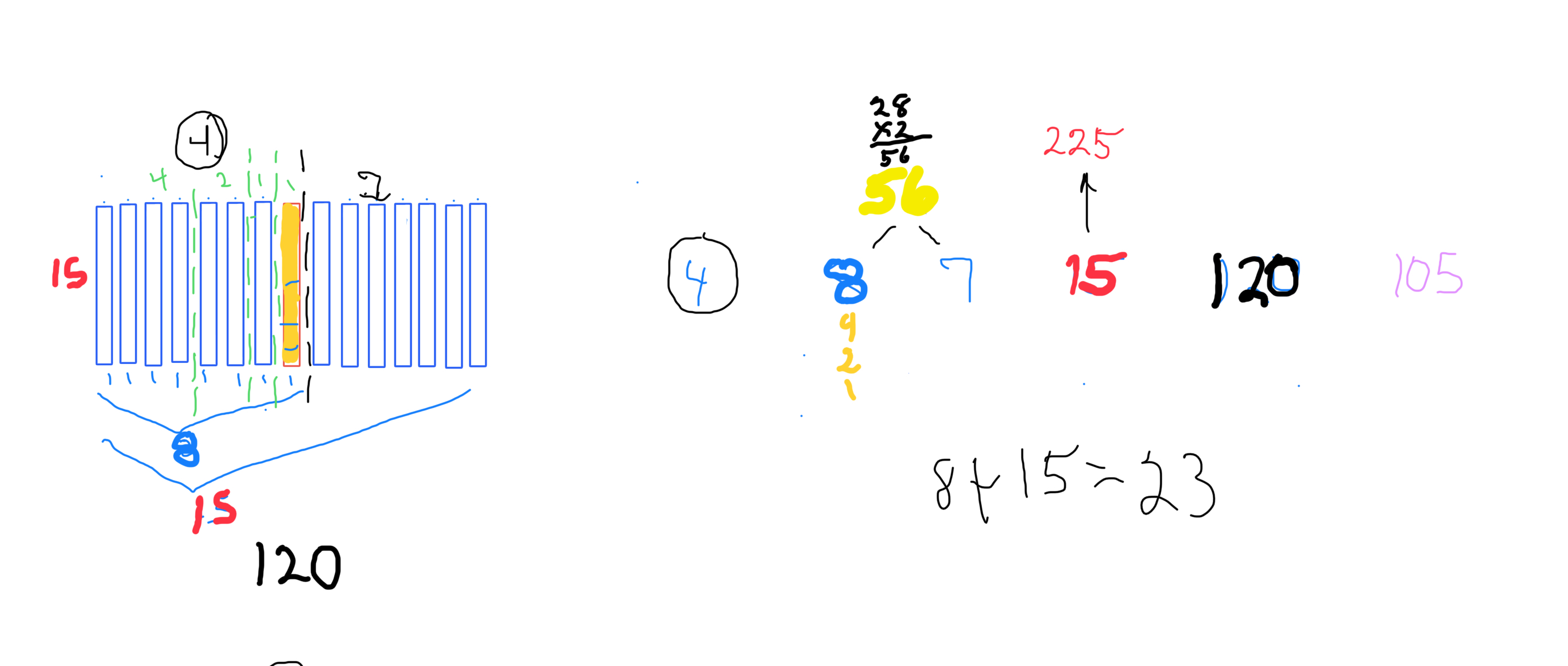
*MPS 225=15² p=4=4 STEPS x=8 y=7 z=15 PN=xz=120 OC=yz=105 CR=xy=56 x²=64 y²=49. container"--Set 2 -- NOT TRUE Mp-Pn.
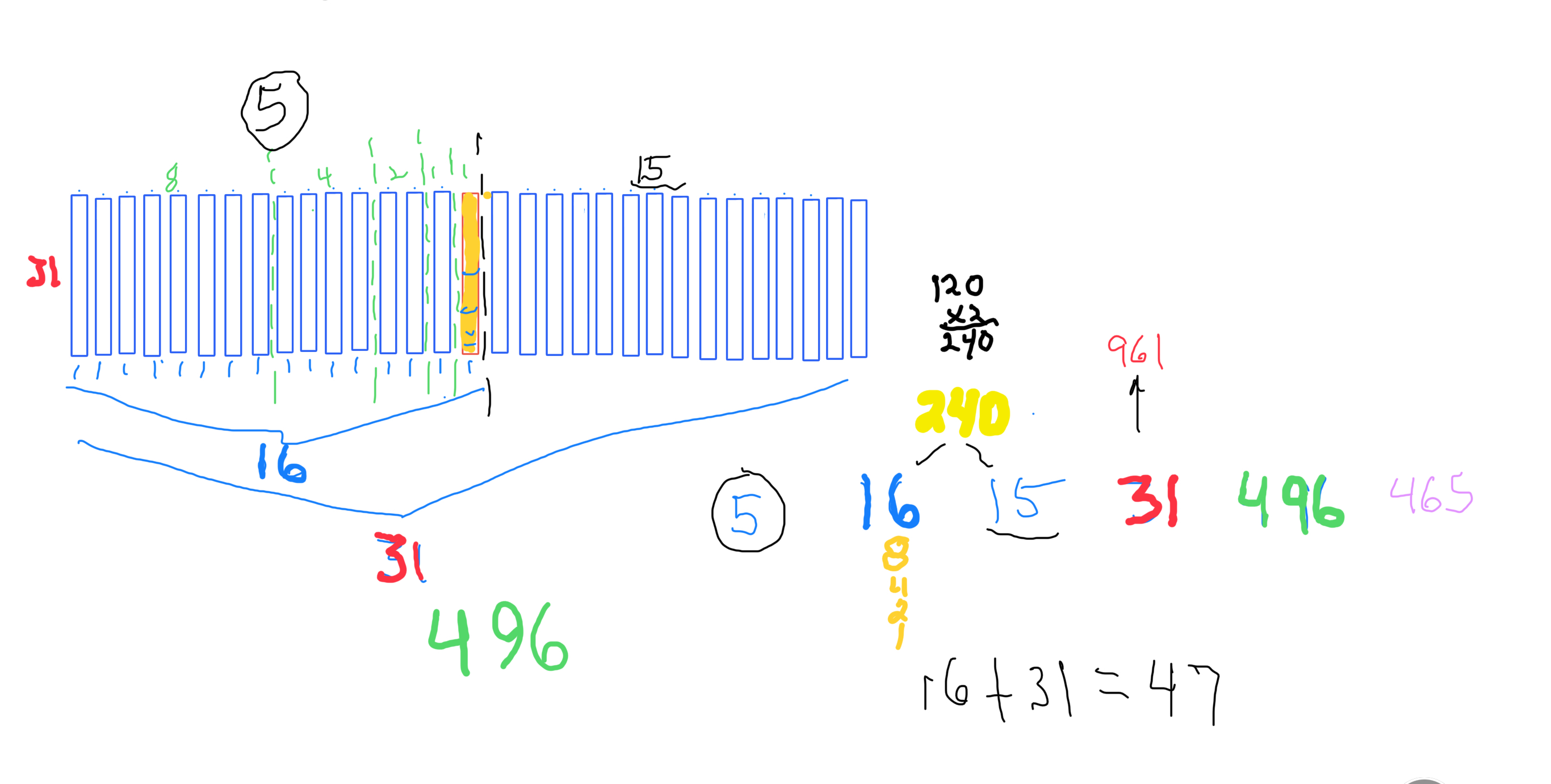
MPS 961=31² p=5=5 STEPS x=16 y=15 z=31 PN=xz=496 OC=yz=465 CR=xy=240 x²=256 y²=225. container"--Set 1 -- TRUE Mp-Pn.
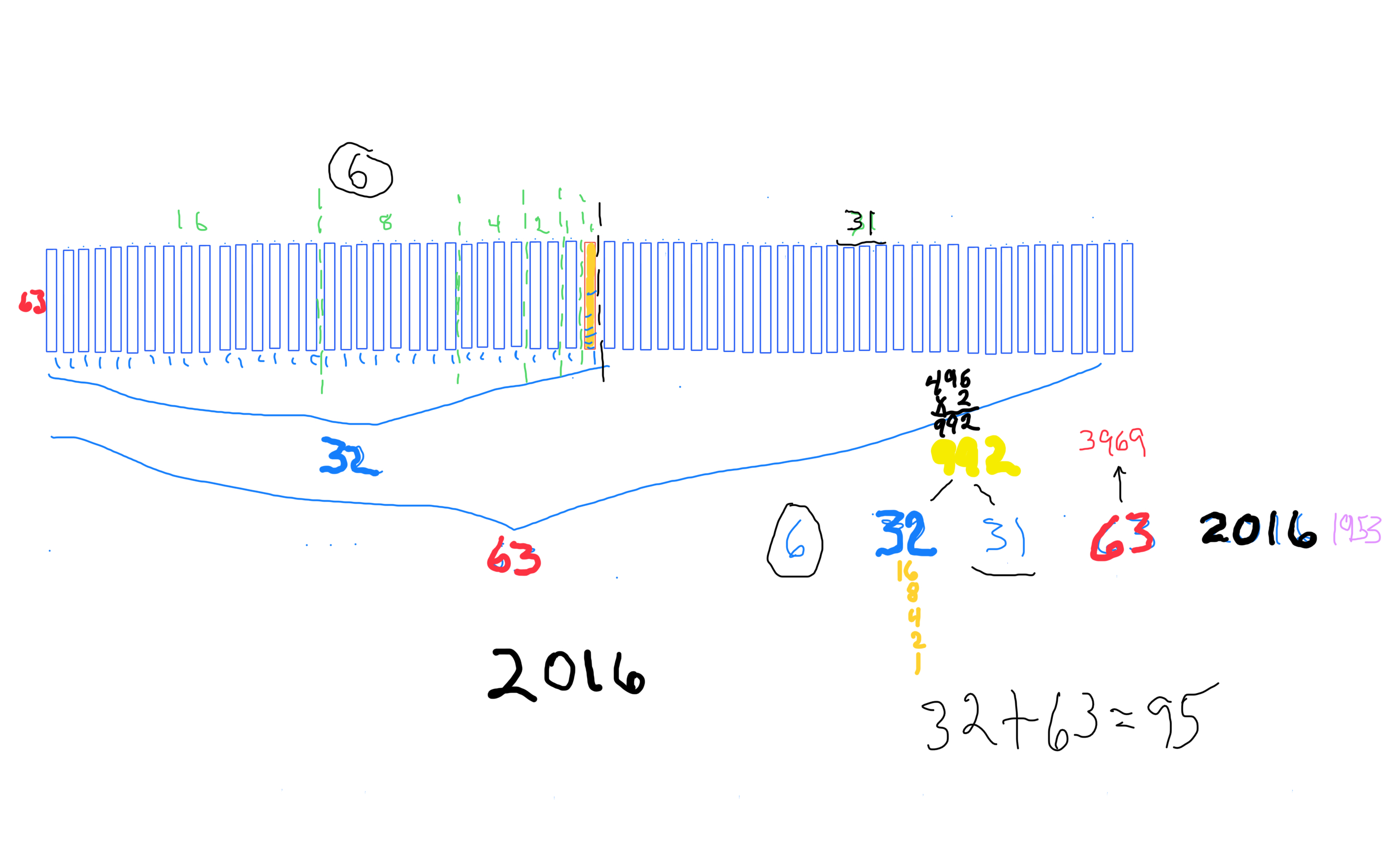
*MPS 3969=63² p=6=6 STEPS x=32 y=31 z=63 PN=xz=2016 OC=yz=1953 CR=xy=992 x²=1024 y²=961. "container"--Set 2 -- NOT TRUE Mp-Pn.
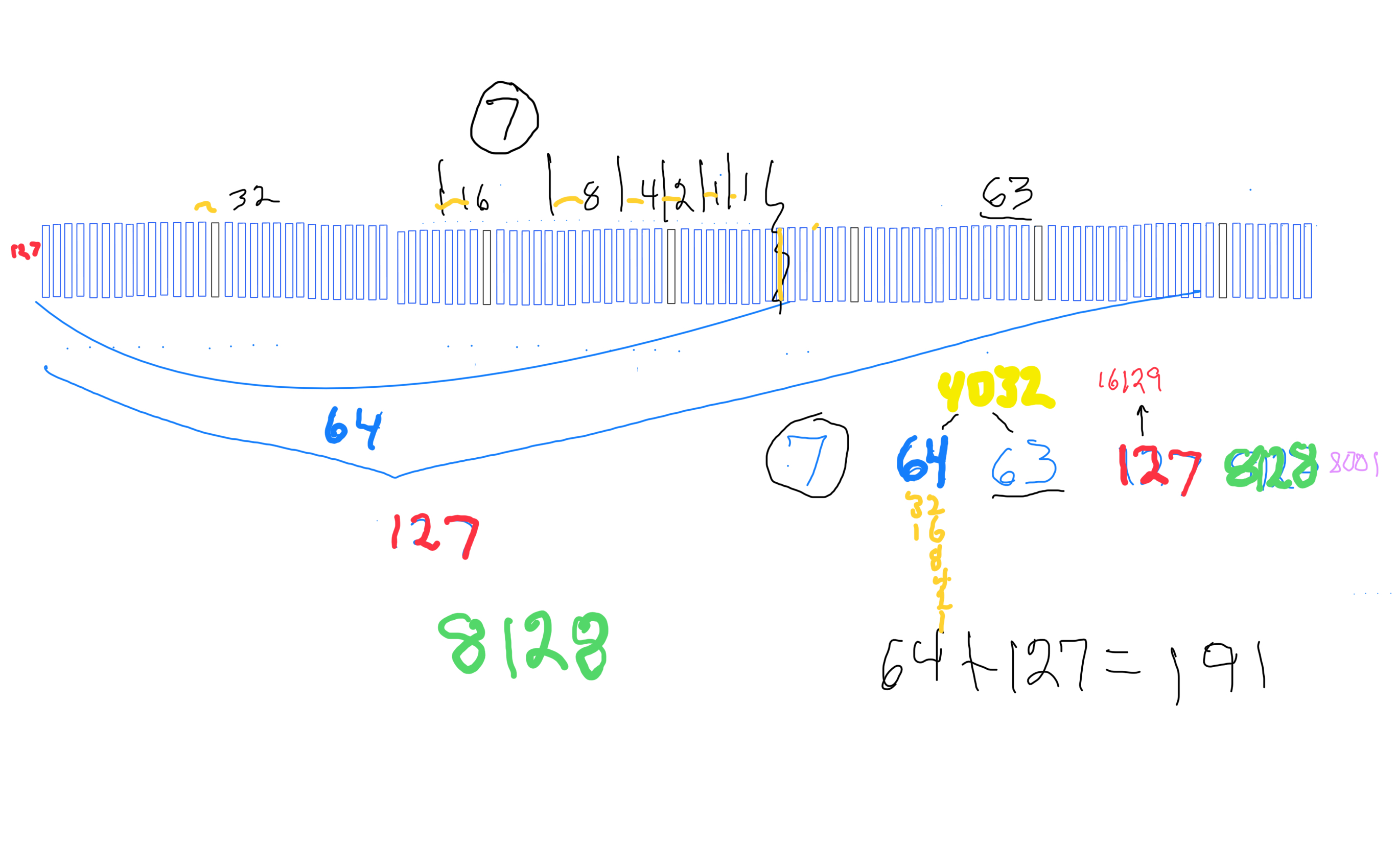
MPS 16129=127² p=7=7 STEPS x=64 y=63 z=127 PN=xz=8128 OC=yz=8001 CR=xy=4032 x²=4096 y²=3969. container"--Set 1 -- TRUE Mp-Pn. (Running out of space.)
*NOTE: The MPS "containers" for ALL FALSE Mp-PN candidates actually contains -- by definition -- more factors and divisors than showed here. The additional factors have not been included. Only those BF1 factors have been included for purposes of comparing with the TRUE Mp-PN, e.i. MPS 225=15² p=4=4 STEPS x=8 y=7 z=15 PN=xz=120 OC=yz=105 CR=xy=56 x²=64 y²=49. container"--Set 2 -- NOT TRUE Mp-Pn. The actual divisors of 120 are: 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120 but only the BF1 related values are used: 1, 2, 4, 8, 15, 30, 60, 120. This also allows for some of the number patterns that the TRUE Mp-PN are embedded in that otherwise would be obscured. An example of this is found in the TIP below.
*TIP*: When ALL "containers" are displayed using ONLY their BF1 related values -- as above -- the z of the current MPS becomes the y of the next MPS, and the MPS of the current MPS becomes the y² value in the next MPS, and vice versa. Also, the PN of the current MPS -- when multiplied by 2 -- equals the CR=xy of the next MPS. There are more: each subsequent MPS has the x value doubled, the y and z values doubled+1. They are completely entangled!
This short video on Vimeo is a good place to start:
The Divisor Matrix Table (DMT) from Reginald Brooks on Vimeo.
How does the BF1 inform the Divisor Matrix Table (DMT) and its sibling tables?
The short answer: it is everything!
The long answer: it is everything and then some!
The DMT, tDMT and EDMT all have their Row 1 Header as the BF1.
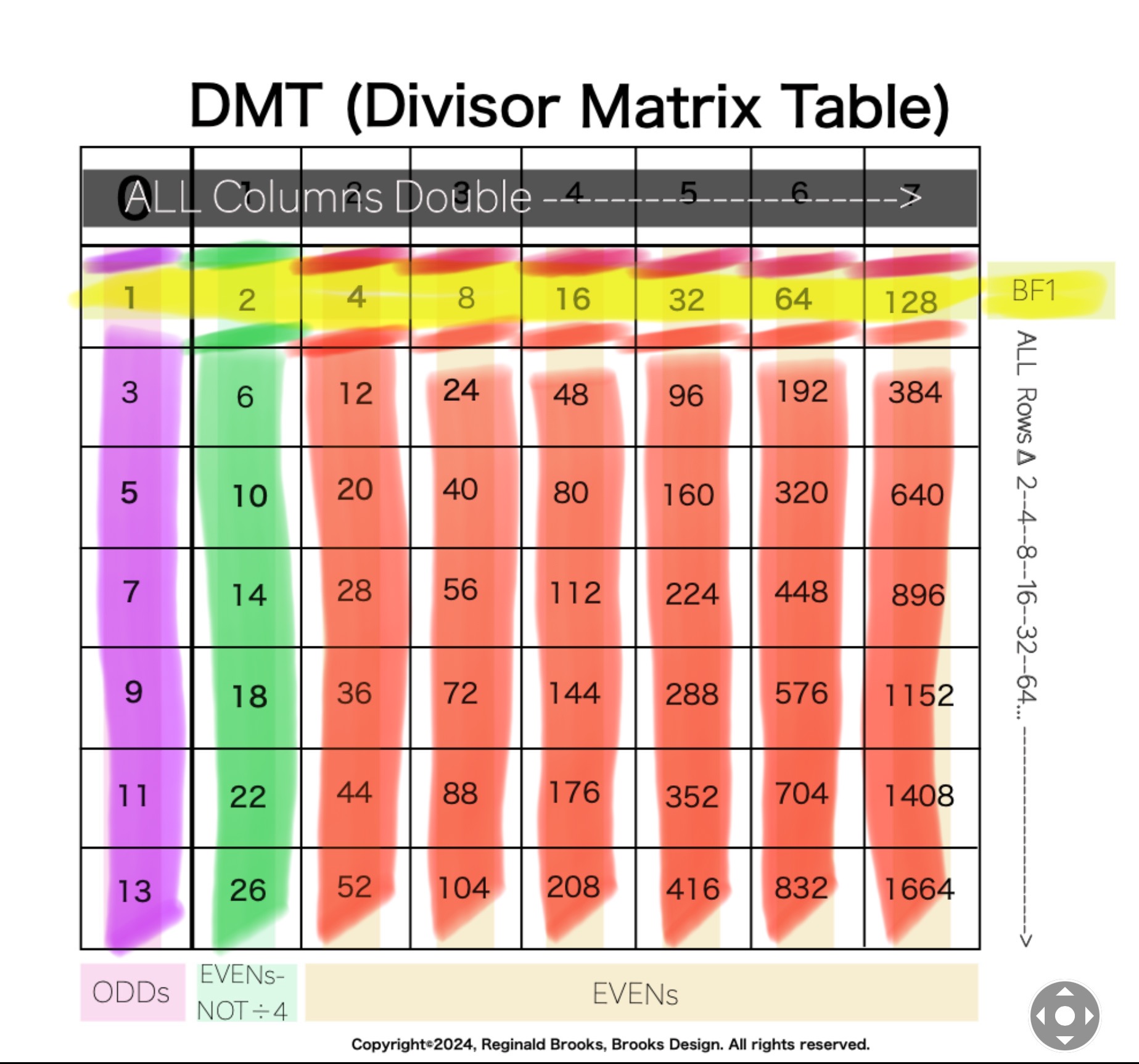
In the DMT, the Column 1 Header is the ODDs -- thus each Row is an ODD number multiple of the top Row 1 Header -- the BF1. It uniquely gives ALL Numbers and ALL of their divisors! See Tables 167-171
The truncated DMT (tDMT) is just the DMT with the Column 1 Header of ODDs reduced to just those ODDs that are the Running Sums (∑) of the initial BF1: 1--3--7--15--31... This eliminates all Rows that are not derived directly from the BF1, i.e. the exponential power of two. When combined with the listings of the ∑ a number of connections between subsequent "containers" are found. See Tables 172-175
The EVENs DMT (EDMT) takes it a step further by substituting the ODDs Column 1 Header with the BF1. That's right, both horizontal and vertical headers of this matrix are the BF1. When combined with the listings of the ∑ a number of connections between subsequent "containers" are found.
Side note:
One may ask: Is not the ODD number sequence that provides the vertical Column Header of the DMT a fractal as well? And you would be so right -- at least in some sense of the concept of the fractal. In fact, the BF1 horizontal Row Header is simply the first Row of the ODD Column 1 doubling sequence: 1--2--4--8--16--.... The ODD Column 1 Header sequence -- 1--3--5--7--9--... is simply doubled to form Column 2, and Column 2 doubled to form 3, and so on. This is actually the easiest way to form the DMT. It also emphasizes an important finding:
Column 1: ODDs
Column 2: EVENs NOT ÷4
Columns 3+: EVENs ÷ 4.
We see that we have two types of EVENs -- one type is NOT÷4 and on type is ÷4. ALL the PNs, except PN 6, are found in the latter. And they ALL end with the number 6! Because the EVENs in Column 1 are only 1 STEP away from the Column 1 ODDs, they too, just like the ODDs, have very minimal number of divisors. This is similar to just one subset group within the Column 3+ EVENs -- the Mp-PNs, and ONLY the Mp-PNs -- also have a minimum number of divisors, distinguishing them from ALL other Column 3+ EVENs who ALWAYS have extra divisors, e.i. PN 28 divisors (factors) are 1-2-4-7-14-28, while the EVEN 36, has 1-2-3-4-6-8-9-12-16-18-36, with 3, 6, 9, 12, and 18 being extra -- resulting from 36 dividing down to 9 a composite number of 3, 3 giving the 3-6-12 extra divisors. This, of course, points to a major divide of ALL ODDs -- are they Prime or Non-Prime (composite) numbers. Composites are always bloated with extras!
Actually, one may think of the ODDs as the ultimate fractal in that all EVENs are but doubled ODDs -- and that includes the EVENs of the BF1!
Side Note 2:
Ultimate Fractal
The ultimate fractal is that of quantity one, usually represented by the numerical symbol "1."
That quantity 1 may be of anything, including SpaceTime (ST) itself. Or it may be a grain of sand, of rice, ...
In the Butterfly Fractal 1 (BF1) -- the "other" ultimate fractal based on the Exponential Power of 2 -- we are presented with the same starting quantity 1 that is doubled. Doubled in the sense that in addition to the starting 1, we have the addition of 2 identical doublings of that 1, giving us 1-2, with a Running Sum (∑) of 3. Do that doubling again gives 1-2-4 with a ∑=7, and so on. The BF1 forms the Top Row Header of the Divisor Matrix Table (DMT) -- a table that holds ALL the natural whole numbers, and, their divisors!
So what forms the First Column Header in the DMT? Why it is the ODDs -- 1-3-5-7... starting with that same quantity 1. The subsequent Rows below the Top Row Header of one BF1 sequence, are simply that BF1 times (1)-3-5-7...
Taking a closer look at the ODDs Column -- 1-3-5-7... -- we see that quantity 1 -- the same quantity 1 that starts the BF1 Row -- is subsequently increased by 2 to give 1-3, and then again by 2 to give 1-3-5, and so on. The quantity 2 is simply added to the quantity before.
If we take the ∑s along the way we get: 1+3=4 -- 4+5=9 -- 9+7=16... i.e., the ∑ sequence of 1-4-9-16...
1-4-9-16... is also the sequence of the squares of 1-2-3-4 and this is the basis of the BIM (BBS-ISL Matrix). The BIM Axis is 1-2-3-4... with a central prime diagonal (PD) of 1-4-9-16=1² - 2² - 3² - 4² ... The Inner Grid (IG) of the BIM is formed from the difference between where the horizontal and vertical intercepts on the PD occur, e.i. IG 7 is the difference (∆) of the horizontal intercept at the PD 16 - vertical intercept at the PD 9. The significance of the BIM is that it not only is the math behind the Inverse Square Law (ISL) that governs our Universe, it is also the source of ALL Pythagorean Triples and ALL Primes (including the rarest of rare Mersenne Primes (Mp).
Back to the ultimate fractal -- the ODDs. 1 is followed by 3 as 1+2=3, and 3 is followed by 5 as 3+2-5, 5 followed by 7,.. It is as if the more efficient way of following the doubling of quantity 1 from that of the more linear "other" ultimate fractal -- the BF1 -- is simply to add the same constant doubling value of 2 to each subsequent ODD Column value. And it turns out to be true!
When the Column 1 ODDs are doubled, they form the Column 2 EVENs. These EVENs are a special subclass of ALL the EVENs: they are NOT ÷4. ALL other EVENs are ÷4.
In fact, when you double Column 2 EVENs (NOT ÷4) you get Column 3 EVENs that are ÷4, and doubling Column 3 gives Column 4 EVENs, and doubling 4 gives 5,... on the DMT. The entire DMT is formed from this simple doubling of the Columns!
Three types of Columns arise:
Col. 1 ODDs
Col. 2 EVENs NOT÷4
Col.3+ EVENs ÷4
And it all started with the Column 1 ODDs -- the ultimate fractal!
But we are not done yet.
If you let the ODDs become the exponent in the Exponential Power of 2 we get:
2¹ =2
2² =4
2³ =8
2⁴ =16
2⁵=32
2⁶ =64
2⁷ =128
2⁸ =256
2⁹ =512
2¹⁰ =1024
2¹¹ =2048
2¹² =4096
2¹³ =8192
This group of EVENs becomes the "x" value of the "containers." They are equivalent to the 2ᵖ⁻¹ values of the Euclid-Euler Theorem [ 2ᵖ⁻¹(2ᵖ -1)]= Perfect Number (PN). They are also identical to the BF1 sequence.
2¹ =2-1=1
2² =4-1=3
2³ =8-1=7
2⁴ =16-1=15
2⁵=32-1=31
2⁶ =64-1=63
2⁷ =128-1=127
2⁸ =256-1=255
2⁹ =512-1=511
2¹⁰ =1024-1=1023
2¹¹ =2048-1=2047
2¹² =4096-1=4096
2¹³ =8192-1=8191
This group of the EVENs-1 becomes the "z" -- z=Mersenne Prime candidate -- value of the "containers." They are equivalent to the 2ᵖ-1 values of the Euclid-Euler Theorem [ 2ᵖ⁻¹(2ᵖ -1)]= Perfect Number (PN). They are also identical to the ∑ of the BF1 sequence.
But wait. "'Foul' you might cry out! These have more than the ODDs included!" And you would be right. This shows ALL the "containers" as well.
So lets stick to strictly the ODDs:
If you let the ODDs become the exponent in the Exponential Power of 2 minus 1, to start with, we get:
2⁰ =1
2² =4
2⁴ =16
2⁶ =64
2⁸ =256
2¹⁰ =1024
2¹² =4096
This group of EVENs becomes the "x" value of the Set 1 "containers." They are equivalent to the 2ᵖ⁻¹ values of the Euclid-Euler Theorem [ 2ᵖ⁻¹(2ᵖ -1)]= Perfect Number (PN).
If you let the ODDs remain the exponent in the Exponential Power of 2, after subtracting 1, we get:
2¹ =1-1=0
2² =4-1=3 *Exception to the rule: Only one Set 2 "container" holds a TRUE Mp -- this one.
2³ =8-1=7
2⁵=32-1=31
2⁷ =128-1=127
2⁹ =512-1=511
2¹¹ =2048-1=2047
2¹³ =8192-1=8191
This group of resulting ODDs (*exception) becomes the "z" -- z=Mersenne Prime candidate -- value of the Set 1 "containers." They are equivalent to the 2ᵖ-1 values of the Euclid-Euler Theorem [ 2ᵖ⁻¹(2ᵖ -1)]= Perfect Number (PN).
Effectively, the ODDs Fractal 1 provides a clear path to the Set 1 "containers" -- and with the *exception, are the exclusive subset of "containers" that hold the sub-subset Mp-PN pairings! Not bad!
In that these same ODDs -- as the ODD number summation series 1+3=4, 4+5=9, 9+16=25,... -- underlie the structure of the BIM, we have indeed, given ample light to the notion that they may be the primary ultimate fractal. Remember, every EVEN divides down to an ODD, every EVEN is composed of two Primes (Goldbach Conjecture), and every Non-Prime ODD is the product of two or more Primes. Where are we going with this? Are the Primes the actual fundamental ultimate fractal? Perhaps one that embraces a more fundamental definition of a true numerical fractal?
See Tables 176-179.
Check out these videos, too:
You will find the four-part video series — “Numbers: Doubling Fractals Fill the Voids."
TIP*: on Vimeo, you can change the playback speed by selecting the “gear” icon.* TIP*: Parts 1-3 give a diagrammatic visualization of the unfolding math that characterizes the Mp-PN pairings and the “containers” that hold them — giving rise to the* DMT*; Part 4 is a pure visualization “summary” if you will, of the entire journey and the one you don’t want to miss. I*
~~~
“Numbers: Doubling Fractals Fill the Voids”
How does the BF1 inform the BBS-ISL Matrix table (BIM)?
The BIM -- up until the discovery of the DMT -- was, and remains, the Pandora's Box of mathematical tables. Everything from Primitive Pythagorean Triples to PRIMES is found within this Inverse Square Law (ISL) matrix, including everything having to do with the Exponential Power of 2 (a.k.a. the BF1). How so? The BIM is but a subset table of the DMT. The advantage of seeing the BF1, Mp-PN pairings and all the 10 ID parameters thereof is also its disadvantage -- details. The BIM really gets you into the details whereas the BF1 and Mp-PNs within the larger, simplified DMT-tDMT-EDMT tables is just that -- simpler to see!
What's "next?"
In Tables 180-181, along with a refreshed Table 130, we take a look at the NEXT Mp-PN pairings from different angles.
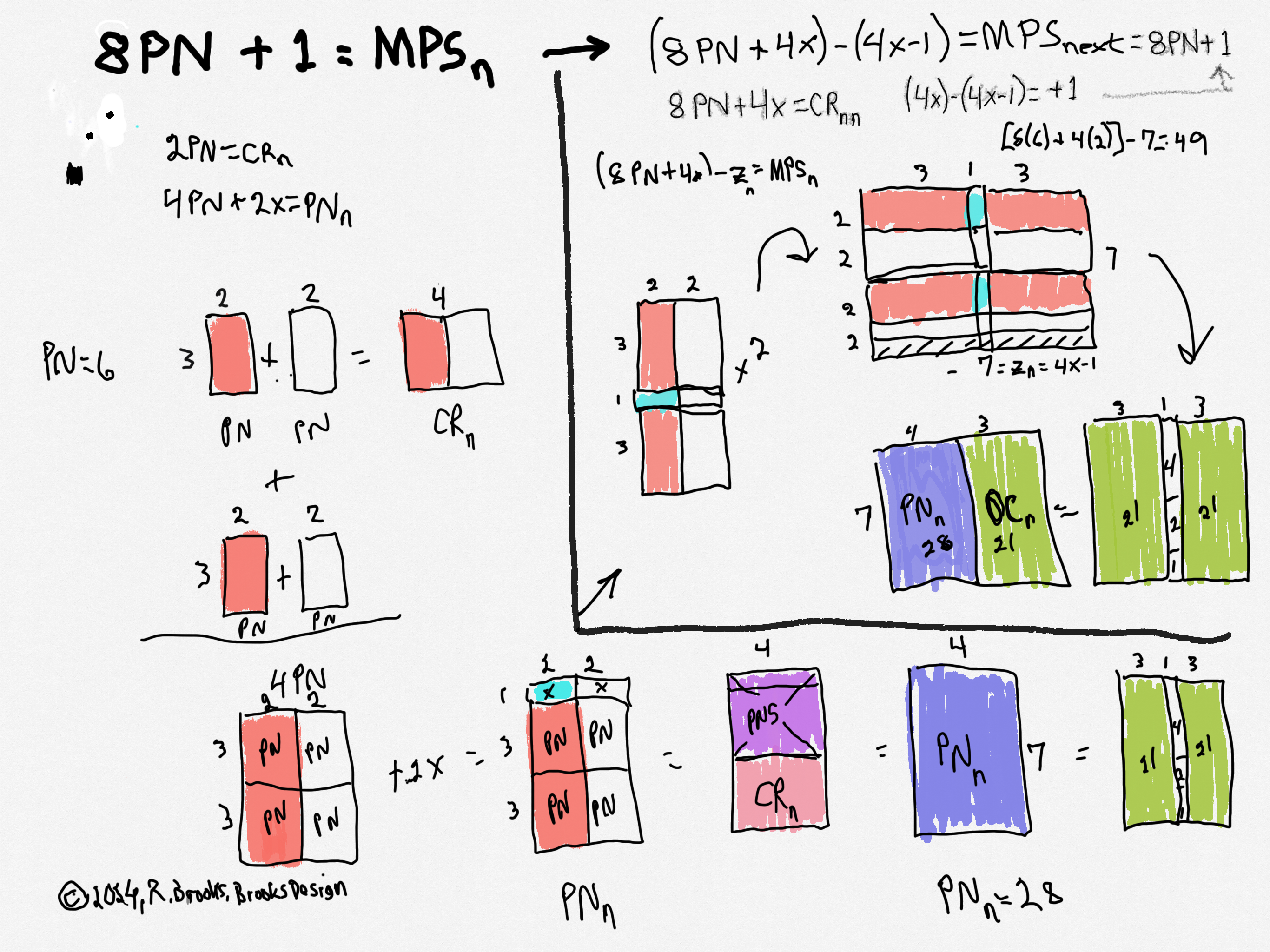
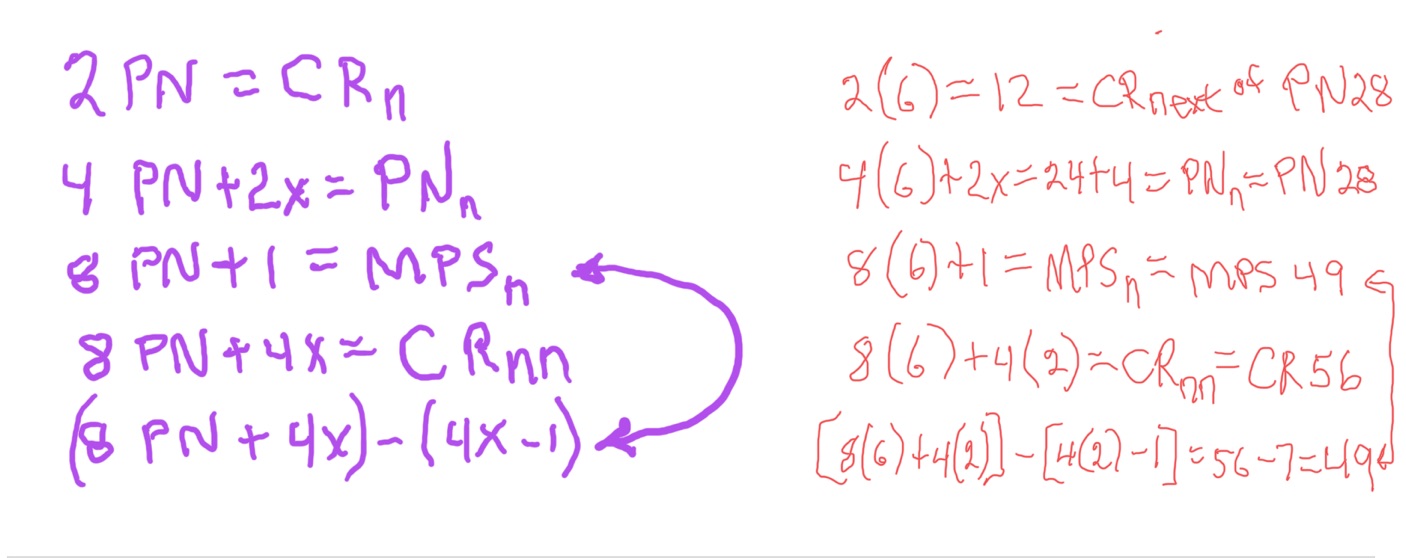
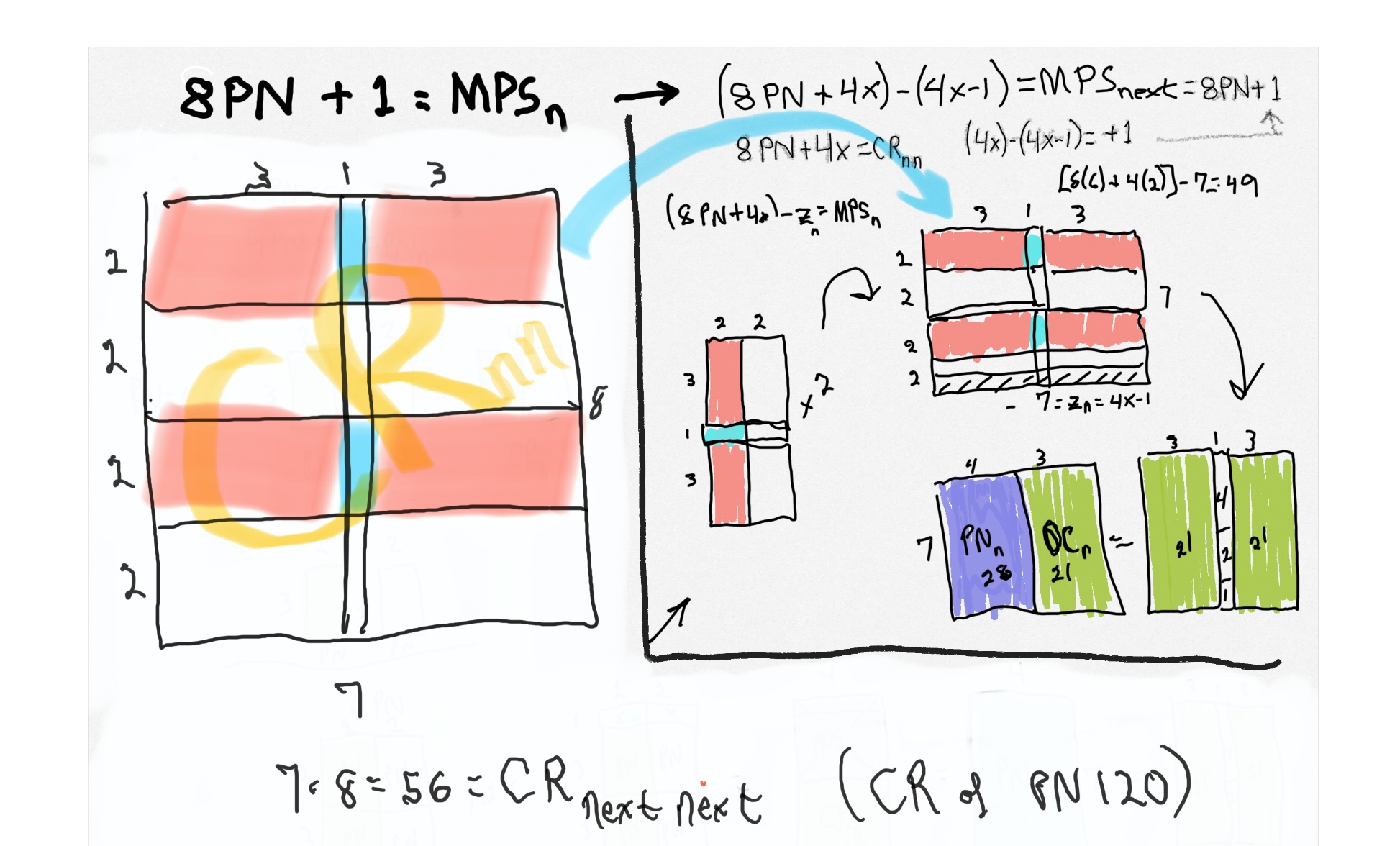
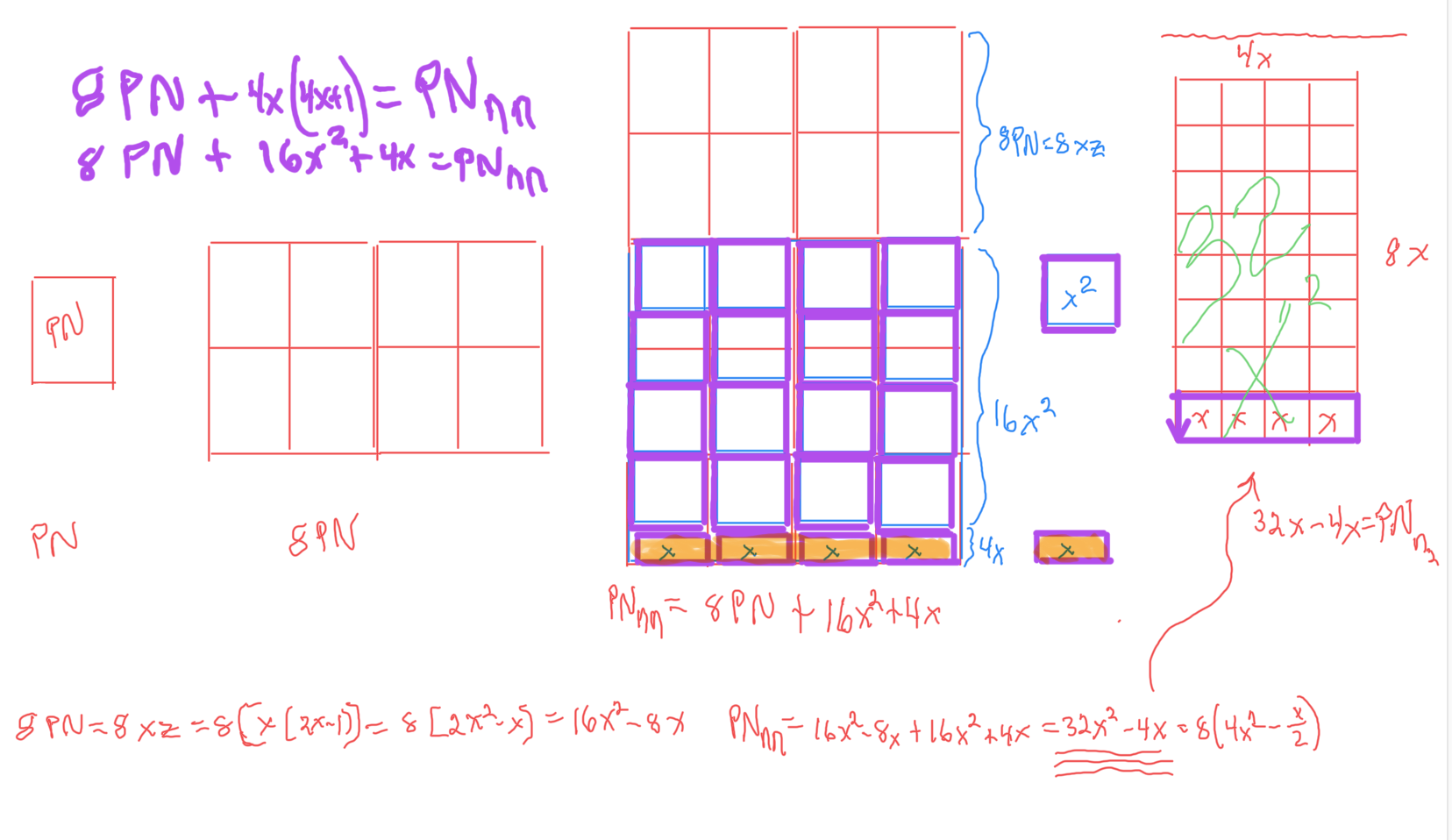



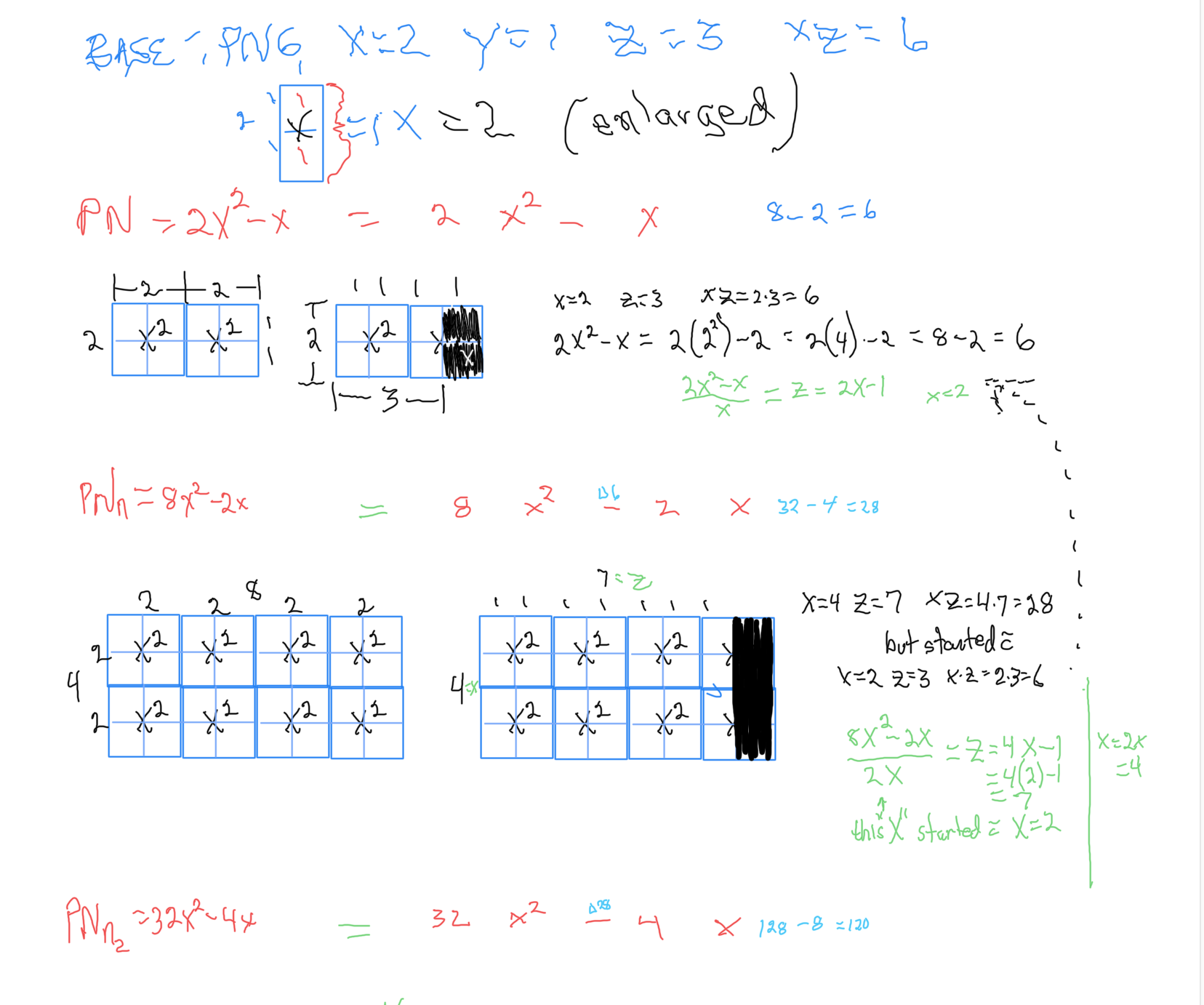


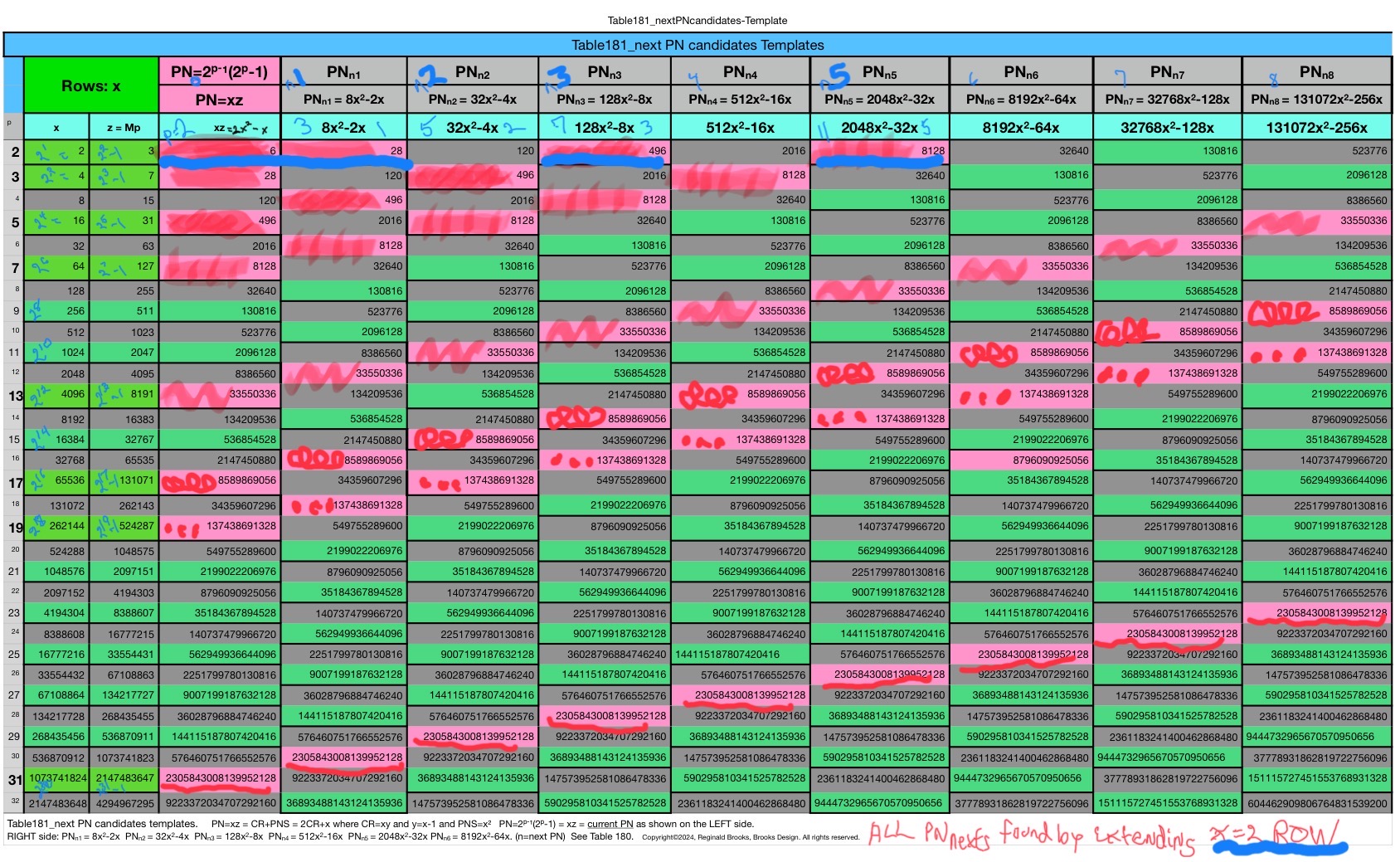
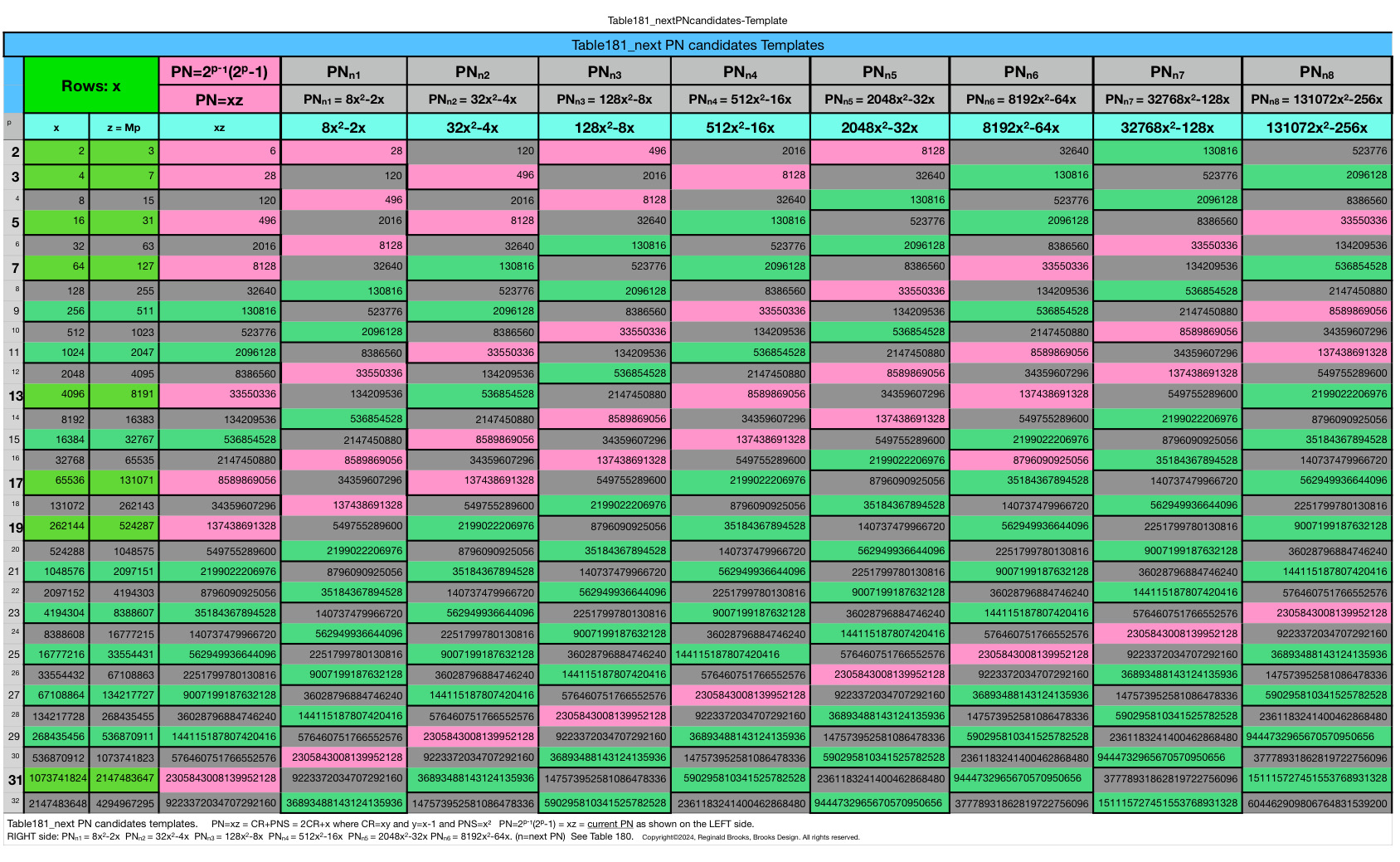
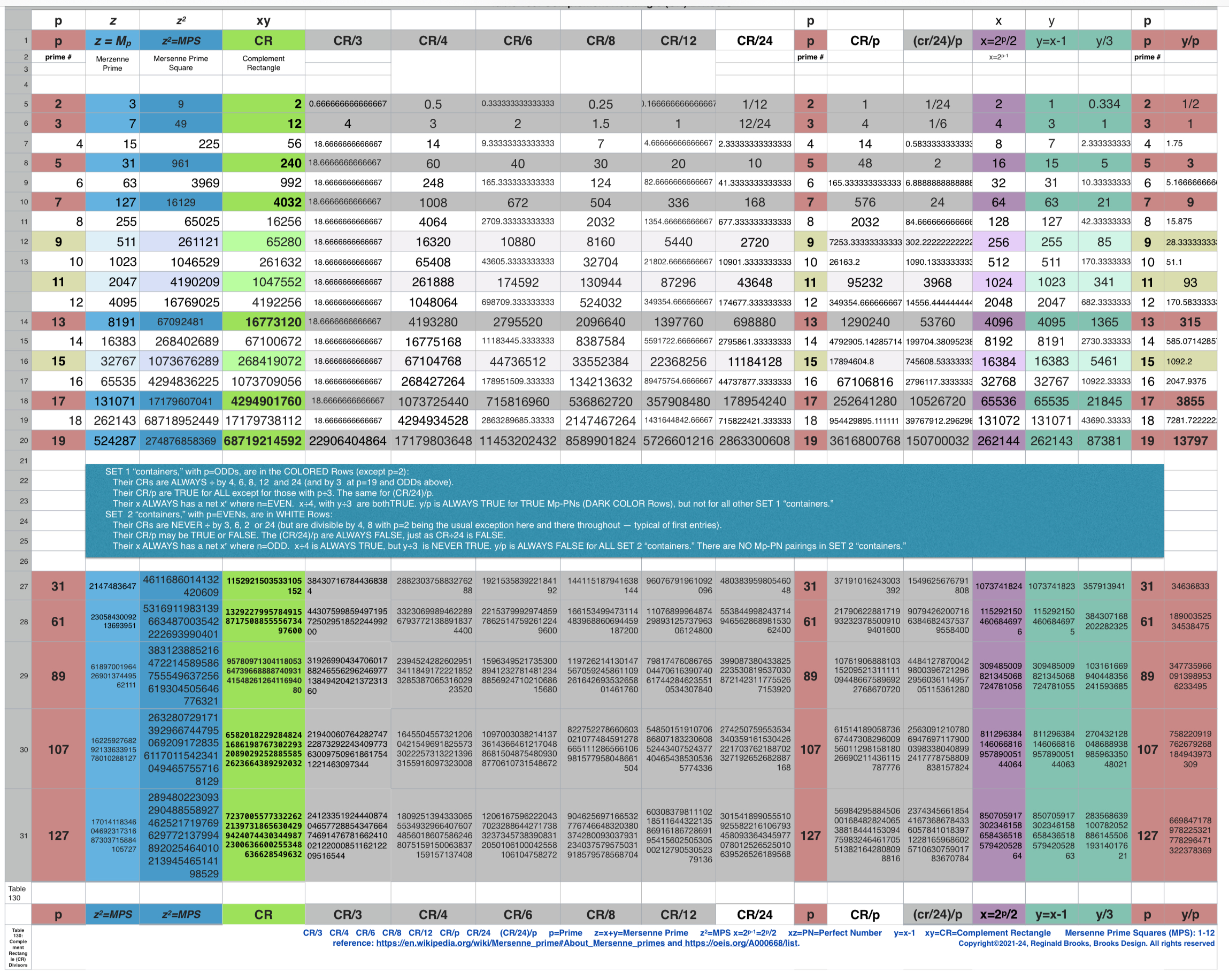
Table 130 has been updated with new information. By now, it should come as no surprise that there are numerous connections between sequential "containers", and, to those further on down the line, by simply incorporating a custom multiplier to any one of the 10 identifying, profiling parameters. The above Tables, especially Table 181 gave ample example!
Or, you just may prefer the simplicity of:
Simple As Can Bee, 2
It’s simple to see
1—2—3 gives y—x—z
Next y comes from z
Simpler and more direct than “8PN+1” page, however “8PN+1” gives insight into the NPS!
2^0=1,
2¹=2,
2²=4,
2³=8,
2⁴=16,
2⁵=32,
2⁶=64,
2⁷=128,
2⁸=256,
2⁹=512,
2¹⁰=1024,
2¹¹=2048,
2¹²=4096,
2¹³=8192,…
1+2=3 a Mersenne Prime = Mp = z
3+4=7 = z
7+8=15
15+16=31 = z
31+32=63
63+64=127 = z
127+128=255
255+256=511
511+512=1023
1023+1024=2047
2047+2048=4095
4095+4096=8191 = z
While deep profiling of the "containers"-- and the TRUE Mp-PN pairings contained within -- has and will continue to be the main area of interest, it is readily apparent that sufficient data has been found and presented to allow some incarnation of AI and Python to readily ferret out the next, and next, and next,... larger Mp-PNs for *those chasing that goal. What remains of great mystery is how these connections play out in the formation of SpaceTime and all the expression(s) that emerge from such. No doubt, the relationship to entanglement, entropy, the arrow of time, and ultimately that which defines consciousness will be uncovered!
What's "next?"
In Tables 182-188 we take a look at the NEXT Mp-PN pairings from different angles.
Table182_zSquared+zOver2EqualsPN.pdf
Table183_Make-Mp-DMT-.pdf
Table184_Mp-DMTdifferences-.pdf
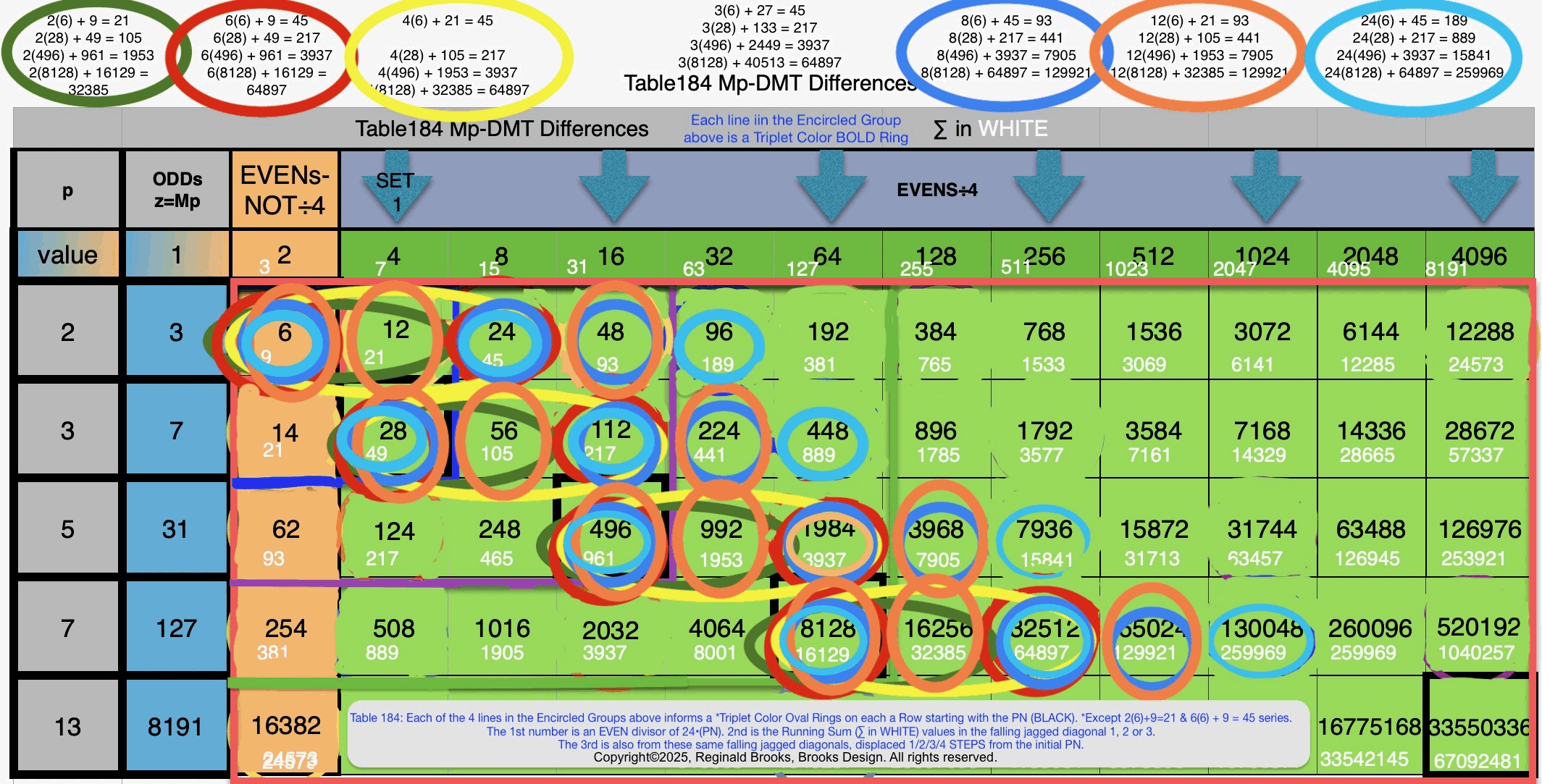
Table184 Mp-DMT Differences-Annotated.gif

Table185_Mp-DMTdifferences-1.gif

Table185_Mp-DMTdifferences+1.gif

Table185_Mp-DMTdifferences-2.gif

Table185_Mp-DMTdifferences+2.gif
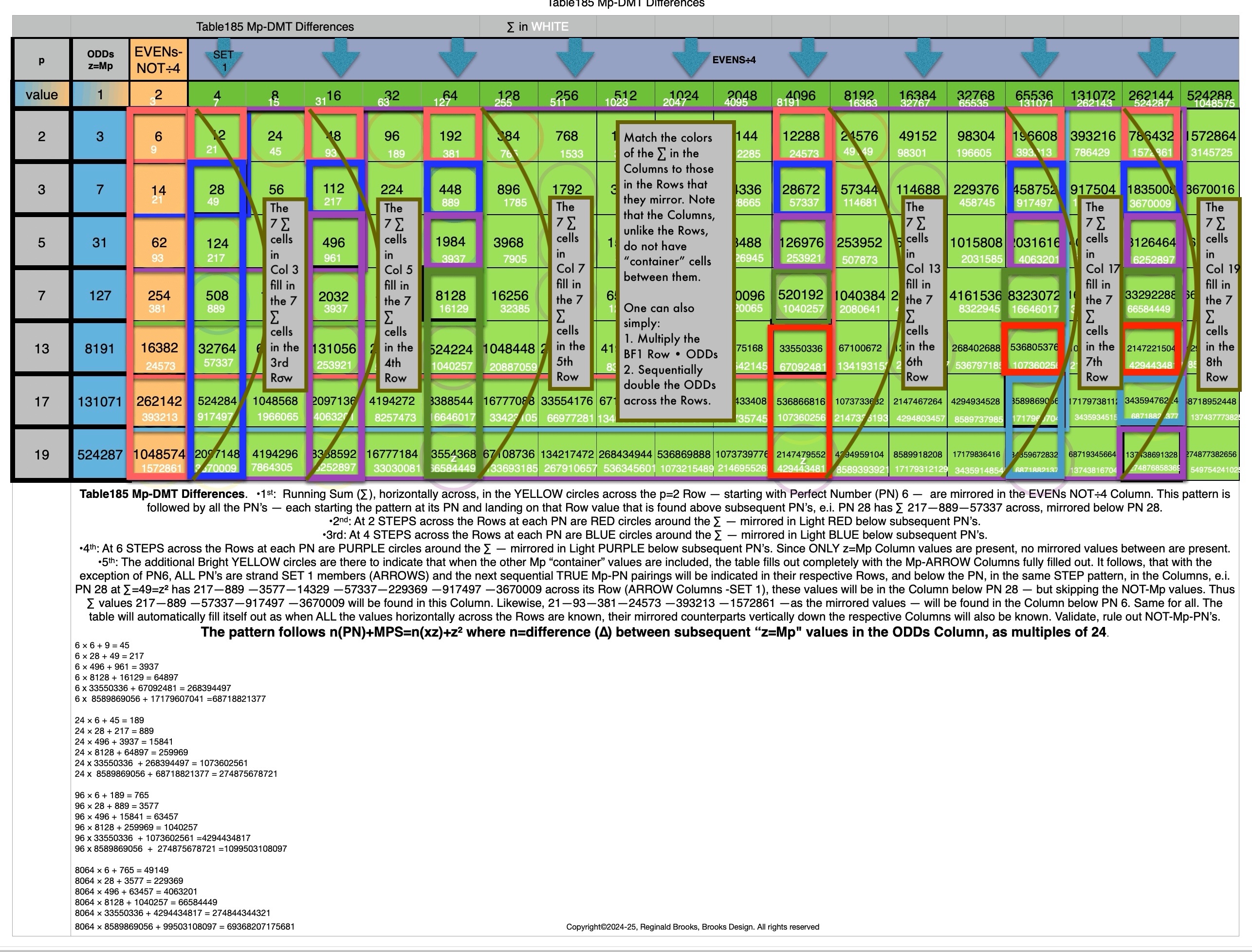
Table185_Mp-DMTdifferences+2A.jpg
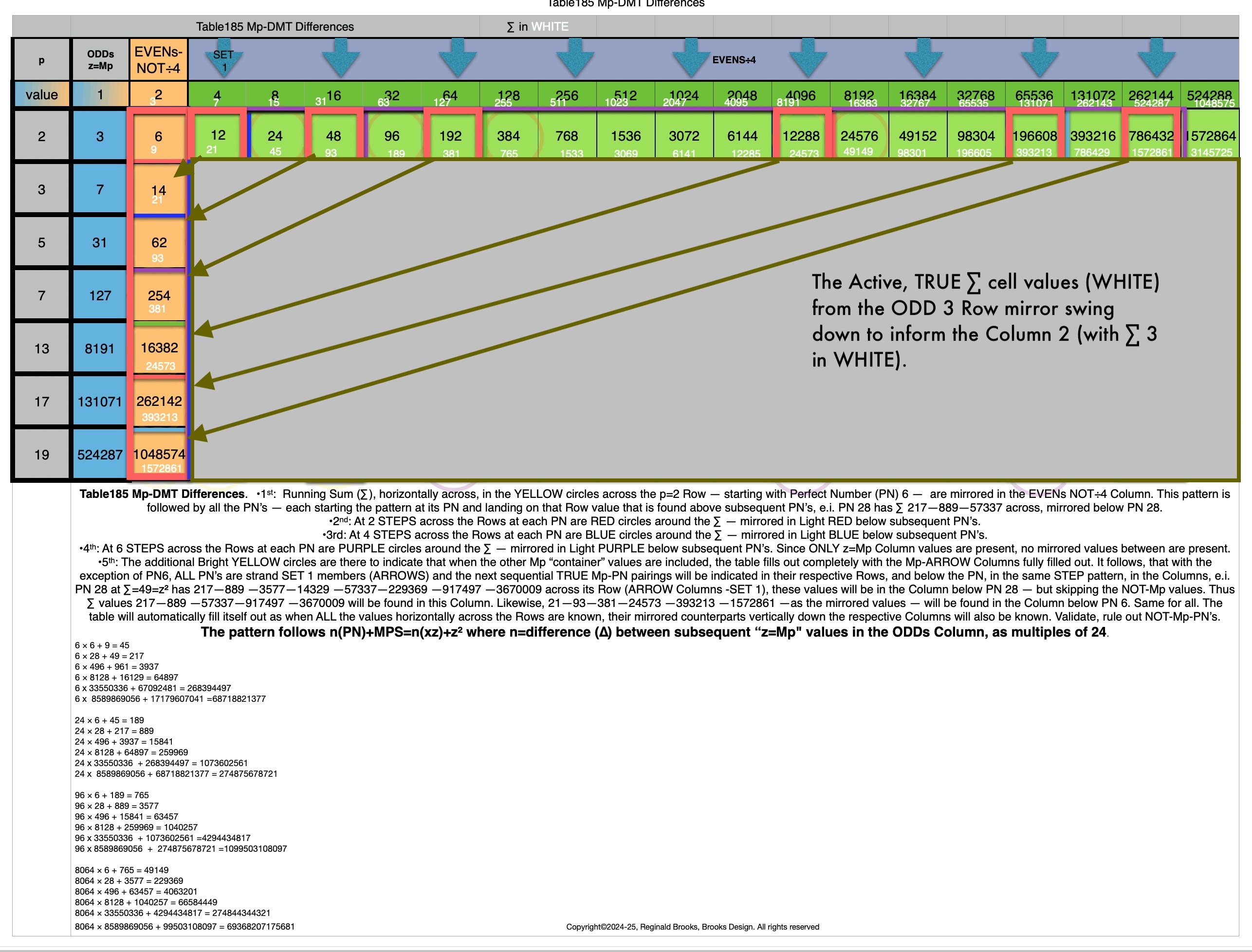
Table185_Mp-DMTdifferences+2B.jpg

Table185_Mp-DMTdifferences+2C.jpeg
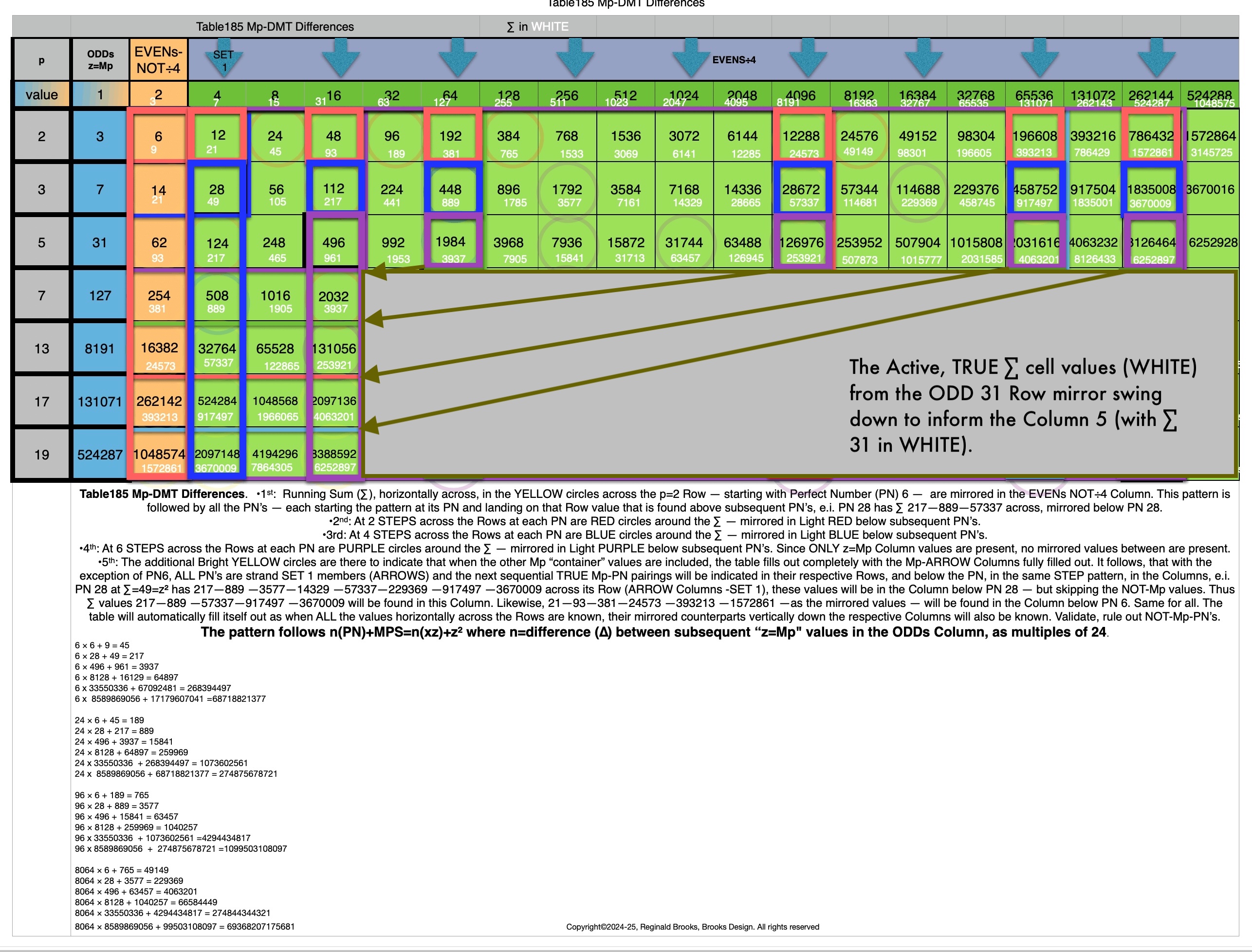
Table185_Mp-DMTdifferences+2D.jpeg

Table185_Mp-DMTdifferences+2E.jpeg

Table185_Mp-DMTdifferences+2F.jpeg

Table185_Mp-DMTdifferences+2G.jpeg
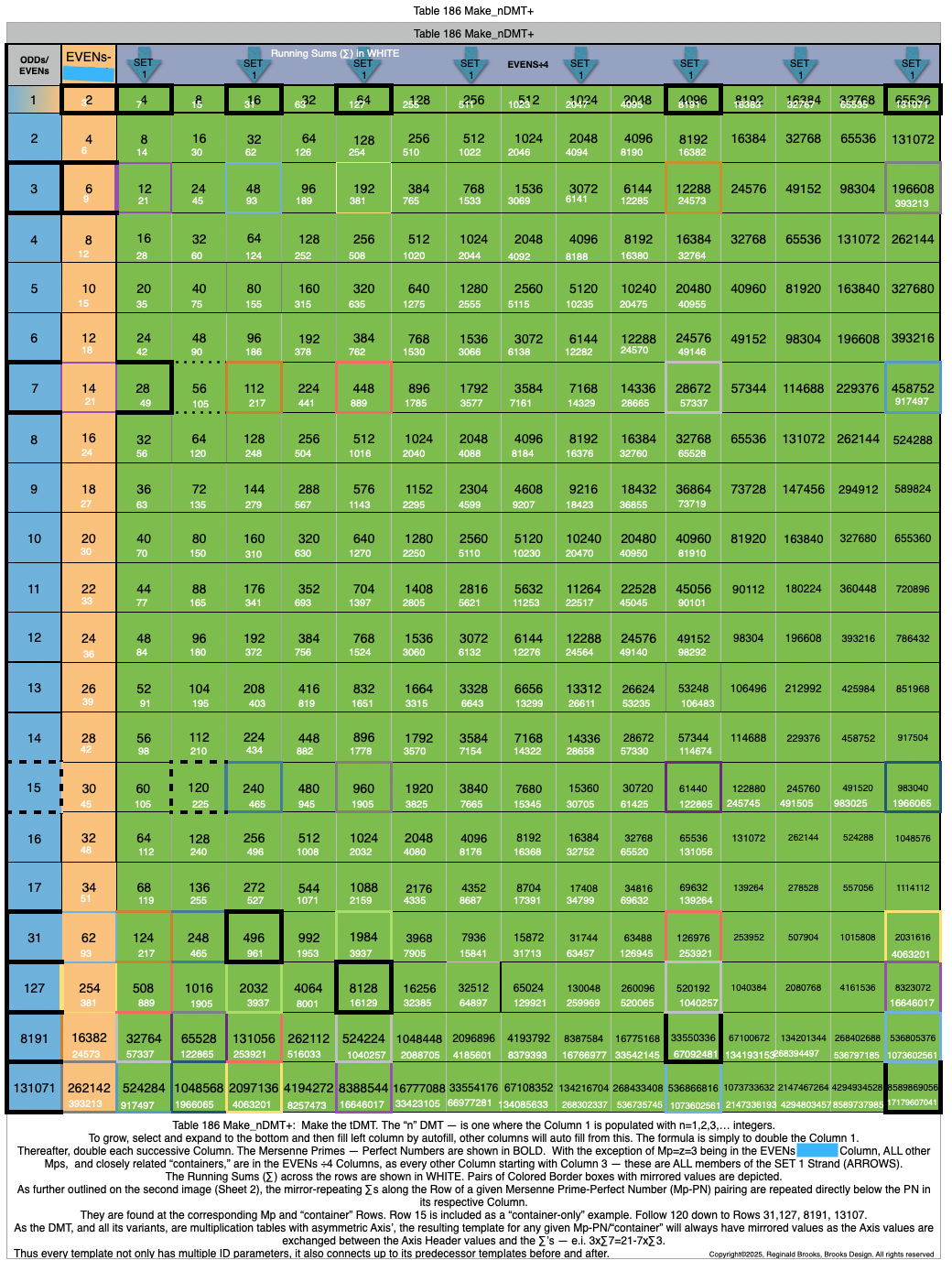
Table186_Make_nDMT+1.png
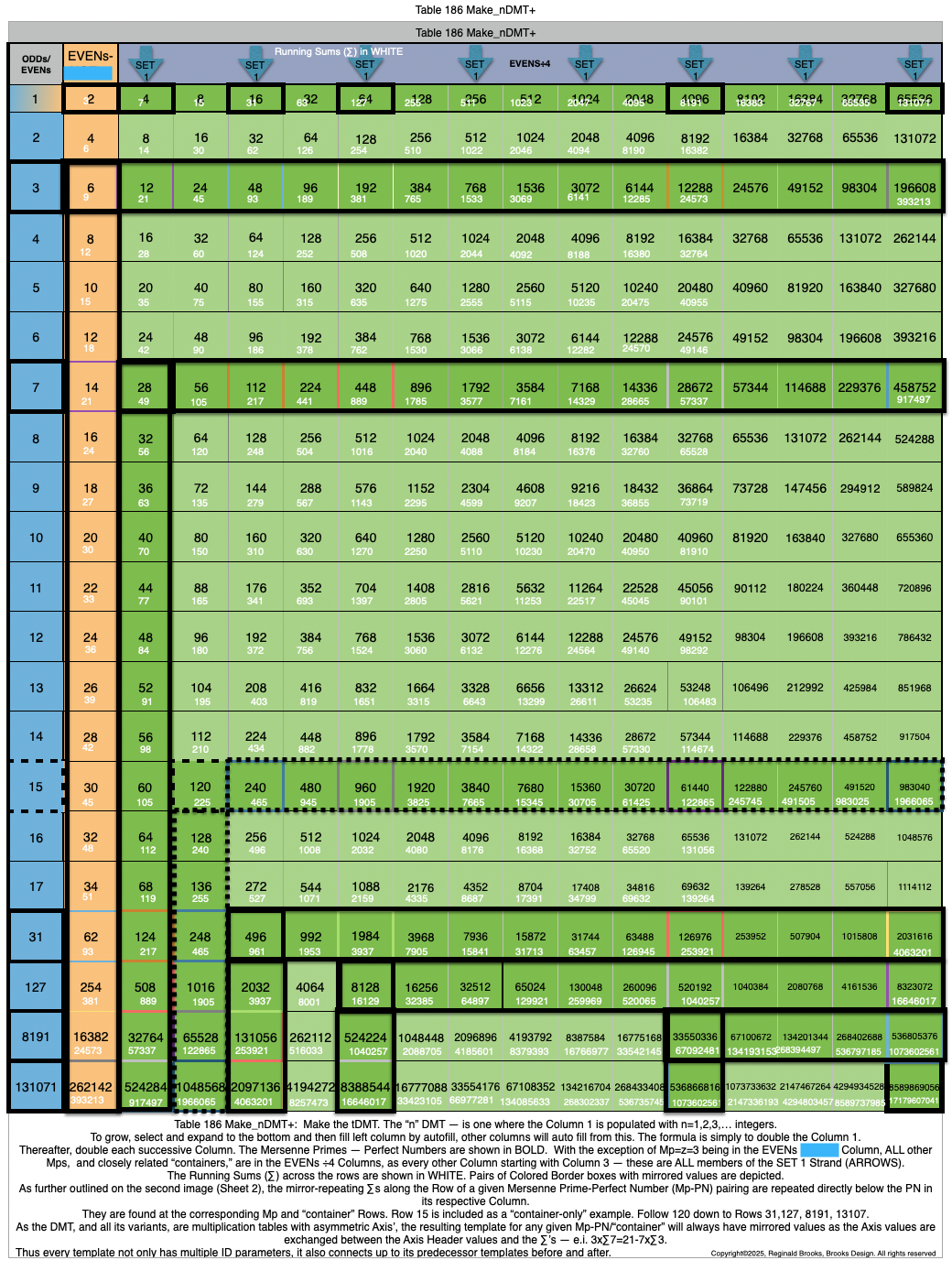
Table186_Make_nDMT+2.png
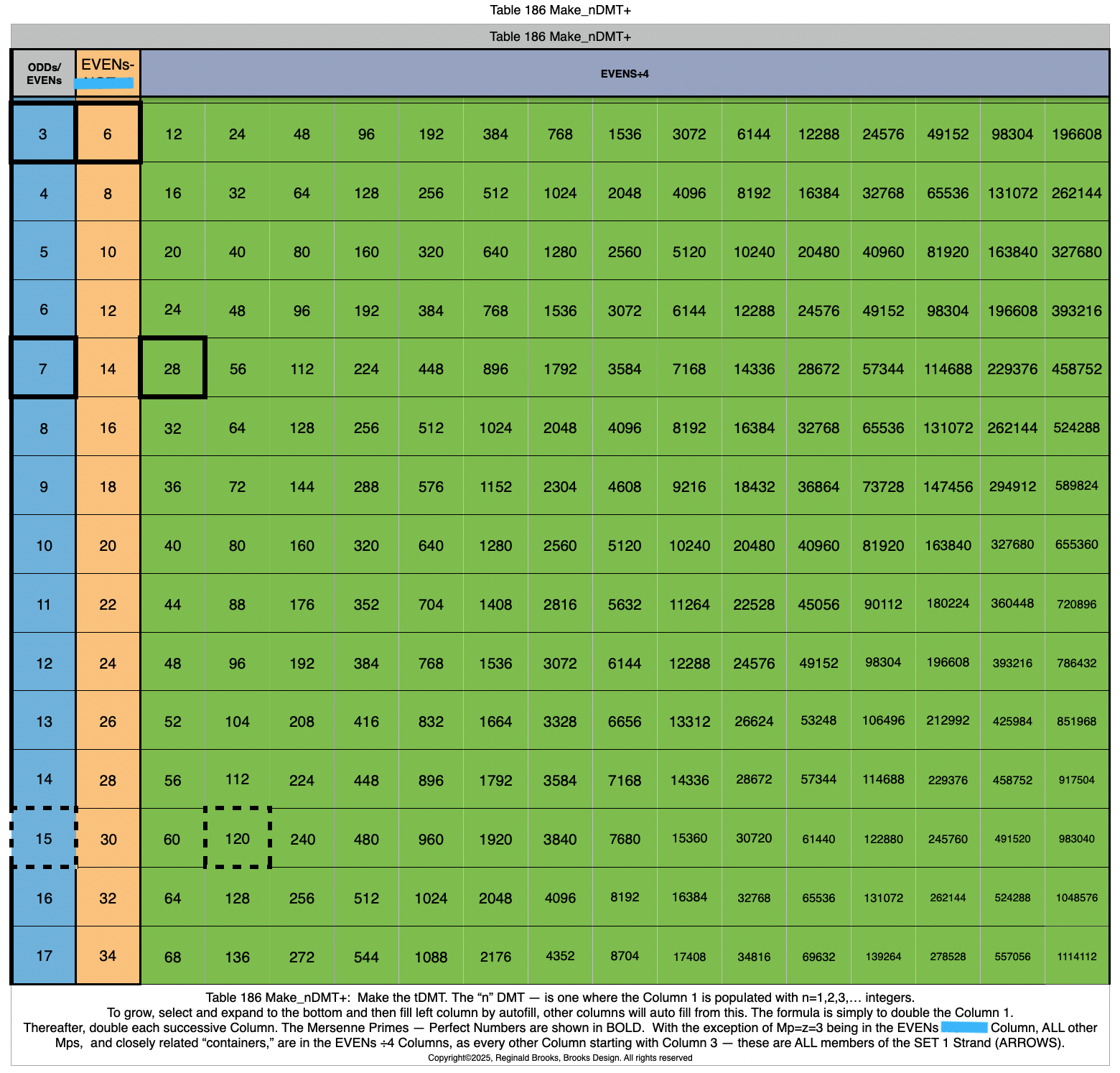
Table186_Make_nDMT+3.png
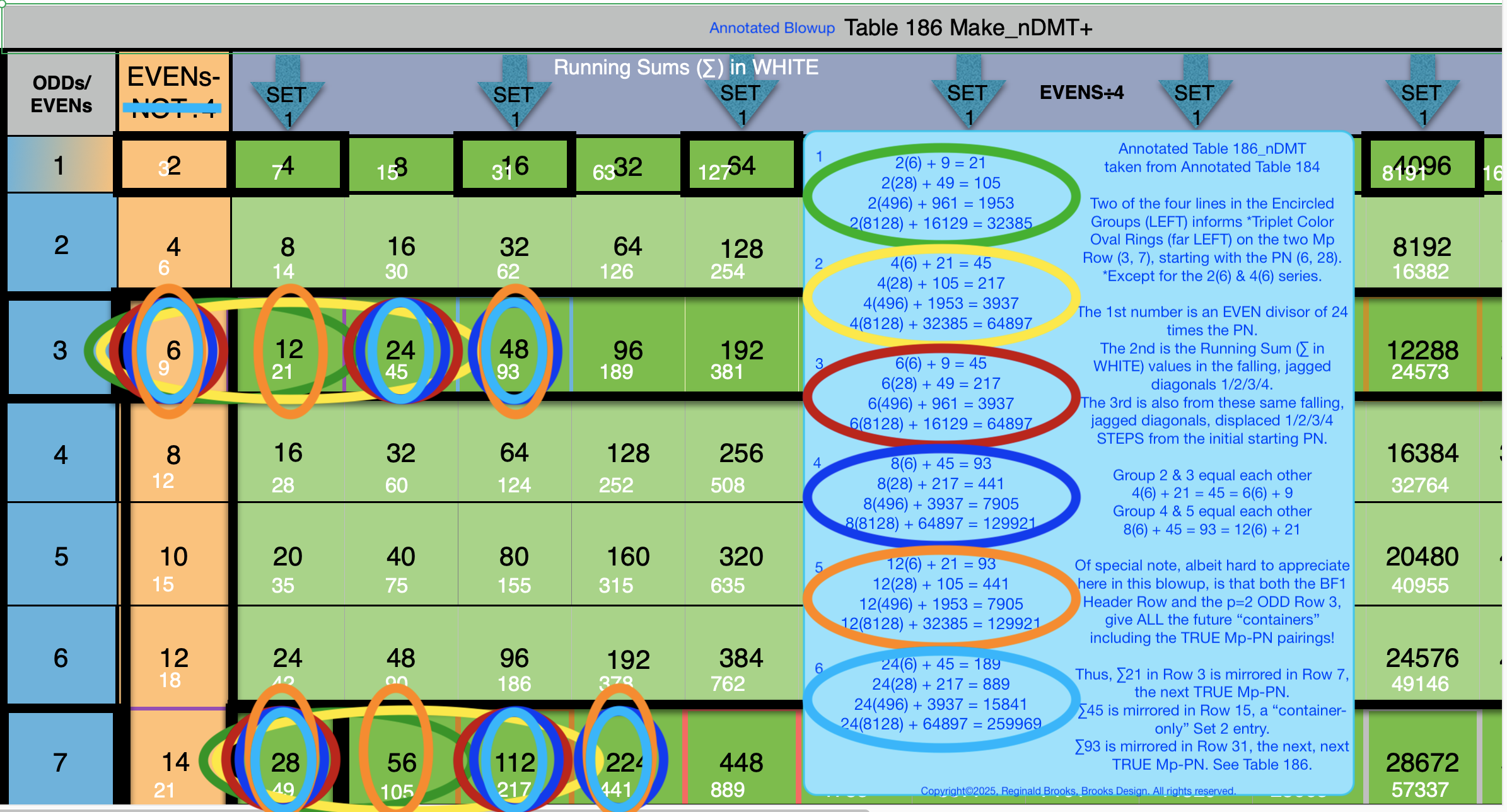
Table186closeUpAnntd2.png
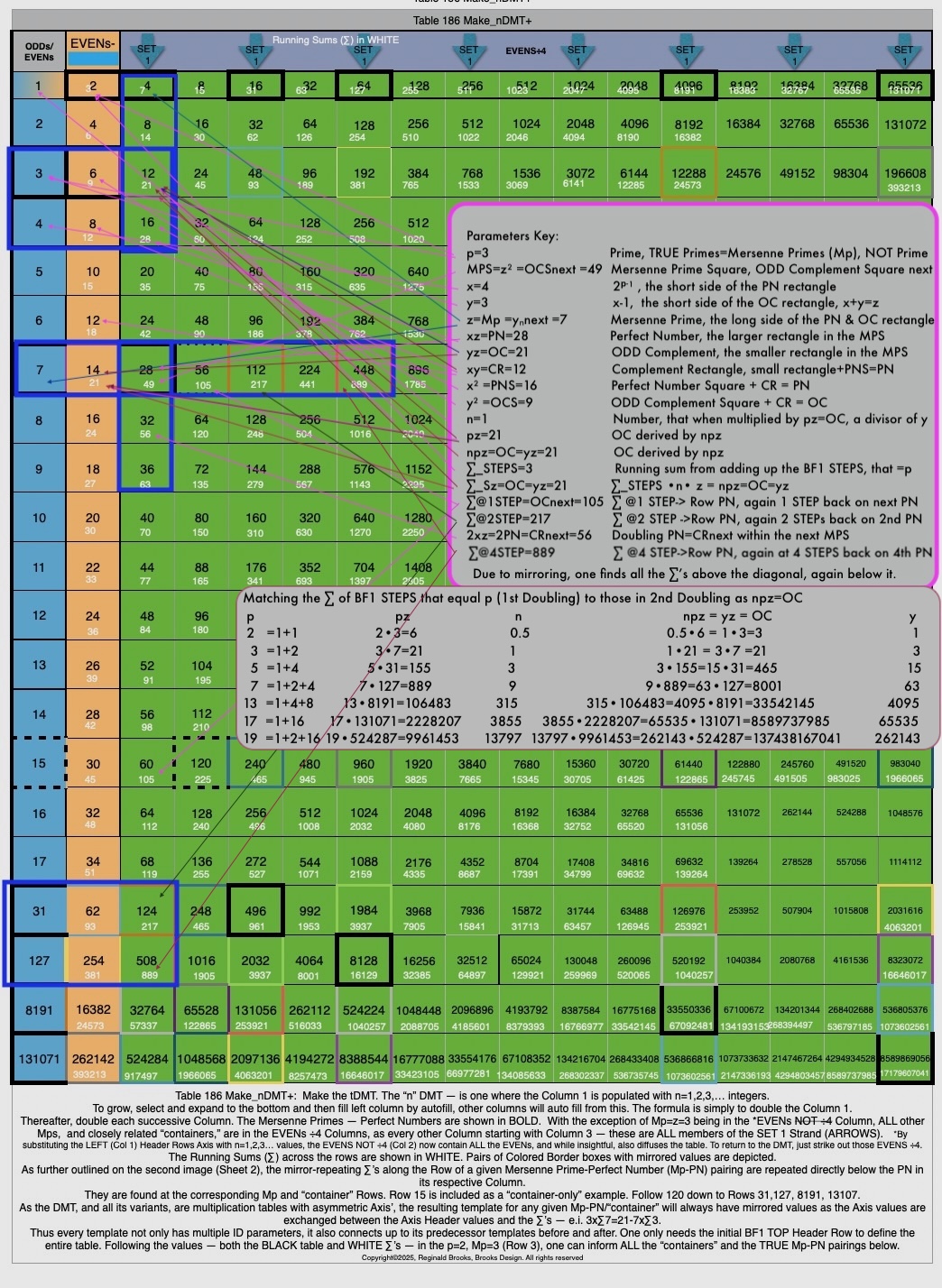
Table186_npzOC-1.jpg
Table186closeUpAnntd2.png
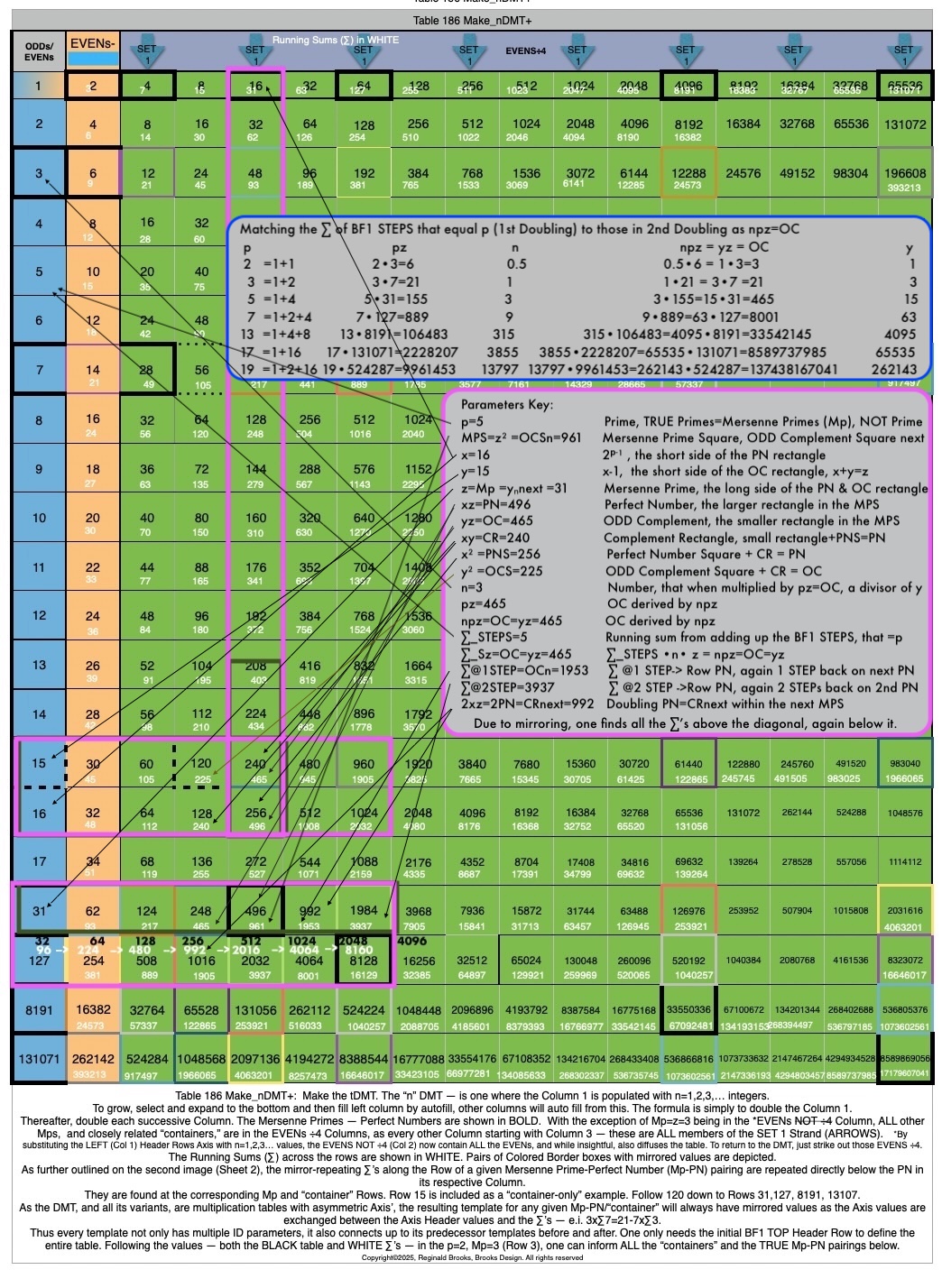
Table186_npzOC-2.jpg
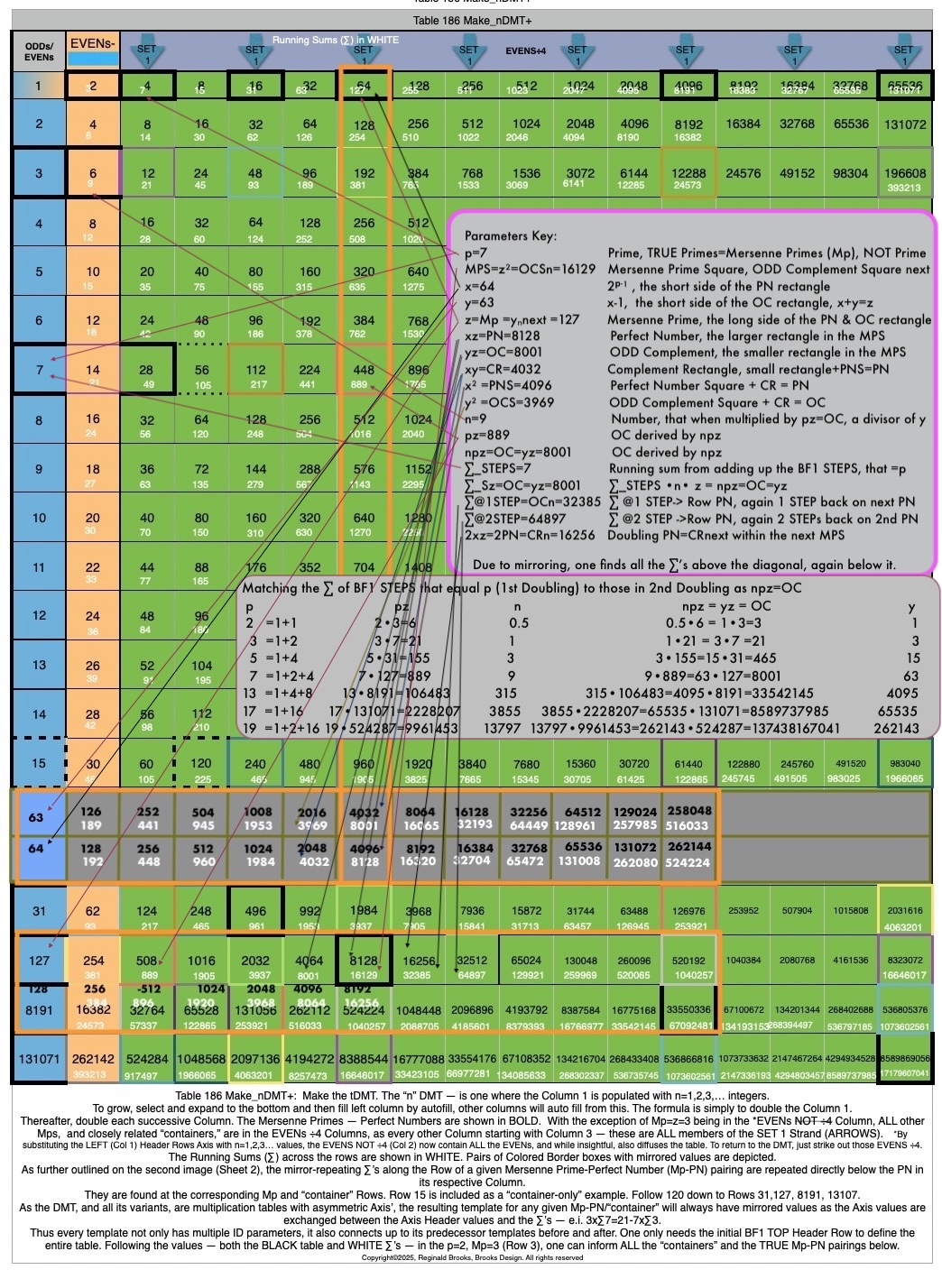
Table186_npzOC-3.jpg
Table187_Squares+n24
Table188_4z+3gives_z.pdf
*As stated early on, any rewards and/or financial assets gained by others -- in or out of academia -- from the use of this information shall have its rightful proportion applied to a trust fund setup for the sole purpose of providing the encouragement and financial support for underprivileged youth with an interest, and aptitude, to pursue studies in the field of mathematics -- specifically mathematics that relates to physics and art.
REFERENCE: Table 124 Mersenne Prime Squares -3+ “Containters”
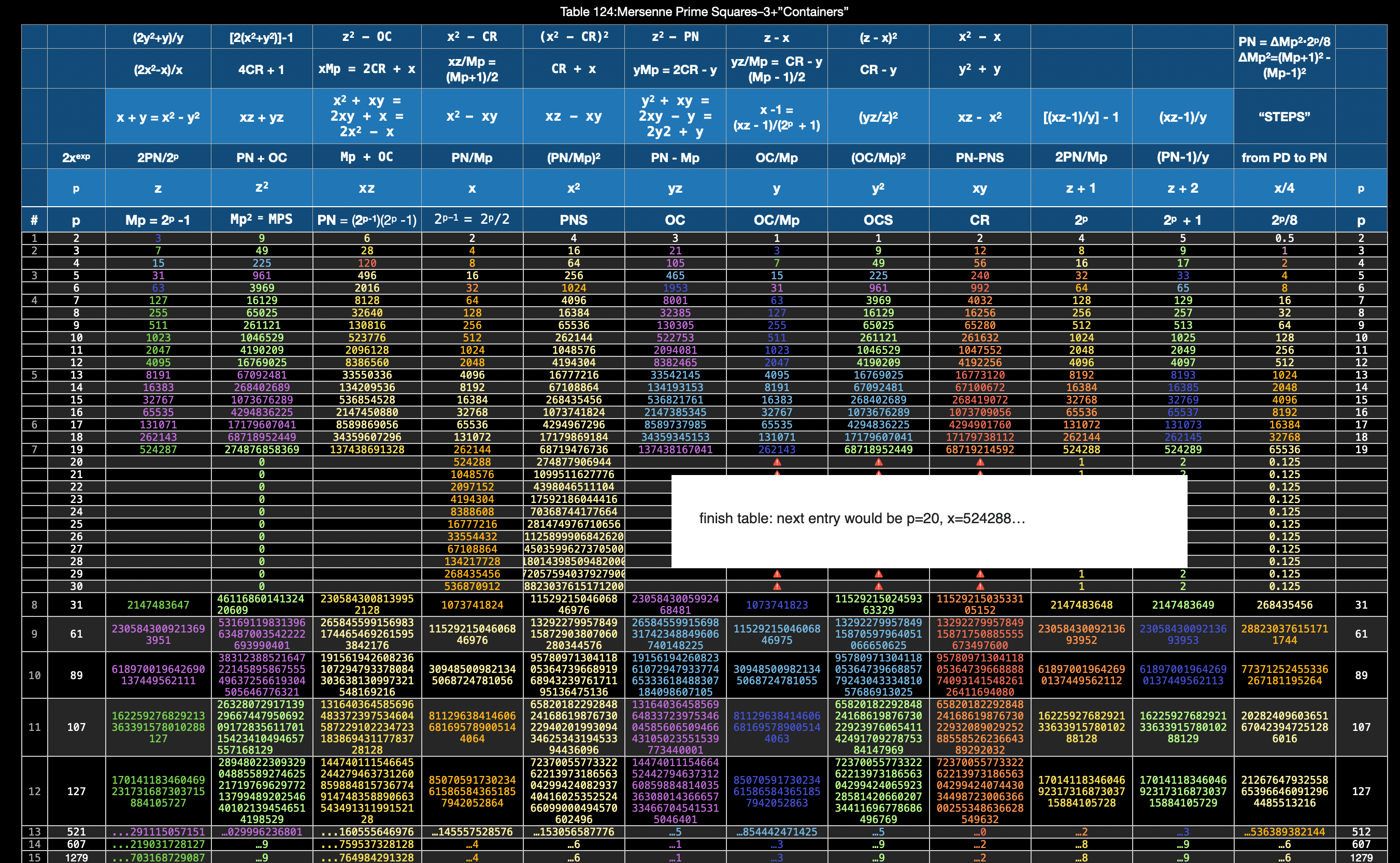
Here are the listings for the 10 ID parameters for the "containers" that include the Mp-PN pairings (PURPLE Dots). Copyright©2021-24, Reginald Brooks, Brooks Design. All rights reserved.