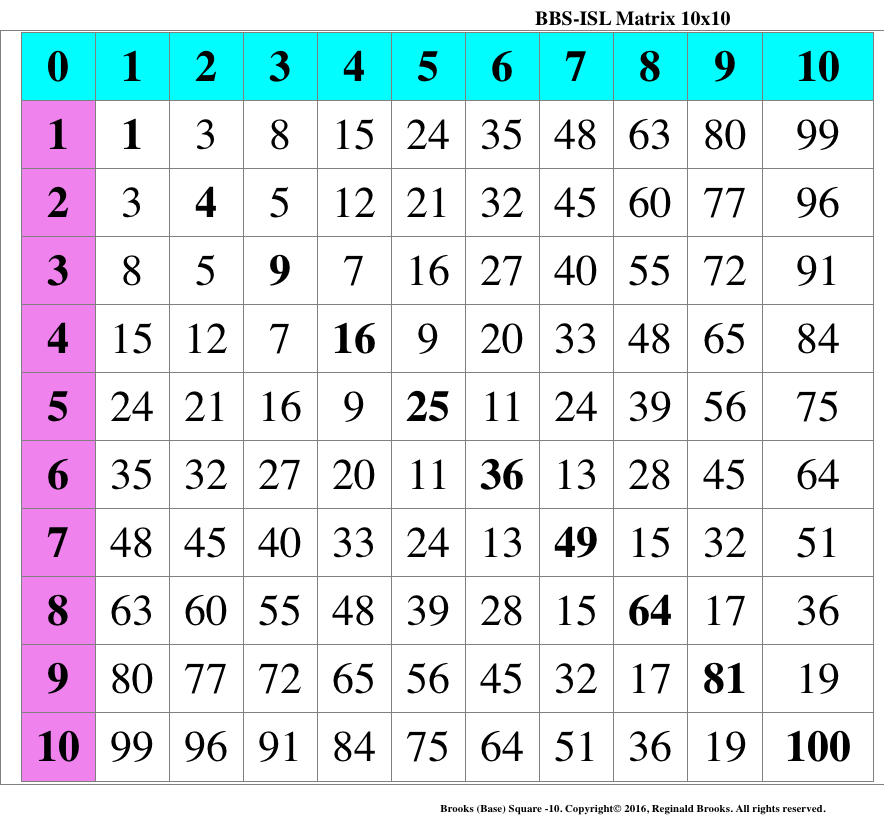
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 3 | 8 | 15 | 24 | 35 | 48 | 63 | 80 | 99 |
| 2 | 3 | 4 | 5 | 12 | 21 | 32 | 45 | 60 | 77 | 96 |
| 3 | 8 | 5 | 9 | 7 | 16 | 27 | 40 | 55 | 72 | 91 |
| 4 | 15 | 12 | 7 | 16 | 9 | 20 | 33 | 48 | 65 | 84 |
| 5 | 24 | 21 | 16 | 9 | 25 | 11 | 24 | 39 | 56 | 75 |
| 6 | 35 | 32 | 27 | 20 | 11 | 36 | 13 | 28 | 45 | 64 |
| 7 | 48 | 45 | 40 | 33 | 24 | 13 | 49 | 15 | 32 | 51 |
| 8 | 63 | 60 | 55 | 48 | 39 | 28 | 15 | 64 | 17 | 36 |
| 9 | 80 | 77 | 72 | 65 | 56 | 45 | 32 | 17 | 81 | 19 |
| 10 | 99 | 96 | 91 | 84 | 75 | 64 | 51 | 36 | 19 | 100 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 3 | 8 | 15 | 24 | 35 | 48 | 63 | 80 | 99 |
| 2 | 3 |
4 | 5 | 12 | 21 | 32 | 45 | 60 | 77 | 96 |
| 3 | 5 |
9 | 7 | 16 | 27 | 40 | 55 | 72 | 91 | |
| 4 | 7 |
16 | 9 | 20 | 33 | 48 | 65 | 84 | ||
| 5 | 9 |
25 | 11 | 24 | 39 | 56 | 75 | |||
| 6 | 11 |
36 | 13 | 28 | 45 | 64 | ||||
| 7 | 13 |
49 | 15 | 32 | 51 | |||||
| 8 | 15 |
64 | 17 | 36 | ||||||
| 9 | 17 |
81 | 19 | |||||||
| 10 | 19 |
100 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 3 | 8 | 15 | 24 | 35 | 48 | 63 | 80 | 99 |
| 2 | 4 | 5 | 12 | 21 | 32 | 45 | 60 | 77 | 96 | |
| 3 | 8 |
9 | 7 | 16 | 27 | 40 | 55 | 72 | 91 | |
| 4 | 12 |
16 | 9 | 20 | 33 | 48 | 65 | 84 | ||
| 5 | 16 |
25 | 11 | 24 | 39 | 56 | 75 | |||
| 6 | 20 |
36 | 13 | 28 | 45 | 64 | ||||
| 7 | 24 |
49 | 15 | 32 | 51 | |||||
| 8 | 28 |
64 | 17 | 36 | ||||||
| 9 | 32 |
81 | 19 | |||||||
| 10 | 36 |
100 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 3 | 8 | 15 | 24 | 35 | 48 | 63 | 80 | 99 |
| 2 | 3 |
4 | 5 | 12 | 21 | 32 | 45 | 60 | 77 | 96 |
| 3 | 8 |
5 |
9 | 7 | 16 | 27 | 40 | 55 | 72 | 91 |
| 4 | 12 |
7 |
16 | 9 | 20 | 33 | 48 | 65 | 84 | |
| 5 | 16 |
9 |
25 | 11 | 24 | 39 | 56 | 75 | ||
| 6 | 20 |
11 |
36 | 13 | 28 | 45 | 64 | |||
| 7 | 24 |
13 |
49 | 15 | 32 | 51 | ||||
| 8 | 28 |
15 |
64 | 17 | 36 | |||||
| 9 | 32 |
17 |
81 | 19 | ||||||
| 10 | 36 |
19 |
100 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 3 | 8 | 15 | 24 | 35 | 48 | 63 | 80 | 99 |
| 2 | 4 | 5 | 12 | 21 | 32 | 45 | 60 | 77 | 96 | |
| 3 | 9 | 7 | 16 | 27 | 40 | 55 | 72 | 91 | ||
| 4 | 15 |
16 | 9 | 20 | 33 | 48 | 65 | 84 | ||
| 5 | 21 |
25 | 11 | 24 | 39 | 56 | 75 | |||
| 6 | 27 |
36 | 13 | 28 | 45 | 64 | ||||
| 7 | 33 |
49 | 15 | 32 | 51 | |||||
| 8 | 39 |
64 | 17 | 36 | ||||||
| 9 | 45 |
81 | 19 | |||||||
| 10 | 51 |
100 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 3 | 8 | 15 | 24 | 35 | 48 | 63 | 80 | 99 |
| 2 | 3 |
4 | 5 | 12 | 21 | 32 | 45 | 60 | 77 | 96 |
| 3 | 8 |
5 |
9 | 7 | 16 | 27 | 40 | 55 | 72 | 91 |
| 4 | 15 |
12 |
7 |
16 | 9 | 20 | 33 | 48 | 65 | 84 |
| 5 | 21 |
16 |
9 |
25 | 11 | 24 | 39 | 56 | 75 | |
| 6 | 27 |
20 |
11 |
36 | 13 | 28 | 45 | 64 | ||
| 7 | 33 |
24 |
13 |
49 | 15 | 32 | 51 | |||
| 8 | 39 |
28 |
15 |
64 | 17 | 36 | ||||
| 9 | 45 |
32 |
17 |
81 | 19 | |||||
| 10 | 51 |
36 |
19 |
100 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 3 | 8 | 15 | 24 | 35 | 48 | 63 | 80 | 99 |
| 2 | 4 | 5 | 12 | 21 | 32 | 45 | 60 | 77 | 96 | |
| 3 | 9 | 7 | 16 | 27 | 40 | 55 | 72 | 91 | ||
| 4 | 16 | 9 | 20 | 33 | 48 | 65 | 84 | |||
| 5 | 24 |
25 | 11 | 24 | 39 | 56 | 75 | |||
| 6 | 32 |
36 | 13 | 28 | 45 | 64 | ||||
| 7 | 40 |
49 | 15 | 32 | 51 | |||||
| 8 | 48 |
64 | 17 | 36 | ||||||
| 9 | 56 |
81 | 19 | |||||||
| 10 | 64 |
100 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 3 | 8 | 15 | 24 | 35 | 48 | 63 | 80 | 99 |
| 2 | 3 |
4 | 5 | 12 | 21 | 32 | 45 | 60 | 77 | 96 |
| 3 | 8 |
5 |
9 | 7 | 16 | 27 | 40 | 55 | 72 | 91 |
| 4 | 15 |
12 |
7 |
16 | 9 | 20 | 33 | 48 | 65 | 84 |
| 5 | 24 |
21 |
16 |
9 |
25 | 11 | 24 | 39 | 56 | 75 |
| 6 | 32 |
27 |
20 |
11 |
36 | 13 | 28 | 45 | 64 | |
| 7 | 40 |
33 |
24 |
13 |
49 | 15 | 32 | 51 | ||
| 8 | 48 |
39 |
28 |
15 |
64 | 17 | 36 | |||
| 9 | 56 |
45 |
32 |
17 |
81 | 19 | ||||
| 10 | 64 |
51 |
36 |
19 |
100 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 3 | 8 | 15 | 24 | 35 | 48 | 63 | 80 | 99 |
| 2 | 4 | 5 | 12 | 21 | 32 | 45 | 60 | 77 | 96 | |
| 3 | 9 | 7 | 16 | 27 | 40 | 55 | 72 | 91 | ||
| 4 | 16 | 9 | 20 | 33 | 48 | 65 | 84 | |||
| 5 | 25 | 11 | 24 | 39 | 56 | 75 | ||||
| 6 | 35 |
36 | 13 | 28 | 45 | 64 | ||||
| 7 | 45 |
49 | 15 | 32 | 51 | |||||
| 8 | 55 |
64 | 17 | 36 | ||||||
| 9 | 65 |
81 | 19 | |||||||
| 10 | 75 |
100 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 3 | 8 | 15 | 24 | 35 | 48 | 63 | 80 | 99 |
| 2 | 3 |
4 | 5 | 12 | 21 | 32 | 45 | 60 | 77 | 96 |
| 3 | 8 |
5 |
9 | 7 | 16 | 27 | 40 | 55 | 72 | 91 |
| 4 | 15 |
12 |
7 |
16 | 9 | 20 | 33 | 48 | 65 | 84 |
| 5 | 24 |
21 |
16 |
9 |
25 | 11 | 24 | 39 | 56 | 75 |
| 6 | 35 |
32 |
27 |
20 |
11 |
36 | 13 | 28 | 45 | 64 |
| 7 | 45 |
40 |
33 |
24 |
13 |
49 | 15 | 32 | 51 | |
| 8 | 55 |
48 |
39 |
28 |
15 |
64 | 17 | 36 | ||
| 9 | 65 |
56 |
45 |
32 |
17 |
81 | 19 | |||
| 10 | 75 |
64 |
51 |
36 |
19 |
100 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 3 | 8 | 15 | 24 | 35 | 48 | 63 | 80 | 99 |
| 2 | 4 | 5 | 12 | 21 | 32 | 45 | 60 | 77 | 96 | |
| 3 | 9 | 7 | 16 | 27 | 40 | 55 | 72 | 91 | ||
| 4 | 16 | 9 | 20 | 33 | 48 | 65 | 84 | |||
| 5 | 25 | 11 | 24 | 39 | 56 | 75 | ||||
| 6 | 36 | 13 | 28 | 45 | 64 | |||||
| 7 | 48 |
49 | 15 | 32 | 51 | |||||
| 8 | 60 |
64 | 17 | 36 | ||||||
| 9 | 72 |
81 | 19 | |||||||
| 10 | 84 |
100 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 3 | 8 | 15 | 24 | 35 | 48 | 63 | 80 | 99 |
| 2 | 3 |
4 | 5 | 12 | 21 | 32 | 45 | 60 | 77 | 96 |
| 3 | 8 |
5 |
9 | 7 | 16 | 27 | 40 | 55 | 72 | 91 |
| 4 | 15 |
12 |
7 |
16 | 9 | 20 | 33 | 48 | 65 | 84 |
| 5 | 24 |
21 |
16 |
9 |
25 | 11 | 24 | 39 | 56 | 75 |
| 6 | 35 |
32 |
27 |
20 |
11 |
36 | 13 | 28 | 45 | 64 |
| 7 | 48 |
45 |
40 |
33 |
24 |
13 |
49 | 15 | 32 | 51 |
| 8 | 60 |
55 |
48 |
39 |
28 |
15 |
64 | 17 | 36 | |
| 9 | 72 |
65 |
56 |
45 |
32 |
17 |
81 | 19 | ||
| 10 | 84 |
75 |
64 |
51 |
36 |
19 |
100 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 3 | 8 | 15 | 24 | 35 | 48 | 63 | 80 | 99 |
| 2 | 4 | 5 | 12 | 21 | 32 | 45 | 60 | 77 | 96 | |
| 3 | 9 | 7 | 16 | 27 | 40 | 55 | 72 | 91 | ||
| 4 | 16 | 9 | 20 | 33 | 48 | 65 | 84 | |||
| 5 | 25 | 11 | 24 | 39 | 56 | 75 | ||||
| 6 | 36 | 13 | 28 | 45 | 64 | |||||
| 7 | 49 | 15 | 32 | 51 | ||||||
| 8 | 63 |
64 | 17 | 36 | ||||||
| 9 | 77 |
81 | 19 | |||||||
| 10 | 91 |
100 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 3 | 8 | 15 | 24 | 35 | 48 | 63 | 80 | 99 |
| 2 | 3 |
4 | 5 | 12 | 21 | 32 | 45 | 60 | 77 | 96 |
| 3 | 8 |
5 |
9 | 7 | 16 | 27 | 40 | 55 | 72 | 91 |
| 4 | 15 |
12 |
7 |
16 | 9 | 20 | 33 | 48 | 65 | 84 |
| 5 | 24 |
21 |
16 |
9 |
25 | 11 | 24 | 39 | 56 | 75 |
| 6 | 35 |
32 |
27 |
20 |
11 |
36 | 13 | 28 | 45 | 64 |
| 7 | 48 |
45 |
40 |
33 |
24 |
13 |
49 | 15 | 32 | 51 |
| 8 | 63 |
60 |
55 |
48 |
39 |
28 |
15 |
64 | 17 | 36 |
| 9 | 77 |
72 |
65 |
56 |
45 |
32 |
17 |
81 | 19 | |
| 10 | 91 |
84 |
75 |
64 |
51 |
36 |
19 |
100 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 3 | 8 | 15 | 24 | 35 | 48 | 63 | 80 | 99 |
| 2 | 4 | 5 | 12 | 21 | 32 | 45 | 60 | 77 | 96 | |
| 3 | 9 | 7 | 16 | 27 | 40 | 55 | 72 | 91 | ||
| 4 | 16 | 9 | 20 | 33 | 48 | 65 | 84 | |||
| 5 | 25 | 11 | 24 | 39 | 56 | 75 | ||||
| 6 | 36 | 13 | 28 | 45 | 64 | |||||
| 7 | 49 | 15 | 32 | 51 | ||||||
| 8 | 64 | 17 | 36 | |||||||
| 9 | 80 |
81 | 19 | |||||||
| 10 | 96 |
100 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 3 | 8 | 15 | 24 | 35 | 48 | 63 | 80 | 99 |
| 2 | 3 |
4 | 5 | 12 | 21 | 32 | 45 | 60 | 77 | 96 |
| 3 | 8 |
5 |
9 | 7 | 16 | 27 | 40 | 55 | 72 | 91 |
| 4 | 15 |
12 |
7 |
16 | 9 | 20 | 33 | 48 | 65 | 84 |
| 5 | 24 |
21 |
16 |
9 |
25 | 11 | 24 | 39 | 56 | 75 |
| 6 | 35 |
32 |
27 |
20 |
11 |
36 | 13 | 28 | 45 | 64 |
| 7 | 48 |
45 |
40 |
33 |
24 |
13 |
49 | 15 | 32 | 51 |
| 8 | 63 |
60 |
55 |
48 |
39 |
28 |
15 |
64 | 17 | 36 |
| 9 | 80 |
77 |
72 |
65 |
56 |
45 |
32 |
17 |
81 | 19 |
| 10 | 96 |
91 |
84 |
75 |
64 |
51 |
36 |
19 |
100 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 3 | 8 | 15 | 24 | 35 | 48 | 63 | 80 | 99 |
| 2 | 4 | 5 | 12 | 21 | 32 | 45 | 60 | 77 | 96 | |
| 3 | 9 | 7 | 16 | 27 | 40 | 55 | 72 | 91 | ||
| 4 | 16 | 9 | 20 | 33 | 48 | 65 | 84 | |||
| 5 | 25 | 11 | 24 | 39 | 56 | 75 | ||||
| 6 | 36 | 13 | 28 | 45 | 64 | |||||
| 7 | 49 | 15 | 32 | 51 | ||||||
| 8 | 64 | 17 | 36 | |||||||
| 9 | 81 | 19 | ||||||||
| 10 | 99 |
100 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 3 | 8 | 15 | 24 | 35 | 48 | 63 | 80 | 99 |
| 2 | 3 |
4 | 5 | 12 | 21 | 32 | 45 | 60 | 77 | 96 |
| 3 | 8 |
5 |
9 | 7 | 16 | 27 | 40 | 55 | 72 | 91 |
| 4 | 15 |
12 |
7 |
16 | 9 | 20 | 33 | 48 | 65 | 84 |
| 5 | 24 |
21 |
16 |
9 |
25 | 11 | 24 | 39 | 56 | 75 |
| 6 | 35 |
32 |
27 |
20 |
11 |
36 | 13 | 28 | 45 | 64 |
| 7 | 48 |
45 |
40 |
33 |
24 |
13 |
49 | 15 | 32 | 51 |
| 8 | 63 |
60 |
55 |
48 |
39 |
28 |
15 |
64 | 17 | 36 |
| 9 | 80 |
77 |
72 |
65 |
56 |
45 |
32 |
17 |
81 | 19 |
| 10 | 99 |
96 |
91 |
84 |
75 |
64 |
51 |
36 |
19 |
100 |

Highlight Interactive BBS-ISL Matrix at:
BBS-ISL_Matrix10x10_TableRowColHighlight.html
BBS-ISL & TPISC Resources at:
MSST-TPISC_resources/netart19.htm
BBS-ISL & TPISC Media Center at:
MediaCenter_MSST-TPISC_resources.html
Interactive Matrix pages at:
BBS-ISL_Matrix-simplified.html
Subtraction/Addition Method:
Every IG cell number value is simply the difference between its two PD numbers.
Adding the IG cell value to the PD number above sums to the intersecting PD number.
Multiplication/Division Method:
Every IG cell number value is also the product of its two Axial numbers intersected by the two diagonal lines — of that IG number — pointing back to the Axis at a 90°angle.
It is also the dividend, the divisor and quotient being the Axial numbers.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 3 | 8 | 15 | 24 | 35 | 48 | 63 | 80 | 99 |
| 2 | 3 | 4 | 5 | 12 | 21 | 32 | 45 | 60 | 77 | 96 |
| 3 | 8 | 5 | 9 | 7 | 16 | 27 | 40 | 55 | 72 | 91 |
| 4 | 15 | 12 | 7 | 16 | 9 | 20 | 33 | 48 | 65 | 84 |
| 5 | 24 | 21 | 16 | 9 | 25 | 11 | 24 | 39 | 56 | 75 |
| 6 | 35 | 32 | 27 | 20 | 11 | 36 | 13 | 28 | 45 | 64 |
| 7 | 48 | 45 | 40 | 33 | 24 | 13 | 49 | 15 | 32 | 51 |
| 8 | 63 | 60 | 55 | 48 | 39 | 28 | 15 | 64 | 17 | 36 |
| 9 | 80 | 77 | 72 | 65 | 56 | 45 | 32 | 17 | 81 | 19 |
| 10 | 99 | 96 | 91 | 84 | 75 | 64 | 51 | 36 | 19 | 100 |
Basic BBS-ISL Rule 1: All numbers (#s) related by the 1—4—9—...PD sequence
Basic BBS-ISL Rule 2: Every # in the PD sequence is the square of an Axial #.
Basic BBS-ISL Rule 3: The Odd-Number Summation sequence forms the PD sequence.
Basic BBS-ISL Rule 4: Every EVEN Inner Grid (IG) # is divisible by 4 & all are present.
Basic BBS-ISL Rule 5: Every IG# is:
A: The difference (∆) between its two PD-sequence #s. (Note: A=B=C=D=E, and, F.)
B: The sum (∑) of the ∆s of each of its PD#s between its two PD-sequence #s (as above).
C: The ∆ between the squares of the two Axial #s forming that IG# (as above).
D: The product of the Addition & Subtraction of the two Axial #s forming that IG# (as above).
E: The product of the Diagonal Axis # — STEPS from the PD — times the ∑ of Row + Column Axis #s.
F: Also, the product of its 2 Axial #s intersected by that IG#'s 90° diagonals.
Basic BBS-ISL Rule 6: Every *ODD IG# is NOT PRIME & all are present.
Corollary: NO PRIME #s are present on the *IG.
Corollary: NO EVEN, NOT divisible by 4 #s are present on the IG.
*Excepting the 3—5—7—… ODD #s of the 1st Parallel Diagonal.
Basic BBS-ISL Rule 7: The ODD-Number sequence 3—5—7—9—..., and the 1—4—9-...PD sequence, form the sequential ∆ between ALL IG#s.
Basic BBS-ISL Rule 8: The ∆ between #s within the Parallel Diagonals is a constant 2 x its Axial #.
Basic BBS-ISL Rule 9: The ∆ between #s in the Perpendicular Diagonals follow:
A: From EVEN PD#s, √PD x 4 starts the sequence & follows x1—x2—x3—x4—....
B: From ODD PD#s, √PD x 4 starts the sequence & follows x1—x2—x3—x4—....
C: From ODD Perpendicular Diagonals between the EVEN-ODD diagonals (above), the sequence starts with the same value as the Axis number ending the diagonal, the sequence following x1—x3—x5—x7—....
Basic BBS-ISL Rule 10: Every #, especially the #s in the ONEs Column, informs both smaller and larger Sub-set symmetries (much larger grids required to demonstrate).
IGGR Rule 1: The IG is formed of two equal & symmetrical 90°-right, isosceles triangles that are bilaterally symmetrical about the PD — and, infinitely expandable.
IGGR Rule 2: The 90°-right-triangle — inherent to ALL squares and rectangles by definition — both forms the alternating EVEN-ODD square grid cells within the Matrix, and, is responsible for all major patterns and sequences, thereupon.
IGGR Rule 3: Subtraction-Addition: Every IG# is simply the ∆ between its two PD#s (subtraction), and, the sum (∑) of any IG# + its PD# above = the PD# on the end of that Row (or, Column).
IGGR Rule 4: Multiplication-Division: Every IG# is simply the product of the two AXIAL #s intersected by the two diagonals — of that said IG# — pointing back to the Axis at a 90° angle (multiplication), and, the dividend of the Axial divisor and quotient (division).
IGGR Rule 5: The actual # of grid-cell steps — i.e., the actual # of STEPS from a given IG# to another by a strictly horizontal, vertical, or 45° diagonal path — forms a simple, yet often fundamental descriptor to the pattern-sequence templates that inform the more advanced patterns, e.i., Exponentials and especially the Pythagorean Triples (PTs). STEPS are particularly important in the geometric visualizations within the BBS-ISL Matrix (as alluded to in IGGR 2, above).
TPISC-BBS-ISL Rule 1: Every IG EVEN Squared # is part of a Paired-Factor Set (PFS) that:
A: Has reciprical PFS members on the PD vertically above.
B: Both PFS members reside on the SAME Row.
C: They represent the a2 and b2 values of a PT, whose c2 value is on the PD intersection.
TPISC-BBS-ISL Rule 2: Every PT is found on the BBS-ISL Matrix and can be located by this intersection of EVERY PD (9>) and a Row with PFSs.
TPISC-BBS-ISL Rule 3: Every PT — including its sides, perimeter, area and proof — can also be found and fully profiled (and, predicted) as r-set, s-,t-set members of the Dickson Method (DM), Expanded Dickson Method (EDM), and the Fully Expanded Dickson Method (FEDM), shown herein.
White papers (freely available):
Works on pure mathematics include:
PIN: Pattern in Number…from primes to DNA (2001).
Butterfly Primes series (2005, 2006, 2006.)
GoDNA: the Geometry of DNA (2001)
.GoMAS: The Geometry of Music, Art and Structure…linking science, art and esthetics (1987, 1996, 1998, 2009) with parts II and III (2012).
Brooks (Base) Square (BS): The Architecture of Space-Time (TOAST) and The Conspicuous Absence of Primes (TCAOP) - the complete work (Rules 1–177) (2009, 2010, 2011, 2012).
Brooks (Base) Square interactive (BBSi) Matrix: Part I: Basics (2011, 2013).
The Architecture of SpaceTime (TAOST) as defined by the Brooks (Base) Square Matrix and the Inverse Square Law (ISL) (2011).
Numbers Of Inevitability (2012).
AFPOP: A Fresh Piece of Pi(e)…and the √2, too…Fractal-Fractal-Fractal (2012).
The BBS-ISL Matrix papers, videos, slideshows, etc. all culminated in MathspeedST (2013) an interactive iBook, published in the iTunes iBooks Store. Free. Most of the white papers are freely available.
TPISC I: Basics: The Pythagorean - Inverse Square Connection – a MathspeedST Supplement (2015) an interactive iBook, published in the iTunes iBooks Store. Free. Most of the white papers are freely available.
TPISC II: Advanced: The Pythagorean - Inverse Square Connection – a MathspeedST Supplement (2015) an interactive iBook, published in the iTunes iBooks Store. Most of the white papers are freely available.
TPISC III: Simplification: The Pythagorean - Inverse Square Connection – a MathspeedST Supplement, Return to Basics – and then some (in progress, 2016–17).
BBS-ISL_Matrix10x10_TableRowColHighlight.html
BBS-ISL_Matrix20x20_TableRowColHighlight.html
BBS-ISL_Matrix35x35_TableRowColHighlight.html
BBS-ISL_Matrix35x35-LARGE_TableRowColHighlight.html
BBS-ISL_Matrix50x50-LARGE-Highlight.html
BBS-ISL_Matrix50x50-LARGE.html
BBS-ISL & TPISC Resources at:
MSST-TPISC_resources/netart19.htm
BBS-ISL & TPISC Media Center at:
MediaCenter_MSST-TPISC_resources.html
Interactive Matrix pages at:
Brooks (Base) Square matrix (BBS) interactive BBS-ISL hands-on matrix grids
BBS-ISL_Matrix: Simplified.html
Find Row-Col Axis number of Any IG number:
BBS_FindRow-Col_Any_IG_number.pdf
BBS_FindRow-Col_Any_IG_number.html
Find Row-Col Axis number of Any IG number:
BBS_ToFindRow-ColAnyIGnumber.pdf
BBS_ToFindRow-ColAnyIGnumber.html
BBS_ToFindRow-ColAnyIGnumber-MARP.pdf
BBS-ISL_IGGR_TPISC_fundamental_rules:
BBS-ISL_IGGR_TPISC_rulesMARP.pdf
BBS-ISL_Matrix_Overview Slideshow:
BBS-ISL_Matrix_Overview_MARP.pdf
Simple Visual Guide to making a BBS-ISL Matrix:
Simple Highlight Table Row/Col:
highlightTableRowCol_BBBS-ISL.html
highlightTableRowCol_BBBS-ISL10x.html
highlightTableRowCol_BBBS-ISL20x.html

Copyright 2016-17, Reginald Brooks, Brooks Design. All rights reserved.
iTunes, iTunes Store, iBooks, iBooks Store, iBooks Author, Mac OS are registered® trademarks of Apple Inc. and their use on this webpage does not reflect endorsement by Apple Inc.