| art theory 101~ Butterfly Primes |
|---|
Butterfly Primes
Copyright 2005, Reginald Brooks. All rights reserved.
Date completed: 12-07-05
Introduction
The lure and elusiveness of prime numbers, those very same numbers which all the other natural whole numbers can be reduced to, is thousands of years in the making, captivating the minds of anyone...perhaps everyone...who has ever contemplated their beauty and mystery. Can this beauty reveal a visual and mathematical pattern?
Given Prime Definition
A prime number (
P ) is any natural whole number ( N ), greater than one, which is reducible only by itself and one.Postulate 1:
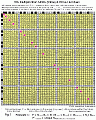
"Axis vs. Matrix, and Unique Squares"On a Multiplication Matrix (Table) where all natural whole numbers 1,2,3,...are placed on the x- and y-axis with 1 at the origin, it follows that (Fig 1, Table I):
a.
b. Similarly, only primes remain when the product of all x-axis numbers times the y-axis numbers are eliminated from all numbers, as:
c. And again, as all primes are odd (except
P=2=P2 ), only primes remain when all odd matrix numbers are eliminated from all the odd numbers (plus N2=2 ), as:P = (Nodd-x-axis + N2)-NM-odd (3)
d. Not only are the squares of all primes (except P2 ) odd, and (except P5 ) end in either 1 or 9, the squares of the squares all end in 1, as:
P2except P2 = Nodd-ends in 1 or 9
(4)(P2)2 = Nodd-ends in 1
(5)e. The squares of all primes are the only unique numbers on the matrix, as:
P2 = NM-unique . (6)
Fig. 1
(click to enlarge image)
Best viewed 800x600, F-11 key
(click here for high resolution image-895 KB)
Table I
Table I. Postulate 1
All numbers, All Matrix numbers, All Prime numbers,
N x-axis - NM = P
2-50... 4-50... from 1-50...
as a group as a group as a group
____________ ___________________ __________________
- 4
2 6 2
3 8 3
4 9
5 10 5
6 12
7 14 7
8 15
9 16
10 18
11 20 11
12 21
13 22 13
14 24
15 25
16 26
17 27 17
18 28
19 30 19
20 32
21 33
22 34
23 35 23
24 36
25 38
26 39
27 40
28 42
29 44 29
30 45
31 46 31
32 48
33 49
34 50
35
36
37 37
38
39
40
41 41
42
43
44
45
46
47 47
48
49
50 |
Commentary
All natural whole numbers,
N = 1, 2, 3,... , placed on the x- and y-axis, with the unit number 1 at the origin to form the Multiplication Matrix (Table). The Multiplication Matrix Numbers, NM , equals the grid of products formed from multiplying the Nx-axis and Ny-axis (excluding N=1 ) numbers. All prime numbers, P , are only found, by definition, on the x- or y-axis and are not part of the matrix numbers, NM . Removing (not actually subtracting) all the numbers from this axis which also appear in the matrix table will leave only the prime numbers. The corollary to this is that the squares of the primes are the only unique numbers within the matrix table. Fig.1.Postulate 2:
"Divisible Differences Predict Primes"a. Except for
where
P> = greater, P7 or higher, and, P< = lesserb. The square root of any squared prime plus a multiple of 24 (n24) equals the next prime, as:
where
P< = P5 or higher.Fig. 2
(click to enlarge image)
Best viewed 800x600, F-11 key
(click here for high resolution image-721 KB)
Table II
Table II Postulate 2
All (a.) (b.)
Primes, |
P squared (P>)2 - (P<)2 = n24 | n24+(P<)2 = P2next (P2next)1/2 = P
____ ______________ _____ | __________ _______ __________ _____
2 |
3 |
5 ^2 = 25 25 -9 = |
7 ^2 = 49 49 -25 = (1)24 | (1)24 + 25 = 49 49 7
11 ^2 = 121 121 -49 = (3)24 | (3)24 + 49 = 121 121 11
13 ^2 = 169 169 -121 = (2)24 | (2)24 + 121 = 169 169 13
17 ^2 = 289 289 -169 = (5)24 | (5)24 + 169 = 289 289 17
19 ^2 = 361 361 -289 = (3)24 | (3)24 + 289 = 361 361 19
23 ^2 = 529 529 -361 = (7)24 | (7)24 + 361 = 529 529 23
29 ^2 = 841 841 -529 = (13)24 | (13)24 + 529 = 841 841 29
31 ^2 = 961 961 -841 = (5)24 | (5)24 + 841 = 961 961 31
37 ^2 = 1369 1369-961 = (17)24 | (17)24 + 961 = 1369 1369 37
41 ^2 = 1681 1681-1369= (13)24 | (13)24 + 1369 = 1681 1681 41
43 ^2 = 1849 1849-1681= (7)24 | (7)24 + 1681 = 1849 1849 43
47 ^2 = 2209 2209-1849= (15)24 | (15)24 + 1849 = 2209 2209 47
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
53 ^2 = 2809 2809-2209= (25)24 | (25)24 + 2209 = 2809 2809 53
59 ^2 = 3481 3481-2809= (28)24 | (28)24 + 2809 = 3481 3481 59
61 ^2 = 3721 3721-3481= (10)24 | (10)24 + 3481 = 3721 3721 61
67 ^2 = 4489 4489-3721= (32)24 | (32)24 + 3721 = 4489 4489 67
71 ^2 = 5041 5041-4489= (23)24 | (23)24 + 4489 = 5041 5041 71
73 ^2 = 5329 5329-5041= (12)24 | (12)24 + 5041 = 5329 5329 73
79 ^2 = 6241 6241-5329= (38)24 | (38)24 + 5329 = 6241 6241 79
83 ^2 = 6889 6889-6241= (27)24 | (27)24 + 6241 = 6889 6889 83
89 ^2 = 7921 7921-6889= (43)24 | (43)24 + 6889 = 7921 7921 89
97 ^2 = 9409 9409-7921= (62)24 | (62)24 + 7921 = 9409 9409 97
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
101 ^2 = 10201 10201-9409= (33)24 | (33)24 + 9409 = 10201 10201 101
103 ^2 = 10609 10609-10201= (17)24 | (17)24 +10201 = 10609 10609 103
107 ^2 = 11449 11449-10609= (35)24 | (35)24 +10609 = 11449 11449 107
109 ^2 = 11881 11881-11449= (18)24 | (18)24 +11449 = 11881 11881 109
113 ^2 = 12769 12769-11881= (37)24 | (37)24 +11881 = 12769 12769 113
127 ^2 = 16129 16129-12769= (140)24 |(140)24 +12769 = 16129 16129 127
131 ^2 = 17161 17161-16129= (43)24 | (43)24 +16129 = 17161 17161 131
137 ^2 = 18769 18769-17161= (67)24 | (67)24 +17161 = 18769 18769 137
139 ^2 = 19321 19321-18769= (23)24 | (23)24 +18769 = 19321 19321 139
149 ^2 = 22201 22201-19321= (120)24 |(120)24 +19321 = 22201 22201 149
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
151 ^2 = 22801 22801-22201= (25)24 | (25)24 +22201 = 22801 22801 151
157 ^2 = 24649 24649-22801= (77)24 | (77)24 +22801 = 24649 24649 157
163 ^2 = 26569 26569-24649= (80)24 | (80)24 +24649 = 26569 26569 163
167 ^2 = 27889 27889-26569= (55)24 | (55)24 +26569 = 27889 27889 167
173 ^2 = 29929 29929-27889= (85)24 | (85)24 +27889 = 29929 29929 173
179 ^2 = 32041 32041-29929= (88)24 | (88)24 +29929 = 32041 32041 179
181 ^2 = 32761 32761-32041= (30)24 | (30)24 +32041 = 32761 32761 181
191 ^2 = 36481 36481-32761= (155)24 |(155)24 +32761 = 36481 36481 191
193 ^2 = 37249 37249-36481= (32)24 | (32)24 +36481 = 37249 37249 193
197 ^2 = 38809 38809-37249= (65)24 | (65)24 +37249 = 38809 38809 197
199 ^2 = 39601 39601-38809= (33)24 | (33)24 +38809 = 39601 39601 199
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
211 ^2 = 44521 44521-39601= (205)24 |(205)24 +39601 = 44521 44521 211
223 ^2 = 49729 49729-44521= (217)24 |(217)24 +44521 = 49729 49729 223
227 ^2 = 51529 51529-49729= (75)24 | (75)24 +49729 = 51529 51529 227
~~~~~~~~~random clusters hereafter through the first 10K primes~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
283 ^2 = 80089 |
293 ^2 = 85849 85849-80089= (240)24 |(240)24 + 80089 = 85849 85849 293
307 ^2 = 94249 94249-85849= (350)24 |(350)24 + 85849 = 94249 94249 307
|
449 ^2 = 201601 |
457 ^2 = 208849 208849-201601=(302)24 |(302)24 +201601 = 208849 208849 457
461 ^2 = 212521 212521-208849=(153)24 |(153)24 +208849 = 212521 212521 461
|
617 ^2 = 380689 |
619 ^2 = 383161 383161-380689=(103)24 |(103)24 +380689 = 383161 383161 619
631 ^2 = 398161 398161-383161=(625)24 |(625)24 +383161 = 398161 398161 631
|
787 ^2 = 619369 |
797 ^2 = 635209 635209-619369=(660)24 |(660)24 +619369 = 635209 635209 797
809 ^2 = 654481 654481-635209=(803)24 |(803)24 +635209 = 654481 654481 809
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
2729 ^2 = 7447441 |
2731 ^2 = 7458361 7458361-7447441= (455)24 | (455)24 +7447441 = 7458361 7458361 2731
2741 ^2 = 7513081 7513081-7458361=(2280)24 |(2280)24 +7458361 = 7513081 7513081 2741
~~~~~~~ headings combined to save space~~~~~~~~~~~~~
4691 ^2 = 22005481
4703 ^2 = 22118209 -22005481= (4697)24 | (4697)24 +22005481 = 22118209 ^1/2 4703
4721 ^2 = 22287841 -22118209= (7068)24 | (7068)24 +22118209 = 22287841 ^1/2 4721
5749 ^2 = 33051001
5779 ^2 = 33396841 -33051001= (14410)24 | (14410)24 +33051001 = 33396841 ^1/2 5779
5783 ^2 = 33443089 -33396841= (1927)24 | (1927)24 +33396841 = 33443089 ^1/2 5783
6841 ^2 = 46799281
6857 ^2 = 47018449 -46799281= (9132)24 | (9132)24 +46799281 = 47018449 ^1/2 6857
6863 ^2 = 47100769 -47018449= (3430)24 | (3430)24 +47018449 = 47100769 ^1/2 6863
7901 ^2 = 62425801
7907 ^2 = 62520649 -62425801= (3952)24 | (3952)24 +62425801 = 62520649 ^1/2 7907
7919 ^2 = 62710561 -62520649= (7913)24 | (7913)24 +62520649 = 62710561 ^1/2 7919
8231 ^2 = 67749361
8233 ^2 = 67782289 -67749361= (1372)24 | (1372)24 +67749361 = 67782289 ^1/2 8233
8237 ^2 = 67848169 -67782289= (2745)24 | (2745)24 +67782289 = 67848169 ^1/2 8237
9719 ^2 = 94458961
9721 ^2 = 94497841 -94458961= (1620)24 | (1620)24 +94458961 = 94497841 ^1/2 9721
9733 ^2 = 94731289 -94497841= (9727)24 | (9727)24 +94497841 = 94731289 ^1/2 9733
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
10141 ^2 = 102839881
10151 ^2 = 103042801 -102839881= (8455)24 | (8455)24 +102839881 =103042801 ^1/2 10151
10159 ^2 = 103205281 -103042801= (6770)24 | (6770)24 +103042801 =103205281 ^1/2 10159
11003 ^2 = 121066009
11027 ^2 = 121594729-121066009= (22030)24 | (22030)24 +121066009 =121594729 ^1/2 11027
11047 ^2 = 122036209-121594729= (18395)24 | (18395)24 +121594729 =122036209 ^1/2 11047
12941 ^2 = 167469481
12953 ^2 = 167780209-167469481= (12947)24 | (12947)24 +167469481 =167780209 ^1/2 12953
12959 ^2 = 167935681-167780209= (6478)24 | (6478)24 +167780209 =167935681 ^1/2 12959
13033 ^2 = 169859089
13037 ^2 = 169963369-169859089= (4345)24 | (4345)24 +169859089 =169963369 ^1/2 13037
13043 ^2 = 170119849-169963369= (6520)24 | (6520)24 +169963369 =170119849 ^1/2 13043
14407 ^2 = 207561649
14411 ^2 = 207676921-207561649= (4803)24 | (4803)24 +207561649 =207676921 ^1/2 14411
14419 ^2 = 207907561-207676921= (9610)24 | (9610)24 +207676921 =207907561 ^1/2 14419
15937 ^2 = 253987969
15959 ^2 = 254689681-253987969= (29238)24 | (29238)24 +253987969 =254689681 ^1/2 15959
15971 ^2 = 255072841-254689681= (15965)24 | (15965)24 +254689681 =255072841 ^1/2 15971
17851 ^2 = 318658201
17863 ^2 = 319086769-318658201= (17857)24 | (17857)24 +318658201 =319086769 ^1/2 17863
17881 ^2 = 319730161-319086769= (26808)24 | (26808)24 +319086769 =319730161 ^1/2 17881
19543 ^2 = 381928849
19553 ^2 = 382319809-381928849= (16290)24 | (16290)24 +381928849 =382319809 ^1/2 19553
19559 ^2 = 382554481-382319809= (9778)24 | (9778)24 +382319809 =382554481 ^1/2 19559
27739 ^2 = 769452121
27743 ^2 = 769674049-769452121= (9247)24 | (9247)24 +769452121 =769674049 ^1/2 27743
27749 ^2 = 770007001-769674049= (13873)24 | (13873)24 +769674049 =770007001 ^1/2 27749
37097 ^2 = 1376187409
37117 ^2 = 1377671689-1376187409=(61845)24 | (61845)24 +1376187409 =1377671689 ^1/2 37117
37123 ^2 = 1378117129-1377671689=(18560)24 | (18560)24 +1377671689 =1378117129 ^1/2 37123
46687 ^2 = 2179675969
46691 ^2 = 2180049481-2179675969= (15563)24 | (15563)24 +2179675969 =2180049481 ^1/2 46691
46703 ^2 = 2181170209-2180049481= (46697)24 | (46697)24 +2180049481 =2181170209 ^1/2 46703
50123 ^2 = 2512315129
50129 ^2 = 2512916641-2512315129= (25063)24 | (25063)24 +2512315129 =2512916641 ^1/2 50129
50131 ^2 = 2513117161-2512916641= (8355)24 | (8355)24 +2512916641 =2513117161 ^1/2 50131
60773 ^2 = 3693357529
60779 ^2 = 3694086841-3693357529= (30388)24 | (30388)24 +3693357529 =3694086841 ^1/2 60779
60793 ^2 = 3695788849-3694086841= (70917)24 | (70917)24 +3694086841 =3695788849 ^1/2 60793
79867 ^2 = 6378737689
79873 ^2 = 6379696129-6378737689= (39935)24 | (39935)24 +6378737689 =6379696129 ^1/2 79873
79889 ^2 = 6382252321-6379696129=(106508)24 |(106508)24 +6379696129 =6382252321 ^1/2 79889
82963 ^2 = 6882859369
82981 ^2 = 6885846361-6882859369=(124458)24 |(124458)24 +6882859369 =6885846361 ^1/2 82981
82997 ^2 = 6888502009-6885846361=(110652)24 |(110652)24 +6885846361 =6888502009 ^1/2 82997
92461 ^2 = 8549036521
92467 ^2 = 8550146089-8549036521= (46232)24 | (46232)24 + 8549036521 =8550146089 ^1/2 92467
92479 ^2 = 8552365441-8550146089= (92473)24 | (92473)24 + 8550146089 =8552365441 ^1/2 92479
99989 ^2= 9997800121
99991 ^2= 9998200081-9997800121= (16665)24 | (16665)24 +9997800121 =9998200081 ^1/2 99991
100003 ^2=10000600009-9998200081= (99997)24 | (99997)24 +9998200081 =10000600009 ^1/2 100003
100019 ^2=10003800361-10000600009=(133348)24|(133348)24 +10000600009=10003800361 ^1/2 100019
104309 ^2=10880367481
104311 ^2=10880784721-10880367481=(17385)24 | (17385)24 +10880367481=10880784721 ^1/2 104311
104323 ^2=10883288329-10880784721=(104317)24|(104317)24 +10880784721=10883288329 ^1/2 104323
104717 ^2=10965650089
104723 ^2=10966906729-10965650089=(52360)24 | (52360)24 +10965650089=10966906729 ^1/2 104723
104729 ^2=10968163441-10966906729=(52363)24 | (52363)24 +10966906729=10968163441 ^1/2 104729
~~~
|
Commentary
Take the squares of any prime number 5 or more, and the difference between it and any other squared prime number is always an exact multiple of 24, n24. Twenty-four, or a multiple of 24, when added to the square of any prime number, and the square root of that sum taken, will always equal the next prime number to follow. This follows from the smallest primes (
P5 or higher) to predicting and calculating the next largest known prime. Please donate your prize money to help fight world hunger, disease and the deterioration of the planet and/or for the education of that under-privileged child. Fig.2.Postulate 3:
"Butterfly Primes"a.
P2candidate = [Neven x (N+2)] + 1 (11)
Pcandidate = ([Neven x (N+2)] + 1)½
(12)b. Applying the principles of Postulates 1 and 2 above eliminates all the spurious entries leaving only the squared primes.
Fig. 3a
(click to enlarge image)
Best viewed 800x600, F-11 key
(click here for high resolution image-709 KB)
Fig. 3b
(click to enlarge image)
Best viewed 800x600, F-11 key
Fig. 3c
(click to enlarge image)
Best viewed 800x600, F-11 key
Table III
Table III Postulate 3
[ Product must equal n24]
[Neven x (N+2)] + 1 = P2candidate (P2candidate)1/2 = Pcandidate
________________________________ ____________ ______________ __________
-
- >=non-prime
-
4 6 1 25 25 5
6 8 1 49 49 7
10 12 1 121 121 11
12 14 1 169 169 13
16 18 1 289 289 17
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
18 20 1 361 361 19
22 24 1 529 529 23
24 26 1 625 625 >25
28 30 1 841 841 29
30 32 1 961 961 31
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
34 36 1 1225 1225 >35
36 38 1 1369 1369 37
40 42 1 1681 1681 41
42 44 1 1849 1849 43
46 48 1 2209 2209 47
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
48 50 1 2401 2401 >49
52 54 1 2809 2809 53
54 56 1 3035 3035 >55
58 60 1 3481 3481 59
60 62 1 3721 3721 61
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
64 66 1 4225 4225 >65
66 68 1 4489 4489 67
70 72 1 5041 5041 71
72 74 1 5329 5329 73
76 78 1 5929 5929 >77
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
78 80 1 6241 6241 79
82 84 1 6889 6889 83
84 86 1 7225 7225 >85
88 90 1 7921 7921 89
90 92 1 8281 8281 >91
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
94 96 1 9025 9025 >95
96 98 1 9409 9409 97
100 102 1 10201 10201 101
102 104 1 10609 10609 103
106 108 1 11449 11449 107
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
108 110 1 11881 11881 109
112 114 1 12769 12769 113
114 116 1 13225 13225 >115
118 120 1 14161 14161 >119
120 122 1 14641 14641 >121
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
124 126 1 15625 15625 >125
126 128 1 16129 16129 127
130 132 1 17161 17161 131
132 134 1 17689 17689 >133
136 138 1 18769 18769 137
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~random samples of know primes~~~~~~~~~~~~~~~~~~~~~
786 788 1 619369 619369 787
796 798 1 635209 635209 797
808 810 1 654481 654481 809
810 812 1 657721 657721 811
2728 2730 1 7447441 7447441 2729
2730 2732 1 7458361 7458361 2731
2740 2742 1 7513081 7513081 2741
4690 4692 1 22005481 22005481 4691
4702 4704 1 22118209 22118209 4703
4720 4722 1 22287841 22287841 4721
5748 5750 1 33051001 33051001 5749
5778 5780 1 33396841 33396841 5779
5782 5784 1 33443089 33443089 5783
6840 6842 1 46799281 46799281 6841
6856 6858 1 47018449 47018449 6857
6862 6864 1 47100769 47100769 6863
7900 7902 1 62425801 62425801 7901
7906 7908 1 62520649 62520649 7907
7918 7920 1 62710561 62710561 7919 |
Commentary
Within the Multiplication Matrix (Table) there are any number of patterns found by delineating the occurrences of a particular number multiple. Here, the concern is with the number 24.
A basic, modular repeating visual pattern is found by highlighting all instances of n24 within the matrix numbers formed from the products of the 1-24 x- and y-axis numbers. This pattern is mirrored in the other three quadrants of an expanded 48 x 48 matrix, and so on...very much a fractal pattern encompassing the products of all numbers.
The original 24 x 24 fractal base pattern is itself composed of four quadrants formed by the crossings of n24s at the product lines of the 12 x- and y-axis. Because the squares of the primes all fall symmetrically on the diagonal drawn from the origin, the focus will be solely on those two quadrants hereafter...though it is to be remembered that the n24 pattern is mirrored in all quadrants as a pattern of eight internal n24s highlights. What remains in this simplification is the "Butterfly Primes" pattern...two diagonally symmetrical quadrant patterns whose eight internal, and 10 axial, n24s highlights radiate out from the center (12 x 12 =144 in this module). This pattern extends diagonally to infinity. In between each and every n24 pair which lies along side the strict diagonal "squares" line (always off the diagonal number by 1), there exists a squared prime number candidate. The pattern is of n24s shepherding the squared primes along the diagonal processional. This pattern defines and predicts all primes when the spurious candidates are eliminated by applying the principles of Postulates 1 and 2.
Twin primes (
P, P+2 ), Prime Triples ( P, P+2, P+6 or P, P+4, P+6 ) and Prime Quadruples ( P, P+2, P+6, P+8 or P, P+2, P+4, P+8 ) and other prime patterns can be seen to result from the logical beauty and order of the "Butterfly" pattern. Fig.3.Conjecture:
"Proof of Riemann's Hypothesis"Taken together, these three postulates prove the order within the prime numbers necessary to establish a non-variance factor (n24)...the landscape at sea level (Riemann's zero points of the zeta function)...the critical line...and it is not "noisy", random or fluctuating, but constant, predictable and straight...and thus proves Riemann's Hypothesis. Each and every prime number square is shepherded along the "squares" diagonal by a series of constant, ordered and symmetrical n24s confirming the larger order of the primes within this "Butterfly" of n24s.
New Prime Definition
= new "Prime Number Theorem"A prime number is any natural whole number, greater than one, which is reducible only by itself and one, and, is always separated from the square of all other primes (except
P2,3,5 ) by multiplies of 24. The infinity of primes can not exceed the infinity of n24.Conjecture:
Primes and the Inverse Square LawThe Inverse Square Law, 1/r2, so fundamental to our physical world...witness gravity and electromagnetism, light and sound, energy, etc...is built on the "odd number summation series", that is, as r, the radius (or distance) increases as 1,2,3,4,5,... the sequential difference between the squares, as r2, follows as 3,5,7,9,11,.... As the distance, r, is doubled, the influence diminishes by 1/4. When r is tripled the influence is reduced by 1/9, when r is quadrupled, the influence drops to 1/16 of the original, and so on. The odd numbers: 1...3...5...7...9... and so on, when added to each other form the sums: 1...4...9...16...25... and so on, forming the "odd number summation series"...the square roots of which form the series: 1,2,3,4,5 and so on.
The "odd number summation series can easily be seen as the diagonal
"squares" line on any of the above figures. The odd numbers which form it (when squared),
are made of prime and non-prime numbers. The non-prime numbers can be shown to be
made of the product of two or more prime numbers. Table IV.
It follows that all odd natural whole numbers, greater than one, are either prime or
composed of the product of two or more prime numbers. See the (1) Caldwell and (4) Brooks reference links below.
Table IV
Table IV. Primes and the Inverse Square Law
All odd (Nodd)2 Non-Prime
numbers, generates Nodd(x-axis)
Nodd(x-axis) the odd numbers are
3-100..., Inverse the product
form the Square of two or more
difference Numbers Prime numbers, P
between the
Inverse
Square
Number's
"odd number
summation
series"
______ _______ __________________
3 squared = 9
5 squared = 25
7 squared = 49
9 squared = 81 9 = 3x3
11 squared = 121
13 squared = 169
15 squared = 225 15 = 3x5
17 squared = 289
19 squared = 361
21 squared = 441 21 = 3x7
23 squared = 529
25 squared = 625 25 = 5x5
27 squared = 729 27 = 3x3x3
29 squared = 841
31 squared = 961
33 squared = 1089 33 = 3x11
35 squared = 1225 35 = 5x7
37 squared = 1369
39 squared = 1521 39 = 3x13
41 squared = 1681
43 squared = 1849
45 squared = 2025 45 = 3x3x5
47 squared = 2209
49 squared = 2401 49 = 7x7
51 squared = 2601 51 = 3x17
53 squared = 2809
55 squared = 3025 55 = 5x11
57 squared = 3249 57 = 3x19
59 squared = 3481
61 squared = 3721
63 squared = 3969 63 = 3x3x7
65 squared = 4225 65 = 5x13
67 squared = 4489
69 squared = 4761 69 = 3x23
71 squared = 5041
73 squared = 5329
75 squared = 5625 75 = 3x5x5
77 squared = 5929 77 = 7x11
79 squared = 6241
81 squared = 6561 81 = 3x3x3x3
83 squared = 6889
85 squared = 7225 85 = 5x17
87 squared = 7569 87 = 3x29
89 squared = 7921
91 squared = 8281 91 = 7x13
93 squared = 8649 93 = 3x31
95 squared = 9025 95 = 5x19
97 squared = 9409
99 squared = 9801 99 = 3x3x11
and so on |
Conclusion
By using an expanded Multiplication Matrix (Table) and plotting the patterns of the prime numbers on the axis and their squares in the matrix, a strict order based on a factor of 24 was found which is both numerically and visually logical. The difference in squared primes of multiples of 24 allows for the validation of all primes past and the prediction and calculation of all new primes to be easily accomplished. Three Postulates and a new Prime Number Theorem have been offered to summarize and codify these findings...and taken together they define a beautiful ordered pattern within the primes revealing the proof of Riemann's Hypothesis.
References
The three excellent website references below provide outstanding information, presentation and resources about primes.
1. Caldwell, Chris, The Prime Pages,
http://primes.utm.edu
First and last source to check out everything you ever wanted to know about primes-history, glossary, proofs, types, lists, resources and more. Well referenced and up to date.
2. du Sautoy, Marcus, The Music of the Primes,
http://www.musicoftheprimes.com
A beautiful site which educates you as you go along the melody of mathematical thought. Particularly insightful presentation of imaginary numbers and the musical landscape metaphor elucidating Riemann's pursuit of the great ordered pattern of the primes.
3. Watkins, Matthew R., Number Theory and Physics,
http://www.maths.ex.ac.uk/~mwatkins/zeta/physics.htm
Embedded in the bigger picture of number theory and its relationship to physics, this wonderful site both teaches and inspires by relating the history of numerical and physical thought by their authors to a contemporary presentation of those ideas. Full of resources and great quotes.
Additional writings on art, math and physics by the author can be found at:
4. Brooks, Reginald, Art Theory 101,
http://www.brooksdesign-ps.net/Code/Html/arthry5.com
Additional and valuable links added post-publication:
5. Alfeld, Peter, http://www.math.utah.edu/~alfeld/
6. Chamness, Mark, http://alumnus.caltech.edu/~chamness/Prime.html
7. Edgington, Will, http://www.garlic.com/~wedgingt/mersenne.html
8. Heinz, Harvey, http://www.geocities.com/~harveyh/primes.htm
9. Leatherland, Adrian J.F., http://yoyo.cc.monash.edu.au/~bunyip/primes/
10. The Mathematical Association of America, http://www.maa.org
11. O'Connor, John and Edmund Robertson, http://www-history.mcs.st-and.ac.uk/history/HistTopics/Prime_numbers.html
12. Peterson, Ivars, http://www.sciencenews.org
13. Woltman, George, http://www.mersenne.org/prime.htm (GIMPS)
_________________________________________________________________________________________Copyright 2005, Reginald Brooks. All rights reserved.
Use
This paper and all its contents
© 2005-06, Reginald Brooks. All rights reserved. This work and all its content are, to the best knowledge of its author, original and solely of and by the author at the time of its creation. Permission is hereby granted for single copies to be made for personal, non-commercial use for students and teachers of schools, colleges and universities provided that: either the entire paper, including figures and tables, is kept intact; or, any extracts of the text, or figures or tables (in part or whole), be properly and visibly cited as to authorship and source.Special thanks to Calc98 (http://www.calculator.org/), whose software calculator eloquently handled the big digits after running out of space on my trusty hand-held Texas Instruments Slimline TI-35 Solar Scientific Calculator
Go to Butterfly Prime Directive
(white paper), or
The Butterfly Prime Determinate Number Array
(white paper), or
Butterfly Primes ~Prejudicial Numbers~ (new media net.art)