INTRO Commentary
There is a very unusual number pattern called the Perfect Number (PN). It is extremely rare. A PN is a number whose divisors--not counting the number itself--add up to equal that number. Only 51 are known as of September 2021. They are ALWAYS an EVEN number. For example 6=1+2+3.
Now what is even stranger and endlessly fascinating is that each PN is paired exactly with another very unusual and rare number pattern called the Mersenne Prime (Mp). Again, only 51 are currently known.
A Mp is a special kind of prime (p) that is a directly -1, related to the exponential power of 2. If you take 2 to the power of p and then subtract 1, if the resulting number is prime you have a Mersenne Prime. For example if p=2, you have 2² -1 = 4 - 1 = 3 a Mersenne Prime.
Euclid found that a PN could be found if one knew what the prime number value was by
PN = (2ᵖ⁻¹)(2ᵖ -1)
Euler, some 1500+ years later proved that ALL PNs could be found with this equation and that they would ALL be EVEN and ALL paired with a Mersenne Prime (Mersenne Primes were discovered by Mersenne during the time of Euler). This has become the Euclid-Euler Theorem.
Why would this EVEN PN always go hand in hand with the ODD Mp?
If the Mp is treated as the side of a square, the resulting area is called a Mersenne Prime Square (MPS). The MPS area ALWAYS contains within it a smaller area, the area of the PN.
That's right, when transformed into geometry the Euclid-Euler Theorem
PN = (2ᵖ⁻¹)(2ᵖ -1)
becomes clearly visible as a natural consequence of geometry. Every MPS formed carries along within its area the smaller PN area.
The fact that the PN is EVEN and the Mp and MPS are ODD will be seen to be another natural consequence of the geometry of the MPS!
All of this will be revealed as the story of the MPS is described in the pages that follow.
Like so many really simple and quite beautiful geometric discoveries, the MPS geometry will ultimately prove to be the source of a plethora of patterns and interconnections between the ODDs and EVENS -- most especially between the ODD PRIMES and the rest of the natural numbers!
Added note 1: The intense research into discovering and profiling each of the MPS that embody the PN & OC within has lead to a great number of very fruitfull pathways -- each that adds something to the portrait template that has unfolded. There really is an almost embarrassment of richness. With that said, what floats to the top are the PNs-- rectangular areas composed of a short "x" and longer "z" side, a.k.a. as
PN = (2ᵖ⁻¹)(2ᵖ -1) = x(Mp) = xz.
In each of the chapters that follow, please keep in mind that one of the main threads that sew this entire quilt of progressively larger MPSs is that of the PN and its two main constituents -- "x" and "z". If you know either one you can easy get the other, and "y" as well, as y=x-1. Next to "1," the next smallest ODD is always "y."
x=y+1
z=2x-1
and
xz = x(2x-1) = 2x² -x
Added note 2: As a preliminary to the more terse Abstract that follows, try this first:
∑ = running sum PN = Perfect Number = xz Mp = Mersenne Prime = z = 2ᵖ - 1 = x + y Mp² = Mersenne Prime Square = MPS = z² x = 2ᵖ⁻¹ = short side of PN rectangle y = x-1 = short side of OC rectangle OC = ODD Complement rectangle to PN = yz
CR = Complement Rectangle = xy
Mp² = PN + OC = xz + yz = z² 2ⁿ = exponential power of 2, where n = 1,2,3,…, e.i. 2ⁿ = 1–2–4–8–16… ∑ of 2ⁿ = 1–3–7–15–31–…, the difference (∆) = 2–4–8–16–..
x² = Perfect Number Square
y² = ODD Complement Square
…more
If you take a Perfect Number (PN) — which is always EVEN — and sequentially divided it by two, it will always land on an ODD number known as a Mersenne Prime (Mp). Euclid — and later, Euler — knew about this and expressed it as the Euclid-Euler Theorem.
That PN ÷ by some number of twos = Mp. The Euclid-Euler Theorem states that formally as an algebraic equation:
PN = 2ᵖ⁻¹ (2ᵖ -1)
where p = prime, 2ᵖ -1 = Mp and 2ᵖ⁻¹ is another way of saying 2ⁿ (where n=1,2,3,..), i.e. how many doublings of two times the Mersenne Prime = the Perfect Number. This works, if and only if, 2ᵖ -1 = Mp, e.i. if p=11, a prime, but 2¹¹ -1 is not a Mp, there is no PN generated.
2ⁿ is the expression for the exponential power of 2, where 20 = 1, 2¹ = 2, 2² = 4, 2³ = 8… Do notice that 2ᵖ⁻¹ always solves to some form of 2ⁿ, e.i. 2( 7-1) = 2⁶ = 64 as p=ODD and subtracting 1 from an ODD = EVEN.
In my installation, “The MPS Project,” in Building 5 in July of 2021, I showed visually why this is true as the new geometry extension of this Euclid-Euler Theorem plays out: namely, that squaring the Mp (treated as a “long” side) to give a geometric Square — Mersenne Prime Square (MPS) — contains within itself two Rectangles, one being the PN, the other its ODD Complement (OC). (The PN has a “short” side = x, the OC = y, with y = x-1 and x + y = z = Mp.)
If you take that PN Rectangle and sequentially diminish it by half (divide by two over and over) until it reaches an ODD, that ODD = the Mersenne Prime (Mp, as 1 x the side of that PN Rectangle).
It simplifies it all to give the short side of the PN = x, and the long side = z
xz = PN
which is the same as
2ᵖ⁻¹ (2ᵖ -1) = PN
such that
x = 2ᵖ⁻¹ z = 2ᵖ -1
and, y = x-1
OC = (x-1)z = yz.
It all fits within the MPS! To date, there have been 51 Mps discovered and each has an associated PN.
z² = 4CR + 1
The Mersenne Prime Square (MPS)
Author: Reginald Brooks
Postal address: 535 NW 107th Ave, Portland, OR, 97229-6211, USA
Home phone: 503-646-1548
Email: bdesign5@frontier.com
ABSTRACT
The Euclid-Euler Theorem is shown to be but a part of a larger composite geometry, the Mersenne Prime Square (MPS).
The MPS — Mp2— is a square area made from squaring the Mersenne Prime (Mp). The MPS is itself composed of two rectangular areas, one an EVEN area and the other a slightly smaller ODD: the Perfect Number (PN) EVEN rectangle and the ODD Complement (OC) ODD rectangle, respectively. These two rectangles can also be subdivided into the Perfect Squares of their respective short sides, and, a common remaining or complement area CR (Complement Rectangle). Assigning the short sides as “x” and “y,” respectively, and letting Mp = z = x + y, a simplified expression describing all Mersenne Prime-Perfect Numbers is found: z2 = xz + xy = (x2 + xy) + (y2 + xy) as z2 = MPS = Mp2 = PN + OC = (PNS + CR) + (OCS + CR). If one knows either x or y (where y = x - 1), one can reconstruct the MPS as PN = (2p−1)(2p -1) = xz.
INTRODUCTION
Euclid-Euler Theorem
Euclid discovered that (2p−1)(2p -1), where p = prime, generates EVEN Perfect Numbers (PN). Euler proved that it generates all the PNs, that they are all EVEN and that there is a one-to-one correspondence with Mersenne Prime numbers (Mp). No ODD PNs are know to exist. To date, their are 51 known Mersenne Prime-Perfect Number pairs, or sets, of numbers, the Mp being those special primes that are based on the powers of two, less 1, when the exponent, p, is prime, and, the resulting product is a prime number. This special insight into the elusive prime sequencing has resulted in the discovery of most of the larger primes.
Mersenne Prime Square (MPS)
Key:
p = prime x = 2p−1 = PN/Mp y = x-1 = OC/Mp z = x + y = 2p -1= Mp (Mersenne Prime) z2 = MPS = Mp2 (Mersenne Prime Square) xz = PN (Perfect Number) yz = OC (ODD Complement) xy = CR (Complement Rectangle) x2 = PNS (Perfect Number Square) y2 = OCS (ODD Complement Square)
CALCULATION and RESULTS
Treating the value of the Mersenne Prime = z as as the side of a square, z2 = Mp2 = MPS. This is an area. It is always an ODD.
Dividing this MPS area into two rectangles whose long side = z, the Mersenne Prime, and whose short side is: (z+1)/2 for the EVEN “x” and (z-1)/ 2 for the ODD “y,” to give xz = PN and yz = OC, respectively.
as
z2 = xz + xy
z2 = MPS = Mp2 = PN + OC
The x-side and PN are always EVEN and ÷4 (except for p=2) and the y-side and OC are always ODD and ÷3.
The PN and OC rectangles can be subdivided into their own Perfect Squares (PNS and OCS) of their respective short sides and a common remaining Complement Rectangle (CR), as:
as
z2 = xz + xy = (x2 + xy) + (y2 + xy)
z2 = MPS = Mp2 = PN + OC = (PNS + CR) + (OCS + CR)
The x-side and x2 are always EVEN and ÷4 (except for p=2) and the y-side and y2 are always ODD and ÷3, with xy ÷3 and ÷4.
z2=xz + xy =(x2 + xy)+(y2 +xy)
z2 = PN + OC = (PNS + CR) + (OCS + CR)
Figure 1 summarizes the geometry of any Mersenne Prime Square.
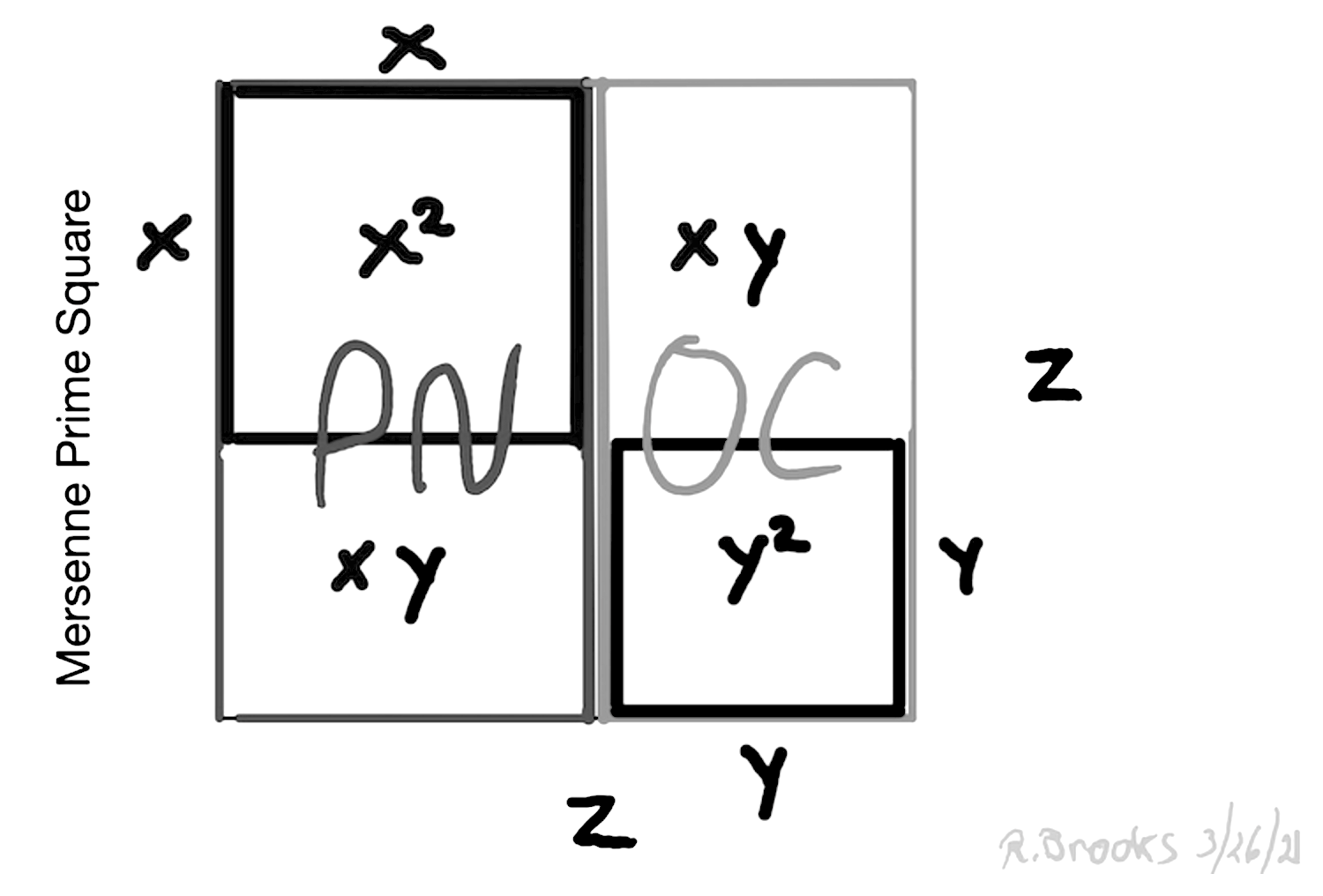
Table 1 summarizes the findings for the first 12 Mersenne Prime Squares.

CONCLUSION
The Euclid-Euler Theorem is shown to be but a part of a larger composite geometry, the Mersenne Prime Square (MPS).
The MPS — Mp2— is a square area made from squaring the Mersenne Prime (Mp). The MPS is itself composed of two rectangular areas, one an EVEN area and the other a slightly smaller ODD: the Perfect Number (PN) EVEN rectangle and the ODD Complement (OC) ODD rectangle, respectively. These two rectangles can also be subdivided into the Perfect Squares of their respective short sides, and, a common remaining or complement area CR (Complement Rectangle). Assigning the short sides as “x” and “y,” respectively, and letting Mp = z = x + y, a simplified expression describing all Mersenne Prime-Perfect Numbers is found: z2 = xz + xy = (x2 + xy) + (y2 + xy) as z2 = MPS = Mp2 = PN + OC = (PNS + CR) + (OCS + CR). If one knows either x or y (where y = x - 1), one can reconstruct the MPS as PN = (2
REFERENCES
https://en.wikipedia.org/wiki/Euclid–Euler_theorem
https://en.wikipedia.org/wiki/Mersenne_prime
https://en.wikipedia.org/wiki/Perfect_number